Векторное произведение векторов, формула и примеры
Определение и формула векторного произведения векторов
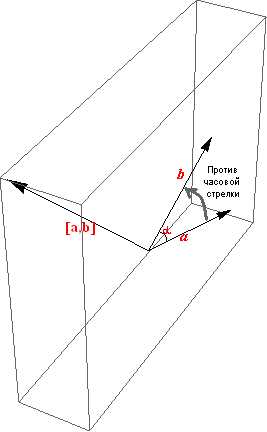
ОПРЕДЕЛЕНИЕ Векторным произведением двух векторов и называется вектор , перпендикулярный к плоскости этих векторов и направленный так, что наименьший поворот от вектора к вектору происходит против хода часовой стрелки, если смотреть с конца вектора (рис. 1), причем
Если векторы и заданы своими координатами: , то их векторное произведение вычисляется по формуле:
где – орты координатных осей соответственно.
Если раскрыть этот определитель по первой строке:
то получаем, что
ПРИМЕР
| Задание | Найти векторное произведение векторов и |
| Решение |
Для нахождения векторного произведения составим определитель, в первой строке которого записаны орты координатных осей, а во второй и третьей строках координаты векторов и соответственно:
Вычислим этот определитель, разложив его по элементам первой строки:
|
| Ответ |
Свойства векторного произведения векторов
1. Геометрический смысл векторного произведения. Модуль векторного произведения двух векторов и равен площади параллелограмма построенного на этих векторах:
ЗАМЕЧАНИЕ Площадь треугольника построенного на векторах и равна половине модуля векторного произведения указанных векторов:
2. Векторное произведение двух ненулевых векторов и равно нулю тогда и только тогда, когда эти векторы коллинеарны.
3. .
4. .
5. .
ПРИМЕР| Задание | Найти площадь треугольника, образованного векторами и , если известно, что , а угол между этими векторами . |
| Решение | Известно, что площадь треугольника, построенного на двух векторах, равна половине длины вектора, который есть их векторным произведением. Модуль векторного произведения векторов и равен произведению модулей этих векторов на синус угла между ними. То есть имеем: (кв. ед.). |
| Ответ | (кв. ед.) |
ru.solverbook.com
13. Векторное произведение векторов, его свойства. Площадь параллелограмма.
Векторным произведениемвектора a на вектор b называется вектор c, длина которого численно равна площади параллелограмма построенного на векторах a и b, перпендикулярный к плоскости этих векторов и направленный так, чтоб наименьшее вращение от a к b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора c (рис. 1).
рис. 1 |
Формулы вычисления векторного произведения векторов
Векторное произведениедвух векторов a = {ax; ay; az} и b = {bx; by; bz} в декартовой системе координат — это вектор, значение которого можно вычислить, используя следующие формулы:
a × b = | i | j | k | = i(aybz — azby) — j(axbz — azbx) + k(axby — ay bx) |
ax | ay | az | ||
bx | by | bz |
a × b = {aybz— azby; azbx— axbz; axby— aybx}
Свойства векторного произведения векторов
Модуль векторного произведения двух векторов a и b равен площади параллелограмма построенного на этих векторах:
Sпарал= a × b]
Площадь треугольника построенного на векторах a и b равна половине модуля векторного произведения этих векторов:
Векторное произведения двух не нулевых векторов a и b равно нулю тогда и только тогда, когда вектора коллинеарны.
Вектор c, равный векторному произведению не нулевых векторов a и b, перпендикулярен этим векторам.
a × b = -b × a
(k a) × b = a × (k b) = k (a × b)
(a + b) × c = a × c + b × c
14. Смешанное произведение векторов, его свойства. Условие компланарности вектора. Объем параллелепипеда. Объём пирамиды.
Смешанным произведением некомпланарныхвекторов,взятых в данном порядке, называетсяобъём параллелепипеда, построенного на данных векторах, снабжённый знаком «+», если базисправый, и знаком «–», если базислевый.
1. Смешанное произведение не меняется при циклической перестановке его сомножителей (не меняется ни объем параллелепипеда, ни ориентация его ребер): .
2. Смешанное произведение не меняетсязнаков векторного и скалярного умножения:, поэтому смешанное произведение записывают.
3. Смешанное произведение меняет свой знак при перемене любых двух вектор-сомножителей: ,.
4. Смешанное произведение ненулевых векторов ,иравно нулю тогда и только тогда, когда они компланарны:,, – компланарны.
Доказательство. Предположим, что векторы ,и– не компланарны. Тогда можно построить параллелепипед имеющий объем, т.е., но это противоречит условию, согласно которого,. Следовательно, векторы,и– компланарны.
Обратно, пусть ,и– компланарны. Тогда вектори перпендикулярен плоскости, в которой находятся векторы,и, значит, он перпендикулярен любому вектору, лежащему в этой плоскости, напримерЭто значит, что .
Смешанное произведение векторов, заданных своими проекциями в декартовой системе координат.
Пусть векторы заданы своими разложениями по ортам в декартовой системе координат:
, и.
Найдем их смешанное произведение, используя выражения в координатах для векторного и скалярного произведений:
.
Итак,
.
Приложения смешанного произведения:
1. Определение взаимной ориентации векторов в пространстве.
Если ,и– правая тройка, еслилевая.
2. Установление компланарности векторов:
( (,, – компланарны).
3. Определение объема параллелепипеда и треугольной пирамиды (тетраэдра):
, .
Пример. Компланарны ли векторы ,и, если .
Решение. Вычислим смешанное произведение векторов:
векторы ,ине компланарны.
Пример. Доказать, что векторы ,икомпланарны.
Решение. Рассмотрим матрицу, составленную из координат векторов ,и
, т. к. определитель матрицы равен нулю, то векторы линейно зависимы, следовательно они компланарны.
Пример. Вычислить объем тетраэдра с вершинами в точках и его высоту, опущенную из вершинына грань, если
Решение. Найдем координаты векторов:
, ,.
Вычислим объем:
.
Поскольку объем тетраэдра , то высота.
Вычислим площадь основания тетраэдра
.
Итак, высота .
studfiles.net
Векторное произведение векторов — это… Что такое Векторное произведение векторов?
Правые и левые тройки векторов
Три вектора называются упорядоченной тройкой, если указано, какой из этих векторов является первым, какой — вторым, а какой — третьим.
Тройка некомпланарных векторов называется правой (левой), если, будучи приведёнными к общему началу, эти векторы располагаются так, как могут быть расположены соответственно большой, несогнутый указательный и средний пальцы правой (левой) руки.
Определение
Векторным произведением вектора на вектор называется вектор , удовлетворяющий следующим требованиям:
- длина вектора равна произведению длин векторов и на синус угла ; между ними
Обозначение:
В различных учебных заведениях определение векторного произведения даётся по-разному. Например, в качестве определения даётся описанное далее выражение векторного произведения в координатах. А далее выводится данное выше определение.
Свойства
Геометрические свойства векторного произведения
Алгебраические свойства векторного произведения
Выражение для векторного произведения в декартовых координатах
Если два вектора и определены своими прямоугольными декартовыми координатами, а говоря точнее — представлены в ортонормированном базисе
то их векторное произведение имеет вид
Для запоминания этой формулы удобно использовать определитель:
или
где — символ Леви-Чивиты.
Обобщения
Кватернионы
Векторное произведение можно также записать в кватернионной форме, поэтому буквы , , — стандартные обозначения для ортов в : они рассматриваются как воображаемые кватернионы.
Заметим, что соотношения через векторное произведение между , и соответствуют правилам умножения для кватернионов i, j и k. Если представить вектор как кватернион a1i + a2j + a3k, то векторное произведение двух векторов получается взятием векторной части от произведения соответствующих им кватернионов. Скалярное произведение этих векторов противоположно скалярной части произведения этих кватернионов.
Преобразование к матричной форме
Векторное произведение двух векторов можно записать как произведение кососимметрической матрицы и вектора:
где
Пусть равен векторному произведению:
тогда
Такая форма записи позволяет обобщить векторное произведение на высшие размерности, представляя псевдовекторы (угловая скорость, индукция и т. п.) как такие кососимметричные матрицы. Ясно, что такие физические величины будут иметь n(n − 1) / 2 независимых компонент в n-мерном пространстве. В трёхмерном пространстве получаются три независимые компоненты, поэтому такие величины можно представлять как векторы этого пространства.
С такой формой записи также зачастую проще работать (например, в en:epipolar geometry).
Из общих свойств векторного произведения следует, что
- и
а так как кососимметрична, то
В такой форме записи легко доказывается тождество Лагранжа (правило «бац минус цаб»).
Распространение на матрицы
В 3-хмерном случае можно определить векторное произведение матриц и произведение матрицы на вектор. Это делает очевидным указанный выше изоморфизм и позволяет упростить многие выкладки. Представим матрицу A как столбец векторов, тогда
Умножение матрицы на вектор слева определяется аналогично, если представить A как строку векторов. Транспонирование матрицы, соответственно, переводит строку векторов в столбец векторов, и наоборот. Легко обобщить многие соотношения для векторов на соотношения для векторов и матриц, например (A — матрица, , — векторы):
После этого можно изменить форму записи для векторного произведения:
E — единичная матрица. Отсюда очевидны существование и вид матрицы, соответствующей векторному умножению на вектор слева. Аналогично можно получить выражение для матрицы умножения на вектор справа. Распространяя операции над векторами на матрицы покомпонентно, представляя их как «векторы из векторов», стандартные соотношения для векторов легко обобщаются на матрицы. Например, теорема Стокса в примет вид:
где ротор матрицы A вычисляется как векторное произведение матрицы A на оператор Гамильтона слева. В этих обозначениях очень легко доказать, например, следующие формы теоремы Стокса:
Размерности, не равные трём
Пусть D — размерность пространства.
Векторное произведение, обладающее всеми свойствами обычного трёхмерного векторного произведения, то есть бинарное билинейное антисимметричное невырожденное отображение , можно ввести только для размерности 3.
Однако есть простое обобщение на остальные натуральные размерности, начиная с 3, а если нужно — и на размерность 2 (последнее, правда, сравнительно специфическим образом). Тогда это обобщение, в отличие от невозможного, описанного чуть выше, вводится не для пары векторов, а лишь для набора (D − 1) векторов-сомножителей. Вполне аналогично смешанному произведению, естественно обобщаемому в D-мерном пространстве на операцию с D сомножителями. Используя символ Леви-Чивиты с D индексами, можно явно записать такое (D − 1)-валентное векторное произведение как
Такое обобщение дает гиперплощадь размерности (D − 1).
Если нужно ввести операцию именно для двух сомножителей, имеющую геометрический смысл, предельно близкий к смыслу векторного произведения (то есть представляющую ориентированную площадь), то результат уже не будет вектором, так как при D < > 3 не найдется единственной, однозначно определённой нормали к двумерной плоскости, натянутой на множители. Можно ввести бивектор, компоненты которого равны проекциям ориентированной площади параллелограмма, натянутого на пару векторов, на координатные плоскости:
- .
Эта конструкция называется внешним произведением.
Для двумерного случая эта операция называется псевдоскалярным произведением, так как получающееся пространство одномерно и результат можно отождествить с псевдоскаляром.
Алгебра Ли векторов
Векторное произведение вводит на структуру алгебры Ли (поскольку оно удовлетворяет обеим аксиомам — антисимметричности и тождеству Якоби). Эта структура соответствует отождествлению с касательной алгеброй Ли so(3) к группе Ли SO(3) ортогональных линейных преобразований трёхмерного пространства.
См. также
Произведения векторов
Другое
Ссылки
Литература
- Кочин Н. Е. Введение в векторный и тензорный анализ.
Wikimedia Foundation. 2010.
dic.academic.ru
Векторное произведение двух векторов. Он-лайн калькулятор.
Выражение векторного произведения через координаты векторов.
Зачем нужно векторное произведение? Существует множество способов применения векторного произведения, например, как уже написано выше, вычислив векторное произведение двух векторов можно выяснить, коллинеарны ли они. Или же его можно использовать как способ вычисления площади параллелограмма, построенного на этих векторах. Исходя из определения, длина результирующего вектора и есть площадь данного параллелограмма. |
dpva.ru
5.2. Векторное произведение двух векторов.
Определение векторного произведения.
О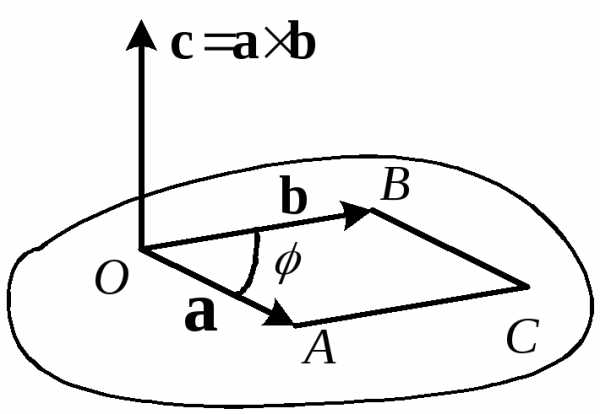 пределение.
Векторным произведением двух векторов
пределение.
Векторным произведением двух векторов  и
и называется вектор,
удовлетворяющий следующим условиям:
называется вектор,
удовлетворяющий следующим условиям:
а) вектор
перпендикулярен плоскости векторов  и
и и направлен так, что тройка векторов
и направлен так, что тройка векторов ,
, ,
, правая;
правая;
б) длина вектора численно равна площади
Рис. 2.19
параллелограмма,
построенного на векторах  и
и ,
т.е.,
где
,
т.е.,
где —
угол между векторами
—
угол между векторами и
и (рис. 2.19).
(рис. 2.19).
Очевидно, что  ,,
,,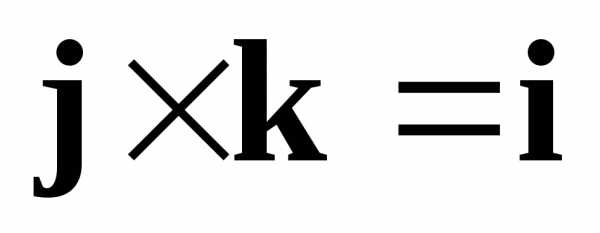 ,
,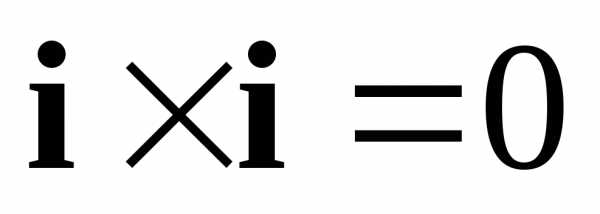 ,
,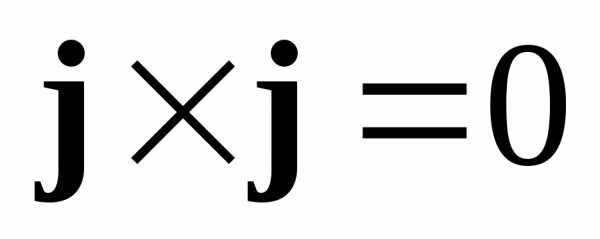 ,.
,.
Пример 11. Проверить справедливость равенства .
Решение. ,,
.
Метод Жуковского.
Рассмотрим метод Жуковского построения вектора .
Пусть угол между
векторами  и
и равен
равен .
.
Векторы  и
и приложим к общему началу
приложим к общему началу (рис. 2.20).
Через точку
(рис. 2.20).
Через точку перпендикулярно вектору
перпендикулярно вектору проведем плоскость
проведем плоскость .
Из конца вектора
.
Из конца вектора опустим перпендикуляр на плоскость
опустим перпендикуляр на плоскость . Точку пересечения этого перпендикуляра
и плоскости обозначим через
. Точку пересечения этого перпендикуляра
и плоскости обозначим через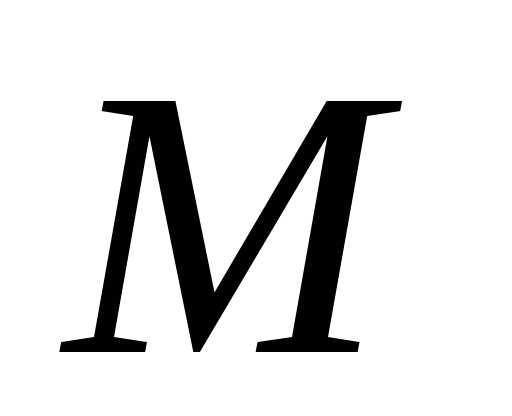 .
Проведем в плоскости
.
Проведем в плоскости вектори построим вектор.
вектори построим вектор.
Рис. 2.20
П окажем,
что вектор.
окажем,
что вектор.
а) Из построения
следует, что вектор 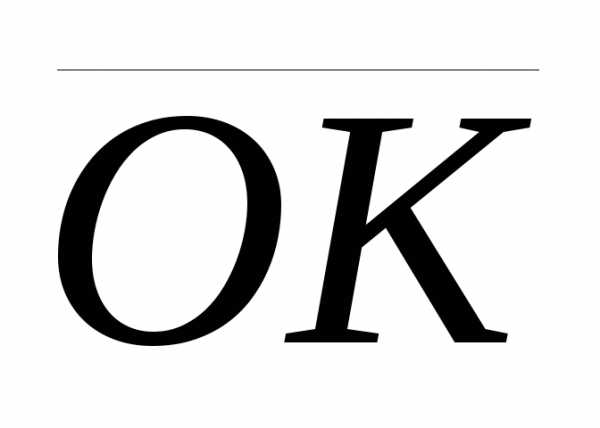 перпендикулярен
векторам
перпендикулярен
векторам ,
, ,
и векторы
,
и векторы ,
, ,
,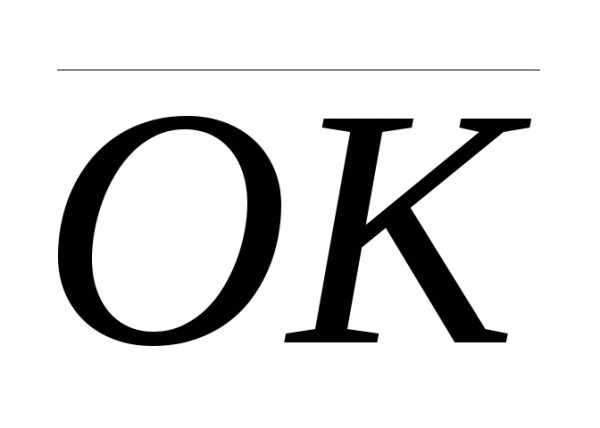 образуют правую тройку.
образуют правую тройку.
б) .
Из а) и б) следует, что .
Если проекцию
вектора  на плоскость
на плоскость обозначить
через
обозначить
через ,
то
,
то
.
Свойства векторного произведения.
Векторное произведение двух векторов обладает следующими свойствами:
1) (векторное произведениеантикоммутативно, т.е. при перестановке сомножителей направление вектора меняется на противоположное, при этом его модуль остаётся неизменным).
Это свойство
следует из определения векторного
произведения. Если тройка векторов 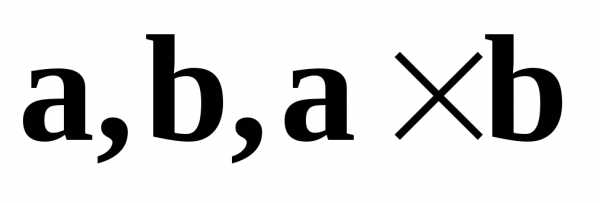 правая, то тройка
правая, то тройка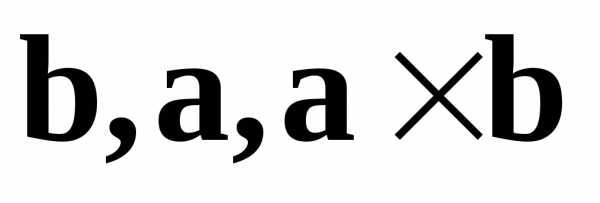 —
левая.
—
левая.
2) (ассоциативный закон). Это свойство легко доказывается из определения векторного произведения.
3) (дистрибутивный закон.) ►.◄
4)
.
Это свойство следует из определения
векторного произведения, а именно из
того, что модуль векторного произведения
равен площади параллелограмма,
построенного на векторах и
и .
Это свойство дает возможность записать в удобной форме параллельность двух векторов.
.
Это свойство дает возможность записать в удобной форме параллельность двух векторов.
Например, означает, что вектор коллинеарен биссектрисе первого
координатного угла.
коллинеарен биссектрисе первого
координатного угла.
Векторное произведение в координатной форме.
Пользуясь свойствами
векторного произведения и равенствами 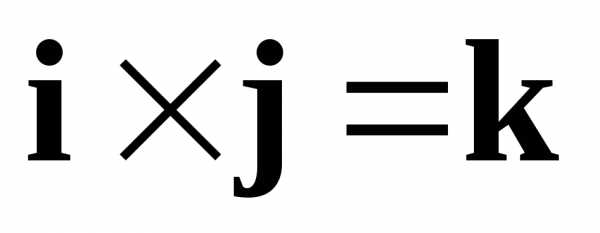 ,,
,,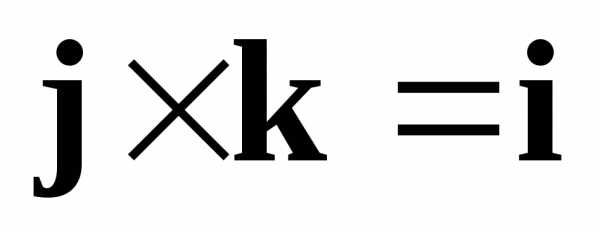 ,
,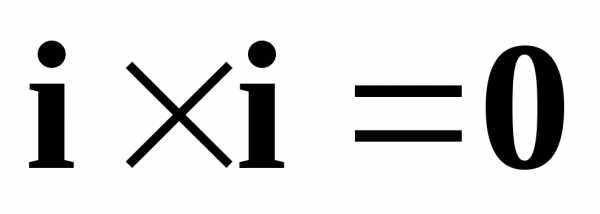 ,
,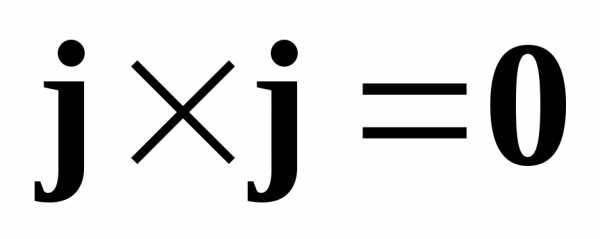 ,,
вычислим
,,
вычислим
=
=
,
т.е.
или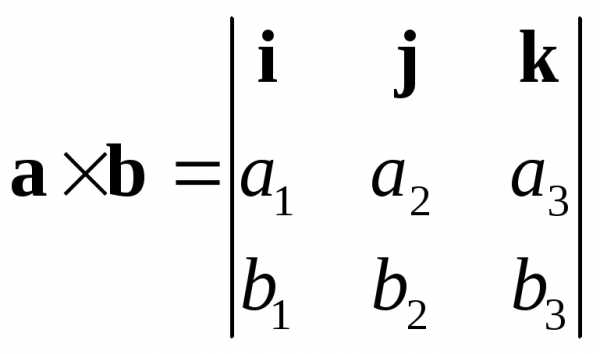 .
.
Применение векторного произведения.
Векторное
произведение векторов  и
и применяется:
применяется:
для нахождения
площади параллелограмма, построенного
на векторах  и
и ;
;
для нахождения
площади треугольника, построенного на
векторах  и
и ;
;
для нахождения
синуса угла между векторами  и
и ;
;
для нахождения
вектора, перпендикулярного векторам  и
и .
.
1) Площадь  параллелограмма, построенного на
векторах
параллелограмма, построенного на
векторах и
и ,
может быть вычислена по формуле,
где-
угол между векторами
,
может быть вычислена по формуле,
где-
угол между векторами и
и .
.
Замечание. Если
и,
то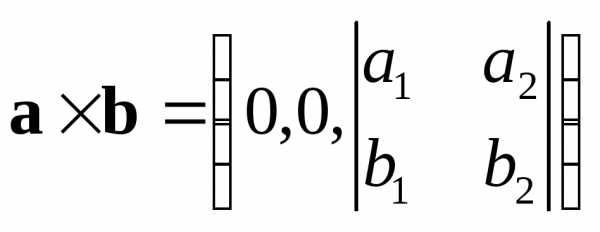 и
и .
Отсюда следует, чтомодуль
определителя второго порядка численно равен площади параллелограмма,
построенного на векторах
и.
.
Отсюда следует, чтомодуль
определителя второго порядка численно равен площади параллелограмма,
построенного на векторах
и.
2) Площадь  треугольника, построенного на векторах
треугольника, построенного на векторах и
и ,
равна половине площади параллелограмма,
построенного на этих же векторах, т.е.,
где
,
равна половине площади параллелограмма,
построенного на этих же векторах, т.е.,
где —
угол между векторами
—
угол между векторами и
и .
.
3) Синус угла между
векторами  и
и может быть вычислен по формуле.
может быть вычислен по формуле.
4) Вектор 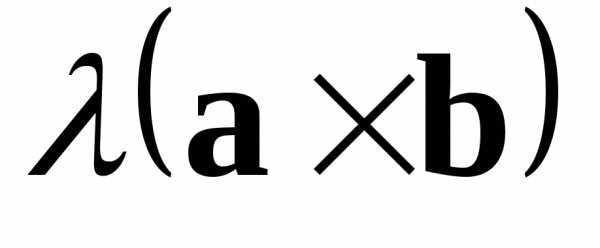 перпендикулярен вектору
перпендикулярен вектору и вектору
и вектору .
.
Замечание. Векторное произведение может быть
использовано при решении системы
линейных однородных уравнений вида 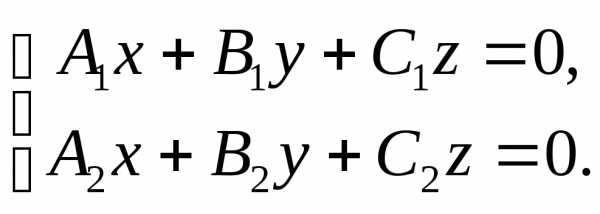 Если векторыинеколлинеарны, тоявляется
решением исходной системы.
Если векторыинеколлинеарны, тоявляется
решением исходной системы.
►Действительно,
из системы уравнений следует, что вектор
перпендикулярен векторам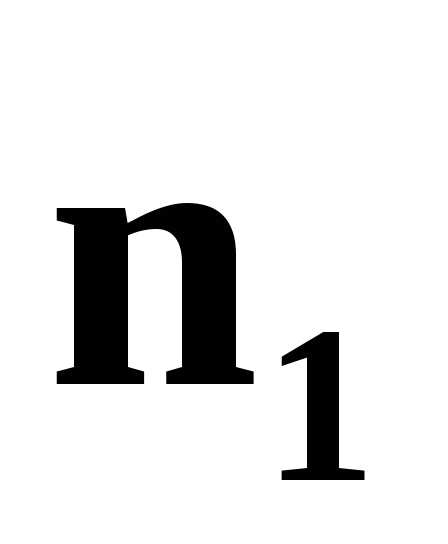 и
и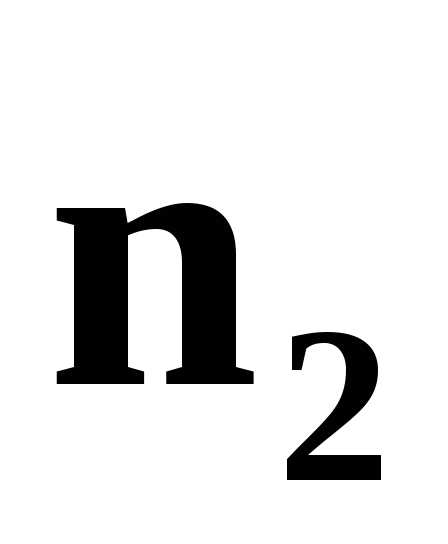 ,
а, следовательно,.◄
,
а, следовательно,.◄
● Пример 12. Дано: 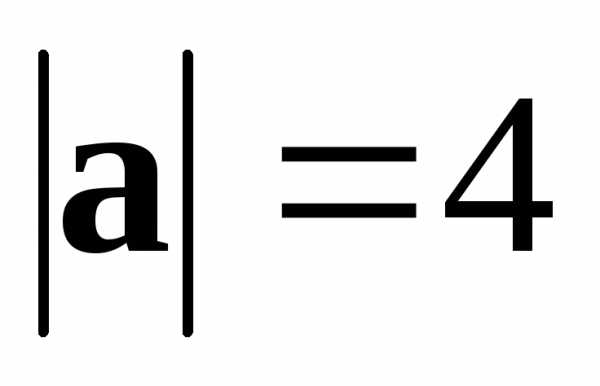 ,
,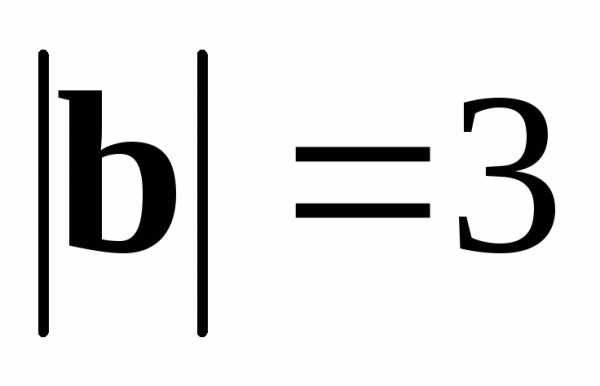 ,
, ,,.
,,.
Найти площадь
параллелограмма, построенного на
векторах 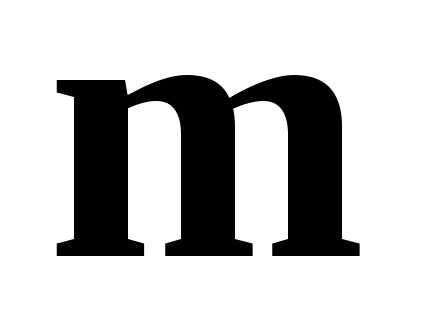 и
и .
.
Найти синус угла  между векторами
между векторами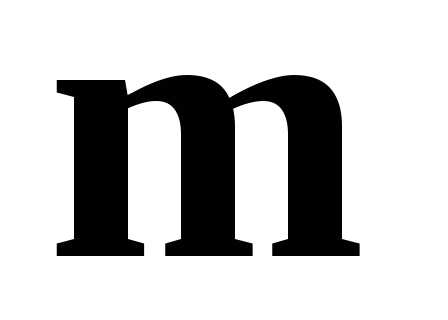 и
и .
.
Решение.
Площадь параллелограмма, построенного
на векторах 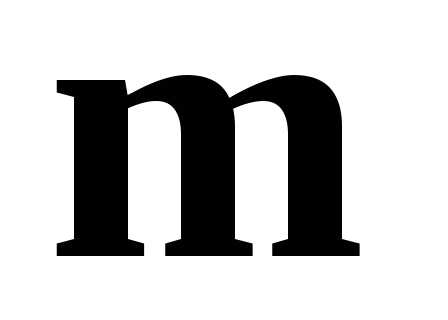 и
и равнамодулю векторного произведения векторов
равнамодулю векторного произведения векторов 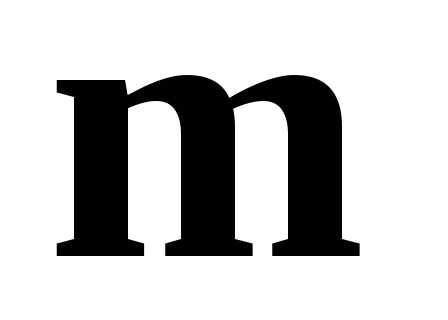 и
и ,
т.е…=.
,
т.е…=.
.
Ответ: 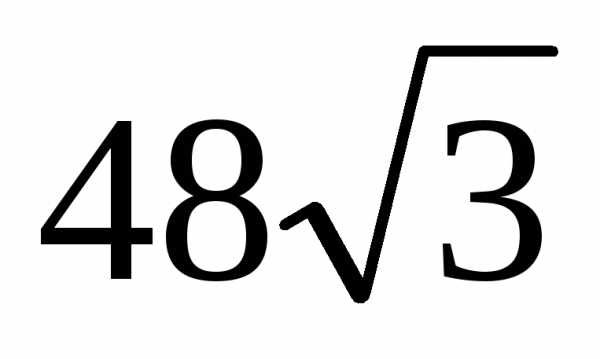 ,
,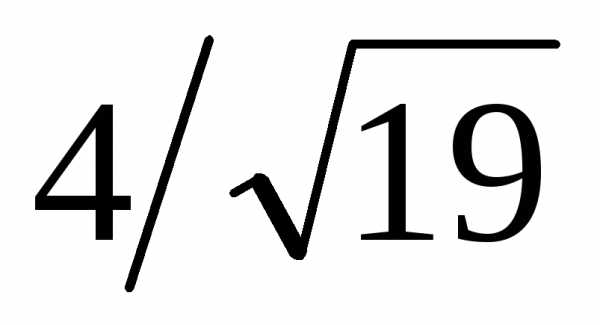 .
.
● Пример 13. Дано: 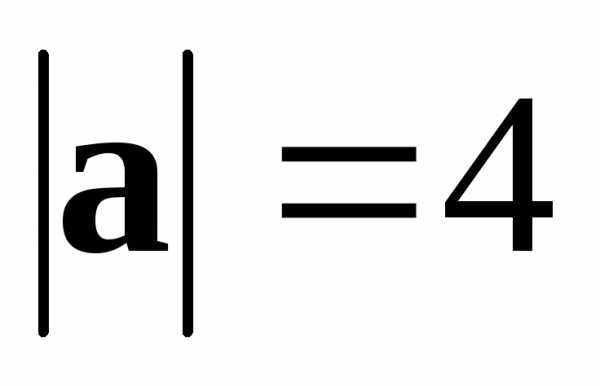 ,
,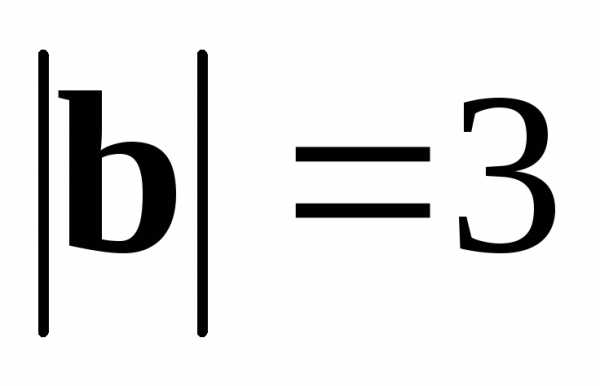 ,
,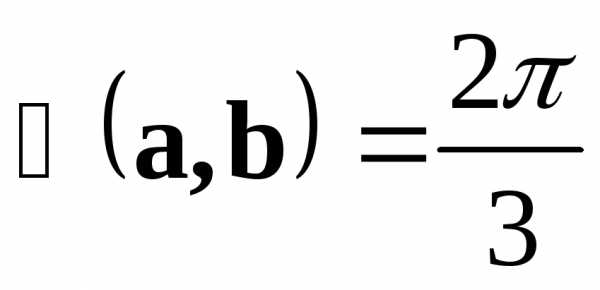 ,,.
,,.
Найти значение
параметра  ,
при котором векторы
,
при котором векторы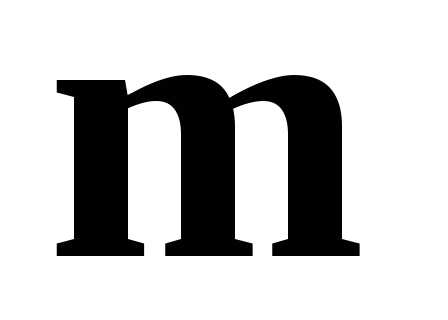 и
и коллинеарны.
коллинеарны.
Решение. Первый способ. Так как векторы 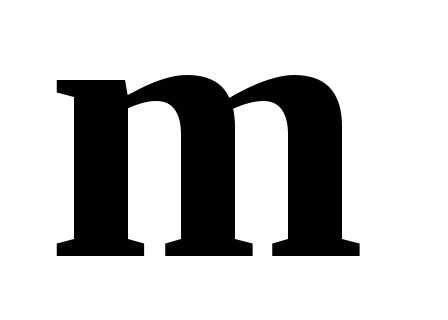 и
и коллинеарны, то их векторное произведение
равно нулю.=0,
а так как,
тои
коллинеарны, то их векторное произведение
равно нулю.=0,
а так как,
тои .
.
Второй способ.
Векторы  и
и составляют базис системы векторов
составляют базис системы векторов ,
, ,
,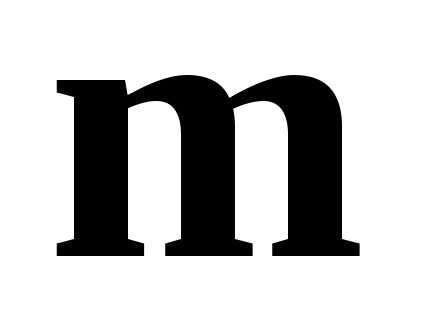 и
и .
В базисе
.
В базисе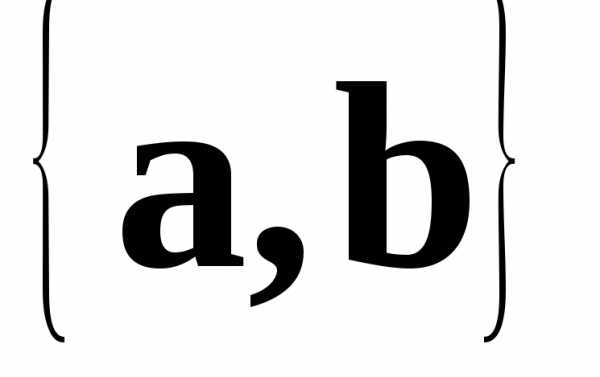 и
и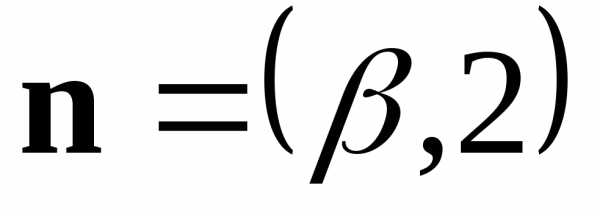 .
Так как векторы
.
Так как векторы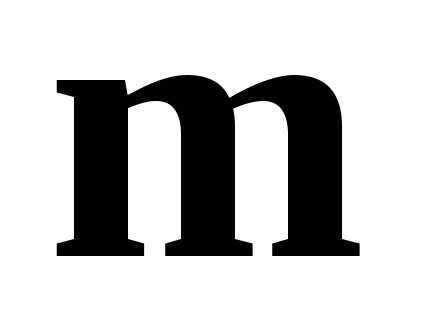 и
и коллинеарны, то
коллинеарны, то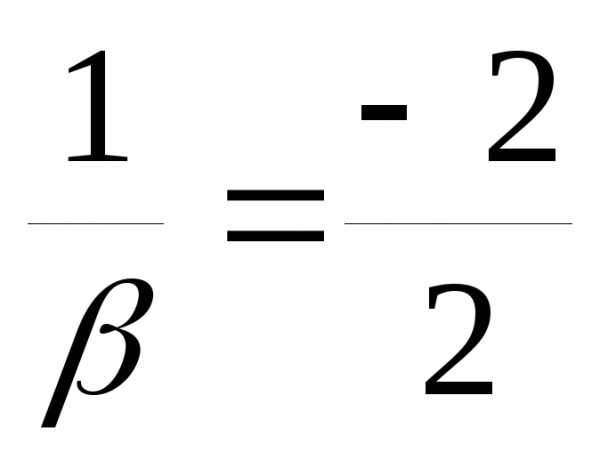 ,
откуда
,
откуда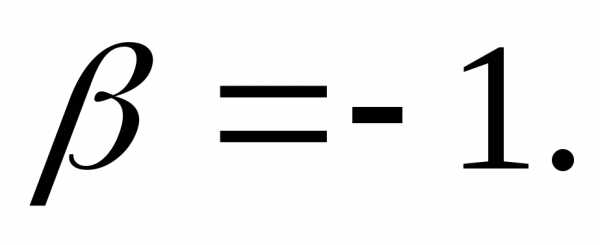 ●
●
● Пример 14. Найти координаты вектора  ,
длина которого равна 15, зная, что он
перпендикулярен оси
,
длина которого равна 15, зная, что он
перпендикулярен оси и векторуи образует острый угол с осью
и векторуи образует острый угол с осью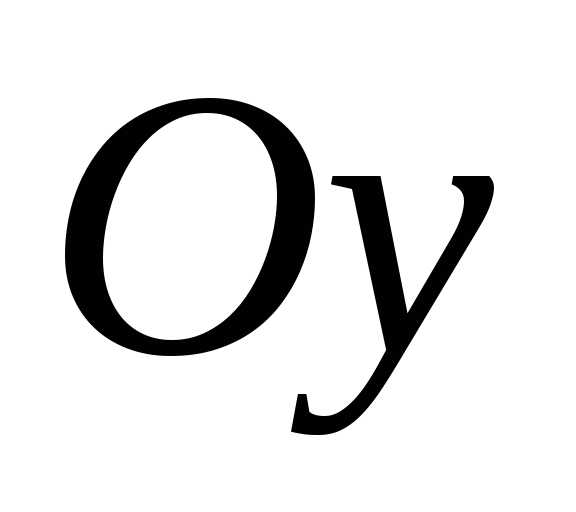 .
.
Решение. и, поэтому.
,
откуда 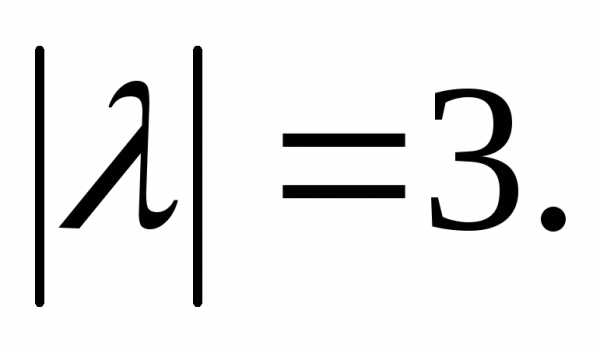
Так как вектор  образует острый угол с осью
образует острый угол с осью ,
то вторая его координата положительна,
тогда
,
то вторая его координата положительна,
тогда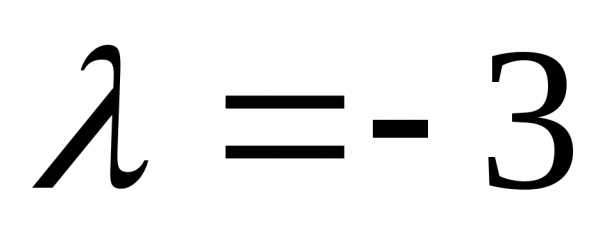 и●
и●
● Пример 15. Найти
площадь параллелограмма 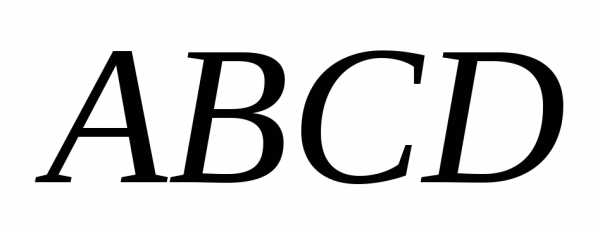 ,
если известны координаты трёх его вершин
,
если известны координаты трёх его вершин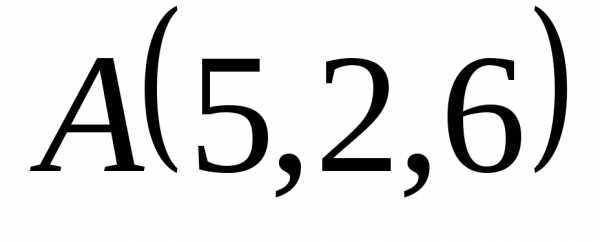 ,
,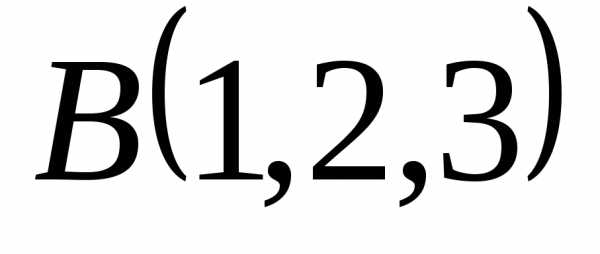 и
и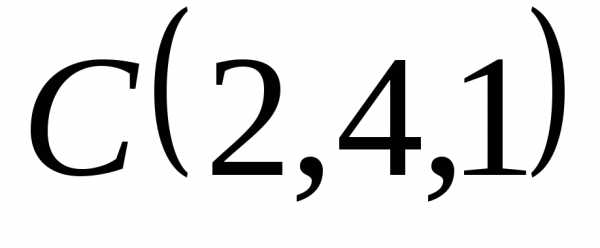 .
.
Решение. .,,,.
● Пример 16. 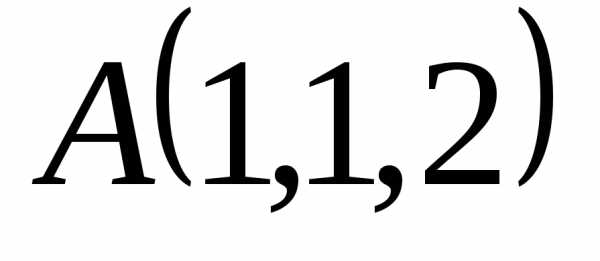 ,
, ,
,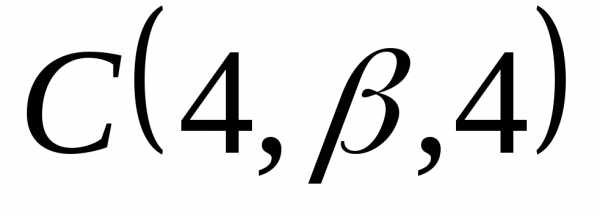 — вершины треугольника
— вершины треугольника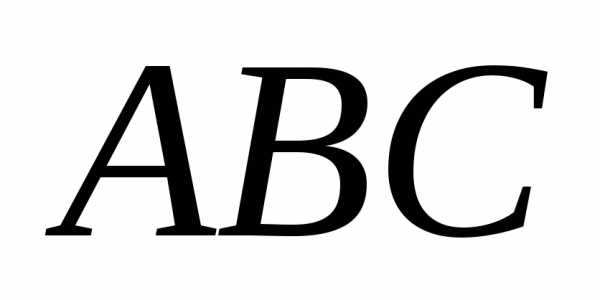 .
Найти недостающую координату
.
Найти недостающую координату точки
точки .
если площадь треугольника
.
если площадь треугольника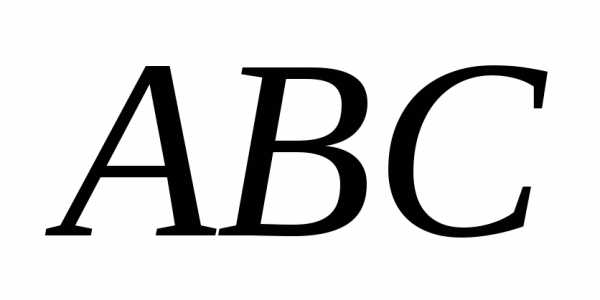 равна 3.
равна 3.
Решение. Площадь 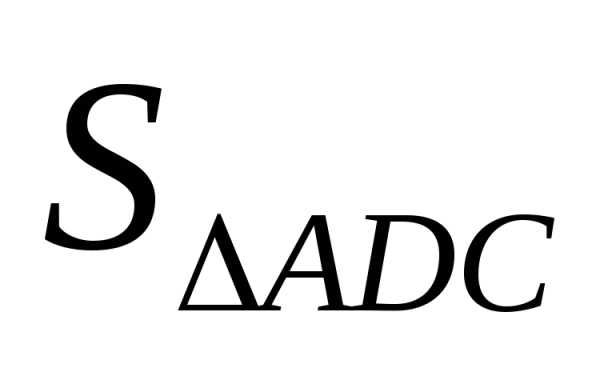 равна половине площади параллелограмма,
построенного на векторах
равна половине площади параллелограмма,
построенного на векторах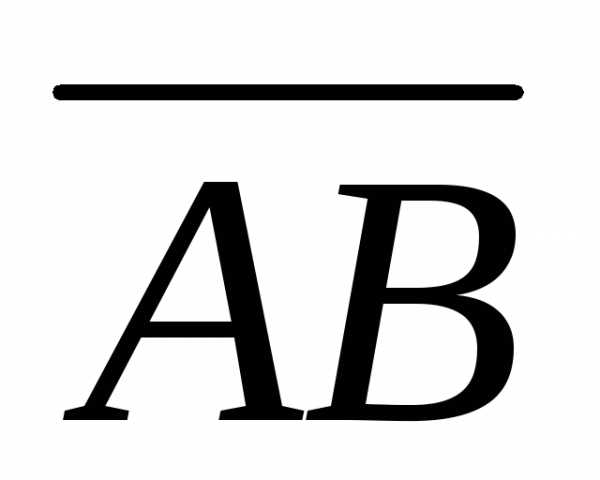 и
и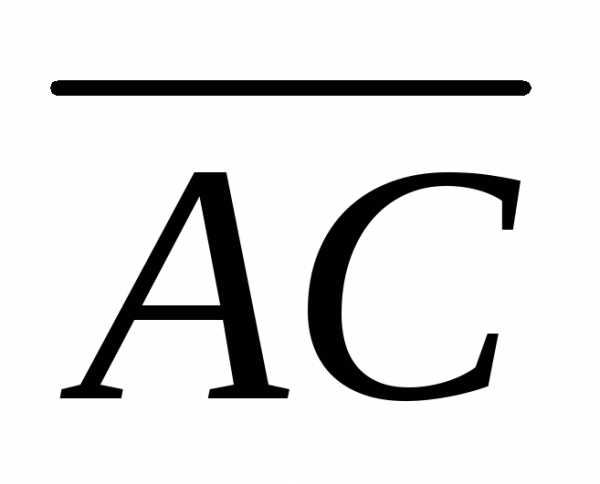 ,
т.е..
,
т.е..
,
,.,
откуда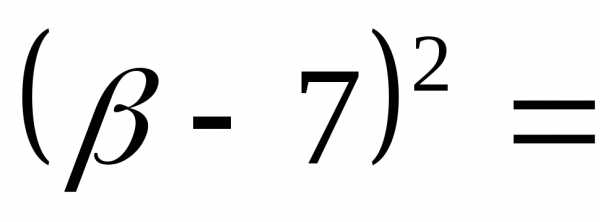 16,
16,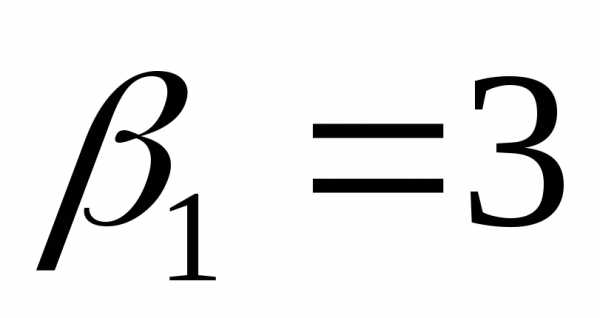 и
и .
.
Ответ: 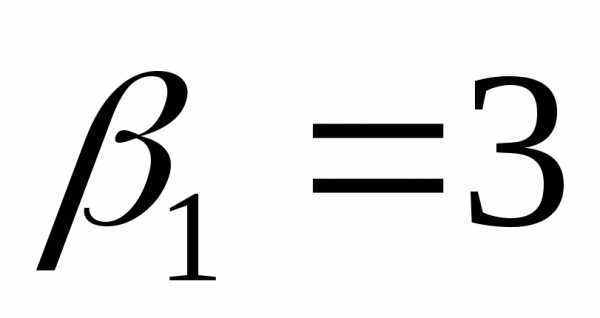 или
или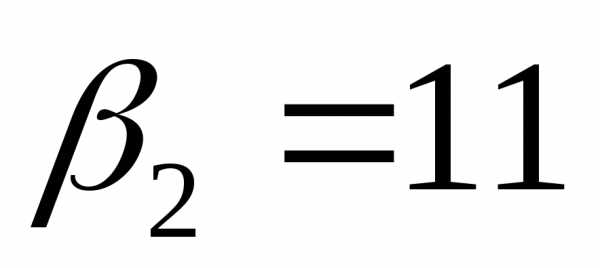 .
.
● Пример 17. Решить систему 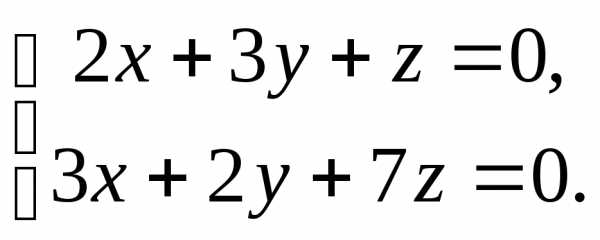
Решение. Из уравнений системы следует, что вектор перпендикулярен векторами. Тогда- решение данной системы. ●
studfiles.net
Как найти произведение векторов 🚩 как найти векторное произведение 🚩 Математика
Инструкция
Если координаты вершин треугольника даны в двухмерном декартовом пространстве, то сначала составьте матрицу из разниц значений координат точек, лежащих в вершинах. Затем используйте определитель второго порядка для полученной матрицы — он будет равен векторному произведению двух векторов, составляющих стороны треугольника. Если обозначить координаты вершин как A(X₁, Y₁), B(X₂, Y₂) и C(X₃, Y₃), то формулу площади треугольника можно записать так: S=|(X₁-X₃)•(Y₂-Y₃)-(X₂-X₃)•(Y₁-Y₃)|/2.Например, пусть даны такие координаты вершин треугольника на двухмерной плоскости: A(-2, 2), B(3, 3) и C(5, -2). Тогда, подставив числовые значения переменных в приведенную на предыдущем шаге формулу, вы получите: S=|(-2-5)•(3-(-2))-(3-5)•(2-(-2))|/2=|-7•5-(-2)•4|/2=|-35+8|/2=27/2=13,5 сантиметров.
Можно действовать по-другому — сначала вычислить длины всех сторон, а затем использовать формулу Герона, которая определяет площадь треугольника именно через длины его сторон. В этом случае сначала найдите длины сторон, используя теорему Пифагора для прямоугольного треугольника, составленного из самой стороны (гипотенуза) и проекций каждой стороны на оси координат (катеты). Если обозначить координаты вершин как A(X₁, Y₁), B(X₂, Y₂) и C(X₃, Y₃), то длины сторон будут следующими: AB=√((X₁-X₂)²+(Y₁-Y₂)²), BC=√((X₂-X₃)²+(Y₂-Y₃)²), CA=√((X₃-X₁)²+(Y₃-Y₁)²). Например, для координат вершин треугольника, приведенных на втором шаге, эти длины составят AB=√((-2-3)²+(2-3)²)=√((-5)²+(-1)²)=√(25+1)≈5,1, BC=√((3-5)²+(3-(-2))²)=√((-2)²)+5²)=√(4+25)≈5,36, CA=√((5-(-2))²+(-2-2)²)=√(7²+(-4)²)=√(49+16)≈8,06.
Найдите полупериметр, сложив известные теперь длины сторон и разделив результат на двойку: p=0,5•(√((X₁-X₂)²+(Y₁-Y₂)²)+√((X₂-X₃)²+(Y₂-Y₃)²)+√((X₃-X₁)²+(Y₃-Y₁)²)). Например, для длин сторон, рассчитанных на предыдущем шаге, полупериметр будет приблизительно равен p≈(5,1+5,36+8,06)/2≈9,26.
Рассчитайте площадь треугольника по формуле Герона S=√(p(p-AB)(p-BC)(p-CA)). Например, для образца из предыдущих шагов: S=√(9,26•(9,26-5,1)•(9,26-5,36)•(9,26-8,06))=√(9,26•4,16•3,9•1,2)=√180,28≈13,42. Как видите, результат на восемь сотых отличается от полученного на втором шаге — это результат округлений, использованных при расчетах на третьем, четвертом и пятом шагах.
www.kakprosto.ru
Векторное произведение двух векторов. Он-лайн калькулятор.
Векторное произведение двух векторов. Он-лайн калькулятор.
|
Векторное произведение двух векторов а и b — это операция над ними, определенная лишь в трехмерном пространстве, результатом которой является вектор со следующими свойствами: Для большей ясности приведем пример — на рисунке справа вектор [a,b] — векторное произведение векторов а и b. Как сказано в определении, мы привели все три вектора к общему началу, и тогда, если смотреть на вектора a и b с конца вектора [a,b], кратчайший поворот от вектора а до вектора b будет против часовой стрелки . |
 |
Очевидно, что в случае векторного произведения, имеет значение порядок, в котором берутся вектора, более того,
Так же, непосредственно из определения следует, что для любого скалярного множителя k (числа) верно следующее:
Векторное произведение коллинеарных векторов равно нулевому вектору. Более того, векторное произведение двух векторов равно нулю тогда и только тогда, когда они коллинеарны. (В случае, если один из них нулевой вектор необходимо вспомнить, что нулевой вектор коллинеарен любому вектору по определению).
Векторное произведение обладает распределительным свойством, то есть
Выражение векторного произведения через координаты векторов.
Пусть даны два вектора
(как найти координаты вектора по координатам его начала и конца — см. статью Скалярное произведение векторов, пункт Альтернативное определение скалярного произведения, или вычисление скалярного произведения двух векторов, заданных своими координатами.)
Тогда
Зачем нужно векторное произведение?
Существует множество способов применения векторного произведения, например, как уже написано выше, вычислив векторное произведение двух векторов можно выяснить, коллинеарны ли они.
Или же его можно использовать как способ вычисления площади параллелограмма, построенного на этих векторах. Исходя из определения, длина результирующего вектора и есть площадь данного параллелограмма.
Он-лайн калькулятор векторного произведения.
Чтобы найти скалярное произведение двух векторов с помощью данного калькулятора, нужно ввести в первую строку по порядку координаты первого вектора, во вторую- второго. Координаты векторов могут быть вычислены по координатам их начала и конца (см. статью Скалярное произведение векторов, пункт Альтернативное определение скалярного произведения, или вычисление скалярного произведения двух векторов, заданных своими координатами. )
tehtab.ru