Конъюнктивная совершенная нормальная форма: Построение таблицы истинности онлайн | СКНФ | СДНФ | Полином Жегалкина | Таблица истинности булевой функции онлайн

НОУ ИНТУИТ | Лекция | Нормальная форма записи

Смотреть на youtube || на ИНТУИТ в качестве: низком | среднем | высоком

Конъюнктивная и дизъюнктивная нормальная форма

Литерой будем называть переменную или ее отрицание.

Дизъюнкт – это дизъюнкция литер.

Совершенный дизъюнкт – это дизъюнкт, число литер в котором совпадает с числом переменных.

Конъюнкт – это конъюнкция литер.

Совершенный конъюнкт – это конъюнкт, число литер в котором совпадает с числом переменных.

Конъюнктивная нормальная форма – это конъюнкция дизъюнктов.

Совершенная конъюнктивная нормальная форма – это конъюнкция совершенных дизъюнктов.

Дизъюнктивная нормальная форма – это дизъюнкция конъюнктов.

Совершенная дизъюнктивная нормальная форма – это дизъюнкция совершенных конъюнктов.

Построение ДНФ — дизъюнктивной нормальной формы

Пусть – логическая функция от n переменных. Построим для нее таблицу истинности. Рассмотрим те кортежи, на которых F принимает значение 1. Для каждого такого кортежа построим совершенный конъюнкт. Если переменная в этом кортеже имеет значение 1, то соответствующая литера в конъюнкте совпадает с , в противном случае литера задает отрицание . По правилам построения так построенный конъюнкт на данном кортеже равен 1 и совпадает со значением функции на этом кортеже. ДНФ – задается как дизъюнкция всех таких конъюнктов.

Построенная ДНФ эквивалентна функции , поскольку совпадает с ней на всех кортежах. Заметьте, что на кортежах, не вошедших в наше построение, все конъюнкты будут иметь значение 0.

Рассмотрим пример построения ДНФ. Пусть – функция от четырех переменных. Она определена на 16 кортежах. Пусть на двух из них она имеет значение 1, а на остальных – 0. Приведем фрагмент таблицы истинности, где показаны только те два кортежа, на которых функция равна 1.

Построим по первому кортежу совершенный конъюнкт :

Построим по второму кортежу совершенный конъюнкт :

Понятно, что по построению, конъюнкт истинен на первом кортеже, а – на втором.

Построим совершенную ДНФ для функции .

На двух рассмотренных кортежах ДНФ имеет значение 1, поскольку один из конъюнктов имеет это значение. На остальных кортежах оба конъюнкта будут иметь значение 0. Поясним на примере. Рассмотрим, например, кортеж . В оба кортежа первая литера входит со знаком отрицания, поэтому на всех кортежах, где первая переменная получает значение 1, оба конъюнкта будут иметь значение 0, и ДНФ будет иметь значение 0. Аналогично обстоит дело и с другими кортежами, на которых функция имеет значение 0, там и конъюнкты будут равны нулю.

Построение КНФ — конъюнктивной нормальной формы

Пусть – логическая функция от переменных. Построим для нее таблицу истинности. Рассмотрим те кортежи, на которых принимает значение 0. Для каждого такого кортежа построим совершенный дизъюнкт. Если переменная в этом кортеже имеет значение 0, то соответствующая литера в конъюнкте совпадает с , в противном случае литера задает отрицание .

По правилам построения так построенный дизъюнкт на данном кортеже равен 0 и совпадает со значением функции на этом кортеже. КНФ – задается как конъюнкция всех таких дизъюнктов. Построенная КНФ эквивалентна функции , поскольку совпадает с ней на всех кортежах. Заметьте, что на кортежах, не вошедших в наше построение, все дизъюнкты будут иметь значение 1.

Рассмотрим пример построения KНФ. Пусть – функция от четырех переменных. Она определена на 16 кортежах. Пусть на двух из них она имеет значение 0, а на остальных – 1. Приведем фрагмент таблицы истинности, где показаны только те два кортежа, на которых функция равна 0.

Построим по первому кортежу совершенный дизъюнкт :

Построим по второму кортежу совершенный конъюнкт :

intuit.ru/2010/edi»>Понятно, что по построению, дизъюнкт ложен на первом кортеже, а – на втором.

Построим совершенную КНФ для функции .

На двух рассмотренных кортежах КНФ имеет значение 0, поскольку один из дизъюнктов имеет это значение. На остальных кортежах оба дизъюнкта будут иметь значение 1. Поясним на примере. Рассмотрим, например, кортеж . В оба кортежа первая литера входит без знака отрицания, поэтому на всех кортежах, где первая переменная получает значение 1, оба дизъюнкта будут иметь значение 1, и КНФ будет иметь значение 1. Аналогично обстоит дело и с другими кортежами, на которых функция имеет значение 1, там и дизъюнкты будут равны единице.

Тема 3 Нормальные формы | Контрольные работы по математике и другим пр

3.1 Разложение булевых функций по переменным

3.2 Алгебра Жегалкина

Выше мы показали, что любая булева функция может быть задана с помощью таблицы истинности. В настоящем разделе излагается переход от табличного перехода задания функции к аналитическому.

3.1 Разложение булевых функций по переменным. Пусть G – параметр, равный 0 или 1. Введем обозначение.

Проверкой легко установить, что

XG=1, тогда и только тогда, когда X=G. Отсюда следует, конъюнкция равна 1 (здесь G равен 0 или 1) тогда и только тогда, когда . Например, конъюнкция (в которой G2=G1=0, G3=G4=1) равна 1 только в случае, когда X1=X2=0, X3=X4=1.

Теорема 1. Всякая булева функция F(X1,X2,…,Xn) может быть представлена в следующей форме:

(1)

Где 1≤K≤N, в дизъюнкции берется по всем наборам значений переменных.

Это представление носит название разложения функции по переменным . Например, при n=4, k=2 разложение (1) имеет вид:

.

Докажем справедливость разложения (1). Для этого возьмем произвольный набор значений переменных . Покажем, что левая и правая части соотношения (1) принимают при нем одно и то же значение. Действительно, так как

XG=1 тогда и только тогда, когда X=G, то среди 2К конъюнкции правой части (1) в единицу обращается только одна, в которой . Все остальные конъюнкции равны нулю.

Поэтому . В качестве следствия из разложения (1) получаем следующие два специальных разложения.

Разложение по переменной XN:

(2)

Если булева функция не есть константа 0, то справедливо разложение

Разложение по всем переменным:

, (3)

Где дизъюнкция берется по всем наборам , при которых значение функции равно 1.

Разложение (3) называется совершенной дизъюнктивной нормальной формой (сокращенная запись СДНФ) функции.

Разложение (3) дает способ построения СДНФ. Для этого в таблице истинности отмечает все строки , в которых . Для каждой такой строки образуем конъюнкцию и затем все полученные конъюнкции соединяем знаком дизъюнкции.

Таким образом, существует взаимно однозначное соответствие между таблицей истинности функции и ее СДНФ. А это значит, что СДНФ для булевой функции единственна.

Единая булева функция, не имеющая СДНФ, есть константа 0.

Пример 1. Найти совершенную дизъюнктивную форму для функции .

Составим таблицы истинности для данной функции:

0	0	0	1	1	0
0	0	1	1	1	1
0	1	0	0	1	0
0	1	1	0	1	1
1	0	0	1	1	0
1	0	1	1	1	1
1	1	0	0	0	1
1	1	1	0	0	1

Отсюда получаем: ==.

Важную роль в алгебре логики играет следующее разложение булевых функций.

Теорема 2. Всякая булева функция Может быть представлена в следующей форме:

(4)

Где 1≤k≤n, а конъюнкция берется По всем 2K наборам значений переменных.

Действительно, пусть – произвольный набор значений переменных. Покажем, что любая и правая части соотношения (4) принимают при нем одно и то же значение. Так как только тогда, когда , то среди 2k дизъюнкций правой части (4) в 0 обращается только одна, в которой . Все остальные дизъюнкции равны 1.

Поэтому ==.

Непосредственно из разложения (4) следуют следующие разложения булевых функций:

(5)

, (6)

Последнее разложение носит название совершенной конъюнктивной нормальной формы (СКНФ). Разложение (6) дает способ построения СКНФ. Для этого в таблице истинности отмечаем все строки , в которых . Для каждой такой строки образуем дизъюнкцию и затем все полученные конъюнкции соединяем знаком конъюнкции. Таким образом, существует взаимно однозначное соответствие между таблицей истинности функции и ее СКНФ. А это значит, что СКНФ для булевой функции единственна.

Единственная булева функция, не имеющая СКНФ, есть константа 1.

Пример 2. Найти совершенную конъюнктивную нормальную форму для функции .

Составим таблицу истинности для данной функции.

0	0	0	1	1	1
0	0	1	1	1	1
0	1	0	1	0	0
0	1	1	1	1	1
1	0	0	0	1	0
1	0	1	0	1	0
1	1	0	1	0	0
1	1	1	1	1	1

Отсюда получаем СКНФ

.

Формула вида (краткая запись ), где — конъюнкции называется Дизъюнктивной нормальной формой.

В силу приведенного определения ДНФ будут, например, выражения: , .

Как отмечено в пункте 2.2, все логические операции можно свести к трем: конъюнкции, дизъюнкции и отрицания. Причем, ввиду закона де Моргана, знак отрицания можно предполагать отнесенным только к переменным.

Теперь, используя дистрибутивный закон, раскрываем скобки и получаем дизъюнктивную нормальную форму. Итак, справедлива следующая теорема.

Теорема 3. Для любой формулы алгебры логики существует равносильная ей дизъюнктивная нормальная форма.

Доказательство данной теоремы дает способ построения дизъюнктивной нормальной формы для любой формулы алгебры логики.

Пример 3. Найти дизъюнктивную нормальную форму для следующей формулы:

.

Исключая знак по закону и применяя законы де Моргана и двойного отрицания, получаем:

Затем, применяя закон дистрибутивности, раскроем скобки

Последнее выражение есть дизъюнктивная нормальная форма.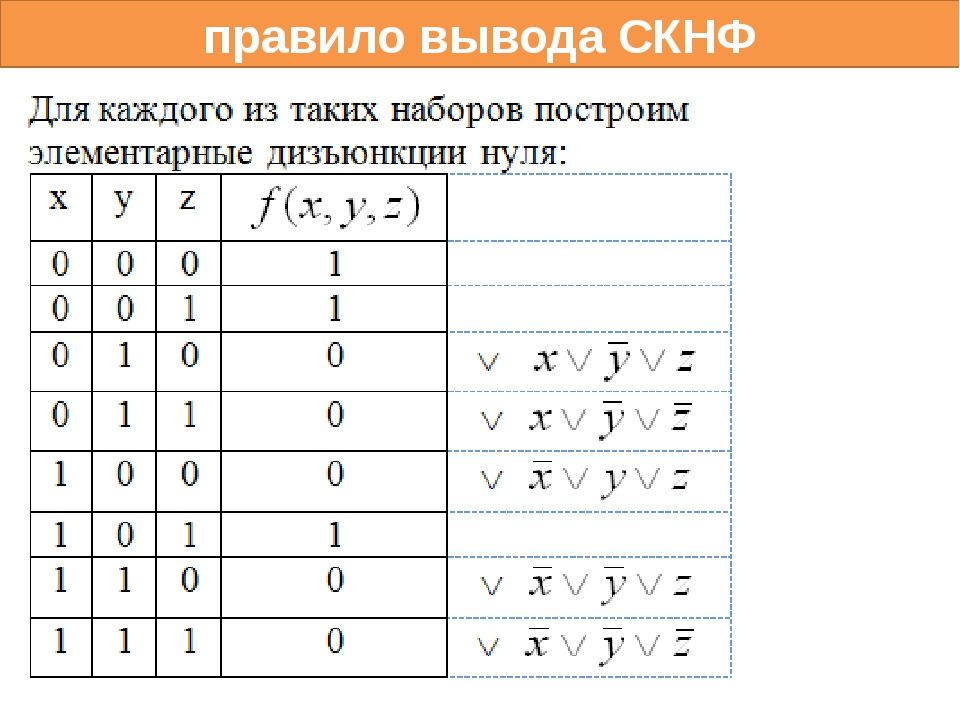

Форма вида

(краткая запись ), где — дизъюнкции называется Конъюнктивной нормальной формой (сокращенно КНФ).

В силу приведенного определения КНФ будут, например, выражения:

, .

Как показано выше, для любой формулы алгебры логики существует равносильная ей дизъюнктивная форма. Используя дистрибутивный закон , из данной ДНФ легко получить КНФ.

Итак, справедлива следующая теорема.

Теорема 4. Для любой формулы алгебры логики существует равносильная ей конъюнктивная нормальная форма.

Доказательство данной теоремы дает способ построения конъюнктивной нормальной формы для любой формулы алгебры логики.

Пример 4. Найти дизъюнктивную и конъюнктивную нормальные формы для следующей формулы: .

Используя закон , исключаем знак .

Получаем формулу .

Используя закон де Моргана, получаем формулу .

Раскрывая скобки, получаем дизъюнктивную нормальную форму

.

Чтобы получить конъюнктивную нормальную форму, применим к формуле

Дистрибутивный закон, получаем:

Последнее выражение является конъюнктивной нормальной формой. Так как и , то полученная КНФ равносильна следующей КНФ:

.

Среди всех нормальных формул данной формулы выделим совершенную нормальную форму как дизъюнктивную, так и конъюнктивную. Учитывая разложение (3), нетрудно заметить, что совершенная дизъюнктивная нормальная форма формулы алгебры логики, содержащей ровно n различный переменных, есть ее дизъюнктивная нормальная форма, в которой:

1) все конъюнкции попарно различны;

2) каждая конъюнкция содержит ровно n переменных;

3) в каждой конъюнкции встречаются все n переменных.

На примере 1 мы рассмотрели один из способов построения СДНФ, основанный на составлении таблицы истинности. Следующий способ построения СДНФ основан на применении законов алгебры логики.

Пример 5. Найти совершенную дизъюнктивную форму формулы .

Используя, что , получаем . Ввиду законов де Моргана и двойного отрицания имеем:

Получили дизъюнктивную нормальную форму. Данная ДНФ равносильна формуле .

Раскрывая скобки, получаем:

.

Используя закон идемпотентности, получаем требуемую СДНФ:

.

Учитывая разложение (6), нетрудно заметить, что совершенная конъюнктивная нормальная форма формулы алгебры логики, содержащей ровно N различных переменных, есть ее конъюнктивная нормальная форма, в которой:

1) все дизъюнкции попарно различны;

2) каждая дизъюнкция содержит ровно n членов;

3) в каждой дизъюнкции встречаются все n переменных.

На примере 2 мы рассмотрели один из способов построения СКНФ, основанный на составлении таблицы истинности. Следующий способ построения СКНФ основан на применении законов алгебры логики.

Пример 6. Найти совершенную конъюнктивную нормальную форму формулы

.

Используя, что , получаем

.

Данная формула является конъюнктивной нормальной формой. Она равносильна формуле

.

Используя закон дистрибутивности, получаем:

Применяя закон идемпотентности, получаем требуемую совершенную конъюнктивную нормальную форму

.

Формула алгебры логики называется Тождественно истинной, если она при всех значениях входящих в нее переменных принимает значение истинно.

Примерами тождественно истинных формул являются формулы:

Формула алгебры логики называется Тождественно ложной, если она при всех значениях, входящих в нее переменных, принимает значение Ложь.

Примерами тождественно ложных формул являются формулы:

,

Формула алгебры логики называется Выполнимой, если она при некоторых значениях, входящих в нее переменных, принимает значение Истинно.

Примерами выполнимых формул являются следующие формулы:

, .

В алгебре логики можно поставить следующую задачу: указать способ (алгоритм), позволяющий для каждой формулы алгебры логики выяснить, является она тождественно истинной или нет. Поставленная задача носит название Проблемы разрешения.

Рассмотрим следующие два способа решения этой задачи.

Способ 1 (табличный). Для того, чтобы определить, является ли данная формула тождественно истинной или нет, достаточно составить ее таблицу истинности.

Однако данный способ, хотя и дает принципиальное решение проблемы разрешимости, он довольно громоздкий.

Способ 2 основан на приведении формул к нормальной форме.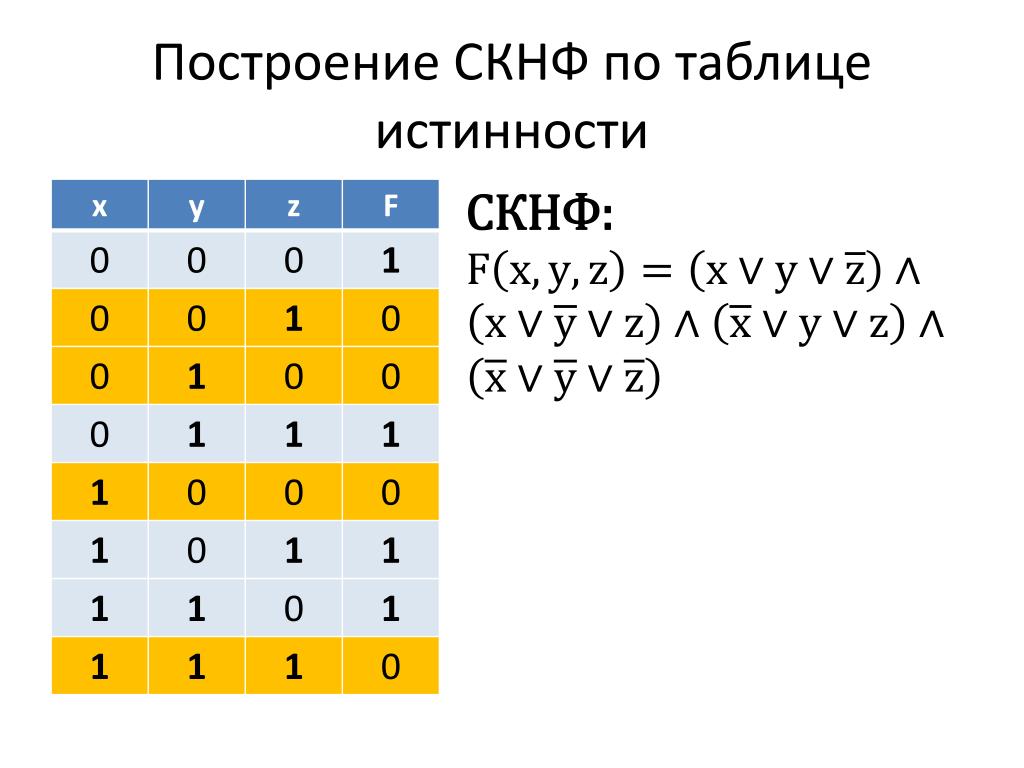

Теорема 4. Формула алгебры логики тогда и только тогда является тождественно истинной, когда каждая дизъюнкция в ее конъюнктивной нормальной форме содержит некоторую переменную вместе с ее отрицанием.

Действительно, если каждая дизъюнкция в конъюнктивной нормальной форме содержит переменную вместе с ее отрицанием, то все дизъюнкции равны 1, ибо , . Отсюда следует, что КНФ является тождественно истинной.

Пусть теперь данная формула является тождественно истинной, и пусть есть некоторая дизъюнкция в КНФ данной формулы. Допустим, что данная дизъюнкция не содержит переменной вместе с ее отрицанием. В таком случае мы может каждой переменной, не стоящей под знаком отрицания, дать значение 0, а каждой переменной, стоящей под знаком отрицания – значение 1. После указанной подстановки все дизъюнкции станут равны 0, следовательно, формула не является тождественно истинной. Получили противоречие.

Пример 7. Выяснить, будет ли тождественно истинной формула

Используя, что , получаем

.

Применяя закон дистрибутивности, получаем КНФ:

.

Так как каждая дизъюнкция содержит некоторую переменную вместе с ее отрицанием, то формула тождественно истинна.

Аналогично предыдущей теореме доказывается теорема:

Теорема 5. Формула алгебры логики тогда и только тогда является тождественно ложной, когда каждая конъюнкция в ее дизъюнктивной форме содержит некоторую переменную вместе с ее отрицанием.

3.2 Алгебра Жегалкина. Множество булевых функций, рассматриваем вместе с операциями конъюнкции и сложения (по модулю два), будем называть алгеброй Жегалкина.

Непосредственно проверкой (с помощью таблиц истинности) устанавливаются следующие законы:

— закон коммутативности;

— закон ассоциативности;

— закон дистрибутивности;

В алгебре Жегалкина роль совершенных нормальных форм булевой алгебры играют полиномы Жегалкина.

Полиномом Жегалкина называется полином вида

Причем в каждом наборе все координаты различны, а суммирование ведется по некоторому множеству таких не совпадающих наборов, А – константа 0 или 1.

Например, выражение является полиномом Жегалкина, а выражения и нет, так как в первом выражении имеется конъюнкция, содержащая две переменные y, а второе выражение содержит два одинаковых слагаемых и .

Если в произвольной форме алгебры Жегалкина раскрыть скобки и произвести все возможные упрощения по указанным выше законам и закону идемпотентности, то получится формула, являющаяся полиномом Жегалкина.

Рассмотрим теперь взаимосвязь, существующую между операциями булевой алгебры и алгебры Жегалкина. Непосредственной проверкой устанавливается

(1)

Ранее мы показали, что любая булева функция может быть выражена в виде формулы через отрицание, конъюнкцию и дизъюнкцию. Согласно законам (1) получаем, что любая булева функция может быть выражена в виде формулы алгебры Жегалкина. Следовательно, существование полинома Жегалкина доказано для любой булевой функции.

Число различных слагаемых (конъюнкций) полинома Жегалкина от переменных равно числу всех подмножеств из n элементов, т. е. 2n. Число различных полиномов, которых можно образовать из этих конъюнкций, равно числу всех подмножеств множества данных конъюнкций, т. е. . Следовательно, число всех полиномов Жегалкина от n переменных равно числу всех булевых функций от n переменных. Отсюда следует единственное представление булевой функции посредством полинома Жегалкина. Итак, справедлива следующая теорема.

Теорема 6. Каждая булева функция может быть единственным образом выражена при помощи полинома Жегалкина.

Пример 8. Выразить в виде полинома Жегалкина.

1 способ. Ищем требуемый полином методом неопределенных коэффициентов: .

При X=y=0 имеем: d=1;

При X=0, y=1 имеем: a=0;

При X=1, y=0 имеем: b=1;

При X=1, y=0 имеем: 1=a+b+c+d =a+1+0+1=a, т. е. а=1.

Отсюда

2 способ.

< Предыдущая		Следующая >

Как с помощью python сделать СДНФ (Совершенная дизъюнктивная нормальная форма)? Что должно получиться на фото ниже

Воспользуйтесь модулем Pandas:

import pandas as pd

исходная таблица истинности в виде Pandas DataFrame:

In [112]: df = pd.DataFrame(
     ...:  [[0,0,0,1],
     ...:   [0,0,1,1],
     ...:   [0,1,0,0],
     ...:   [0,1,1,0],
     ...:   [1,0,0,1],
     ...:   [1,0,1,1],
     ...:   [1,1,0,0],
     ...:   [1,1,1,1]],
     ...:   columns = ["x1", "x2", "x3", "F(x1,x2,x3)"]
     .  x3)

UPDATE: вспомогательная инвертированная матрица нужна для удобства.

Правило: Если значение переменной равно 0, то она записывается с инверсией. Если значение переменной равно 1, то без инверсии.

В ответе используется следующий трюк:

In [29]: '!' * 0 + 'x1'
Out[29]: 'x1'

In [30]: '!' * 1 + 'x1'
Out[30]: '!x1'

т.е. чтобы поставить отрицание (восклицательный знак) надо чтобы соответствующее значение в матрице равнялось единице, а по правилу построения СДНФ, отрицание ставиться в случае если элемент равен нулю. Поэтому удобнее воспользоваться инвертированной таблицей, чтобы использовать трюк, орисанный выше.

Совершенная конъюнктивная нормальная форма — Студопедия

Для одной и той же формулы можно составить множество равносильных ей КНФ. Но среди них существует единственная КНФ со свойствами совершенства.

Перечислим свойства совершенства для КНФ:

1. Каждый логический множитель формулы содержит все переменные, входящие в функцию.

2. Все логические множители различны.

3. Ни один множитель не содержит одновременно переменную и ее отрицание.

4. Ни один множитель не содержит одну и ту же переменную дважды.

КНФ, для которой выполняются свойства совершенства называется совершенной КНФ (СКНФ).

Любая не тождественно истинная формула имеет единственную СКНФ.

Один из способов получения СКНФ состоит в использовании таблицы истинности для :

1. Составляют СДНФ.

2. Для получения СКНФА строят отрицание СДНФ, т.е.

Или из наборов переменных, при которых А ложна, составляют элементарные дизъюнкции, в которых переменная, вошедшая со значением истина вводится с отрицанием, а со значением ложь – без отрицания. Из полученных элементарных дизъюнкций составляют конъюнкцию.

Другой способ основан на равносильных преобразованиях

Приведем соответствующий алгоритм:

1. Путем равносильных преобразований получить какую – либо КНФ.

2. Если какая-либо элементарная дизъюнкция В не содержит переменную х_i , то вводят ее, используя равносильность . И используют свойство дистрибутивности.

3. Если в КНФ входят две одинаковые дизъюнкции В, то лишнюю отбрасывают, используя свойство идемпотентности В B º B.

4. Если какая-либо дизъюнкция содержит x_i вместе с отрицанием, то В º 1. И В исключают из КНФ.

5. Если какая-либо дизъюнкция содержит переменную x_i дважды, то одну из них отбрасывают, используя свойство x_iv x_i º x_i.

Примеры.

1. Составить СКНФ для формулы по таблице истинности и путем равносильных преобразований.

Составим таблицу истинности, которая содержит 4 строки, для

Тогда

Такую же формулу мы получили бы, строя СКНФА на наборах, при которых А ложна.

Преобразуем формулу:

2.Аналогичное задание для формулы

Таблица истинности имеет вид:

Составим СКНФА на наборах, при которых А=0:

Преобразуем формулу:

3. Путем равносильных преобразований получить СКНФА.

Задачи для самостоятельного решения.

1. Для следующих формул найти СДНФ и СКНФ, каждую двумя способами (путем равносильных преобра­зований и используя таблицы истинности):

2. Найдите СДНФ для всякой тождественно ис­тинной формулы, содержащей: 1) одно переменное, 2) два переменных, 3) три переменных.

3.Найдите СКНФ для всякой тождественно лож­ной формулы, содержащей: 1) одно переменное, 2) два переменных, 3) три переменных.

4. Докажите равносильность формул и сравнением их совершенных нормальных форм (конъюнктивных или дизъюнктивных).

5. Найдите более простой вид формул, имеющих следующие совершенные нормальные формы:

Контрольные вопросы

1. Перечислить свойства совершенства для ДНФ.

2. Перечислить свойства совершенства для КНФ.

3. Сколько для одной формулы можно составить СДНФ и СКНФ?

4. Как по таблице истинности составить СДНФ?

5. Связь между СДНФА и СКНФА.

6. Как путем равносильных преобразований составить СДНФ и СКНФ формулы?

3. Совершенная дизъюнктивная нормальная форма и совершенная конъюнктивная нормальная форма.

Известно два способа задания логических функций: с помощью формулы и с помощью таблицы истинности. По формуле легко составляется таблица. На практике при конструировании различных электронных устройств часто возникает обратная задача – от таблицы истинности перейти к формуле, чтобы на ее основе построить функциональную схему.

Введем следующие определения:

Элементарной конъюнкцией называется конъюнкция нескольких переменных, взятых с отрицанием или без отрицания, причем среди переменных могут быть одинаковые.

Элементарной дизъюнкцией называется дизъюнкция нескольких переменных, взятых с отрицанием или без отрицания, причем среди переменных могут быть одинаковые.

Всякую дизъюнкцию элементарных конъюнкций назовем дизъюнктивной нормальной формой (ДНФ).

Всякую конъюнкцию элементарных дизъюнкций назовем конъюнктивной нормальной формой (КНФ).

Совершенной дизъюнктивной нормальной формой (СДНФ) называется ДНФ, в которой нет одинаковых элементарных конъюнкций и все конъюнкции состоят из одного и того же набора переменных, в который каждая переменная входит только один раз (возможно, с отрицанием).

Совершенной конъюнктивной нормальной формой (СКНФ) называется КНФ, в которой нет одинаковых элементарных дизъюнкций и все дизъюнкции состоят из одного и того же набора переменных, в который каждая переменная входит только один раз (возможно, с отрицанием).

Приведем примеры формул, соответствующих и не соответствующих этим определениям:

НАЗВАНИЕ ФОРМУЛЫ В ОПРЕДЕЛЕНИИ	Формула, соответствующая определению	ФОРМУЛА, НЕ СООТВЕТСТВУЮЩАЯ ОПРЕДЕЛЕНИЮ
Элементарная дизъюнкция
Элементарная конъюнкция
ДНФ		ДНФ можно построить для всякой формулы (путем преобразования)
КНФ		КНФ можно построить для всякой формулы (путем преобразования)
СДНФ
СКНФ

Любую функцию, кроме констант 0 и 1, можно представить в виде как СДНФ, так и СКНФ.

Этот факт является теоремой алгебры логики. Из него следует, что любая формула (кроме констант 0 и 1) может быть преобразован к виду как СДНФ, так и СКНФ. Константа 0 может быть представлена только СКНФ (), а константа 1 – только СДНФ (). Из вышесказанного следует, что если надо построить формулу некоторой функции по таблице истинности этой функции, то всегда можно получить СКНФ или СДНФ этой функции.

Алгоритм получения СДНФ по таблице истинности:

1. Отметить те строчки таблицы истинности, в последнем столбце которых стоят 1:

X	Y	F(X,Y)
0	0	0
0	1	1*
1	0	1*
1	1	0

2. Выписать для каждой отмеченной строки конъюнкциювсех переменных следующим образом: если значение некоторой переменной в данной строкеравно 1, то в конъюнкцию включатьсаму эту переменную, еслиравно 0, то ееотрицание:

– для 2-й строки;

– для 3-й строки.

3. Все полученные конъюнкции связать в дизъюнкцию: .

Алгоритм получения СКНФ по таблице истинности:

1. Отметить те строки таблицы истинности, в последнем столбце которых стоит 0:

X	Y	F(X,Y)
0	0	0*
0	1	1
1	0	1
1	1	0*

2. Выписать для каждой отмеченной строки дизъюнкциювсех переменных следующим образом: если значение некоторой переменной в данной строкеравно 0, то в дизъюнкцию включатьсаму эту переменную, еслиравно 1, то ееотрицание:

– для 1-й строки;

– для 4-й строки.

3. Все полученные дизъюнкции связать в конъюнкцию: .

Покажем, что полученные по двум алгоритмам СДНФ и СКНФ эквивалентны. Преобразуем СКНФ по правилам алгебры логики: .

Примечание: для нахождения формулы по таблице истинности рекомендуется использовать тот из двух алгоритмов, в котором в таблице помечается меньше строк.

4. ТИПОВЫЕ ЛОГИЧЕСКИЕ УСТРОЙСТВА ЭВМ.

К типовым логическим устройствам ЭВМ относятся сумматоры, полусумматоры, триггеры, счетчики, регистры, шифраторы, дешифраторы.

1. СУММАТОРЫ.

Сумматор является основным узлом арифметико-логического устройства ЭВМ и служит для суммирования чисел посредством поразрядного сложения.

Сумматор выполняет сложение многозначных двоичных чисел. Он представляет собой последовательное соединение одноразрядных двоичных сумматоров, каждый из которых осуществляет сложение в одном разряде. При этом если сумма двух цифр в данном разряде больше или равна основанию используемой системы счисления, то возникает перенос старшего разряда в соседний сумматор.

Одноразрядный сумматор должен иметь два выхода: для суммы и для переносимого значения. У него может быть два или три (для складываемых значений и значения переноса) входа.

Одноразрядный двоичный сумматор на два входа и два выхода называется одноразрядным полусумматором.

Одноразрядный двоичный сумматор на три входа и два выхода называется одноразрядным сумматором на три входа.

Тематика	Число статей
Аварийное восстановление	369
Авиационная медицина	25. 624
Авиация	90.734
Австралийское выражение	9.071
Австралия	12
Австрийское выражение	21
Австрия	2
Автоматика	93.908
Автоматическое регулирование	983
Автомобили	66.024
Авторское право	244
Агрономия	7
Агрохимия	10.624
Аддитивные технологии и 3D-печать	153
Административное деление	28
Административное право	359
Азартные игры	965
Айкидо	4
Аккумуляторы	84
Акридология	4
Акробатика	3
Активный отдых и экстремальный спорт	5
Акупунктура	9
Акустика  раздел физики	1. 711
Акушерство	458
Албанский язык	1
Алгебра	61
Алжир	7
Алкалоиды	132
Аллергология	164
Альпинизм	397
Альтернативное урегулирование споров	2.679
Алюминиевая промышленность	2.171
Американская фондовая биржа	13
Американский вариант английского языка	7
Американский футбол	48
Американское выражение  не вариант языка	28.451
Амфибии и рептилии	6.029
Анатомия	11. 979
Английский язык	225
Анестезиология	255
Антарктика	186
Антенны и волноводы	8.741
Антильские острова	3
Антимонопольное законодательство	9
Античность  кроме мифологии	443
Антропология	253
Арабский язык	661
Арагон	6
Аргентина	16
Арго	70
Артиллерия	6.940
Архаизм	1.353
Археология	1.180
Архивное дело	158
Архитектура	15. 263
Астрология	156
Астрометрия	29
Астрономия	7.872
Астроспектроскопия	8
Астрофизика	344
Атомная и термоядерная энергетика	13.419
Аудиотехника	13
Аудит	2.516
Африка	121
Африканское выражение	27
Аэрогидродинамика	17.514
Аэродинамика	245
Аэропорты и управление водзушным движением	195
Аэрофотосъемка и топография	29
Базы данных	1. 510
Бактериология	617
Балет	4
Баллистика	173
Банки и банковское дело	31.492
Баскетбол	711
Бейсбол	137
Беларусь	20
Бельгийское выражение	3
Бережливое производство	40
Бетон	163
Библиография	62
Библиотечное дело	208
Библия	2.821
Бизнес	73.434
Бильярд	414
Биоакустика	13
Биогеография	37
Биология	59. 845
Биометрия	98
Бионика	47
Биотехнология	3.724
Биофизика	218
Биохимия	5.875
Биоэнергетика	140
Биржевой термин	5.692
Благотворительные организации	31
Бодибилдинг	1
Боевые искусства и единоборства	17
Боеприпасы	13
Бокс	353
Бондарное производство	2
Борьба	113
Борьба с вредителями	324
Борьба с коррупцией	45
Ботаника	34. 869
Бразилия	16
Британский вариант английского языка	11
Британское выражение  не вариант языка	4.700
Бронетехника	20.866
Буддизм	20
Буквальное значение	290
Бурение	21.058
Бухгалтерский учет  кроме аудита	20.469
Бытовая техника	7.912
Валютный рынок  форекс	39
Валюты и монетарная политика  кроме форекс	789
Вежливо	21
Вексельное право	231
Великобритания	112
Велосипеды  кроме спорта	1. 809
Велоспорт	49
Венгерский язык	16
Венерология	27
Венесуэла	1
Вентиляция	319
Верлан	2
Вертолёты	242
Ветеринария	2.925
Ветроэнергетика	5
Взрывчатые вещества	870
Вибромониторинг	361
Видеозапись	16
Виноградарство	191
Виноделие	1.029
Вирусология	690
Внешняя политика	1.102
Внешняя торговля	268
Водные лыжи	5
Водные ресурсы	523
Водоснабжение	3. 323
Военная авиация	801
Военно-морской флот	1.488
Военный жаргон	1.477
Военный термин	307.219
Возвышенное выражение	572
Воздухоплавание	812
Волейбол	20
Волочение	12
Восклицание	126
Восточное выражение	4
Всемирная торговая организация	224
Вулканология	113
Вульгаризм	317
Выборы	1.498
Высокопарно	321
Высокочастотная электроника	464
Выставки	132
Вьетнамский язык	6
Вяжущие вещества	1
Гавайский	29
Газовые турбины	3. 346
Газоперерабатывающие заводы	4.968
Галантерея	314
Гальванотехника	48
Гандбол	5
Гастроэнтерология	367
Гватемала	1
ГДР  история	2
Гельминтология	135
Гематология	1.152
Геммология	6
Генеалогия	24
Генетика	12.651
Генная инженерия	823
Геоботаника	12
География	15.253
Геодезия	1.510
Геология	67. 954
Геометрия	368
Геомеханика	35
Геоморфология	186
Геофизика	16.891
Геохимия	165
Геохронология	24
Геральдика	326
Германия	56
Герпетология  вкл. с серпентологией	219
Гигиена	196
Гидравлика	449
Гидроакустика	89
Гидробиология	2.755
Гидрогеология	187
Гидрография	681
Гидрология	9.998
Гидрометрия	66
Гидромеханика	79
Гидропланы	1
Гидротехника	217
Гидроэлектростанции	326
Гимнастика	65
Гинекология	1. 201
Гипсокартон и сис-мы сухого строительства	1
Гироскопы	2.333
Гистология	411
Гляциология	110
Голландский  нидерландский  язык	35
Голубиные гонки	1
Гольф	110
Гомеопатия	35
Гонки и автоспорт	11
Горное дело	47.408
Горные лыжи	145
Городская застройка	16
Горюче-смазочные материалы	448
ГОСТ	1.342
Гостиничное дело	1.123
Государственный аппарат и госуслуги	59
Гравиметрия	34
Гражданско-процессуальное право	42
Гражданское право	210
Грамматика	2. 164
Гребной спорт	34
Греческий язык	1.067
Грубо	2.390
Грузовой транспорт	67
Гэльский  шотландский  язык	1
Дактилоскопия	84
Дамбы	4
Даосизм	1
Датский язык	21
Двигатели внутреннего сгорания	615
Дегустация	26
Деловая лексика	874
Делопроизводство	61
Демография	282
Дербетский диалект	1
Деревообработка	6. 584
Дерматология	579
Детали машин	823
Детская речь	374
Дефектоскопия	124
Дзюдо	10
Диалектизм	8.997
Диетология	42
Дизайн	45
Дипломатия	33.420
Дистанционное зондирование Земли	20
Дистилляция	134
Договоры и контракты	28
Документооборот	150
Домашние животные	161
Доменное производство	26
Доминиканская Республика	1
Дорожное движение	673
Дорожное дело	13. 320
Дорожное покрытие	136
Дорожное строительство	386
Дорожный знак	49
Дословно	4
Древнегреческая и древнеримская мифология	696
Древнегреческий язык	117
Древнееврейский язык	23
Европейский банк реконструкции и развития	24.924
Евросоюз	1.234
Египтология	601
Единицы измерений	576
Жаргон	4.142
Жаргон наркоманов	3.344
Железнодорожный термин	33.602
Жестяные изделия	11
Живопись	591
Животноводство	7. 526
Журналистика  терминология	921
Заболевания	398
Занятость	397
Звукозапись	72
Звукоподражание	162
Звукорежиссура	9
Здравоохранение	1.767
Землеведение	9
Зенитная артиллерия	230
Значение 2	4
Золотодобыча	8.816
Зоология	8.542
Зоотехния	219
Зубная имплантология	4.510
Зубчатые передачи	936
Иврит	76
Игрушки	28
Игры  кроме спорта	24
Идиоматическое выражение	15.154
Идиш	178
Издательское дело	647
Измерительные приборы	3.490
Изоляция	68
ИКАО	2
Имена и фамилии	4.749
Иммиграция и гражданство	55
Иммунология	19.210
Имя	3
Имя собственное	8.130
Инвестиции	5.103
Индия	57
Индонезийское выражение	16
Инженерная геология	295
Инженерное дело	99
Иностранные дела	3.195
Инструменты	1.052
Интегральные схемы	90
Интернет	6.493
Информационная безопасность	1.100
Информационные технологии	99.667
Инфракрасная техника	8
Иран	3
Ирландский язык	367
Ирландское выражение	6
Ирония	1.699
Искусственный интеллект	3.528
Искусство	3.174
Ислам	205
Исландский язык	12
Испания	2
Испано-американский жаргон	39
Испанский язык	305
Исторические личности	7
История	13.013
Итальянский язык	845
Иудаизм	14
Ихтиология	20.453
Кабели и кабельное производство	10.427
Кадры	1.707
Казахстан	19
Калька	22
Каменные конструкции	21
Канада	454
Канадское выражение	17
Канализация и очистка сточных вод	153
Канцеляризм	1.519
Канцтовары	11
Карате	12
Карачаганак	2.991
Кардиология	4.456
Картография	12.547
Карточные игры	1.149
Карцинология	33
Карьерные работы	102
Каспий	8.756
Католицизм	1.861
Квантовая механика	1.328
Квантовая электроника	120
Керамика	130
Керамическая плитка	9
Кибернетика	183
Кинематограф	10.145
Киноосветительная аппаратура	19
Киносъёмочная аппаратура	25
Кинотехника	90
Кипр	6
Кирпич	3
Китай	18
Китайский язык	796
Классификация видов экон. деятельности	288
Классификация минералов	5
Климатология	516
Клинические исследования	4.256
Клише	822
Книжное/литературное выражение	4.369
Ковка	15
Кожевенная промышленность	1.149
Кокни  рифмованный сленг	2
Коллекционирование	5
Коллоидная химия	239
Колумбия	1
Комиксы	134
Коммунальное хозяйство	220
Компьютерная графика	690
Компьютерная защита	172
Компьютерная томография	17
Компьютерные игры	1.290
Компьютерные сети	17.467
Компьютерный жаргон	604
Компьютеры	22.490
Конвертерное производство	7
Кондитерские изделия	98
Кондиционеры	119
Коневодство	924
Конный спорт	282
Консалтинг	218
Консервирование	150
Контекстуальное значение	552
Контроль качества и стандартизация	14.167
Конькобежный спорт	14
Кораблевождение	1
Коран	4
Корейский язык	23
Корма	39
Короткие текстовые сообщения	11
Корпоративное управление	4.459
Косметика и косметология	1.780
Космонавтика	66.873
Космос	447
Коста-Рика	1
Кофе	20
Красители	255
Красота и здоровье	6
Крахмально-паточная промышленность	6
Крикет	1
Криминалистика	970
Криминология	7
Криптография	862
Кристаллография	671
Куба	1
Кулинария	10.614
Культурология	969
Культы и прочие духовные практики	2
Кыргызстан	30
Лабораторное оборудование	928
Лазерная медицина	946
Лазеры	2.436
Лакокрасочные материалы	509
Ландшафтный дизайн	68
Ласкательно	114
Латиноамериканский сленг	8
Латиноамериканское выражение	7
Латынь	3.094
ЛГБТ	40
Легкая атлетика	27
Лесоводство	39.215
Лесозаготовка	591
Лесосплав	66
Лесохимия	11
Лимнология	1
Лингвистика	15.936
Линии электропередач	15
Литейное производство	867
Литература	4.206
Литология	19
Лифты	143
Логика	644
Логистика	12.550
Логопедия	5
Ложный друг переводчика	7
Лыжный спорт	69
Льдообразование	267
Магнетизм	316
Магнитная запись изображения	5
Магнитнорезонансная томография	42
Майкрософт	25.963
Макаров	604.933
Малайский язык	15
Малакология	158
Малярное дело	98
Маммология	382
Маори	197
Маркетинг	3.436
Маркшейдерское дело	9
Марокко	1
Мартеновское производство	11
Масложировая промышленность	43
Математика	124.303
Математический анализ	329
Материаловедение	2.053
Машиностроение	7.116
Машины и механизмы	907
Мебель	710
Медико-биологические науки	330
Медицина	251.014
Медицинская техника	5.062
Международная торговля	276
Международное право	1.075
Международное частное право	14
Международные отношения	1.106
Международные перевозки	433
Международный валютный фонд	10.603
Мексиканское выражение	17
Мелиорация	444
Менеджмент	3.881
Местное название	34
Металловедение	469
Металлообработка	64
Металлургия	47.845
Метеорология	7.869
Метрология	11.770
Метрополитен и скоростной транспорт	559
Механика	15.683
Механика грунтов	21
Микология	514
Микробиология	1.684
Микроскопия	377
Микроэлектроника	13.413
Минералогия	2.754
Мифология	1.435
Млекопитающие	9.396
Мобильная и сотовая связь	1.063
Мода	751
Молдавский язык	2
Молекулярная биология	2.567
Молекулярная генетика	853
Моликпак	2.428
Молодёжный сленг	90
Молочное производство	472
Монтажное дело	250
Морское право	18
Морской термин	98.185
Морфология	3
Мостостроение	2.082
Мотоциклы	253
Мрачно	10
Музеи	245
Музыка	11.200
Музыкальные инструменты	81
Мультимедиа	7
Мультфильмы и мультипликация	223
Мучное производство	69
Мясное производство	4.091
Навигация	410
Надёжность	59
Название компании	3
Название лекарственного средства	2.286
Название организации	4.006
Название произведения	11
Названия учебных предметов	104
Налоги	4.364
Нанотехнологии	56.806
Напитки	308
Народное выражение	185
НАСА	54
Наследственное право	66
Насосы	815
Настольные игры	11
Настольный теннис	144
НАТО	2.509
Научно-исследовательская деятельность	1.439
Научный термин	11.512
Неаполитанское выражение	1
Небесная механика	6
Неврология	1.457
Негритянский жаргон	156
Недвижимость	1.741
Нейролингвистика	6
Нейронные сети	650
Нейропсихология	99
Нейрохирургия	137
Нелинейная оптика	4
Немецкий язык	505
Неодобрительно	1.227
Неологизм	486
Неорганическая химия	841
Непрерывная разливка	5
Нефрология	174
Нефтегазовая техника	19.044
Нефтеперерабатывающие заводы	9.064
Нефтепромысловый	13.427
Нефть	95.312
Нефть и газ	60.161
Нидерланды	1
Новозеландское выражение	143
Норвежский язык	12
Нотариальная практика	10.524
Нумизматика	112
Нью-Йоркская фондовая биржа	9
Обмотки	9
Обогащение полезных ископаемых	708
Обработка данных	1.710
Обработка кинофотоматериалов	21
Образное выражение	4.239
Образование	12.895
Обувь	1.363
Общая лексика	1.511.623
Общее право  англосаксонская правовая система	96
Общественное питание	1.557
Общественные организации	652
Общественный транспорт	17
Обществоведение	135
Огнеупорные материалы	154
Одежда	3.256
Океанология  океанография	5.755
Окна	40
Окружающая среда	5.413
Онкология	3.033
ООН  Организация Объединенных Наций	7.020
Операционные системы	220
Оптика  раздел физики	1.573
Оптическое волокно	57
Оптометрия	4
Организационно-правовые формы компаний	91
Организация производства	1.129
Органическая химия	2.594
Оргтехника	605
Орнитология	16.856
Ортопедия	279
Оружие и оружейное производство	10.744
Оружие массового поражения	11.184
Отопление	254
Официальный стиль	2.925
Офтальмология	2.109
Оффшоры	15
Охота и охотоведение	988
Охрана труда и техника безопасности	2.633
Ошибочное или неправильное	106
Паблик рилейшнз	748
Палеоботаника	32
Палеозоология	2
Палеонтология	949
Палинология	114
Панама	4
Паразитология	147
Парапланеризм	3
Парапсихология	108
Парикмахерское дело	474
Парусные суда	55
Парусный спорт	18
Парфюмерия	13.317
Паспорт безопасности вещества	383
Патенты	16.940
Патология	405
Педагогика	17
Педиатрия	392
Пенитенциарная система	7
Переключатели	99
Переносный смысл	31.233
Переплётное дело	44
Персидский язык  фарси	73
Перу	9
Петанк	7
Петрография	649
Печатные платы	374
Пивоварение	580
Письменная речь	10
Пишущие машинки, машинопись	6
Пищевая промышленность	23.281
Плавание	83
Планирование	346
Пластмассы	4.465
Поговорка	1.573
Погрузочное оборудование	366
Подводное плавание	982
Подводные лодки	425
Пожарное дело и системы пожаротушения	11.641
Полезные ископаемые	164
Полиграфия	31.711
Полимеры	29.546
Полинезийское выражение	4
Политика	26.187
Политэкономия	385
Полицейский жаргон	31
Полиция	2.322
Полупроводники	756
Польский язык	25
Порошковая металлургия	144
Португальский язык	39
Пословица	17.248
Почвоведение	993
Почта	474
Почтительно	13
Пошив одежды и швейная промышленность	1.169
Поэзия  терминология	471
Поэтический язык	2.717
Пояснительный вариант перевода	736
Права человека и правозащитная деят.	26
Правоохранительная деятельность	346
Православие	3
Прагматика	15
Превосходная степень	22
Презрительно	998
Пренебрежительно	447
Прессовое оборудование	62
Преступность	370
Приводы	155
Прикладная математика	644
Природные ресурсы и охрана природы	53
Программирование	133.055
Программное обеспечение	3.435
Проекторы	5
Проигрыватели виниловых дисков	37
Производственные помещения	559
Производство	20.192
Производство спирта	281
Производство электроэнергии	16
Прокат  металлургия	4.053
Промышленная гигиена	116
Промышленность	2.276
Просторечие	1.398
Противовоздушная оборона	204
Протистология	31
Профессиональный жаргон	1.239
Профсоюзы	2.561
Процессуальное право	104
Прыжки в высоту	1
Прыжки на батуте	1
Прыжки с парашютом	143
Прыжки с трамплина	12
Прядение	52
Прямой и переносный смысл	1.280
Психиатрия	4.662
Психогигиена	38
Психолингвистика	246
Психология	19.337
Психопатология	160
Психотерапия	1.028
Психофизиология	163
Птицеводство	395
Публицистический стиль	229
Публичное право	368
Пульмонология	619
Пуэрто-риканский диалект испанского языка	11
Пчеловодство	512
Радио	3.043
Радиоастрономия	32
Радиобиология	51
Радиогеодезия	12
Радиолокация	1.577
Разговорная лексика	148.724
Ракетная техника	1.456
Распределение энергии	4
Расстройства речи	5
Растениеводство	1.269
Расходометрия	205
Расширение файла	16
Реактивные двигатели	1
Регби	11
Региональные выражения  не варианты языка	114
Регулирование движения	85
Редко	8.569
Резиновая промышленность	380
Реклама	37.311
Релейная защита и автоматика	1.115
Религия	36.780
Рентгенография	232
Рентгенология	628
Риторика	4.561
Ритуал	2
Робототехника	10.252
Россия	266
Ругательство	1.619
Рудные месторождения	37
Рукоделие	240
Румынский язык	7
Русский язык	319
Рыбалка  хобби	241
Рыбоводство	10.750
Рыболовство  промысловое	2.750
Садоводство	793
Санитария	224
Санный спорт	2
Санскрит	48
Сантехника	272
Сарказм	63
Сахалин А	1.140
Сахалин Р	4.233
Сахалин Ю	1.475
Сахалин	31.184
Сахарное производство	85
Сварка	4.381
Светотехника  кроме кино	793
Связь	7.969
Северная Ирландия	2
Североамериканское выр.  США, Канада	34
Сейсмология	1.723
Сейсмостойкость сооружений	60
Секс и психосексуальные субкультуры	39
Сексопатология	258
Селекция	73
Сельское хозяйство	49.240
Сенситометрия	7
Сестринское дело	20
Сигнализация	194
Силикатная промышленность	11.104
Силовая электроника	168
Синтоизм	2
Система наряд-допусков	17
Систематика организмов	65
Системы безопасности	28.488
Сказки	158
Скандинавская мифология	123
Скачки	246
Складское дело	587
Скорая медицинская помощь	6
Скульптура	31
Славянское выражение	5
Сленг	63.537
Слоистые пластики	14
Слуховые аппараты	9
Снабжение	380
Сниженный регистр	545
Сноуборд	3
Собаководство  кинология	1.549
Собирательно	2.162
Советский термин или реалия	924
Современное выражение	296
Сокращение	9.783
Солнечная энергетика	3.848
Соматика	238
Сопротивление материалов	215
Социализм	291
Социальное обеспечение	915
Социальные сети	248
Социологический опрос	10
Социология	6.015
Союз-Аполлон	3.098
Спектроскопия	1.362
Спелеология	2
Специи	51
Спецслужбы и разведка	2.171
СПИД	10
Спичечное производство	63
Спорт	21.673
Спорттовары	18
Спутниковая связь	51
Средне-китайский	16
Средства индивидуальной защиты	33
Средства массовой информации	14.459
Станки	604
Старая орфография	1
Старомодное  выходит из употребления	28
Старофранцузский	3
Статистика	5.392
Стеклоделие	76
Стеклотарная промышленность	59
Стерео	8
Стилистика	95
Стоматология	26.696
Стратиграфия	58
Страхование	9.955
Стрелковый спорт	28
Стрельба из лука	28
Строительная техника	7
Строительные конструкции	991
Строительные материалы	1.866
Строительство	125.060
Студенческая речь	165
Суда на воздушной подушке	162
Суда на подводных крыльях	102
Судебная лексика	234
Судебная медицина	97
Судостроение	16.851
Сухопутные силы	70
Сценарное мастерство	11
США	1.449
Сыроварение	20
Табачная промышленность	452
Табуированная  обсценная  лексика	18.102
Тавромахия	1
Тагмемика	1
Тайвань	1
Тайский язык	12
Таможенное дело	936
Танцы	10
Татарский язык	3
Театр	2.559
Текстильная промышленность	46.823
Тектоника	108
Телевидение	3.879
Телеграфия	180
Телекоммуникации	90.612
Телемеханика	60
Телефония	1.584
Тенгизшевройл	7.530
Теннис	431
Теория права	66
Тепличные технологии	120
Теплообменные аппараты	189
Теплопередача	104
Теплотехника	14.693
Теплоэнергетика	53
Тератология	81
Термодинамика	86
Техника	545.508
Типографика	343
Ткачество	149
Токсикология	971
Топография	199
Топология	129
Топоним	272
Торговая марка	1.189
Торговля	3.814
Торговый флот	34
Торпеды	682
Травматология	217
Трансплантология	641
Транспорт	4.294
Трансформаторы	99
Трибология	371
Трикотаж	203
Трубопроводная арматура	175
Трубопроводы	4.802
Трудовое право	1.392
Туннелестроение и проходческие работы	32
Турбины	30
Турецкий язык	143
Туризм	3.719
Турция	1
Тюремный жаргон	319
Тюркские языки	10
Тяжёлая атлетика	12
Увеличительно	16
Уголовное право	1.950
Уголовный жаргон	304
Уголь	804
Удобрения	12
Узкоплёночное кино	4
Украина	56
Украинский язык	6
Украинское выражение	3
Ультразвук	14
Уменьшительно	461
Университет	819
Уничижительно	542
Упаковка	1.333
Управление проектами	1.227
Управление рисками	27
Управление скважиной	483
Уровнеметрия	154
Урология	603
Уругвайский диалект испанского языка	2
Устаревшее	37.787
Устная речь	39
Утилизация отходов	345
Уфология	68
Уэльс	9
Фалеристика	14
Фамилия	3
Фамильярное выражение	771
Фантастика, фэнтези	747
Фармакология	11.540
Фармация	5.970
Федеральное бюро расследований	14
Фелинология	4
Ферментация	4
Фехтование	97
Фигурное катание	193
Физика металлов	42
Физика твёрдого тела	249
Физика	10.086
Физиология	3.844
Физиотерапия	3
Физическая химия	979
Филателия	333
Филиппины	17
Филология	123
Философия	3.468
Финансы	24.755
Финский язык	53
Фитопатология	315
Фольклор	652
Фонетика	620
Фортификация	14
Фотографическая запись звука	1
Фотография	1.709
Фотометрия	2
Фразеологизм	10.204
Французский язык	2.210
Фундаментостроение	19
Футбол	2.386
Хакерство	39
Хальцидология	1
Химическая номенклатура	674
Химическая промышленность	720
Химические волокна	163
Химические соединения	965
Химия	66.057
Хинди	924
Хирургия	2.844
Хлеб и хлебопечение	342
Хобби, увлечения, досуг	193
Хозйственное  предпринимательское  право	135
Хозяйственные общества и товарищества	3
Хоккей	2.095
Холодильная техника	17.319
Хореография	37
Христианство	9.540
Хроматография	2.207
Цветная металлургия	157
Цветоводство	112
Целлюлозно-бумажная промышленность	2.114
Цемент	7.899
Ценные бумаги	1.024
Центральная Америка	2
Церковный термин	3.591
Цинкование	163
Цирк	69
Цитаты, афоризмы и крылатые выражения	2.025
Цитогенетика	40
Цитология	632
Цифровая обработка звука	14
Цифровые и криптовалюты	60
Часовое дело	276
Чаты и интернет-жаргон	42
Черчение	190
Чешский язык	9
Чили	7
Шахматы	18.849
Шведский язык	7
Швейцарское выражение	47
Школьное выражение	591
Шотландия	593
Шотландское выражение	1.168
Шоу-бизнес  индустрия развлечений	254
Штамповка	23
Шутливое выражение	2.875
Эволюция	68
Эвфемизм	926
Эзотерика	204
Эквадор	1
Экология	43.298
Эконометрика	1.188
Экономика	132.646
Экструзия	29
Электрические машины	612
Электричество	2.106
Электродвигатели	17
Электролиз	4
Электромедицина	30
Электрометаллургия	30
Электроника	49.920
Электронная почта	140
Электронная торговля	17
Электронно-лучевые трубки	39
Электротермия	18
Электротехника	25.196
Электротяга	12
Электрофорез	48
Электрохимия	7.362
Эмбриология	362
Эмоциональное выражение	706
Эндокринология	332
Энергетика	60.568
Энергосистемы	4.750
Энтомология	14.605
Эпидемиология	217
Эпистолярный жанр	1
Эскимосское выражение	3
Эсперанто	7
Эстонский язык	1
Этнография	676
Этнология	1.011
Этнопсихология	10
Этология	187
Ювелирное дело	616
Южная Америка	29
Южноафриканское выражение	139
Южнонидерландское выражение	1
Юридическая лексика	121.230
Ядерная физика	2.464
Ядерная химия	50
Ямайский английский	67
Япония	6
Японский язык	240
Яхтенный спорт	2.198
ASCII	118
Hi-Fi акустика	919
SAP технические термины	7.504
SAP финансы	4.393
SAP	7.233
Всего:	7.846.786

Персональный сайт Лаптевой З.А. — СДНФ и СКНФ

СДНФ и СКНФ

Нормальная форма логической функции – если логическая функция представлена дизъюнкцией, конъюнкцией и инверсией.

Ранг элементарной конъюнкции или дизъюнкции — это число аргументов ее образующих.

Пример:   

Элементарная конъюнкция третьего порядка.

Элементарная дизъюнкция второго порядка.

Конъюнктивная нормальная форма (КНФ) содержит элементарные дизъюнкции, связанные между собой операциями конъюнкции.

Пример:

Дизъюнктивная нормальная форма (ДНФ) содержит элементарные конъюнкции, связанные между собой операциями дизъюнкции.

Совершенная конъюнктивная нормальная форма (СКНФ):

• нет двух элементарных дизъюнкций;
• ни одна элементарная дизъюнкция не содержит двух одинаковых переменных;
• ни одна элементарная дизъюнкция не содержит переменную вместе с ее инверсией;
• все дизъюнкции имеют один и тот же ранг.

Совершенная дизъюнктивная нормальная форма (СДНФ)

• нет двух одинаковых элементарных конъюнкций
• ни одна элементарная конъюнкция не содержит двух одинаковых переменных;
• ни одна элементарная конъюнкция не содержит переменную вместе с ее инверсией;
• все конъюнкция имеют один и тот же ранг.

Убедиться, является ли данная формула ДНФ, КНФ, СДНФ или  СКНФ:

Решение

а) Данная формула является КНФ (конъюнкция элементарных дизъюнкций),  но не  СКНФ,  так как  элементарные  дизъюнкции  не являются полными.

б) Формула не является ДНФ,  так как  последняя конъюнкция не является элементарной. Но формулу можно с помощью закона Де Моргана преобразовать к равносильному виду который является ДНФ, но не СДНФ (не все элементарные конъюнкции полны).

в) Формула не является ни ДНФ, ни КНФ, поскольку содержит импликацию.

г) СДНФ, состоящая из одной элементарной полной конъюнкции; либо КНФ, но не СКНФ, так как  состоит из трех элементарных неполных дизъюнкций.

д) СКНФ.

 е) СДНФ.

Алгоритм образования СКНФ и СДНФ по таблице истинности

1. Выделить в таблице истинности все строки, в которых функция принимает значения 0.

2. Для каждого выбранного набора записать элементарные дизъюнкции, содержащие переменные:

а) если значение переменной равно 0, то записывается сама переменная,

б) если значение переменной равно 1, то записывается инверсия этой переменной

3. Соединить элементарные дизъюнкции знаком конъюнкции.

Алгоритм образования СКНФ и СДНФ по таблице истинности

1. Выделить в таблице истинности все строки, в которых функция принимает значения 1.

2. Для каждого выбранного набора записать элементарные конъюнкции, содержащие переменные:

а) если значение переменной равно 0, то записывается инверсия этой переменной,

б) если значение переменной равно 1, то записывается сама переменная.

3. Соединить элементарные конъюнкции знаком дизъюнкции.

нормальных форм

нормальных форм

• Когда мы рассматривали логические операции высказываний, мы определили несколько вещей, использующих и / или не использующих.
  • Например: \ [\ begin {align *} p \ oplus q & \ Equiv (p \ vee q) \ клин \ neg (p \ клин q) \ ,, \\ p \ rightarrow q & \ Equiv \ neg p \ vee q \ ,, \\ п \ leftrightarrow q & \ Equiv (p \ rightarrow q) \ wedge (q \ rightarrow p) \ Equ (\ neg p \ vee q) \ wedge (\ neg q \ vee p) \ ,. \ конец {выравнивание *} \]
• Мы сделали это, чтобы помочь нам понять новые символы с точки зрения того, что мы уже знали.
  • Но также хорошо иметь стандартное определение операторов, которые мы можем использовать.
  • При доказательстве эквивалентности он позволяет нам применять эквивалентности, которые у нас уже были, которые использовались и / или / или нет.
• У нас также были некоторые правила эквивалентности, которые помогли нам перестроить предложения, чтобы мы могли добраться до нужных нам частей:

  Имя	Эквиваленты
  Двойное отрицание	\ (\ neg (\ neg p) \ Equiv p \)
  Commutative	\ (p \ vee q \ Equiv q \ vee p \\ p \ клин q \ эквив q \ клин p \)
  Ассоциативный	\ ((p \ vee q) \ vee r \ Equiv p \ vee (q \ vee r) \\ (p \ wedge q) \ клин г \ эквив р \ клин (д \ клин г) \)
  Распределительный	\ (р \ ви (д \ клин г) \ экв (р \ ви д) \ клин (р \ ви г) \ \ p \ wedge (q \ vee r) \ Equiv (p \ wedge q) \ vee (p \ wedge r) \)
  Закон Де Моргана	\ (\ neg (p \ wedge q) \ Equiv \ neg p \ vee \ neg q \\\ neg (p \ vee q) \ Equiv \ neg p \ wedge \ neg q \)

  • [И другие, но давайте пока придерживаемся их.]
• Мы можем быть немного строже в оформлении предложения.

• Помните, что мы также называли «или» «дизъюнкцией» и «и» «соединением».
• Предложение, содержащее только \ (\ vee \), называется дизъюнктивным предложением , а только \ (\ wedge \) называется конъюнктивным предложением .
  • Отрицание разрешено, но только непосредственно для переменных.
  • \ (p \ vee \ neg q \ vee r \): дизъюнктивное предложение
  • \ (\ neg p \ wedge q \ wedge \ neg r \): конъюнктивное предложение
  • \ (\ neg p \ wedge \ neg q \ vee r \): ни один из
• Если мы соединим кучу дизъюнктивных предложений вместе с \ (\ клином \), это называется конъюнктивной нормальной формой .
  • Например: \ ((p \ vee r) \ wedge (\ neg q \ vee \ neg r) \ wedge q \) находится в конъюнктивной нормальной форме.
• Точно так же, если объединить конъюнктивные предложения вместе с \ (\ vee \), это называется дизъюнктивной нормальной формой .
  • Например: \ ((p \ wedge \ neg q \ wedge r) \ vee (\ neg q \ wedge \ neg r) \) находится в дизъюнктивной нормальной форме.
• Еще примеры:
  • \ ((p \ wedge q \ wedge \ neg r \ wedge s) \ vee (\ neg q \ wedge s) \ vee (p \ wedge s) \) находится в дизъюнктивной нормальной форме.
  • \ ((p \ vee q \ vee \ neg r \ vee s) \ wedge (\ neg q \ vee s) \ wedge \ neg s \) находится в конъюнктивной нормальной форме.
  • \ ((p \ vee r) \ wedge (q \ wedge (p \ vee \ neg q)) \) не в нормальной форме.
  • \ (\ neg p \ vee q \ vee r \) и \ (\ neg p \ wedge q \ wedge r \) находятся в обеих нормальных формах.
• Оказывается, мы можем преобразовать любое предложение в любую нормальную форму.
  • Мы можем использовать определения, чтобы избавиться от \ (\ rightarrow \), \ (\ leftrightarrow \) и \ (\ oplus \).
  • Используйте законы ДеМоргана, чтобы переместить любые \ (\ neg \) в скобки прошедшего времени, чтобы они располагались на переменных.
  • Используйте двойное отрицание, чтобы избавиться от всех появившихся \ (\ neg \ neg \).
  • Используйте правила распределения, чтобы перемещать элементы в / из пар, когда нам нужно.
• Например, преобразование в конъюнктивную нормальную форму: \ [\ begin {align *} \ Нег ((\ Нег п \ Стрелка вправо \ Нег q) \ клин \ Нег г) & \ Equiv \ neg ((\ neg \ neg p \ vee \ neg q) \ wedge \ neg r) & \ mbox {[определение]} \\ & \ Equiv \ neg ((p \ vee \ neg q) \ wedge \ neg r) & \ mbox {[двойное отрицание]} \\ & \ Equiv \ neg (p \ vee \ neg q) \ vee \ neg \ neg r & \ mbox {[ДеМорган]} \\ & \ Equiv \ neg (p \ vee \ neg q) \ vee r & \ mbox {[двойное отрицание]} \\ & \ Equiv (\ neg p \ wedge \ neg \ neg q) \ vee r & \ mbox {[ДеМорган]} \\ & \ Equiv (\ neg p \ wedge q) \ vee r & \ mbox {[двойное отрицание]} \\ & \ Equiv (\ neg p \ vee r) \ wedge (q \ vee r) & \ mbox {[дистрибутив]} \ конец {выравнивание *} \]
  • На самом деле он был в дизъюнктивной нормальной форме на втором-последнем шаге.
• Почему нам нужно преобразовать в нормальную форму?
  • Может быть проще доказать эквивалентность: показать \ (A \ Equiv B \), преобразовать оба в нормальную форму, а затем переписать одно доказательство в обратном порядке.
  • Может быть, мы сильно упростим: если мы получим \ ((p \ vee \ neg p \ vee \ cdots) \) термины, мы узнаем, что они верны.
  • Доказательство теорем обо всех предложениях: нужно обрабатывать только логические выражения в нормальной форме, и это покрывает каждое предложение.
  • Показывает, что мы можем использовать схему для вычисления любого логического выражения с двумя уровнями логических вентилей.
• Другой пример: \ [\ begin {align *} (p \ rightarrow q) \ rightarrow (\ neg r \ wedge q) & \ Equiv \ neg (p \ rightarrow q) \ vee (\ neg r \ wedge q) & \ mbox {[определение]} \\ & \ Equiv \ neg (\ neg p \ vee q) \ vee (\ neg r \ wedge q) & \ mbox {[определение]} \\ & \ Equiv (\ neg \ neg p \ wedge \ neg q) \ vee (\ neg r \ wedge q) & \ mbox {[DeMorgan’s]} \\ & \ Equiv (p \ wedge \ neg q) \ vee (\ neg r \ wedge q) & \ mbox {[двойное отрицание]} \\ \ конец {выравнивание *} \]
  • На данный момент это DNF.Продолжая…
  \ [\ begin {align *} (p \ rightarrow q) \ rightarrow (\ neg r \ wedge q) & \ Equiv (p \ wedge \ neg q) \ vee (\ neg r \ wedge q) & \ mbox {[как указано выше]} \\ & \ Equiv (p \ vee (\ neg r \ wedge q)) \ wedge (\ neg q \ vee (\ neg r \ wedge q)) & \ mbox {[дистрибутив]} \\ & \ Equiv (p \ vee (\ neg r \ wedge q)) \ wedge (\ neg q \ vee \ neg r) \ wedge (\ neg q \ vee q) & \ mbox {[распределительный]} \\ & \ Equiv (p \ vee (\ neg r \ wedge q)) \ wedge (\ neg q \ vee \ neg r) \ wedge \ mathbf {T} & \ mbox {[отрицание]} \\ & \ Equiv (p \ vee (\ neg r \ wedge q)) \ wedge (\ neg q \ vee \ neg r) & \ mbox {[идентичность]} \\ & \ Equiv (p \ vee \ neg r) \ wedge (p \ vee q) \ wedge (\ neg q \ vee \ neg r) & \ mbox {[дистрибутив]} \ конец {выравнивание *} \]

Вернуться на главную страницу заметок к курсу.Авторское право © 2013, Грег Бейкер.

Нормальные и основные формы — GeeksforGeeks

Нормальные и основные формы

1. Дизъюнктивные нормальные формы (DNF):
   Формула, которая эквивалентна данной формуле и состоит из суммы элементарных произведений, называется дизъюнктивной нормальной формой. данной формулы.

   Пример:
   (P ∧ ~ Q) ∨ (Q ∧ R) ∨ (~ P ∧ Q ∧ ~ R)

   • DNF формулы не уникален.
2. Конъюнктивная нормальная форма (CNF):
   Формула, эквивалентная данной формуле и состоящая из произведения элементарных произведений, называется конъюнктивной нормальной формой данной формулы.

   Пример:
   (P ~ ∨ Q) ∧ (Q ∨ R) ∧ (~ P ∨ Q ∨ ~ R)

   • CNF формулы не уникален.
   • Если каждая элементарная сумма в КНФ является тавтологией, то данная формула также является тавтологией.
3. Принцип дизъюнктивной нормальной формы (PDNF):
   Эквивалентная формула, состоящая только из дизъюнкций минтермов, называется основной дизъюнктивной нормальной формой формулы.
   

   Также известна как каноническая форма суммы произведений .

   Пример:
   (P ∧ ~ Q ∧ ~ R) ∨ (P ∧ ~ Q ∧ R) ∨ (~ P ∧ ~ Q ∧ ~ R)

   • Минтерм состоит из союзов, в которых каждая переменная оператора или его отрицание, но не оба, появляется только один раз.
   • Минтермы записываются путем включения переменной, если ее значение истинности равно Т, и отрицания, если ее значение истинности равно F.
4. Принцип конъюнктивной нормальной формы (PCNF):
   Эквивалентная формула, состоящая из конъюнкций максимальных терминов. только называется основной конъюнктивной нормальной формой формулы.

   Также известна как каноническая форма произведения сумм .

   Пример:
   (P ∨ ~ Q ∨ ~ R) ∧ (P ∨ ~ Q ∨ R) ∧ (~ P ∨ ~ Q ∨ ~ R)

   • maxterm состоит из дизъюнкций, в которых каждая переменная или ее отрицание, но не оба, появляется только один раз.
   • Двойной минтерм называется макстерм.
   • Каждый из maxterm имеет значение истинности F ровно для одной комбинации значений истинности переменных.
   • Максимальные термины записываются путем включения переменной, если ее значение истинности равно F, и отрицания, если ее значение истинности равно T.

DNF, PPF, SDNF, SKFF. Дизъюнктивные и конъюнктивные совершенные нормальные формы Алгоритм построения КНФ

Введем понятие элементарной дизъюнкции.

Элементарная дизъюнкция называется выражением

Конъюнктивная нормальная форма (PFF) логической функции — это конъюнкция любого конечного набора пар различных элементарных дизъюнкций. Например, логические функции

представляют собой соединения элементарных дизъюнкций.Следовательно, они записываются в соединительной нормальной форме.

Произвольная логическая функция, заданная аналитическим выражением, может быть передана PFF, выполнив следующие операции:

Использование правила инверсии, если операция отрицания применяется к логическому выражению;

Использование аксиом распределения относительно умножения:

Использование операции абсорбции:

Исключения в дизъюнкции повторяющихся переменных или их отрицания;

Удаление всех одинаковых элементарных дизъюнкций, кроме одного;

Удаление всех дизъюнкций, одновременно вводящих переменную и ее отрицание.

Справедливость перечисленных операций следует из главных осей и идентичного соотношения логической алгебры.

Конъюнктивная нормальная форма называется совершенной, если каждая входящая элементарная дизъюнкция содержит в прямой или обратной форме все переменные, от которых зависит функция.

Преобразование CNF в совершенную CNF осуществляется путем выполнения следующих операций:

Добавление к каждой элементарной дизъюнкции конъюнктуры переменных и их отрицаний, если они не входят в эту элементарную дизъюнкцию;

Использование аксиом распределения;

Удаление всех одинаковых элементарных дизъюнкций, кроме одного.

В совершенной CNF может быть представлена ​​любая логическая функция, кроме

тождественно равен единице (). Отличительной чертой совершенного KNF является то, что представление логической функции уникально.

Элементарные дизъюнкции, включенные в идеальную функцию PFF, называются составляющей нуля. Каждая составляющая нуля, которая включена в идеальный KNF, обращается в ноль на единственном наборе переменных, который является нулевым набором функций. Следовательно, количество нулевых наборов логической функции совпадает с количеством составляющих нуля, включенных в ее совершенный PFF.

Логическая функция нулевой константы в совершенном KNF — это конъюнкция 2N, составляющая ноль. Сформулируем правило компиляции логической функции SCFF по таблице соответствия.

Для каждой строки таблицы соответствия, в которой функция равна нулю, составляется элементарная дизъюнкция всех переменных. В то же время сама переменная входит в дизъюнкцию, если ее значение равно нулю, или в отрицание, если ее значение равно единице. Полученные элементарные дизъюнкции объединяются знаком конъюнкции.

Пример 3.4. Для логической функции z (x), данной таблице соответствия 2.2, мы определяем совершенную конъюнктивную форму.

Для первой строки таблицы, которая соответствует нулевому набору функции 000, мы находим составляющую нуля. Выполняя аналогичные операции для второй, третьей и пятой строк, мы определяем желаемую идеальную функцию PFF:

Следует отметить, что для функций, количество единичных наборов которых превышает количество нулевых наборов, более компактной является их запись в виде SCFF и наоборот.

Стандартное основание. Элементарные формулы — литералы. Элементарное соединение (дизъюнкция). Дизъюнктивное (соединительное) Нормальная форма и совершенная форма. Теорема: Любая логическая функция, отличная от 0 (от 1), присутствует в форме SDNF (SCPF). Полнота стандартной базы. Примеры полных баз: основа Жегалкина, штрих-код Шеффера, стрелка пирса.

Стандартное основание — Это набор из трех исходных операций булевой алгебры: сложение (ассоциация), умножение (пересечение) и отрицание.

Здесь мы будем называть литералом Переменная x или ее отрицание X и обозначение x. Булево пересечение нескольких литералов, определяемых различными переменными, т.е.выражение вида x = x 1 x 2.. . X l, называется Элементарное соединение . Требование, чтобы все переменные были разными, обусловлено следующим. Если в конъюнкции несколько одинаковых литералов, то за счет коммутации, ассоциативности и идемпотенциала конъюнкцию можно перевести в эквивалентную формулу, оставить только один литерал (например, x 1 x 1 = x 1).Если в конъюнкцию входит переменная и ее отрицание, то формула эквивалентна константе 0, так как x x = 0 и для любой формулы y имеем y x x = 0.

Дизъюнкция нескольких элементарных союзов называется дизъюнктивная нормальная форма или DNF. . Например,

х 1 х 3 + х 2 х 3 х 4 + х 1 х 2 х 3 х 5.

Если состав переменных в каждом элементарном соединении этой DNF одинаков, то DNF называется perfect .Приведенный выше пример — это DNF, который не идеален. Напротив, формула

х 1 х 2 х 3 х 4 + х 1 х 2 х 3 х 4 + х 1 х 2 х 3 х 4

есть совершенная форма.

Поскольку в булевой алгебре сложение и умножение — симметричные операции и всегда могут интерпретироваться сложением как умножение, а умножение как сложение, существует двойственное понятие — конъюнктивная нормальная форма ( КНФ. ), который представляет собой соединение элементарных дизъюнкций, и совершенная конъюнктивная форма ( SKFF ).Из принципа двойственности для симметричных полукольцов следует, что любое утверждение относительно DNF соответствует двойственному утверждению относительно CNF, которое получается заменой сложения (дизъюнкции) умножением, умножения (конъюнкции) добавлением, константы 0 константа 1, константа 1 константа 0, отношение порядка двойного (обратного) порядка. Поэтому далее мы сосредоточимся на изучении только ДНФ.

Теорема 1.4. Любая логическая функция, отличная от Постоянного 0 Представителя в форме SDNF.

◀ Договариваемся под x σ понимать формулу X, если σ = 1, и формулу X, если σ = 0. Пусть функция f (y 1, .., Yn) принимает значение 1 на векторе ( T 1, …, TN) (такой вектор называется составляющей Unity ). Тогда элементарная конъюнкция также принимает значение 1 на этом наборе, но обращается в ноль на всех других N-мерных логических векторах. Рассмотрим формулу

, в котором сумма (слияние) применяется ко всем тем наборам (T 1, .., Tn) значений аргументов, на которых указанная функция принимает значение 1.Учтите, что многие такие наборы не пустые, поэтому в сумме присутствует хотя бы одна Скорость.

Легко заметить, что формула φ относится к 1 с теми и только теми значениями переменных, в которых указана функция. Итак, формула ψ представляет функцию f.

Следствие 1.1. Стандартная база в комплекте.

◀ Действительно, если функция не является константой 0, то она представляется либо в форме SDNF, которая является формулой над стандартным базисом.Константу 0 можно представить, например, формулой F (x 1, x 2, …, X n) = x 1 x 1.

Пример 1.2. Рассмотрим функцию трех переменных M (x 1, x 2, x 3) (таблица 1.4), называемую мажоритарными функциями ̆. Эта функция принимает значение 1, если более половины ее аргументов имеют значение 1. Поэтому ее часто называют функцией голосования. Строим для нее NDNF.

Полнота стандартной базы позволяет выбрать другие полные функции функций.Полноту множества F можно установить из следующих соображений. Предположим, что каждая из трех функций стандартного BUZISS будет представлять формулу над f. Тогда по теореме 1.3 индекс F будет полным.

Пример 1.3. Многие операции сложения модуля 2, умножения и константы 1 вызывают базис Жегалкина . Сложение модуля 2 и умножение — основные операции кольца Z2, составленные с их помощью выражения являются многочленами над кольцом Z2.Connect 1 В этом случае это необходимо для регистрации бесплатного члена. Поскольку xx = x, то все множители в многочлене имеют степень 1. Поэтому при записи многочлена можно обойтись без понятия степени. Примеры формул над базой Жегалкина:

xy⊕x⊕y, x⊕1, xyz⊕xz⊕x⊕y⊕1.

Любая такая формула называется полиномом жегалкина. Фактически полином Жегалкина является полиномом над кольцом Z2.

Легко построить формулы над базисом жегалкина, представляющие операции сложения и отрицания стандартного базиса (умножение двух базисов в целом):

x + y = x⊕y⊕xy, x = x⊕1.

Следовательно, основа Жегалкина — это полный комплект.
Можно показать, что для любой логической функции Полиник Жегалкин определенно определен

(Точнее с точностью порядка составных частей). Коэффициенты многочленов Жегалкине с небольшим количеством переменных могут быть найдены методом неопределенных коэффициентов.

Пример 1.4. Считай многое от единственной функции — росчерка читателя *. Это очень много, что следует из следующих легко проверяемых тождеств:

х = х | х, ху = х | у = (х | у) | (x | y), x + y = x | у = (х | х) | (у | у).

Пример 1.5. Основа, состоящая из единственной функции — стрелок пирса, тоже в комплекте. Проверка аналогична случаю накопительного хода. Однако такой вывод можно сделать на основе принципа двойственности для симметричных полукольцов.

* Шаферера — бинарный штрих-код, а не ассоциативная операция. Поэтому при использовании инфиксной формы следует быть внимательным: результат зависит от порядка выполнения операций. В этом случае рекомендуется явно указывать порядок операций с помощью скобок, например, запись (x | y) | z, а не x | Y | z, хотя обе формы эквивалентны.

Пример. Найдите формулу CNF

~ ~

Совершенная дизъюнктивная нормальная форма SDNF может быть построена с использованием следующего алгоритма:

1. = 1. Алгоритм DNF

2. = 2. Алгоритм DNF

3. = 3. Алгоритм DNF

4. = 4. Алгоритм DNF

5. Младшие идентично ложные термины, т. Е.

6. Пополнить остальные компоненты недостающих переменных

7. Повторить пункт 4.

Пример. Найдите формулу CDFF.

~

Для построения SCPF можно использовать следующую схему:

Пример. Найдите формулу CDFF.

~

Известно (теоремы 2.11, 2.12), что SDNF и SCPF определенно определены, и это означает, что они могут быть построены на таблице истинности формулы.

Схема построения SDNF и SCFF на таблице истинности показана ниже для формулы ~:

			~
			1 0 1 0 1 1 0 1	SDNF; SKFF.

2.2. Задание.

2.2.1 Ниже приведены логические выражения. Максимально упростите выражения своей версии, используя законы Bul Logic.Затем с помощью таблиц истинности сравните ваше упрощенное выражение с исходным.

2.2.2. Выясните вопрос об эквивалентности F 1 и F 2, сообщив их SDNF (Таблица 1).

2.2.3. Найдите двойственную функцию для F 3 по обобщенному и логическому принципу (таблица 1). Сравните полученные результаты.

2.3. Контрольные вопросы.

2.3.1. Дайте определение утверждению.

2.3.2. Перечислите основные операции над выпиской.

2.3.3. Что такое таблица истинности?

2.3.4. Создайте таблицы истинности для следующих формул:

~ ~ ~;

2.3.5. Учитывая договоренности о порядке выполнения операций, в формулах опустить «лишние» скобки и знак «»:

;

2.3.6. Применяя эквивалентные преобразования, докажите тождественную истинность формул:

2.3.7. Найдите двойные формулы:

)

2.3.8. Привести к идеальным формулам DNF (CDNF):

~

2.3.9. Привести к идеальным формулам CNF (SKPF):

~

Лабораторная работа № 3

Тема: «Минимизация логических функций. Логика»

Цель: Приобретение практических навыков работы с методами минимизации логических функций.

3.1. Теоретическая информация.

Минимальные формы

Как было показано в, любая функция бушеля представляется в совершенной нормальной форме (дизъюнктивной или конъюнктивной).Более того, такое представление является первым шагом перехода от табличной задачи функции к ее аналитическому выражению. В дальнейшем мы будем исходить из дизъюнктивной формы, а соответствующие результаты для конъюнктивной формы будут получены на основе принципа двойственности.

Каноническая задача синтеза логических схем в булевом базисе сводится к минимизации булевых функций, т.е.к представлению их в дизъюнктивной нормальной форме, содержащей наименьшее количество букв (переменных и их отрицаний).Такие формы называются минимальными. При каноническом синтезе предполагается, что на входы схемы поступают как сигналы, так и их инверсии.

Формула, представленная в дизъюнктивной нормальной форме, упрощается за счет многократного использования операции склеивания и операции поглощения и (двойные тождества для конъюнктивной нормальной формы: и). Здесь под и вы можете понять любую формулу булевой алгебры. В результате мы приходим к такому аналитическому выражению, когда дальнейшие преобразования уже невозможны, т.е.е. Получаем тупиковую форму.

Среди тупиковых форм есть минимальная дизъюнктивная форма, и она может не использоваться. Чтобы убедиться, что эта тупиковая форма минимальна, необходимо найти все тупиковые формы и сравнить их по количеству букв в них.

Пусть, например, функция задана в идеальной нормальной дизъюнктивной форме:

Группирование элементов и применение операции склейки у нас есть.

При другом методе группировки получаем:

Обе тупиковые формы не минимальны.Чтобы получить минимальную форму, нужно предположить, что один член повторяется в исходной формуле (это всегда можно сделать, потому что). В первом случае такой член может быть. Потом. Добавляя участника, мы получаем:. Пройдя все возможные варианты, вы можете убедиться, что последние две формы минимальны.

Работа с формулами на таком уровне похожа на блуждание по точкам. Процесс поиска минимальных форм становится более наглядным и целенаправленным, если вы используете некоторые графические и аналитические представления и символику, специально разработанную для этой цели.

Многокомпонентный кубический

Каждую вершину объемного куба можно поставить в соответствии с Составной частью единицы. Следовательно, подмножество отмеченных вершин является отображением на размерной Кубе булевой функции из переменных в совершенной дизъюнктивной нормальной форме. На рис. 3.1 показано такое отображение для функции пункта 3.7.

Рис.3.1 Отображение трехмерных объектов Кубы, представленных в SDNF

Чтобы отобразить функцию из переменных, представленных в любой дизъюнктивной нормальной форме, необходимо установить соответствие между ее минитерами и элементами размерного куба.

MiniTer (-1) -go rank можно рассматривать как результат склейки двух miniternal rank (составляющих единиц), т.е. On-мерной Кубы, он соответствует замене двух вершин, которые различаются только значениями \ u200b. координаты, соединяющей эти вершины, ребро (говорят, что ребро покрывает вершины инцидентов). Таким образом, порядок minimets (-1) -go соответствует реберно-мерному кубу. Точно так же соответствие miniters (-2) -go порядка — это ребра размерного куба, каждое из которых покрывает четыре вершины (и четыре ребра).

Элементы объемного куба, характеризующиеся размерами, называются -кубами. Итак, вершины — 0 кубов, ребра — 1 кубик, грани — 2 куба и т. Д. Обобщая приведенные выше рассуждения, можно предположить, что miniterm () -go ранг в дизъюнктивной нормальной форме для функции переменных отображается -cub, и каждая шишка покрывает всех тех детенышей меньших размеров, которые связаны с его вершинами. В качестве примера на рис. 3.2 заявлены функции трех переменных. Здесь минтеры и соответствуют 1-м кубам (), а минтеры отображаются 2-кубическими ().

Рис. 3.2 Функциональное покрытие

Итак, любая дизъюнктивная нормальная форма отображается на — мерном кубинском множестве — кубах, которые покрывают все вершины, соответствующие Составляющим единицы (0 Куба). Верно и обратное утверждение: если некоторый set -cube покрывает множество всех вершин, соответствующих единичным значениям функции, то дизъюнкция соответствующих этим кускам минитеров является выражением этой функции в дизъюнктивном виде. нормальная форма.Говорят, что такая комбинация -кубов (или соответствующих минитеров) образует функциональное покрытие.

Стремление к минимальной форме интуитивно понимается как поиск такого покрытия, количество кубиков которого было бы меньше, а их размер — больше. Покрытие, соответствующее минимальной форме, называется минимальным покрытием. Например, функции покрытия на рис. 3.3 соответствуют минимальным формам и.

Рис. 3.3 Функциональные крышки.

левый -; справа —

Отображение функции на трехмерном Кубе визуально и просто когда. Четырехмерный куб можно изобразить так, как показано на рис. 3.4, где отображается функция четырех переменных и ее минимальное покрытие, соответствующее выражению. . Использование этого метода, когда требуются настолько сложные конструкции, что теряются все его преимущества.

Рис. 3.4 Отображение функции на четырехмерном кубе

Гвоздики

В другом методе графического отображения логических функций используются гвоздик, карты , которые представляют собой специально организованные таблицы соответствия.Столбцы и строки таблицы соответствуют всевозможным наборам, содержащим не более двух значений переменных, и эти наборы расположены таким образом, что каждое последующее значение отличается от предыдущего значения только одной из переменных. Благодаря этому соседние ячейки горизонтальной таблицы и вертикальные ячейки различаются значением только одной переменной. Ячейки, расположенные по краям стола, также считаются смежными и обладают этим свойством. На рис. 3.5 показаны карты Карно для двух, трех, четырех переменных.

Рис. 3.5 Карты Карно для двух, трех и четырех переменных

Как и в обычных таблицах истинности, ячейки наборов, на которых функция принимает значение 1, заполнены единицами измерения (нули обычно не подходят, они соответствуют пустым ячейкам). Например, на рис. 3.6, но Карта автомобиля может быть показана для функции, отображение которой на четырехмерной Кубе приведено на рис. 3.4. Для упрощения строки и столбцы, соответствующие значениям 1 для определенной переменной, выделены фигурной скобкой с обозначением этой переменной.

Рис. 3.6 Отображение на карте Карно Four Variables

(а) и его минимальное покрытие (б)

Между функциями отображения на n. — Великолепная Куба и на карте Карны есть взаимно недвусмысленное соответствие. На карте Карно с. -Куба соответствует комбинации 2 соседних ячеек, размещенных в строке, столбце, квадрате или прямоугольнике (с учетом соседства противоположных краев карты). Следовательно, все положения, изложенные выше (см. Стр. многокомпонентный кубик ), справедливы для карт карно. Итак, на рис. 3.6, б. Показано покрытие блоков карты, соответствующее минимальной дизъюнктивной форме. Рассматриваемая функция.

Чтение майнитеров с карты carno осуществляется по простому правилу.Клетки образующие с. -cub, дать miniter (n-s) -Ho rank, в котором те переменные (n-s) , которые сохраняют те же значения, что и эти s. -куб, а сами переменные соответствуют значению 1, а значения 0 запрещены. Переменные, не сохраняющие свои значения с. -куб, минитерма нет. Различные способы чтения приводят к разному представлению функции в дизъюнктивной нормальной форме (крайняя правая минимальная) (рис.3.7).

Использование карточек Carno требует более простых конструкций по сравнению с дисплеем на n. — Заслуга Кубы, особенно в случае четырех переменных. Для отображения функций пяти переменных используются две карты карно для четырех переменных, а для функции шести переменных — четыре таких карты. При дальнейшем увеличении количества переменных карты карно становится практически непригодным.

Известных в литературе waich карт Они отличаются только другим порядком наборов переменных и обладают теми же свойствами, что и карты Карно.

Кубический комплекс

Несостоятельность графических методов с большим количеством переменных компенсируется различными аналитическими методами представления булевых функций. Одна из этих идей — комплекс кубов , использующий терминологию многомерного логического пространства в сочетании со специально разработанной символикой.

). 0-Кубы, соответствующие составляющим единицам, представлены наборами переменных, на которых функция равна единице.Очевидно в записи

Рис. 3.8 Сложные кубы, функция трех переменных (, но ) и его символическое представление ( b. )

Комплекс куба формирует максимальных функций, покрывающих . Не считая всех тех с. -Кубики, покрытые кубиками наибольшей размерности, получаем покрытия, соответствующие тупиковым формам. Итак, для рассматриваемого примера (рис. 3.8) имеем тупиковое покрытие

,

, что соответствует функции.В этом случае такое покрытие минимальное.

Для двух булевых функций операция дизъюнкции соответствует комбинации их кубических комплексов, а операция конъюнкции — это пересечение кубических комплексов. Отказ от функции соответствует сложению комплекса кубов, т.е. определяется всеми вершинами, на которых функция принимает значение 0. Таким образом, существует взаимно однозначное соответствие (изоморфизм) между алгеброй булевых функций и булевы множества, представляющие кубические комплексы.

Представление функций в виде комплексов кубов менее понятно, однако его наиболее важные преимущества заключаются в том, что при использовании вычислительных машин снимаются ограничения на количество переменных и упрощается кодирование информации.

Минимизация логических функций

Постановка задачи. Минимизация схемы в булевом базисе сводится к поиску минимальной дизъюнктивной формы, соответствующей минимальному покрытию.Общее количество букв, входящих в нормальную форму, выражается ценой покрытия. , где — число — кубики, образующие покрытие этой функции от n переменных. Минимальное покрытие характеризуется наименьшим значением его цены.

Обычно задача минимизации решается в два этапа. Во-первых, они ищут уменьшенное покрытие, которое включает в себя все максимальные размеры, но не содержит ни одного куба, покрывающего любой куб этого покрытия. Соответствующая дизъюнктивная нормальная форма называется сокращенной, а ее минитеры — простыми импликантами.Для этой функции сокращенное покрытие является единственным, но оно может быть избыточным из-за того, что некоторые кубы покрыты наборами других кубов.

На втором этапе происходит переход от сокращенных дизъюнктивных нормальных форм к тупиковым, из которых выбираются минимальные формы. Тупические формы образуются путем исключения из сокращенного покрытия всех избыточных кубов, без которого оставшийся набор кубиков по-прежнему образует покрытие этой функции, но, за дальнейшим исключением любого из кубов, он больше не покрывает наборы всех вершин. соответствующие единичным значениям функции, т.е.е. перестает быть покрытием.

Сокращенный куб покрытия, который покрывает вершины этой функции, не покрытый другими кубами, не может быть избыточным и всегда будет иметь минимальное покрытие. Такой куб, как и соответствующая имипиканта, называется экстремальным (существенным импликантом), а покрываемые им вершины — сокращенными вершинами. Многие экстремали составляют ядро ​​покрытий, понятно, что при переходе от сокращенного покрытия к минимуму, прежде всего, необходимо выделить экстремаль.Если многие экстремали не образуют покрытий, это дополняют нанесением покрытий сокращенными кубиками покрытия.

Указанные определения проиллюстрированы на рис. 3.9, где уменьшенное покрытие (см. Рис. 3.9a, ) и минимальные покрытия (рис. 3.9б) и (см. Рис. 3.9, б) выражаются следующим образом.

Нормальная форма Логическая формула не содержит знаков иммунизации, эквивалентности и отрицания неэлементарных формул.

Нормальная форма существует двух типов:

конъюнктивная нормальная форма (KNF) — соединение нескольких дизъюнкций, например, $ \ left (A \ Vee \ Overline (B) \ Vee C \ \ Вправо) \ КЛИН \ ВЛЕВО (A \ Vee C \ Right) $;

diaunctive Normal Form (DNF) — дизъюнкция нескольких союзов, например, $ \ left (A \ Wedge \ Overline (B) \ WEDGE C \ RIGHT) \ Vee \ Left (B \ \ Клин C \\ Вправо) $.

SKFF

Идеальное соединение нормальной формы (SCFF) — Это CNF, удовлетворяющая трем условиям:

не содержит такой же элементарной дизъюнкции;

ни одна из дизъюнкций не содержит одинаковых переменных;

каждая элементарная дизъюнкция содержит каждую переменную из тех, что включены в этот PFF.

Любая логическая формула, которая не является тождественной истинной, может быть представлена ​​в SKFF.

Правила построения SCFF для таблицы истинности

Для каждого набора переменных, в котором функция равна 0, записывается сумма, а переменные с 1 берутся с отрицанием.

SDNF.

Совершенная дизъюнктивная нормальная форма (SDNF) — Это ДНФ, удовлетворяющая трем условиям:

не содержит одинаковых элементарных союзов;

ни одно из союзов не содержит одинаковых переменных;

каждая элементарная конъюнкция содержит каждую переменную из тех, что включены в эту DNF, причем в том же порядке.

Любая логическая формула, которая не является тождественно ложной, может быть представлена ​​в SDNF, кроме единственного способа.

Правила построения SDNF на таблице истинности

Для каждого набора переменных, в котором функция равна 1, записывается произведение, а переменные, имеющие значение 0, берутся с отрицанием.

Примеры поиска SCPF и SDNF

Пример 1.

Запишите логическую функцию по ее таблице истинности:

Рисунок 1.

Решение:

Мы используем Правило построения SDNF:

Рисунок 2.

Мы получим SDNF:

Мы используем Правило построения SCPF.

Конъюнктивная нормальная форма удобна для автоматического доказательства теорем. Любая логическая формула может быть дана PFF. Для этого можно использовать: закон двойного отрицания, закон де Морганы, распределение.

Энциклопедический YouTube.

• 1 / 5

  Формулы в PFF :

  ¬ A ∧ (B ∨ C), (\ DisplayStyle \ NEG A \ WEDGE (B \ Vee C),) (A ∨ B) ∧ (¬ B ∨ C ∨ ¬ D) ∧ (D ∨ ¬ E), (\ DisplayStyle (A \ VEE B) \ WEDGE (\ NEG B \ Vee C \ Vee \ \ NEG D) \\ КЛИН (D \\ Vee \\ NEG E),) А ∧ б.(\ DisplayStyle A \ Wedge B.)

  Формулы отсутствуют в PFF :

  ¬ (B ∨ C), (\ DisplayStyle \ NEG (B \ Vee C),) (A ∧ B) ∨ C, (\ DisplayStyle (A \ WEDGE B) \ Vee C,) A ∧ (B ∨ (D ∧ E)). (\ DisplayStyle A \ WEDGE (B \ Vee (D \ Wedge E)).)

  Но эти 3 формулы не эквивалентны следующим формулам в PBF:

  ¬ В ∧ ¬ С, (\ Displaystyle \ NEG B \ клин \ NEG C,) (A ∨ C) ∧ (B ∨ C), (\ DisplayStyle (A \ Vee C) \ WEDGE (B \ Vee C),) A ∧ (B ∨ D) ∧ (B ∨ E).(\ DisplayStyle A \ Wedge (B \ Vee D) \ WEDGE (B \ Vee E).)

  Строительство CNF.

  Алгоритм построения украинского ПБФ

  1) избавиться от всех логических операций, содержащихся в формуле, заменив их основными: соединение, дизъюнкция, отрицание. Это можно сделать с помощью эквивалентных формул:

  A → B = ¬ A ∨ B, (\ DisplayStyle A \ Rightarrow B = \ NEG A \ VEE B,) A ↔ B = (¬ A ∨ B) ∧ (A ∨ ¬ B). (\ DisplayStyle A \ Leftrightarrow B = (\ NEG A \ VEE B) \ Wedge (A \ Vee \ NEG B).)

  2) Заменить знак отрицания, относящийся ко всему выражению, знаки отрицания, относящиеся к определенным операторам переменных, на основе формул:

  ¬ (a ∨ b) = ¬ a ∧ ¬ b, (\ displaystyle \ NEG (A \ Vee B) = \ NEG A \ WEDGE \ NEG B,) ¬ (a ∧ b) = ¬ A ∨ ¬ b. (\ DisplayStyle \ NEG (A \ WEDGE B) = \ NEG A \ Vee \ NEG B.)

  3) избавиться от знаков двойного отрицания.

  4) При необходимости применять к операциям соединения и дизъюнкции свойств распределения и формул поглощения.

  Пример построения CNF.

  Приведем формулу PFF

  F = (x → y) ∧ ((¬ y → z) → ¬ x). (\ DisplayStyle F = (X \ Rightarrow y) \ WEDGE ((\ NEG Y \ Rightarrow z) \ Rightarrow \ NEG X).)

  Преобразуем формулу F (\\ DisplayStyle F) в формулу, которая не содержит → (\\ DISPLAYSTYLE \\ RIGHTARROW):

  F = (¬ x ∨ y) ∧ (¬ (¬ y → z) ∨ ¬ x) = (¬ x ∨ y) ∧ (¬ (¬ ¬ y ∨ z) ∨ ¬ x). (\ DisplayStyle F = (\ NEG X \ VEE Y) \ Wedge (\ NEG (\ NEG Y \ Rightarrow z) \ vee \ neg x) = (\ NEG X \ \ VEE y) \\ WEDGE (\\ NEG (\\ NEG \\ В полученной формуле мы перенесем отрицание в переменные и уменьшим двойные отрицания:

  F = (¬ x ∨ y) ∧ ((¬ y ∧ ¬ z) ∨ ¬ x).(\ DisplayStyle F = (\ NEG X \ VEE Y) \ Wedge (((\ NEG Y \\ Wedge \ NEG Z) \ Vee \ NEG X).)

  Например, в 2-КПФ записана следующая формула:

  (A ∨ B) ∧ (¬ B ∨ C) ∧ (B ∨ ¬ C). (\ DisplayStyle (A \ Lor B) \ Land (\ NEG B \ LOR C) \ Land (B \ Lor \ NEG C).)

  Общее:

(PDF) Минимизация конъюнктивных нормальных форм булевых функций комбинаторным методом

ИНФОРМАЦИОННО-УПРАВЛЯЮЩИЕ СИСТЕМЫ:

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ

55 ТЕХНОЛОГИЧЕСКИЙ АУДИТ И ПРОИЗВОДСТВЕННЫЕ ЗАПИСИ — № 5/2 (43148), 2018

3780

Возможности.Возможностями дальнейшего исследования

комбинаторного метода может стать разработка

протокола для вычисления минимальных функций для симметричных

булевых функций.

Дополнительные возможности для практической реализации

комбинаторного метода минимизации CNF

булевых функций состоят в установлении новых критериев

комбинаторной оптимизации булевых функций, определяемых знаком минимальной функции и Boolean

Минимизация функций на полной таблице истинности.

Угрозы. Процесс минимизации КНФ булевых функций

комбинаторным методом не зависит от

процессов минимизации другими методами, поэтому

не существует угрозы отрицательного воздействия на объект

исследования внешних факторов.

Аналогом комбинаторного метода минимизации

КНФ булевых функций является алгебраический метод [18].

Алгебраический метод минимизации КНФ булевых функций лучше всего тем, что для него созданы уже заданные законы

упрощения, обнаруженные свойства и алгоритмы

минимизации булевых функций.Однако

алгебраический метод представляет собой словесную процедуру для оперативных преобразований

, которая в меньшей степени влияет на качество

минимизации по сравнению с образным преобразованием комбинаторного метода.

8. Выводы

1. Установлено, что минимизация CNF

булевых функций комбинаторным методом

основана на блок-схеме с повторением.Это таблица истинности

этой функции. Это позволяет сосредоточиться на принципе минимизации

в рамках протокола для вычисления

логической функции (в таблице истинности функции)

и, таким образом, отказаться от вспомогательных объектов, таких как карта Карно

, диаграммы Вейча. , ациклический граф, кубическое представление

и т.д.

2. Выявлено, что табличная организация

математического аппарата блок-схемы с повторением

позволяет получить больше информации об ортогональности,

смежности , уникальность блоков комбинаторной системы

и, как следствие, блоков таблицы истинности

этой функции.Эквивалентные образные преобразования по

своим свойствам обладают большой информационной емкостью, способной

заменить словесные процедуры алгебраических преобразований, в частности

, используя библиотеку протоколов для минимизации

CNF булевых функций.

3. Выявлено, что образные преобразования

упрощают процедуру установления знаков минимальной логической функции

(примеры 8–10), что гарантирует

оптимальное сокращение числа переменных логики

функционировать без потери своей функциональности.

4. Выявлено, что для достижения наилучшего результата булевой

минимизация функций может быть получена в ДНФ и в КНФ минимальной функции

(примеры 6, 8–11). Отсюда

следует, что минимизация данной функции должна быть

выполнена в двух нормальных формах — DNF и CNF, используя

полную таблицу истинности, а минимальная функция должна быть

, выбранной в соответствии с результатами минимизации две нормальные формы

— ДНФ и ЦНФ.

Литература

1. Ризник В.В., Соломко М.М. Минимизация булевых функций комбинаторным методом

// Технологический аудит и производство

Запасы. 2017. Т. 4, выпуск 2 (36). С. 49–64. doi: http: //

doi.org/10.15587/2312-8372.2017.108532

2. Ризник В., Соломко М. Применение алгебраической операции суперприлипания

переменных для минимизации булевых функций комбинаторным методом

// Аудит технологий и производства

Запасы.2017. Т. 6, выпуск 2 (38). С. 60–76. doi: http: //

doi.org/10.15587/2312-8372.2017.118336

3. Ризник В., Соломко М. Исследование 5-битных булевых функций mini-

протоколов преобразования комбинаторным методом // Технологический аудит

и производственные запасы. 2018. Т. 4, выпуск 2 (42). С. 41–52.

doi: http://doi.org/10.15587/2312-8372.2018.140351

4. Cepek O., Kucera P., Savicky P. Булевы функции с простым сертификатом

для сложности CNF // Discrete Applied Mathe —

мат.2012. Т. 160, выпуск 4-5. С. 365–382. doi: http://doi.org/

10.1016 / j.dam.2011.05.013

5. Хемаспандра Э., Шнор Х. Минимизация для обобщенных

булевых формул // Труды двадцать второй In-

международная совместная конференция по искусственному интеллекту. 2012.

С. 566–571.

6. Борос Э., Чепек О., Кучера П. Метод декомпозиции для CNF

доказательств минимальности // Теоретическая информатика.2013. Т. 510.

С. 111–126. doi: http://doi.org/10.1016/j.tcs.2013.09.016

7. Гурский С. Минимизация согласованных формул // WDS’11

Proceedings of Contributed Papers. Часть 1. 2011. С. 101–105.

8. Бернаскони А., Чириани В., Луччио Ф., Пагли Л. Трехуровневая логика

минимизация на основе функциональных закономерностей // IEEE Transac-

tions on Computer Aided Design of Integrated Circuits and

Systems .2003. Vol. 22. Вып. 8. С. 1005–1016. doi: http: //

doi.org/10.1109/tcad.2003.814950

9. Носрати М., Карими Р. Алгоритм минимизации булевых функций

на основе Graph DS // World Applied Program-

ming . 2011. Т. 1, вып. 3. Р. 209–214.

10. Валли М., Периясами д-р Р., Амудхавел Дж. Состояние правил минимизации булевых функций.2017.

Выпуск 12. С. 1322–1341. URL: http://www.jardcs.org/abstract.

php? Archiveid = 1323 #

11. Бояр Дж., Перальта Р. Новая минимальная комбинационная логика.

Метод замещения с приложениями к криптологии. Лекция

Заметки по информатике. Берлин: Springer, 2010. С. 178–189.

doi: http://doi.org/10.1007/978-3-642-13193-6_16

12. Фисер П., Томан Д. Быстрый минимизатор СОП для логических функций

, описанный во многих терминах продукта // 2009 12-я конференция Euromicro

по проектированию цифровых систем, архитектурам, методам

и инструментам.Patras, 2009. doi: http://doi.org/10.1109/dsd.2009.157

13. Пынько А. П. Минимальные секвенциальные исчисления для монотонных цепных конечно-

значных логик // Вестник раздела логики. 2014. Т. 43,

Выпуск 1-2. С. 99–112.

14. Пынько А. П. Минимизация КНФ частично-монотонных бу-

левых функций // Доповіді Национальной академии наук Украины.

2017. Вып. 3. С. 18–21.

15. Булевы функции. URL: http: // любая-книга.org / download / 88296.html

16. Рыцарь Б.Е. Новый метод минимизации логических функций в теоретико-множественном полиномиальном формате

. 1. Обобщенные правила упрощения кон-

переходов // Управляющие системы и машины.

2015. Вып. 2. С. 39–57. URL: http://dspace.nbuv.gov.ua/handle/

123456789/87194

17. Рыцарь Б.Е. Минимизация системы лохичных функций метод

паралельного розчепления конъюнктермив // Вісник Националь-

ноуниверситету «Львовская политехника».Радиоэлектроника

та телекомуникации. 2013. Выпуск 766. С. 18–27. URL: http: //

nbuv.gov.ua/UJRN/VNULPPT_2013_766_6

18. Мартынюк О. М. Основы дискуссионной математики. Конспект

лекций. Одесса: Одесский национальный политехнический университет:

Наука и техника, 2008. 300 с.

Ризник Владимир, д-р техн. Наук, профессор, De-

отдел автоматизированных систем управления, Национальный университет

Львовская политехника, Украина, е-mail: rvv @ polynet.lviv.ua, ORCID: http: //

orcid.org/0000-0002-3880-4595

Соломко Михаил, кандидат технических наук, доцент кафедры компьютерной инженерии, Национальный университет воды и окружающей среды

Инженерное дело, Ровно, Украина, e-mail: [email protected], ORCID:

http://orcid.org/0000-0003-0168-5657

Конъюнктивная нормальная форма логической функции. Дизъюнктивные и конъюнктивные совершенные нормальные формы

Обычный соединение называется соединение один или несколько переменных , в этот каждый соответствует переменная больше соответствует умножить на ( или сам , или ее отрицание ).

Например, простое соединение,

дизъюнктивная нормальная форма (DNF) называется дизъюнкция простая конъюнкция .

Например, выражение — DNF.

Perfect дизъюнктивная нормальная форма (SDNF) называется так дизъюнктивная нормальная форма , при включены все переменные данные список ( или сами , или их отказов ), более того в и один тот же хорошо .

Например, выражение — это DNF, но не SDNF. Выражение — SDNF.

Аналогичные определения (с заменой конъюнкции дизъюнкцией и наоборот) действительны для CNF и SKNF. Вот точные составы.

Обычный дизъюнкция называется дизъюнкция одна или несколько переменные , в это каждый 9028 9028 9028 9028 9028 9028 9028 умножить на ( или сам , или ее отрицание ) Например, выражение представляет собой простую дизъюнкцию,

Конъюнктив нормальный форма (CNF) называется конъюнкция простая дизъюнкция (например, выражение CNF).

Совершенная конъюнктивная нормальная форма (SCNF) — это CNF, в которой каждая простая дизъюнкция содержит все переменные данного списка (либо сами себя, либо их отрицания) и в том же порядке.

Например, выражение — СКНФ.

Вот алгоритмы переходов из одной формы в другую. Естественно, что в конкретных случаях (при определенном творческом подходе) использование алгоритмов более трудоемко, чем простые преобразования с использованием определенного типа заданной формы:

а) переход от DNF к CNF

Алгоритм этого перехода следующий: мы помещаем два отрицания поверх DNF и, используя правила де Моргана (не касаясь верхнего отрицания), мы возвращаем отрицание DNF обратно в DNF.В этом случае вы должны раскрыть скобки, используя правило поглощения (или правило Блейка). Отрицание (верхнее) полученного DNF (опять же по правилу де Моргана) сразу дает нам CNF:

Обратите внимание, что CNF также может быть получена из исходного выражения, если мы вынесем на за скобки;

б) переход с CNF на DNF

Этот переход осуществляется простым открытием скобок (здесь снова используется правило поглощения)

Таким образом, мы получили ДНФ.

Обратный переход (от SDNF к DNF) связан с проблемой минимизации DNF. Подробнее об этом будет сказано в гл. 5, здесь мы покажем, как упростить DNF (или SDNF) в соответствии с правилом Блейка. Этот DNF называется укороченный DNF;

c) сокращение DNF (или SDNF) правилом Blake

Применение этого правила состоит из двух частей:

Если среди непересекающихся термов в DNF есть термы, то ко всей дизъюнкции мы добавляем член TO 1 TO 2.Мы выполняем эту операцию несколько раз (она может быть последовательной, может быть одновременно) для всех возможных пар термов, а затем применяем обычное поглощение;

Если добавленный термин уже содержался в DNF, то его можно вообще отбросить, например,

или

Конечно, сокращенный DNF не определен однозначно, но все они содержат одинаковое количество букв (например, есть DNF, после применения к нему правила Блейка вы можете прийти к DNF, эквивалентному этому):

в) переход от ДНФ к СДНФ

Если переменная отсутствует в каком-либо простом соединении, например, z , вставьте в нее выражение, а затем разверните круглые скобки (в этом случае мы не записываем повторяющиеся непересекающиеся термины).Например:

г) переход от CNF к SKNF

Этот переход осуществляется аналогично предыдущему: если в простой дизъюнкции отсутствует какая-либо переменная (например, z , то мы добавляем к ней выражение (это не меняет саму дизъюнкцию), после чего мы раскрыть скобки, используя закон распределения):

Таким образом, SKNF получают из CNF.

Обратите внимание, что минимальный или сокращенный CNF обычно получается из соответствующего DNF.

Определение 1. Конъюнктивный моном (элементарная конъюнкция) от переменных называется конъюнкцией этих переменных или их отрицаниями.

например , является элементарным соединением.

Определение 2. Дизъюнкция мономов (элементарная дизъюнкция) от переменных называется дизъюнкцией этих переменных или их отрицаниями.

например , является элементарной дизъюнкцией.

Определение 3. Формула, эквивалентная данной формуле алгебры высказываний и являющаяся дизъюнкцией элементарных конъюнктивных мономов, называется дизъюнктивной нормальной формой (ДНФ) этой формулы.

Например, — DNF.

Определение 4. Формула, эквивалентная данной формуле алгебры высказываний и являющаяся конъюнкцией элементарных дизъюнктивных мономов, называется конъюнктивной нормальной формой (CNF) этой формулы.

например , — CNF.

Для каждой формулы алгебры высказываний можно найти набор дизъюнктивных и конъюнктивных нормальных форм.

Алгоритм построения нормальных форм

Используя эквивалентности алгебры логики, заменить все операции в формуле на базовые: конъюнкция, дизъюнкция, отрицание:

Избавьтесь от знаков двойного отрицания.

Примените, если необходимо, к операциям соединения и дизъюнкции свойства распределенности и формулы поглощения.

2.6. Совершенные дизъюнктивные и совершенные конъюнктивные нормальные формы

Любая логическая функция может иметь множество представлений в форме DNF и CNF. Особое место среди этих представлений занимают совершенные ДНФ (SDNF) и совершенные CNF (SKNF).

Определение 1. Совершенная дизъюнктивная нормальная форма (SDNF) — это ДНФ, в которой в каждом конъюнктивном мономе каждая переменная из набора встречается ровно один раз, и появляется либо сама по себе, либо ее отрицание.

Конструктивно SDNF для каждой формулы алгебры высказываний, приведенной к DNF, может быть определена следующим образом:

Определение 2. Совершенная дизъюнктивная нормальная форма (SDNF) формулы алгебры высказываний называется ее ДНФ, которая обладает следующими свойствами:

Определение 3. Совершенная конъюнктивная нормальная форма (СКНФ) — это КНФ, в которой в каждом дизъюнктивном мономе каждая переменная из набора встречается ровно один раз, и появляется либо сама по себе, либо ее отрицание.

Структурно SKNF для каждой формулы алгебры высказываний, приведенной к CNF, может быть определен следующим образом.

Определение 4. Совершенная конъюнктивная нормальная форма (СКНФ) данной формулы алгебры высказываний называется ее КНФ, которая удовлетворяет следующим свойствам.

Теорема 1. Каждая булева функция переменных, которая не является тождественно ложной, может быть представлена ​​в SDNF и, более того, уникальным образом.

Способы поиска SDNF

1-й способ

2-й способ

выберите строки, в которых формула принимает значение 1;

составляем дизъюнкцию конъюнкций при условии, что если переменная включена в конъюнкцию со значением 1, то мы записываем эту переменную, если со значением 0, то ее отрицание.Получаем SDNF.

Теорема 2. Каждая булева функция переменных, которая не является тождественно истинной, может быть представлена ​​в СКНФ, причем уникальным образом.

Способы поиска SKNF

1-й способ — с использованием эквивалентных преобразований:

2-й способ — с использованием таблиц истинности:

выберите строки, в которых формула принимает значение 0;

мы составляем конъюнкцию дизъюнкций при условии, что если в дизъюнкцию входит переменная со значением 0, то мы записываем эту переменную, если со значением 1, то ее отрицание.Получаем СКНФ.

Пример 1. Постройте функции CNF.

Решение

Исключим связь «» с помощью законов преобразования переменных:

= / законы де Моргана и двойное отрицание / =

/ законы распределения / =

Пример 2. Приведем формулу к DNF.

Решение

Выразим логические операции через, и:

= / относим отрицание к переменным и сводим двойные отрицания / =

= / закон распределения /.

Пример 3. Запишите формулу в DNF и SDNF.

Решение

Используя законы логики, приведем эту формулу к форме, содержащей только дизъюнкции элементарных союзов. Результирующая формула будет желаемой DNF:

Чтобы построить SDNF, мы составим таблицу истинности для этой формулы:

Мы отмечаем те строки таблицы, в которых формула (последний столбец) принимает значение 1. Для каждой такой строки мы выписываем формулу, которая истинна на множестве переменных данной строки:

строка 1 :;

строка 3 :;

строка 5 :.

Дизъюнкция этих трех формул примет значение 1 только на наборах переменных в строках 1, 3, 5 и, следовательно, будет желаемой идеальной дизъюнктивной нормальной формой (SDNF):

Пример 4. Bring формула СКНФ двумя способами:

а) с использованием эквивалентных преобразований;

б) с использованием таблицы истинности.

Решение:

Преобразуем вторую элементарную дизъюнкцию:

Формула:

б) составляем таблицу истинности для этой формулы:

Отмечаем те строки таблицы, в которых формула (последний столбец) принимает значение 0.Для каждой такой строки мы выписываем формулу, которая истинна на множестве переменных данной строки:

строка 2 :;

строка 6 :.

Соединение этих двух формул примет значение 0 только на наборах переменных в строках 2 и 6, и, следовательно, будет требуемой идеальной конъюнктивной нормальной формой (SCNF):

Вопросы и задачи для независимого решения

1 . С помощью эквивалентных преобразований переведите формулы в DNF:

2. С помощью эквивалентных преобразований перенесите формулы в CNF:

3.Используйте второй закон распределения для преобразования DNF в CNF:

a);

4. Преобразуйте заданные DNF в SDNF:

5. Преобразуйте заданные CNF в SKNF:

6. Для заданных логических формул создайте SDNF и SKNF двумя способами: используя эквивалентные преобразования и используя таблицу истинности.

б);

Стандартное основание. Элементарные формулы — это литералы. Элементарное соединение (дизъюнкция). Дизъюнктивная (конъюнктивная) нормальная форма и совершенная форма. Теорема: любая логическая функция, отличная от 0 (от 1), может быть представлена ​​в форме SDNF (SKNF).Полнота стандартной базы. Примеры полных основ: основа Жегалкина, штрих Шеффера, стрела Пирса.

Стандартное основание — это набор из трех начальных операций булевой алгебры: сложение (объединение), умножение (пересечение) и отрицание.

Здесь мы будем называть литералом переменную x или ее отрицание x и обозначим xˆ. Логическое пересечение нескольких литералов, определенных разными переменными, т.е. выражение вида X = xˆ 1 xˆ 2…. … xИ л называется элементарным соединением … Требование различий всех переменных обусловлено следующим. Если конъюнкция содержит несколько одинаковых литералов, то в силу коммутативности, ассоциативности и идемпотентности конъюнкции можно, переходя к эквивалентной формуле, оставить только один литерал (например, x 1 x 1 = x 1) . Если в конъюнкцию входит переменная и ее отрицание, то формула эквивалентна константе 0, так как x x = 0 и для любой формулы Y имеем Y x x = 0.

Дизъюнкция нескольких элементарных союзов называется дизъюнктивная нормальная форма или DNF … Например,

х 1 х 3 + х 2 х 3 х 4 + х 1 х 2 х 3 х 5.

Если состав переменных в каждом элементарном соединении данной DNF одинаков, то DNF называется perfect … Данный пример — DNF, что не идеально. Напротив, формула

х 1 х 2 х 3 х 4 + х 1 х 2 х 3 х 4 + х 1 х 2 х 3 х 4

есть совершенная форма.

Поскольку в булевой алгебре сложение и умножение являются симметричными операциями, и вы всегда можете интерпретировать сложение как умножение, а умножение как сложение, существует также двойственная концепция — конъюнктивная нормальная форма ( CNF ), который представляет собой соединение элементарных дизъюнкций, и совершенная конъюнктивная форма ( СКНФ ). Из принципа двойственности для симметричных полуколец следует, что любое утверждение о ДНФ соответствует двойственному утверждению о КНФ, которое получается заменой сложения (дизъюнкции) умножением, умножения (конъюнкции) на сложение, константы 0 на константу 1, константы 1 на константа 0, отношение порядка по двойственному (обратному) порядку.Поэтому в дальнейшем мы сосредоточимся на изучении только ДНФ.

Теорема 1.4. Любая логическая функция, кроме константы 0, может быть представлена ​​как SDNF.

◀ Условимся под x σ обозначать формулу x, если σ = 1, и формулу x, если σ = 0. Пусть функция f (y 1, …, Yn) принимает значение 1 на векторе ( t 1, …, Tn) (такой вектор называется составляющей единицы ). Тогда элементарная конъюнкция также принимает значение 1 на этом множестве, но обращается в нуль на всех других n-мерных булевых векторах.Рассмотрим формулу

, в котором сумма (объединение) распространяется на все те наборы (t 1, …, tn) значений аргументов, для которых данная функция принимает значение 1. Обратите внимание, что набор таких наборов не пуст, значит, в сумме есть хотя бы одно слагаемое.

Легко видеть, что формула Φ становится 1 для тех и только тех значений переменных, для которых рассматриваемая функция становится равной 1. Следовательно, формула function представляет функцию f.

Следствие 1.1. Стандартная база полная.

◀ Действительно, если функция не является константой 0, то она может быть представлена ​​либо в форме SDNF, которая является формулой на стандартном базисе. Константу 0 можно представить, например, формулой f (x 1, x 2, …, X n) = x 1 x 1.

Пример 1.2. Рассмотрим функцию трех переменных m (x 1, x 2, x 3) (таблица 1.4), называемую функцией большинства ̆. Эта функция принимает значение 1, если более половины ее аргументов равны 1.Поэтому ее часто называют функцией голосования. Давайте построим для него SDNF.

Полнота стандартной основы позволяет выбирать другие полные системы функций. Полноту множества F можно установить из следующих соображений. Предположим, что каждая из трех стандартных бизнес-функций представима формулой над F. Тогда по теореме 1.3 множество F полно.

Пример 1.3. Набор операций сложения по модулю 2, умножения и константы 1 называется базис Жегалкина … Сложение по модулю 2 и умножение являются основными операциями кольца Z2, составленные с их помощью выражения являются многочленами над кольцом Z2. Константа 1 в этом случае нужна для записи свободного члена. Поскольку xx = x, все множители в многочлене имеют степень 1. Поэтому при написании многочлена можно обойтись без понятия степени. Примеры формул над базисом Жегалкина:

xy⊕x⊕y, x⊕1, xyz⊕xz⊕x⊕y⊕1.

Любая такая формула называется полиномом Жегалкина.Фактически полином Жегалкина является полиномом над кольцом Z2.

Нетрудно построить формулы над базисом Жегалкина, представляющие операции сложения и отрицания стандартного базиса (умножение является общим для двух базисов):

x + y = x⊕y⊕xy, x = x⊕1.

Следовательно, основа Жегалкина — это полный комплект.
Можно показать, что для любой булевой функции полином Жегалкина определяется однозначно

(точнее, по порядку терминов).Коэффициенты полинома Жегалкина для небольшого числа переменных могут быть найдены методом неопределенных коэффициентов.

Пример 1.4. Рассмотрим набор одной функции, ход Schaeffer *. Этот набор является полным, что следует из следующих легко проверяемых тождеств:

х = х | х, ху = х | у = (х | у) | (x | y), x + y = x | у = (х | х) | (у | у).

Пример 1.5. Основа, состоящая из единственной функции, стрелки Пирса, также завершена.Проверка аналогична случаю удара Шеффера. Однако такой вывод можно сделать на основе принципа двойственности для симметричных полуколец.

* Штрих Шеффера — бинарная, но не ассоциативная операция. Поэтому при использовании инфиксной формы следует соблюдать осторожность: результат зависит от порядка выполнения операций. В этом случае рекомендуется явно указывать порядок операций с помощью круглых скобок, например, write (x | y) | z, а не x | y | z, хотя обе формы эквивалентны.

Пример. Найдите формулы CNF

~ ~

Совершенная дизъюнктивная нормальная форма SDNF может быть построена с использованием следующего алгоритма:

1. = 1. алгоритм DNF

2. = 2. алгоритма DNF

3. = 3. Алгоритм DNF

4. = 4. алгоритма DNF

5. Отбросьте идентично ложные термины, то есть термины формы

6. Пополнить оставшиеся члены недостающими переменными

7. Повторите шаг 4.

Пример. Найдите формулы SDNF.

~

Для построения СКНФ можно использовать следующую схему:

Пример. Найдите формулы SDNF.

~

Известно (теоремы 2.11, 2.12), что SDNF и SKNF определяются формулой однозначно и, следовательно, они могут быть построены из таблицы истинности формулы.

Схема построения SDNF и SKNF по таблице истинности приведена ниже для формулы ~:

			~
			1 0 1 0 1 1 0 1	SDNF; СКНФ.

2.2. Задание.

2.2.1 Ниже приведены логические выражения. Максимально упростите выражения вашего варианта, используя логические законы Буля.Затем используйте таблицы истинности, чтобы сравнить ваше упрощенное выражение с оригиналом.

2.2.2. Выясните вопрос об эквивалентности f 1 и f 2, сведя их к SDNF (Таблица 1).

2.2.3. Найдите двойственную функцию для f 3 в соответствии с обобщенным и булевым принципом (таблица 1). Сравните полученные результаты.

2.3. Контрольные вопросы.

2.3.1. Дайте определение утверждению.

2.3.2. Перечислите основные операции с оператором.

2.3.3. Что такое таблица истинности?

2.3.4. Создайте таблицы истинности для следующих формул:

~ ~ ~;

2.3.5. Учитывая соглашения о порядке операций, опустите «лишние» круглые скобки и знак «» в формулах:

;

2.3.6. Используя эквивалентные преобразования, докажите тождественную истинность формул:

2.3.7. Найдите двойные формулы:

)

2.3.8. Приведите следующие формулы к идеальной форме DNF (SDNF):

~

2.3.9. Приведите следующие формулы к идеальной форме CNF (SKNF):

~

Лабораторная работа № 3

Тема: «Минимизация булевых функций. Логика »

Цель: Приобретение практических навыков работы с методами минимизации булевых функций.

3.1. Теоретическая информация.

Минимальные формы

Как показано на, любая логическая функция может быть представлена ​​в совершенной нормальной форме (дизъюнктивной или конъюнктивной). Более того, такое представление — это первый шаг в переходе от табличного определения функции к ее аналитическому выражению. В дальнейшем мы будем исходить из дизъюнктивной формы, а соответствующие результаты для конъюнктивной формы получены на основе принципа двойственности.

Каноническая проблема синтеза логических схем в булевом базисе сводится к минимизации булевых функций, т.е.е. представить их в дизъюнктивной нормальной форме, содержащей наименьшее количество букв (переменных и их отрицаний). Такие формы называются минимальными. В каноническом синтезе предполагается, что на входы схемы поступают как сигналы, так и их инверсии.

Формула, представленная в дизъюнктивной нормальной форме, упрощается за счет многократного применения операции склеивания и операции поглощения и (двойные тождества для конъюнктивной нормальной формы: и). Здесь и можно понимать любую формулу булевой алгебры.В результате мы приходим к такому аналитическому выражению, когда дальнейшие преобразования уже невозможны, т.е. получаем тупиковую форму.

Среди тупиковых форм есть минимальная дизъюнктивная форма, и она не может быть уникальной. Чтобы убедиться, что заданная тупиковая форма минимальна, необходимо найти все тупиковые формы и сравнить их по количеству содержащихся в них букв.

Например, пусть функция задана в идеальной нормальной дизъюнктивной форме:

Группируем элементы и применяем операцию склеивания.

При другом способе группировки получаем:

Обе тупиковые формы не минимальны. Чтобы получить минимальную форму, нужно угадать повторить один член в исходной формуле (это всегда можно сделать, т.к.). В первом случае такой член может быть. Потом. Добавляя участника, мы получаем :. Перебрав все возможные варианты, вы можете убедиться, что последние две формы минимальны.

Работа с формулами на этом уровне похожа на блуждание в темноте. Процесс поиска минимальных форм станет более наглядным и целенаправленным, если мы будем использовать некоторые графические и аналитические представления и символы, специально предназначенные для этой цели.

Многомерный куб

Каждая вершина -мерного куба может быть связана с единичным компонентом. Следовательно, подмножество отмеченных вершин является отображением на -мерном кубе булевой функции переменных в совершенной дизъюнктивной нормальной форме. На рис. 3.1 показывает такое отображение для функции из раздела 3.7.

Рис. 3.1 Отображение на трехмерном кубе функции, представленной в SDNF

Чтобы отобразить функцию переменных, представленную в любой дизъюнктивной нормальной форме, необходимо установить соответствие между ее минитермами и элементами -мерного куба.

Минитерм (-1) -го ранга можно рассматривать как результат склейки двух минитермов -го ранга (составляющих единицы), т.е. на -мерном кубе это соответствует замене двух вершин, которые отличаются только значения координаты, соединяющей эти вершины ребром (говорят, что ребро покрывает инцидентные вершины). Таким образом, минитерммы (-1) -го порядка соответствуют ребрам -мерного куба. Аналогичным образом устанавливается соответствие минитерм (-2) -го порядка граням -мерного куба, каждая из которых покрывает четыре вершины (и четыре ребра).

Элементы -мерного куба, характеризующиеся размерами, называются -кубами. Итак, вершины — это 0-кубы, ребра — 1-кубы, грани — 2-кубы и т. Д. Обобщая приведенные выше рассуждения, можно предположить, что miniterm () -го ранга в дизъюнктивной нормальной форме для функции переменных отображается с помощью -куба, и каждый -куб покрывает все те -кубы самого низкого измерения, которые связаны с его вершинами. В качестве примера на рис. 3.2 показано отображение функции трех переменных.Здесь miniterms и соответствуют 1-кубам (), а miniterms отображаются как 2-кубы ().

Рисунок 3.2 Охват функций

Итак, любая дизъюнктивная нормальная форма отображается на -мерном кубе набором -кубов, которые покрывают все вершины, соответствующие составляющим единицы (0-куб). Верно и обратное: если некоторый набор -кубов покрывает множество всех вершин, соответствующих единичным значениям функции, то дизъюнкция мини-термов, соответствующих этим -кубам, является выражением этой функции в дизъюнктивной нормальной форме .Говорят, что такой набор -кубов (или соответствующих miniterms) образует покрытие функции.

Стремление к минимальной форме интуитивно понимается как поиск такого покрытия, количество -кубов которого было бы меньше, а их размер — больше. Покрытие, соответствующее минимальной форме, называется минимальным покрытием. Например, для функции покрытие на рис. 3.3 соответствует минимальным формам и.

Рисунок: 3.3 крышки функций

левый -; справа —

Отображение функции на -мерном кубе для. Четырехмерный куб можно нарисовать, как показано на рис. 3.4, где функция четырех переменных и ее минимальное покрытие, соответствующее выражению … Использование этого метода требует таких сложных конструкций, что все его преимущества теряются.

Рисунок: 3.4 Отображение функций на четырехмерном кубе

Карты Карно

Другой метод графического представления логических функций использует карт Карно , которые представляют собой специально организованные справочные таблицы.Столбцы и строки таблицы соответствуют всем возможным наборам значений не более двух переменных, и эти множества расположены в таком порядке, что каждый последующий отличается от предыдущего на значение только одной из переменные. Благодаря этому как по горизонтали, так и по вертикали соседние ячейки таблицы отличаются значением только одной переменной. Ячейки, расположенные по краям таблицы, также считаются смежными и обладают этим свойством. На рис. 3.5 показаны диаграммы Карно для двух, трех, четырех переменных.

Рисунок: 3.5 Карты Карно для двух, трех и четырех переменных

Как и в обычных таблицах истинности, ячейки наборов, на которых функция принимает значение 1, заполняются единицами (нули обычно не помещаются, они соответствуют пустым ячейкам). Например, на рис. 3.6, a показывает карту Карно для функции, отображение которой на четырехмерном кубе показано на рис. 3.4. Для простоты строки и столбцы, соответствующие значениям 1 для некоторой переменной, заключены в фигурные скобки с обозначением этой переменной.

Рисунок: 3.6 Отображение функции четырех переменных на диаграмме Карно

(а) и его минимальное покрытие (б)

Между отображениями функций на n -мерном кубе и на карте Карно существует взаимно однозначное соответствие. На карте Карно s -куб соответствует набору из 2-х соседних ячеек, расположенных в строке, столбце, квадрате или прямоугольнике (с учетом близости противоположных краев карты).Следовательно, все положения, изложенные выше (см. Стр. многомерный куб ), действительны для карт Карно. Итак, на рис. 3.6, b показывает покрытие единиц карты, соответствующее минимальной дизъюнктивной форме рассматриваемой функции.

Считывание минитерм с карты Карно осуществляется по простому правилу. Ячейки, которые образуют s -куб, дают miniter (n — s) -й ранг, который включает те переменные (n — s) , которые хранят те же значения, что и этот s -куб, где значение 1 соответствует самим переменным, а значения 0 — их отрицаниям.Переменные, не хранящие своих значений для s -куб, в miniterm отсутствуют. Различные способы чтения приводят к разному представлению функции в дизъюнктивной нормальной форме (крайняя правая — минимальная) (рис. 3.7).

Использование карт Карно требует более простых конструкций, чем отображение на n -мерном кубе, особенно в случае четырех переменных. Для отображения функций пяти переменных используются две карты Карно для четырех переменных, а для функции шести переменных используются четыре таких карты.При дальнейшем увеличении числа переменных карты Карно становятся практически непригодными.

Известные в литературе карты Weich отличаются только другим порядком наборов значений переменных и имеют те же свойства, что и карты Карно.

Комплекс кубиков

Несогласованность графических методов с большим количеством переменных компенсируется различными аналитическими методами представления булевых функций. Одним из таких представлений является комплекс кубов , использующий терминологию многомерного логического пространства в сочетании со специально разработанной символикой.

). 0-кубы, соответствующие составляющим единицы, представлены наборами значений переменных, на которых функция равна единице. Очевидно в записи

Рисунок: 3.8 Комплекс кубов функции трех переменных ( a ) и его символьное представление ( b )

Комплекс кубов образует максимальное покрытие функций … Исключив из него все те s -кубов, которые покрыты кубами наибольшей размерности, мы получим покрытия, соответствующие тупиковым формам.Итак, для рассматриваемого примера (рис. 3.8) имеем заглушку тупиковую

,

, что соответствует функции … В этом случае и это покрытие минимально.

Для двух булевых функций операция дизъюнкции соответствует объединению их комплексов кубов, а операция соединения соответствует пересечению комплексов кубов. Отрицание функции соответствует дополнению комплекса кубов, т.е. определяется всеми вершинами, в которых функция принимает значение 0.Таким образом, существует взаимно однозначное соответствие (изоморфизм) между алгеброй булевых функций и булевыми множествами, представляющими комплексы кубов.

Представление функции в виде комплексов кубов менее понятно, но его наиболее важные преимущества заключаются в том, что он снимает ограничения на количество переменных и упрощает кодирование информации при использовании компьютеров.

Минимизация логических функций

Постановка задачи. Минимизация схемы в булевом базисе сводится к нахождению минимальной дизъюнктивной формы, соответствующей минимальному покрытию. Общее количество букв в нормальной форме выражается ценой обложки, где — количество — кубиков, образующих обложку данной функции от n переменных. Минимальное покрытие характеризуется наименьшим значением его цены.

Обычно задача минимизации решается в два этапа. Во-первых, ищите сокращенное покрытие, которое включает все -кубы максимальной размерности, но не содержит ни одного куба, покрытого каким-либо кубом этого покрытия.Соответствующая дизъюнктивная нормальная форма называется сокращенной, а ее минимальные термины — простыми импликантами. Для этой функции покрытие разреза является единственным, но оно может быть избыточным из-за того, что некоторые кубы покрыты наборами других кубов.

На втором этапе происходит переход от приведенных к тупиковым дизъюнктивным нормальным формам, из которых выбираются минимальные формы. Тупиковые формы формируются путем исключения всех избыточных кубов из сокращенного покрытия, без которого оставшийся набор кубов по-прежнему образует покрытие данной функции, но при дальнейшем исключении любого из кубов он больше не охватывает наборы всех вершины, соответствующие единичным значениям функции, т.е.е., перестает быть покрытием …

Куб с уменьшенным покрытием, который покрывает вершины данной функции, не покрытые другими кубами, не может быть избыточным и всегда будет включаться в минимальное покрытие. Такой куб, как и соответствующая импликанта, называется экстремалью (существенной импликантой), а покрываемые им вершины называются сокращенными вершинами. Набор экстремалей составляет ядро ​​покрытия, понятно, что при переходе от сокращенного покрытия к минимальному в первую очередь необходимо выделить все экстремали.Если набор экстремалей не образует покрытие, то его дополняют для покрытия кубиками из уменьшенного покрытия.

Эти определения проиллюстрированы на рис. 3.9, где уменьшенное покрытие (см. Рис. 3.9a, ) и минимальное покрытие (рис. 3.9б) и (см. Рис. 3.9, б) выражаются следующим образом.

Конъюнктивная нормальная форма удобна для автоматического доказательства теорем. Любая логическая формула может быть преобразована в CNF. Для этого можно использовать: закон двойного отрицания, закон де Моргана, распределительность.

Энциклопедический YouTube

• 1 / 5

  Формулы в KNF :

  ¬ A ∧ (В ∨ С), (\ Displaystyle \ Neg A \ клин (B \ vee C),) (A ∨ B) ∧ (¬ B ∨ C ∨ ¬ D) ∧ (D ∨ ¬ E), (\ displaystyle (A \ vee B) \ клин (\ neg B \ vee C \ vee \ \ neg D) \\ клин (D \\ vee \\ neg E),) А ∧ Б. (\ Displaystyle А \ клин Б.)

  Формулы отсутствуют в KNF :

  ¬ (В ∨ С), (\ displaystyle \ neg (B \ vee C),) (A ∧ В) ∨ С, (\ Displaystyle (A \ клин B) \ vee C,) A ∧ (B ∨ (D ∧ E)).(\ Displaystyle A \ клин (B \ vee (D \\ клин E)).)

  Но эти 3 формулы не в CNF эквивалентны следующим формулам в CNF:

  ¬ В ∧ ¬ С, (\ Displaystyle \ Neg B \ клин \ Neg C,) (A ∨ C) ∧ (B ∨ C), (\ displaystyle (A \ vee C) \ клин (B \ vee C),) A ∧ (B ∨ D) ∧ (B ∨ E). (\ Displaystyle A \ клин (B \ vee D) \ клин (B \ vee E).)

  Построение CNF

  Алгоритм построения CNF

  1) Избавьтесь от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкция, дизъюнкция, отрицание.Это можно сделать с помощью эквивалентных формул:

  A → B = ¬ A ∨ B, (\ displaystyle A \ rightarrow B = \ neg A \ vee B,) A ↔ B = (¬ A ∨ B) ∧ (A ∨ ¬ B). (\ displaystyle A \ leftrightarrow B = (\ neg A \ vee B) \ клин (A \ vee \ neg B).)

  2) Замените знак отрицания, относящийся ко всему выражению, знаками отрицания, относящимся к отдельным операторам переменных на основе формул:

  ¬ (A ∨ B) = ¬ A ∧ ¬ B, (\ displaystyle \ neg (A \ vee B) = \ neg A \ клин \ neg B,) ¬ (A ∧ B) = ¬ A ∨ ¬ B.(\ Displaystyle \ neg (A \ клин B) = \ neg A \ vee \ neg B.)

  3) Избавьтесь от знаков двойного отрицания.

  4) Примените, если необходимо, к операциям соединения и дизъюнкции свойства распределенности и формулы поглощения.

  Пример построения CNF

  Приведем в CNF формулу

  F = (X → Y) ∧ ((¬ Y → Z) → ¬ X). (\ displaystyle F = (X \ rightarrow Y) \ wedge ((\ neg Y \ rightarrow Z) \ rightarrow \ neg X).)

  Давайте преобразуем формулу F (\ displaystyle F) в формулу, которая не содержит → (\ displaystyle \ rightarrow):

  F = (¬ X ∨ Y) ∧ (¬ (¬ Y → Z) ∨ ¬ X) = (¬ X ∨ Y) ∧ (¬ (¬ ¬ Y ∨ Z) ​​¬ X). (\ displaystyle F = (\ neg X \ vee Y) \ клин (\ neg (\ neg Y \\ rightarrow Z) \ vee \ neg X) = (\ neg X \ \ vee Y) \ wedge (\ neg (\ neg \\) В полученной формуле переносим отрицание на переменные и уменьшаем двойное отрицание:

  F = (¬ X ∨ Y) ∧ ((¬ Y ∧ ¬ Z) ∨ ¬ X).(\ displaystyle F = (\ neg X \ vee Y) \ клин ((\ neg Y \ клин \ neg Z) \ vee \ neg X).)

  Например, в 2-CNF записана следующая формула:

  (A ∨ B) ∧ (¬ B ∨ C) ∧ (B ∨ ¬ C). (\ displaystyle (A \ lor B) \ land (\ neg B \ lor C) \ land (B \ lor \ neg C).)

  Предыдущая статья

Грамматика: der Konjunktiv II

	Если бы я хотел прелюдию, я бы так и сказал.

The Subjunctive Mood на английском языке:

В английском языке, как и в немецком, есть общее сослагательное наклонение, система для обсуждения гипотетических ситуаций:

• «На вашем месте я бы этого не сделал».
• «Если бы она знала это, она бы не пошла с ним на свидание».
• «Давайте представим, что мы пираты».
• «Если бы вы жили здесь, вы были бы сейчас дома».
• «Я бы пошел, но я слишком устал.«
• «Если бы я этого не сказал!»

Эти формы очень распространены, но ораторы не всегда сознательно используют их правильно: мы слышим, как хулиганы говорят: «На вашем месте я бы держал рот на замке», а спортивные комментаторы утверждают, «Если я тренер, я доволен тем, как идет игра». В разговорной речи наиболее удобны конструкции, в которых используется слово «было бы» (сослагательное наклонение «воля»): «Я бы сделал это, если бы мог».

Общее сослагательное наклонение иногда называют «прошедшим сослагательным наклонением». потому что оно построено на формах прошедшего времени, но не обязательно относится к прошедшему.Фактически, «Если бы я был богат …» относится к неопределенному времени , а не к в прошлом — оно могло быть в настоящем или будущем. Чтобы говорить о нереальной ситуации в прошлом, мы должны были бы сказать: «Если бы я был богат …»

	Должен . Было бы . Может . Будет . До . Берлину нужно еще садов !

Общее сослагательное наклонение в немецком языке (Konjunktiv II).

Так же, как и в английском, немецкий использует простые формы прошедшего времени как основу для общего сослагательного наклонения. На самом деле сослагательная форма слабых глаголов неотличима от простое прошлое:

Wenn ich diesen Wagen haben wollte, kaufte ich ihn sofort.

Если бы я хотел иметь эту машину, я бы сразу ее купил.

Сильные глаголы также используют простое прошедшее, добавляя умляут, где это возможно, вместе с теми же окончаниями, которые следуют за «-t-» слабого простое прошлое:

ich wär e	wir wär en
du wär est	ihr wär et
	Sie wär en
er / sie / es wär e	sie wär ru

	Если бы вы могли поцеловать только одного человека в своей жизни, кто бы это был?

неправильные слабые глаголы добавьте умляут к несовершенной форме: brächte, dächte, hätte, wüsste, хотя некоторые из них заменяют «-ä-» на «-e-»: brennte, kennte, nennte, rennte, sendete, wendete.

Модальные окна также добавьте умляут к несовершенной форме — если он был в инфинитиве: dürfte, könnte, möchte, müsste. «Sollen» и «wollen», однако, не добавляют умлаут: sollte, wollte.

(Некоторые глаголы сохранили сослагательные формы, отражающие архаические конструкции. Таким образом, «helfen» традиционно становится «hülfe». Однако теперь эти формы кажутся педантичными, и мы все чаще находим «hälfe». Вы можете щелкнуть здесь, чтобы просмотреть список сослагательных форм наиболее распространенных сильных глаголов).

Таким образом, мы можем составить такие предложения, как:

Wenn ich dieses Lied wüsste, sänge ich es.	Если бы я знал эту песню, я бы ее спел.
Wenn es nicht regnete, gingen wir schwimmen.	Если бы не дождь, мы бы купались.
Ich kaufte das Buch, wenn ich Italienisch lesen könnte.	Я бы купил книгу, если бы умел читать по-итальянски.
Ich brächte Blumen mit, wenn die Geschäfte nicht zu hätten.	Я бы взял с собой цветы, если бы магазины не закрывались.
Wenn das Wörtchen «wenn» nicht wär ‘, wär’ mein Vater Millionär.	Если бы не словечко «если бы», мой отец был бы миллионером (~ «Если бы желания были лошадьми, то нищие могли бы ездить верхом».).
Wenn ich ein Vöglein wär ‘, / Und auch zwei Flüglein hätt’ / flöge ich zu dir ‘.	Если бы я был маленькой птичкой / И имел бы два маленьких крылышка, / Я бы полетел к тебе. [из народной песни].
Wenn deine Großmutter Räder hätte, wäre sie eine Straßenbahn.	Если бы у вашей бабушки были колеса, она была бы троллейбусом [= пословица на идише].

	Если бы мой парень нарушил столько же обещаний, сколько канцлер, я бы его выгнал.

Подобно использованию английского слова «would», в разговорном немецком языке наиболее удобно использовать «würde» , сослагательное наклонение «werden». В условных предложениях («если … то») «würde» обычно является частью «then-clause»:

Wenn ich dieses Lied wüsste, würde ich es singen.	Если бы я знал эту песню, я бы ее спел.
Wenn es nicht regnete, würden wir schwimmen gehen.	Если бы не дождь, мы бы купались.

Времена в общем сослагательном наклонении:

Обратите внимание, что конструкции с «würden» напоминают будущее время (например, «werden» + инфинитив), но не обязательно подразумевается будущее значение. В отличие от особого сослагательного наклонения, общее сослагательное наклонение на самом деле имеет только два времени — непрошедшее и прошедшее — но мы можем построить каждое из этих времен несколькими способами.

Не прошедшее , неопределенное время в настоящем или будущем, может быть построено с или без «» würde «:

Wenn ich schneller führe, hätte ich bestimmt einen Unfall.

Wenn ich schneller führe, würde ich bestimmt einen Unfall haben.

Если бы я ехал быстрее, я бы наверняка попал в аварию.

Чтобы создать прошедшее время , неопределенное время до настоящего, мы используем совершенную конструкцию, использование сослагательных форм haben или sein в качестве вспомогательных глаголов:

Wenn ich schneller gefahren wäre, hätte ich bestimmt einen Unfall gehabt.

Wenn ich schneller gefahren wäre, dann würde ich bestimmt einen Unfall gehabt haben.

Если бы я ехал быстрее, я бы наверняка попал в аварию.

Когда этого требует смысл, можно использовать оба времени:

Wenn ich das damals gewusst hätte, wäre ich jetzt ein reicher Mann.

Wenn ich das damals gewusst hätte, würde ich jetzt ein reicher Mann sein.

Если бы я знал это тогда, я был бы теперь богатым человеком.

Обратите внимание, что только «нереальная» часть предложения находится в сослагательном наклонении:

Wenn ich damals gewusst hätte, was ich jetzt weiß, wäre ich ein reicher Mann.

Если бы я знал тогда то, что знаю сейчас, я был бы богатым человеком.

Другие формы предложений «если-то»:

Обратный порядок слов может заменить «wenn» (сравните с английским «Если бы я знал… «):

Hätte ich gewusst, wer ihr Vater ist, hätte ich etwas anderes gesagt.	Если бы я знал, кто ее отец, я бы сказал что-нибудь другое.
Regnete es, gingen wir nach Hause.	Если бы пошел дождь, поехали бы домой.

	Боишься стареть … Больной туберкулезом в Третий мир был бы в восторге от этого.

Другое использование сослагательного наклонения:

1) Как и в английском, просьбы или другие утверждения могут быть смягчены общим сослагательным наклонением:

Ich hätte gern das große Frühstück.	Я бы хотел обильный завтрак.
Ich möchte einen Döner ohne Soße.	Дёнер без соуса.
Könnten Sie mir bitte auch etwas Brot geben?	Не могли бы вы также дать мне хлеба?
Hätten Sie vielleicht etwas Salz?	Может быть, есть немного соли?
Würden Sie mir bitte Ihren Bleistift leihen?	Не могли бы вы одолжить мне свой карандаш?
Wie wäre es mit einer Tasse Kaffee?	Как будет чашка кофе?
Dürfte ich sie bitten, das Fenster aufzumachen?	Могу я попросить вас открыть окно?
Es wäre jetzt Zeit, dass du gingest.	Тебе пора идти.
Ich müsste eigentlich jetzt gehen.	Мне правда пора.
Ich wüsste nicht, was ich dir sagen könnte.	Я не знаю, что вам сказать.
Das dürfte richtig sein.	Наверное, верно.
Ich hätte noch einen Wunsch.	У меня еще одна просьба.
Das wäre alles.	Это все [запросов больше нет].
Sie möchten bitte nach Hause anrufen.	Пожалуйста, позвоните домой.
Jetzt wären wir am Ende.	Теперь мы закончили. (Это все.)

2) «als ob» , «als wenn» : Когда «как будто» подразумевает нереальное состояние, оно требует сослагательного наклонения. «als ob» — самая обычная форма, но «als wenn» тоже возможно. Вы также можете использовать «als» с обратным порядком слов.

Er tut, als ob er die Antwort wüsste.	Он действует так, как будто знает ответ.
Sie tun, als ob sie kein Wort verstanden hätten.	Они ведут себя так, как будто не поняли ни слова.
Die Amerikaner sprechen, als ob sie heiße Kartoffeln im Munde hätten.	Американцы говорят так, как будто у них есть горячий картофель.
Er sieht aus, als ob er zu lange in der Sonne gelegen hätte.	Похоже, он слишком долго пролежал на солнышке.
Sie redet, als wenn sie meine beste Freundin wäre.	Она говорит так, как будто она моя лучшая подруга.
Sie tut, als hätte sie das Pulver erfunden.	Она ведет себя так, как будто она изобрела порох [~ «была ученым-ракетчиком»].

3) Пожелания могут быть выражены в сослагательном наклонении. Обратите внимание, что глаголы, выражающие желание, в отличие от английского, также находятся в сослагательном наклонении:

Ich wünschte, ich könnte fliegen.	Я бы хотел летать.
Ich wollte, er würde den Mund halten.	Я бы хотел, чтобы он держал рот на замке.

4) Одно сослагательное наклонение также может означать желание:

Das wäre der Wagen für mich!	Я бы хотел такую ​​машину!
Man müsste jung sein!	Ах, быть молодым!

5) «Если бы» (или обратный порядок слов) + сослагательное наклонение:

Wenn du nur hier wärest!	Если бы ты был здесь!
Wenn ich nur ihren Namen wüsste!	Если бы я только знал ее имя!
Wenn sie nur anrufen würde!	Хоть бы она позвонила!
Regnete es nur!	Хоть бы дождь!
Hätten sie nur die richtige Größe!	Хоть бы у них был правильный размер!

6) Использование сослагательного наклонения для противоречия предыдущему утверждению:

Wann hätte ich так было gesagt?	Когда я должен был сказать такое?
Wie sollte er es gefunden haben?	Как он мог это найти?
Schön wäre es!	Было бы неплохо [если бы это было правдой].
Nicht dass ich wüsste.	Насколько мне известно.

7) Утверждать что-то фантастическое:

Ich dachte, ich wäre im Kino.	Я думал, что мне снится [«в кино»; т.е. ситуация была нелепой]
Wir hatten Angst, dass er vor Wut platzen würde.	Мы боялись, что он взорвется от гнева.

8) Использование общего сослагательного наклонения в косвенный дискурс, особенно, если сомневаетесь в правдивости говорящего:

Er sagt, dass sein Wecker nicht geklingelt hätte.	Он говорит, что его будильник не сработал.
Siebeeeptet, dass sie die ganze Zeit zu Hause gewesen wäre.	Она утверждает, что все время была дома.
Der Hund hätte Ihre Arbeit gefressen?	[Вы говорите, что] Собака съела вашу бумагу?

9) Еще несколько примеров:

Er wäre der letzte, den ich um Hilfe bitte würde.	Он был бы последним, кого бы я попросил о помощи.
Das Buch is so teuer, wie es sein könnte.	Книга настолько дорогая, насколько это возможно.
Ich habe Angst, dass ich das Spiel verlieren könnte.	Боюсь проиграть партию.
Wo ist einer, der das tun wollte?	Где тот, кто захочет это сделать?

---

(Для получения дополнительной информации см. Специальное сослагательное наклонение (Konjunktiv I)

Несовершенное сослагательное наклонение в испанском

Несовершенное сослагательное наклонение ( el imperfecto de subjuntivo ) следует многим из тех же правил, что и настоящее сослагательное наклонение.Введенное с помощью глагола preterite, несовершенного, условного или прошедшего совершенного WEIRDO в независимом предложении, несовершенное сослагательное наклонение часто относится к предыдущему опыту, но также может относиться к маловероятным событиям или возможностям.

Обратите внимание на эти примеры несовершенного сослагательного наклонения.

примеры
Si tuviera más dinero, viajaría por todo el mundo. Если бы у меня было больше денег, я бы путешествовал по всему миру.
Si yo fuera tú, no lo haría. На вашем месте я бы не стал этого делать.

Несовершенные формы сослагательного наклонения

В поисках несовершенного сослагательного наклонного ствола

Чтобы спрягать глагол в несовершенном сослагательном наклонении, вам нужно знать форму третьего лица множественного числа ( ellos, ellas ), претерит формы глагола, который вы используете. Почему? Вместо использования инфинитива для основы, несовершенное сослагательное наклонение использует третье лицо множественного числа претерита (минус -ron ).Каким бы ни было претерите от третьего лица глагола, правильным или неправильным, оно становится основой несовершенного сослагательного наклонения.

Формула несовершенного сослагательного ствола

несовершенный сослагательный стержень = форма претерита множественного числа третьего лица минус -рон окончание

Примеры несовершенного сослагательного ствола

Вот несовершенные основы сослагательного наклонения некоторых распространенных испанских глаголов.

левая сторона 68

		Cupie-
		die-
		dije-
		durmie- 9			durmie-
		хаби-
		хабла-
		hicie-
		tuvie-
		pidie-
		pudie-
		quisie-
		supie-
		sintie-
		fue-
		traduje-			traduje-
		vie-

Окончания несовершенного сослагательного наклонения

При спряжении несовершенного сослагательного наклонения вы можете выбрать один из двух разных наборов окончаний.Оба верны, хотя использование первого набора, у которого yo окончание -ra , более распространено.

llas

лет	-ra	-se
tú	-ras	-ses
él, ella, usted	-ra -ra	-se
nosotros	-ramos	-semos
vosotros	-rais	-seis
elloste -ран	-сен

Остерегайтесь акцентов

Nosotros несовершенные спряжения сослагательного наклонения имеют тильду на гласной, которая идет непосредственно перед окончанием сослагательного наклонения.Например:

• написать éramos / написать ésemos

Вот три общих глагола, спряженных в несовершенном сослагательном наклонении с каждым набором окончаний.

Слагательное наклонение 1

930 ellas, ustedes

лет
tú
él, ella, usted
nosotros

Слагательное наклонение 2

930 ellas, ustedes

лет
tú
él, ella, usted
nosotros

Несовершенное употребление сослагательного наклонения

Несовершенное сослагательное наклонение может использоваться, чтобы говорить о прошлых событиях, текущих мнениях о прошлых событиях, сомнениях и желаниях, а также в if предложениях и вежливых просьбах.

1. Прошлые события

Если глагол WEIRDO в независимом предложении находится в претерите или несовершенном, то последующий сослагательный глагол будет несовершенным.

примеры
Quería que vinieras / vinieses a mi fiesta. Я хотел, чтобы вы пришли ко мне на вечеринку.
Tenía miedo de que no lloviera / lloviese. Я боялся, что дождя не будет.
Le iba a prestar dinero para que se comprara un abrigo. Я собирался одолжить ему денег, чтобы он мог купить пальто.

2. Текущее мнение о прошлых событиях

Несовершенное сослагательное наклонение также может использоваться для выражения текущих эмоций, сомнений и т. Д. По поводу того, что произошло в прошлом.

примеры
Es bueno que él se casara / casase. Хорошо, что женился.
No me parece que el viaje fuera / french largo. Мне не кажется, что путь был долгим.

3. Сомнения и пожелания

Часто можно увидеть, что ojalá или ojalá que используются с несовершенным сослагательным наклонением, чтобы выразить идею надежды на что-то, что маловероятно или невозможно.

примеры
Ojalá que nevara / nevase en Panamá. Я бы хотел, чтобы в Панаме пошел снег.
Ojalá mi hermano se casara / casase. Я бы хотел, чтобы мой брат женился.

4. Пункты If

Когда перед ним стоит si (, если ), несовершенное сослагательное наклонение часто используется, чтобы говорить о гипотезах. Обратите внимание, что другой глагол в этих конструкциях находится в условном выражении.

примеры
Si yo fuera / french reina, viajaría por todo el mundo. Если бы я была королевой, я бы путешествовала по всему миру.
Pintaría más seguido si tuviera / tuviese más tiempo. Я бы рисовал чаще, если бы у меня было больше времени.

5. Относительные статьи

Несовершенное сослагательное наклонение используется в придаточных предложениях с несуществующим, неопределенным или отрицательным антецедентом.

примеры
Buscaba una casa que tuviera / tuviese una piscina. Я искал дом с бассейном.
No conocía a nadie que viviera / viviese en Buenos Aires. Я не знал никого, кто жил в Буэнос-Айресе.

6. Вежливые предложения и просьбы

Несовершенное сослагательное наклонение может использоваться для очень вежливых предложений или официальных просьб.

No related posts.