Модуль вектора — это… Что такое Модуль вектора?
- Модуль вектора
Модулем (длиной) вектора
 называется длина(норма) соответствующего вектора AB и обозначается как
называется длина(норма) соответствующего вектора AB и обозначается как  .
.В евклидовом n-мерном пространстве длина вектора рассчитывается как корень из скалярного произведения этого вектора на себя, в том случае если это произведение задано как (x,y)=x1 * y1 + x2 * y2,…,xn * yn),где (x1,x2,…,xn) (y1,y2,…,
 .
.Вектор, модуль которого равен 1, называется единичным вектором или ортом.
Wikimedia Foundation. 2010.
- Мусульманские страны
- Ракетный подводный крейсер стратегического назначения
Смотреть что такое «Модуль вектора» в других словарях:
модуль вектора — величина вектора — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы величина вектора EN absolute value of a vector … Справочник технического переводчика
модуль вектора — vektoriaus modulis statusas T sritis fizika atitikmenys: angl. absolute value of vector vok. Vektorbetrag, m rus. длина вектора, f; модуль вектора, m pranc. module d’un vecteur, m … Fizikos terminų žodynas
Модуль — (от лат. modulus «маленькая мера»): В Викисловаре есть статья «модуль» Мо … Википедия
Модуль (значения) — Модуль (от лат. modulus «маленькая мера») составная часть, отделимая или хотя бы мысленно выделяемая из общего. Модульной обычно называют вещь, состоящую из чётко выраженных частей, которые нередко можно убирать или добавлять, не разрушая вещь… … Википедия
Модуль числа — Абсолютная величина или модуль вещественного или комплексного числа x есть расстояние от x до начала координат. Более точно: Абсолютная величина вещественного числа x есть неотрицательное число, обозначаемое |x| и определяемое следующим образом:… … Википедия
модуль волнового вектора — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN magnitude of propagation vector … Справочник технического переводчика
модуль конвольвера кодового вектора огибающей — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN shape codevector convolution module … Справочник технического переводчика
Модуль комплексного числа — Модулем комплексного числа называется длина вектора, соответствующего этому числу: . Модуль комплексного числа z обычно обозначается | z | или r. Пусть и вещественные числа такие, что комплексное число (обычные обозначения). Тогда Числа … Википедия
Модуль (в математике) — Модуль в математике, 1) М. (или абсолютная величина) комплексного числа z = х + iy есть число ═(корень берётся со знаком плюс). При представлении комплексного числа z в тригонометрической форме z = r(cos j + i sin j) действительное число r равно… … Большая советская энциклопедия
МОДУЛЬ — абелева группа с кольцом операторов. М. является обобщением (линейного) векторного пространства над полем Кдля случая, когда Кзаменяется нек рым кольцом. Пусть задано кольцо А. Аддитивная абелева группа Мназ. левым А модулем, если определено… … Математическая энциклопедия
5.6.3 Вектор, модуль вектора, равенство векторов; сложение векторов и умножение вектора на число
Видеоурок 1: Понятие вектора
Видеоурок 2: Равенство векторов
Видеоурок 3: Сложение и вычитание векторов
Видеоурок 4: Умножение вектора на число
Лекция: Вектор, модуль вектора, равенство векторов; сложение векторов и умножение вектора на число

Вектор – это тело, которое изучается в математике, но используется в большом количестве наук. Например, в физике существуют скалярные величины (те, что характеризуются значением – масса, температура и т.д.), а также векторные величины (сила, работа и другие).
Вектор – это величина, которая характеризуется не только значением, но и направлением. Иными словами, это направленный отрезок.

Но кроме его длины, нам также важно, где находится его начало, а где конец.
Если вектор имеет свое начало в некоторой точке А, а заканчивается в точке В, то его обозначают следующим образом:
Кроме двух букв, вектор можно обозначить одной буквой со значком вектора сверху.
Длиной вектора (его модулем) называют расстояние между концом вектора и его началом.
Для определения модуля вектора следует воспользоваться следующей формулой:
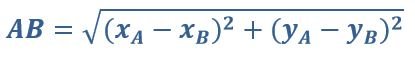
Кроме этого, модуль вектора может обозначаться следующим образом:

Если некоторый вектор имеет начало и конец в одной и той же точке, то такой вектор называют нулевым. Нулевой вектор обозначают, как
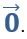
Если длина некоторого вектора равна единичному отрезку, то его называют единичным.
Если некоторые векторы расположены на одной прямой или же параллельны друг другу, то такие векторы называются коллинеарными.
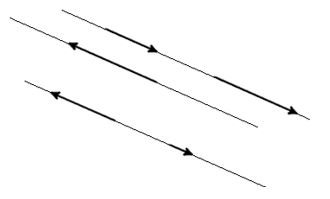
Если некоторые векторы можно назвать коллинеарными, но кроме этого они направлены в одну сторону, то их можно назвать сонаправленными.
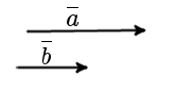
Если же наоборот два коллинеарных вектора смотрят в разные стороны, то их называют противоположно направленными.
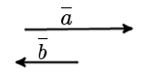
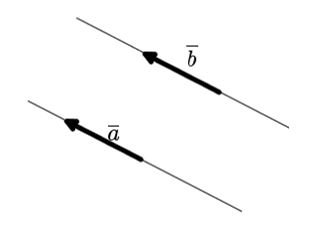
Если же некоторые векторы являются коллинеарными, сонаправленными, а также имеют одинаковую длину (модуль), то их можно назвать равными.
 Координаты вектора
Координаты вектора
Для нахождения координаты вектора следует вычесть соответствующие координаты его конца и начала.
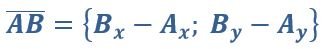
Например, если начало вектора А (3; 6), а конец В (5;9), то этот вектор будет иметь следующие координаты: {2;3}.
 Сложение и вычитание векторов
Сложение и вычитание векторов
Чтобы сложить два вектора для получения нового, необходимо сложить соответствующие координаты.
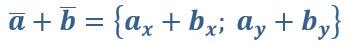
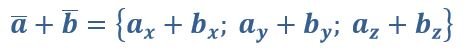
Например, сложим вектор {2;3} с вектором {5;7}. В результате получим новый вектор с координатами {7;10}. С вычитанием все аналогично.
 Умножение вектора на некоторое число
Умножение вектора на некоторое число
Чтобы умножить вектор на некоторое число, следует умножить каждую его координату на данное число.
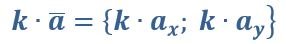
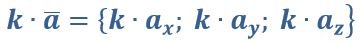
Свойства:
- Первоначальный вектор и вектор умноженный на некоторое число, который равный ему, являются параллельными.
- Если число, на которое умножался вектор, больше нуля, то новый вектор будет сонаправлен первоначальному. Если же число меньше нуля, то векторы будут противоположно направленны.

Векторы. Модуль вектора. Равенство векторов. Сложение векторов. Умножение вектора на число
Во многих разделах математики, механики, физики, технических наук
различают величины скалярные и векторные. Величина, для определения которой достаточно задать только ее численное значение, называется скалярной. Примерами скалярных величин служат длина, площадь, масса, температура, сопротивление и др. Объекты, которые характеризуются не только численным значением, но и направлением в пространстве, называ-ются векторными. Векторами являются, к примеру, скорость, сила, напряженность электрического или магнитного поля и др.
Векторную величину можно изобразить направленным отрезком.
Определение. Вектором называется отрезок, концы которого упорядочены. Первый из его концов называется началом, второй – концом вектора.
Обозначается a, MN , где М – начало вектора, N – его конец (рис.3).
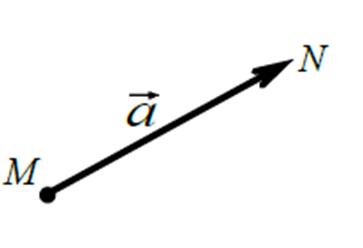
Рис. 3.
Если вектор обозначен одной буквой, то в печати обычно стрелка над ней
не ставится, а сама буква выделяется жирным шрифтом: 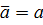 .
.
Введем ряд понятий.
1) Вектор 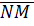 называется противоположным вектору
называется противоположным вектору 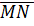
2) Нулевой вектор – вектор, у которого начало и конец совпадают.
Обозначается 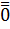 или 0. Нулевой вектор не имеет направления.
или 0. Нулевой вектор не имеет направления.
3) Модуль (длина) вектора – это расстояние между его началом и концом.
Обозначается | 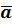 |, |
|, | 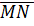 | Модуль нулевого вектора равен нулю |
| Модуль нулевого вектора равен нулю | 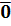 | 0.
| 0.
4) Единичный вектор – вектор, длина которого равна единице.
Определение. Коллинеарные векторы – векторы,
лежащие на одной прямой или на параллельных прямых
(рис.4). Обозначаются a b. Нулевой вектор считается
коллинеарным любому вектору.
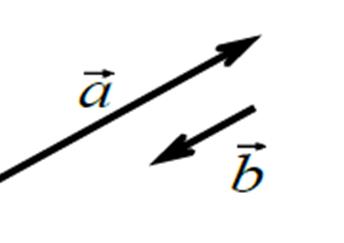
Рис. 4.
Определение. Компланарные векторы – векторы, лежащие в одной
плоскости или в параллельных плоскостях.
Заметим, что любые два вектора всегда компланарны.
Определение.Векторы а и b называются равными,
если они: 1) коллинеарны, 2) их длины равны, 3) они имеют одинаковое направление
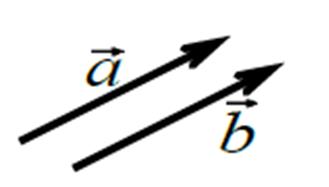
(рис.5).
Обозначение: a = b.
Если точка приложения вектора может быть любой, то есть его можно
переносить, то вектор называется свободным.
Вектор называется скользящим, если его можно перемещать вдоль прямой, проходящей через начало и конец вектора.
Векторы, для которых точка приложения имеет существенное значение, называются связанными (например, радиус-вектор точки, который будет определен ниже, или сила, действующая на тело).
Модуль вектора Википедия
 Вектор A
B → {\displaystyle {\overrightarrow {AB}}} .ts-Боковая_навигационная_таблица-preTitle{padding-top:0}.mw-parser-output .ts-Боковая_навигационная_таблица-image{padding:0.4em 0 0.4em}.mw-parser-output .ts-Боковая_навигационная_таблица-title{padding:0.2em 0.4em 0.2em;font-size:125%;line-height:1.15em;font-weight:bold;background:#cfe3ff}.mw-parser-output .ts-Боковая_навигационная_таблица-above,.mw-parser-output .ts-Боковая_навигационная_таблица-below{padding:0.2em 0.4em 0.2em;font-weight:bold}.mw-parser-output .ts-Боковая_навигационная_таблица-heading{padding:0.2em 0;font-weight:bold;background:#eaf3ff}.mw-parser-output .ts-Боковая_навигационная_таблица-list{padding:0.2em 0}]]>
Вектор A
B → {\displaystyle {\overrightarrow {AB}}} .ts-Боковая_навигационная_таблица-preTitle{padding-top:0}.mw-parser-output .ts-Боковая_навигационная_таблица-image{padding:0.4em 0 0.4em}.mw-parser-output .ts-Боковая_навигационная_таблица-title{padding:0.2em 0.4em 0.2em;font-size:125%;line-height:1.15em;font-weight:bold;background:#cfe3ff}.mw-parser-output .ts-Боковая_навигационная_таблица-above,.mw-parser-output .ts-Боковая_навигационная_таблица-below{padding:0.2em 0.4em 0.2em;font-weight:bold}.mw-parser-output .ts-Боковая_навигационная_таблица-heading{padding:0.2em 0;font-weight:bold;background:#eaf3ff}.mw-parser-output .ts-Боковая_навигационная_таблица-list{padding:0.2em 0}]]>У этого термина существуют
4.2. Разложение вектора по ортам. Модуль вектора
10.Разложение вектора по ортам. Из прямоугольного параллелепипеда (рис. 4.1) следует:
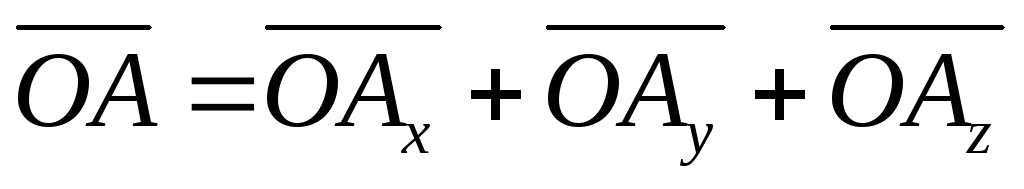 .
.
Но 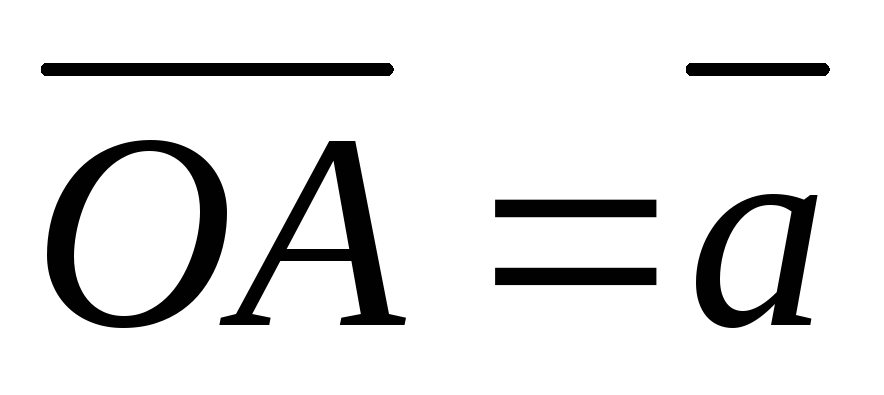 ,
,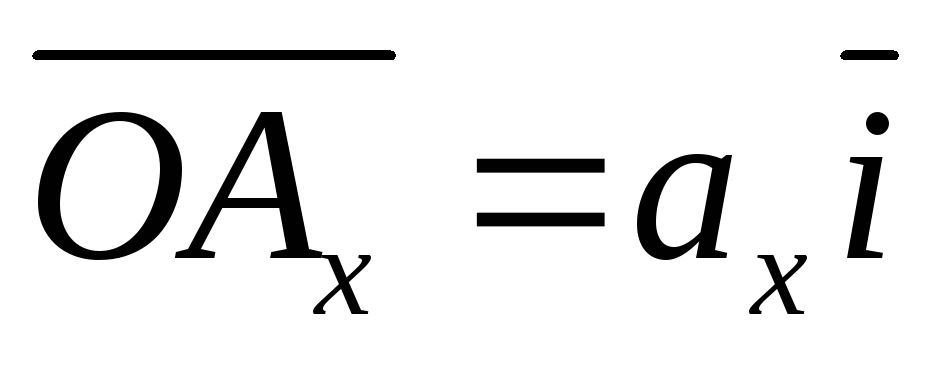 ,
,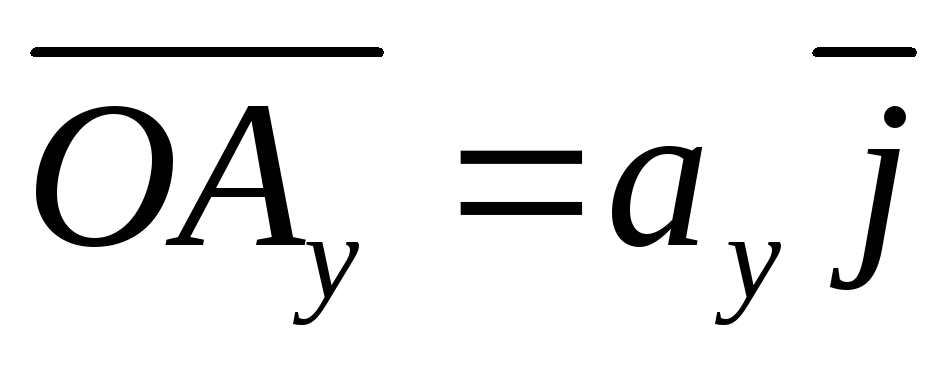 ,
,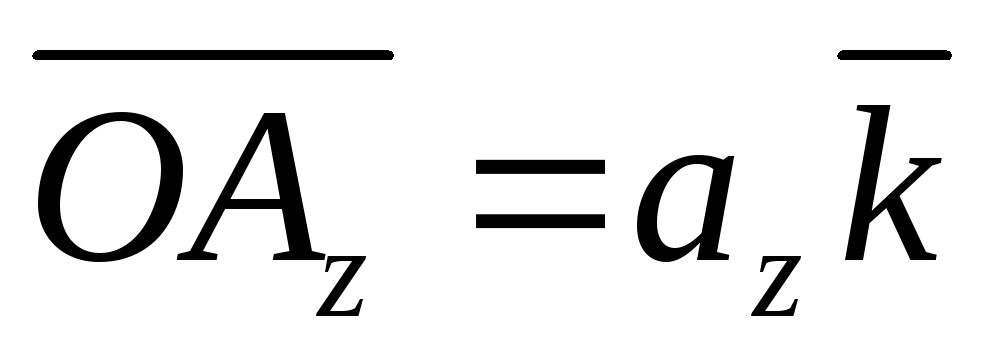 ,
Следовательно,
,
Следовательно,
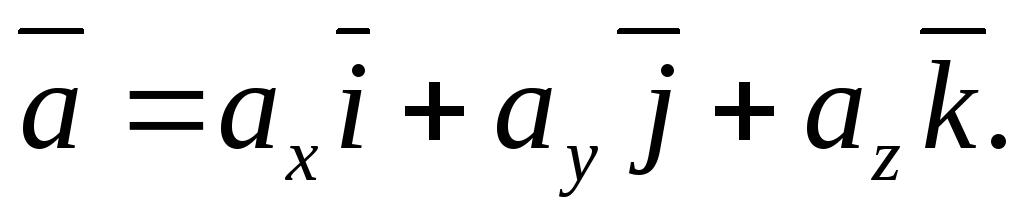 (4.3)
(4.3)
Равенство (4.3) и есть формула разложения
вектора  по ортам координатных осей.
по ортам координатных осей.
Таким образом, координатная запись вектора может быть осуществлена двумя способами:
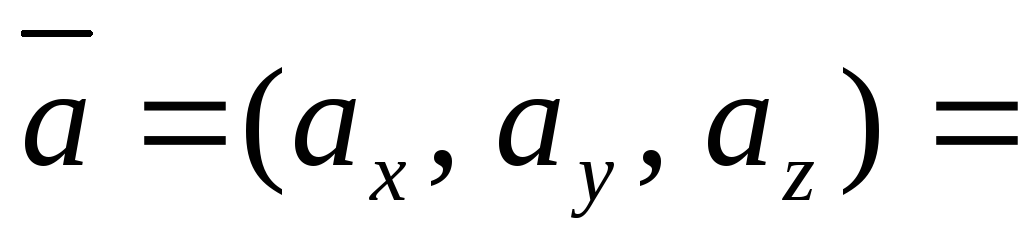
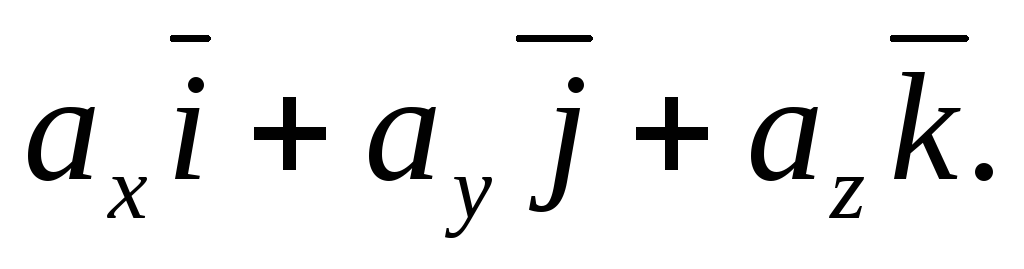
20.Модуль вектора. Вектор является диагональю прямоугольного
параллелепипеда (рис. 4.1). Квадрат длины
диагонали равен сумме квадратов трех
его измерений:
является диагональю прямоугольного
параллелепипеда (рис. 4.1). Квадрат длины
диагонали равен сумме квадратов трех
его измерений:
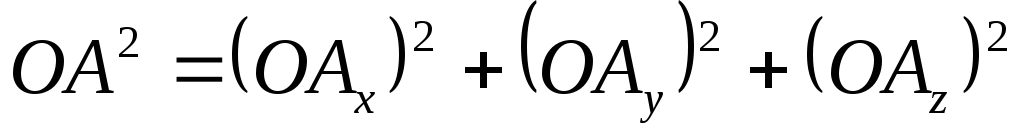 ,
,
отсюда следует: 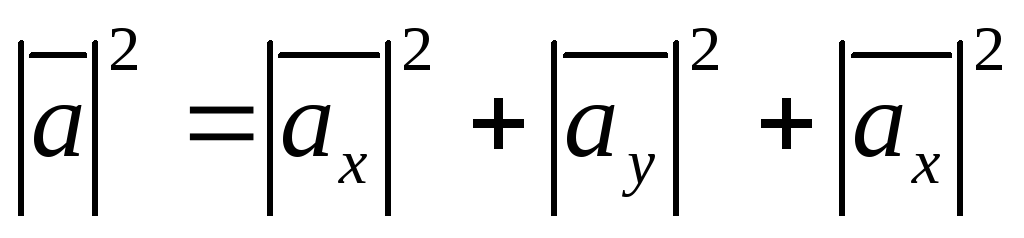 ,
и наконец, получаем искомую формулу:
,
и наконец, получаем искомую формулу:
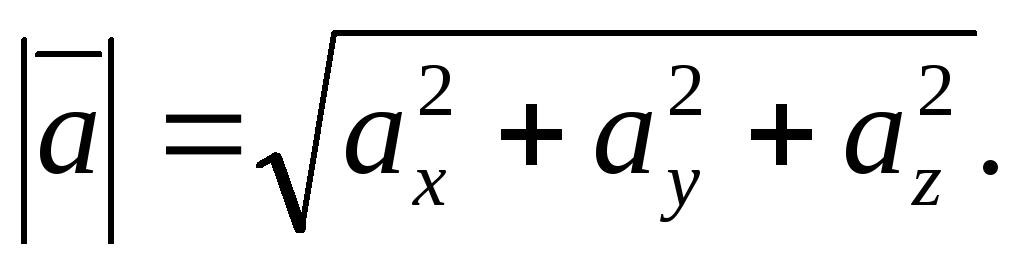 (4.4)
(4.4)
Модуль вектора равен корню квадратному из суммы квадратов его координат.
4.3. Линейные операции над векторами.
Сформулируем правила действийнад векторами в координатной форме.
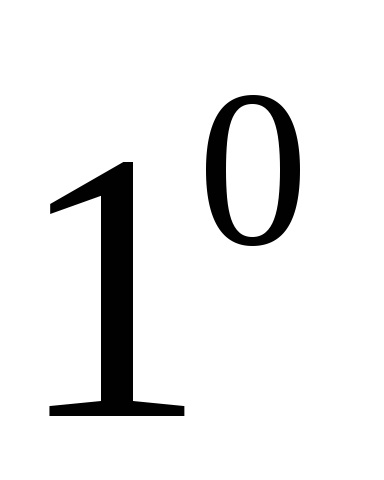 .Координаты суммы (разности) векторов
равны суммам (разностям) соответствующих
координат этих векторов.
.Координаты суммы (разности) векторов
равны суммам (разностям) соответствующих
координат этих векторов.
Пусть 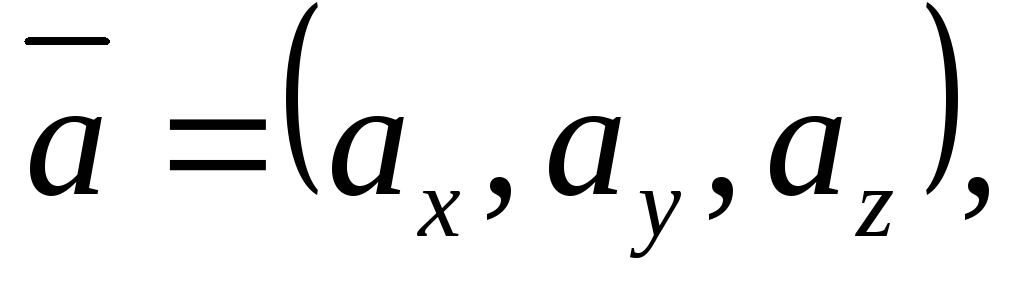
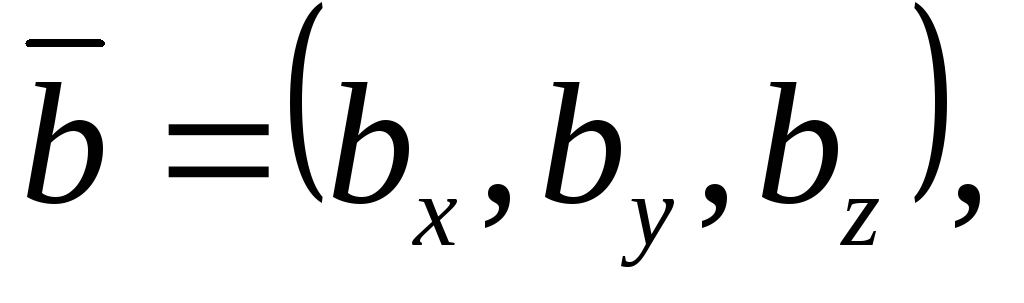 тогда
тогда
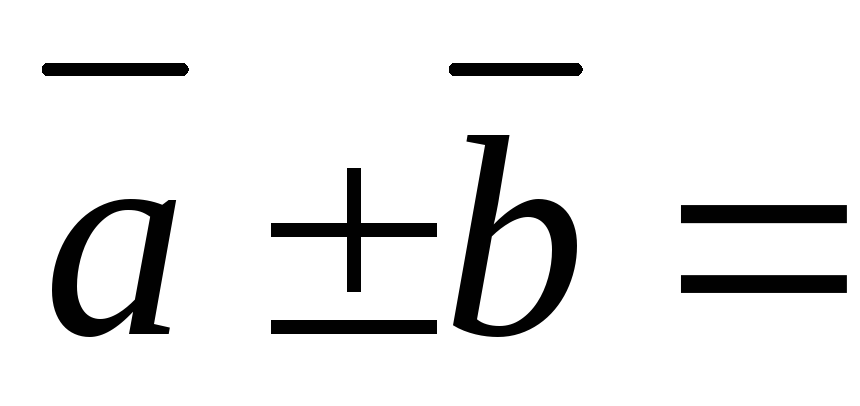
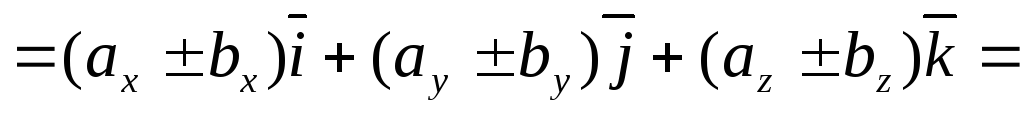
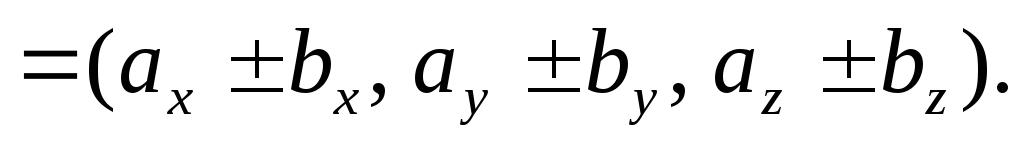 (4.5)
(4.5)
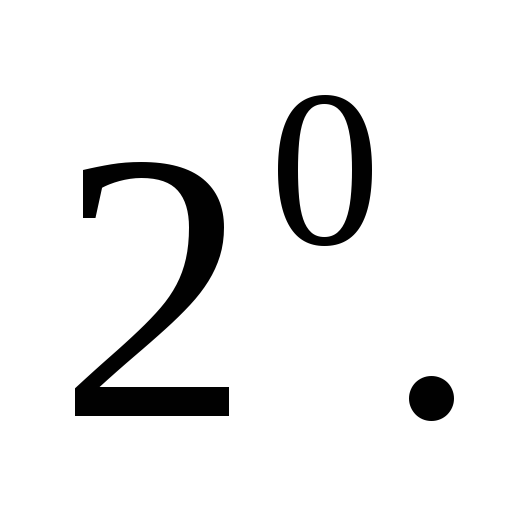 При умножении вектора на скаляр его
координаты умножаются на этот скаляр.
При умножении вектора на скаляр его
координаты умножаются на этот скаляр.
Если 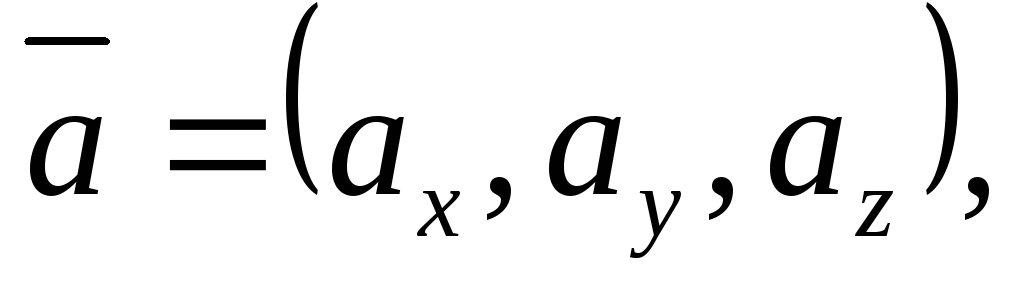 и
и – скалярная величина, то
– скалярная величина, то
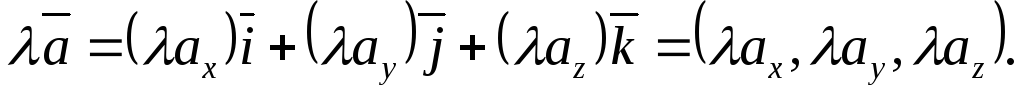 (4.6)
(4.6)
Покажем применение рассмотренного в этой главе материала к решению практической задачи.
Задача 4.1. Даны векторы:
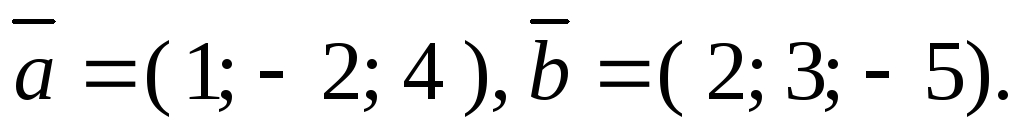
Найти: координаты и модуль вектора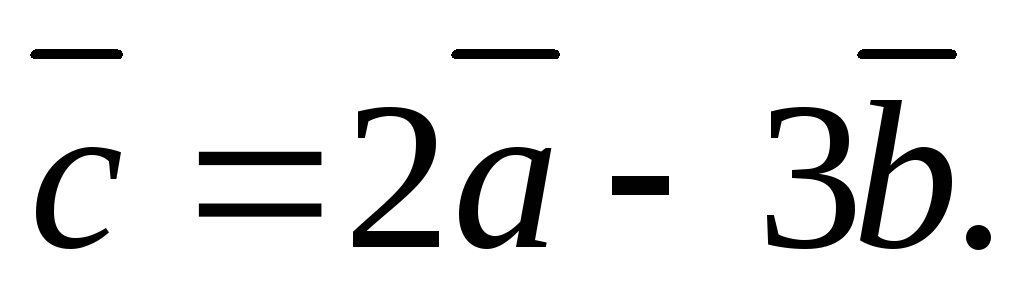
Решение.Используем координатную запись векторов и правила линейных операций над ними:
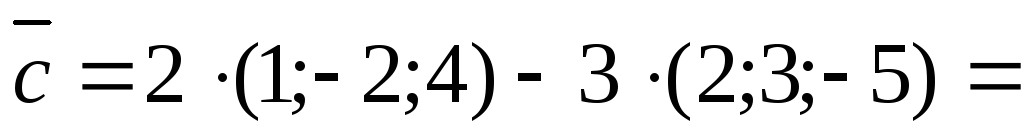
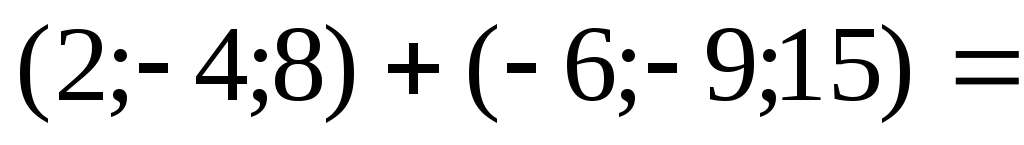
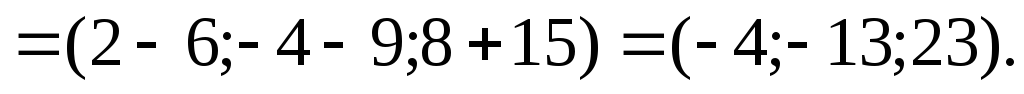
Модуль вектора 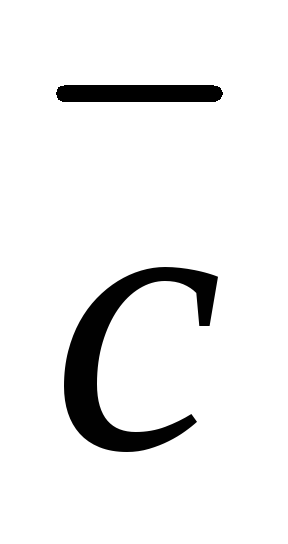 вычислим по формуле (4.4):
вычислим по формуле (4.4):
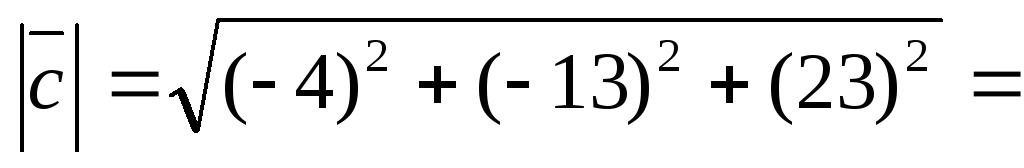
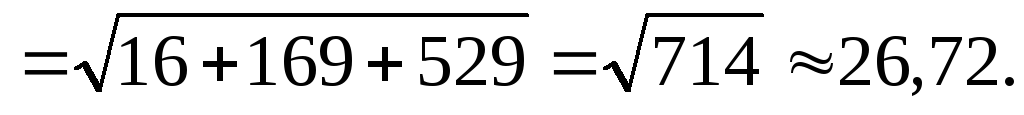
Ответ.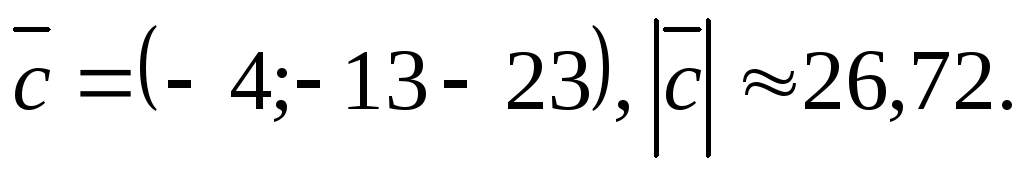
4.4. Направляющие косинусы вектора
О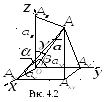 пределение
4.2. Направляющими косинусами
ненулевого вектора называются косинусы
углов, которые этот вектор образуют с
осями координат (рис. 4.2).
пределение
4.2. Направляющими косинусами
ненулевого вектора называются косинусы
углов, которые этот вектор образуют с
осями координат (рис. 4.2).
Выразим координаты вектора  через его модуль и углы
через его модуль и углы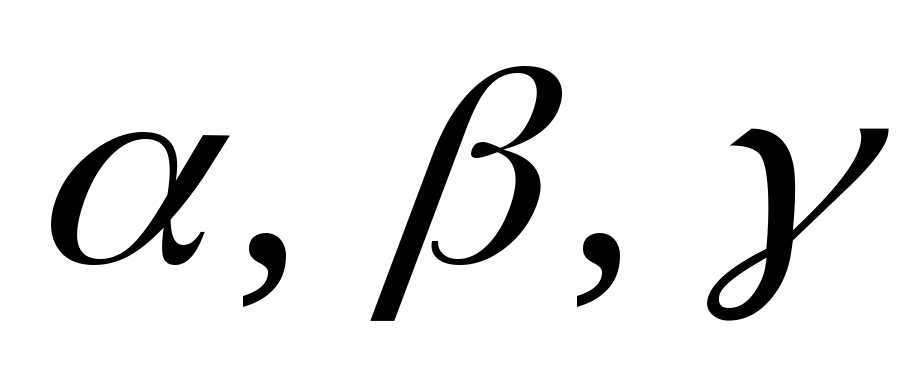 :
:
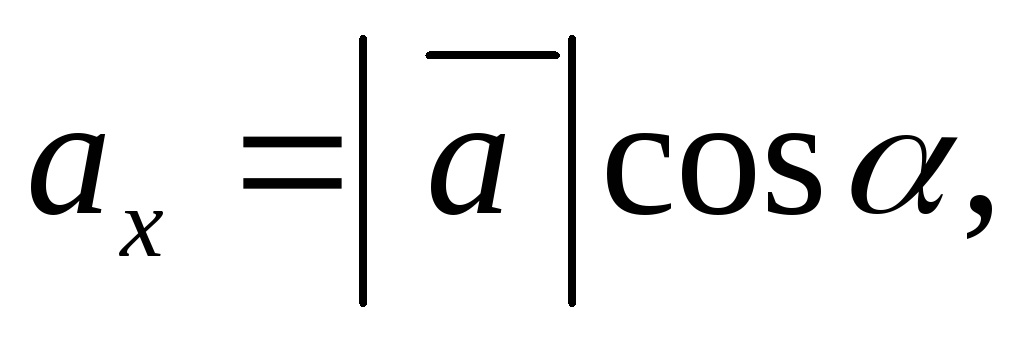
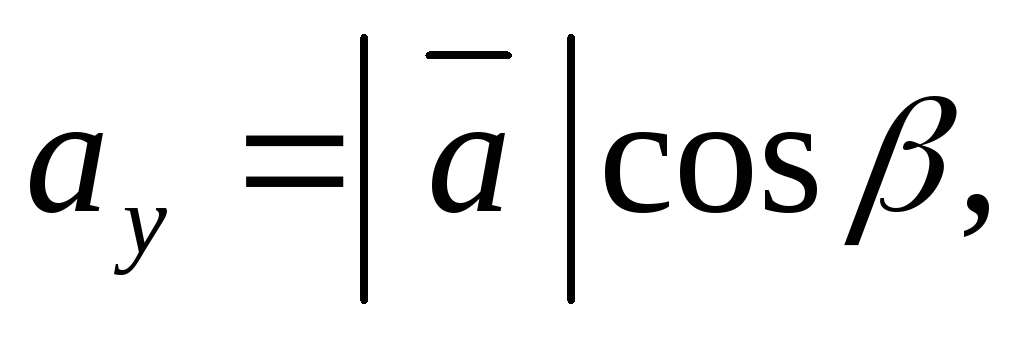
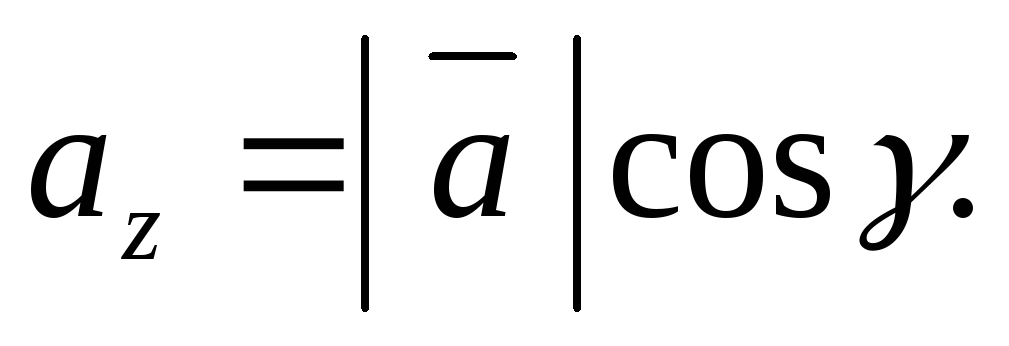
С помощью данных равенств найдем
выражения направляющих косинусов через
координаты вектора  и его модуль:
и его модуль:
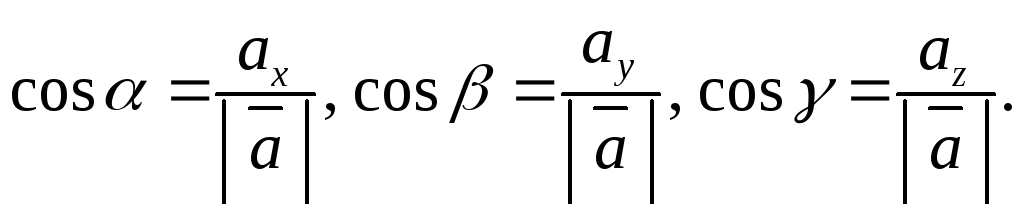 (4.7)
(4.7)
Вычислим сумму квадратов направляющих
косинусов вектора  :
:
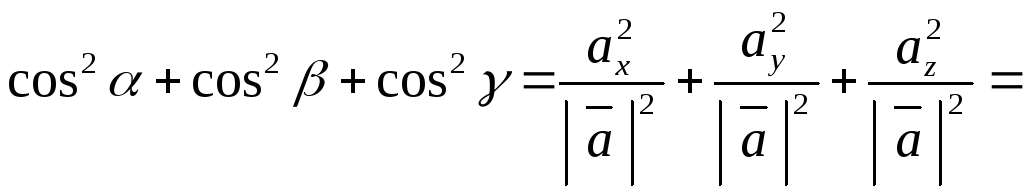
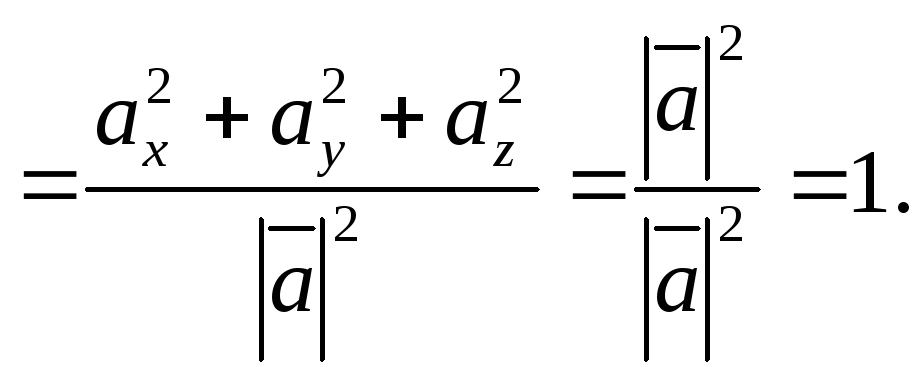
Полученный результат в векторной алгебре сформулирован в виде следующего утверждения:
Сумма квадратов направляющих косинусов ненулевого вектора равна единице:
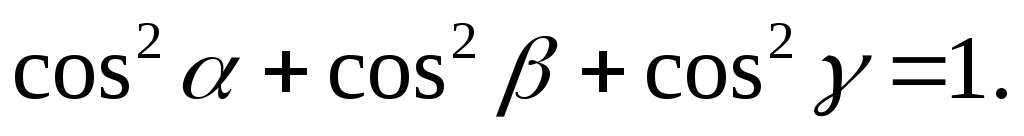 (4.8)
(4.8)
Задача 4.2.Определить направляющие
косинусы вектора 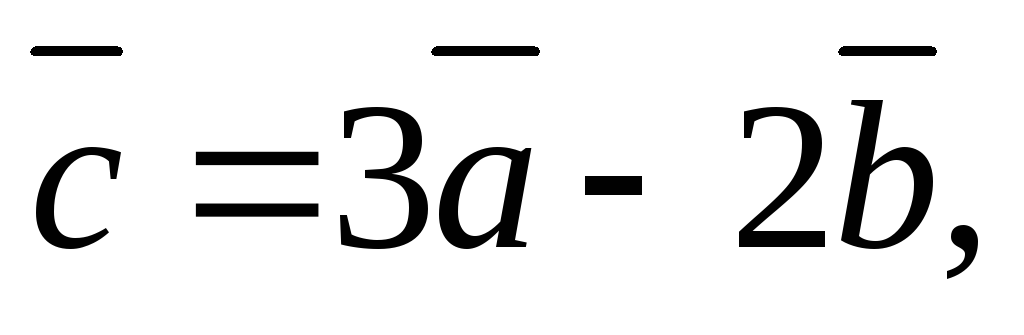
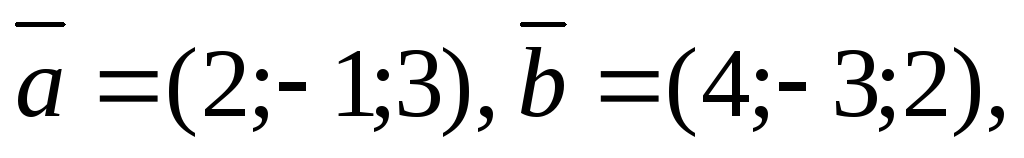 а также убедиться в справедливости
тождества(4.8).
а также убедиться в справедливости
тождества(4.8).
Решение.10. Определим координаты
и модуль вектора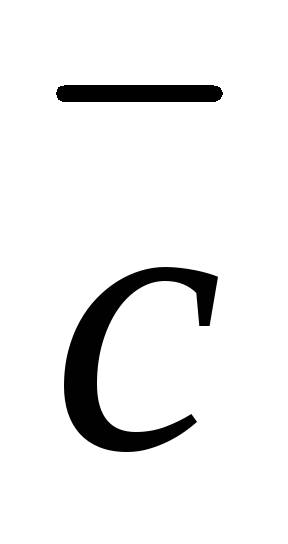 :
:
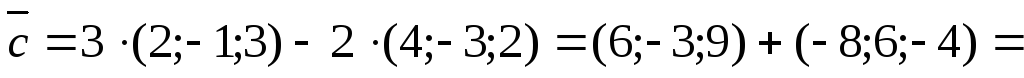
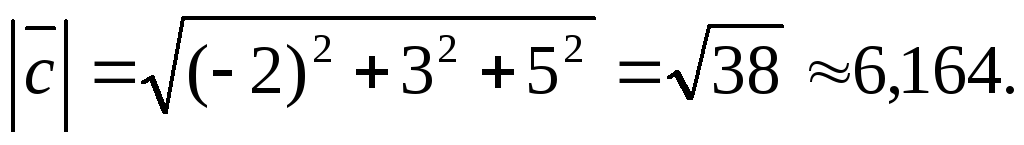
20. Вычислим направляющие косинусы
вектора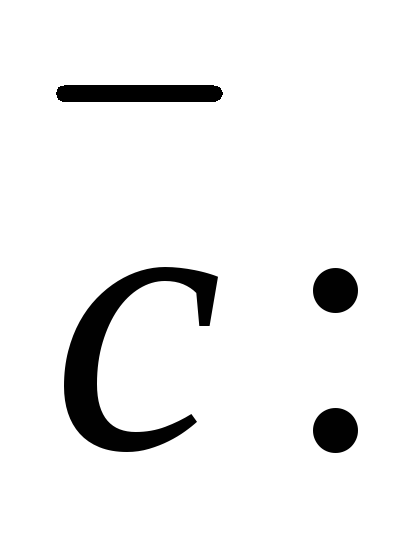
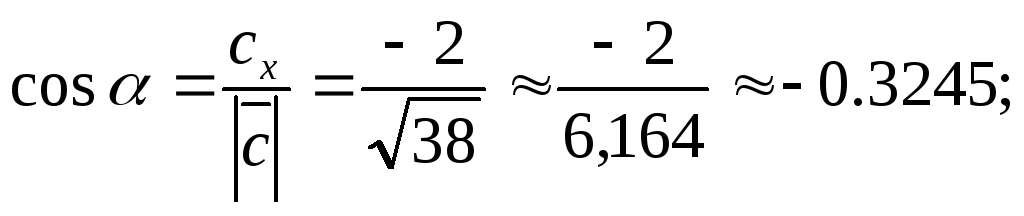
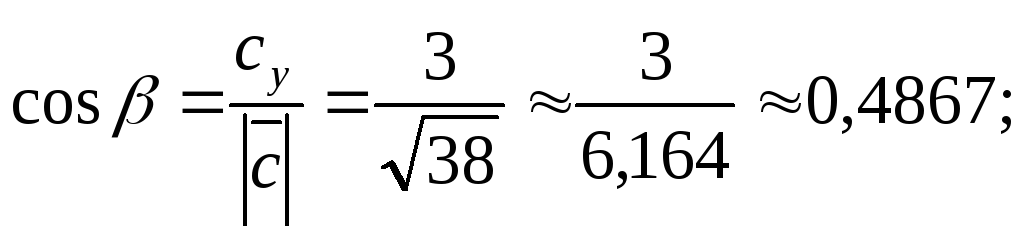
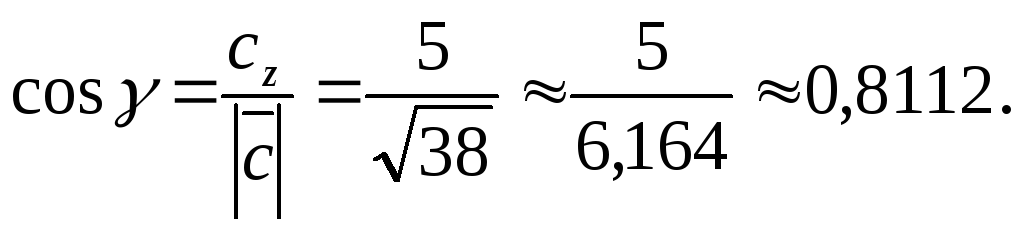
30. Проверим справедливость тождества (4.8):
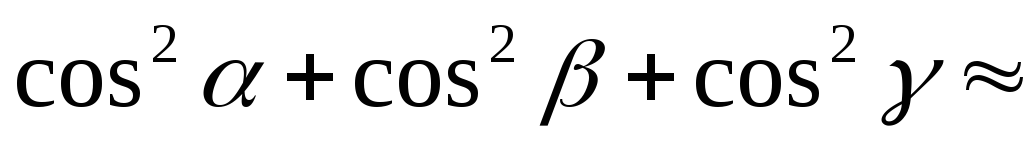
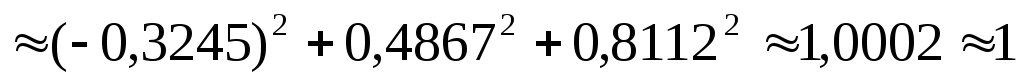
Ответ.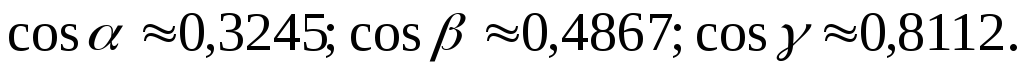
4.5. Координаты точки в пространстве. Вычисление координат вектора и его модуля по координатам его начала и конца.
В ведем
понятие координат точки в пространстве
через понятие радиус-вектора.
ведем
понятие координат точки в пространстве
через понятие радиус-вектора.
Определение 4.3. Радиус-вектором
точки М называется вектор 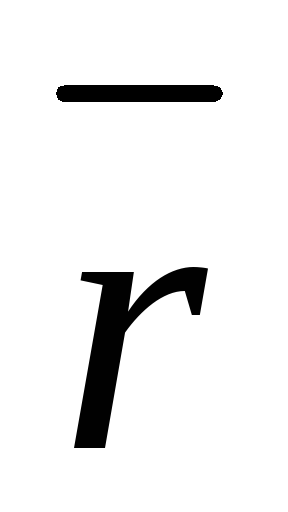 с началом в начале координат и концом
в точке М, то есть вектор
с началом в начале координат и концом
в точке М, то есть вектор  (рис. 4.3).
(рис. 4.3).
В качестве координат точки М примем координаты радиус-вектора.
Определение 4.4. Координатами точки в пространстве называются координаты ее радиус-вектора.
Координаты точки М (рис. 4.3) обозначаются
символом: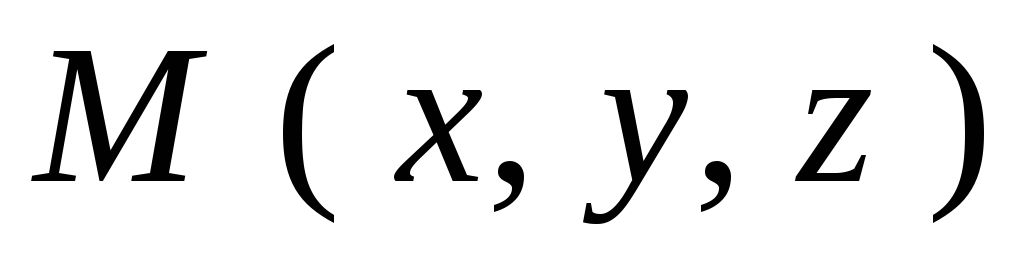 ,
или
,
или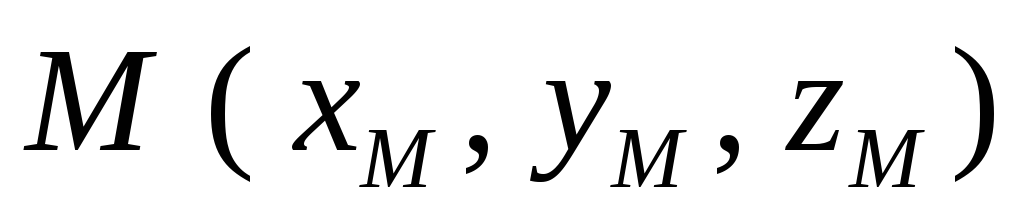 .
Таким образом,
.
Таким образом,
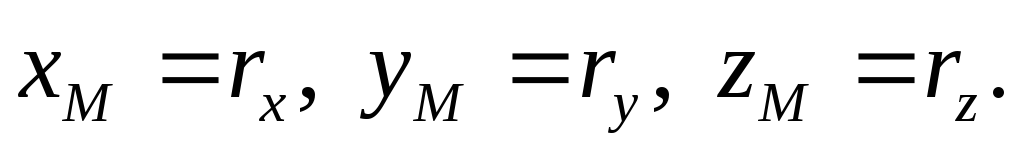
Поставим задачу:найти координаты
и модуль вектора 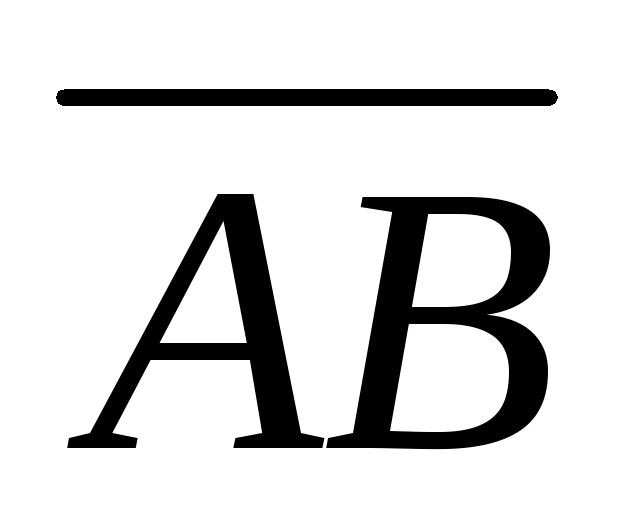 ,
если известны координаты его начала и
конца:
,
если известны координаты его начала и
конца: 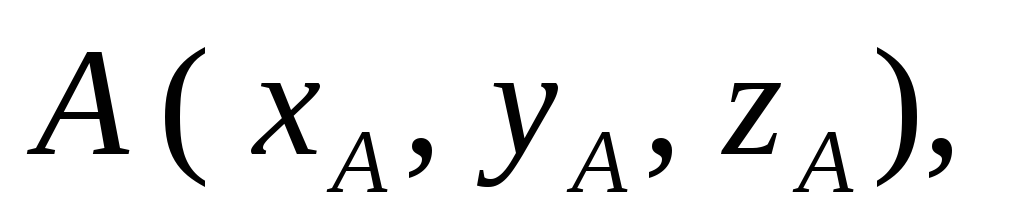
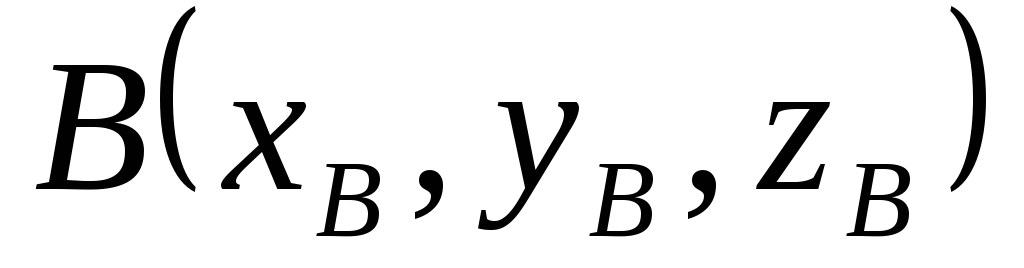 (рис. 4.4).
(рис. 4.4).
Р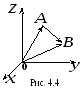 ешение.Проведем в точкиАиВ радиус-векторы
ешение.Проведем в точкиАиВ радиус-векторы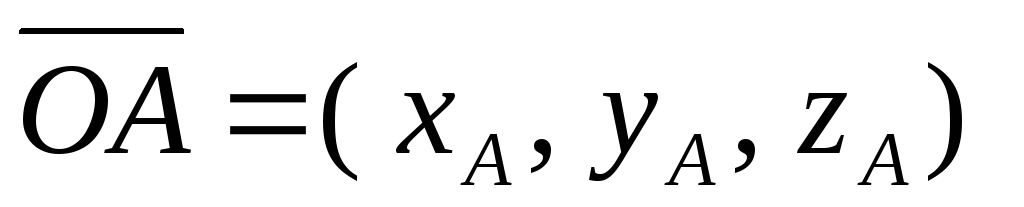 и
и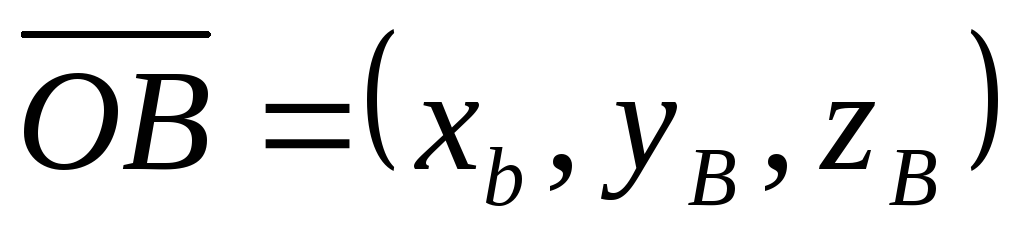 ,
выразим координаты вектора
,
выразим координаты вектора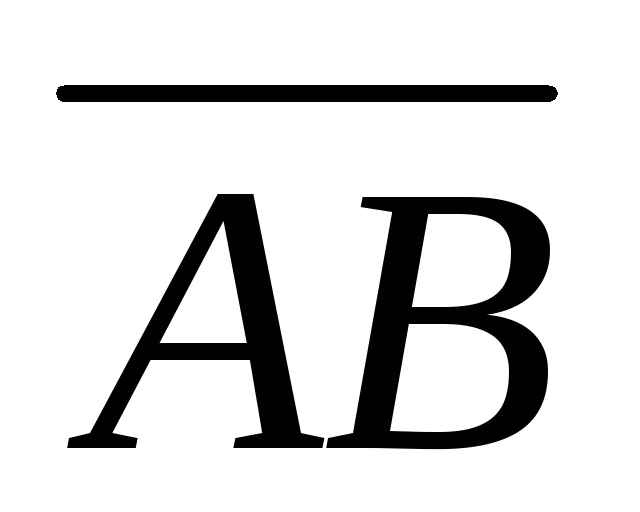 через координаты векторов
через координаты векторов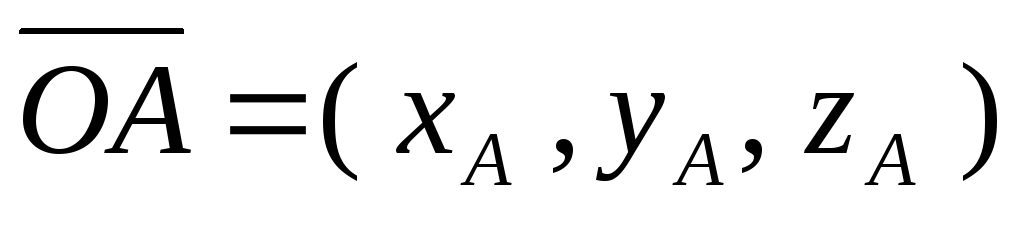 и
и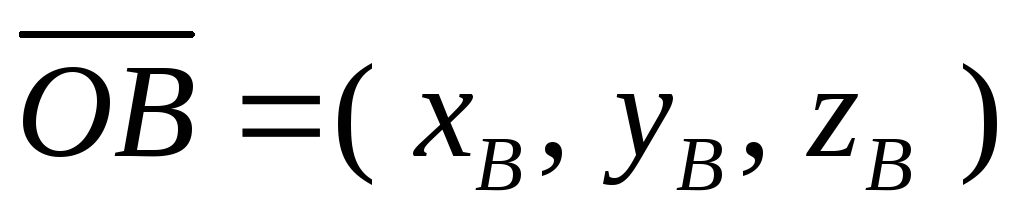 (см. определение 4.4), получим:
(см. определение 4.4), получим:
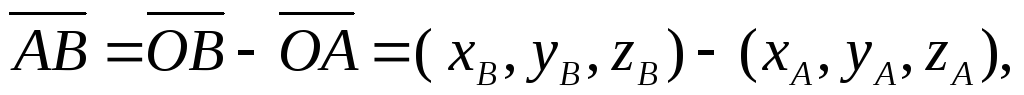
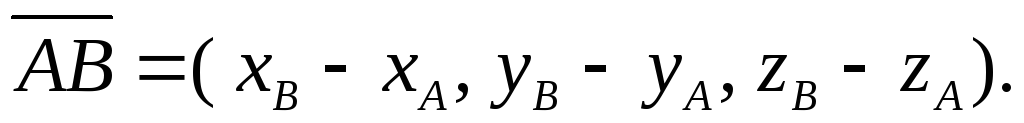 (4.9)
(4.9)
Координаты вектора равны соответствующим разностям координат конца и начала этого вектора.
Задача 4.3.Даны две точки: 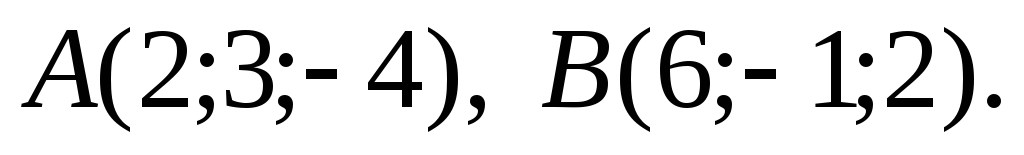 Найти координаты, разложение по ортам
координатных осей, модуль и направляющие
косинусы вектора
Найти координаты, разложение по ортам
координатных осей, модуль и направляющие
косинусы вектора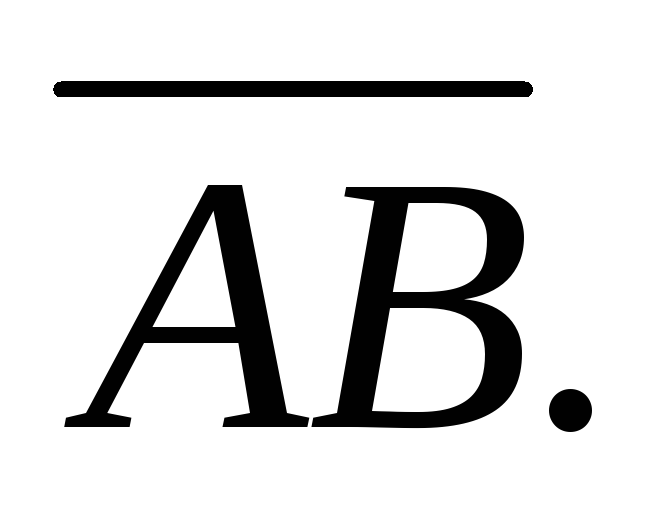
Решение.Для определения координат
вектора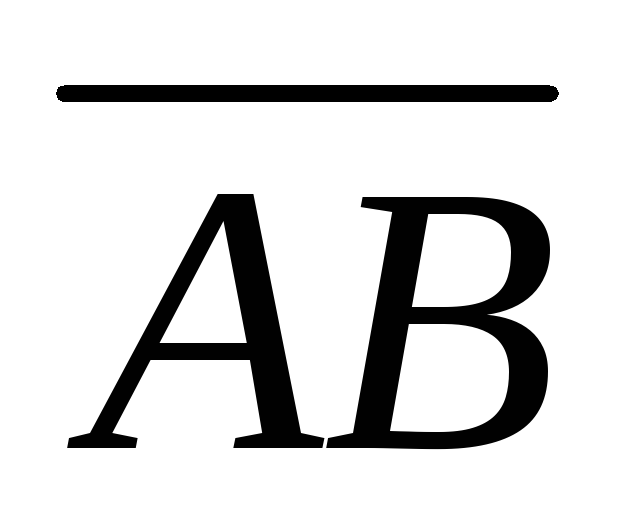 воспользуемся
формулой (4.9):
воспользуемся
формулой (4.9):
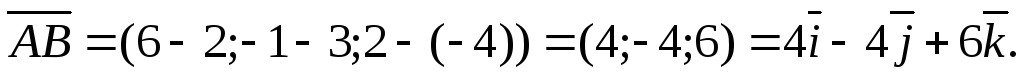
По формуле (4.4) вычислим модуль вектора 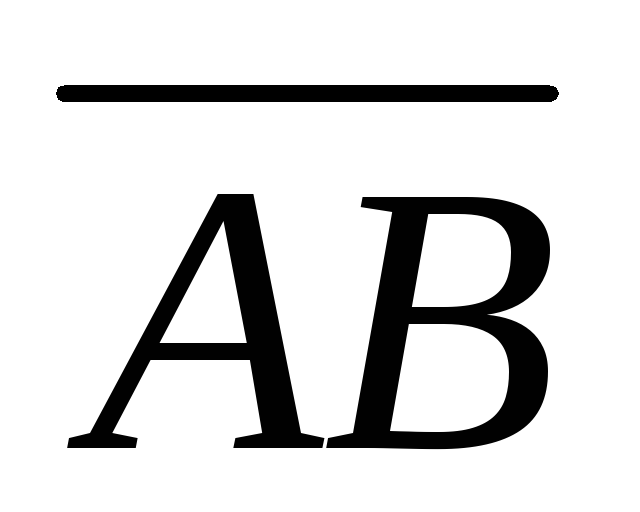 :
:
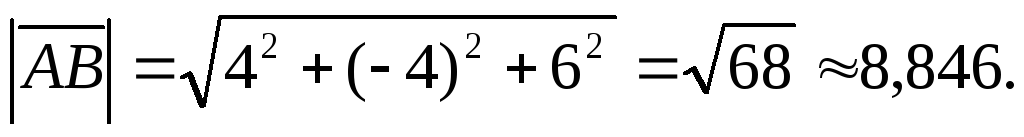
Найдем направляющие косинусы вектора 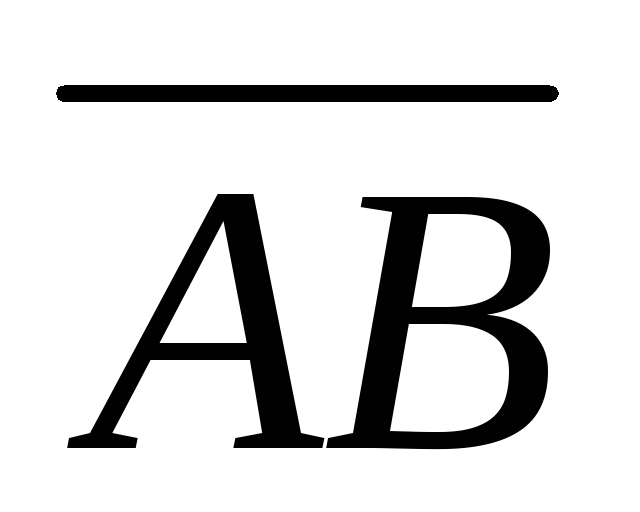 :
:
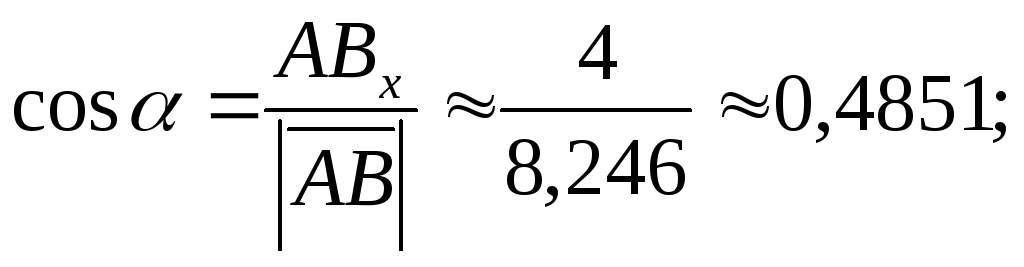
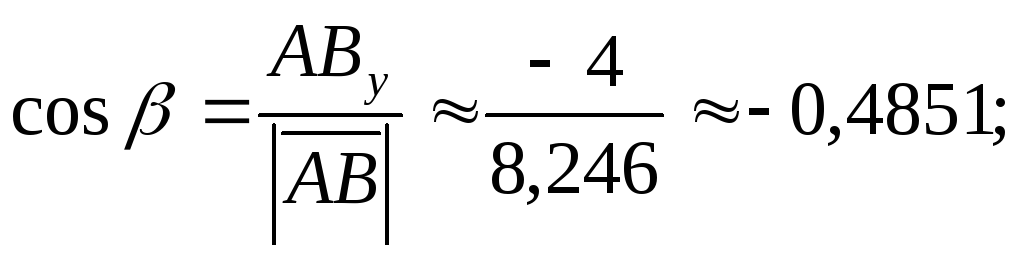

Вычислим сумму квадратов направляющих косинусов:
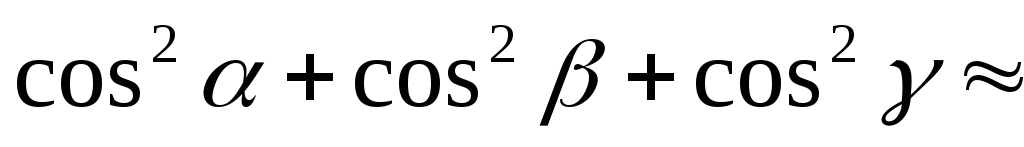
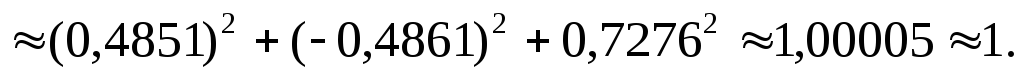
Ответ.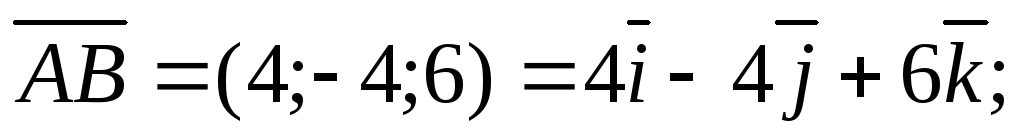
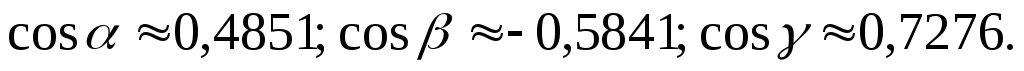
Скалярное произведение векторов
Геометрическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная произведению модулей этих векторов умноженного на косинус угла между ними:a · b = |a| · |b| cos α
Алгебраическая интерпретация. Скалярным произведением двух векторов a и b будет скалярная величина, равная сумме попарного произведения координат векторов a и b.
Формулы скалярного произведения векторов заданных координатами
Формула скалярного произведения векторов для плоских задач
В случае плоской задачи скалярное произведение векторов a = {ax ; ay} и b = {bx ; by} можно найти воспользовавшись следующей формулой:
a · b = ax · bx + ay · by
Формула скалярного произведения векторов для пространственных задач
В случае пространственной задачи скалярное произведение векторов a = {ax ; ay ; az} и b = {bx ; by ; bz} можно найти воспользовавшись следующей формулой:
a · b = ax · bx + ay · by + az · bz
Формула скалярного произведения n -мерных векторов
В случае n-мерного пространства скалярное произведение векторов a = {a1 ; a2 ; … ; an} и b = {b1 ; b2 ; … ; bn} можно найти воспользовавшись следующей формулой:
a · b = a1 · b1 + a2 · b2 + … + an · bn
Примеры задач на вычисление скалярного произведения векторов
Примеры вычисления скалярного произведения векторов для плоских задач
Пример 1. Найти скалярное произведение векторов a = {1; 2} и b = {4; 8}.Решение: a · b = 1 · 4 + 2 · 8 = 4 + 16 = 20.
Пример 2. Найти скалярное произведение векторов a и b, если их длины |a| = 3, |b| = 6, а угол между векторами равен 60˚.Решение: a · b = |a| · |b| cos α = 3 · 6 · cos 60˚ = 9.
Пример 3. Найти скалярное произведение векторов p = a + 3b и q = 5a — 3 b, если их длины |a| = 3, |b| = 2, а угол между векторами a и b равен 60˚.Решение:
p · q = (a + 3b) · (5a — 3b) = 5 a · a — 3 a · b + 15 b · a — 9 b · b == 5 |a|2 + 12 a · b — 9 |b|2 = 5 · 32 + 12 · 3 · 2 · cos 60˚ — 9 · 22 = 45 +36 -36 = 45.
Пример 4. Найти скалярное произведение векторов (a + 2i)·(b — 2j),если a = {1; 2} и b = {4; -8}.Решение: Запишем вектора a и b через ортонормированные базисные вектора i и j:
a = i + 2jb = 4i — 8j
Тогда используя свойства ортов (i2 = 1, j2 = 1, i·j = 0)
(a + 2i)·(b — 2j) = (i + 2j + 2i)·(4i — 8j — 2j) = (3i + 2j)·(4i — 10j) = 12i2 — 30i·j + 12j·i — 20j2 = 12 — 0 + 0 — 20 = -8
Пример вычисления скалярного произведения векторов для пространственных задач
Пример 5. Найти скалярное произведение векторов a = {1; 2; -5} и b = {4; 8; 1}.Решение: a · b = 1 · 4 + 2 · 8 + (-5) · 1 = 4 + 16 — 5 = 15.
Пример вычисления скалярного произведения для n -мерных векторов
Пример 6. Найти скалярное произведение векторов a = {1; 2; -5; 2} и b = {4; 8; 1; -2}.Решение: a · b = 1 · 4 + 2 · 8 + (-5) · 1 + 2 · (-2) = 4 + 16 — 5 -4 = 11.
модуль вектора — с русского на английский
См. также в других словарях:
модуль вектора — величина вектора — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы величина вектора EN absolute value of a vector … Справочник технического переводчика
модуль вектора — vektoriaus modulis statusas T sritis fizika atitikmenys: angl. absolute value of vector vok. Vektorbetrag, m rus. длина вектора, f; модуль вектора, m pranc. module d’un vecteur, m … Fizikos terminų žodynas
Модуль вектора — Модулем (длиной) вектора называется длина(норма) соответствующего вектора AB и обозначается как . В евклидовом n мерном пространстве длина вектора рассчитывается как корень из скалярного произведения этого вектора на себя, в том случае если это… … Википедия
Модуль — (от лат. modulus «маленькая мера»): В Викисловаре есть статья «модуль» Мо … Википедия
Модуль (значения) — Модуль (от лат. modulus «маленькая мера») составная часть, отделимая или хотя бы мысленно выделяемая из общего. Модульной обычно называют вещь, состоящую из чётко выраженных частей, которые нередко можно убирать или добавлять, не разрушая вещь… … Википедия
Модуль числа — Абсолютная величина или модуль вещественного или комплексного числа x есть расстояние от x до начала координат. Более точно: Абсолютная величина вещественного числа x есть неотрицательное число, обозначаемое |x| и определяемое следующим образом:… … Википедия
модуль волнового вектора — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN magnitude of propagation vector … Справочник технического переводчика
модуль конвольвера кодового вектора огибающей — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN shape codevector convolution module … Справочник технического переводчика
Модуль комплексного числа — Модулем комплексного числа называется длина вектора, соответствующего этому числу: . Модуль комплексного числа z обычно обозначается | z | или r. Пусть и вещественные числа такие, что комплексное число (обычные обозначения). Тогда Числа … Википедия
Модуль (в математике) — Модуль в математике, 1) М. (или абсолютная величина) комплексного числа z = х + iy есть число ═(корень берётся со знаком плюс). При представлении комплексного числа z в тригонометрической форме z = r(cos j + i sin j) действительное число r равно… … Большая советская энциклопедия
МОДУЛЬ — абелева группа с кольцом операторов. М. является обобщением (линейного) векторного пространства над полем Кдля случая, когда Кзаменяется нек рым кольцом. Пусть задано кольцо А. Аддитивная абелева группа Мназ. левым А модулем, если определено… … Математическая энциклопедия
Как найти модуль вектора?
Наука
- Анатомия и физиология
- Астрономия
- Астрофизика
- Биология
- Химия
- наука о планете Земля
- Наука об окружающей среде
- Органическая химия
- Физика
Математика
- Алгебра
- Исчисление
- Геометрия
Векторов
Это вектор:
Вектор имеет величину , (размер) и направление :
Длина линии показывает ее величину, а стрелка указывает направление.
Мы можем сложить два вектора, соединив их голова к хвосту:
И неважно, в каком порядке мы их добавляем, результат будет тот же:
Пример: самолет летит на север, но ветер дует с северо-запада.
Два вектора (скорость, создаваемая воздушным винтом, и скорость ветра) приводят к немного меньшей путевой скорости при движении немного к востоку от севера.
Если бы вы смотрели на самолет с земли, казалось бы, он немного поскользнулся.
Вы когда-нибудь видели это? Возможно, вы видели птиц, борющихся с сильным ветром, которые, кажется, летят боком. Векторы помогают это объяснить.
Скорость, ускорение, сила и многое другое — векторы.
Вычитание
Мы также можем вычесть один вектор из другого:
- сначала мы меняем направление вектора, который хотим вычесть,
- , затем добавьте их как обычно:
а — б
Обозначение
Вектор часто пишется жирным шрифтом , например a или b .
| Вектор также можно записать как буквы его головы и хвоста со стрелкой над ним, например: |
Расчеты
Сейчас… как мы делаем расчеты?
Самый распространенный способ — сначала разбить векторы на части x и y, например:
Вектор a разбит на
, два вектора a x и a y
(Позже мы увидим, как это сделать.)
Добавление векторов
Затем мы можем сложить векторы на , сложив части x и , добавив части y :
Вектор (8, 13) и вектор (26, 7) складываются в вектор (34, 20)
Пример: складываем векторы a = (8, 13) и b = (26, 7)
c = a + b
c = (8, 13) + (26, 7) = (8 + 26, 13 + 7) = (34, 20)
Когда мы разбиваем такой вектор, каждая часть называется компонентом :
Вычитание векторов
Для вычитания сначала переверните вектор, который мы хотим вычесть, а затем сложите.
Пример: вычесть k = (4, 5) из v = (12, 2)
a = v + — k
a = (12, 2) + — (4, 5) = (12, 2) + (−4, −5) = (12−4, 2−5) = (8, −3)
Величина вектора
Величина вектора показана двумя вертикальными полосами по обе стороны от вектора:
| a |
ИЛИ можно написать с двойной вертикальной чертой (чтобы не путать с абсолютным значением):
|| a ||
Для его вычисления мы используем теорему Пифагора:
| a | = √ (х 2 + у 2 )
Пример: какова величина вектора b = (6, 8)?
| b | = √ (6 2 + 8 2 ) = √ (36 + 64) = √100 = 10
Вектор с величиной 1 называется единичным вектором.
Вектор против скалярного
Скаляр имеет величину (размер) только .
Скаляр: просто число (например, 7 или -0,32) … определенно не вектор.
Вектор имеет величину и направление и часто выделяется полужирным шрифтом , поэтому мы знаем, что это не скаляр:
- , поэтому c — вектор, его величина и направление
- , но c — это просто значение, например 3 или 12.4
Пример: k b на самом деле является скаляром k, умноженным на вектор b .
Умножение вектора на скаляр
Когда мы умножаем вектор на скаляр, это называется «масштабированием» вектора, потому что мы изменяем размер вектора.
Пример: умножить вектор m = (7, 3) на скаляр 3
| a = 3 м = (3 × 7, 3 × 3) = (21, 9) |
Он по-прежнему указывает в том же направлении, но в 3 раза длиннее
(И теперь вы знаете, почему числа называются «скалярами», потому что они «масштабируют» вектор вверх или вниз.)
Умножение вектора на вектор (скалярное произведение и перекрестное произведение)
Как умножить два вектора вместе? Есть несколько способов! (Подробности см. На этих страницах.) |
Более двух размеров
Векторы также отлично работают в трех и более измерениях:
Вектор (1, 4, 5)
Пример: складываем векторы a = (3, 7, 4) и b = (2, 9, 11)
c = a + b
c = (3, 7, 4) + (2, 9, 11) = (3 + 2, 7 + 9, 4 + 11) = (5, 16, 15)
Пример: какова величина вектора w = (1, −2, 3)?
| w | = √ (1 2 + (−2) 2 + 3 2 ) = √ (1 + 4 + 9) = √14
Вот пример с 4-мя измерениями (но его сложно нарисовать!):
Пример: вычесть (1, 2, 3, 4) из (3, 3, 3, 3)
(3, 3, 3, 3) + — (1, 2, 3, 4)
= (3, 3, 3, 3) + (−1, −2, −3, −4)
= (3 −1, 3−2, 3−3, 3−4)
= (2, 1, 0, −1)
Звездная величина и направление
Мы можем знать величину и направление вектора, но нам нужны его длины по осям x и y (или наоборот):
| <=> | ||
| Вектор a в полярных координатах | Вектор a в декартовых координатах |
Вы можете прочитать, как преобразовать их в полярные и декартовы координаты, но вот краткое описание:
| От полярных координат (r, θ ) до декартовых координат (x, y) | От декартовых координат (x, y) до полярных координат (r, θ) | |
|---|---|---|
|
|
Пример
Сэм и Алекс тянут ящик.
- Сэм тянет с силой 200 Ньютонов при 60 °
- Алекс тянет с усилием 120 Ньютонов под углом 45 °, как показано на рисунке
Что такое объединенная сила и ее направление?
Давайте сложим два вектора голова к хвосту:
Первое преобразование из полярной в декартову (до 2 десятичных знаков):
Вектор Сэма:
- x = r × cos ( θ ) = 200 × cos (60 °) = 200 × 0,5 = 100
- y = r × sin ( θ ) = 200 × sin (60 °) = 200 × 0.8660 = 173,21
Вектор Алекса:
- x = r × cos ( θ ) = 120 × cos (-45 °) = 120 × 0,7071 = 84,85
- y = r × sin ( θ ) = 120 × sin (-45 °) = 120 × -0,7071 = -84,85
Теперь у нас:
Добавьте их:
(100, 173,21) + (84,85, -84,85) = (184,85, 88,36)
Этот ответ верен, но давайте вернемся к полярному, поскольку вопрос был в полярном:
- r = √ (x 2 + y 2 ) = √ (184.85 2 + 88,36 2 ) = 204,88
- θ = tan -1 (y / x) = tan -1 (88,36 / 184,85) = 25,5 °
И у нас есть (округленный) результат:
А для Сэма и Алекса это выглядит так:
Они могли бы получить лучший результат, если бы стояли плечом к плечу!
.модуль вектора — это … Что такое модуль вектора?
Модуль непрерывности — В математическом анализе модуль непрерывности — это функция, используемая для количественного измерения однородной непрерывности функций. Таким образом, функция допускает ω как модуль непрерывности тогда и только тогда, когда для всех x и y в области определения f. Поскольку модули… Википедия
Геометрическая алгебра — В математической физике геометрическая алгебра — это полилинейная алгебра, технически описываемая как алгебра Клиффорда над реальным векторным пространством, снабженная невырожденной квадратичной формой.Неформально геометрическая алгебра — это алгебра Клиффорда, которая…… Wikipedia
твердое тело, механика — ▪ физика Введение в науку о напряжении (напряжении), деформации (деформации и течении) и разрушении твердых материалов и конструкций. Что же такое твердое тело? Любой материал, жидкий или твердый, может выдерживать нормальные силы.…… Universalium
Определяющее уравнение (физика) — Общую номенклатуру основных величин, используемых в этой статье, см. В разделе Физическая величина.Для 4-х векторных модификаций, используемых в теории относительности, см. Четыре вектора. Очень часто определяющие уравнения имеют форму определяющего уравнения, поскольку параметры…… Wikipedia
Комплексное число — Комплексное число может быть визуально представлено как пара чисел, образующих вектор на диаграмме, называемой диаграммой Аргана, представляющей комплексную плоскость. Re — действительная ось, Im — мнимая ось, а i — квадратный корень из –1. Комплекс…… Википедия
Дислокация — синтаксические операции см. В разделе Дислокация (синтаксис).Чтобы узнать о медицинских терминах, см. Вывих сустава. В материаловедении дислокация — это кристаллографический дефект или неоднородность кристаллической структуры. Наличие вывихов…… Википедия
Алгоритм Шёнхаге-Штрассена — Алгоритм Шёнхаге-Штрассена представляет собой асимптотически быстрый алгоритм умножения для больших целых чисел. Он был разработан Арнольдом Шёнхаге и Фолькером Штрассеном в 1971 году. [А. Шёнхаге и В. Штрассен, Schnelle Multiplikation großer Zahlen,…… Википедия
Углеродная нанотрубка — Не путать с углеродным волокном.Часть серии статей о наноматериалах фуллеренов… Wikipedia
Абсолютное значение — Философский термин см. В разделе Ценность (этика). Об альбоме Akrobatik см. Абсолютное значение (альбом). В математике абсолютное значение (или модуль) | a | действительного числа a — это числовое значение a независимо от его знака. Так, например,…… Википедия
Комплексное число с разбиением — Часть плоскости с комплексным числом разбиения, показывающая подмножества с модулем ноль (красный), один (синий) и минус один (зеленый).В абстрактной алгебре разделенные комплексные числа (или гиперболические числа) представляют собой двумерную коммутативную алгебру над действительной… Wikipedia
Линейная эластичность — Механика сплошной среды… Википедия
векторов Модуль вектора — это его величина.
Презентация на тему: «Векторы. Модуль вектора — это его величина» — стенограмма презентации:
1 Векторы Модуль вектора — это его величина.
Модуль упругости записывается как.Модуль записывается как Единичные векторы — это векторы с единичной величиной. — единичный вектор в направлении a. i, j и k — единичные векторы, параллельные осям Ox, Oy и Oz Вектор положения и его величина Вектор смещения 
2
Пример векторов Точки A, B и C имеют координаты (4, -2), (3, 3) и (-2, 1) соответственно, а O — начало координат. Найдите в терминах i и j векторы, параллельные векторам параллельны и в s раз больше его длины.
3 Единичные векторы Величина вектора Пример
Найдите величину каждого из этих векторов Единичные векторы в этих направлениях равны 
4
Пример Найдите вектор величиной 30 в направлении 6i -8j. Пример p = 4i + j q = 6i — 5j r = 3i + 4j. Найдите числа m и n, такие что mp + nq = r.i-й компонент: 4m + 6n = 3 [1] j-й компонент: m — 5n = 4 [2] [1] — 4 [2]: 26n = — 13 n = — ½ m = 1.5
5
Пример Найти вектор AB AB (iii) Вектор положения середины AB (i) (ii) (iii)
6
Пример. Учитывая, что v = i + 2j — 6k, найдите такое, что v = 7. Пример v1 = 3i + 2j — k, r2 = 2i — k.Найдите единичный вектор в направлении 2v1 — v2. Длина 2v1 — v2 =

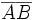 называется длина(норма) соответствующего вектора AB и обозначается как
называется длина(норма) соответствующего вектора AB и обозначается как 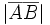 .
.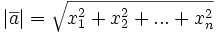 .
.