Задачи на нахождение периметра и площади
Площадь одной клетки равна 1см.
Найдите площадь фигуры, изображённой на рисунке A.
Найдите площадь фигуры, изображённой на рисунке B.
Найдите площадь фигуры, изображённой на рисунке C.
Найдите площадь фигуры, изображённой на рисунке D.
Найдите площадь фигуры, изображённой на рисунке E.
Определение:
Неправильный четырехугольник – фигура, у которой стороны не равны и не параллельны.
Решение:
разобьём неправильные четырехугольники A, B, D на два прямоугольных треугольника и прямоугольник, а неправильные четырехугольники C, E на два прямоугольных треугольника и квадрат.
Применив формулы площади треугольника, квадрата и прямоугольника легко решим поставленную задачу
Фигура A
S = a · b — формула площади прямоугольника, тогда
3 · 4 = 12 см² — площадь прямоугольника a
S = ½ · a · h — формула площади треугольника, тогда
½ ·1 · 5 = 2,5 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника
½ ·2 · 4 = 4 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры A
12 + 2,5 + 4 = 18,5 см²
Ответ: площадь фигуры A 18,5 см²
Фигура B
S = a · b — формула площади прямоугольника, тогда
5 · 1 = 5 см² — площадь прямоугольника a
S = ½ · a · h — формула площади треугольника, тогда
½ ·6 · 5 = 15 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ ·1 · 1 = 0,5 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры B
5 + 15 + 0,5 = 18,5 см²
Ответ: площадь фигуры B 20,5 см²
Фигура C
S = a · a; S = a² — формула площади квадрата, тогда
5 · 5 = 25 см² — площадь квадрата a
S = ½ · a · h — формула площади треугольника, тогда
½ · 1 · 6 = 3 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ · 1 · 5 = 2,5 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры C
25 + 3 + 2,5 = 30,5 см²
Ответ: площадь фигуры C 30,5 см²
Фигура D
S = a · b — формула площади прямоугольника, тогда
3 · 4 = 12 см² — площадь прямоугольника a
S = ½ · a · h — формула площади треугольника, тогда
½ ·1 · 5 = 2,5 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ ·2 · 4 = 4 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры A
12 + 2,5 + 4 = 18,5 см²
Ответ: площадь фигуры A 18,5 см²
Фигура E
S = a · a; S = a² — формула площади квадрата, тогда
2 · 2 = 4 см² — площадь квадрата a
S = ½ · a · h — формула площади треугольника, тогда
½ · 3 · 4 = 6 см² — площадь прямоугольного треугольника b
S = ½ · a · h — формула площади треугольника, тогда
½ · 2 · 2 = 2 см² — площадь прямоугольного треугольника c
теперь сложив полученные площади узнаем полную площадь фигуры E
4 + 6 + 2 = 12 см²
Ответ: площадь фигуры E 12 см²
xn--80abl6aqcjc8ic.xn--p1ai
Периметр квадрата, прямоугольника и треугольника в младших классах
Уже в младших классах школьники начинают изучать такие геометрические понятия, как периметр квадрата, периметр прямоугольника, периметр треугольника, площади геометрических фигур и даже объёмы простейших тел. Подготовить своего ребенка к продуктивному восприятию этих тем по геометрии можно и дома. Задачи с решениями для начальных классов, которые приведены ниже, могут послужить учителю младших классов при подготовке к уроку по математике. Их могут использовать родители, которые пожелают закрепить пройденный материал по математике со своими детьми.
Задача 1: Сторона квадрата равна длине прямоугольника. На сколько периметр квадрата больше периметра прямоугольника, если ширина прямоугольника 4 см, причем она на 1 см меньше чем его длина?
Решение: opened=0
Найдем длину прямоугольника 4 см + 1 см = 5 см.
Найдем периметр прямоугольника 5 см + 5 см + 4 см + 4 см = 18 см.
Поскольку сторона квадрата равна длине прямоугольника, то сторона квадрата 5 см.
Найдем периметр квадрата 5 см + 5 см +5 см + 5 см = 20 см.
20 см – 18 см = 2 см – на столько сантиметров периметр квадрата больше периметра прямоугольника.
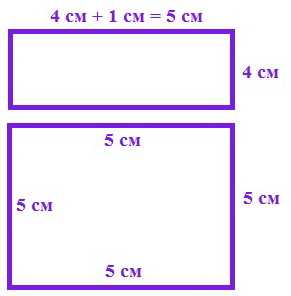
Комментарии: Ученику следует объяснить, что означает «больше на», «меньше на» и как найти некоторую величину по таким зависимостям. Важно напомнить, что такое квадрат и что такое прямоугольник. Чем похожи эти фигуры? В чем их разница? Что такое периметр? Что нужно знать, чтобы найти периметр квадрата, прямоугольника? В чем может измеряться периметр? Зачем знать периметр фигуры?
Школьнику нужно сразу показывать, где применяются знания по математике, чтобы он понимал, что математика везде. Для ученика, который успевает по математике, это будет, как минимум интересно, а для того, кому математика не по душе, это станет подспорьем собрать свою волю в кулак и разобраться с неясностями. Ведь без математики никуда!
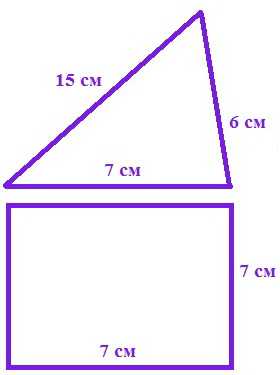
Задача 2: Длина сторон треугольника 15 см, 7 см, 6 см. Его периметр равен периметру квадрата. Найдите сторону такого квадрата.
Решение: opened=0
Найдем периметр треугольника 15 см + 7 см + 6 см = 28 см.
У квадрата и треугольника одинаковые периметры, значит периметр квадрата тоже 28 см. У квадрата 4 одинаковые стороны, значит длина его стороны 28:4 = 7 см.
Задача 3: Ширина прямоугольника 3 см, она на 4 см меньше его длины. Периметр прямоугольника на 8 см больше периметра квадрата. Найдите сторону квадрата.
Решение: opened=0
Найдем длину прямоугольника 3 см + 4 см = 7 см.
Найдем периметр этого прямоугольника 7 см + 7 см + 3 см + 3 см = 7 см + 3 см + 7 см + 3 см = 10 см + 10 см = 20 см.
Найдем периметр квадрата 20 см — 8 см = 12 см. Поскольку у квадрата 4 одинаковые стороны, а его периметр равен 12 см, то длина одной стороны 12:4 = 3 см.
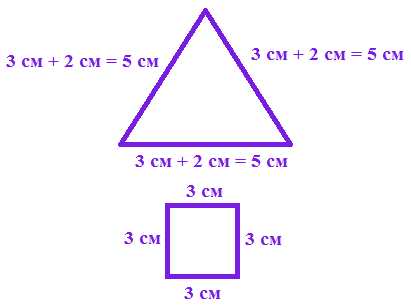
Задача 4: Имеется треугольник с равными сторонами и квадрат, сторона которого на 2 см короче, чем сторона треугольника. На сколько сантиметров периметр треугольника больше периметра квадрата, если сторона квадрата 3 см?
Решение: opened=0
Найдем длину стороны треугольника 3 см + 2 см = 5 см.
Найдем периметр квадрата 3 см + 3 см + 3 см + 3 см = 12 см.
Найдем периметр треугольника 5 см + 5 см + 5 см + 5 см = 20 см.
20 см – 12 см = 8 см – на столько сантиметров периметр треугольника больше периметра квадрата.
Задача 5: Периметр прямоугольника равен половине разности периметра треугольника ABC и 1 см. Найди ширину прямоугольника, если его длина равна меньшей стороне треугольника ABC, у которого сторона ВС вдвое длиннее стороны АС, сторона АВ равна 3 см 3 мм, а сторона АС на 14 мм короче стороны АВ.
Решение этой и других задач, которые находятся на нашем сайте вы можете узнать абсолютно бесплатно, обратившись к администратору Этот адрес электронной почты защищен от спам-ботов. У вас должен быть включен JavaScript для просмотра..
Изучите еще больше задач по геометрии для детей младшего школьного возраста.
belmathematics.by
1)Периметр и площадь треугольника и квадрата. 2)
1)Периметр и площадь треугольника и квадрата. 2)
Ответы:
Формула для вычисления площади квадрата имеет следующий вид: S=a*a=a2 Формула для вычисления периметра квадрата: P=4*a где a — сторона квадрата.
Прямоугольник — это четырёхугольник, у которого четыре прямых угла. Размеры прямоугольника задаются длиной его сторон, обозначаемых обычно a и b. Прямоугольник, все стороны которого равны (a=b) называется квадратом. Свойства прямоугольника противолежащие стороны равны и параллельны друг другу; диагонали равны и в точке пересечения делятся пополам; сумма квадратов диагоналей равна сумме квадратов всех (четырех) сторон; прямогугольниками одного размера можно полностью замостить плоскость; прямоугольник можно двумя способами разделить на два равных между собой прямоугольника; прямоугольник можно разделить на два равных между собой прямогульных треугольника; вокруг прямоугольника можно описать окружность, диаметр которой равен диагонали прямоугольника; в прямогульник (кроме квадрата) нельзя вписать окружность так, чтобы она касалась всех его сторон. Параллельность сторон, одинаковость углов и возможность замощения плоскости делают прямоугольник самой удобной геометрической фигурой при разбиении площади на участки будь то на местности, в помещении или внутри технического устройства. Участок можно считать прямоугольным, если его отклонения от идеального прямоугольника не превышают допустимой в расчетах погрешности. Тогда для периметр и площадь участка можно определять по формулам расчета периметра и площади прямоугольника. Периметр P прямоугольника равен удвоенной сумме сторон, прилежащих к одному углу P = 2(a + b). Длина диагонали d прямоугольника вычисляется по теореме Пифагора: d = √(a2 + b2). Углы между диагоналями прямоугльника определяются соотношением сторон: α = 2arctg(a/b), β = 2arctg(b/a), α + β = 180°. Площадь S прямоугольника равна произведению сторон, прилежащих к одному углу (произведению длины на ширину): S = a·b. Также можно выразить площадь прямоугольника через длину диагоналей и угол между ними: S = d2·sin(α/2)·cos(α/2). Радиус описанной вокруг прямоугольника окружности равен половине длины диагонали: R = √(a2 + b2)/2. В прямоугольник (если он не квадрат) нельзя вписать окружность так, чтобы она касалась всех его сторон. Максимальный радиус окружности, которая может поместиться внутри прямоугольника, равен половине его меньшей стороны.
cwetochki.ru
