Площадь квадрата
Площадь квадрата – это численная характеристика, характеризующая размер плоскости, ограниченной четырьмя последовательно соединенными отрезками (сторонами) одинаковой длины, у которой противоположные стороны попарно параллельны, а угол между любыми двумя смежными сторонами равен 90 градусов.
Для вычисления площади квадрата применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор, который поможет вычислить площадь или проверить уже выполненные вычисления.
1
Площадь квадрата через его сторону
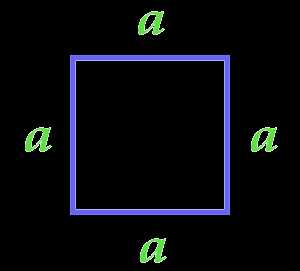
a — сторона
… подготовка …
2
Площадь квадрата через его диагональ

d — диагональ
… подготовка …
3
Площадь квадрата через периметр

P — периметр
… подготовка …
4
Площадь квадрата через отрезок проведенный из вершины квадрата к середине противоположной стороны

k — отрезок
… подготовка …
5
Площадь квадрата через радиус вписанной окружности

r — радиус вписанной окружности
… подготовка …
6
Площадь квадрата через радиус описанной окружности
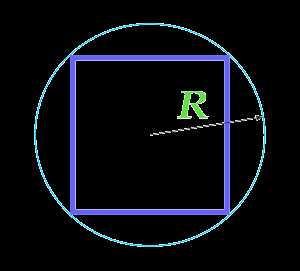
R — радиус описанной окружности
… подготовка …
Определения
Квадрат – это геометрическая фигура, образованная четырьмя последовательно соединенными отрезками (сторонами) одинаковой длины, у которой противоположные стороны попарно параллельны, а угол между любыми двумя смежными сторонами равен 90 градусов.
Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.
Площадь измеряется в единицах измерения в квадрате: км2, м2, см2, мм2 и т.д.
doza.pro
Как найти площадь и периметр квадрата 3 класс формула
В прямоугольном треугольнике один из катетов равен * Треугольник Математика / Русский язык 9 класс.
Площадь фигур
Две фигуры называют равными, если одну их них можно так наложить на другую, что эти фигуры совпадут.
Площади равных фигур равны. Их периметры тоже равны.
Площадь квадрата
Для вычисления площади квадрата нужно умножить его длину на саму себя.
Формулу площади квадрата, зная определение степени, можно записать следующим образом:
Площадь прямоугольника
Для вычисления площади прямоугольника нужно умножить его длину на ширину.
Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т. д.
Площадь сложных фигур
Площадь всей фигуры равна сумме площадей её частей.
Задача: найти площадь огородного участка.
Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя правило выше.
Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.
Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = 30 + 35 = 65 м 2
Ответ: S = 65 м 2 — площадь огородного участка.
Свойство ниже может вам пригодиться при решении задач на площадь.
Диагональ прямоугольника делит прямоугольник на два равных треугольника.
Площадь любого из этих треугольников равна половине площади прямоугольника.
Вначале найдём площадь прямоугольника по формуле.
Как найти площадь и периметр квадрата 3 класс формула
Площадь фигур
Две фигуры называют равными, если одну их них можно так наложить на другую, что эти фигуры совпадут.
Площади равных фигур равны. Их периметры тоже равны.
Площадь квадрата
Для вычисления площади квадрата нужно умножить его длину на саму себя.
Формулу площади квадрата, зная определение степени, можно записать следующим образом:
Площадь прямоугольника
Для вычисления площади прямоугольника нужно умножить его длину на ширину.
Нельзя вычислять периметр или площадь, если длина и ширина выражены в разных единицах длины.
Обязательно проверяйте, чтобы и длина, и ширина были выражены в одинаковых единицах, то есть обе в см, м и т. д.
Площадь сложных фигур
Задача: найти площадь огородного участка.
Так как фигура на рисунке не является ни квадратом, ни прямоугольником, рассчитать её площадь можно используя правило выше.
Разделим фигуру на два прямоугольника, чьи площади мы можем легко рассчитать по известной формуле.
Чтобы найти площадь всей фигуры, сложим площади найденных прямоугольников.
S = 30 + 35 = 65 м 2
Ответ: S = 65 м 2 — площадь огородного участка.
Свойство ниже может вам пригодиться при решении задач на площадь.
Диагональ прямоугольника делит прямоугольник на два равных треугольника.
Площадь любого из этих треугольников равна половине площади прямоугольника.
Вначале найдём площадь прямоугольника по формуле.
Как найти площадь и периметр квадрата 3 класс формула
Как найти площадь и периметр квадрата 3 класс формула
V — скорость t — время
1)Чтобы найти скорость, надо расстояние разделить на время
2)чтобы найти время, надо расстояние разделить на скорость
Формула площади прямоугольникаФормула площади квадрата
Формула площади прямоугольного треугольника
(Площадь прямоугольного треугольника равна половине произведения его катетов)
Формула периметра прямоугольника
Формула периметра квадрата
Формула объёма прямоугольного параллелепипеда
1.Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше.
2.Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше.
1.Чтобы найти часть числа, выраженную дробью, надо это число разделить на знаменатель и умножить на числитель дроби.
2. Чтобы найти число по его части, выраженной дробью, надо разделить эту часть на числитель и умножить на знаменатель дроби.

3 способа как найти площадь квадрата, формула
Квадра́т — правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.
Википедия
Способ № 1: Расчёт площади квадрата по размеру стороны
Расчёт по стороне
Введите размер стороны квадрата
Площадь квадрата равна
Рассчитать
Способ № 2: Найти площадь квадрата по диагонали
Расчёт по диагонали квадрата
Введите размер диагонали
Площадь квадрата равна
Рассчитать
Способ № 3: Найти площадь квадрата зная периметр
Расчёт по диагонали квадрата
Введите периметр
Площадь квадрата равна
Рассчитать

Как рассчитать площадь квадрата формулы, примеры расчёта
Находим площадь по стороне квадрата, формула расчёта
Формула: S=A²
S- площадь квадрата
А- сторона квадрата
Пример расчёта
А= 10см
Рассчёт будет таким:
S = 10²=10×10=100
Ответ: площадь квадрата равна 100см
Как найти площадь квадрата по диагонали, формула расчёта
Формула: S=D²/2
S- площадь квадрата
D- диагональ квадрата
Пример расчёта площади по диагонали
Диагональ D= 30см
Рассчёт будет таким:
S = 30²/2=(30×30)/2 =450см
Ответ: площадь квадрата равна 450см
Как найти площадь квадрата если известен периметр формулы, пример расчёта
Формула: S=(Р/4)²
S- площадь квадрата
P- периметр квадрата
Пример расчёта
Р= 40см
Рассчёт будет таким:
S = 40/4=10×10=100
Ответ: площадь квадрата равна 100см
home-my.ru
Как найти площадь квадрата | Треугольники
Как найти площадь квадрата?
Площадь квадрата может быть найдена по его стороне, диагонали, радиусам вписанной и описанной окружности.
1. Площадь квадрата равна квадрату его стороны.
Формула для нахождения площади квадрата по его стороне:
Например, площадь квадрата ABCD можно найти как квадрат его стороны AB:
2. Площадь квадрата равна половине квадрата диагонали его стороны.
Формула для нахождения площади квадрата по его диагонали:
Например, площадь квадрата ABCD можно найти через его диагональ AC:
3. Площадь квадрата в четыре раза больше квадрата радиуса вписанной к него окружности.
Так как
то из формулы площади квадрата по стороне получаем
формулу для нахождения площади квадрата через радиус вписанной окружности:
4. Площадь квадрата равна удвоенному квадрату радиуса описанной около него окружности.
Так как
то из формулы площади квадрата по стороне вытекает
формула для нахождения площади квадрата через радиус вписанной окружности:
www.treugolniki.ru
Площадь квадрата
Квадрат — это правильный четырёхугольник, у которого все стороны и углы равны между собой.
Площадь квадрата равна квадрату его стороны:
Доказательство
Начнем с того случая, когда a = 1/n, где n является целым числом.
Возьмем квадрат со стороной 1 и разобьем его на n2 равных квадратов так, как показано на рисунке 1.
Так как площадь большого квадрата равна единице, то площадь каждого маленького квадрата равна 1/n2. Сторона каждого маленького квадрата равна 1/n, т. е. равна a. Итак,
Пусть теперь число a представляет собой конечную десятичную дробь, содержащую n знаков после запятой (в частности, число a может бать целым, и тогда n = 0)
При этом каждая сторона данного квадрата разобьется на m равных частей, и, значит, сторона любого маленького квадрата равна
a/m = a / (a · 10n) = 1/10n.
По формуле (1) площадь маленького квадрата равна (1/10n)2. Следовательно, площадь S данного квадрата равна
m2 · (1/10n)2 = (m/10n)2 = ((a · 10n)/10n)2 = a2.
Наконец, пусть число a представляет собой бесконечную десятичную дробь. Рассмотрим число an, получаемое из a отбрасыванием всех десятичных знаков после запятой, начиная с (n + 1)-го. Так как число a отличается от an не более чем на 1/10n, то an ≤ a ≤ an + 1/10n, откуда
an2 ≤ a2 ≤ (an + 1/10n)2. (2)
Ясно, что площадь S данного квадрата заключена между площадью квадрата со стороной an и площадью квадрата со стороной an + 1/10n:
т. е. между an2 и (an + 1/10n)2:
an2 ≤ S ≤ (an + 1/10n)2. (3)
Будем неограниченно увеличивать число n. Тогда число 1/10n будет становиться сколь угодно малым, и, значит, число (an + 1/10n)2 будет сколь угодно мало отличаться от числа an2. Поэтому из неравенств (2) и (3) следует, что число S сколь угодно мало отличается от числа a2. Следовательно, эти числа равны: S = a2, что и требовалось доказать.
Так же площадь квадрата можно найти с помощью следующих формул:
S = 4r2,
S = 2R2,
где r — радиус вписанной в квадрат окружности,
R — радиус описанной вокруг квадрата окружности.
Другие заметки по алгебре и геометрии
edu.glavsprav.ru
что такое площадь квадрата и как её найти?
я это знал уже в 3-4 классе
одна сторона, умноженная на другую, равна площади квадрата. Например 10 х 10 = 100 кв. м
площадь это то сколько места занимает этот квадрат и это размер квадрата умнажаешь две стороны друг на друга Например, сторона квадрата равна 3 сантиметра значит площадь равна 3 см умножено на 3 см равно девять Формула: S=a*a=3см*3см=9см2 Или если проходили степени то площадь равна сторона в квадрате (во второй степени) S=a2=(3см) 2=9см2
Площадь-это размер пространства до границ фигуры внутри. площадь квадрата, если обозначить сторону за А равна А^2 (А в квадрате)
площадь это сторона + сторона
что это? Это член в жопу (секс)
touch.otvet.mail.ru
Формула площади квадрата
Площадь квадрата равна квадрату его стороны.
Что такое Квадрат? Квадрат — это четырехугольник, у которого все стороны равны, а все углы прямые (равны 90°).
На рисунке изображен квадрат ABCD
у него:
AB=BC=CD=DA
\( \angle A \) = \( \angle B \) = \( \angle C \) = \( \angle D \) = \( 90^{o} \)
1. Площадь квадрата со стороной a равна квадрату стороны, то есть:
\( \LARGE S = a^{2} \)
2. Если известна диагональ квадрата d, то его площадь равна:
\( \LARGE S = \frac{ d^{2} }{2} \)
Свойства квадрата
Диагонали квадрата равны и пересекаются под прямым углом: AC = BD, \( \angle O \) = \( 90^{o} \)
В любой квадрат можно вписать окружность и вокруг любого квадрата можно описать окружность. Центром вписанной и описанной окружностей есть точка пересечения диагоналей квадрата. При этом радиусы и вписанной rи описанной R окружностей связаны с длиной его стороны aследующими соотношениями:
\[ r = \frac{ a }{2} \]
\[ R = \frac{ \sqrt{2} }{2} \cdot a \]
Свойства и признаки квадрата (необходимые и достаточные условия того, что четырехугольник — квадрат)
- Если четырехугольник — квадрат, то для него справедливы все следующие утверждения.
- Если для четырехугольника справедливо хотя бы одно из следующих утверждений, то он — квадрат.
Утверждения.
- Все стороны равны и среди внутренних углов есть прямой угол.
- Диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.
- Четырехугольник имеет 4 оси симметрии: прямые, перпендикулярные сторонам и проходящие через их середины; прямые, содержащие диагонали.
- Четырехугольник обладает поворотной симметрией: он не изменится при повороте на 90°
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Не можешь написать работу сам?
Доверь её нашим специалистам
от 100 р.стоимость заказа
2 часамин. срок
Узнать стоимость
Поделитесь с другими:
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
calcsbox.com
