Площадь определяется как – * (). , , ,

Приказ Министерства экономического развития Российской Федерации (Минэкономразвития России) от 30 сентября 2011 г. N 531 г. Москва «Об утверждении Требований к определению площади здания, помещения»

Зарегистрирован в Минюсте РФ 7 ноября 2011 г.

Регистрационный N 22231

В соответствии с частью 10 статьи 41 Федерального закона от 24 июля 2007 г. N 221-ФЗ «О государственном кадастре недвижимости» (Собрание законодательства Российской Федерации, 2007, N 31, ст. 4017; 2008, N 30, ст. 3597, 3616; 2009, N 1, ст. 19; N 19, ст. 2283; N 29, ст. 3582; N 52, ст. 6410, 6419; 2011, N 1, ст. 47; N 23, ст. 3269; N 27, ст. 3880; N 30, ст. 4563, 4594) приказываю:

Утвердить Требования к определению площади здания, помещения согласно приложению.

Министр Э. Набиуллина

Требования к определению площади здания, помещения

I. Общие требования к определению площадей

1. Площадь и общая площадь здания, помещения определяются как площадь простейшей геометрической фигуры (прямоугольник, трапеция, прямоугольный треугольник и т. п.) или путем разбивки такого объекта на простейшие геометрические фигуры и суммирования площадей таких фигур.

2. Значение площади и общей площади здания, помещения определяется в квадратных метрах с округлением до 0,1 квадратного метра, а значения измеренных расстояний, применяемые для определения площадей, — метрах с округлением до 0,01 метра.

3. Для помещений в зданиях, возведенных по типовым проектам из сборных конструкций заводского изготовления с типовой планировкой на этажах, допускается производить определение площадей по подвальному, первому и типовому этажу. Для последующих этажей площадь может быть принята по типовому, за исключением помещений, в которых имеются изменения планировки.

II. Определение площади здания, помещения

4. Площадь здания определяется как сумма площадей всех надземных и подземных этажей (включая технический, мансардный, цокольный).

Площадь этажа следует измерять в пределах внутренних поверхностей наружных стен на высоте 1,1 — 1,3 метра от пола.

Площадь этажа при наклонных наружных стенах измеряется на уровне пола.

В площадь здания включается площадь антресолей, галерей и балконов зрительных и других залов, веранд, наружных застекленных лоджий и галерей.

В площадь здания отдельно включается также площадь открытых неотапливаемых планировочных элементов здания (включая площадь эксплуатируемой кровли, открытых наружных галерей, открытых лоджий и т.п.).

Площадь многосветных помещений, а также пространство между лестничными маршами более ширины марша и проемы в перекрытиях более 36 квадратных метров следует включать в площадь здания в пределах только одного этажа.

5. Площадь помещения определяется как сумма площадей всех частей такого помещения, рассчитанных по их размерам, измеряемым между отделанными поверхностями стен и перегородок на высоте 1,1 — 1,3 метра от пола.

III. Определение общей площади жилого помещения, жилого дома

6. Общая площадь жилого помещения, жилого дома состоит из суммы площади всех частей такого помещения, жилого дома, включая площадь помещений вспомогательного использования, предназначенных для удовлетворения гражданами бытовых и иных нужд, связанных с их проживанием в жилом помещении, за исключением балконов, лоджий, веранд и террас.

К площади помещений вспомогательного использования относятся площади кухонь, коридоров, ванн, санузлов, встроенных шкафов, кладовых, а также площадь, занятая внутриквартирной лестницей.

Измерение расстояний, применяемых для определения общей площади жилого помещения, жилого дома, производится по всему периметру стен на высоте 1,1 — 1,3 метра от пола.

При определении общей площади жилого помещения, жилого дома надлежит:

— площадь ниш высотой 2 метра и более включать в общую площадь помещений, в которых они расположены. Площади арочных проемов включать в общую площадь помещения, начиная с ширины 2 метра;

— площадь пола под маршем внутриквартирной лестницы, при высоте от пола до низа выступающих конструкций марша 1,6 метра и более, включать в общую площадь помещения, в котором расположена лестница;

— площадь, занятую выступающими конструктивными элементами и отопительными печами, а также находящуюся в пределах дверного проема, в общую площадь помещений не включать.

При определении общей площади помещений мансардного этажа учитывается площадь этого помещения с высотой от пола до наклонного потолка:

1,5 метра — при наклоне 30 градусов к горизонту;

1,1 метра — при 45 градусах;

0,5 метра — при 60 градусах и более.

При промежуточных значениях высота определяется по интерполяции.

rg.ru

Общая площадь здания: состав, измерение, расчет

Общую площадь здания необходимо знать для определения:

• стоимости строения;
• объемов и характера перепланировочных или реконструкционных работ;
• размера доли в праве общей долевой собственности и т. д.

В основу определения общей площади зданий положен:

• свод нормативных правил СНиП 31−06−2009, утвержденный приказом № 635/10 Мин-ва рег. развития РФ от 29.12. 2011 г.;
• приказ № 876/пр Минстроя РФ от 3.12.2016 г. об изменениях в правилах.

Здание — это сложное сооружение, в которое, кроме обычных этажей, входят цокольный и подвальный этажи, надстройки, мансарды, лоджии, переходы, лестничные марши, шахты и пр. Все это необходимо также рассчитать. Как рассчитывается общая площадь здания — тема настоящей статьи.

Содержание страницы

Общая площадь здания: что включает, как измерить ее и посчитать

Состав ОПЗ

Общая площадь здания (ОПЗ) определяется как сумма общих площадей:

• каждого этажа, в т. ч.технического, подвального, цокольного, а также надстроек типа мансарды;
• всех помещений, вне зависимости от их высоты:
  • зрительных галерей, веранд, балконов;
  • застекленных балконов, лоджий и галерей наружного типа;
  • переходов в другие здания;
  • антресолей;
• пространственных помещений, маршей, проемов и шахт в пределах одного этажа:
  • многосветных пространств, занимающих по своей высоте несколько этажей;
  • лестничных проемов, ширина которых превышает 1.5 м;
  • проемы в перекрытиях свыше 36 м²;
  • вентиляционные и лифтовые шахты;
• открытых наружных неотапливаемых элементов планировки (используемой части кровли, галерей, террас, лоджий, тамбуров и пр.), которые отдельно включаются в общую площадь.

Все конструктивно глухие (засыпанные) пространства в подвальных помещениях в ОПЗ не включаются.

Измерение площади этажа (ПЭ)

Каждый этаж здания ограждается наружными стенами, которые имеют внутреннюю поверхность с финишной отделкой. Именно от этих поверхностей (а не от голого бетона) следует измерять площадь этажа. Это означает, что точное значение ПЭ можно знать после полного завершения строительных отделочных работ. Измерять S этажа следует на уровне пола. Это правило касается как прямых, так и наклонных наружных стен.

Что такое полезная площадь здания

В полезную площадь здания (ППЗ) входят площади всех помещений, включая внутренние балконы или антресоли (атрибуты залов, вестибюльных помещений или фойе). Не принимаются во внимание при расчете полезной площади коммуникационные, инженерные технические и лифтовые шахты, лестничные клетки, неогражденные лестницы внутри помещения, пандусы.

Расчетная площадь

Расчетная площадь здания (РПЗ) — почти то же самое, что и полезная, но из нее дополнительно вычитается S коридоров, переходов между зданиями, тамбуров.

Внимание: площадь коридоров входит в расчетную площадь в учебных заведениях, медицинских учреждениях, санаториях, домах отдыха, административных зданиях, ведущих прием населения и подобных учреждениях.

Не включается в РПЗ пространство под лестницами, если их высота ниже 1.5 м.

Что нельзя считать общей или полезной площадью

К ОПЗ и ППЗ не относятся площади:

• подполий для вентиляции в зданиях, построенных в зонах вечной мерзлоты;
• технических подполий, при высоте выступающих в нем конструкций менее, чем 1.8 м;
• крылец, наружных лестниц и пандусов;
• наружных балконов;
• подвальных пространств, заполненных землей.

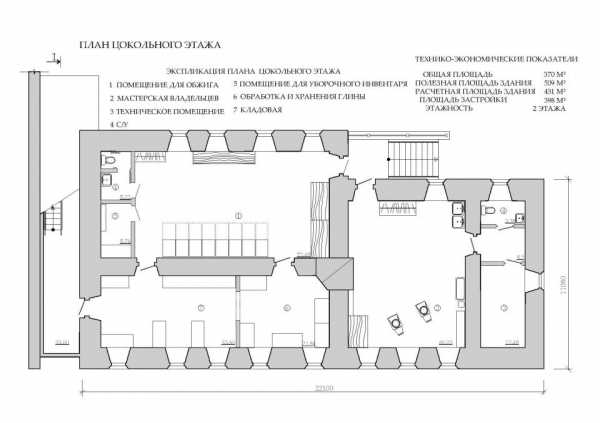
Как определить площадь помещения здания (ППЗ)

Помещение ограничивается как наружными стенами, так и внутренними перегородками, отделяющими его от других помещений. Внутренние поверхности наружных стен и перегородок — вот пределы, между которыми необходимо считать ППЗ. Измерение проводится на уровне пола, но выше плинтусов, то есть данный элемент отделки в расчет не принимается.

Измерение площади мансарды (ПМ)

Мансардный этаж ограничивается наружными стенами и ограждениями, примыкающими к пазухам чердака. S мансарды рассчитывается от внутренних поверхностей этих ограничений. Особенностью мансарды является наклон стен или потолка, иногда значительный. Поэтому для определения ПМ используют понижательный коэффициент (ПК), уменьшающий измеренную площадь на 30%, то есть расчетную площадь следует умножить на 0.7. Но применить ПК можно не во всех случаях, а в зависимости от высоты мансарды и угла наклона ее стен (потолка):

• при угле наклона 30º, высота не должна превышать 1.5 м;
• 45º — 1.1 м;
• 60º и более — до 0.5 м (непонятно, как вообще можно находиться в столь низком помещении).

Что такое строительный объем здания

Здание состоит из наземной и подземной частей, разделенных линией пола.

Строительный объем — это сумма объемов:

• надземной части, включая купола и фонари, но без следующих элементов:
  • выступающих конструкций в виде балконов, портиков, террас;
  • проездов, устроенных прямо под зданием.
• подземной части, за исключением:
  • подземного пространства для зданий на опорах;
  • подполий для проветривания в зданиях северных широт;
  • подпольных технических каналов.

Как определить площадь застройки

Общая площадь здания и площадь застройки — это разные понятия.

Площадь застройки здания определяется как S горизонтального сечения здания на уровне цоколя вместе с выступающими его частями, в том числе и расположенные выше линии сечения.

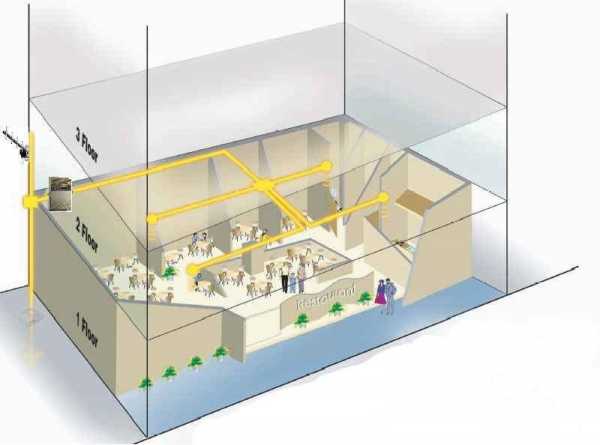
Учитываются при подсчете:

• ступени, террасы, колонны, подвальные входы, веранды и пр.;
• консольные элементы, выступающие за пределы наружных стен, расположенные на высоте не более 4.5 м;
• проезды.

Выступающие консоли, расположенные выше 4.5 м, не учитываются при определении площади застройки.

Как посчитать количество этажей

Этажность здания и количество этажей — разные вещи, что не вполне отражено в своде правил.

Под этажностью обычно понимают количество надземных этажей в построенном и сданном в эксплуатацию здании.

К надземным этажам относятся:

• обычные этажи;
• технический этаж;
• цокольный (полуподвальный) этаж, если его потолочное перекрытие находится не ниже двух метров от уровня земной поверхности;
• антресоли, площадки и другие поверхности площадью не более 40% от ПЭ.

Не считаются надземными этажами:

• чердаки высотой менее 1.8 м;
• подполье;
• пространство между этажами;
• технические надстройки на крыше (выходы вентиляционных и лифтовых шахт, этажных лестниц и др.).

При проектировании здания и его регистрации используется также термин «кол-во этажей», однако он шире и включает в себя надземные, технические, цокольные, подвальные, мансардные этажи. Все они вносятся в кадастр недвижимости.

• Здание может быть многоуровневым, то есть в разных его частях может быть разное количество этажей (частая причина этому уклон местности).
• Для расчета высоты подъема лифта учитывается только технический этаж (чердаки во внимание не принимаются).

Что такое торговая площадь

В торговую площадь магазина входят:

• S торговых залов;
• помещений для оформления и выдачи заказов;
• кафетерии и детские площадки;
• другие помещения для обслуживания покупателей.

Краткие итоги

• Общая площадь здания слагается не только из S этажей, а и других помещений (лоджий, антресолей, террас и пр.), в том числе и пространственного типа (световых и шахтовых), и наружных элементов планировки.
• При проектировании и эксплуатации здания необходимо отличать общую площадь от полезной и расчетной, а также уметь определить площадь застройки здания.
• Хотя здание и состоит из внутренних помещений (квартир, офисов, торговых залов и пр.) их площади не суммируются для определения S этажа: она определяется в границах внутренних поверхностей наружных стен дома.
• Знать площадь помещения в здании важно, например, для расчета арендной платы.
• Визуальное количество этажей здания может быть меньше, чем в техническом плане в ЕГРН.

Оценка статьи:

Загрузка…

moezhile.ru

ЛЕКЦИЯ_2_текст — Стр 2

Правила подсчета основных объемно-планировочных параметров общественных зданий

Общая площадь общественного здания определяется как сумма площадей всех этажей (включая технические, мансардный, цо­кольный и подвальные).

Площадь этажей зданий следует измерять в пределах внутрен­них поверхностей наружных стен. Площадь антресолей, перехо­дов в другие здания, остекленных веранд, галерей и балконов зрительных и других залов следует включать в общую площадь здания. Площадь многосветных помещений следует включать в общую площадь здания в пределах только одного этажа. При на­клонных наружных стенах площадь этажа измеряется на уровне пола.

Полезная площадь общественного здания определяется как сум­ма площадей всех размещаемых в нем помещений, а также балко­нов и антресолей в залах, фойе и т.п., за исключением лестнич­ных клеток, лифтовых шахт, внутренних открытых лестниц и пан­дусов.

Расчетная площадь общественных зданий определяется как сум­ма площадей всех размещенных в нем помещений, за исключени­ем коридоров, тамбуров, переходов, лестничных клеток, лифто­вых шахт, внутренних открытых лестниц, а также помещений, предназначенных для размещения инженерного оборудования и инженерных сетей.

В нормируемую площадь здания включаются:

— S коридоров, используемых в качестве рекреационных помещений в зданиях учебных заведений, зданиях боль­ниц, санаториев, домов отдыха, кинотеатров, клубов и других учреждений, предназначенных для отдыха или ожидания,

— S радиоузлов, коммуникационных, подсобных поме­щений при эстрадах и сценах, киноаппаратных, ниш шириной не менее 1 м, высотой 1,8 м и более (за исключением ниш инже­нерного назначения), а также встроенных шкафов (за исключе­нием встроенных шкафов инженерного назначения)

В общую, полезную и расчетную площади зданий не включается:

— S подполья для проветривания здания, (строительство на вечномерзлых грунтах),

— S чердака, техни­ческого подполья (технического чердака) при высоте от пола до низа выступающих конструкций менее 1,8 м,

— S лоджий, тамбуров, наружных балконов, портиков, крылец, наружных от­крытых лестниц.

Площадь помещений зданий следует определять по их разме­рам, измеряемым между отделанными поверхностями стен и пе­регородок на уровне чистого пола (без учета плинтусов). При определении площади мансардного помещения учитывается пло­щадь этого помещения с высотой наклонного потолка не менее 1,6 м.

Строительный объем

здания определяется как сумма строи­тельного объема выше отметки +0,00 (наземная часть) и ниже этой отметки (подземная часть). Строительный объем надземной и подземной частей здания определяется в пределах ограничива­ющих поверхностей с включением ограждающих конструкций, световых фонарей, куполов, начиная с отметки чистого пола каждой из частей здания, без учета выступающих архитектурных деталей и конструктивных элементов, подпольных каналов, пор­тиков, террас, балконов, объема проездов и пространства под зданием на опорах (в чистоте), а также проветриваемых подпо­лий под зданиями, проектируемыми для строительства на веч­номерзлых грунтах.

Площадь застройки здания определяется как площадь горизон­тального сечения по внешнему обводу здания на уровне цоколя, включая выступающие части. Площадь под зданием, расположен­ным на столбах, а также проезды под зданием включаются в пло­щадь застройки.

При определении этажности здания в количество этажей вклю­чаются все надземные этажи, в том числе технический, мансард­ный, а также цокольный этаж, если верх его перекрытия нахо­дится выше средней планировочной отметки земли не менее чем на 2 м.

Подполье для проветривания под зданиями, проектируемыми для строительства на вечномерзлых грунтах, в количество надземных этажей не включается.

При различном количестве этажей в разных частях здания, а также при размещении здания на участке с уклоном, когда за счет уклона увеличивается количество этажей, этажность опреде­ляется отдельно для каждой части здания.

Технический этаж, расположенный над верхним этажом, при определенной этажности здания не учитывается.

Торговая площадь магазина определяется как сумма площадей торговых залов, помещений приема и выдачи заказов, зала кафе­терия, площадей для дополнительных услуг покупателей.

studfiles.net

ПЛОЩАДЬ ЗАСТРОЙКИ, ОБЩАЯ ПЛОЩАДЬ И ДРУГИЕ

Трудно найти понимание, когда люди разговаривают на разном языке. Заказчик, строитель и проектировщик иногда по-разному понимают такие термины, как площадь застройки, общая площадь и т.д. Давайте рассмотрим основные определения этих терминов:

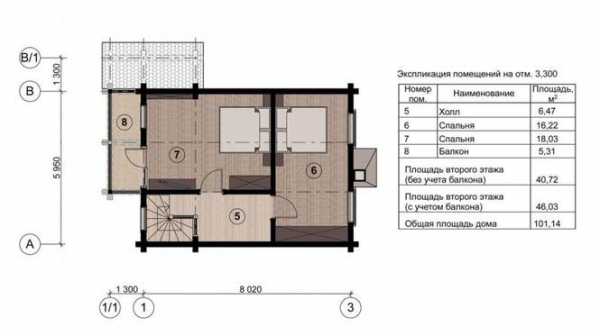
Площадь застройки

Площадь застройки — площадь горизонтального сечения здания на уровне цоколя, включая его выступающие части. Крыльцо и пандус также включаются в площадь застройки, а выступающие части крыши — нет. Логика такая: на площади участка выделяются площадь застройки, отмостки, площадок, проездов, дорожек и т.д. Балкон на втором этаже, выступающий за пределы цоколя, не будет включен в площадь застройки, если только он не расположен на несущих столбах. Для владельца земельного участка существенным является «разрешенная площадь застройки», которая обычно не может превышать 30% общей площади участка.

 

Площадь помещения

Площадь помещения определяется после отделки стен и перегородок как площадь на уровне пола без учета плинтусов. Если печь (камин) является частью отопления, она исключается из площади помещения. Площади балконов и террас определяются по внутреннему контуру без учета ограждений. В мансардных помещениях, где высоты стены меньше 1.8 м, делаются поправки.

 

Общая площадь

Общая площадь определяется как сумма площадей помещений, куда включаются также встроенные шкафы, лоджии, веранды, тамбуры, кладовые и другие помещения. По определению это суммарная площадь жилых и подсобных помещений квартиры с учетом лоджий, балконов, веранд, террас, холодных кладовых и встроенных шкафов.

 

Жилая площадь

Жилая площадь это сумма площадей жилых комнат. Какие комнаты относятся к жилым определяется в проекте здания. Считается, что высота жилых помещений должна быть не менее 2.2 м. По смыслу жилая комната «предназначена для постоянного проживания граждан». В ЖП включается площадь гардеробных.

 

Полезная площадь

Полезная площадь в российской архитектурно-строительной практике означает сумму площадей помещений, а также балконов и антресолей в залах, фойе и т.п., за исключением лестничных клеток, лифтовых шахт, внутренних открытых лестниц и пандусов. В зарубежных стандартах полезная площадь это «используемая» площадь.

 

Примечания:

 

1. Для многоквартирных домов площадь застройки определяется СНиП 31-01-2003 «Здания жилые многоквартирные». Эти определения обычно используются и для частных жилых домов. Приложение В:

В.1 Площадь помещений жилых зданий следует определять по их размерам, измеряемым между отделанными поверхностями стен и перегородок на уровне пола (без учета плинтусов). Площадь, занимаемая печью, в том числе печью с камином, которые входят в отопительную систему здания, а не являются декоративными, в площадь помещений не включаются.

В.2 Площадь открытых помещений (балконов, лоджий, террас) следует определять по их размерам, измеряемым по внутреннему контуру (между стеной здания и ограждением) открытого помещения без учета площади, занятой ограждением.

В.4 Площадь застройки здания определяется как площадь горизонтального сечения по внешнему обводу здания на уровне цоколя, включая выступающие части. Площадь под зданием, расположенным на опорах, а также проезды под ним включаются в площадь застройки.

В.5 При определении этажности здания в число надземных этажей включаются все надземные этажи, в том числе технический этаж, мансардный, а также цокольный этаж, если верх его перекрытия находится выше средней планировочной отметки земли не менее чем на 2 м. Подполье под зданием независимо от его высоты, а также междуэтажное пространство с высотой менее 1,8 м в число надземных этажей не включаются. При различном числе этажей в разных частях здания, а также при размещении здания на участке с уклоном, когда за счет уклона увеличивается число этажей, этажность определяется отдельно для каждой части здания.

 

2. Для садовых товариществ действует свод правил СП 53.13330.2011 (Актуализированная редакция СНиП 30-02-97):

6.11 На садовых, дачных участках площадью 0,06—0,12 га под строения, отмостки, дорожки и площадки с твердым покрытием следует отводить не более 30 % территории.

Приложение В. Термины и определения: общая площадь жилого строения, жилого дома: Сумма площадей его помещений, встроенных шкафов, а также лоджий, балконов, веранд, террас и холодных кладовых, подсчитываемых со следующими понижающими коэффициентами: для лоджий — 0,5, для балконов и террас — 0,3, для веранд и холодных кладовых — 1,0; площадь, занимаемая печью, в площадь помещений не включается. Площадь под маршем внутриквартирной лестницы при высоте от пола до низа выступающих конструкций 1,6 м и более включается в площадь помещений, где расположена лестница;

 

3. Для ИЖС используется местная нормативная база, которая, к сожалению, не всегда доступна — наверное, потому, что просто не существует..

 

4. Правила подсчета площадей приведены также в СНиП 2.08.01-89. Приложение 2:

п.2. Общую площадь квартир следует определять как сумму площадей их помещений, встроенных шкафов, а также лоджий, балконов, веранд, террас и холодных кладовых, подсчитываемых со следующими понижающими коэффициентами: для лоджий — 0,5, для балконов и террас — 0,3, для веранд и холодных кладовых — 1,0. Площадь, занимаемая печью, в площадь помещений не включается. Площадь под маршем внутриквартирной лестницы при высоте от пола до низа выступающих конструкций 1,6 м и более включается в площадь помещений, где расположена лестница.

 

п.5. Площадь жилого здания следует определять как сумму площадей этажей здания, измеренных в пределах внутренних поверхностей наружных стен, а также площадей балконов и лоджий. Площадь лестничных клеток, лифтовых и других шахт включается в площадь этажа с учетом их площадей в уровне данного этажа. Площадь чердаков и хозяйственного подполья в площадь здания не включается.

 

п.6.* Площадь помещений жилых зданий следует определять по их размерам, измеряемым между отделанными поверхностями стен и перегородок на уровне пола (без учета плинтусов). При определении площади мансардного помещения учитывается площадь этого помещения с высотой наклонного потолка 1,5 м при наклоне 30° к горизонту, 1,1 м — при 45 , 0,5 м — при 60° и более. При промежуточных значениях высота определяется по интерполяции. Площадь помещения с меньшей высотой следует учитывать в общей площади с коэффициентом 0,7, при этом минимальная высота стены должна быть 1,2 м при наклоне потолка 30°, 0,8 м при — 45° — 60° , не ограничивается при наклоне 60° и более.

 

5. Министерство экономического развития РФ 30 сентября 2011 г. утвердило Приказ N 531 «Об утверждении Требований к определению площади здания, помещения», который ссылается на часть 10 статьи 41 Федерального закона от 24 июля 2007 г. N 221-ФЗ «О государственном кадастре недвижимости» (Собрание законодательства Российской Федерации, 2007, N 31, ст. 4017; 2008, N 30, ст. 3597, 3616; 2009, N 1, ст. 19; N 19, ст. 2283; N 29, ст. 3582; N 52, ст. 6410, 6419; 2011, N 1, ст. 47; N 23, ст. 3269; N 27, ст. 3880; N 30, ст. 4563, 4594):
6. 
   Общие требования к определению площадей
7. Площадь и общая площадь здания, помещения определяются как площадь простейшей геометрической фигуры (прямоугольник, трапеция, прямоугольный треугольник и т.п.) или путем разбивки такого объекта на простейшие геометрические фигуры и суммирования площадей таких фигур.
8. Значение площади и общей площади здания, помещения определяется в квадратных метрах с округлением до 0,1 квадратного метра, а значения измеренных расстояний, применяемые для определения площадей, — метрах с округлением до 0,01 метра.
9. Для помещений в зданиях, возведенных по типовым проектам из сборных конструкций заводского изготовления с типовой планировкой на этажах, допускается производить определение площадей по подвальному, первому и типовому этажу. Для последующих этажей площадь может быть принята по типовому, за исключением помещений, в которых имеются изменения планировки.

 

1. Определение площади здания, помещения
2. Площадь здания определяется как сумма площадей всех надземных и подземных этажей (включая технический, мансардный, цокольный). Площадь этажа следует измерять в пределах внутренних поверхностей наружных стен на высоте 1,1 — 1,3 метра от пола. Площадь этажа при наклонных наружных стенах измеряется на уровне пола. В площадь здания включается площадь антресолей, галерей и балконов зрительных и других залов, веранд, наружных застекленных лоджий и галерей. В площадь здания отдельно включается также площадь открытых неотапливаемых планировочных элементов здания (включая площадь эксплуатируемой кровли, открытых наружных галерей, открытых лоджий и т.п.). Площадь многосветных помещений, а также пространство между лестничными маршами более ширины марша и проемы в перекрытиях более 36 квадратных метров следует включать в площадь здания в пределах только одного этажа.
3. Площадь помещения определяется как сумма площадей всех частей такого помещения, рассчитанных по их размерам, измеряемым между отделанными поверхностями стен и перегородок на высоте 1,1 — 1,3 метра от пола.

 

III. Определение общей площади жилого помещения, жилого дома

6. Общая площадь жилого помещения, жилого дома состоит из суммы площади всех частей такого помещения, жилого дома, включая площадь помещений вспомогательного использования, предназначенных для удовлетворения гражданами бытовых и иных нужд, связанных с их проживанием в жилом помещении, за исключением балконов, лоджий, веранд и террас. К площади помещений вспомогательного использования относятся площади кухонь, коридоров, ванн, санузлов, встроенных шкафов, кладовых, а также площадь, занятая внутриквартирной лестницей. Измерение расстояний, применяемых для определения общей площади жилого помещения, жилого дома, производится по всему периметру стен на высоте 1,1 — 1,3 метра от пола. При определении общей площади жилого помещения, жилого дома надлежит:

 

• площадь ниш высотой 2 метра и более включать в общую площадь помещений, в которых они расположены. Площади арочных проемов включать в общую площадь помещения, начиная с ширины 2 метра;
• площадь пола под маршем внутриквартирной лестницы, при высоте от пола до низа выступающих конструкций марша 1,6 метра и более, включать в общую площадь помещения, в котором расположена лестница;
• площадь, занятую выступающими конструктивными элементами и отопительными печами, а также находящуюся в пределах дверного проема, в общую площадь помещений не включать.

При определении общей площади помещений мансардного этажа учитывается площадь этого помещения с высотой от пола до наклонного потолка:1,5 метра — при наклоне 30 градусов к горизонту; 1,1 метра — при 45 градусах; 0,5 метра — при 60 градусах и более. При промежуточных значениях высота определяется по интерполяции.

 

 

6. В словаре ЖКХ написано (видимо, приказ Минстроя РФ от 30.10.95 г. № 17-115):

Жилая комната — конструктивно обособленная неделимая функциональная часть квартиры, площадь которой в соответствии о правилами государственного учета учитывается в составе жилой площади квартиры. Площадь жилой комнаты или жилых комнат квартиры является площадью основного (главного) назначения. К термину «жилая комната» относятся спальни, гостиные, кабинеты, комнаты отдыха, столовые и иные аналогичные места. К этому термину не относятся чуланы, холлы, лестницы, помещения для стирки и ванные комнаты.

xn--80aqdcadzpik.xn--p1ai

как определить и считать площадку участка

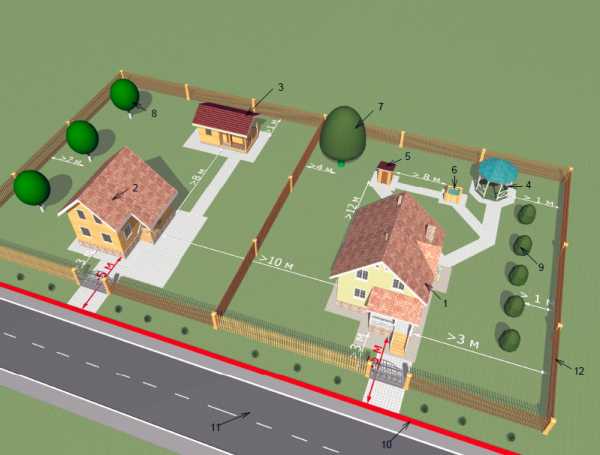
При осуществлении строительства и освоении земельного участка необходимо понимать, что представляет собой площадь застройки, а также что входит в неё. При этом может определяться площадь застройки, например, жилого здания, площадь дома или же площадь застройки земельного участка. Существуют также нормативы, которые считаются основой и контролируют определяемую площадь. Согласно этим правилам осуществлять строительство без определения площади многоквартирного или иного дома нельзя.

Понятие и значение

Что такое площадь застройки, которая должна определяться как у жилого дома, так и у земли под строительные работы? Она представляет собой показатели, определяющиеся параллельно горизонтальному цоколю, в которые входит и выступающая часть территории. Этих показателей будет достаточно, чтобы застраивать выделенные территории. При этом необходимо понимать, что просчитать подобную площадь можно с учётом нескольких показателей сразу.

Недостаточно определить размер той территории, которая, в принципе, входит во владение лица. Важно также определять выступающие точки. Не каждая из них, даже если она будет входить в общую площадь, окажется частью застройки. Если у дома есть крыльцо или иные помосты, а также подъездные дорожки, они должны признаваться как входящие в площадь застройки. Считается, что когда дом имеет балконы, которые не закреплены какими-то несущие столбами, то они, напротив, не должны учитываться в процессе расчёта площади. Соответственно, по конструкции строения могут требовать больше территории, чем показатели рассчитанных площадей.

Для регламентации деятельности по расчёту площадей необходимо брать за основу Строительные нормы и правила, которые были приняты в 2003 году и могут применяться как к частным домам, так и к жилым многоквартирным.

Чтобы найти точные показатели по площади необходимо определить, что нужно просчитывать.

Речь идёт о нескольких видах площадей застройки, к которым относят следующие:

Рекомендуем ознакомиться:

1. Общая площадь. Это сумма всех показателей по площади. Сюда должны входить площади комнат, всех внутренних и внешних помещений, выступающих частей и иных элементов, имеющих значение для установления рассматриваемого показателя.
2. Площадь только помещения. Она определяется после отделки внутренних стен, при этом плинтуса учитываться не будут. Если это не многоквартирный дом, а частный, то при наличии печи она не будет входить в данную площадь, но только в том случае, если является частью общей системы отопления.
3. Площадь жилых помещений. Здесь будут учитываться только те комнаты, которые признаются жилыми, иные помещения в здании входить в сумму этих показателей не будут.
4. Полезная или используемая площадь. Она включает в себя всё — от комнат до балконов. Однако некоторые объекты, например, шахты лифтов и пандусы, включены сюда не будут.

Если нанять специалистов, то они за счёт применения специального оборудования смогут установить необходимые показатели. Однако допускается посчитать площадь самостоятельно, если на руках будут нужные для этого средства.

Основные требования и коэффициенты

Чтобы ответить на вопрос, как определить площадь, необходимо обратиться к нормативной базе, принятой на федеральном уровне и регламентирующей точные правила проведения требуемых расчётов. Однако особенности регионов вынуждают их принимать свои правила, которые хоть и не должны идти в серьёзный разрез с теми, что установлены государством, но при этом отличаются от общепринятых показателей. В первую очередь это касается коэффициентов.

Данные показатели представляют собой соотношение площади конкретной определённой территории и той площади, что отводится непосредственно под возводимое в ходе строительных работ здание. Соответственно в каждом отдельном регионе такой коэффициент будет отличаться. Более того, он нередко расходится с нормативами, установленными на федеральном уровне. Например, в Московской области коэффициент может составлять сорок процентов, но согласно СНиП он равен двадцати процентам.

Коэффициент признаётся основной величиной, необходимой для осуществления строительства, так как подразумевает соотношение всех площадей, а значит, обеспечивает максимальное количество вариантов объёмов строений.

Помимо необходимых показателей, которые должны учитываться при определении размера территории застройки, важно обращать внимания на требования, изложенные в СНиП и распространяющиеся на все варианты площадей:

1. При определении площади самого здания и общих показателей необходимо проводить измерения по самым простым фигурам геометрии. Это могут быть прямоугольники или же квадраты. Если объект имеет сложную форму, то его необходимо разбить на подобные простые фигуры, а после суммировать полученные показатели площадей.
2. Все значения, получаемые в результате измерения площади, должны быть зафиксированы в квадратных метрах и обязательно округлены до одной десятой квадратного метра. Когда осуществляется расчёт расстояния, то отражается он в метрах, с округлением до одной сотой метра.
3. Когда строительство основывается на типовых проектах и используются конструкции строений, уже ранее изготовленные также по типовому варианту, то допускается упрощённый расчёт площадей. Нет необходимости рассчитывать площадь каждого этажа, достаточно взять за основу либо подвал, либо первый и типовой этажи, а дальше суммировать всю площадь по одному полученному ранее показателю.

Данные требования не должны быть изменены, а нарушение может повлечь за собой привлечение к ответственности. Более того, несоблюдение порядка расчёта, а также предложенных выше нормативов, может привести к ошибкам в измерениях, а соответственно, неверным данным, которые будут позже вноситься в технические документы объекта.

Принципы расчёта

Рекомендуем ознакомиться:

Первое, что необходимо знать, при определении площади застройки, это какой коэффициент действует и соответствует ли конкретный участок и проект этому показателю. Проще всего в такой ситуации обратиться к архитектурным схемам, так как специалисты, вычисляя необходимые показатели и формируя проект здания, всегда указывают его площадь. Следовательно, достаточно узнать, какова площадь всего участка и установить соответствие принятому коэффициенту.

Определяя точные принципы расчёта площади, нужно разграничивать общую площадь и площадь помещения. Второй вариант определяется просто и представляет собой сумму площадей каждого из этажей. Измеряется он при этом в пределах внутренних стен, которые уже были отделаны. Осуществлять подобные замеры необходимо не по поверхности пола, а на высоте не менее одного метра. Однако если стены имеют наклонный вид, то тогда площадь определяется по полу, так как должны устанавливаться максимальные показатели помещения.

В площадь здания будут входить не только показатели каждого из этажей, но и такие объекты, как неотапливаемые и планировочные элементы зданий, к которым относят лоджии, открытую используемую кровлю и так далее.

Когда речь идёт о первом варианте, то есть об общей площади, то считать необходимо все части здания, а не только этажи.

Определяя площадь нужно уделять внимание порядку, позволяющему рассчитать площадь следующих элементов:

• площадь всех ниш, если они имеют высоту больше двух метров, а также арок шириной не меньше двух метров;
• площадь пола под специальным маршем лестницы, находящейся внутри помещения, а также общая его площадь, при этом марш должен достигать как минимум полутора метров;
• площадь элементов, которые являются выступающими, под печами или иными отопительными сооружениями, а также отведённую под дверные проёмы измерять нет необходимости.

При наличии мансардного этажа его площадь также должна учитываться. Измерения будут происходить от пола до потолка, который имеет наклонную форму. При этом расчёт должен осуществляться на уровне полутора метров, если угол тридцать градусов, одного метра десяти сантиметров, если угол сорок пять градусов, и полуметра, если угол шестьдесят градусов.

Таким образом, площадь застройки — это размер здания, отражённый в квадратных метрах. Она включает в себя множество показателей, от площадей отдельных помещений до общего размера постройки.

Рассчитывать её при этом необходимо опираясь только на нормативы, устанавливаемые в СНиП и региональными органами власти.

zhiloepravo.com

Площадь — это… Что такое Площадь?

Площадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры^[1], неформально говоря, показывающая размер этой фигуры. Исторически вычисление площади называлось квадратурой. Фигура, имеющая площадь, называется квадрируемой. Конкретное значение площади для простых фигур однозначно вытекает из предъявляемых к этому понятию практически важных требований (см. ниже). Фигуры с одинаковой площадью называются равновеликими.

Общий метод вычисления площади геометрических фигур предоставило интегральное исчисление. Обобщением понятия площади стала теория меры множества, пригодная для более широкого класса геометрических объектов.

Для приближенного вычисления площади на практике используют палетку или специальный измерительный прибор — планиметр.

Свойства

Для фигур на плоскости, не состоящих из целого количества единичных квадратов, а также для искривлённых трёхмерных поверхностей, площадь определяется с помощью предельного перехода; при этом требуется, чтобы как фигура, так и её граница были кусочно-гладкими^[2].

Общий метод определения площади

Площадь плоской фигуры

Декартовы координаты

Определённый интеграл как площадь фигуры Площадь между графиками двух функций равна разности интегралов от этих функций в одинаковых пределах интегрирования

Площадь, заключённая между графиком непрерывной функции на интервале и горизонтальной осью, может быть вычислена как определённый интеграл от этой функции:

Площадь, заключённая между графиками двух непрерывных функций на интервале находится как разность определённых интегралов от этих функций:

Полярные координаты

В полярных координатах: площадь, ограниченная графиком функции и лучами вычисляется по формуле:

.

Площадь поверхности

Площадь искривлённой поверхности A, заданной вектор-функцией , даётся двойным интегралом:

То же в координатах:

Здесь .

Единицы измерения площади

Метрические единицы

Русские устаревшие

Мерами земли при налоговых расчетах были выть, соха, обжа, размеры которых зависели от качества земли и социального положения владельца. Существовали и различные местные меры земли:коробья, веревка, жеребья и др.

Античные

Формулы вычисления площадей простейших фигур

Планиметрические фигуры

Фигура	Формула	Переменные
Квадрат		— длина стороны квадрата.
Правильный треугольник		— длина стороны треугольника.
Правильный шестиугольник		— длина стороны шестиугольника.
Правильный восьмиугольник		— длина стороны восьмиугольника.
Правильный многоугольник		— периметр, а  — количество сторон.
Прямоугольный треугольник		и  — катеты треугольника.
Произвольный треугольник		— сторона треугольника,  — высота, проведенная к этой стороне.
		,  — любые две стороны,  — угол между ними.
	(формула Герона)	, ,  — стороны треугольника,  — полупериметр .
		в случае обхода вершин треугольника по часовой стрелке получим положительный результат, иначе отрицательный.
Прямоугольник		и  — длины сторон прямоугольника (его длина и ширина).
Параллелограмм		и  — длина стороны и опущенной на неё высоты соответственно.
		и  — соседние стороны параллелограмма,  — угол между ними.
Ромб		и  — длины диагоналей ромба.
Эллипс		и  — длины малой и большой полуосей.
Трапеция		та  — параллельные стороны, и  — расстояние между ними (высота трапеции).

Формулы для вычисления площади круга, его частей, описанных и вписанных в круг фигур

Фигура	Формула	Переменные
Круг	или	— радиус, а  — диаметр круга.
Сектор круга		— радиус круга,  — центральный угол сектора (в радианах).
Сегмент		— радиус круга,  — центральный угол сегмента (в радианах).
Треугольник, вписанный в окружность		, ,  — стороны треугольника,  — радиус описанной окружности.
Произвольный многоугольник, описанный вокруг окружности		— радиус окружности, вписанной в многоугольник, и  — периметр многоугольника.

Формулы для вычисления площади поверхности тел в пространстве

См. также

Литература

• Рашевский П. К. Риманова геометрия и тензорный анализ. Изд. 3-е, М.: Наука, 1967.
• Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — М.: ФИЗМАТЛИТ, 1960. — Т. 2. — 680 с. — ISBN 5-9221-0155-2

Ссылки

Примечания

dic.academic.ru

Площадь — Википедия

Пло́щадь — численная характеристика двумерной (плоской или искривлённой) геометрической фигуры^[1], неформально говоря, показывающая размер этой фигуры. Исторически вычисление площади называлось квадратурой. Фигура, имеющая площадь, называется квадрируемой. Конкретное значение площади для простых фигур однозначно вытекает из предъявляемых к этому понятию практически важных требований (см. ниже). Фигуры с одинаковой площадью называются равновеликими.

Общий метод вычисления площади геометрических фигур предоставило интегральное исчисление. Обобщением понятия площади стала теория меры множества, пригодная для более широкого класса геометрических объектов.

Для приближенного вычисления площади на практике используют палетку или специальный измерительный прибор — планиметр.

Определение понятия площади

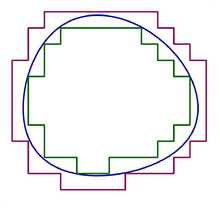Множество измеримо по Жордану, если внутренняя мера Жордана равна внешней мере Жордана

Площадь — функция, которая обладает следующими свойствами^[2][1]:

• Положительность, то есть площадь неотрицательна;
• Аддитивность, то есть площадь фигуры равна сумме площадей составляющих её фигур без общих внутренних точек;
• Инвариантность, то есть площади конгруэнтных фигур равны;
• Нормированность, то есть площадь единичного квадрата равна 1.

Из данного определения площади следует её монотонность, то есть площадь части фигуры меньше площади всей фигуры^[2].

Первоначально определение площади было сформулировано для многоугольников, затем оно было расширено на квадрируемые фигуры. Квадрируемой называется такая фигура, которую можно вписать в многоугольник и в которую можно вписать многоугольник, причём площади обоих многоугольников отличаются на произвольно малую величину. Такие фигуры называются также измеримыми по Жордану^[1]. Для фигур на плоскости, не состоящих из целого количества единичных квадратов, площадь определяется с помощью предельного перехода; при этом требуется, чтобы как фигура, так и её граница были кусочно-гладкими^[3]. Существуют неквадрируемые плоские фигуры^[1]. Предложенное выше аксиоматическое определение площади в случае плоских фигур обычно дополняют конструктивным, при котором с помощью палетки осуществляется собственно вычисление площади. При этом для более точных вычислений на последующих шагах используют палетки, у которых длина стороны квадрата в десять раз меньше длины у предыдущей палетки^[4].

Площадь квадрируемой плоской фигуры существует и единственна. Понятие площади, распространённое на более общие множества, привело к определению множеств, измеримых по Лебегу, которыми занимается теория меры. В дальнейшем возникают более общие классы, для которых свойства площади не гарантируют её единственность^[1].

Под площадью в обобщённом смысле понимают численную характеристику k-мерной поверхности в n-мерном пространстве (евклидовом или римановом), в частности, характеристику двумерной поверхности в трёхмерном пространстве^[1].

Видео по теме

Общий метод определения площади

Площадь плоской фигуры

На практике чаще всего требуется определить площадь ограниченной фигуры с кусочно-гладкой границей. Математический анализ предлагает универсальный метод решения подобных задач.

Декартовы координаты

Определённый интеграл как площадь фигуры Площадь между графиками двух функций равна разности интегралов от этих функций в одинаковых пределах интегрирования

Площадь, заключённая между графиком непрерывной функции на интервале [a,b]{\displaystyle [a,b]} и горизонтальной осью, может быть вычислена как определённый интеграл от этой функции:

S=∫abf(x)dx{\displaystyle S=\int \limits _{a}^{b}f(x)\,dx}

Площадь, заключённая между графиками двух непрерывных функций f(x),g(x){\displaystyle f(x),\,g(x)} на интервале [a,b]{\displaystyle [a,b]} находится как разность определённых интегралов от этих функций:

S=∫ab|f(x)−g(x)|dx{\displaystyle S=\int \limits _{a}^{b}\left|f(x)-g(x)\right|\,dx}

Полярные координаты

В полярных координатах: площадь, ограниченная графиком функции r=r(θ){\displaystyle r=r(\theta )} и лучами θ=θ1,θ=θ2,θ1<θ2{\displaystyle \theta =\theta _{1},\theta =\theta _{2},\theta _{1}<\theta _{2}} вычисляется по формуле:

S=12∫θ1θ2r2(θ)dθ{\displaystyle S={1 \over 2}\int \limits _{\theta _{1}}^{\theta _{2}}r^{2}(\theta )\,d\theta }.

Площадь поверхности

Для определения площади кусочно гладкой поверхности в трёхмерном пространстве используют ортогональные проекции к касательным плоскостям в каждой точке, после чего выполняют предельный переход. В результате, площадь искривлённой поверхности A, заданной вектор-функцией r=r(u,v),{\displaystyle \mathbf {r} =\mathbf {r} (u,v),}, даётся двойным интегралом^[1]:

S=∬A|∂r∂u×∂r∂v|dudv.{\displaystyle S=\iint \limits _{A}\left|{\frac {\partial \mathbf {r} }{\partial u}}\times {\frac {\partial \mathbf {r} }{\partial v}}\right|\,du\,dv.}

То же в координатах:

S=∬A(D(x,y)D(u,v))2+(D(y,z)D(u,v))2+(D(z,x)D(u,v))2dudv{\displaystyle S=\iint \limits _{A}{\sqrt {\left({\frac {D(x,y)}{D(u,v)}}\right)^{2}+\left({\frac {D(y,z)}{D(u,v)}}\right)^{2}+\left({\frac {D(z,x)}{D(u,v)}}\right)^{2}}}\;\mathrm {d} \,u\,\mathrm {d} \,v}

Здесь D(y,z)D(u,v)=|yu′yv′zu′zv′|,D(z,x)D(u,v)=|zu′zv′xu′xv′|,D(x,y)D(u,v)=|xu′xv′yu′yv′|{\displaystyle {\frac {D(y,z)}{D(u,v)}}={\begin{vmatrix}y’_{u}&y’_{v}\\z’_{u}&z’_{v}\end{vmatrix}},\quad {\frac {D(z,x)}{D(u,v)}}={\begin{vmatrix}z’_{u}&z’_{v}\\x’_{u}&x’_{v}\end{vmatrix}},\quad {\frac {D(x,y)}{D(u,v)}}={\begin{vmatrix}x’_{u}&x’_{v}\\y’_{u}&y’_{v}\end{vmatrix}}}.

Теория площадей

Теория площадей занимается изучением обобщений, связанных с распространением определения k-мерной площади с кусочно-гладкого погружения на более общие пространства. Для кусочно-гладкого погружения f площадь определяют способом, аналогичным указанному выше, при этом у площади сохраняются такие свойства как положительность, аддитивность, нормированность, а также ряд новых.

Единицы измерения площади

В одном квадратном сантиметре сто квадратных миллиметров

Метрические единицы

Русские устаревшие

Мерами земли при налоговых расчётах были выть, соха, обжа, размеры которых зависели от качества земли и социального положения владельца. Существовали и различные местные меры земли: коробья, верёвка, жеребья и др.

Античные

Другие

Формулы вычисления площадей простейших фигур

Многоугольники

Фигура	Формула	Переменные
Правильный треугольник	a234{\displaystyle a^{2}{\frac {\sqrt {3}}{4}}}	a{\displaystyle a} — длина стороны треугольника
Прямоугольный треугольник	ab2{\displaystyle {\frac {ab}{2}}}	a{\displaystyle a} и b{\displaystyle b} — катеты треугольника
Произвольный треугольник	12ah{\displaystyle {\frac {1}{2}}ah}	a{\displaystyle a} — сторона треугольника, h{\displaystyle h} — высота, проведённая к этой стороне
	12absin⁡α{\displaystyle {\frac {1}{2}}ab\sin \alpha }	a{\displaystyle a} и b{\displaystyle b} — любые две стороны, α{\displaystyle \alpha } — угол между ними
	p(p−a)(p−b)(p−c){\displaystyle {\sqrt {p(p-a)(p-b)(p-c)}}} (формула Герона)	a{\displaystyle a}, b{\displaystyle b} и c{\displaystyle c} — стороны треугольника, p{\displaystyle p} — полупериметр (p=a+b+c2){\displaystyle \left(p={\frac {a+b+c}{2}}\right)}
	12|x0y01x1y11x2y21|{\displaystyle {\frac {1}{2}}{\begin{vmatrix}x_{0}&y_{0}&1\\x_{1}&y_{1}&1\\x_{2}&y_{2}&1\end{vmatrix}}}	(x0;y0){\displaystyle (x_{0};y_{0})}, (x1;y1){\displaystyle (x_{1};y_{1})}, (x2;y2){\displaystyle (x_{2};y_{2})} — координаты вершин треугольника (в случае обхода вершин по часовой стрелке получим положительный результат, иначе отрицательный)
Квадрат	a2{\displaystyle a^{2}}	a{\displaystyle a} — длина стороны квадрата
Прямоугольник	ab{\displaystyle ab}	a{\displaystyle a} и b{\displaystyle b} — длины сторон прямоугольника (его длина и ширина)
Ромб	12cd{\displaystyle {\frac {1}{2}}cd}	c{\displaystyle c} и d{\displaystyle d} — длины диагоналей ромба
Параллелограмм	ah{\displaystyle ah}	a{\displaystyle a} и h{\displaystyle h} — длины стороны и опущенной на неё высоты соответственно
	absin⁡α{\displaystyle ab\sin \alpha }	a{\displaystyle a} и b{\displaystyle b} — соседние стороны параллелограмма, α{\displaystyle \alpha } — угол между ними
Трапеция	12(a+b)h{\displaystyle {\frac {1}{2}}(a+b)h}	a{\displaystyle a} и b{\displaystyle b} — основания трапеции, h{\displaystyle h} — высота трапеции
Произвольный четырёхугольник	(p−a)(p−b)(p−c)(p−d)−abcdcos⁡α{\displaystyle {\sqrt {(p-a)(p-b)(p-c)(p-d)-abcd\cos \alpha }}} (формула Брахмагупты)	a{\displaystyle a}, b{\displaystyle b}, c{\displaystyle c}, d{\displaystyle d} — стороны четырёхугольника, p{\displaystyle p} — его полупериметр, α{\displaystyle \alpha } — полусумма противолежащих углов четырёхугольника
Правильный шестиугольник	a2332{\displaystyle a^{2}{\frac {3{\sqrt {3}}}{2}}}	a{\displaystyle a} — длина стороны шестиугольника
Правильный восьмиугольник	2a2(1+2){\displaystyle 2a^{2}(1+{\sqrt {2}})}	a{\displaystyle a} — длина стороны восьмиугольника
Правильный многоугольник	P2/n4tg⁡(π/n){\displaystyle {\frac {P^{2}/n}{4\operatorname {tg} (\pi /n)}}}	P{\displaystyle P} — периметр, n{\displaystyle n} — количество сторон
Произвольный многоугольник (выпуклый и невыпуклый)	12|∑i=1n(xi+1−xi)(yi+1+yi)|{\displaystyle {\frac {1}{2}}\left|\sum _{i=1}^{n}(x_{i+1}-x_{i})(y_{i+1}+y_{i})\right|} (метод трапеций)	(xi;yi){\displaystyle (x_{i};y_{i})} — координаты вершин многоугольника в порядке их обхода, замыкая последнюю с первой: (xn+1;yn+1)=(x1;y1){\displaystyle (x_{n+1};y_{n+1})=(x_{1};y_{1})}; при наличии отверстий направление их обхода противоположно обходу внешней границы многоугольника

Площади круга, его частей, описанных и вписанных в круг фигур

Фигура	Формула	Переменные
Круг	πr2{\displaystyle \pi r^{2}} или πd24{\displaystyle {\frac {\pi d^{2}}{4}}}	r{\displaystyle r} — радиус, d{\displaystyle d} — диаметр круга
Сектор круга	αr22{\displaystyle {\frac {\alpha r^{2}}{2}}}	r{\displaystyle r} — радиус круга, α{\displaystyle \alpha } — центральный угол сектора (в радианах)
Сегмент круга	r22(α−sin⁡α){\displaystyle {\frac {r^{2}}{2}}(\alpha -\sin \alpha )}	r{\displaystyle r} — радиус круга, α{\displaystyle \alpha } — центральный угол сегмента (в радианах)
Эллипс	πab{\displaystyle \pi ab}	a{\displaystyle a}, b{\displaystyle b} — большая и малая полуоси эллипса
Треугольник, вписанный в окружность	abc4R{\displaystyle {\frac {abc}{4R}}}	a{\displaystyle a}, b{\displaystyle b} и c{\displaystyle c} — стороны треугольника, R{\displaystyle R} — радиус описанной окружности
Четырёхугольник, вписанный в окружность	(p−a)(p−b)(p−c)(p−d){\displaystyle {\sqrt {(p-a)(p-b)(p-c)(p-d)}}} (формула Брахмагупты)	a{\displaystyle a}, b{\displaystyle b}, c{\displaystyle c}, d{\displaystyle d} — стороны четырёхугольника, p{\displaystyle p} — его полупериметр
Многоугольник, описанный около окружности	12Pr{\displaystyle {\frac {1}{2}}Pr}	r{\displaystyle r} — радиус окружности, вписанной в многоугольник, P{\displaystyle P} — периметр многоугольника
Прямоугольная трапеция, описанная около окружности	ab{\displaystyle ab}	a{\displaystyle a}, b{\displaystyle b} — основания трапеции

Площади поверхностей тел в пространстве

Исторический очерк

Площадь плоских фигур

Многие годы площадь считалась первичным понятием, не требующим определения. Основной задачей математиков являлось вычисление площади, при этом были известны основные свойства площади^[2]. В Древнем Египте использовались точные правила вычисления площади прямоугольников, прямоугольных треугольников и трапеций, площадь произвольного четырёхугольника определялась приближённо как произведение полусумм пар противоположных сторон. Применение такой приближённой формулы связано с тем, что участки, площадь которых надо было померить, были в основном близки к прямоугольным и погрешность в таком случае оставалась небольшой. Историк математики А. П. Юшкевич предполагает, что египтяне могли и не знать, что пользуются приближённой формулой. В задаче 50 папируса Ринда содержится формула вычисления площади круга, которая считалась равной площади квадрата со стороной 8/9 диаметра круга^[5]. Такими же формулами пользовались и в Вавилоне, однако для площади круга приближение было менее точным. Кроме того, вавилоняне могли приближённо посчитать площади правильных пяти-, шести- и семиугольника со стороной равной единице. В шестидесятиричной системе им соответствовали 1,40, 2,37,20 и 3,41, соответственно^[6].

Основным приёмом вычисления площади при этом являлось построение квадрата, площадь которого равна площади заданной многоугольной фигуры, в частности в книге I «Начал» Евклида, которая посвящена планиметрии прямолинейных фигур, доказывается, что треугольник равновелик половине прямоугольника, имеющего с ним равные основания и высоту^[7]. Метод разложения, основанный на том, что две равносоставленные фигуры равновелики, позволял также вычислить площади параллелограммов и любых многоугольников^[4].

Следующим шагом было вычисление площадей круга, кругового сектора, лунок и других фигур. Основу вычислений при этом составлял метод исчерпывания многоугольниками^[1][4], с которого берёт начало теория пределов. Метод заключается в построении последовательности площадей, которые при постепенном нарастании «исчерпывают» требуемую площадь. Метод исчерпывания, получивший своё название только в XVII веке, основан на аксиоме непрерывности Евдокса — Архимеда и приписывается Евдоксу Книдскому, который с его помощью показал, что площади кругов относятся друг к другу как квадраты их диаметров. Метод описан в «Началах» Евклида: аксиома Евдокса сформулирована в книге V, а сам метод исчерпывания и основанные на нём отношения — в книге XII^[7]. Особого совершенства в применении метода достиг Архимед, который с его помощью посчитал площадь сегмента параболы и другие^[8][9]. Труд Архимеда «О спиралях» включает много утверждений, касающихся площадей различных витков спирали и их отношений^[10]. Архимеду принадлежит идея использования площадей или объёмов как вписанных, так и описанных фигур для определения требуемой площади или объёма^[11].

Индийцы поначалу пользовались той же формулой для вычисления четырёхугольников, что египтяне и греки. Брахмагупта пользовался формулой для площади четырёхугольников, выраженной через его полупериметр., которая верна для вписанного в окружность четырёхугольника. Формулы вычисления площади обычно не доказывались, но демонстрировались с наглядными рисунками^[12]. Формула Брахмагупты представляет собой аналог формулы Герона для площади треугольника, которую тот привёл в своей «Метрике»^[13].

Развитие и обобщение метода исчерпывания произошло только в XVII веке. В 1604 году в работе «Три книги о центре тяжести тел» Валерио широко использует теорему, по которой разность между площадями вписанной и описанной фигур, составленных из параллелограммов можно сделать меньше любой данной площади^[14]. Настоящий прорыв был сделан Кеплером, которому для астрономических расчётов нужно было уметь вычислять площадь эллипса. Кеплер рассматривал площадь как «сумму линий» и, разлиновывая эллипс с шагом в один градус, показал^[15], что ∫0φsin⁡xdx=1−cos⁡φ{\displaystyle \int \limits _{0}^{\varphi }\sin xdx=1-\cos \varphi }. Кавальери, обосновывая подобный метод, названный «методом неделимых», сравнивал площади плоских фигур, используя сечение фигур параллельными прямыми^[16]. Применение первообразной для нахождения площади плоской фигуры является наиболее универсальным методом. С помощью первообразной доказывается принцип Кавальери, по которому две плоские фигуры имеют равную площадь, если при пересечении каждой из них прямой, параллельной фиксированной, получаются отрезки одинаковой длины. Принцип был известен задолго до формирования интегрального исчисления^[1][4].

Площадь поверхности

Вычислением площадей кривых поверхностей занимался Архимед, определив, в частности, площадь поверхности шара^[11]. В общем случае для определения площади поверхности нельзя пользоваться ни развёрткой (не подходит для сферы), ни приближением многогранными поверхностями, то есть аналогом метода исчерпывания. Последнее показал Шварц, построив для боковой последовательности цилиндра последовательности, которые приводят к разным результатам (так называемый сапог Шварца)^[1][17].

Общий приём вычисления площади поверхности на рубеже XIX—XX веков предложил Минковский, который для каждой поверхности строил «окутывающий слой» малой постоянной толщины, тогда площадь поверхности будет приближённо равна объёму этого слоя, делённому на его толщину. Предельный переход при толщине, стремящейся к нулю даёт точное значение площади. Однако, для площади по Минковскому не всегда выполняется свойство аддитивности. Обобщение данного определения приводит к понятию линии по Минковскому и другим^[18].

Примечания

1. ↑ ^{1 2 3 4 5 6 7 8 9 10} Площадь // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 4.
2. ↑ ^{1 2 3} Геометрия, 1966, с. 7—13.
3. ↑ Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — Изд. 6-е. — М.: ФИЗМАТЛИТ, 1966. — Т. 2. — С. 186—224. — 800 с.
4. ↑ ^{1 2 3 4} Болтянский В. О понятиях площади и объёма. Квант, № 5, 1977, c.2—9
5. ↑ История математики, т. I, 1970, с. 30—32.
6. ↑ История математики, т. I, 1970, с. 47—53.
7. ↑ ^{1 2} История математики, т. I, 1970, с. 111—114.
8. ↑ Исчерпывания метод // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 2.
9. ↑ История математики, т. I, 1970, с. 101—105.
10. ↑ Boyer & Merzbach, 2010, p. 127—128.
11. ↑ ^{1 2} История математики, т. I, 1970, с. 117—124.
12. ↑ История математики, т. I, 1970, с. 197—198.
13. ↑ Boyer & Merzbach, 2010, p. 172, 219.
14. ↑ История математики, т. II, 1970, с. 131—135.
15. ↑ История математики, т. II, 1970, с. 166—171.
16. ↑ История математики, т. II, 1970, с. 174—181.
17. ↑ В. Н. Дубровский, В поисках определения площади поверхности. Квант. 1978. № 5. С.31—34.
18. ↑ В. Н. Дубровский, Площадь поверхности по Минковскому. Квант. 1979. № 4. С.33—35.

Литература

wiki2.red

No related posts.