Подготовка школьников к ЕГЭ в учебном центре «Резольвента» (Справочник по математике — Стереометрия
Введем следующие обозначения:
Используя эти обозначения, составим таблицу с формулами для вычисления объемов, площадей боковой поверхности и площадей полной поверхности различных видов призм.
| Призма | Рисунок | Формулы для объема, площади боковой и полной поверхности |
| Куб | V = a3, Sбок = 4a2, Sполн = 6a2, где a – длина ребра куба. | |
| Прямоугольный параллелепипед | V = abc, Sбок = 2ac + 2bc, Sполн = 2ac + 2bc +2ab, где | |
| Прямой параллелепипед, в основании которого лежит параллелограмм со сторонами a, b и углом φ | Sосн = ab sin φ, V = Sоснh = abh sin φ, Sбок = 2ah + 2bh, Sполн = 2ab sin φ + 2ah +2bh, где | |
| Произвольный параллелепипед | Sосн = ab sin φ, V = Sоснh = abh sin φ, V = Sперпс, Sбок = Pперпс, Sполн = 2ab sin φ + Pперпс, где | |
| Прямая призма | V = Sоснh, Sбок = Pоснh, Sполн = 2Sосн + Sбок, где | |
| Правильная n – угольная призма | (см. раздел «правильные многоугольники»), V = Sоснh, Sбок = Pоснh = anh, Sполн = 2Sосн + Sбок, где | |
| Произвольная призма | V = Sоснh, V = Sперпl, Sбок = Pперпl, Sполн = 2Sосн + Sбок, где |
| Куб |
Формулы для объема, площади боковой и полной поверхности: V = a3, Sбок = 4a2, Sполн = 6a2, где a – длина ребра куба. |
| Прямоугольный параллелепипед |
Формулы для объема, площади боковой и полной поверхности: V = abc, Sбок = 2ac + 2bc, Sполн = 2ac + 2bc +2ab, где |
| Прямой параллелепипед, в основании которого лежит параллелограмм со сторонами a, b и углом φ |
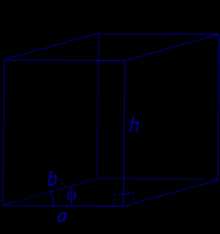 Формулы для объема, площади боковой и полной поверхности: Sосн = ab sin φ, V = Sоснh = abh sin φ, Sбок = 2ah + 2bh, Sполн = где |
| Произвольный параллелепипед |
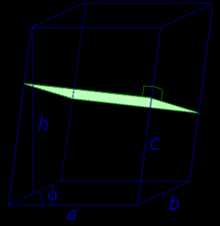 Формулы для объема, площади боковой и полной поверхности: Sосн = ab sin φ, V = Sоснh = abh sin φ, V = Sперпс, Sбок = Pперпс, Sполн = где |
| Прямая призма |
Формулы для объема, площади боковой и полной поверхности: V = Sоснh, Sбок = Pоснh, Sполн = 2Sосн + Sбок, где |
| Правильная n – угольная призма |
Формулы для объема, площади боковой и полной поверхности: (см. раздел «правильные многоугольники»), V = Sоснh, Sбок = Pоснh = anh, Sполн = 2Sосн + Sбок, где |
| Произвольная призма |
Формулы для объема, площади боковой и полной поверхности: V = Sоснh, V = Sперпl, Sбок = Pперпl, Sполн = 2Sосн + Sбок, где |
Замечание 1. С понятием призмы и различными видами призм можно ознакомиться в разделе «Призмы».
Замечание 2. С определением сечения призмы и способами построения сечений призмы можно ознакомиться в разделе «Сечения призмы. Перпендикулярные сечения призмы».
На нашем сайте можно также ознакомиться с разработанными преподавателями учебного центра «Резольвента» учебными материалами для подготовки к ЕГЭ по математике.
Приглашаем школьников (можно вместе с родителями) на бесплатное тестирование по математике, позволяющее выяснить, какие разделы математики и навыки в решении задач являются для ученика «проблемными». Запись по телефону (495) 509-28-10 |
Для школьников, желающих хорошо подготовиться и сдать ЕГЭ по математике или русскому языку на высокий балл, учебный центр «Резольвента» проводит
У нас также для школьников организованы
МОСКВА, СВАО, Учебный центр «РЕЗОЛЬВЕНТА»
www.resolventa.ru
Формулы объема и площади поверхности. Призма, пирамида
 Изучение стереометрии начинается со знания формул. Для решения задач ЕГЭ по стереометрии нужны всего две вещи:
Изучение стереометрии начинается со знания формул. Для решения задач ЕГЭ по стереометрии нужны всего две вещи:
- Формулы объёма — например, объём куба, объём призмы, объем пирамиды — и формулы площади поверхности.
- Элементарная логика.
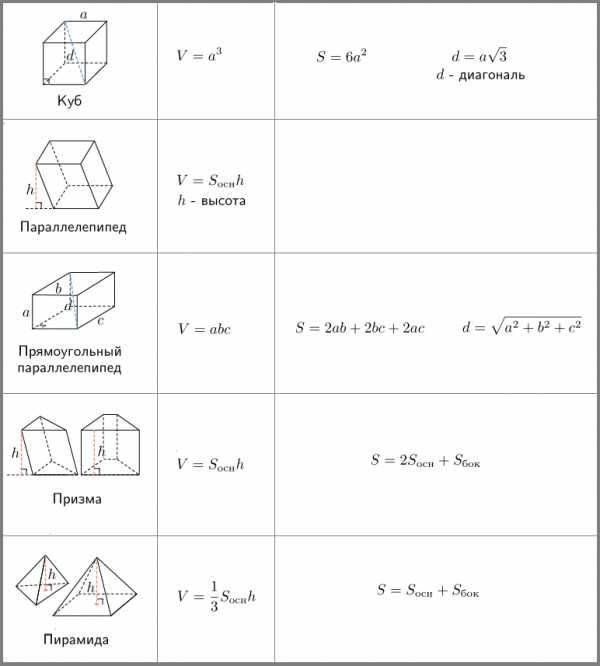
Все формулы объёма и формулы площади поверхности многогранников есть в нашей таблице.
Ты нашел то, что искал? Поделись с друзьями!
Проще всего найти объём куба — это куб его стороны. Вот, оказывается, откуда берётся выражение «возвести в куб».
Объём параллелепипеда тоже легко найти. Надо просто перемножить длину, ширину и высоту.
Объём призмы — это произведение площади её основания на высоту. Если в основании треугольник — находите площадь треугольника. Если квадрат — ищите площадь квадрата. Напомним, что высота — это перпендикуляр к основаниям призмы.
Объём пирамиды — это треть произведения площади основания на высоту. Высота пирамиды — это перпендикуляр, проведенный из её вершины к основанию.
Некоторые задачи по стереометрии решаются вообще без формул! Например, эта.
Объём куба равен . Найдите объём четырёхугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.
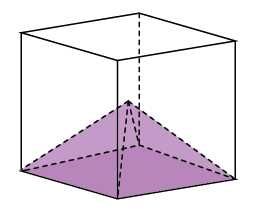
Обойдёмся без формул! Просто посчитайте, сколько нужно таких четырёхугольных пирамидок, чтобы сложить из них этот куб 🙂
Иногда в задаче надо посчитать площадь поверхности куба или призмы.
Напомним, что площадь поверхности многогранника — это сумма площадей всех его граней.
В некоторых задачах каждое ребро многогранника увеличили, например, в три раза. Очевидно, что при этом площадь поверхности увеличится в девять раз, а объём — в раз.
Стереометрия — это просто! Для начала выучите формулы объёма и площади поверхности многогранников и тел вращения. А дальше — читайте о приемах решения задач по стереометрии.
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
Прямые призмы (Sполн=2Sосн+Sбок; V=Sосн•H) |
|
| Куб |
Прямоугольный параллелепипед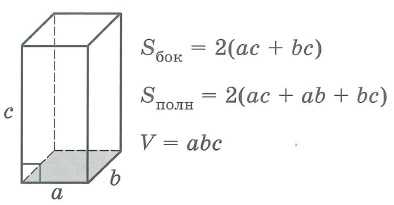 |
| Правильная треугольная призма |
Правильная шестиугольная призма |
Правильные пирамиды (Sполн=Sосн+Sбок; V=1/3•Sосн•H) |
|
| Тертраэдр |
Правильная треугольная пирамида |
| Правильная четырехугольная пирамида |
Правильная шестиугольная пирамида |
| Sбок— площадь боковой поверхности многогранника, Sполн — площадь полной поверхности многогранника, Sосн — площадь основания многогранника, V — объем многогранника. | |
Круговые цилиндры (Sполн=2Sосн+Sбок; V=Sосн•H) |
|
| Прямой цилиндр |
Прямой полый цилиндр |
Круговые конусы |
|
| Прямой конус | |
dpva.ru
Площадь поверхности и объём призмы — урок. Геометрия, 11 класс.
Площадь полной поверхности призмы — сумма площадей всех граней призмы.
Она состоит из площади боковой поверхности и площади оснований
Sполн.=Sбок.+2⋅Sосн.
Все грани куба — квадраты, поэтому рациональнее использовать формулу
Sполн. пов. куба=6⋅a2.
Объём прямой призмы находится по формуле:
V=Sосн.⋅H.
Для прямоугольного параллелепипеда можно использовать формулу \(V = abc\) , где \(a\), \(b\), \(c\) — измерения прямоугольного параллелепипеда (длина, ширина, высота).
Для куба используется формула V=a3, где \(a\) — ребро куба.
Основанием призмы может быть любой \(n\)-угольник, поэтому важно знать формулы вычисления их площадей.
Важные формулы нахождения площади \(n\)-угольников
| Квадрат | a2 | ||
| Прямоугольник | a⋅b | ||
| Ромб | a⋅b⋅sinα | a⋅h | d1⋅d22 |
| Параллелограмм | a⋅b⋅sinα | a⋅h | |
| Равносторонний треугольник | a234 | ||
| Прямоугольный треугольник | a⋅b2 | a⋅h3 | |
| Произвольный треугольник | a⋅b⋅sinα2 | a⋅h3 | p⋅p−ap−bp−c |
| Трапеция | a+b2⋅h |
Формула нахождения площади правильного шестиугольника
Правильный шестиугольник состоит из \(6\) правильных треугольников.
Sправ. ш.=6⋅a234, где \(a\) — сторона шестиугольника |
www.yaklass.ru
Площадь поверхности конуса — формулы, пример расчета
Пусть α– плоскость, точка S– точка, не лежащая в этой плоскости. Возьмем на плоскости произвольный круг с радиусом R. Соединим произвольную точку A этого круга с точкой S отрезком AS. Если точка А будет описывать круг с радиусом R, то отрезки AS будут заполнять некоторое тело. Это тело называют 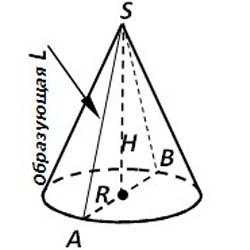
Границей конуса является круг радиуса R и боковая поверхность конуса.
Боковую поверхность описывает отрезок AS , когда точка A описывает круг.
Точка S является вершиной конуса. Множество отрезков AS, соединяющих вершину с окружностью основания являются направляющими конуса.Если перпендикуляр, опущенный из точки S, совпадает с центром основания, то конус называется прямым.Очень часто говорят, что прямой конус образуется в результате вращения прямоугольного треугольника вокруг оси, содержащий его катет.
На данном рисунке прямой конус получился в результате вращения прямоугольного треугольника AOS вокруг катета SO. Тогда говорят, что
- Катет SO –это высота конуса;
- Гипотенуза AS –образующая конуса;
- Катет AO – радиус конуса.
Площадь боковой поверхности конуса через его радиус и направляющую
Пусть дан конус с радиусом R и образующей L
AS=L, AO=R
Разрежем конус по образующей L и развернем его боковую поверхность.
Дуга AA` -это вытянутая окружность основания конуса с радиусом R. Следовательно, длина дуги AA` будет равна 2πR
Площадь боковой поверхности будет равна площади сектора круга с радиусом R.
Если угол α – радиальная мера угла, то:
где α=∠{ASA`}
Чтобы найти угол ∠{ASA`} воспользуемся формулой длины дуги, которая стягивает данный угол:
Но с другой стороны:
Приравняем правые части равенств. Имеем:
Выразим α:
Подставим полученное выражение в формулу площади сектора:
Следовательно, боковая поверхность конуса равна произведению числа π на радиус конуса и его образующую.
Формула боковой поверхности конуса будет иметь следующий вид:
Пример расчета площади боковой поверхности конуса, если известны его радиус и направляющая
Найти площадь боковой поверхности конуса с радиусом равным 3 см, образованным направляющей равной 7 см
Формула боковой поверхности конуса:
Подставив в формулу значения из условия задачи, имеем:
Площадь боковой поверхности конуса через его радиус и высоту
Очень часто в задачах на вычисление площади боковой поверхности конуса известна высота конуса вместо его направляющей.
Так как конус прямой, то треугольник AOS – прямоугольный, где AO и OS – катеты, а AS –гипотенуза. Воспользовавшись теоремой Пифагора, получаем:
Отсюда:
Но
Тогда:
Подставим данное выражение в формулу площади боковой поверхности конуса:
Боковая поверхность конуса равна произведению числа на радиус конуса и корень квадратный из суммы квадратов радиуса и высоты конуса
Найти площадь боковой поверхности конуса с радиусом равным 1 см и высотой, равной 5 см
По условию задачи Н = 5см, R=1см
Формула боковой поверхности конуса:
Подставив в формулу значения из условия задачи, имеем:
Полная поверхность конуса
Полная поверхность конуса – это сумма площади его боковой поверхности и площади основания конуса:
Основанием конуса является круг с радиусом R. Его площадь равна произведению числа π на квадрат его радиуса:
Площадь боковой поверхности вычисляется по формуле: или
Тогда площадь полной поверхности конуса равна:
или
Таким образом, площадь полной поверхности конуса равна произведению числа {pi} на радиус конуса и сумму направляющей и радиуса.
Формула имеет следующий вид:
Площадь полной поверхности конуса равна произведению числа π на радиус конуса и сумму корня квадратного из суммы квадратов радиуса и высоты конуса и радиуса конуса.
Формула имеет следующий вид:
2mb.ru
Площадь поверхности сфероида — Циклопедия
Сфероид вытянутый Сфероид сплюснутыйПлощадь сфероида
Сфероид — это тело, ограниченное эллипсоидом вращения.
Эллипсоид вращения — это поверхность в трёхмерном пространстве, образованная вращением эллипса вокруг одной из его осей.
[править] Виды сфероидов
- вытянутый;
- сплюснутый;
- нормальный.
Вытянутый сфероид ограничен вытянутым эллипсоидом вращения.
Вытянутый эллипсоид вращения — это геометрическое место точек пространства, для которых сумма расстояний до двух заданных точек (фокусов) постоянна (равна большой оси). Вытянутый эллипсоид вращения получается вращением эллипса вокруг большой оси. У вытянутого эллипсоида вращения одна большая ось и две малые оси.
Сплюснутый сфероид ограничен сплюснутым эллипсоидом вращения.
Сплюснутый эллипсоид вращения — это геометрическое место точек пространства, для которых сумма расстояний до ближайшей и до наиболее удалённой точки заданной окружности постоянна (равна малой оси). Сплюснутый эллипсоид вращения получается вращением эллипса вокруг малой оси. У сплюснутого эллипсоида вращения две большие оси и одна малая ось.
Нормальный сфероид — это шар (ограничен сферой).
Введём обозначения:
a — большая полуось;
b — малая полуось;
Sсфер.вытян — площадь вытянутого сфероида.
Sсфер.сплюсн — площадь сплюснутого сфероида.
[править] Формула 1
[править] Формула 2
[править] Другие формулы
cyclowiki.org
