Правило треугольника вычитание векторов – Сложение и вычитание векторов

8 класс. Геометрия. Векторы. Сложение и вычитание векторов. — Сложение и вычитание векторов.

Комментарии преподавателя

Сло­же­ние и вы­чи­та­ние век­то­ров

На преды­ду­щем уроке мы опре­де­ли­ли по­ня­тие век­то­ра, ска­за­ли, какие век­то­ры на­зы­ва­ют­ся рав­ны­ми, кол­ли­не­ар­ны­ми, со­на­прав­лен­ны­ми и про­ти­во­на­прав­лен­ны­ми.

Те­перь пусть за­да­но два век­то­ра – век­то­ра  и . Най­дем сумму этих двух век­то­ров . Для этого от­ло­жим из неко­то­рой точки А век­тор . Из точки В от­ло­жим век­тор . Тогда век­тор  на­зы­ва­ют сум­мой за­дан­ных век­то­ров:  (см. Рис. 1).

Рис. 1

Дан­ное опре­де­ле­ние можно объ­яс­нить так: пусть был задан груз, и сна­ча­ла на него по­дей­ство­ва­ла сила  – он пе­ре­ме­стил­ся из точки А в точку В, после этого по­дей­ство­ва­ла сила  – груз пе­ре­ме­стил­ся из точки В в точку С. Но в ре­зуль­та­те дей­ствия двух этих сил груз пе­ре­ме­стил­ся из точки А в точку С.

Таким об­ра­зом, мы по­лу­чи­ли опре­де­ле­ние суммы двух век­то­ров – пра­ви­ло тре­уголь­ни­ка.

Пра­ви­ло тре­уголь­ни­ка

Для того чтобы по­лу­чить сумму двух век­то­ров, нужно из про­из­воль­ной точки от­ло­жить пер­вый век­тор, из конца по­лу­чен­но­го век­то­ра от­ло­жить вто­рой век­тор, и по­стро­ить век­тор, со­еди­ня­ю­щий на­ча­ло пер­во­го с кон­цом вто­ро­го – это и будет сумма двух век­то­ров.

Можно про­ве­сти ана­ло­гию с чис­ла­ми. Мы ввели по­ня­тие числа, на­учи­лись скла­ды­вать числа, опре­де­ли­ли за­ко­ны сло­же­ния и так далее. Те­перь мы ввели по­ня­тие век­то­ра, на­учи­лись на­хо­дить рав­ные век­то­ра, скла­ды­вать век­то­ра. Те­перь нужно опре­де­лить за­ко­ны сло­же­ния.

За­ко­ны сло­же­ния век­то­ров

Для любых век­то­ров ,  и  спра­вед­ли­вы сле­ду­ю­щие ра­вен­ства:

 – пе­ре­ме­сти­тель­ный закон.

До­ка­за­тель­ство: от­ло­жим из точки сна­ча­ла век­тор , по­лу­ча­ем точку В, из нее от­кла­ды­ва­ем век­тор , по­лу­ча­ем точку С и век­тор .

Те­перь от­ло­жим из точки А сна­ча­ла век­тор  по­лу­чим точку В, из нее от­ло­жим век­тор, по­лу­чим точку С и век­тор .

www.kursoteka.ru

Вычитание векторов

Вам уже знакомы правила сложения векторов.

Чтобы сложить неколлинеарные векторы  и   по правилу треугольника, нужно от некоторой точки А отложить вектор , равный вектору . Далее от точки B отложить вектор , равный вектору . Вектор  является вектором суммы двух векторов  и .

Для сложения этих же векторов можно использовать правило параллелограмма. При этом нужно отложить от произвольной точки А векторы  и , равные векторам  и  соответственно, и построить на них параллелограмм ABCD. Тогда вектор  равен сумме векторов  и .

Для сложения нескольких векторов применяют правило многоугольника. При этом от некоторой точки последовательно откладывают векторы друг за другом, и вектором их суммы является вектор, проведённый от начала первого вектора к концу последнего.

Так же вам известны законы сложения векторов: переместительный и сочетательный.

На этом уроке поговорим о разности двух векторов. Её обозначают так .

Разностью векторов  и  называют такой вектор , сумма которого с вектором  равна вектору .

Чтобы получить представление о разности двух векторов, решим задачу.

Задача. По данным векторам  и  построить вектор .

Построение

 

 

 

.

Вектор  — искомый.

Эту задачу можно решить другим способом.

Но перед тем как его привести введём понятие вектора, противоположного данному.

Для произвольного

ненулевого вектора  вектор  будет противоположным, если:

Вектор, противоположный вектору , обозначается так . И говорят «вектор минус a».

Очевидно, что сумма вектора  с противоположным ему равна нулевому вектору .

Запишем теорему о разности двух векторов.

Для любых векторов  и  справедливо равенство .

Докажем данную теорему.

Доказательство.

Что и требовалось доказать.

Опираясь на эту теорему, приведём ещё одно решение задачи на построение разности векторов .

Способ

 

Отметим произвольную точку О и от неё отложим вектор . Далее отложим от точки А вектор .

По правилу треугольника сумма .

 

А значит, пользуясь теоремой о разности двух векторов, можем сделать вывод о том, что разность векторов . И вектор  — искомый.

Итак, можем сделать вывод, что вектор разности двух векторов можно строить двумя способами.

Можно от некоторой точки О отложить векторы  и , равные векторам . При этом вектором их разности будет вектор , направленный от конца вектора-вычитаемого к концу вектора-уменьшаемого.

Так же, пользуясь теоремой о разности двух векторов, разность векторов  можно представить в виде суммы вектора .

Тогда, отложив от некоторой точки О вектор , равные вектору , а от точки А — вектор , равный вектору , по правилу треугольника получим вектор .

Он является вектором суммы вектора . И, соответственно, вектором разности векторов .

Задача. Начертить попарно неколлинеарные векторы ,  и . Построить на них векторы: , , , ,  и .

Построение.

Для начала построим векторы, противоположные данным.

Векторы являются противоположными, если их длины равны и они противоположно направлены.

Выберем точки А, B и C, от которых будем откладывать противоположные векторы.

Далее через каждую из этих точек проведём прямые параллельные векторам ,  и   соответственно.

От отмеченных точек на проведённых прямых можно изобразить векторы, равные данным, и, противоположные данным. Нам нужны те, которые противоположны векторам ,  и    соответственно.

Так мы построили векторы ,  и .

Задача. Сторона квадрата  равна . Найти  и .

Построение.

Решение.

 

По  теореме Пифагора: 

Ответ: ; .

Подведём итоги нашего урока.

Сегодня вы познакомились с понятием противоположного вектора. Противоположные векторы имеют равные длины и противоположно направлены.

Мы ввели понятие разности двух векторов. Разностью векторов ,  называют такой вектор , сумма которого с вектором    равна вектору .

Для построения вектора разности мы выделили два способа.

Можно от некоторой точки О отложить векторы  и , равные векторам  и . При этом вектором их разности будет вектор, направленный от конца вектора-вычитаемого к концу вектора-уменьшаемого.

Так же, пользуясь теоремой о разности двух векторов, разность векторов  и  можно представить в виде суммы вектора  и вектора, противоположного вектору  .

Тогда, отложив от некоторой точки О вектор , равный вектору , а от точки А — вектор , равный вектору , по правилу треугольника получим вектор .

Он является вектором суммы вектора  и вектора, противоположного вектору . И, соответственно, вектором разности векторов  и .

Теперь вы владеете не только правилами сложения, а ещё и правилом вычитания векторов.

videouroki.net

Вычитание векторов

Вектор называется противоположным вектору , если их сумма равна нулевому вектору: . Противоположный вектор имеет длину , коллинеарен и противоположно направлен вектору (рис.1.8,а,б). Нулевой вектор является противоположным самому себе.

Разностью векторов и называется сумма вектора с вектором , противоположным вектору :

Для нахождения разности векторов и приложим к произвольной точке векторы и , а также вектор , противоположный вектору (рис.1.9,а). Искомую разность находим по правилу параллелограмма

Для нахождения разности проще использовать правило треугольника (рис. 1.9,6). Для этого прикладываем к произвольной точке векторы и . Вектор при этом равен искомой разности

Вычитание векторов — действие, обратное сложению — можно определить также следующим образом: разностью векторов и называется такой вектор , который в сумме с вектором дает вектор (рис.1.9,в), т.е. разность — это решение линейного векторного уравнения .

Решение. Учитывая равенство , получаем по правилу треугольника .

Поскольку и , то .

По правилу параллелограмма . Так как и , находим

Умножение вектора на число

Произведением ненулевого вектора на действительное число называется вектор , удовлетворяющий условиям:

1) длина вектора равна , т.е. ;

2) векторы и коллинеарные ;

3) векторы и одинаково направлены, если , и противоположно направлены, если .

Произведение нулевого вектора на любое число считается (по определению) нулевым вектором: ; произведение любого вектора на число нуль также считается нулевым вектором: . Из определения произведения следует, что:

а) при умножении на единицу вектор не изменяется: ;

б) при умножении вектора на получается противоположный вектор: ;

в) деление вектора на отличное от нуля число сводится к его умножению на число , обратное .

г) при делении ненулевого вектора на его длину, т.е. при умножении на число получаем единичный вектор, одинаково направленный с вектором .

Действительно, длина вектора равна единице: .

Вектор коллинеарен и одинаково направлен с вектором , так как ;

д) при умножении единичного вектора на число получаем коллинеарный ему вектор, длина которого равна .

вектора на и , а также противоположный вектор .

Свойства линейных операций над векторами

Сложение векторов и умножение вектора на число называются линейными операциями над векторами. Для любых векторов , , и любых действительных чисел справедливы равенства:

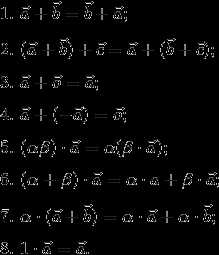
Свойства 1, 2 выражают коммутативность и ассоциативность операции сложения векторов, свойство 5 — ассоциативность операции умножения на число, свойства 6,7 — законы дистрибутивности, свойство 8 называется унитарностью.

Свойства линейных операций устанавливают такие же правила действия с векторами, как с алгебраическими выражениями.

Линейные комбинации векторов

Применяя линейные операции, можно составлять суммы векторов, умноженных на числа.

Вектор называется линейной комбинацией векторов , если он может быть представлен в виде

,

где — некоторые числа. В этом случае говорят, что вектор разложен по векторам , а числа называют коэффициентами разложения.

Линейная комбинация с нулевыми коэффициентами называется тривиальной.

Отметим следующие свойства линейных комбинаций векторов:

1. Если векторы — коллинеарны, то любая их линейная комбинация им коллинеарна.

2. Если векторы — компланарны, то любая их линейная комбинация им компланарна.

Докажем, например, первое свойство. При умножении вектора на число получаем (по определению) вектор, колпинеарный данному. При сложении двух векторов, параллельных некоторой прямой, получаем (по определению) вектор, параллельный той же самой прямой. Поэтому линейная комбинация двух коллинеарных векторов и коллинеарна им. По индукции свойство распространяется на любое конечное число коллинеарных векторов.

Аналогично доказывается второе свойство.

studfiles.net

Сложение и вычитание векторов

На уроках геометрии вы уже познакомились с простейшими операциями над векторами: нахождением их суммы и разности. Напомним это.

Сложение векторов. Чтобы найти сумму двух векторов, необходимо: а) параллельным переносом совместить начала векторов; б) дополнить чертёж двумя отрезками так, чтобы получился параллелограмм; в) провести вектор суммы из точки начал векторов в точку соединения дополняющих отрезков (по диагонали параллелограмма).

Проиллюстрируем это правило на примере из § 12-в, когда автомобиль перемещается сначала по вектору AВ1 и затем по вектору В1В2 до поворота на мост (см. чертёж слева). Другими словами, мы ищем вектор суммы или, что то же самое, сумму векторов AВ1 и В1В2.

Сделаем новые чертежи обсуждаемых векторов (см. ниже). На чертеже «а» применим параллельный перенос и переместим вектор В1В2 началом в точку А (то есть совместим начала векторов). Чертёж «б» дополним двумя отрезками СВ2 и В1В2 до образования параллелограмма. На чертеже «в» проведём вектор суммы из точки А начал векторов в точку В2 соединения дополняющих отрезков (по диагонали параллелограмма).

Итак, мы нашли вектор суммы или сумму векторов:

Проверим правильность результата: автомобиль, переместившись из точки А в точку В1, затем переместился из точки В1 в точку В2. Иначе говоря, он совершил перемещение «по» вектору АВ2, который мы только что построили, применив правило паралеллограмма.

Вычитание векторов. Чтобы найти разность двух векторов, нужно: а) параллельным переносом совместить начала векторов; б) дополнить чертёж отрезком так, чтобы получился треугольник; в) придать отрезку направление от вычитаемого к уменьшаемому, создав вектор разности.

Проиллюстрируем это правило на том же примере из § 12-в, когда автомобиль подъезжает к середине моста. Для этого из вектора полного перемещения АВ3 вычтем перемещение на третьем этапе, вектор B2В3.

Другими словами, сейчас мы ищем вектор разности:

На чертеже «а» применим параллельный перенос и переместим вектор В2В3 началом в точку А (то есть совместим начала векторов). Чертёж «б» дополним отрезком DВ3 до образования треугольника. На чертеже «в» придадим отрезку направление от вычитаемого (синего вектора) к уменьшаемому (красному вектору), создав вектор разности DВ3.

Контурной стрелкой показан параллельный перенос найденного вектора разности в точку А. Важно: построенный вектор DВ3 равен искомому вектору разности АВ2. Это, по сути, проверка правильности результата, поскольку этот вектор мы уже находили по правилу параллелограмма.

Заметим, что векторы можно складывать и «треугольником», а вычитать «параллелограммом». Но мы рекомендуем запомнить именно правило параллелограмма для суммы векторов и правило треугольника для разности векторов, поскольку в дальнейшем эти правила понадобятся нам именно в таком виде.

questions-physics.ru

Сложение и вычитание векторов

Линейными операциями над векторами называется сложение, вычитание векторов и умножение вектора на число.

Результатом сложения векторов является их сумма. Сумма векторов и обозначается .

Существует два правила сложения двух векторов: правило треугольника и правило параллелограмма.

Правило треугольника

Чтобы сложить векторы и , надо взять произвольную точку и от нее отложить последовательно сначала вектор , затем вектор . Вектор, начало которого совпадает с началом вектора (т.е. первого вектора), а конец – с концом вектора (т.е. второго вектора), есть искомая сумма. На рис. 4 .

 

 

По правилу треугольника можно складывать любые векторы.

Коротко правило треугольника можно записать так:

для любых трех точек А,В и С .

Правило параллелограмма

Чтобы сложить векторы и , надо привести их к общему началу, т.е. взять произвольную точку А, построить такие точки В и С, что и , и достроить полученную фигуру до параллелограмма . Вектор — искомая сумма (рис. 5).

 

 

По правилу параллелограмма можно складывать тольконеколлинеарные векторы.

Свойства сложения векторов:

1⁰. .

2⁰. .

3⁰. .

4⁰. .

Суммой трех векторов и называется вектор . Учитывая свойство 4⁰, скобки можно опустить и обозначать сумму в виде .

Суммой n векторовназывается вектор и обозначается так: .

При построении суммы n векторов пользуются правилом многоугольника.

Правило многоугольника

Чтобы найти сумму n векторов, надо взять произвольную точку и отложить от нее последовательно эти векторы. Вектор, начало которого совпадает с началом первого вектора, а конец – с концом последнего (n-го вектора), есть искомая сумма.

Разностью векторов и называется такой вектор , что . Разность – это результат вычитания векторов. Разность векторов и обозначается так: .

Правило построения разности двух векторов

Чтобы построить разность векторов и , надо привести их к общему началу. Тогда вектор, начало которого совпадает с концом второго вектора (т.е. вектора ), а конец – с концом первого (т.е. ), есть искомая разность .

На рис. 6 .

 

 

По правилу треугольника

,

откуда получаем краткую запись правила нахождения разности векторов:

.

Умножение вектора на число

Рассмотрим еще одну линейную операцию над векторами – умножение вектора на число. Результатом этой операции является произведение вектора на число.

Произведением вектора на действительное число a называется вектор , обозначаемый через и удовлетворяющий двум условиям:

1) его длина ;

2) если a 0, то ; если <0, то .

Алгоритм построения произведения вектора число a таков.

Берем произвольную точку М. Проводим луч , сонаправленный с вектором , если a 0, и противоположно направленный с вектором , если <0. На луче от начала М откладываем отрезок MP, длина которого в раз больше длины вектора . Вектор — искомый вектор .

Продемонстрируем этот алгоритм на конкретном примере. Построим вектор , если — данный вектор.

Возьмем произвольную точку А. Так как <0, то проводим луч (рис. 7). На луче строим такую точку С, что . Тогда — искомый вектор.

 

Свойства умножения вектора на число

1⁰. и .

2⁰. .

3⁰. .

4⁰. .

Теорема 1 (о коллинеарных векторах).Пусть . Векторы и коллинеарны тогда и только тогда, когда существует такое действительное число a, что .

Теорема 2 (о компланарных векторах).Пусть || . Векторы компланарны тогда и только тогда, когда существуют такие действительные числа a и b, что .

Лекция 2

Линейная зависимость векторов

Линейная зависимость векторов и ее свойства

Линейной комбинацией векторовназывается вектор , где .

Примеры линейных комбинаций:

1. Вектор есть линейная комбинация векторов (здесь ).

2. Вектор есть линейная комбинация векторов (здесь ).

Система векторов называется линейно зависимой, если существуют такие действительные числа , не все равные 0 одновременно, что выполняется векторное равенство:

.

Если равенство выполняется только при , то система векторов называетсялинейно независимой.

Примеры

1. Система векторов линейно зависима, т.к. если возьмем , то получим, что , т.е. существуют такие действительные числа , не все равные 0 одновременно ( ), что выполняется равенство .

2. Система двух неколлинеарных векторов и линейно независима, т.к. сумма двух неколлинеарных векторов и равна нулевому вектору только при .

---

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

zdamsam.ru

Сложение и вычитание векторов — КиберПедия

Линейными операциями над векторами называется сложение, вычитание векторов и умножение вектора на число.

Результатом сложения векторов является их сумма. Сумма векторов и обозначается .

Существует два правила сложения двух векторов: правило треугольника и правило параллелограмма.

Правило треугольника

Чтобы сложить векторы и , надо взять произвольную точку и от нее отложить последовательно сначала вектор , затем вектор . Вектор, начало которого совпадает с началом вектора (т.е. первого вектора), а конец – с концом вектора (т.е. второго вектора), есть искомая сумма. На рис. 4 .

 

 

По правилу треугольника можно складывать любые векторы.

Коротко правило треугольника можно записать так:

для любых трех точек А,В и С .

Правило параллелограмма

Чтобы сложить векторы и , надо привести их к общему началу, т.е. взять произвольную точку А, построить такие точки В и С, что и , и достроить полученную фигуру до параллелограмма . Вектор — искомая сумма (рис. 5).

 

 

По правилу параллелограмма можно складывать тольконеколлинеарные векторы.

Свойства сложения векторов:

1⁰. .

2⁰. .

3⁰. .

4⁰. .

Суммой трех векторов и называется вектор . Учитывая свойство 4⁰, скобки можно опустить и обозначать сумму в виде .

Суммой nвекторовназывается вектор и обозначается так: .

При построении суммы n векторов пользуются правилом многоугольника.

Правило многоугольника

Чтобы найти сумму nвекторов, надо взять произвольную точку и отложить от нее последовательно эти векторы. Вектор, начало которого совпадает с началом первого вектора, а конец – с концом последнего (n-го вектора), есть искомая сумма.

Разностью векторов и называется такой вектор , что . Разность – это результат вычитания векторов. Разность векторов и обозначается так: .

Правило построения разности двух векторов

Чтобы построить разность векторов и , надо привести их к общему началу. Тогда вектор, начало которого совпадает с концом второго вектора (т.е. вектора ), а конец – с концом первого (т.е. ), есть искомая разность .

На рис. 6 .

 

 

По правилу треугольника

,

откуда получаем краткую запись правила нахождения разности векторов:

.

Умножение вектора на число

Рассмотрим еще одну линейную операцию над векторами – умножение вектора на число. Результатом этой операции является произведение вектора на число.

Произведением вектора на действительное число a называется вектор , обозначаемый через и удовлетворяющий двум условиям:

1) его длина ;

2) если a 0, то ; если <0, то .

Алгоритм построения произведения вектора числоa таков.

Берем произвольную точку М. Проводим луч ,сонаправленный с вектором , если a 0, и противоположно направленный с вектором , если <0. На луче от начала М откладываем отрезок MP, длина которого в раз больше длины вектора .Вектор — искомый вектор .

Продемонстрируем этот алгоритм на конкретном примере. Построим вектор , если — данный вектор.

Возьмем произвольную точку А. Так как <0, то проводим луч (рис. 7). На луче строим такую точку С, что . Тогда — искомый вектор.

 

cyberpedia.su

Тема: Вычитание векторов — Документ

МАСТЕР-КЛАСС

ГЕОМЕТРИЯ, 9 КЛАСС, УРОК: «ВЫЧИТАНИЕ ВЕКТОРОВ»

Предмет: Геометрия

Тема: Вычитание векторов

Класс: 9 класс
Учащиеся должны:

Знать, какой вектор является разностью двух векторов, теорему о разности векторов.

Уметь строить разность двух векторов двумя способами, применять эти знания при решении задач.

Ход урока.

1. Организационный момент: назвать уели урока.

2. Проверка пройденного материала:

Тестирование:

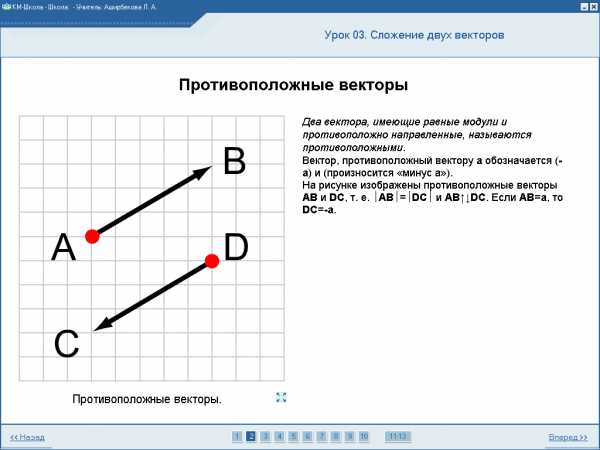1. Как называются векторы, имеющие равные модули и противоположно направленные?

А) противоположные

Б) противоположно направленные

В) равные

2. Тело переместили из точки А в точку В, а потом из точки В в точку С. Какой вектор представляет суммарное перемещение тела?

А)

Б)

В)

3. Закончите предложение:

Суммой двух векторов называется вектор, построенный по правилу…. (треугольника)

4. Вставьте пропущенное слово:

Чтобы сложить два неколлинеарных вектора и, нужно отложить от произвольной точки О векторы = и = и построить …. ОАСВ, тогда =+

(параллелограмм)

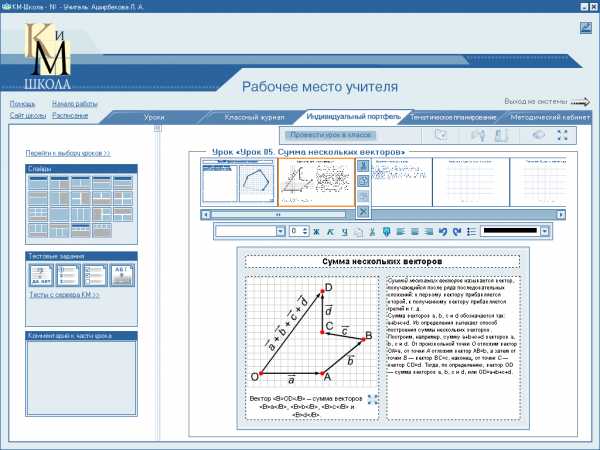5. Изображенный на рисунке способ построения суммы нескольких векторов называется правилом…

(многоугольника)

III. Объяснение нового материала:

План объяснения:

1. Разность векторов

Вычитание векторов, как и вычитание чисел, — это действие, обратное сложению. Разность двух векторов и называется такой вектор , который в сумме с вектором дает вектор . Разность векторов и обозначается так: — . Построить разность векторов и можно следующим образом. Отложим от произвольной точки О векторы и . Получим векторы = и =. Тогда вектор и будет разностью — , поскольку

=+. Итак, == — = — .

Вычитание векторов можно свести к сложению точно так же, как и в случае чисел а и b:

а — b = а + (- b), где числа b и + (- b) — противоположные.

Итак, нам надо доказать, что результат вычитания вектора из вектора тот же, что и результат сложения векторов а + (- b).

2. Теорема о разности двух векторов.

Теорема (о разности векторов)

Для любых векторов и справедливо равенство — = + (- ).

Доказательство:

Отложим от произвольной точки О векторы и . Получим векторы = и =. Тогда, согласно определению, разность векторов и есть вектор , т.е. = — = — . По правилу треугольника = + . Кроме того, = — = -. Поэтому — = = + = (-) + =+(-)=+(-). Теорема доказана.

3. Построение разности векторов.

Доказанная теорема подсказывает еще один способ построения разности векторов и .

Отложим от произвольной точки О отложим вектор = , затем от точки А отложим вектор = -. Тогда по теореме о разности двух векторов — = + (-), поэтому — = + = . Итак, мы построили разность векторов и .

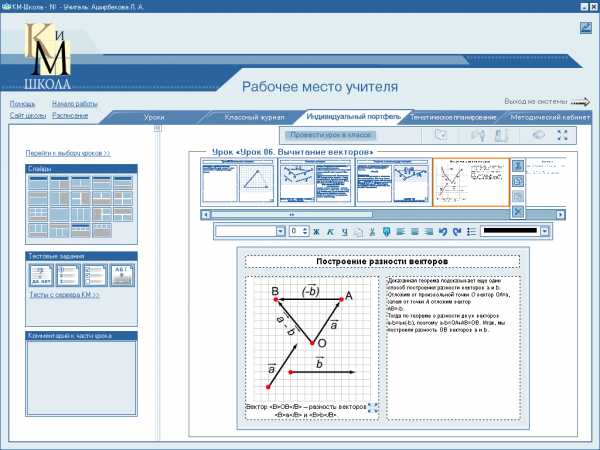
Выводы по уроку:

1. Разностью двух векторов и называется такой вектор , который в сумме с вектором дает вектор .

2. Теорема ( о разности двух векторов): Для любых векторов и справедливо равенство:

— = + (-).

IV. Закрепление полученных знаний.

Тестирование.

1. Какой вектор называется разностью векторов и ?

А) Разностью двух векторов и называется такой вектор , построенный по правилу треугольника.

Б) Разностью двух векторов и называется такой вектор , который получается после ряда последовательных сложений

В) Разностью двух векторов и называется такой вектор , который в сумме с вектором дает вектор

2. Какой вектор, изображенный на рисунке, является разностью векторов и ?

А)

Б)

В)

3. №767. Дан треугольник АВС. Выразите векторы = и = вектор .

а) —

б) —

в) +

4. №762. Сторона равностороннего треугольника АВС равна а .Модуль  —  = а

да нет

V. Подведение итогов.

VI. Задание на дом: п.82, №№754, 756, 767

gigabaza.ru