§2 Предел функции двух переменных
Рассмотрим плоскость и систему Oxyдекартовых прямоугольных координат на ней (можно рассматривать и другие системы координат).
Из аналитической геометрии знаем, что каждой упорядоченной паре чисел ( x, y )можно сопоставить единственную точкуMплоскости и наоборот, каждой точкеMплоскости соответствует единственная пара чисел.
Поэтому в дальнейшем, говоря о точке, мы будем часто подразумевать соответствующую ей пару чисел ( x, y )и наоборот.
Определение 1.2 Множество пар чисел ( x, y ), удовлетворяющих неравенствам, называется прямоугольником (открытым).
На плоскости он изобразится прямоугольником (рис. 1.2) со сторонами, параллельными осям координат, и с центром в точке M0(x
Прямоугольник принято обозначать следующим символом:
Введем важное для дальнейшего изложения понятие: окрестность точки.
Определение 1.3 Прямоугольной δ-окрестностью (дельта-окрестностью) точкиM0(x0y0)называется прямоугольник
с центром в точке M0и с одинаковыми по длине сторонами2δ.
Определение 1.4 Круговой δ— окрестностью точкиM0(x0y0)называется круг радиусаδс центром в точкеM 0, т. е. множество точекM(xy), координаты которых удовлетворяют неравенству:
Можно ввести понятия окрестностей и других видов, но для целей математического анализа технических задач, в основном, используются лишь прямоугольные и круговые окрестности.
Введём следующее понятие предела функции двух переменных.
Пусть функция z = f ( x, y )определена в некоторой областиζиM0(x0y0)— точка, лежащая внутри или на границе этой области.
Определение 1.5Конечное число Aназываетсяпределом функции f ( x, y )при
и
если для любого положительного числа εможно найти такое положительное числоδ, что неравенство
выполняется для всех точек
Смысл этого определения состоит в том, что значения функции f ( х, у )как угодно мало отличаются от числа А в точках достаточно малой окрестности точкиМ0.
Здесь в основу определения положены прямоугольные окрестности М0. Можно было бы рассматривать круговые окрестности точкиМ0и тогда нужно было бы требовать выполнения неравенства
во всех точках М(х,у)областиζ, отличных отМ0и удовлетворяющих условию:
где
— расстояние между точками МиМ0.
Употребительны следующие обозначения предела:
Учитывая определение предела функции двух переменных, можно перенести основные теоремы о пределах для функций одной переменной на функции двух переменных.
Например, теоремы о пределе суммы, произведения и частного двух функций.
§3 Непрерывность функции двух переменных
Пусть функция z = f ( x ,y )определена в точкеM0(x0y0)и её окрестности.
Определение 1.6 Функция называется непрерывной в точке M0(x0y0), если
Если функция f ( x ,y )непрерывна
в точке
Поскольку
То есть, если функция f ( x ,y )непрерывна в точкеM0(x0y0), то бесконечно малым приращениям аргументов в этой области соответствует бесконечно малое приращениеΔzфункцииz.
Справедливо и обратное утверждение: если бесконечно малым приращениям аргументов соответствует бесконечно малое приращение функции, то функция непрерывна
Функцию, непрерывную в каждой точке области, называют непрерывной в области. Для непрерывных функций двух переменных, так же, как и для функции одной переменной, непрерывной на отрезке, справедливы основополагающие теоремы Вейерштрасса и Больцано — Коши.
Справка: Карл Теодор Вильгельм Вейерштрасс (1815 — 1897) — немецкий математик. Бернард Больцано (1781 — 1848) — чешский математик и философ. Огюстен Луи Коши (1789 — 1857) — французский математик, президент французской Академии наук (1844 — 1857).
Пример 1.4. Исследовать на непрерывность функцию
Решение
Данная функция определена при всех значениях переменных xиy, кроме начала координат, где знаменатель обращается в нуль.
Многочлен x2+y2непрерывен всюду, а значит и непрерывен корень квадратный из непрерывной функции.
Дробь же будет непрерывной всюду, кроме точек, где знаменатель равен нулю. То есть рассматриваемая функция непрерывна на всей координатной плоскости Оху, исключая начало координат.
Пример 1.5. Исследовать на непрерывность
функцию
При каждом фиксированном «k»уравнение (1.11) определяет гиперболу. Поэтому рассматриваемая функция является непрерывной функциейx и y , исключая точки, лежащие на кривых (1.11).
studfiles.net
Предел функции многих переменных
Предел функции в точке.
Напомним, что окрестностью \(O(x^0)\) точки \(x^0\) в метрическом пространстве \(X\) называется любое множество, для которого точка \(x^0\) является внутренней. Проколотая окрестность \(\dot{O}(x^0)\) получается из \(O(x^0)\) удалением самой точки \(x^0\), то есть \(\dot{O}(x^0)=O(x^0)\backslash\{x^0\}\).
Будем рассматривать функции \(f: \ M\rightarrow R\), где \(M\) есть некоторое множество, принадлежащее метрическому пространству \(X\). Если \(X=R^n\), то функция \(f: \ M\rightarrow R\) называется функцией многих переменных и обозначается обычно следующим образом:
$$
f(x)=f(x_1,\ldots,x_n),\quad x\in M.\nonumber
$$
Например, функция \(\displaystyle \sqrt{1-x_1^2-x_2^2}\) определена в единичном круге пространства \(R^2\) с центром в точке \((0,0)\), а функция \(\operatorname{ln}(x_1^2+x_2^2)\) определена в любой проколотой окрестности точки \((0,0)\).
Определение 1.
Пусть функция \(f(x)\) определена в проколотой окрестности \(\dot{O}(x^0)\) точки \(x^0\) метрического пространства \(X\). Говорят, что число \(A\) есть предел функции \(f(x)\) при \(x\rightarrow x_0\), если \(\forall\ \varepsilon > 0 \ \exists \ \delta > 0\) такое, что для \(\forall \ x\in\dot{O}(x^0)\), удовлетворяющего условию \(\rho(x,x^0) < \delta\), выполнено неравенство \(|f(x)-A| < \varepsilon\).
Определение 2.
Говорят, что функция \(f(x)\), определенная в \(\dot{O}(x^0)\), имеет при \(x\rightarrow x_0\) предел \(A\), если для любой последовательности \(x^{(k)}\in\dot{O}(x^0)\) такой, что \(\displaystyle\lim_{k\rightarrow\infty}x^{(k)}=x^0\), выполнено равенство \(\displaystyle\lim_{k\rightarrow\infty}f(x^{(k)})=A\).
Эквивалентность двух определений предела доказывается так же, как и для функций одной переменной.
Если число \(A\) есть предел функции \(f(x)\) при \(x\rightarrow x_0\), то будем писать
$$
A=\lim_{x\rightarrow x^0}f(x).\nonumber
$$
Если функция двух переменных \(f(x,y)\) определена в \(\dot{O}((a,b))\), a число \(A\) есть ее предел при \((x,y)\rightarrow(a,b)\), то пишут
$$
A=\lim_{x\rightarrow a,y\rightarrow b}f(x,y)\nonumber
$$
и называют иногда число \(A\) двойным пределом.
Аналогично, для функции \(n\) переменных наряду с обозначением \(A=\displaystyle\lim_{x\rightarrow x^0}f(x)\) будем использовать обозначение
$$
A=\lim_{x\rightarrow x_1^0,\ldots,x_n\rightarrow x_n^0}f(x_1,\ldots,x_n).\nonumber
$$
Лемма 1.
Пусть функции \(f(x)\) и \(\varphi(x)\) определены в \(\dot{O}(x^0)\) и \(|f(x)|\leq \varphi(x)\) в \(\dot{O}(x^0)\). Если \(\displaystyle\lim_{x\rightarrow x^0}\varphi(x)=0\), то и \(\displaystyle\lim_{x\rightarrow x^0}f(x)=0\).
Доказательство.
\(\circ\) Так как \(\displaystyle\lim_{x\rightarrow x^0}\varphi(x)=0\), то для любого \(\varepsilon > 0\) найдется шар \(S_{\delta}(x^0)\) такой, что для всех \(x\in S_{\delta}(x^0)\) выполнено неравенство \(|\varphi(x)| < \varepsilon\). Тем более для всех \(x\in S_{\delta}(x^0)\) выполнено неравенство \(|f(x)| < \varepsilon\), то есть \(\displaystyle\lim_{x\rightarrow x^0}f(x)=0\). \(\bullet\)
Пример 1.
Доказать, что \(\displaystyle\lim_{x\rightarrow 0,y\rightarrow 0}(x^2+y^2)^a=0\), если \(a > 0\).
Решение.
\(\triangle\) Возьмем любое \(\varepsilon > 0\). Положим \(\delta=\varepsilon^{1/(2a)}\). Пусть \((x,y)\in S_\delta(0, 0)\), тогда
$$
(x^2+y^2)^a < \delta^{2a} < \varepsilon,\nonumber
$$
то есть
$$
\lim_{x\rightarrow 0,y\rightarrow 0}(x^2+y^2)^a=0.\nonumber
$$
Что и требовалось доказать. \(\blacktriangle\)
Пример 2.
Показать, что \(\displaystyle \lim_{x\rightarrow 0,y\rightarrow 0}\frac{|x|^{\alpha}|y|^{\beta}}{(x^2+y^2)^{\gamma}}=0\), если \(\alpha+\beta-2\gamma > 0\).
Решение.
\(\triangle\) Так как
$$
|x| < \sqrt{x^2+y^2},\qquad |y| < \sqrt{x^2+y^2},\nonumber
$$
то при \(x^2+y^2 > 0\) имеем неравенства
$$
0\leq f(x,y)=\frac{\vert x\vert^\alpha\vert y\vert^\beta}{(x^2+y^2)^\gamma}\leq\frac{(x^2+y^2)^{\alpha/2}(x^2+y^2)^{\beta/2}}{(x^2+y^2)^\gamma}=\\(x^2+y^2)^{(\alpha+\beta-2\gamma)/2}=\varphi(x,y).\nonumber
$$
В силу примера выше \(\displaystyle\lim_{x\rightarrow 0,y\rightarrow 0}\varphi(x,y)=0.\), так как \(\alpha+\beta-2\gamma > 0\). Применяя лемму 1, получаем, что
$$
\lim_{x\rightarrow 0,y\rightarrow 0}f(x,y)=0.\nonumber
$$
Что и требовалось доказать. \(\blacktriangle\)
Пример 3.
Функция
$$
f(x,y)=\frac{2xy}{x^2+y^2}\label{ref1}
$$
не имеет предела при \((x,y)\rightarrow (0,0)\).
Решение.
\(\triangle\) Рассмотрим последовательность точек \((x_n,y_n)=\displaystyle\left(\frac{1}{n},\frac{1}{n}\right)\). Тогда \(f(x_n,y_n)=1\) и, следовательно, \(\displaystyle \lim_{n\rightarrow\infty}f(x_n,y_n)=1\). Если же взять последовательность точек \((x_n’,y_n’)=\displaystyle\left(\frac{1}{n},-\frac{1}{n}\right)\), то \(\displaystyle \lim_{n\rightarrow\infty}f(x_n’,y_n’)=-1\).
Так как при любом \(n\in \mathbb{N}\) точки \((x_n,y_n)\) и \((x_n’,y_n’)\) не совпадают с точкой \((0,0)\), а последовательности точек \((x_n,y_n)\) и \((x_n’,y_n’)\) сходятся к точке \((0,0)\), то, используя определение 2 предела, получаем, что функция \(f(x,y)\) не имеет предела при \((x,y)\rightarrow (0,0)\). \(\blacktriangle\)
Пример 4.
Функция
$$
f(x,y)=\frac{2x^2y}{x^4+y^2}\label{ref2}
$$
не имеет предела при \((x,y)\rightarrow (0,0)\).
Решение.
\(\triangle\) Повторяя рассуждения примера 3, построим две последовательности точек \((x_n,y_n)=\displaystyle\left(\frac{1}{n},\frac{1}{n}\right)\) и \((x_n’,y_n’)=\displaystyle\left(\frac{1}{n},\frac{1}{n^2}\right)\). Так как \((x_n,y_n)\rightarrow(0,0)\) и \((x_n’,y_n’)\rightarrow(0,0)\), а \(\displaystyle\lim_{n\rightarrow\infty}f(x_n,y_n)=0\) и \(\displaystyle\lim_{n\rightarrow\infty}f(x_n’,y_n’)=1\), то двойной предел функции \(f(x,y)\) при \((x,y)\rightarrow(0,0)\) не существует. \(\blacktriangle\)
Предел по множеству.
Предел \(\displaystyle\lim_{x\rightarrow x^0}f(x)\) был определен ранее для функции, заданной в \(\dot{O}(x^0)\). Расширим определение предела, введя понятие предела по множеству.
Определение 3.
Пусть \(M\) есть подмножество области определения функции \(f(x)\), \(x^0\) — предельная точка множества \(M\). Будем говорить, что число \(A\) есть предел функции \(f(x)\) по множеству \(M\) при \(x\rightarrow x^0\), если \(\forall\varepsilon > 0 \ \exists \delta > 0\) такое, что \(\forall x\in{\dot S}_\delta(x^0)\cap M\) выполнено неравенство \(|f(x)-A| < \varepsilon\). В этом случае пишут
$$
A=\lim_{x\rightarrow x^0, \ x\in M}f(x).\nonumber
$$
Пусть функция двух переменных \(f(x,y)\) определена в проколотой окрестности \(\dot{O}(x_0,y_0)\). Пределом функции \(f(x,y)\) в точке \((x_0,y_0)\) по направлению \(l=(\cos\alpha,\sin\alpha)\) будем называть выражение
$$
\lim_{t\rightarrow+0}f(x_0+t\cos\alpha, \ y_0+t\sin\left(\alpha\right))=\lim_{\begin{array}{c}(x,y)\rightarrow(x_0,y_0)\\(x,y)\in\dot O(x_0,y_0)\cap L\\\end{array}}f(x,y),\nonumber
$$
где \(L\) есть луч, выходящий из точки \((x_0,y_0)\) в направлении \(l\).
Пример 5.
Показать, что предел функции \(f(x,y)=\displaystyle \frac{2xy}{x^2+y^2}\) в точке \((0,0)\) по любому направлению \(l=(\cos\alpha, \ \sin\alpha)\) существует и равен \(\sin 2\alpha\).
Решение.
\(\triangle\) Так как при \(t > 0\) выполнено равенство
$$
f(t\cos\alpha, \ t\sin\alpha)=2\sin\alpha\cos\alpha=\sin 2\alpha,\nonumber
$$
то
$$
\lim_{t\rightarrow 0}f(t\cos\alpha, \ t\sin\alpha)=\sin 2\alpha.\quad\blacktriangle\nonumber
$$
Пример 6.
Показать, что предел функции \(f(x,y)=\displaystyle \frac{2x^2y}{x^4+y^2}\) в точке \((0,0)\) по любому направлению \(l=(\cos\alpha, \ \sin\alpha)\) существует и равен нулю.
Решение.
\(\triangle\) При \(t > 0\) справедливо равенство
$$
f(t\cos\alpha, \ t\sin\alpha)=\frac{2t\cos^2\alpha\sin\alpha}{t^2\cos^4\alpha+\sin^2\alpha}.\nonumber
$$
Если \(\sin\alpha=0\), то \(f(t\cos\alpha, \ t\sin\alpha)=0\) и, следовательно,
$$
\lim_{t\rightarrow +0}f(t\cos\alpha, \ t\sin\alpha)=0.\nonumber
$$
Если \(\sin\alpha\neq 0\), то
$$
\lim_{t\rightarrow +0}f(t\cos\alpha, \ t\sin\alpha)=0.\quad\blacktriangle\nonumber
$$
Ясно, что из существования \(\displaystyle\lim_{x\rightarrow x^0, \ x\in M}f(x)\) следует существование \(\displaystyle\lim_{x\rightarrow x^0, \ x\in M’}f(x)\) для любого подмножества \(M’\subset M\), для которого \(x’\) есть предельная точка. В частности, из существования двойного предела функции \(f(x,y)\) при \((x,y)\rightarrow (x_0,y_0)\) следует существование предела функции \(f(x,y)\) в точке \((x_0,y_0)\) по любому направлению и равенство этих пределов двойному пределу функции \(f(x,y)\) при \((x,y)\rightarrow (x_0,y_0)\).
Из результатов примеров 4 и 6 следует, что из существования и равенства пределов по любому направлению в точке \((x_0,y_0)\) не вытекает существование в этой точке предела функции.
Предел функции \(f(x)\) в точке \(x^0\in R^n\) по направлению \(l=(l_1,\ldots,l_n)\), где \(l_1^2+\ldots+l_n^2=1\), определяется по аналогии со случаем функции двух переменных.
Повторные пределы. Бесконечные пределы.
Пусть функция двух переменных \(f(x,y)\) определена на множестве
$$
\Pi={(x,y):\quad 0 < |x-x_0| < a,\quad 0 < |y-y_0| < b}.\nonumber
$$
Пусть \(\forall x\in (x_0-a, \ x_0+a), \ x\neq x_0\), существует \(\displaystyle\lim_{y\rightarrow y_0}f(x,y)=g(x)\), а функция \(g(x)\) определена в проколотой окрестности точки \(x_0\). Если существует \(\displaystyle\lim_{x\rightarrow x_0}g(x)=\lim_{x\rightarrow x_0}\lim_{y\rightarrow y_0}f(x,y)\), то этот предел называется повторным. Аналогично определяется другой повторный предел \(\displaystyle\lim_{y\rightarrow y_0}\lim_{x\rightarrow x_0}f(x,y)\).
Как показывают простые примеры, из существования двойного предела не следует существование повторных пределов, а из существования и равенства повторных пределов не следует существование двойного предела.
Так для функции \(\displaystyle f(x,y)=\frac{2xy}{x^2+y^2}\) примера 3 двойной предел при \((x,y)\rightarrow (0,0)\) не существует, но оба повторных предела равны нулю, так как
$$
\lim_{x\rightarrow0}f(x,y)=\lim_{y\rightarrow0}f(x,y)=0.\nonumber
$$
Для функции
$$
f(x,y)=\left\{\begin{array}{lc}x\sin\frac1y,&y\neq0,\\0,&y=0,\end{array}\right.\nonumber
$$
справедливо неравенство \(|f(x,y)|\leq|x|\). В силу леммы 1 двойной предел этой функции при \((x,y)\rightarrow (0,0)\) равен нулю. Но при \(x\neq 0\) не существует
$$
\lim_{y\rightarrow0}x\sin\frac1y,\nonumber
$$
а поэтому не существует и соответствующий повторный предел.
Бесконечные пределы для функций многих переменных определяются по той же схеме, что и для функций одной переменной. Например, \(\displaystyle\lim_{x\rightarrow x^0}f(x)=+\infty\), если для любого числа \(C > 0\) число \(\delta > 0\), что для всех \(x\) из проколотой окрестности \(\dot{O}(x^0)\) точки \(x^0\) выполнено неравенство \(f(x) > C\).
Пример 7.
Показать, что
$$
\lim_{x\rightarrow +\infty,y\rightarrow +\infty}(x^2+y^2)e^{-(x+y)}=0.\nonumber
$$
Решение.
\(\triangle\) Так как при \(x > 0, \ y > 0\) справедливо неравенство
$$
0\leq (x^2+y^2)e^{-(x+y)}\leq(x+y)^2e^{-(x+y)}\nonumber
$$
и \(\displaystyle\lim_{t\rightarrow +\infty}t^2e^{-t}=0\), то \(\forall \varepsilon > 0 \ \exists\delta > 0\) такое, что \(\forall t > \delta\) выполнено неравенство \(t^2e^{-t} < \varepsilon\). Но тогда \(\forall x > \displaystyle\frac{\delta}{2}\) и \(\forall y > \displaystyle\frac{\delta}{2}\) справедливо неравенство
$$
0\leq(x^2+y^2)e^{-(x+y)} < \varepsilon.\quad\blacktriangle\nonumber
$$
univerlib.com
1.2. Предел функции двух переменных. Непрерывность
При рассмотрении предела функции одной переменной было введено понятие окрестности точки. Под окрестностью точки Принимался интервал, содержащий эту точку. При введении понятия предела функции двух переменных будем рассматривать окрестность точки в плоскости .
Окрестностью точки Называется внутренность круга с центром в этой точке. Если радиус круга равен , то говорят о -окрестности точки . Очевидно, что любая точка , принадлежащая -окрестности точки , находится от этой точки на расстоянии, меньшем .
Число называется Пределом функции двух переменных при , если для любого числа найдется такая -окрестность точки , что для любой точки этой окрестности (за исключением, быть может, точки ) имеет место неравенство , или .
При этом пишут или , так как при , очевидно, , .
Заметим, что если число Есть предел функции , то как это следует из определения предела, разность является бесконечно-малой, когда точка Произвольным образом (по любому направлению) неограниченно приближается к точке .
Пример 5. Вычислить .
Решение. Предел функции вычисляется при .
Следует обратить внимание на то, что функция не определена в точке , но имеет предел при .
Функция двух переменных называется Бесконечно-малой при , , если ее предел равен нулю, т. е. .
Понятие Непрерывности функции нескольких переменных устанавливается с помощью понятия предела.
Функция нескольких переменных называется Непрерывной в точке , если .
Заметим, что функция , непрерывная в точке , должна быть определена в этой точке и некоторой ее окрестности (иначе нельзя было бы осуществить переход к пределу). Точка , в которой функция нескольких переменных непрерывна, называется Точкой непрерывности функции.
Для непрерывных в точке функций справедлива следующая теорема.
Теорема. Если функции и непрерывны в точке , то в этой точке непрерывны и их сумма , разность и произведение ; если, кроме того, , то частное также есть непрерывная функция в точке .
Если условие непрерывности нарушено (или функция не определена, или не существует предел, или не выполняется равенство), точка называется Точкой разрыва. Точки разрыва могут быть изолированными или образовывать Линии разрыва.
Функция Называется Непрерывной в области, если она непрерывна в каждой точке этой области.
Теорема. Если функция непрерывна в ограниченной замкнутой области , то она в этой области:
1. ограничена: ;
2. имеет наименьшее и наибольшее Значения:
;
3. принимает хотя бы в одной точке области любое численное значение, заключенное между и .
| < Предыдущая | Следующая > |
|---|
matica.org.ua
1.2. Предел и непрерывность функции двух переменных
Для функции двух (и большего числа) переменных вводится понятие предела функции и непрерывность, аналогично случаю функции одной переменной.
Пусть функция определена в некоторой окрестности точки, кроме, может быть, самой этой точки.
Определение 1.3.Число называетсяпределом функциипри
называетсяпределом функциипри и
и (или, что то же самое, при
(или, что то же самое, при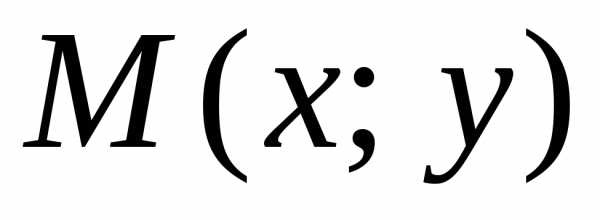 ),
если для любого
),
если для любого существует
существует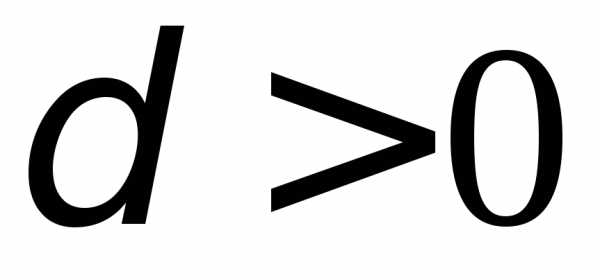 такое, что для всех
такое, что для всех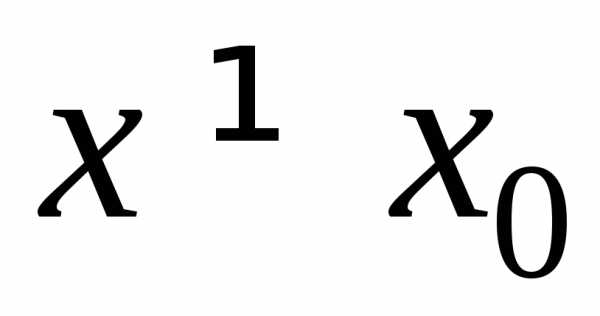 и
и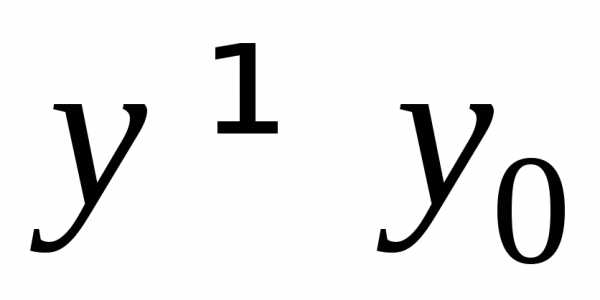 ,
и удовлетворяющих неравенствувыполняется неравенство.
Записывают:
,
и удовлетворяющих неравенствувыполняется неравенство.
Записывают:
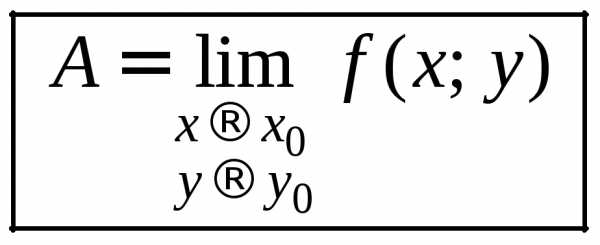
или
.
Из определения следует, что если предел
существует, то он не зависит от пути, по
которому 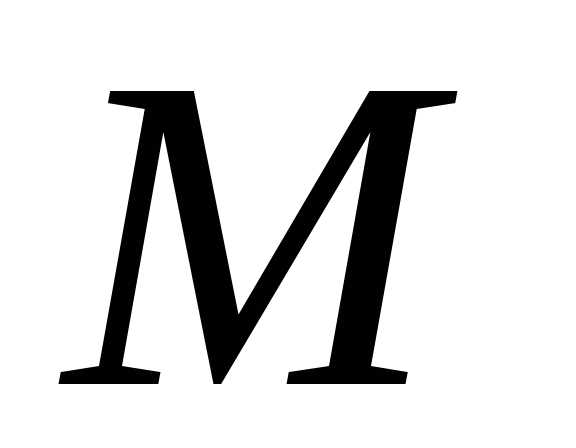 стремится к
стремится к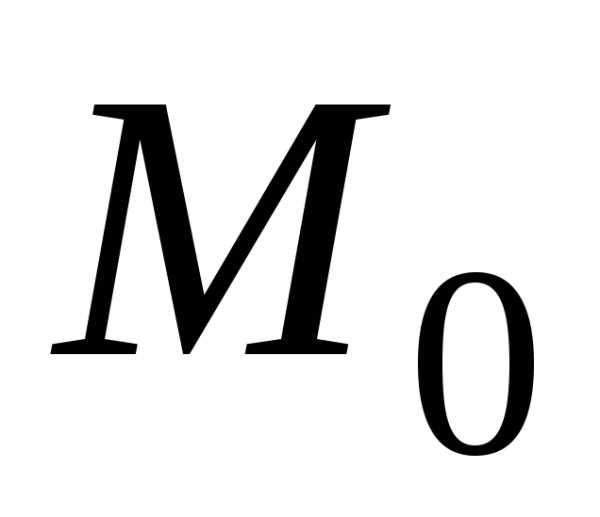 (число таких направлений бесконечно).
Определения бесконечно малых и бесконечно
больших величин являющихся функциями
двух переменных, аналогичны соответствующим
определениям для функций одной переменной.
(число таких направлений бесконечно).
Определения бесконечно малых и бесконечно
больших величин являющихся функциями
двух переменных, аналогичны соответствующим
определениям для функций одной переменной.
Предел функции двух переменных обладает свойствами, аналогичными свойствам предела функции одной переменной.
Определение 1.4.Функция(или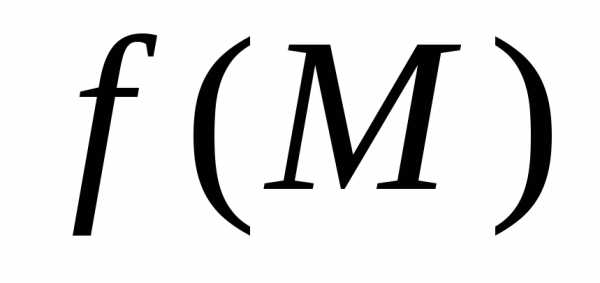 )
называетсянепрерывной в точке ,
если она:
)
называетсянепрерывной в точке ,
если она:
определена в этой точке и некоторой ее окрестности;
имеет предел ;
этот предел равен значению функции
 в точке
в точке ,
т.е.
,
т.е.
или.
Функция, непрерывная в каждой точке
некоторой области, называется непрерывной
в этой области. Точки, в которых
непрерывность нарушается (не выполняется
хотя бы одно из условий непрерывности
функции в точке), называютсяточками
разрываэтой функции. Точки разрывамогут образовывать целыелинии разрыва.
Так, например, функция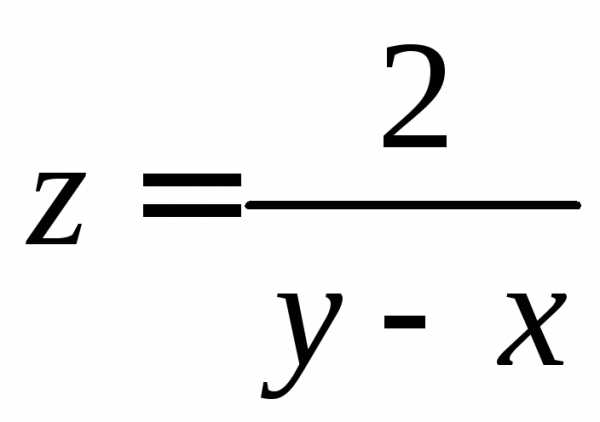 имеет линю разрыва
имеет линю разрыва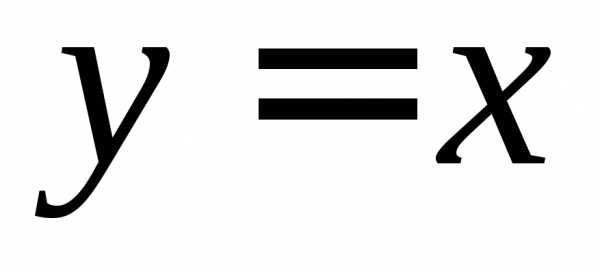 .
.
Можно дать другое, равносильное
приведенному выше, определение
непрерывности функции
в точке. Обозначим,.
Значит,и.
Величины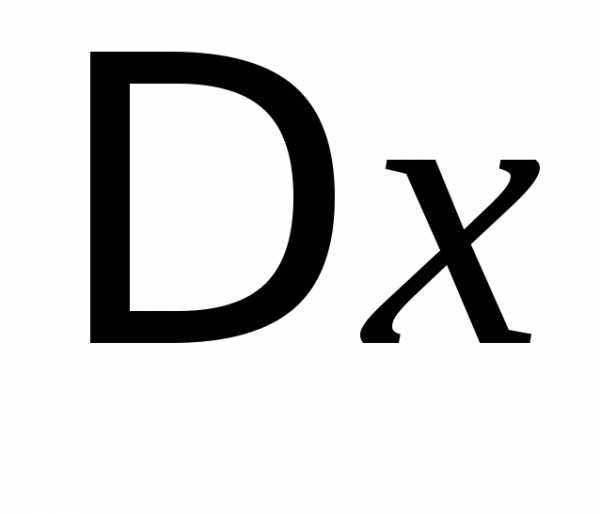 и
и называютсяприращениями аргументов
называютсяприращениями аргументов и
и .
Тогда.
Величина
.
Тогда.
Величина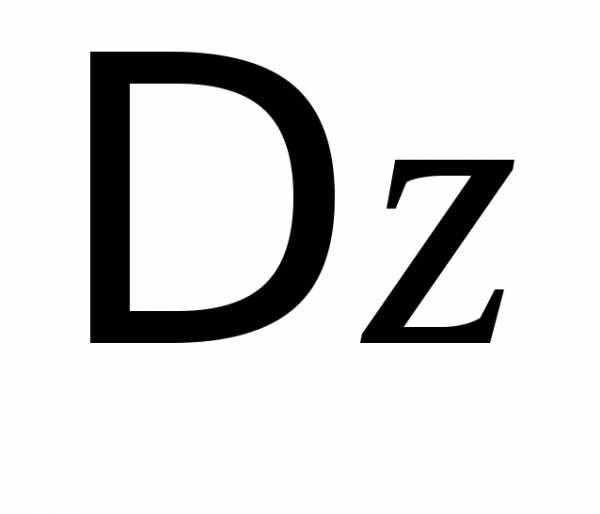 называетсяполным приращением
функциив точке.
называетсяполным приращением
функциив точке.
Определение 1.5.Функцияназывается непрерывной в точке,
если полное приращение функции в этой
точке стремится к нулю, когда приращения
ее аргументов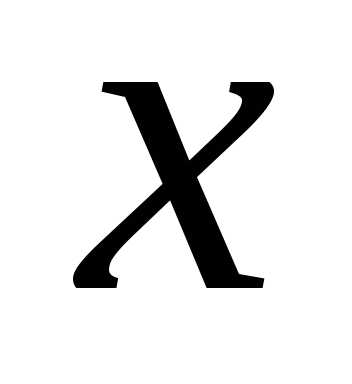 и
и стремится к нулю, т.е.
стремится к нулю, т.е.
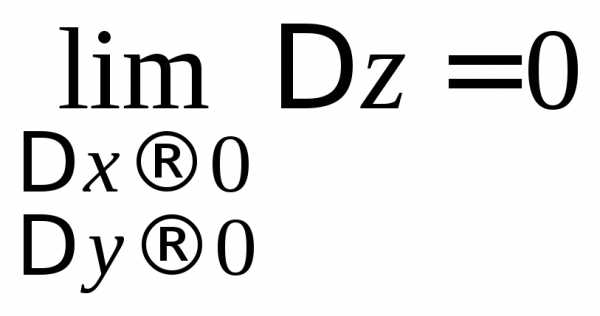 .
.
Пользуясь определением непрерывности и теоремами о пределах, можно доказать, что арифметические операции над непрерывными функциями и построение сложной функции из непрерывных функций приводит к непрерывным функциям – подобные теоремы имели для функций одной переменной.
1.3. Частные производные фнп
Рассмотрим линию  пересечения поверхностис плоскостью,
параллельной плоскости
пересечения поверхностис плоскостью,
параллельной плоскости
 сохраняет постоянное значение, то
сохраняет постоянное значение, то вдоль кривой
вдоль кривой будет меняться только в зависимости от
изменения
будет меняться только в зависимости от
изменения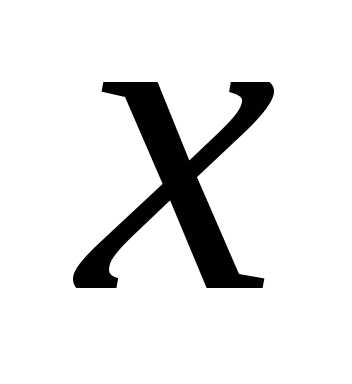 .
Дадим независимой переменной
.
Дадим независимой переменной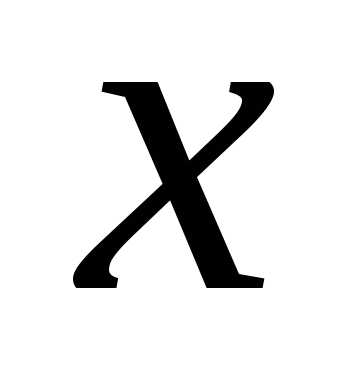 приращение
приращение ,
тогда
,
тогда получит приращение, которое называетсячастным приращением
получит приращение, которое называетсячастным приращением по
по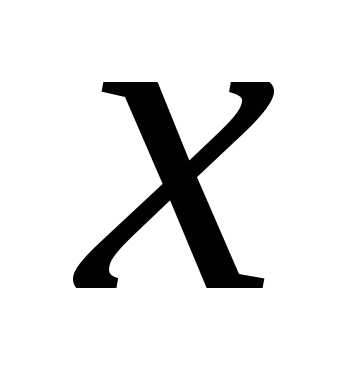
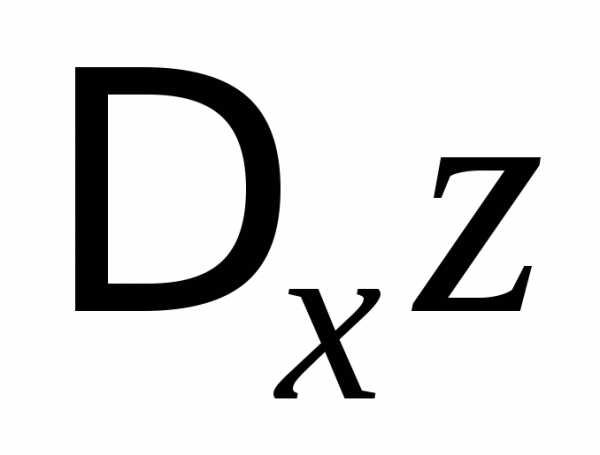 (на рисунке отрезок
(на рисунке отрезок ),
так что
),
так что.
Аналогично, если 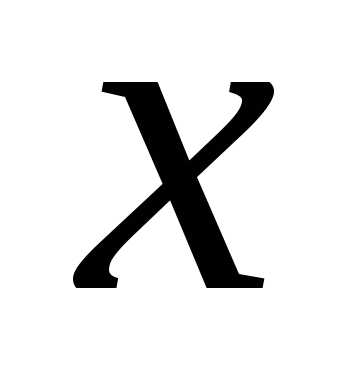 сохраняет постоянное значение, а
сохраняет постоянное значение, а получает приращение
получает приращение
параллельной плоскости  .
.
Наконец, придав аргументу 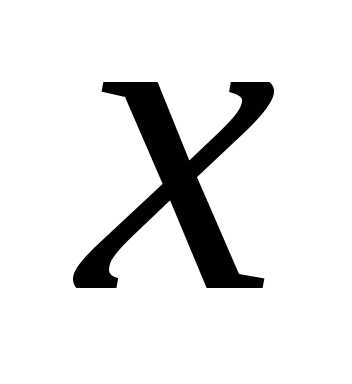 приращение
приращение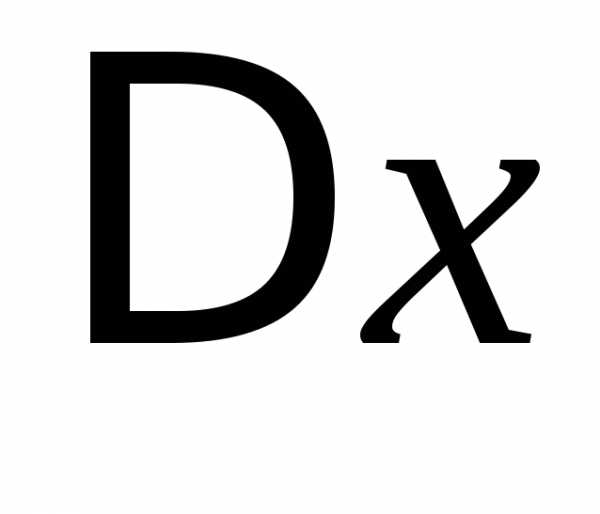 ,
а аргументу
,
а аргументу приращение
приращение ,
получим для
,
получим для
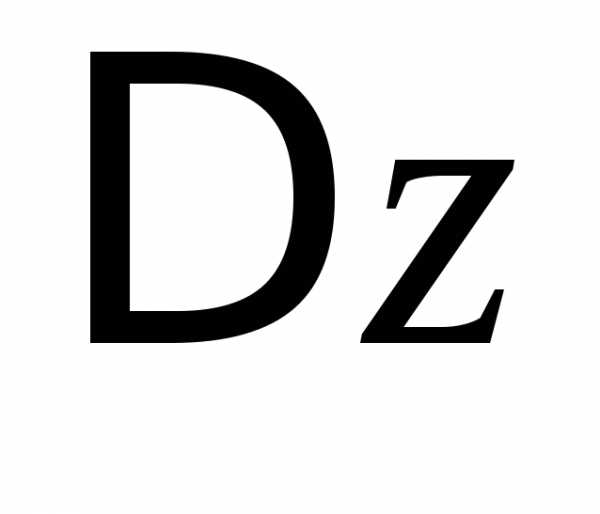 ,
которое называетсяполным приращениемфункции
,
которое называетсяполным приращениемфункции и определяется формулой
и определяется формулой.
На рисунке 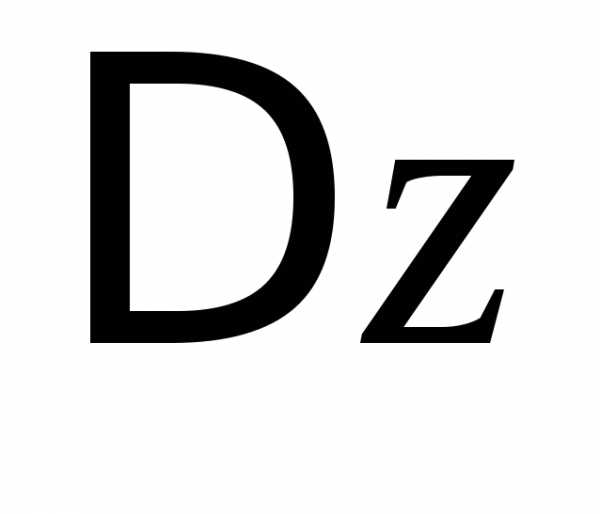 изображено отрезком
изображено отрезком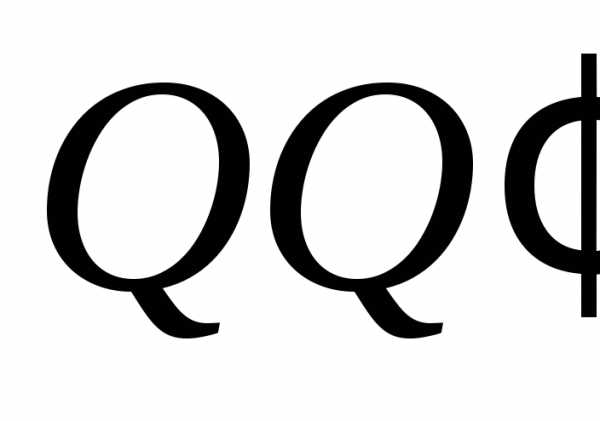 .
.
Надо отметить, что, вообще говоря, полное приращение не равно сумме частных приращений, т.е. .
Определение 1.6.Частной производной
по 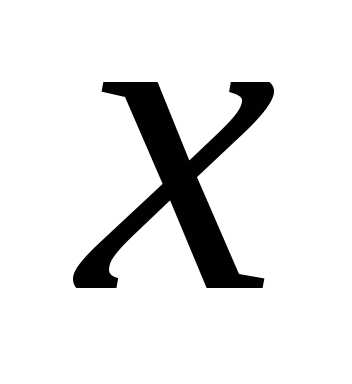 от функцииназывается предел отношения частного
приращения
от функцииназывается предел отношения частного
приращения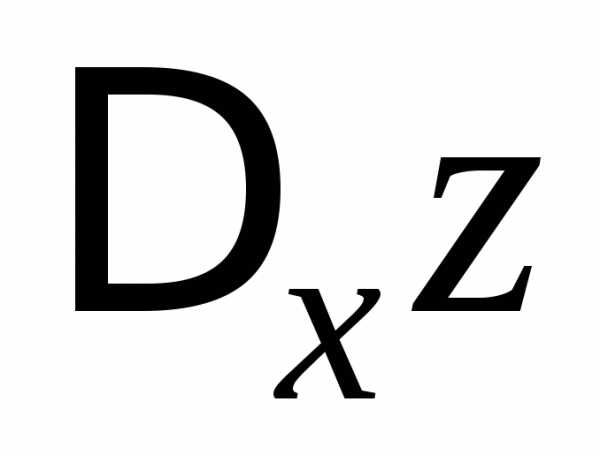 по
по 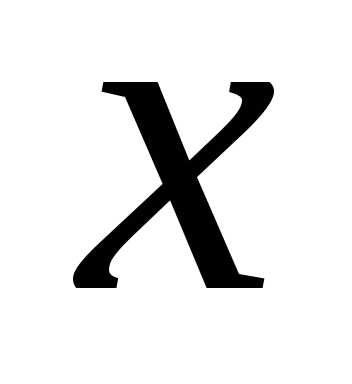
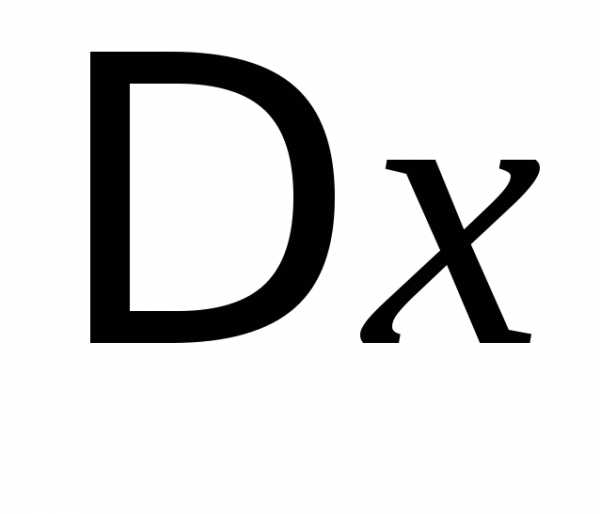 при стремлении
при стремлении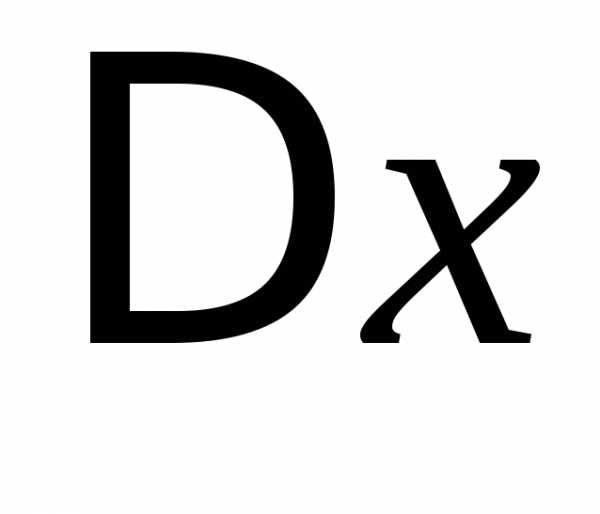 к нулю. Обозначается:.
Тогда
к нулю. Обозначается:.
Тогда.
Определение 1.7.Частной производной
по  от функцииназывается предел отношения частного
приращения
от функцииназывается предел отношения частного
приращения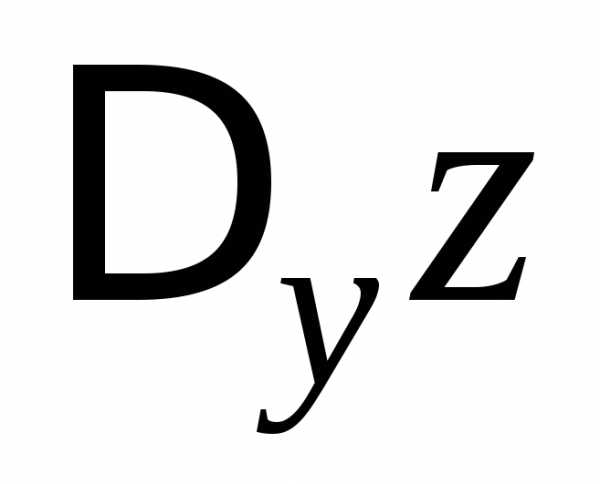 по
по  к
приращению
к
приращению при стремлении
при стремлении к нулю. Обозначается:.
Тогда
к нулю. Обозначается:.
Тогда
.
Таким образом, частная производная
функции нескольких (двух, трех и больше)
переменных определяется как производная
функции одной из этих переменных при
условии постоянства значений остальных
независимых переменных. Поэтому частные
производные функции
находят по формулам и правилам вычисления
производных функции одной переменной
(при этом соответственно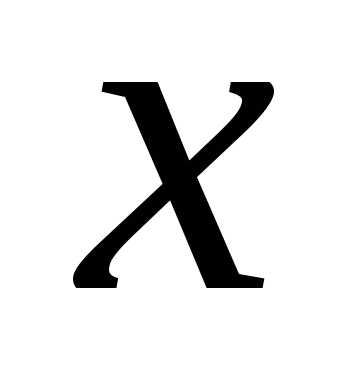 или
или считаются постоянной величиной).
считаются постоянной величиной).
Пример 1.2.Для данной функции
требуется найти частные производные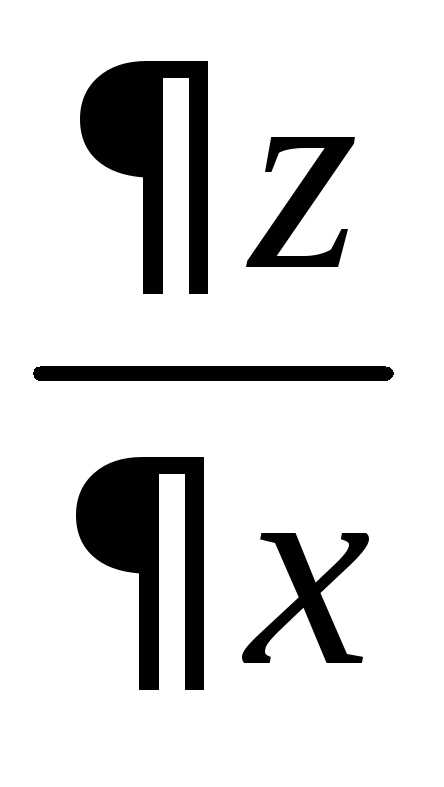 и
и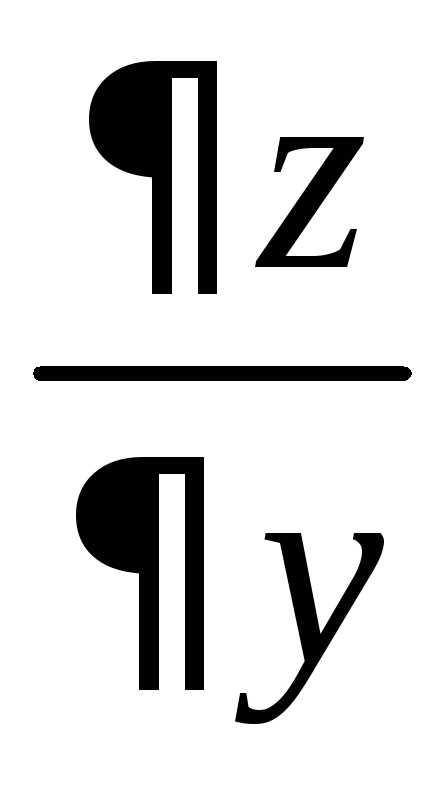 .
Найти значения частных производных в
точке
.
Найти значения частных производных в
точке :
:
.
Решение.Находим частные производные в общем виде:
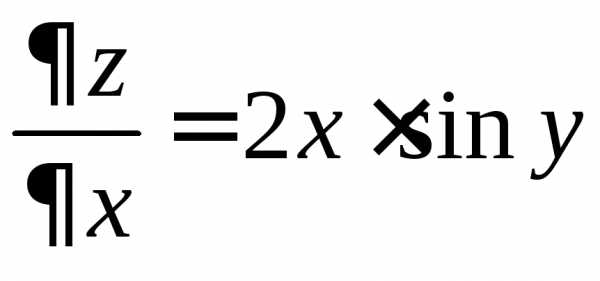 ,
,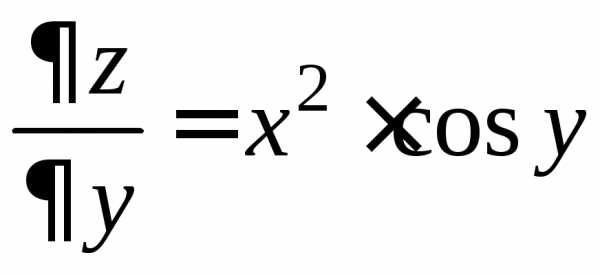 .
.
Находим значения частных производных
в точке 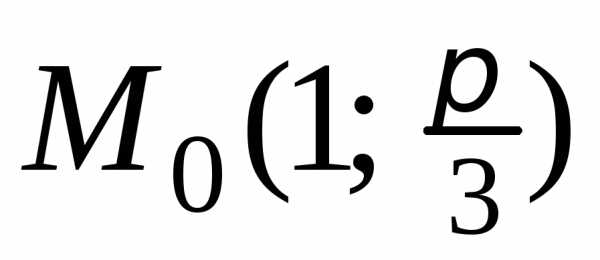 :
:
,.
studfiles.net
7. Функции двух переменных, область определения, линии уровня. Предел и непрерывность функции двух переменных.
Число z из некоторого множества Z (z ϵ Z) по некоторому правилу f, то говорят, что на множестве х задана функция: z = f (n—переменных – называются независимыми переменными или аргументами.z—Зависимая переменная или функция множеств, x—область определения, Z – область значения функции.
Линия уровня. z = f(x,y) – линия удовлетворяющая уравнению f(x,y)=c
c = const
То есть линия уровня – линия, по которой функция принимает одно и тоже значение.
Число А – называется пределом (в точке ()). Если для любойнайдена такая проколотая, что для всех точек М(х, у)ϵ() соответствует значениеf(x,y)ϵ
– называется множество всех точек, располагающихся от точки меньше чем на б.
Функция z=f(x,y) называется прерывной в точке () (непрерывная по совокупности переменных), если она определена в этой точке и некоторой её окружности и
Точка (называется точкой разрыва функцииz=f(x, y), если это условие не выполняется.
8. Частные производные функции двух переменных, их геометрический смыслю
Частная производная функции двух переменных характеризирует скорость изменения функции при изменении только одной переменной, то есть движение вдоль координатных осей. Для характеристики скорости изменения функции в направлении заданного вектора вводится понятие производной по направлению.
Геометрический смысл. Значение частной производной в точке равно тангенсу угла у составленного с осью касательной, проведенной в точке к линии пересечения поверхности и плоскости у В этом заключается геометрический смысл частной производной.
9. Частные производные высших порядков. Теорема о равенстве смешанных производных
Частные производные иназываются частными производными 1-ого порядка, они так же являются функцией 2 переменных. Частные производные от частных производных 1-ого порядка называются частными производными 2-ого порядка.
Частная производная 2-ого или более высокого порядков, взятые по различным переменным называются смешанными частными производными.
Если функция z=f(x,y) и её частные производные иопределены в некоторой окрестности точки (и непрерывна в этой точке, то=в точке (. Результат дифференцирования функции нескольких переменных не зависит от порядка дифференцирования по различным переменным.
10. Понятие дифференцируемости функции 2 переменных. Необходимые и достаточные условия дифференцируемости функции 2 переменных
Функция z = z (x, y) называется дифференцируемой в точке ,если её полное приращение в этой точке представлено в видеZ=Ax+By+(x, y)x+(x,y)y, где А, В – некоторые числа (не зависит от x,y)
Необходимые условия. Если функция дифференцируема в некоторой точке, то она непрерывна в этой точке. Обратное не верно.
Если функция дифференцируема в некоторой точке, то в этой точке существую частные производные.
= А и = В. Обратноене верно
Достаточные условия. Если функция z=f(x,y) в некоторой окрестности точке (х0, у0) имеет частные производные и эти частные производные непрерывны в самой точке (х0, у0), то функция z=f(x, y) дифференцируема в самой точке (х0, у0).
studfiles.net
Предел функции двух переменных.
Говорят,
что последовательность точек  с координатами
с координатами 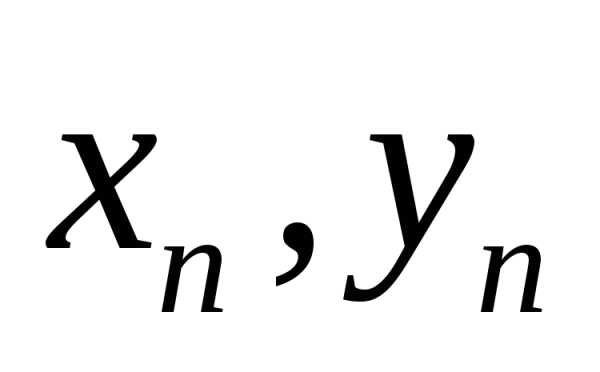 стремится к точке
стремится к точке 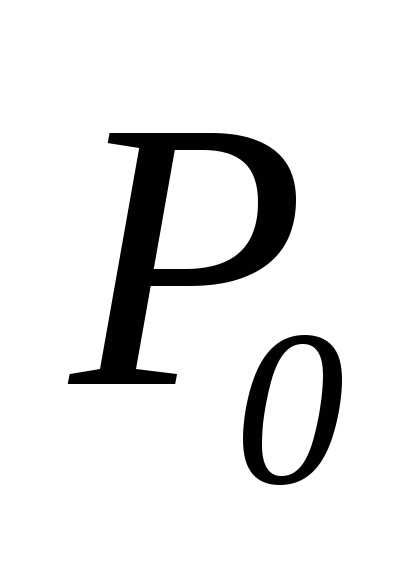 с координатами
с координатами 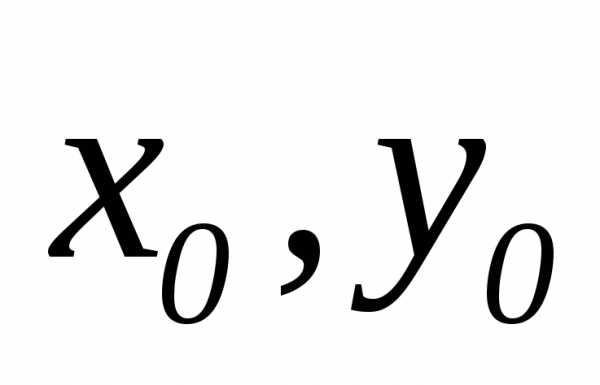 ,
если последовательность расстояний
,
если последовательность расстояний 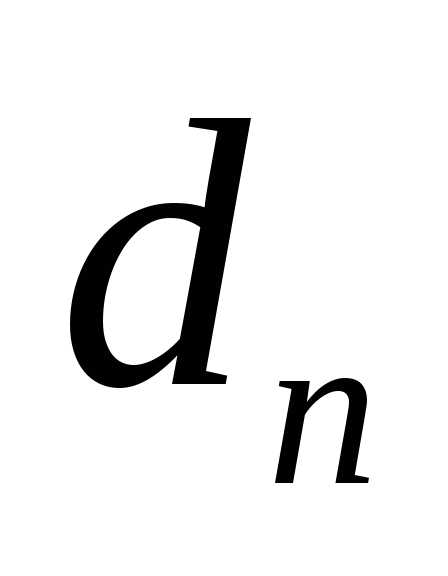 точек
точек 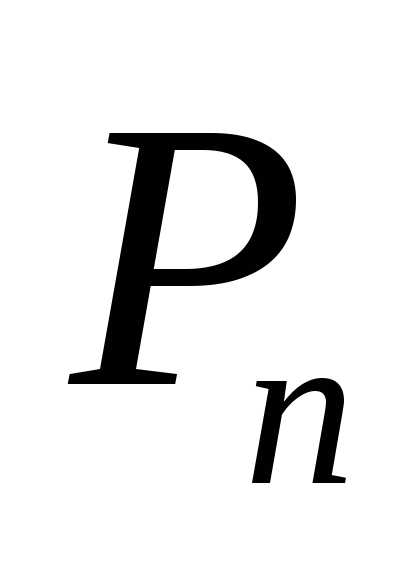 от точки
от точки 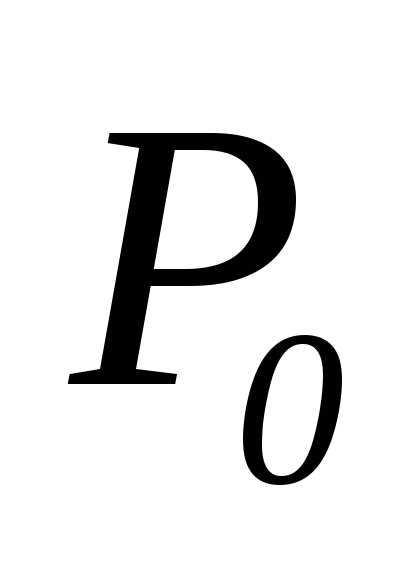 стремится к нулю при
.
Таким образом,
последовательность точек
стремится к нулю при
.
Таким образом,
последовательность точек 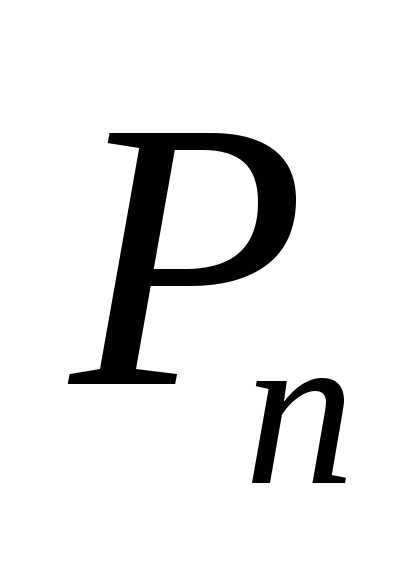 стремится к
стремится к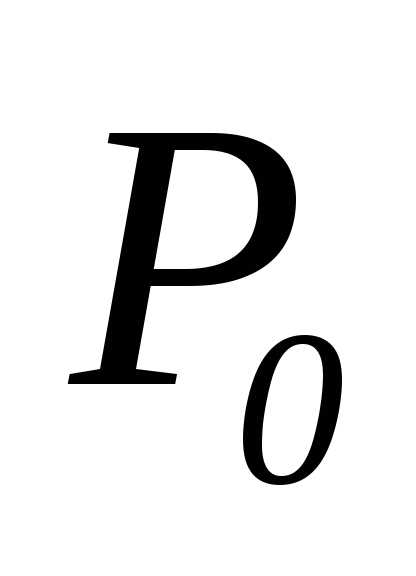 ,
если
,
если
т.
е. если 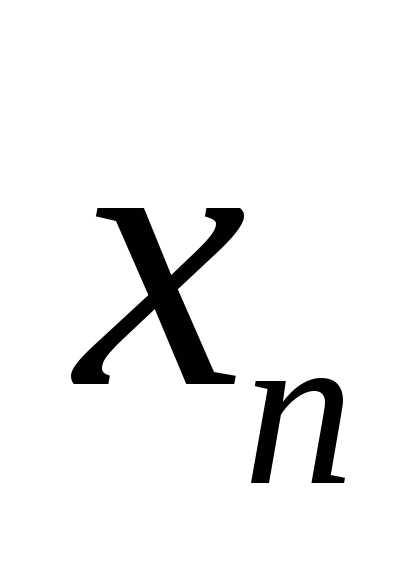 стремится к
стремится к 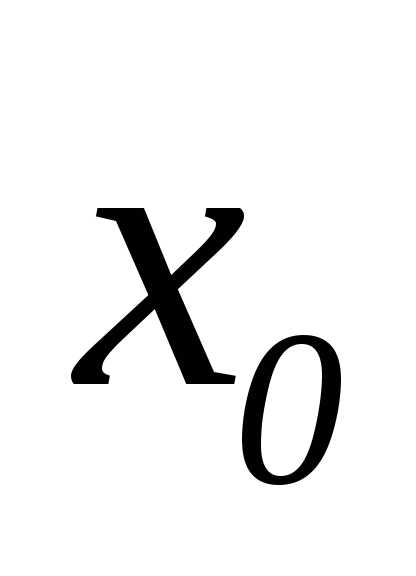 ,
а
,
а 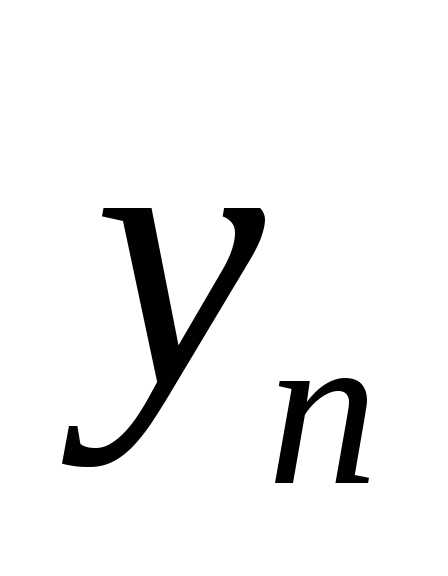 —
к
—
к 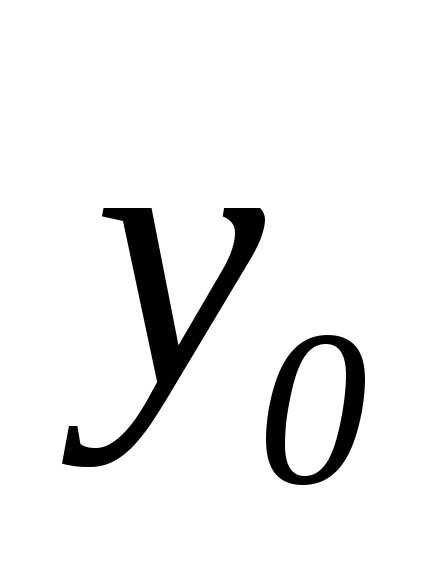 .
.
Говорят,
что 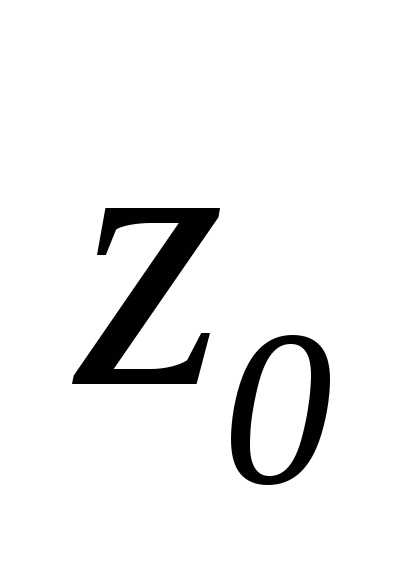 есть предел функции
есть предел функции 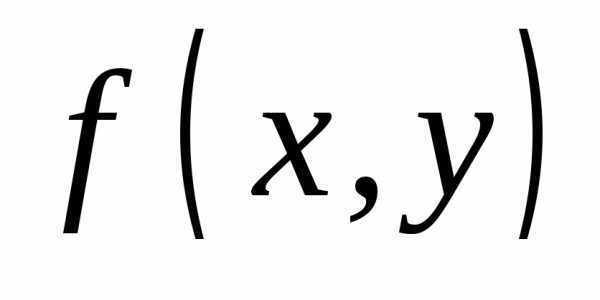 ,
где (х,
у) стремится к
,
где (х,
у) стремится к 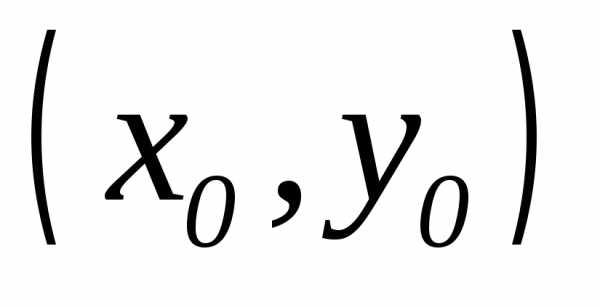 ,
если для каждой последовательности
точек
,
если для каждой последовательности
точек 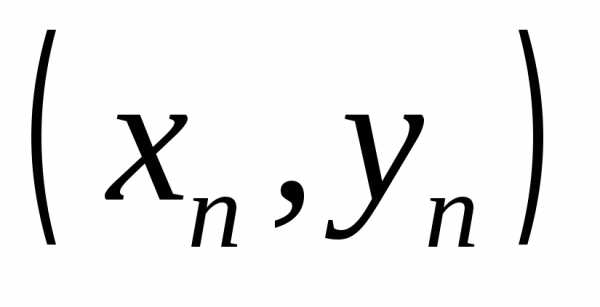 ,
отличных от
,
отличных от 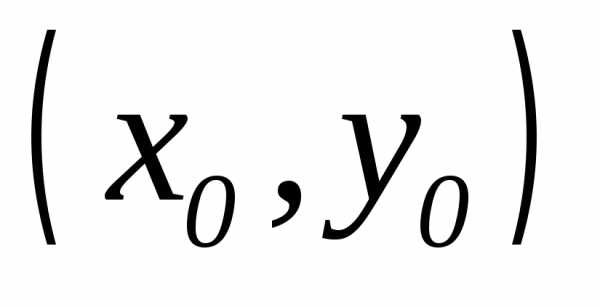 и стремящихся к
и стремящихся к 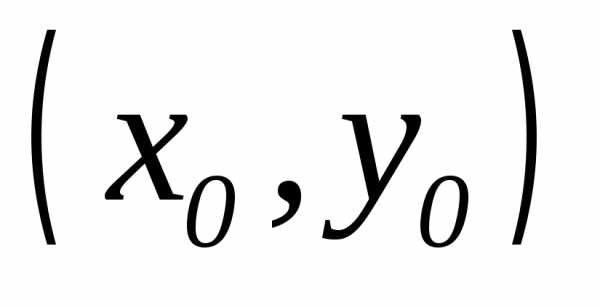 ,
последовательность
,
последовательность 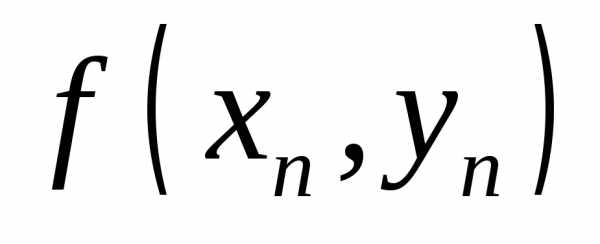 стремится к
стремится к 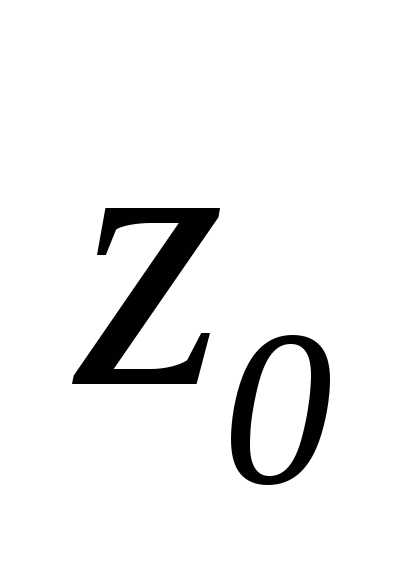 при
.
Это записывается
следующим образом:
при
.
Это записывается
следующим образом:
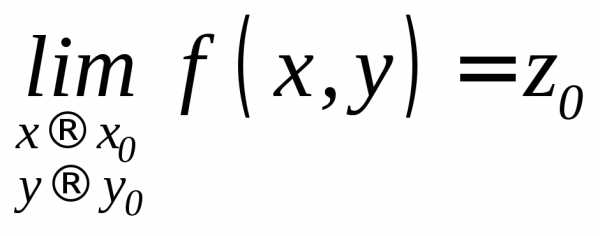
Частные производные первого порядка
Рассмотрим
функцию 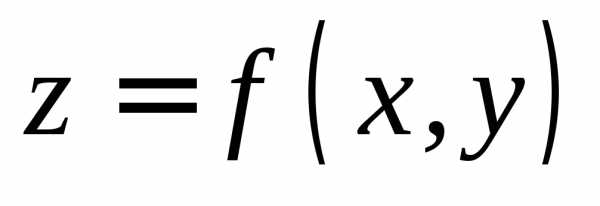 .
Пусть независимая переменная у приняла постоянное значение
.
Пусть независимая переменная у приняла постоянное значение 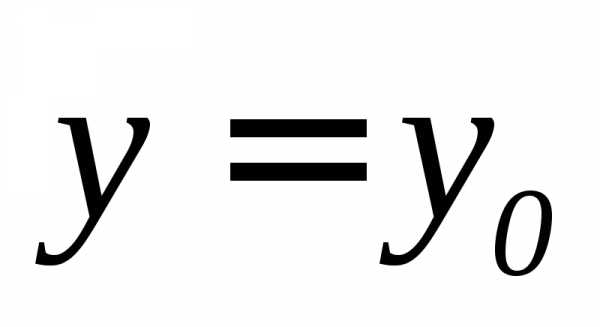 ,
а переменная
,
а переменная 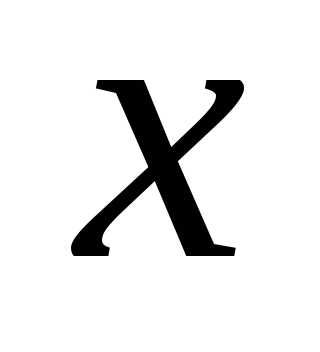 изменяется. Тогда из функции двух
переменных получим функцию одной
независимой переменной .
изменяется. Тогда из функции двух
переменных получим функцию одной
независимой переменной .
Ее
графиком является линия пересечения
поверхности 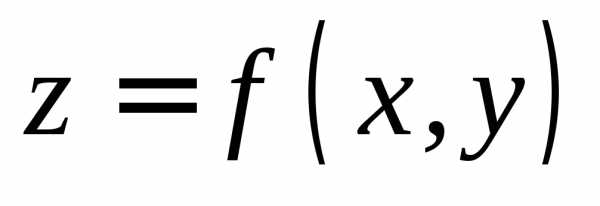 и плоскости
и плоскости 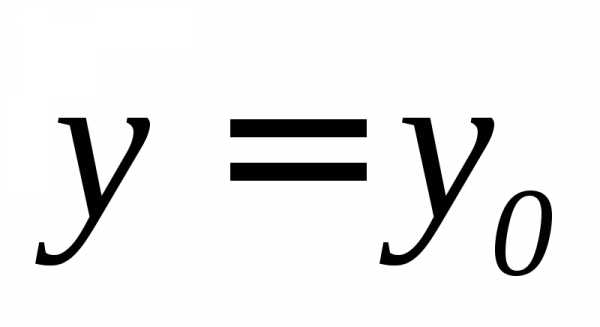 (рис 10).
(рис 10).
Поскольку является функцией одной переменной, ее
производная 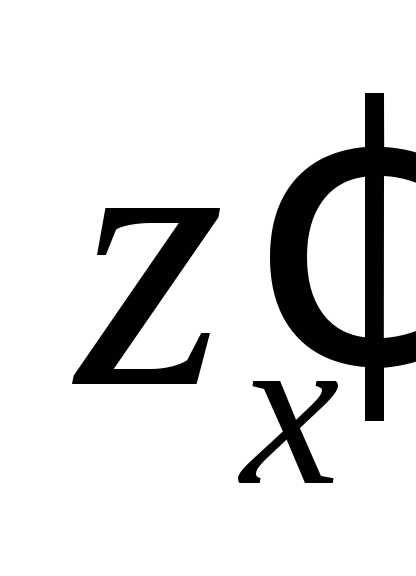 в точке
в точке 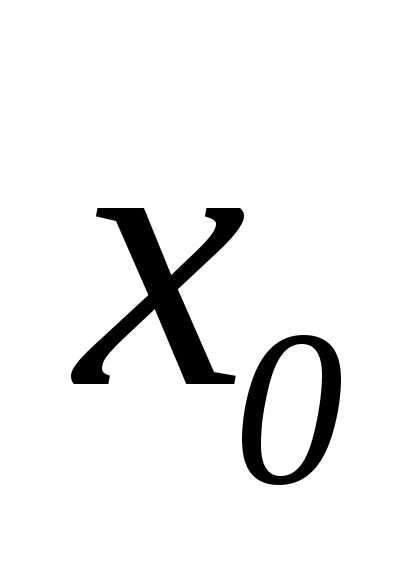 вычисляется по формуле
вычисляется по формуле
Рис. 10.
Эта
производная называется частной
производной 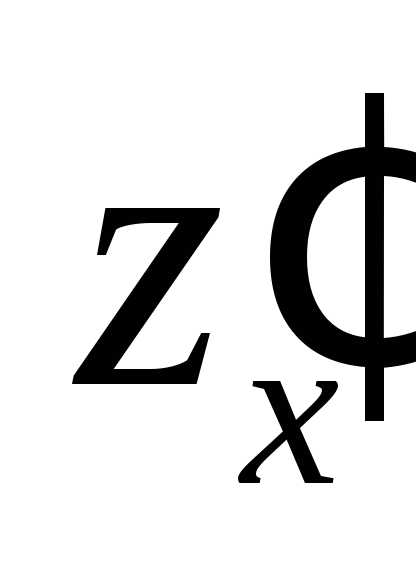 от функции двух переменных
от функции двух переменных 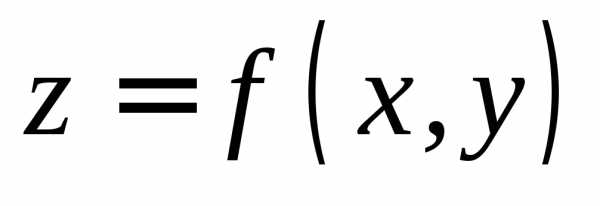 в точке
в точке 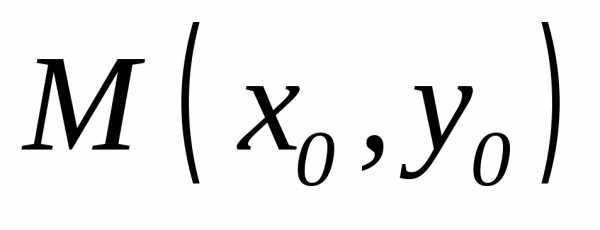 .
.
Обозначим
через  приращение переменной х;
введем также обозначение
приращение переменной х;
введем также обозначение
Приращение 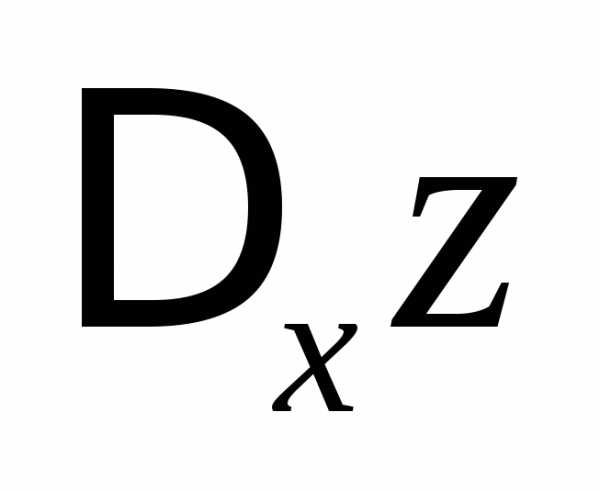 называют частным
приращением функции z по переменной х.
называют частным
приращением функции z по переменной х.
Аналогично,
если переменная у получает приращение  ,
а х остается постоянной, то частное приращение
функции z по переменной у имеет следующий вид:
,
а х остается постоянной, то частное приращение
функции z по переменной у имеет следующий вид:
Если существует предел
то этот предел называется частной производной первого порядка или первой частной производной по переменной х; она обозначается следующими символами:
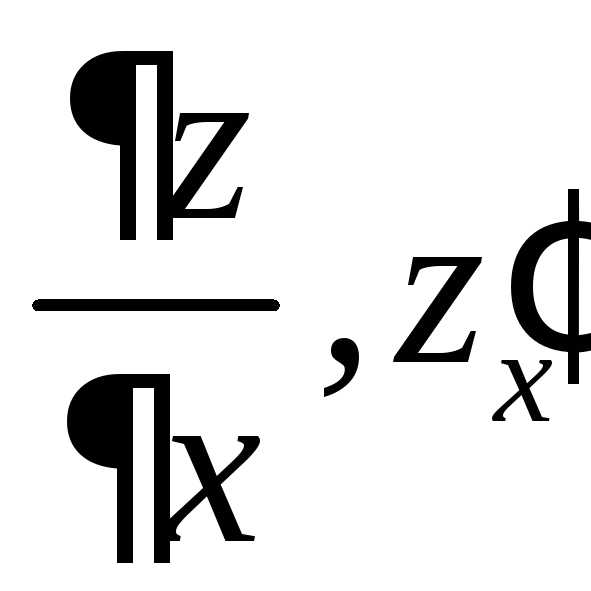 .
.
Аналогично определяется первая частная производная по переменной у
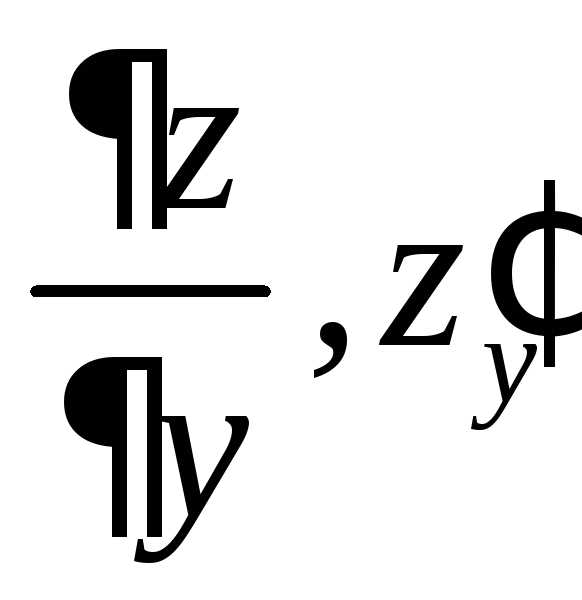
как предел отношения
.
Пример 1. Найти первые частные производные функции
.
Решение. Чтобы найти частную производную по 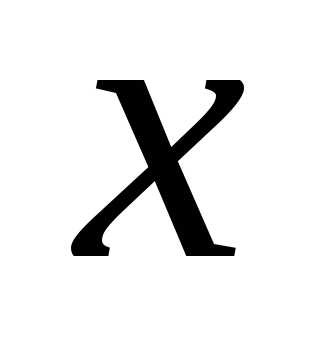 ,
принимаем у за постоянную и находим
производную по х:
,
принимаем у за постоянную и находим
производную по х:
(Производную 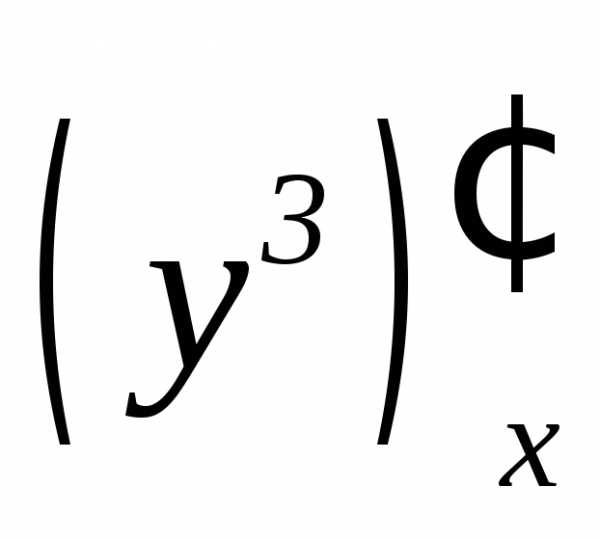 приняли равной нулю, поскольку у считаем
постоянным числом. В первом слагаемом
постоянную
приняли равной нулю, поскольку у считаем
постоянным числом. В первом слагаемом
постоянную 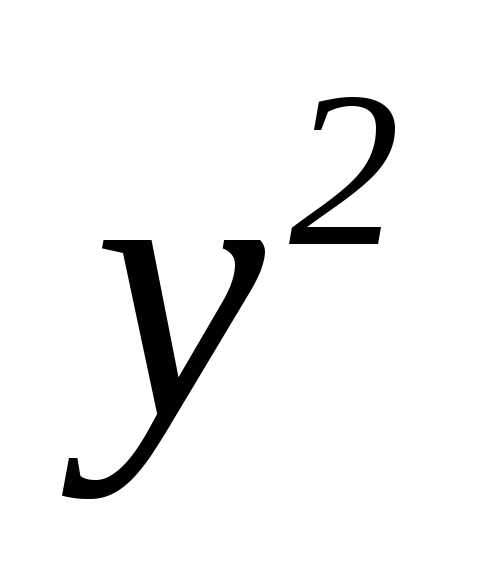 вынесли за знак производной.)
вынесли за знак производной.)
Чтобы найти частную производную по у, принимаем х за постоянную и находим производную по у.
Пример 2. Найти первые частные производные функции
.
Решение. Чтобы
найти частную производную по 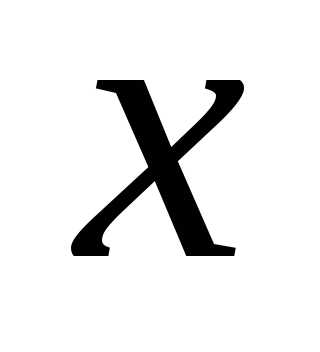 ,
принимаем у за постоянную и находим
производную по х:
,
принимаем у за постоянную и находим
производную по х:
Чтобы
найти частную производную по у, принимаем 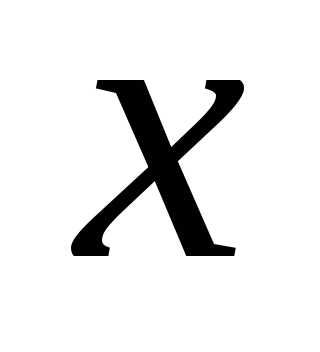 за постоянную и находим производную по
у:
за постоянную и находим производную по
у:
.
Градиент функции. Производная по направлению вектора.
Градиентом
функции 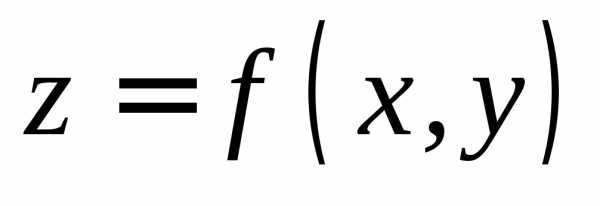 называется вектор, проекциями которого
на оси координат являются частные
производные данной функции:
называется вектор, проекциями которого
на оси координат являются частные
производные данной функции:
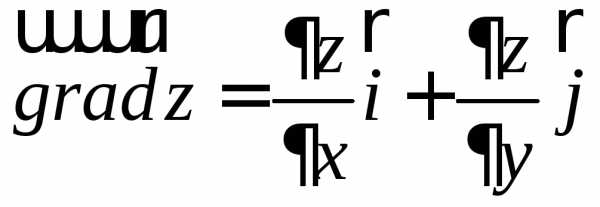 .
.
Производной
функции  в данном направлении
в данном направлении  называется
называется
.
Если
функция  дифференцируемая, то производную
в данном направлению можно найти по формуле
дифференцируемая, то производную
в данном направлению можно найти по формуле
,
где — направляющие косинусы вектора  .
.
● Пример
4. Дана
функция ,
точка 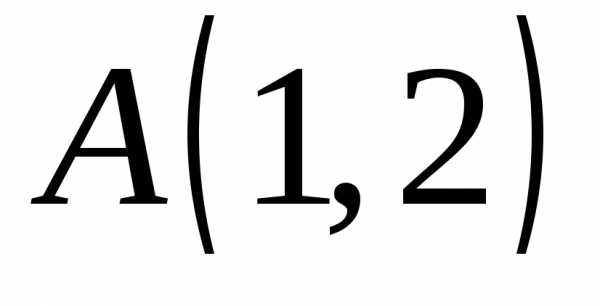 и вектор
и вектор 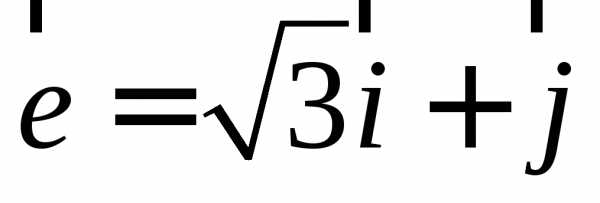 .
Найти: 1)
.
Найти: 1)  в точке
в точке  ;
2) производную в точке по направлению
вектора
;
2) производную в точке по направлению
вектора  .
.
Решение. 1)
Найдем частные производные данной
функции: 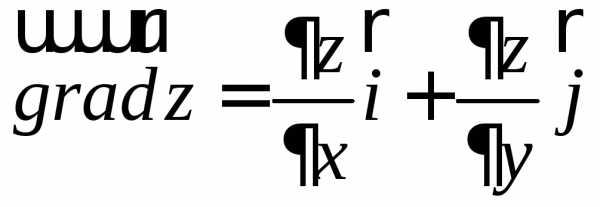
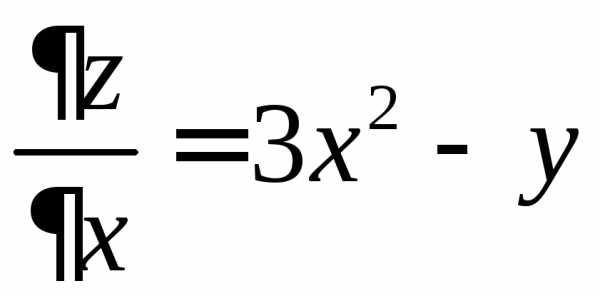 ;
; 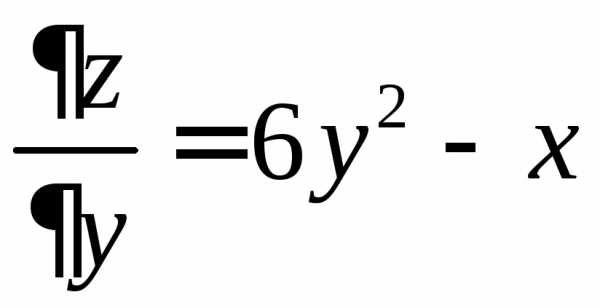 .
.
Градиент
данной функции в произвольной точке  равен
равен
.
Определим
градиент в точке 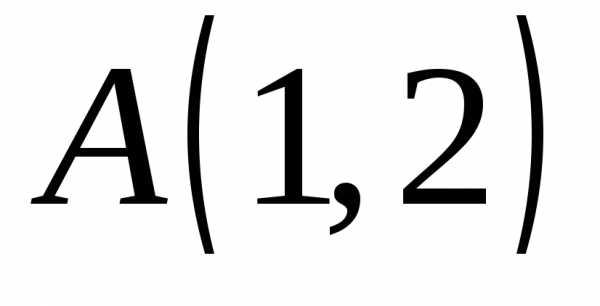
.
2)
Найдем производную функции в точке 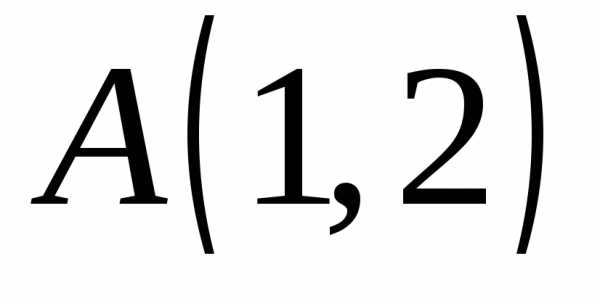 по направлению вектора
по направлению вектора .
.
Частные производные функции в точке равны
 ;
;  .
.
Определим
направляющие косинусы вектора 
;
Отсюда, искомая производная
.●
Вопросы для самоконтроля
Понятие о функции нескольких переменных.
Полное и частное приращение функции.
Частные производные функций нескольких переменных.
Полный дифференциал.
Касательная плоскость и нормаль к поверхности.
Частные производные и дифференциалы высших порядков.
Необходимый признак экстремума функций двух переменных.
Нахождение функции на основании экспериментальных данных по методу наименьших квадратов.
studfiles.net
Предел и непрерывность функции двух переменных
2.1. Предел функции
Для функции двух
(и большего числа) переменных вводится
понятие предела функции и непрерывности,
аналогично случаю функции одной
переменной. Введем понятие окрестности
точки. Множество всех точек  плоскости, координаты которых удовлетворяют
неравенству,
называется-окрестностью
точки
плоскости, координаты которых удовлетворяют
неравенству,
называется-окрестностью
точки 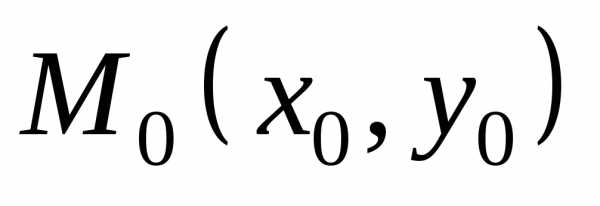 .
Другими словами,-окрестность
точки
.
Другими словами,-окрестность
точки 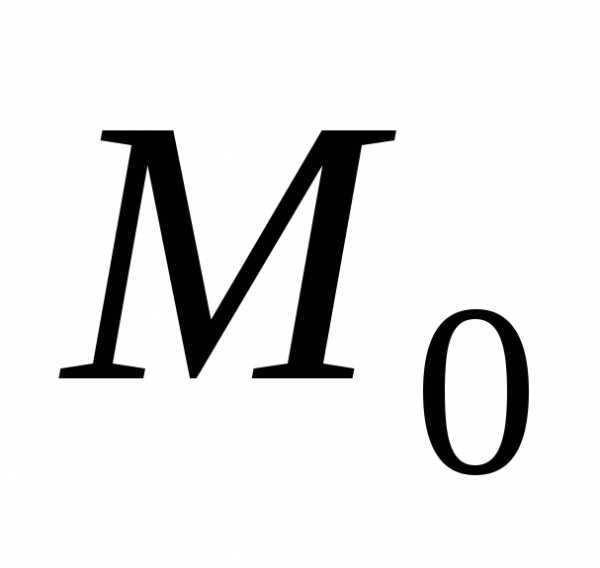 – это все внутренние точки круга с
центром
– это все внутренние точки круга с
центром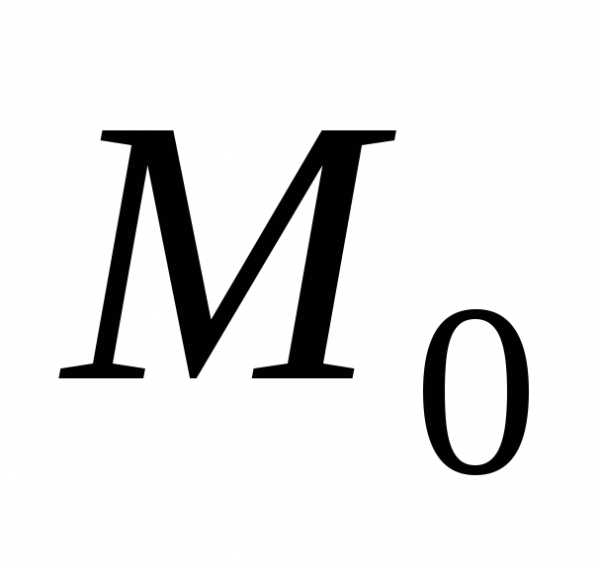 и радиусом
(рис. 2).
и радиусом
(рис. 2).
Рис. 2
Пусть функция
определена в некоторой окрестности
точки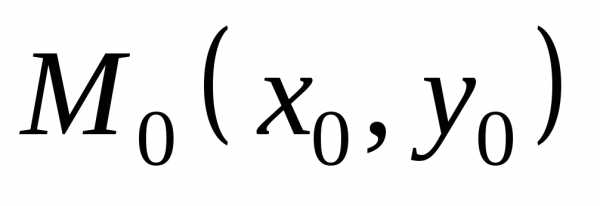 ,
кроме, быть может, самой этой точки.
Число А называетсяпределом
функции при(или, что то же самое, при
,
кроме, быть может, самой этой точки.
Число А называетсяпределом
функции при(или, что то же самое, при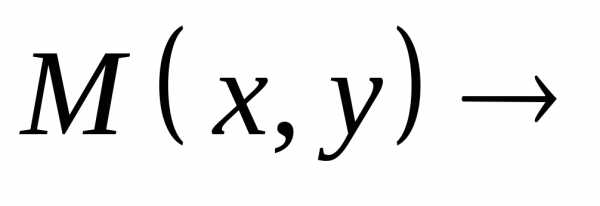
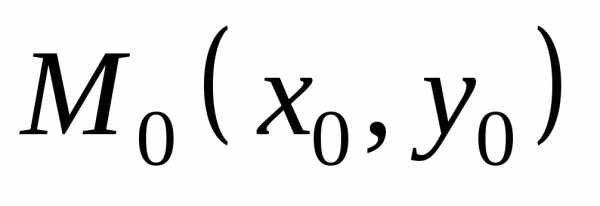 ),
если для любого
),
если для любого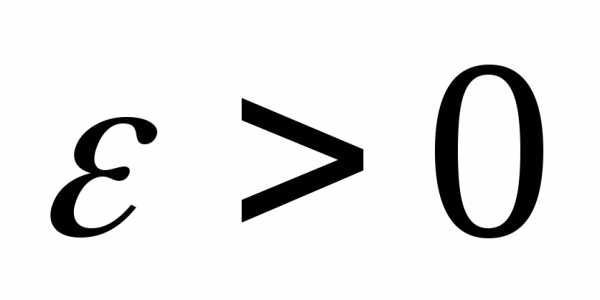 существует
существует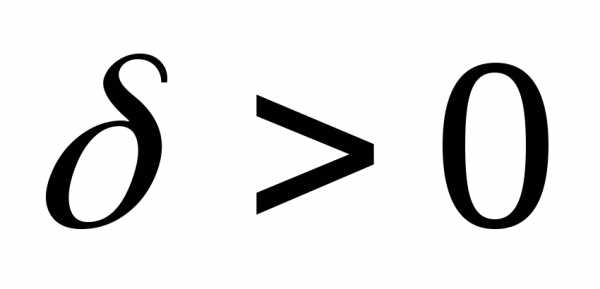 такое, что для всехи удовлетворяющих неравенствувыполняется неравенствоЗаписывают:
такое, что для всехи удовлетворяющих неравенствувыполняется неравенствоЗаписывают:
Из определения
следует, что если предел существует, то
он не зависит от пути, по которому М
стремиться к М0 (число таких направлений бесконечно;
для функции одной переменной 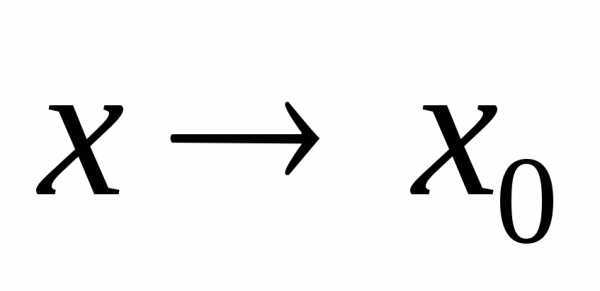 по
двум направлениям: справа и слева).
по
двум направлениям: справа и слева).
Геометрический
смысл предела функции двух переменных
состоит в следующем. Каково бы ни было
число 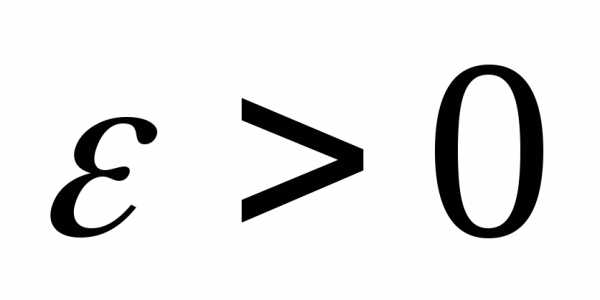 ,
найдется-окрестность
точки
,
найдется-окрестность
точки 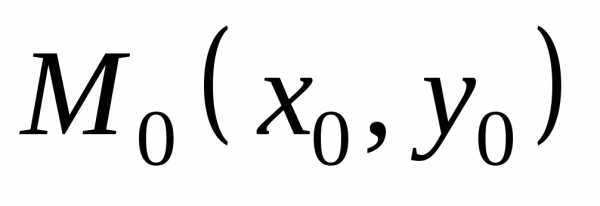 ,
что во всех её точках
,
что во всех её точках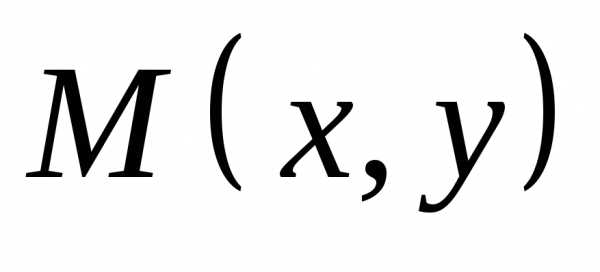 ,
отличных от
,
отличных от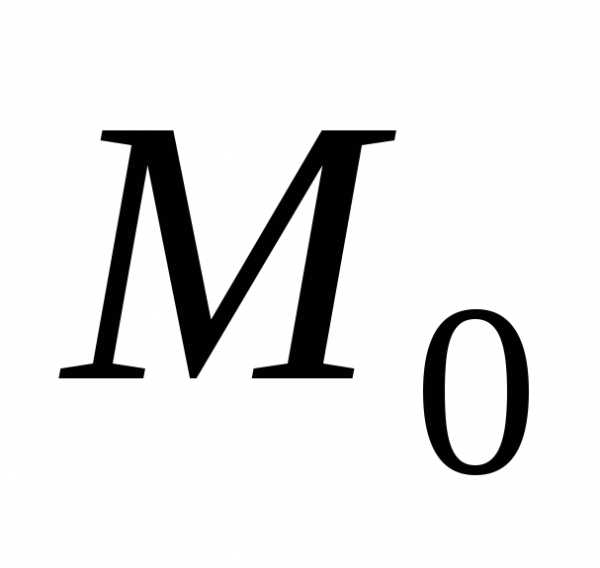 ,
аппликаты соответствующих точек
поверхностиотличаются от числа А по модулю меньше,
чем на.
,
аппликаты соответствующих точек
поверхностиотличаются от числа А по модулю меньше,
чем на.
Пример 1.
Найти предел 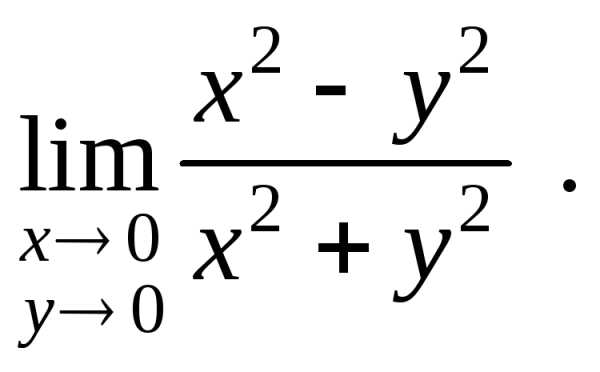
Решение: Будем приближаться к 0(0;0) по прямой 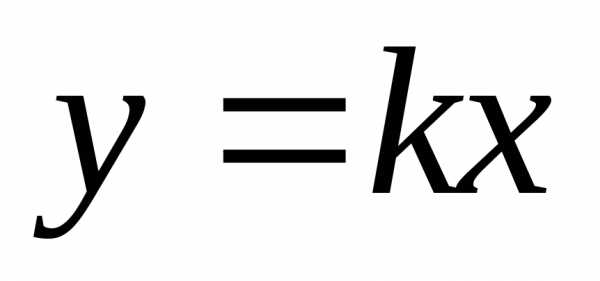 ,
гдеk – некоторое
число. Тогда
,
гдеk – некоторое
число. Тогда
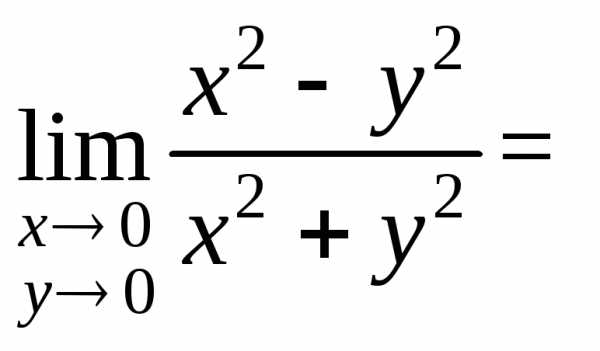
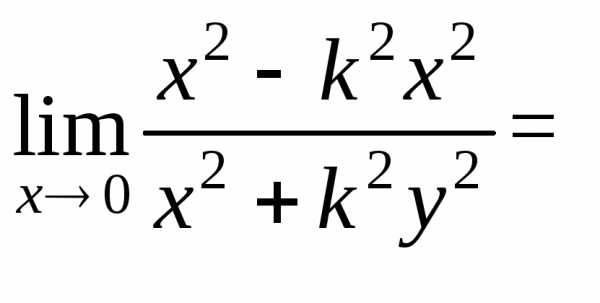
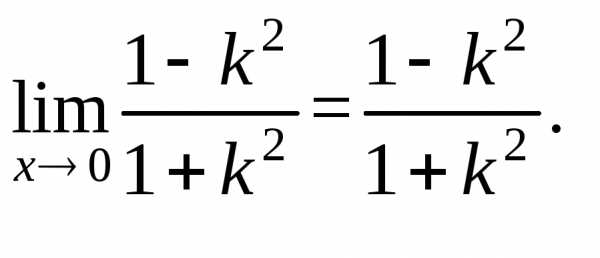
Функция 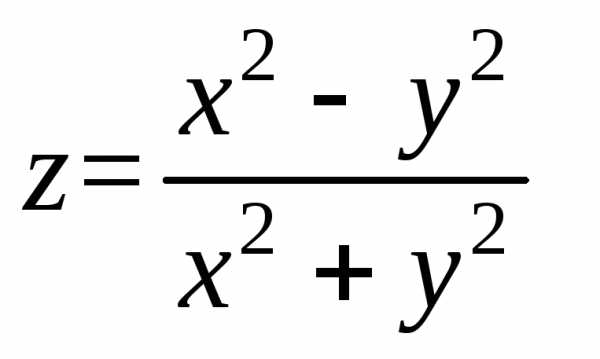 в
точке 0(0;0) предела не имеет, т. к. при
разных значенияхk предел функции не одинаков (функция
имеет различные предельные значения).
в
точке 0(0;0) предела не имеет, т. к. при
разных значенияхk предел функции не одинаков (функция
имеет различные предельные значения).
Предел функции
двух переменных обладает свойствами,
аналогичными свойствами предела функции
одной переменной. Это означает, что
справедливы утверждения: если функции
определены на множествеD и имеют в точке  этого множества пределы А и В соответственно,
то и функции
этого множества пределы А и В соответственно,
то и функции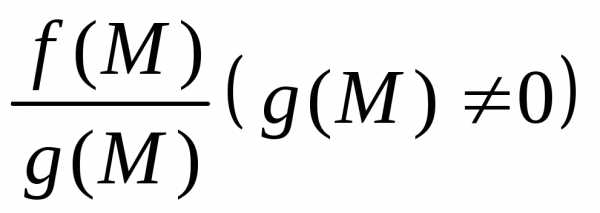 имеют
в точке М0 пределы, которые соответственно равны
имеют
в точке М0 пределы, которые соответственно равны 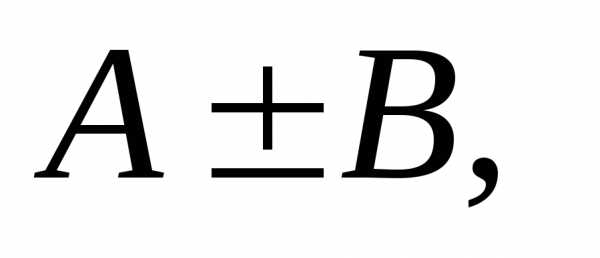
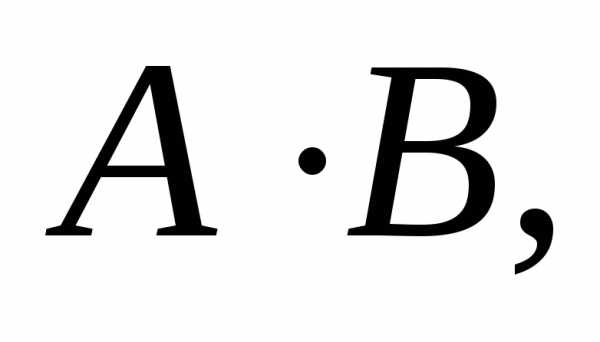
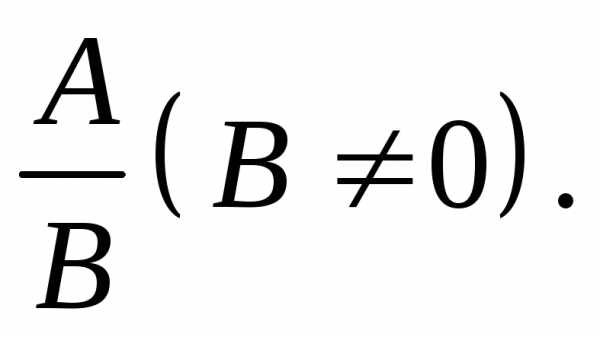
Непрерывность функции двух переменных
Функция
(илиf(M))
называется непрерывной
в точке 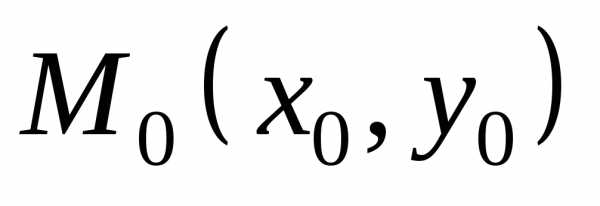 ,
если она: а) определена в этой точке
и некоторой её окрестности;
,
если она: а) определена в этой точке
и некоторой её окрестности;
б) имеет предел 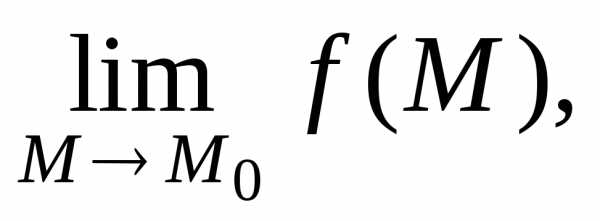
в) этот предел равен значению функции z в точке М0, т. е.
или
Функция, непрерывная
в каждой точке некоторой области,
называется непрерывной в этой области. Точки, в которых непрерывность нарушается
(не выполняется хотя бы одно из условий
непрерывности функции в точке), называются точками
разрыва этой функции. Точки разрыва
могут образовывать целыелинии
разрыва. Так,
функция 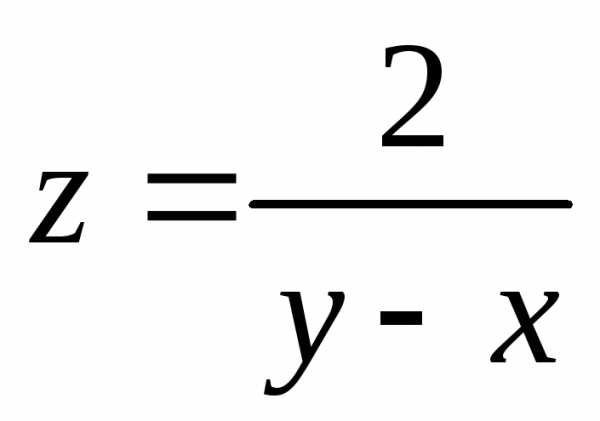 имеет линию разрыва
имеет линию разрыва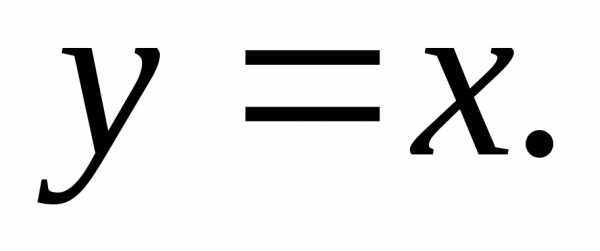
Можно дать другое,
равносильное приведенному выше,
определение непрерывности функции
в точке. Обозначим.
Величины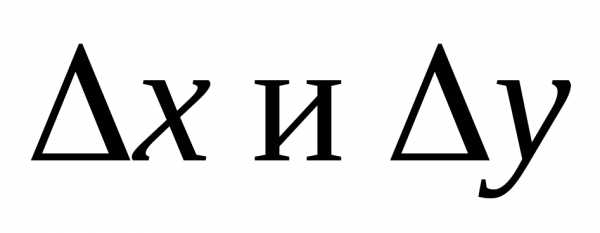 называютсяприращениями
аргументов х и у, а
называютсяприращениями
аргументов х и у, а  –полным
приращением функции
–полным
приращением функции 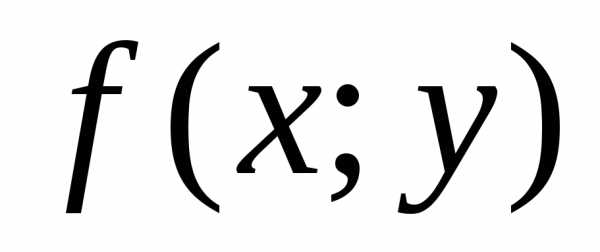 в точке
в точке .
.
Функция
называется непрерывной в точкеесли выполняется равенство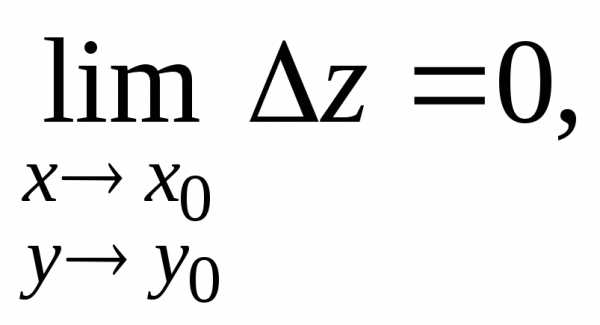 т.
е. полное приращение функции в этой очке
стремится к нулю, когда приращения её
аргументовх и у стремятся к нулю.
т.
е. полное приращение функции в этой очке
стремится к нулю, когда приращения её
аргументовх и у стремятся к нулю.
Пользуясь определением непрерывности и теоремами о пределах, можно доказать, что арифметические операции над непрерывными функциями и построение сложной функции из непрерывных функций приводит к непрерывным функциям – подобные теоремы имели место для функций одной переменной.
Свойства функций, непрерывных в ограниченной замкнутой области
Приведем свойства функций, непрерывных в ограниченной замкнутой области (они аналогичны свойствам непрерывных на отрезке функций одной переменной). Предварительно уточним понятие области.
Областью называется множество точек плоскости, обладающих свойствами открытости и связности.
Свойство открытости: каждая точка принадлежит ей вместе с некоторой окрестностью этой точки.
Свойство связности: любые две точки области можно соединить непрерывной линией, целиком лежащей в этой области.
Точка N0 называется граничной
точкой области
D,
если она не принадлежит D,
но в любой окрестности её лежат точки
этой области. Совокупность граничных
точек области D
называется границей D. Область D
с присоединенной к ней границей называется замкнутой областью,
обозначается 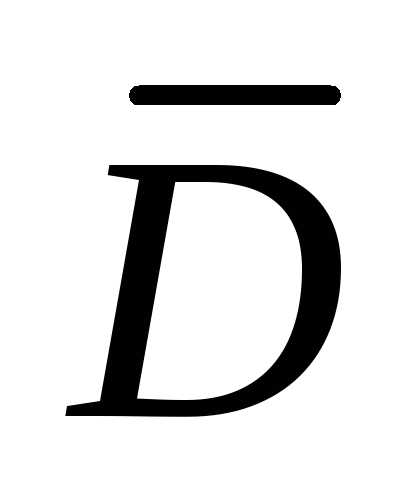 .
Область называетсяограниченной, если все её
точки принадлежат некоторому кругу
радиуса R.
В противном случае область называется неограниченной. Примером неограниченной области может
служить множество точек первого
координатного угла, а примером ограниченной
–
.
Область называетсяограниченной, если все её
точки принадлежат некоторому кругу
радиуса R.
В противном случае область называется неограниченной. Примером неограниченной области может
служить множество точек первого
координатного угла, а примером ограниченной
–  -окрестность
точки
-окрестность
точки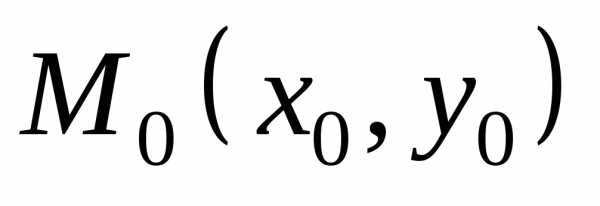 .
.
Теорема. Если функция
непрерывна в ограниченной замкнутой
области, то она в этой области: а)
ограничена, т. е. существует такое числоR
> 0, что для всех точек N
в этой области выполняется неравенство 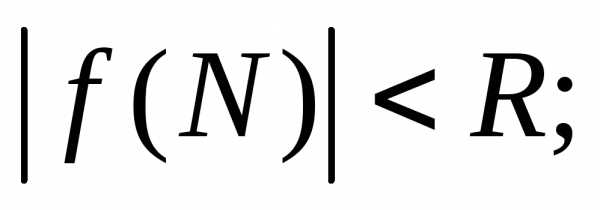 б)
имеет точки, в которых принимает
наименьшееm
и наибольшее M
значения; в) принимает хотя бы в одной
точке области любое численное значение,
заключенной между m
и M
(дается без доказательства).
б)
имеет точки, в которых принимает
наименьшееm
и наибольшее M
значения; в) принимает хотя бы в одной
точке области любое численное значение,
заключенной между m
и M
(дается без доказательства).
studfiles.net

 в точке
в точке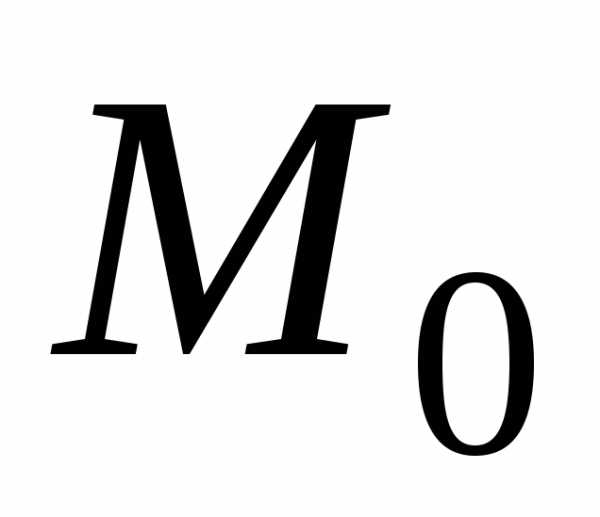 ,
т.е.
,
т.е.