Представить в алгебраической форме – Алгебраическая форма комплексного числа

1. Алгебраическая форма записи комплексного числа

2
10.	Восстановление функции комплексного переменного по её действительной или мнимой
части	21
10.1		Способ №1. С помощью криволинейного интеграла……………………………………………..	21
10.2		Способ №2. Непосредственное применение условий Коши-Римана……………………..	22
10.3		Способ №3. Через производную искомой функции……………………………………………….	23
11.	Интегрирование функций комплексного переменного…………………………………………………		24
12.	Интегральная формула Коши ……………………………………………………………………………………….		26
13.	Разложение функций в ряды Тейлора и Лорана ……………………………………………………………		28
14.	Нули и особые точки функции комплексного переменного …………………………………………		31
14.1		Нули функции комплексного переменного……………………………………………………………	31
14.2		Изолированные особые точки функции комплексного переменного …………………….	32

14.3Бесконечно удалённая точка как особая точка функции комплексного переменного

34

15.	Вычеты………………………………………………………………………………………………………………………….		35
15.1		Вычет в конечной точке…………………………………………………………………………………………	35
15.2		Вычет функции в бесконечно удаленной точке……………………………………………………..	37
16.	Вычисление интегралов с помощью вычетов……………………………………………………………….		41
17.	Вопросы для самопроверки…………………………………………………………………………………………..		43
18.	Литература ……………………………………………………………………………………………………………………		45
19.	Предметный указатель………………………………………………………………………………………………….		47

Оглавление Е.Е. Красновский, В.Д. Морозова «Теория функций комплексного переменного»

3

Предисловие

Правильно распределить время и силы при подготовке к теоретической и практической частям экзамена или аттестации по модулю достаточно сложно, тем более что в период сессии времени всегда не хватает. И как показывает практика, справиться с этим получается не у всех. В результате на экзамене одни студенты правильно решают задачи, но затрудняются ответить на простейшие теоретические вопросы, а другие могут сформулировать теорему, но не могут её применить.

Настоящие методические рекомендации для подготовки к экзамену по курсу «Теория функций комплексного переменного» (ТФКП) являются попыткой разрешить это противоречие и обеспечить одновременное повторение теоретического и практического материала курса. Руководствуясь принципом «Теория без практики мертва, практика без теории слепа», они содержат как теоретические положения курса на уровне определений и формулировок, так и примеры, иллюстрирующие применение каждого приведенного теоретического положения, и, тем самым, облегчающие его запоминание и понимание.

Цель предлагаемых методических рекомендаций – помочь студенту подготовиться к экзамену на базовом уровне. Иными словами, составлен расширенный рабочий справочник, содержащий основные моменты, используемые на занятиях по курсу ТФКП, и необходимые при выполнении домашнего задания и подготовке к контрольным мероприятиям. Помимо самостоятельной работы студентов, настоящее электронное учебное издание можно использовать при проведении занятий в интерактивной форме с использованием электронной доски или для размещения в системе дистанционного обучения.

Содержание справочника отвечает требованиям утверждённых учебных программ для факультетов ФН и СМ МГТУ им . Н.Э. Баумана, составленных в рамках перехода к блочномодульному построению учебных курсов и балльно-рейтинговойсистеме оценки знаний.

Обращаем внимание, что настоящий труд не заменяет собой ни учебников, ни конспекта лекций. Для углублённого изучения материала рекомендуется обращаться к соответствующим разделам изданного в МГТУ им. Н.Э. Баумана базового учебника [7].

В конце пособия помещён список рекомендуемой литературы и предметный указатель, в который входят все выделенные в текстеполужирным курсивом термины. Предметный указатель состоит из гиперссылок на разделы, в которых эти термины строго определены или описаны и где приведены примеры, иллюстрирующие их применение.

Пособие предназначено для студентов 2 курса всех факультетов МГТУ им. Н.Э. Баумана.

Оглавление Е.Е. Красновский, В.Д. Морозова «Теория функций комплексного переменного»

4

Запись вида z = x +iy , гдеx,y — действительные числа,i — мнимая единица (т.е.i2 = −1)

называют алгебраической формой записи комплексного числаz. При этом x называют действительной частью комплексного числаи обозначают Re z ( x = Re z ), y называют мнимой частью комплексного числаи обозначают Im z ( y = Im z ).

Пример. У комплексного числаz = 4−3i действительная часть Rez = 4 , а мнимая Imz = −3 .

2.Плоскость комплексных чисел

Втеории функций комплексного переменного рассматривают плоскость комплексных чисел, которую обозначают либо , либо используют буквы, обозначающие комплексные числаz ,w и т.п.

Горизонтальная ось комплексной плоскости называется действительной осью, на ней располагают действительные числаz = x +0i = x .

Вертикальная ось комплексной плоскости называется мнимой осью, на ней располагают

чисто мнимые числа z = 0+iy .	Мнимая ось в дань исторической традиции обозначается y (а
не iy ).
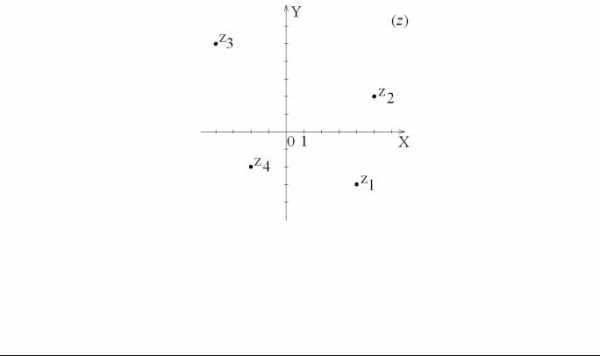
Пример. Изобразить на	комплексной плоскости 4 числа z1 = 4−3i ,z2 = 5+2i ,
z3 = −4+5i ,z4 = −2−2i .

Оглавление Е.Е. Красновский, В.Д. Морозова «Теория функций комплексного переменного»

5

3. Комплексно сопряжённые числа

Числа z = x +iy иz = x −iy называюткомплексно сопряжёнными. На комплексной плоскости им соответствуют точки, симметричные относительно действительной оси.

4.Действия с комплексными числамив алгебраической форме

4.1Сложение комплексных чисел

Суммой двух комплексных чисел

z1= x1+iy1

и z2 = x2 +iy2 называется комплексное число

z1+ z2

= (x1+iy1)+(x2+iy2)= (x1+ x2)+i (y1+ y2).

Таким

образом,

операция

сложения

комплексных чисел аналогична операции сложения алгебраических двучленов.

Пример. Суммой двух комплексных чиселz1 = 3+7i иz2

= −1+2i

будет комплексное число

z1 +z2 =(3 +7i)+(−1+2i)=(3 −1)+(7 +2)i =2 +9i .

Очевидно,

суммой комплексно

сопряжённых

чисел

является

действительное

число:

z + z = (x+iy)+(x−iy)= 2x= 2 Re z.

4.2 Вычитание комплексных чисел

Разностью двух комплексных чисел z1 = x1 +iy1

и

z2

= x2 +iy2

называется

комплексное

число z1− z2= (x1+iy1)−(x2+iy2)= (x1− x2)+i (y1− y2).

Пример. Разностью двух комплексных чисел

z1 =3 −4i

и z2

= −1+2i

будет комплексное

число z1 − z2 = (3−4i)−(−1+2i)= (3−(−1))+(−4−2)i = 4−6i .

Разностью

комплексно сопряжённых

чисел

является

чисто

мнимое

число

z − z = (x+iy)−(x−iy)= 2iy= 2iIm z.

4.3 Умножение комплексных чисел

Произведением двух комплексных чисел

z1= x1+iy1

и z2= x2+iy2

называется комплексное

число

z1z2= (x1+iy1)(x2+iy2)= x1x2+iy1x2+iy2x1+i2 y1y2

= (x1x2− y1y2)+i (y1x2+ y2x).

Таким

образом, операция умножения комплексных чисел аналогична операции умножения алгебраических двучленов с учётом того, что i2 = −1.

Оглавление Е.Е. Красновский, В.Д. Морозова «Теория функций комплексного переменного»

studfiles.net

Действия над комплексными числами в алгебраической и тригонометрической форме. Сопряженность — ПриМат

Сложение

Пусть , и .
Тогда получается простым приведением подобных:

Вычитание

Пусть , и .
Тогда получается аналогично со сложением:

Умножение

Пусть , и .
Тогда .
Что делать на этом шаге? Все довольно просто, как Вы наверно и подумали, надо всего лишь раскрыть скобки и привести подобные:

Определение комплексно сопряженного числа

Пусть , и .
называют комплексно сопряженным к , если и , т.е. и .
И при перемножении
Это потребуется для нашего следующего действия.

Деление

Пусть , и .
Тогда
На этом шаге обычно все и остановилось бы, но мы сможем еще упростить выражение благодаря знанию комплексно сопряженных чисел. Умножим числитель и знаменатель на комплексно сопряженное число к знаменателю, получим:

Умножение

Произведением двух комплексных чисел и будет комплексное число вида

Деление

Частным двух комплексных чисел и будет комплексное число вида

ib.mazurok.com

Действия над комплексными числами в алгебраической форме — ПриМат

Сложение

Пусть , и .

Тогда получается простым приведением подобных:

Вычитание

Пусть , и .
Тогда получается аналогично со сложением:

Умножение

Пусть , и .
Тогда .
Что делать на этом шаге? Все довольно просто, как Вы наверно и подумали, надо всего лишь раскрыть скобки и привести подобные:

Определение комплексно сопряженного числа

Пусть , и .
называют комплексно сопряженным к , если и , т.е. и .
И при перемножении
Это потребуется для нашего следующего действия.

Деление

Пусть , и .
Тогда
На этом шаге обычно все и остановилось бы, но мы сможем еще упростить выражение благодаря знанию комплексно сопряженных чисел. Умножим числитель и знаменатель на комплексно сопряженное число к знаменателю, получим:

Умножение

Произведением двух комплексных чисел и будет комплексное число вида

Деление

Частным двух комплексных чисел и будет комплексное число вида

Возведение в степень

Извлечение корня

,

Лимит времени: 0

Информация

Тест поможет Вам проверить, как Вы усвоили материал

Вы уже проходили тест ранее. Вы не можете запустить его снова.

Тест загружается…

Вы должны войти или зарегистрироваться для того, чтобы начать тест.

Вы должны закончить следующие тесты, чтобы начать этот:

Правильных ответов: 0 из 4

Ваше время:

Время вышло

Вы набрали 0 из 0 баллов (0)

Средний результат
Ваш результат

Рубрики

1. Алгебра 0%
2. Математический анализ 0%

Ваш результат был записан в таблицу лидеров

1. С ответом
2. С отметкой о просмотре

ib.mazurok.com

Комплексные числа. Алгебраическая форма комплексного числа. — КиберПедия

Комплексные числа — расширение множества вещественных чисел, обычно обозначается . Любое комплексное число может быть представлено как формальная сумма , где и — вещественные числа, — мнимая единица.

Запись комплексного числа в виде , , называется алгебраической формой комплексного числа.

 

 

Свойства комплексных чисел. Геометрическая интерпретация комплексного числа.

Действия над комплексными числами, заданными в алгебраической форме:

Рассмотрим правила, по которым производятся арифметические действия над комплекс­ными числами.

Если даны два комплексных числа α = a + bi и β = c + di, то

α + β = (a + bi) + (c + di) = (a + c) + (b + d)i,

α – β = (a + bi) – (c + di) = (a – c) + (b – d)i . (11)

Это следует из определения действий сложения и вычитания двух упорядоченных пар действительных чисел (см. формулы (1) и (3)). Мы получили правила сложения и вычитания комплексных чисел: чтобы сложить два комплексных числа, надо отдельно сложить их действительные части и соответственно мни­мые части; чтобы из одного комплексного числа вычесть другое, необходимо вычесть соответственно их действительные и мнимые части.

Число – α = – a – bi называют противополож­ным числу α = a + bi . Сумма двух этих чисел равна нулю: — α + α = (- a — bi) + (a + bi) = (-a + a) + (-b + b)i = 0.

Для получения правила умножения комплексных чисел воспользуемся формулой (6), т. е. тем, что i2 = -1. Учитывая это соотношение, находим (a + bi)( c + di) = ac + adi + bci + bdi2 = ac + (ad + bc)i – bd, т.е.

(a + bi)( c + di) = (ac — bd) + (ad + bc)i . (12)

Эта формула соответствует формуле (2), которой определялось умножение упорядоченных пар дей­ствительных чисел.

Отметим, что сумма и произведение двух комп­лексно сопряженных чисел являются действительными числами. Всамомделе, еслиα = a + bi, = a – bi, тоα = (a + bi)( a — bi) = a2 – i2b2 = a2 + b2 , α + = ( a + bi) + (a — bi) = (a + a) + (b — b)i= 2a, т.е.

α + = 2a, α = a2 + b2. (13)

При делении двух комплексных чисел в алгеб­раической форме следует ожидать, что частное вы­ражается также числом того же вида, т. е. α/β = u + vi, где u, v R. Выведем правило деления комплексных чисел. Пусть даны числа α = a + bi, β = c + di, причем β ≠ 0, т. е. c2 + d2 ≠ 0. Послед­нее неравенство означает, что c и d одновременно в нуль не обращаются (исключается случай, когда с = 0, d = 0). Применяя формулу (12) и вто­рое из равенств (13), находим:

.

Следовательно, частное двух комплексных чисел определяется формулой:

, (14)

соответствующей формуле (4).

С помощью полученной формулы для числа β = с + di можно найти обратное ему число β-1 = 1/β. Полагая в формуле (14) а = 1, b = 0, получаем

.

Эта формула определяет число, обратное данному комплексному числу, отличному от нуля; это число также является комплексным.

Например: (3 + 7i) + (4 + 2i) = 7 + 9i;

(6 + 5i) – (3 + 8i) = 3 – 3i;

(5 – 4i)(8 – 9i) = 4 – 77i;

Действия над комплексными числами в алгебраической форме.

 

55. Аргумент комплексного числа. Тригонометрическая форма записи комплексного числа (вывод).

Арг.ком.числа. – между положительным направлением действительной оси Х вектором изображающим данное число.

Формула тригон. Числа : ,

 

cyberpedia.su