Квадратные неравенства — урок. Алгебра, 8 класс.
Общий вид квадратных неравенств — это ax2+bx+c>0(<0,≤0,≥0),гдеa≠0.
Множество решений квадратного неравенства легко определить, приблизительно начертив график функции y=ax2+bx+c (параболу).
Шаги решения квадратного неравенства:
1. определяются точки пересечения параболы и оси \(x\) с помощью решения уравнения ax2+bx+c=0.
Вспомним формулы корней квадратного уравнения:
D=b2−4ac;x1=−b+D2a,x2=−b−D2a.
Если \(D > 0\), у уравнения — два разных корня,
| |
Если \(D = 0\), у уравнения — два одинаковых корня,
| |
Если \(D < 0\), у уравнения нет реальных корней, парабола не пересекает ось \(x\) |
2. Учитывая количество корней и знак коэффициента \(a\), чертится график параболы.
Обрати внимание!
Если \(a > 0\), то ветви параболы устремлены вверх, если \(a < 0\), то вниз.
Совет: если хочешь, чтобы ветви параболы всегда были уcтремлены вверх, в случаях, когда \(a < 0\), сначала обе части неравенства перемножь на (\(-1\)).
Не забудь, что на противоположный поменяется также знак неравенства.
3. Выбираются пустые или закрашенные точки, в зависимости от вида знака неравенства:
•, если стоит знак нестрогого неравенства — ≤ или ≥;
о, если стоит знак строгого неравенства — \(<\) или \(>\).
4. Закрашивается правильный интервал.
5. Записывается ответ.
Пример:
решить квадратное неравенство −2×2+4x−5≤0.
Решение:
−2×2+4x−5≤0|⋅(−1)2×2−4x+5≥0;D=16−4⋅2⋅5=−24;парабола не пересекает осьOx.
По рисунку видно, что график положителен любому значению \(x\).
Ответ: x∈−∞;+∞, илиx∈R |
www.yaklass.ru
8 класс. Алгебра. Решение квадратных неравенств. — Решение квадратных неравенств графическим методом.
Комментарии преподавателя
На данном уроке будет рассмотрена тема: «Решение квадратных неравенств». Вы узнаете, что решение квадратных неравенств полностью базируется на свойствах квадратичных функций.
Тема: Неравенства
Урок: Решение квадратных неравенств
Квадратными называются неравенства вида
Причем важно, что старший коэффициент не может быть равен нулю: .
Решить неравенство:
Умножаем обе части неравенства на , чтобы старший коэффициент стал числом положительным. Получаем:
Так, мы видим, что любое квадратное неравенство можно преобразовать таким образом, чтобы старший коэффициент был положительным, поэтому будем рассматривать квадратные неравенства для случая .
Итак, решим заданное неравенство для положительного старшего коэффициента:
Рассмотрим функцию: , применяем теорему Виета,
Раскладываем на линейные множители:
Построим график функции (Рис. 1):
Рис. 1. График квадратичной функции
I способ решения неравенства
Произведение двух скобок – число отрицательное.
Произведение двух чисел отрицательное тогда, когда они разных знаков.
Если , тогда или , тогда
Исходное неравенство распалось на совокупность двух линейных систем.
или
Проиллюстрируем решение первой системы неравенств (рис. 2):
Рис. 2. Решение системы линейных неравенств
Красным показано множество решений первого неравенства. Зеленым – второго. Нас интересуют те значения, которые удовлетворят одновременно и первому неравенству, и второму. Очевидно, что это множество значений находится там, где присутству
www.kursoteka.ru
Решение квадратных неравенств. Видеоурок. Алгебра 8 Класс
На данном уроке будет рассмотрена тема: «Решение квадратных неравенств». Вы узнаете, что решение квадратных неравенств полностью базируется на свойствах квадратичных функций.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Уравнения и неравенства»
Квадратными называются неравенства вида
Причем важно, что старший коэффициент не может быть равен нулю: .
Решить неравенство:
Умножаем обе части неравенства на , чтобы старший коэффициент стал числом положительным. Получаем:
Так, мы видим, что любое квадратное неравенство можно преобразовать таким образом, чтобы старший коэффициент был положительным, поэтому будем рассматривать квадратные неравенства для случая .
Итак, решим заданное неравенство для положительного старшего коэффициента:
Рассмотрим функцию: , применяем теорему Виета,
Раскладываем на линейные множители:
Построим график функции (Рис. 1):
Рис. 1. График квадратичной функции
I способ решения неравенства
Произведение двух скобок – число отрицательное.
Произведение двух чисел отрицательное тогда, когда они разных знаков.
Если , тогда или , тогда
Исходное неравенство распалось на совокупность двух линейных систем.
или
Проиллюстрируем решение первой системы неравенств (рис. 2):
Рис. 2. Решение системы линейных неравенств
Красным показано множество решений первого неравенства. Зеленым – второго. Нас интересуют те значения, которые удовлетворят одновременно и первому неравенству, и второму. Очевидно, что это множество значений находится там, где присутствуют оба цвета. Так, решение первой системы:
Проиллюстрируем решение второй системы (Рис. 3):
interneturok.ru
Квадратные неравенства повышенной сложности. Видеоурок. Алгебра 8 Класс
Квадратными называются неравенства вида .
Методы решения квадратных неравенств, основанных на свойствах квадратичной функции.
1. Чтобы решить, например, неравенство , нужно рассмотреть функцию:
2. Найти корни функции, с целью построить схематический график параболы. Корни в данном случае
3. Рассмотреть схематический график функции (Рис. 1).
Ветви параболы направлены вверх. Внутри интервала корней и вне интервала корней функция сохраняет знак. Если старший коэффициент больше нуля, то вне интервала корней функция положительная. Внутри интервала корней функция отрицательная.
Рис. 1. График квадратичной функции
4. Решением данного неравенства являются все значения в интервале: . Границы интервала входят в ответ, т. к. условие допускает равенство трехчлена нулю.
Рассмотрим аналогичное неравенство: . Мы можем построить график функции для данного квадратного трехчлена (Рис. 2):
Интересующие нас значения находятся все на том же интервале
Так, мы видим, что при умножении неравенства на минус единицу ответ не изменяется, и любое неравенство с отрицательным старшим коэффициентом можно преобразовать и получить положительное
Рис. 2. График квадратичной функции
Решить неравенство:
Один из корней явно угадывается , потому что получаем верное числовое решение
Поскольку один корень уравнения найден, дискриминант его больше либо равен нулю.
Второй корень находим по теореме Виета. Произведение и сумма корней легко выражаются через коэффициенты.
Находим второй корень:
Строим схематический график параболы (Рис. 3):
Ветви параболы направлены вверх, проходят через точки . Вне интервала корней функция положительна, внутри интервала корней функция отрицательна. Нам нужны те значения, при которых функция отрицательна. Это
Рис. 3. График квадратичной функции
Ответ: .
Какие могут быть сопутствующие задачи для такого вида неравенств?
Допустим: найти целочисленные решения для данного неравенства.
находится левее , затем , а не входит в ответ, значит, целочисленное решение:
Решить неравенство:
Обозначим за новую переменную ; Тогда неравенство превращается в следующее квадратное неравенство
Решение:
Рассматриваем функцию:
Находим корни, используя обратную теорему Виета.
Схематически рисуем график функции (Рис. 4).
Ветви параболы направлены вверх. Внутри интервала корней и вне интервала корней функция сохраняет знак. Если старший коэффициент больше нуля, то вне интервала корней функция положительная. Внутри интервала корней функция отрицательная.
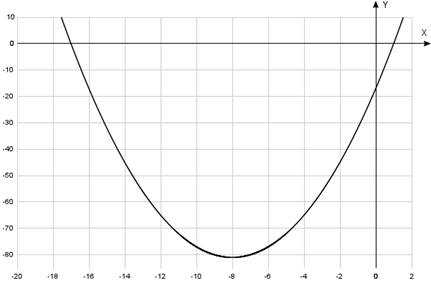
Рис. 4. График квадратичной функции
Решение неравенства: , но Так, получаем
Переходим к старой переменной.
Переходим к системе:
Первое неравенство системы выполняется всегда.
Рассматриваем график функции: (Рис. 5).
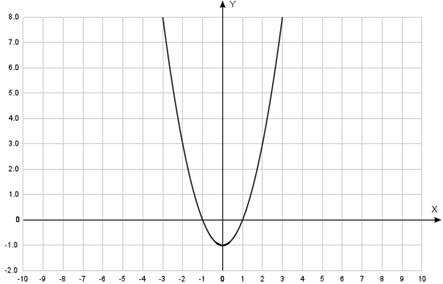
Рис. 5. График квадратичной функции
Корни:
График очевиден. Ветви параболы направлены вверх. Внутри интервала корней все значения отрицательные.
Решение неравенства:
Решить неравенство:
Обозначим за новую переменную ; Тогда неравенство превращается в следующее квадратное неравенство
Решение:
1. Рассматриваем функцию:
2. Находим корни, используя обратную теорему Виета.
3. Схематически рисуем график функции (Рис. 6).
Ветви параболы направлены вверх. Внутри интервала корней и вне интервала корней функция сохраняет знак. Если старший коэффициент больше нуля, то вне интервала корней функция положительная. Внутри интервала корней функция отрицательная.
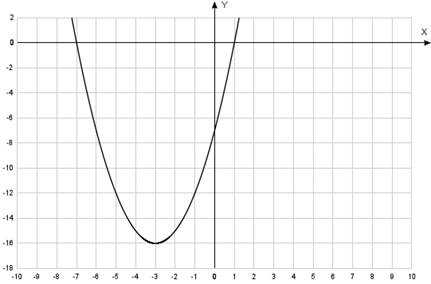
Рис. 6. График квадратичной функции
4. Решение неравенства: или но
5. Переходим к старой переменной.
6. Переходим к системе: ; первое неравенство не имеет решений.
7. Рассматриваем график функции: (рисунок 53.5). Корни:
8. График очевиден. Ветви параболы направлены вверх. Внутри интервала корней все значения отрицательные, вне интервала – положительные.
9. Решение неравенства: или
Подведение итога урока
На данном уроке была рассмотрена тема: «Квадратные неравенства повышенной сложности». Вы вспомнили свойства квадратичных функций, на основании которых решаются квадратные неравенства любой сложности. К квадратичной функции сводятся любые неравенства, несмотря на их сложность.
Список литературы
- Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.
- Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. 5 издание. – М.: Просвещение, 2010.
- Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- ЕГЭ по математике (Источник).
- Frezzii.narod.ru (Источник).
- Фестиваль педагогических идей «Открытый урок» (Источник).
- Видеоуроки для школьников (Источник).
Домашнее задание
- Р
interneturok.ru
| 1. |
Рисунок с множеством решений неравенства
Сложность: лёгкое |
1 |
| 2. |
Решение неравенства с готовым графиком
|
1 |
| 3. |
Решение неравенства без графика
Сложность: лёгкое |
2 |
| 4. |
Замена квадратного неравенства системами неравенств
Сложность: лёгкое |
1 |
| 5. |
Нахождение ответа квадратного неравенства
Сложность: среднее |
1 |
| 6. |
Нахождение решения квадратного неравенства
Сложность: среднее |
1 |
| 7. |
Решение квадратного неравенства
Сложность: среднее |
1 |
| 8. |
Решение полного квадратного неравенства
Сложность: среднее |
1 |
| 9. |
Решение квадратного неравенства
Сложность: среднее |
2 |
| 10. |
Решение квадратного неравенства, неполный квадратный трёхчлен
Сложность: среднее |
4 |
| 11. |
Метод интервалов (произведение биномов)
Сложность: среднее |
7 |
| 12. |
Квадратное неравенство (произведение биномов)
Сложность: среднее |
7 |
| 13. |
Наименьшее или наибольшее решение неравенства
Сложность: сложное |
6 |
| 14. |
Значения, при которых имеет смысл выражение
Сложность: среднее |
8 |
| 15. |
Неотрицательные или неположительные значения трёхчлена
Сложность: сложное |
7 |
| 16. |
Положительные или неотрицательные значения трёхчлена
Сложность: сложное |
7 |
www.yaklass.ru
Квадратные неравенства. Как решать квадратные неравенства?
Квадратными неравенствами называют неравенства, которые можно привести к виду \(ax^2+bx+c\) \(⋁\) \(0\), где \(a\),\(b\) и \(с\) — любые числа (причем \(a≠0\)), \(x\) – неизвестная переменная, а \(⋁\) – любой из знаков сравнения (\(>\),\(<\),\(≤\),\(≥\)).
Проще говоря, такие неравенства выглядят как квадратные уравнения, но со знаком сравнения вместо знака равно.
Примеры:
\(x^2+2x-3>0\)
\(3x^2-x≥0\)
\((2x+5)(x-1)≤5\)
Как решать квадратные неравенства?
Квадратные неравенства обычно решают методом интервалов. Ниже приведен алгоритм, как решать квадратные неравенства с дискриминантом больше нуля. Решение квадратных неравенств с дискриминантом равным нулю или меньше нуля – разобраны отдельно.
-
Приведите неравенство к виду \(ax^2+bx+c⋁0\).
Примеры:\(x^2-6x-16<0\) \(-9x^2+x+8≤0\)
-
Разложите выражение слева на множители. Для этого приравняйте его к нулю и решите получившееся уравнение, найдя корни \(x_1\) и \(x_2\). Затем запишите исходное выражение в виде \(a(x-x_1 ) (x-x_2 )\) Подробнее об этом можно почитать здесь.
\(x^2-6x-16=0\) \(-9x^2+x+8=0\)
\(D=36-4 \cdot 1 \cdot (-16)=100=10^2\) \(D=1-4 \cdot (-9) \cdot 8=289\)
\(x_1=\frac{6-10}{2}=-2\) \(x_1=\frac{-1+17}{-18}=\frac{16}{-18}=-\frac{8}{9}\) \(x_2=\frac{6+10}{2}=8\) \(x_2=\frac{-1-17}{-18}=\frac{-18}{-18}=1\)
\((x-8)(x+2)<0\) \(-9(x+\frac{8}{9})(x-1)≤0\) -
Начертите числовую ось и отметьте на ней найденные корни. Если неравенство строгое (со знаком \(<\) или \(>\)) то точки должны быть выколоты, если неравенство нестрогое (со знаком \(≤\) или \(≥\)), то точки должны быть закрашены.
-
Нанесенные корни разбивают числовую ось на несколько интервалов.
В первом справа интервале поставьте:
\(-\) знак плюс если перед скобками ничего не стоит или стоит положительное число
\(-\) знак минус если перед скобками стоит знак минус.
В следующих за ним интервалах поставьте чередующиеся знаки. -
Заштрихуйте подходящие интервалы, то есть числовые промежутки:
\(-\) со знаком «\(+\)», если в неравенстве стояло «\(>0\)» или «\(≥0\)»
\(-\) со знаком «\(-\)», если в неравенстве стояло «\(<0\)» или «\(≤0\)» -
Выпишите в ответ те интервалы, которые вы заштриховали.
Внимание! При строгих знаках неравенства (\(<\) или \(>\)) границы интервала НЕ ВХОДЯТ в решение, при этом в ответе сам интервал записывается в виде \((x_1;x_2)\) – скобки круглые. При нестрогих знаках неравенства (\(≤\) или \(≥\)) — границы интервала ВХОДЯТ в решение, и ответ записывается в виде \([x_1;x_2]\), с квадратными скобками на точках.Ответ: \((-2;8)\) Ответ: \((-∞;\frac{8}{9}]∪[1;∞)\)
Пример. Решите квадратное неравенство \(\frac{x^2}{5}+\frac{2x}{3}\)\(≥\) \(\frac{8}{15}\)
Решение:
|
\(\frac{x^2}{5}+\frac{2x}{3}\)\(≥\) \(\frac{8}{15}\) |
Чтобы избавиться от дробей, умножим обе части неравенство на \(15\). |
|
|
\(3x^2+10x≥8\) |
Перенесем \(8\) влево. |
|
|
\(3x^2+10x-8≥0\) |
Вот мы и привели неравенство к виду \(ax^2+bx+c⋁0\). Запишем квадратное уравнение вида \(ax^2+bx+c=0\). |
|
|
\(3x^2+10x-8=0\) |
Решим полученное квадратное уравнение. |
|
|
\(D=100+4⋅3⋅8=196=14^2\) |
Когда корни найдены, запишем неравенство в разложенном на множители виде. |
|
|
\(3(x+4)(x-\frac{2}{3})≥0\) |
Теперь начертим числовую ось, отметим на ней корни и расставим знаки на интервалах. |
|
|
Выпишем в ответ интересующие нас интервалы . Так как знак неравенства \(≥\), то нам нужны интервалы со знаком \(+\), при этом сами корни мы включаем в ответ (скобки на этих точках – квадратные). |
Ответ: \(x∈(-∞;-4]∪[ \frac{2}{3};∞)\)
Квадратные неравенства с отрицательным и равным нулю дискриминантом
Алгоритм выше работает, когда дискриминант больше нуля, то есть квадратный трехчлен имеет \(2\) корня. Что делать в остальных случаях? Например, таких:
|
\(1) x^2+2x+9>0\) |
\(2) x^2+6x+9≤0\) |
\(3)-x^2-4x-4>0\) |
\(4) -x^2-64<0\) |
|
\(D=4-36=-32<0\) |
\(D=36-36=0\) |
\(D=16-16=0\) |
\(D=-4 \cdot 64<0\) |
Если \(D<0\), то квадратный трехчлен имеет постоянный знак, совпадающий со знаком коэффициента \(a\) (тем, что стоит перед \(x^2\)).
То есть, выражение:
\(x^2+2x+9\) – положительно при любых \(x\), т.к. \(a=1>0\)
\(-x^2-64\) — отрицательно при любых \(x\), т.к. \(a=-1<0\)
Если \(D=0\), то квадратный трехчлен при одном значении \(x\) равен нулю, а при всех остальных имеет постоянный знак, который совпадает со знаком коэффициента \(a\).
То есть, выражение:
\(x^2+6x+9\) — равно нулю при \(x=-3\) и положительно при всех остальных иксах, т.к. \(a=1>0\)
\(-x^2-4x-4\) — равно нулю при \(x=-2\) и отрицательно при всех остальных, т.к. \(a=-1<0\).
Как найти икс, при котором квадратный трехчлен равен нулю? Нужно решить соответствующее квадратное уравнение.
С учетом этой информации давайте решим квадратные неравенства:|
1) \(x^2+2x+9>0\) |
Неравенство, можно сказать, задает нам вопрос: «при каких \(x\) выражение слева больше нуля?». Выше мы уже выяснили, что при любых. В ответе можно так и написать: «при любых \(x\)», но лучше туже самую мысль, выразить на языке математики. |
|
|
Ответ: \(x∈(-∞;∞)\) |
||
|
2) \(x^2+6x+9≤0\) |
Вопрос от неравенства: «при каких \(x\) выражение слева меньше или равно нулю?» Меньше нуля оно быть не может, а вот равно нулю – вполне. И чтобы выяснить при каком иске это произойдет, решим соответствующие квадратное уравнение. |
|
|
\(x^2+6x+9=0\) |
Давайте соберем наше выражение по формуле \(a^2+2ab+b^2=(a+b)^2\). |
|
|
\((x+3)^2=0\) |
Сейчас нам мешает только квадрат. Давайте вместе подумаем — какое число в квадрате равно нулю? Ноль! Значит, квадрат выражения равен нулю только если само выражение равно нулю. |
|
|
\(x+3=0\) |
Это число и будет ответом. |
|
|
Ответ: \(-3\) |
|
|
|
3)\(-x^2-4x-4>0\) |
Когда выражение слева больше нуля? Как выше уже было сказано выражение слева либо отрицательно, либо равно нулю, положительным оно быть не может. Значит ответ – никогда. Запишем «никогда» на языке математике, с помощью символа «пустое множество» — \(∅\). |
|
|
Ответ: \(x∈∅\) |
||
|
4) \(-x^2-64<0\) |
Когда выражение слева меньше нуля? Всегда. Значит неравенство выполняется при любых \(x\). |
|
|
Ответ: \(x∈(-∞;∞)\) |
|
Смотрите также:
Дробно-рациональные неравенства
Скачать статью
cos-cos.ru
Урок алгебры «Квадратные неравенства» (8 класс)
Определение
квадратного уравнения
Квадратным уравнением называют уравнение вида ах2 +bx +с =0,
где а, b, с – любые действительные числа, причём а0.
Определение
квадратного уравнения
Квадратным уравнением называют уравнение вида ах2 +bx +с =0,
где а, b, с – любые действительные числа, причём а0.
Определение
квадратного уравнения
Квадратным уравнением называют уравнение вида ах2 +bx +с =0,
где а, b, с – любые действительные числа, причём а0.
Определение
квадратного уравнения
Квадратным уравнением называют уравнение вида ах2 +bx +с =0,
где а, b, с – любые действительные числа, причём а0.
Определение
линейного неравенства
Линейным неравенством называется неравенство, сводящееся к виду
ах + b 0 ( или ах + b <0)
где а, b – любые действительные числа, причём а0.
Определение
линейного неравенства
Линейным неравенством называется неравенство, сводящееся к виду
ах + b 0 ( или ах + b <0)
где а, b – любые действительные числа, причём а0.
Определение
линейного неравенства
Линейным неравенством называется неравенство, сводящееся к виду
ах + b 0 ( или ах + b <0)
где а, b – любые действительные числа, причём а0.
Определение
линейного неравенства
Линейным неравенством называется неравенство, сводящееся к виду
ах + b 0 ( или ах + b <0)
где а, b – любые действительные числа, причём а0.
infourok.ru
