Кривые второго порядка
Содержание
Введение
1.Кривые второго порядка
1.1 Эллипс
1.2 Гипербола
1.3 Парабола
2.Теоремы, связанные с кривыми второго порядка
Литература
Введение
Впервые кривые второго порядка изучались одним из учеников Платона. Его работа заключалась в следующем: если взять две пересекающиеся прямые и вращать их вокруг биссектрисы угла, ими образованного, то получится конусная поверхность. Если же пересечь эту поверхность плоскостью, то в сечении получаются различные геометрические фигуры, а именно эллипс, окружность, парабола, гипербола и несколько вырожденных фигур.
Однако эти научные знания нашли применение лишь в XVII, когда стало известно, что планеты движутся по эллиптическим траекториям, а пушечный снаряд летит по параболической. Ещё позже стало известно, что если придать телу первую космическую скорость, то оно будет двигаться по окружности вокруг Земли, при увеличении этой скорости — по эллипсу, а по достижении второй космической скорости тело по параболе покинет поле притяжения Земли.
1. Кривые второго порядка
Кривой 2-го порядка называется линия на плоскости, которая в некоторой декартовой системе координат определяется уравнением
ax2 + 2bxy + cy2 + 2dx + 2ey + f = 0
где a, b, c, d, e, f — вещественные коэффициенты, причем a2 + b2 + c2 ≠ 0 .
Вид кривой зависит от четырёх инвариантов:
инварианты относительно поворота и сдвига системы координат:
инвариант относительно поворота системы координат (полуинвариант):
Многие важные свойства кривых второго порядка могут быть изучены при помощи характеристической квадратичной формы, соответствующей уравнению кривой:
Так, например, невырожденная кривая
оказывается вещественным эллипсом, мнимым эллипсом, гиперболой или параболой в зависимости от того, будет ли положительно определённой, отрицательно определённой, неопределённой или полуопределённой квадратичной формой, что устанавливается по корням характеристического уравнения: Илиλ2 − Iλ + D = 0.
Корни этого уравнения являются собственными значениями вещественной симметричной матрицы и, как следствие этого, всегда вещественны:
Кривые второго порядка классифицируются на невырожденные кривые и вырожденные.
Доказано, что кривая 2–го порядка, определяемая этим уравнением принадлежит к одному из следующих типов: эллипс, гипербола, парабола, пара прямых (пересекающихся, параллельных или совпадающих), точка, пустое множество.
Иными словами, для каждой кривой 2-го порядка (для каждого уравнения) существует такая система координат, в которой уравнение кривой имеет вид:
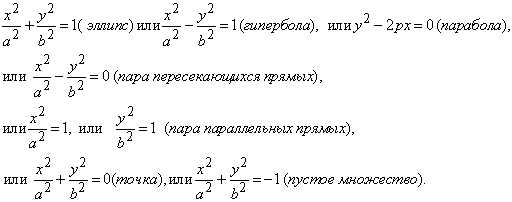
1.1 Эллипс
Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух фиксированных точек плоскости, называемых фокусами эллипса, есть величина постоянная. Отрезки, соединяющие точку эллипса с фокусами, называются фокальными радиусами точки.
Если эллипс описывается каноническим уравнением
где a > 0 , b > 0, a > b > 0 — большая и малая полуоси эллипса, то фокусы эллипса расположены симметрично на оси абсцисс и имеют координаты (−c, 0) и ( c, 0), где
Величина e = c/a называется эксцентриситетом эллипса.
По определению эллипса r1 + r2 = 2a, r1 и r2 − фокальные радиусы, их длины вычисляются по формулам
Если фокусы эллипса совпадают, то эллипс является окружностью.
1.2 Гипербола
Гиперболой называется кривая второго порядка, которая в некоторой декартовой системе координат описывается уравнением
где a > 0, b > 0 — параметры гиперболы.
Это уравнение называется каноническим уравнением гиперболы, а система координат, в которой гипербола описывается каноническим уравнением, называется канонической.
В канонической системе оси координат являются осями симметрии гиперболы, а начало координат — ее центром симметрии.
Точки пересечения гиперболы с осью OX ( ± a, 0) называются вершинами гиперболы.
С осью OY гипербола не пересекается.
Отрезки a и b называются полуосями гиперболы.
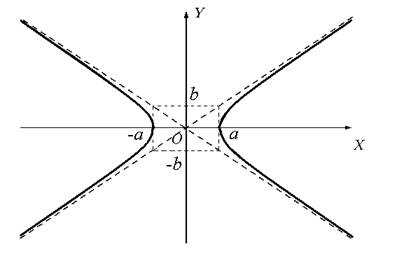
Рис.1
Прямые ay − bx = 0 и ay + bx = 0 — асимптоты гиперболы, при удалении точки гиперблы в бесконечность, соответствующая ветвь гиперболы приближается к одной из асимптот.
Уравнение описывает гиперболу, вершины которой лежат на оси OY в точках (0, ± b).

Рис.2
Такая гипербола называется сопряженной к гиперболе её асимптоты — те прямые ay − bx = 0 и ay + bx = 0. Говорят о паре сопряжённых гипербол.
1.3 Парабола
Параболой называется кривая второго порядка, которая в некоторой декартовой системе координат описывается уравнением
y2 = 2 px
где p > 0 — параметр параболы.
Такое уравнение называется каноническим уравнением параболы, а система координат, в которой парабола описывается каноническим уравнением, называется канонической.
В канонической системе ось абсцисс является осью симметрии параболы, а начало координат — её вершиной.
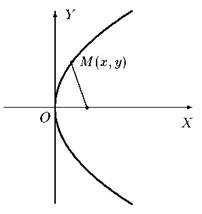
Рис.3
Уравнения y2 = −2 px, x2 = 2 py, и x2 = −2 py, p > 0, в той же самой канонической системе координат также описывают параболы:
2. Теоремы, связанные с кривыми второго порядка
Теоремма Паскамля — теорема проективной геометрии, которая гласит, что:
Если шестиугольник вписан в окружность либо любое другое коническое сечение (эллипс, параболу, гиперболу, даже пару прямых), то точки пересечения трёх пар противоположных сторон лежат на одной прямой.Теорема Паскаля двойственна к теореме Брианшона.
Теорема Брианшона является классической теоремой проективной геометрии. Она сформулируется следующим образом:
Если шестиугольник описан около конического сечения, то три диагонали, соединяющие противоположные вершины этого шестиугольника, проходят через одну точку.
В частности, в вырожденном случае:
Если стороны шестиугольника проходят поочерёдно через две данные точки, то три диагонали, соединяющие его противоположные вершины, проходят через одну точку.
Теорема Брианшона двойственна к теореме Паскаля, а её вырожденный случай двойственен к теореме Паппа.
Литература
1. Корн Г., Корн Т. Кривые второго порядка (конические сечения) // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 64-69.
2. Корн Г., Корн Т. 2.4-5. Характеристическая квадратичная форма и характеристическое уравнение // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 64.
3. В.А. Ильин, Э.Г. Позняк. Аналитическая геометрия, гл. 6. М.: «Наука», 1988.
Кривые второго порядка — Мегаобучалка
Пример 1. Найти центр и радиус окружности, заданной уравнением .
Решение. Приведем исходное уравнение к виду (4.13). Для этого сгруппируем члены с и члены с , и выделим в скобках полные квадраты.
, или
— это уравнение окружности с центром в точке и радиусом 2.
Пример 2. Найти координаты фокусов и эксцентриситет эллипса, описываемого уравнением .
Решение. Приведем уравнение к виду ( 4.14 ) разделив обе части уравнения 36
, откуда , .
Определяем расстояние фокусов от центра: .
Так как то фокусы эллипса лежат на оси : , .
Эксцентриситет данного эллипса определяем по формуле:
.
Пример 3. Написать уравнение гиперболы, если ее фокусы находятся в точках , , а длина ее действительной оси равна 1.
Решение. Для записи уравнения гиперболы в виде (4.15 ) необходимо знать величины и . Величина по условию задачи (длина действительной оси). Определим величину .
Из условия задачи можно определить величину . Это первая координата фокуса, то есть .
По формуле определяем величину :
Подставляем в уравнение (4.15 ), получаем .
Пример 4. Вывести каноническое уравнение параболы, если известно, что ее вершина расположена в начале координат, она расположена симметрично оси , и проходит через точку .
Решение. По условию парабола симметрична оси и вершина расположена в начале координат, следовательно, для нахождения параметра параболы можно воспользоваться каноническим уравнением ( 4.16 ).
Подставим в уравнение (4.16 ) координаты точки, через которую проходит парабола: , откуда .
Следовательно, уравнение параболы можно записать как ; .
Пример 5. Определить вид кривой второго порядка
и её параметры .
Решение. Преобразуем уравнение линии, группируя члены с и члены с , и вынося за скобки коэффициенты при квадратах:
,
;
выделим в скобках полные квадраты:
,
,
,
разделим обе части уравнения на (144):
Получили уравнение эллипса (4.18) с центром в точке .
Выполним параллельный перенос
.
Получили каноническое уравнение эллипса в системе , где — новое начало. Полуоси , поэтому большая ось параллельна оси .
Найдем фокусы
Вершины эллипса
Задачи для самостоятельного решения
1. Составить уравнение эллипса, полуоси которого , центр в точке (-2; 3)
2. Для гиперболы найти действительную и мнимую полуоси, координаты фокусов и эксцентриситет.
3. Составить уравнение параболы с вершиной (-1; 1) и фокусом .
4. Определить вид кривых второго порядка , их параметры. Построить кривые
а) ;
б) ;
в) ;
г)
Ответы
2. , , , ,
1. .
Полярная система координат
Пример 1. Построить в полярной системе координат точки:
Решение.
Пример 2. — координаты точки М. Найти полярные координаты точки М.
Решение.
Равенства (4.25) примут вид:
Отсюда имеем:
Таким образом, полярные координаты точки М равны:
Пример 3.. Дано полярное уравнение линии . Построить эту линию по точкам. Найти ее декартово уравнение.
Решение. Выражение в правой части имеет смысл при , то есть и . Учитывая периодичность функции (период Т= ) достаточно рассмотреть . Составим таблицу значений функции, ограничиваясь точностью 0,01:
Проведем лучи, соответствующие выбранным значениям , и на каждом из них отложим вычисленное значение . Полученные точки соединим плавной кривой (см. рис. ниже). Построенная линия называется лемнискатой Бернулли.
Чтобы перейти к декартовым координатам, запишем уравнение в виде и воспользуемся формулами (4.26, 4.28):
– уравнение линии в декартовой системе координат.
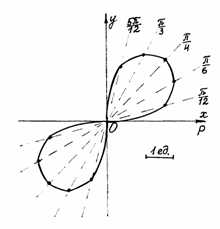
Рис.
Пример 4. Найти полярное уравнение окружности
Решение. Запишем уравнение в виде
или
Воспользуемся формулами (4.25):
– искомое уравнение.
megaobuchalka.ru
1. Определение кривой второго порядка
Кривой второго порядка называется линия, определяемая уравнением второй степени относительно текущих декартовых координат.
В общем случае это уравнение имеет следующий вид:
(1)
где
коэффициенты и 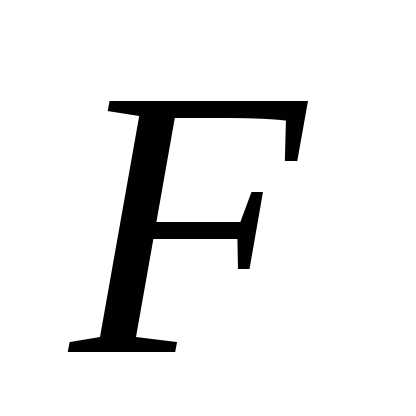 — действительные числа и, кроме того,
по крайней мере одно из чисел:
— действительные числа и, кроме того,
по крайней мере одно из чисел: 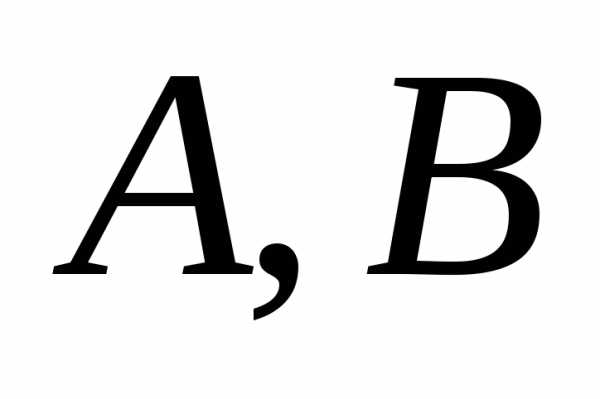 или
или  отлично
от нуля. Коэффициенты при
отлично
от нуля. Коэффициенты при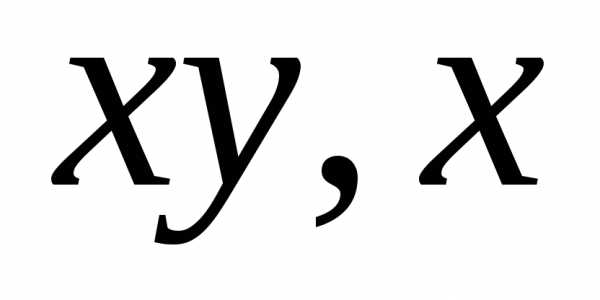 и
и обозначены соответственно через
обозначены соответственно через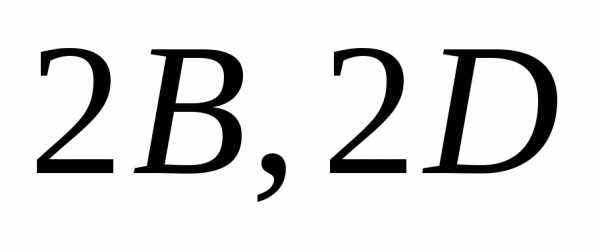 и
и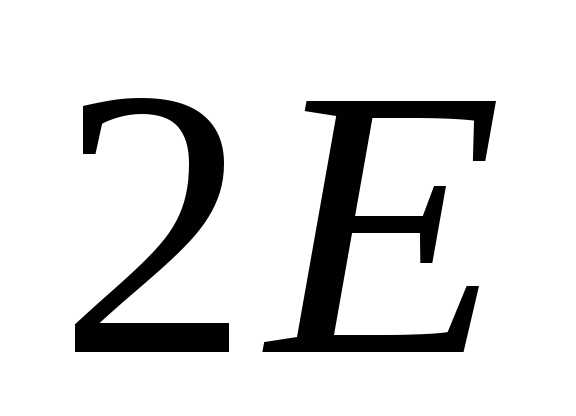 для удобства преобразований уравнения.
Известно, что уравнение окружности с
центром в точке
для удобства преобразований уравнения.
Известно, что уравнение окружности с
центром в точке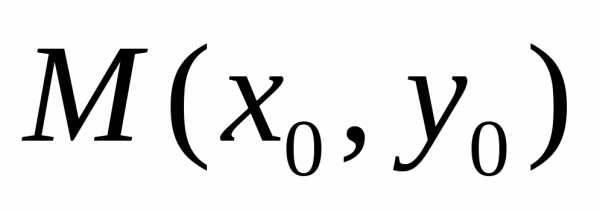 и радиуса
и радиуса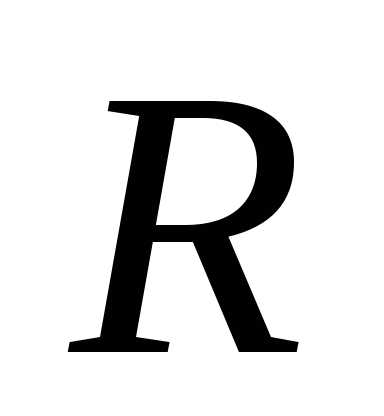 имеет вид
имеет вид
(2)
Это
уравнение второй степени относительно  и
и  .
Следовательно,
окружность есть кривая
второго порядка. Далее будут рассмотрены
четыре кривые второго порядка: окружность,
эллипс, гипербола и парабола.
.
Следовательно,
окружность есть кривая
второго порядка. Далее будут рассмотрены
четыре кривые второго порядка: окружность,
эллипс, гипербола и парабола.
2. Окружность
Раскрыв скобки в уравнении (2) и выполнив некоторые тождественные преобразования, мы получим уравнение окружности в следующем виде:
При
сравнении этого уравнения с общим
уравнением (1) кривой второго порядка
легко заметить, что для уравнения
окружности выполнены два условия: 1)
отсутствует член с произведением
координат 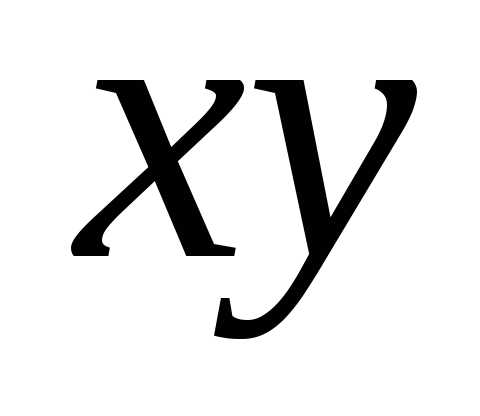 ;
2) коэффициенты при
;
2) коэффициенты при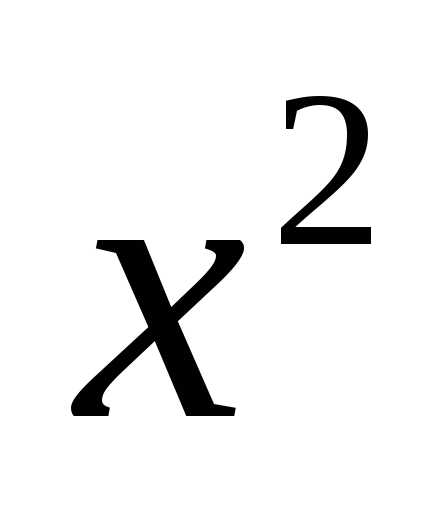 и
и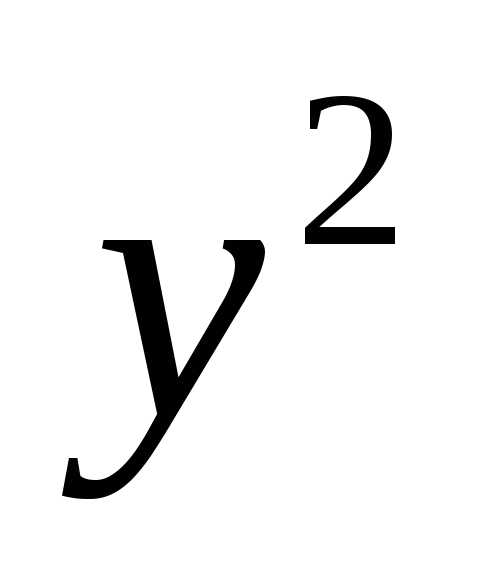 равны между собой.
равны между собой.
Пример. Показать, что уравнение определяет окружность, и найти координаты ее центра и радиус.
Решение.
Условия и 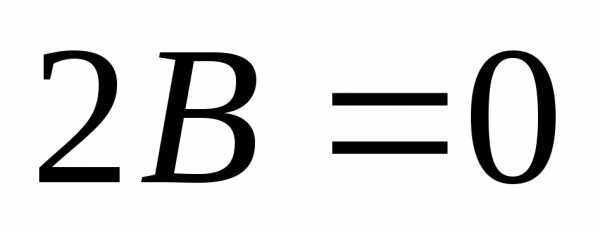 здесь выполняются. Преобразуем данное
уравнение:
здесь выполняются. Преобразуем данное
уравнение:
или
Мы
получили уравнение окружности с центром  и радиусом
и радиусом .
.
Пример. Показать, что уравнение не определяет никакой линии.
Решение. Преобразуем это уравнение:
или
Теперь ясно, что данное уравнение не определяет никакой линии.
3. Эллипс
Определение. Эллипсом называется геометрическое место точек плоскости, сумма расстояний каждой из которых от двух данных точек этой плоскости, называемых фокусами, есть постоянная величина (при условии, что эта величина больше расстояния между фокусами).
Обозначим
фокусы через и
и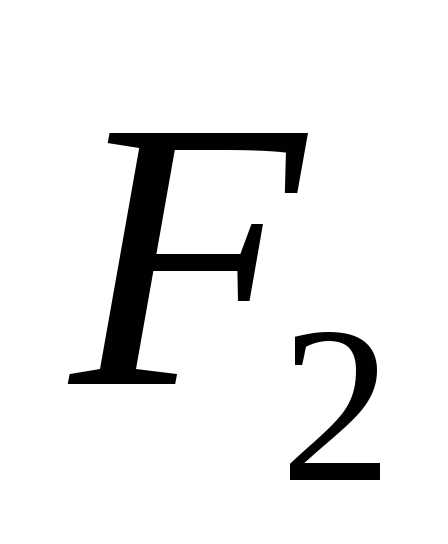 ,
расстояние между ними – через
,
расстояние между ними – через 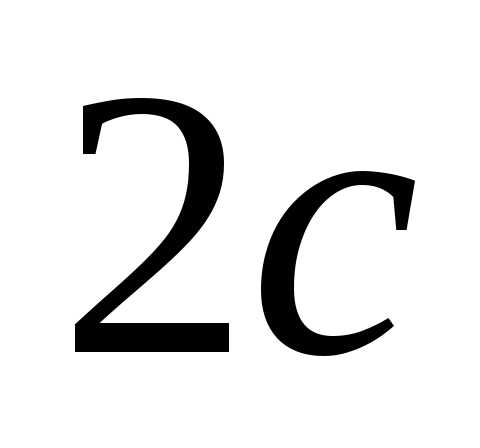 ,
а постоянную величину, равную сумме
расстояний от каждой точки эллипса до
фокусов, – через
,
а постоянную величину, равную сумме
расстояний от каждой точки эллипса до
фокусов, – через 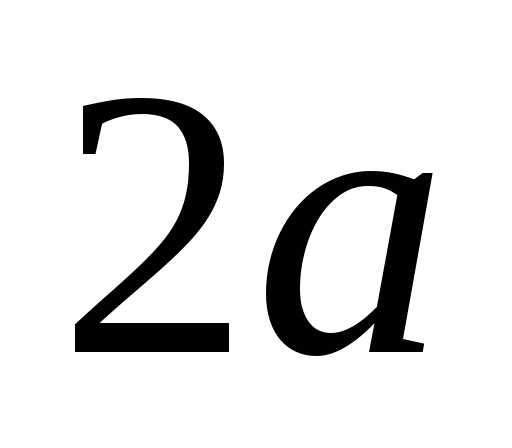 (по условию
(по условию ).
).
Построим
декартову систему координат так, чтобы
фокусы  и
и 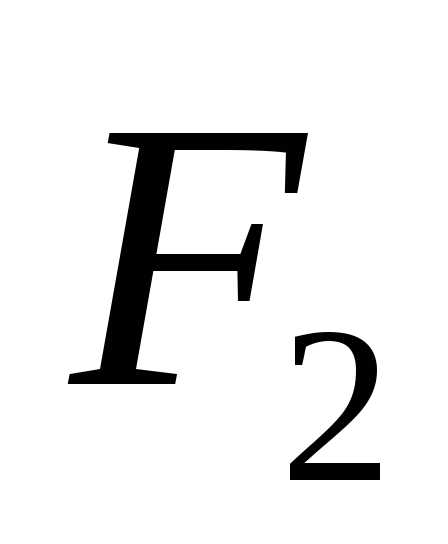 оказались на оси абсцисс, а начало
координат совпало с серединой отрезка
оказались на оси абсцисс, а начало
координат совпало с серединой отрезка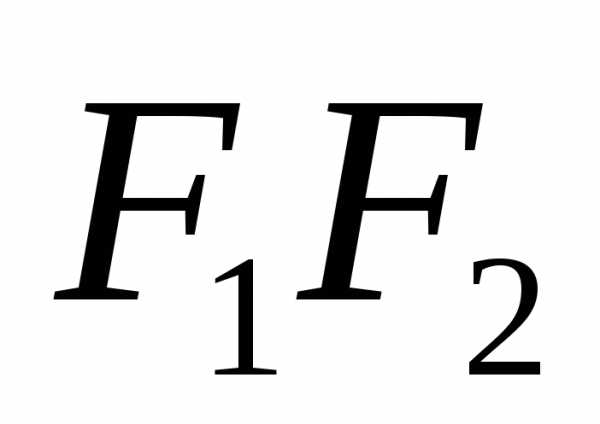 (рис.2.3). Тогда фокусы будут иметь следующие
координаты: левый фокус
(рис.2.3). Тогда фокусы будут иметь следующие
координаты: левый фокус 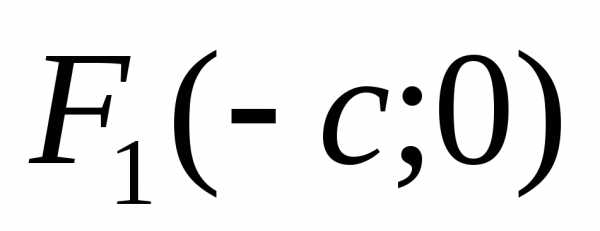 и правый фокус
и правый фокус  .
Выведем уравнение эллипса в выбранной
нами системе координат. С этой целью
рассмотрим произвольную точку
.
Выведем уравнение эллипса в выбранной
нами системе координат. С этой целью
рассмотрим произвольную точку 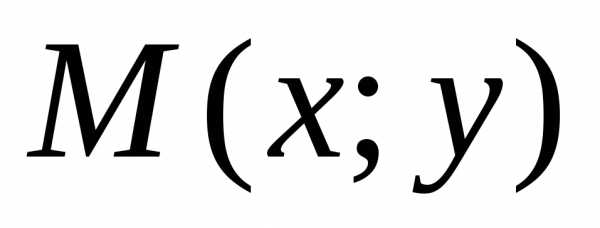 эллипса. По определению эллипса сумма
расстояний от этой точки до фокусов
эллипса. По определению эллипса сумма
расстояний от этой точки до фокусов и
и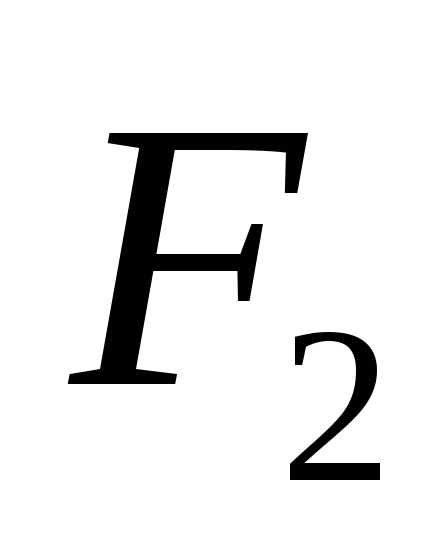 равна
равна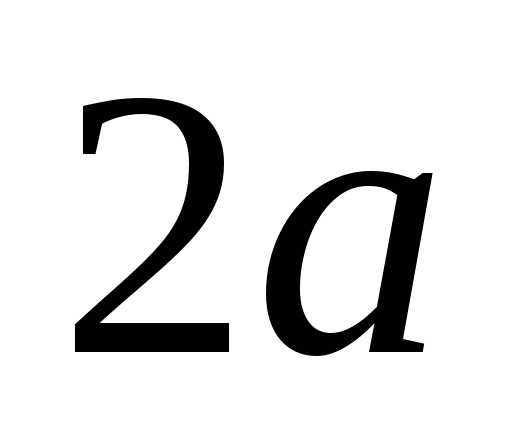 :
:
Пользуясь формулой для расстояния между двумя точками, получим , ; следовательно,
Для упрощения этого уравнения запишем его в форме
Возведя затем обе части уравнения в квадрат, получим
или, после очевидных упрощений:
Теперь опять возводим обе части уравнения в квадрат, после чего будем иметь
или после тождественных преобразований:
Так
как согласно условию в определении
эллипса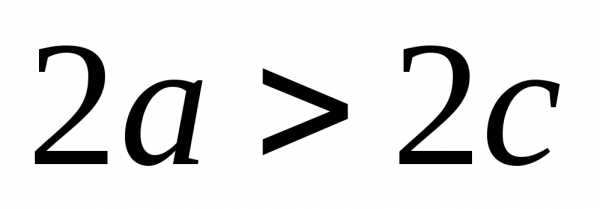 ,
то
,
то — число положительное. Введем обозначение
— число положительное. Введем обозначение
Тогда уравнение примет следующий вид:
или
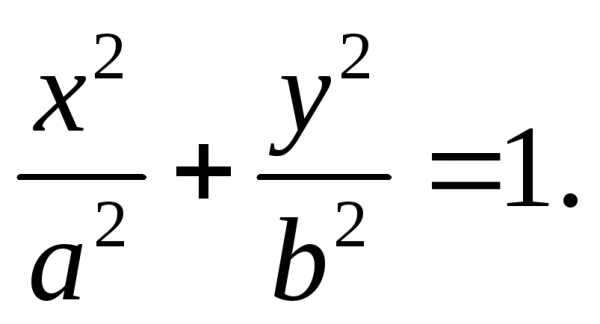
Можно
показать, что эллипс имеет форму,
изображенную на рис. 2.4. Точки пересечения
эллипса с осями называются вершинами эллипса. Из
симметрии эллипса следует, что, кроме
вершин 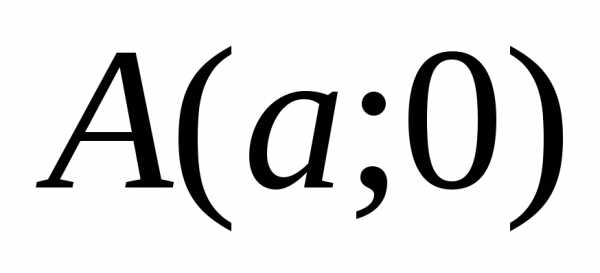 и
и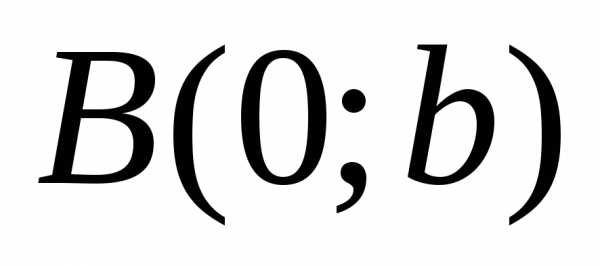 ,
эллипс имеет еще две вершины:и
,
эллипс имеет еще две вершины:и (см. рис. 2.4). Отрезки
(см. рис. 2.4). Отрезки и
и 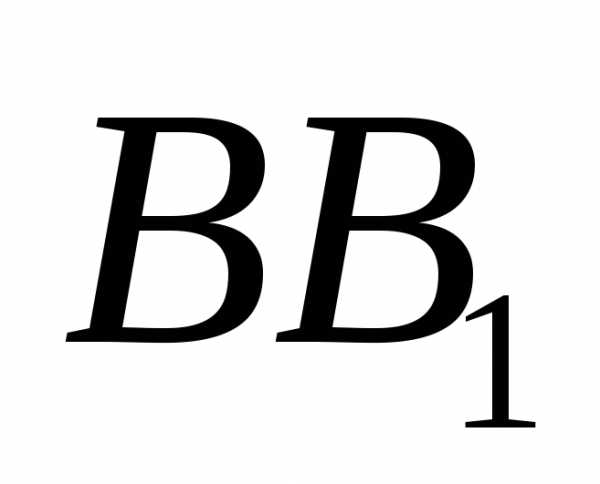 ,
соединяющие противоположные вершины
эллипса, а также их длины
,
соединяющие противоположные вершины
эллипса, а также их длины 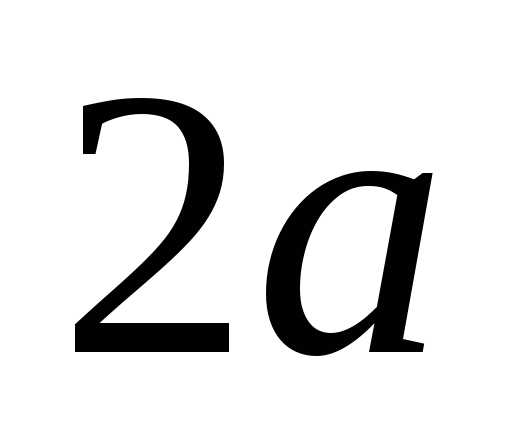 и
и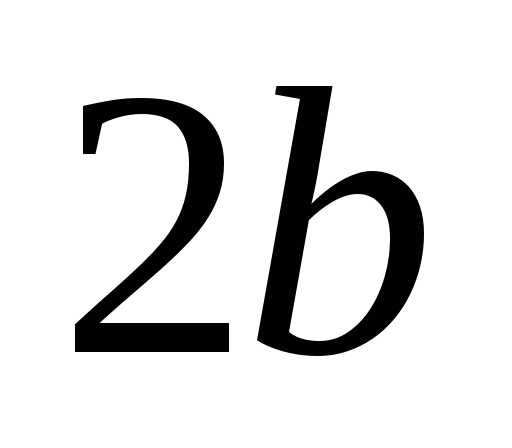 ,
называются соответственнобольшой и малой осями эллипса. Числа
,
называются соответственнобольшой и малой осями эллипса. Числа  и
и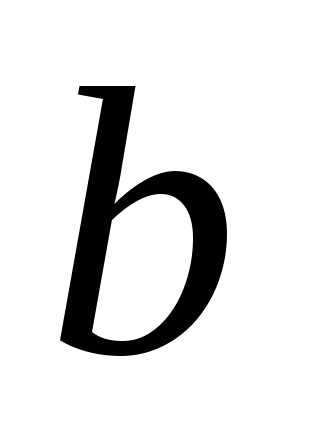 называются соответственнобольшой и малой
полуосями эллипса.
Отношение
называются соответственнобольшой и малой
полуосями эллипса.
Отношение  половины расстояния между фокусами к
большой полуоси эллипса называетсяэксцентриситетом эллипса и обозначается обычно буквой
половины расстояния между фокусами к
большой полуоси эллипса называетсяэксцентриситетом эллипса и обозначается обычно буквой  :
:
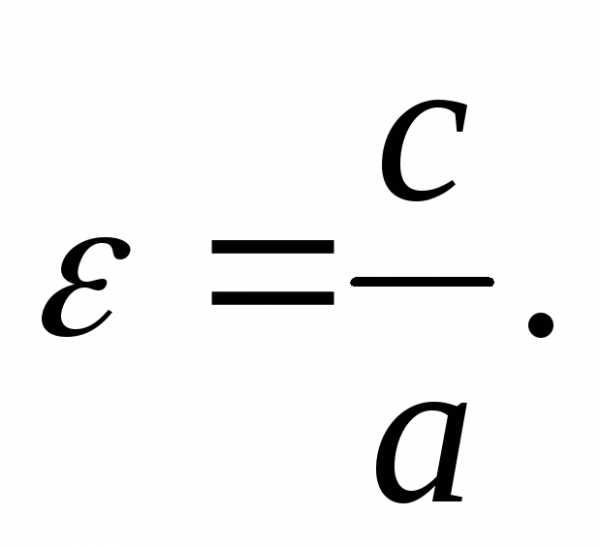
Так
как  ,
то эксцентриситет эллипса меньше
единицы:
,
то эксцентриситет эллипса меньше
единицы:  .
.
Пример. Найти каноническое уравнение эллипса,
зная его большую полуось 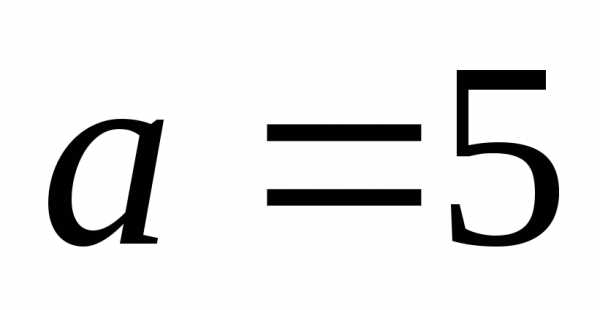 и эксцентриситет
и эксцентриситет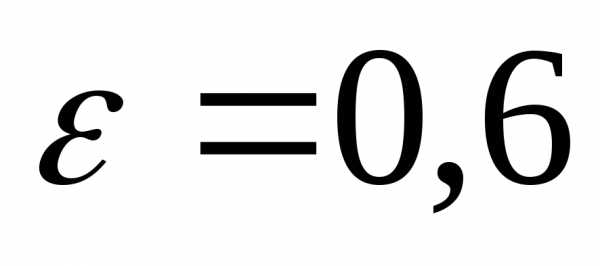 .
.
Решение.
По условию 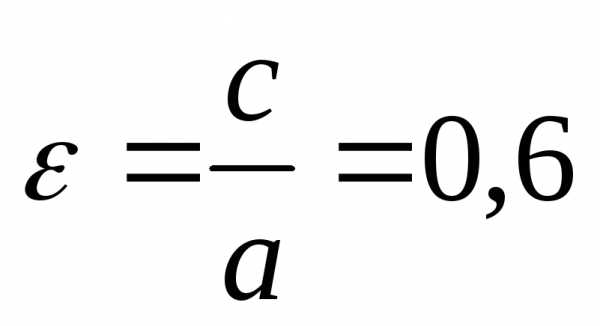 .
Следовательно, половина расстояния
между фокусами
.
Но тогда квадрат малой полуоси эллипса .
Таким образом, искомое каноническое
уравнение эллипса имеет следующий вид:
.
Следовательно, половина расстояния
между фокусами
.
Но тогда квадрат малой полуоси эллипса .
Таким образом, искомое каноническое
уравнение эллипса имеет следующий вид:
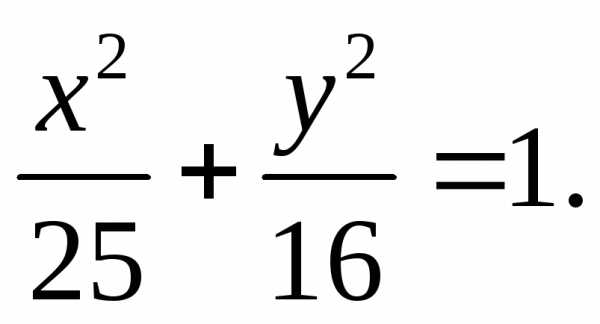
Пример. Составить каноническое уравнение
эллипса, проходящего через точку 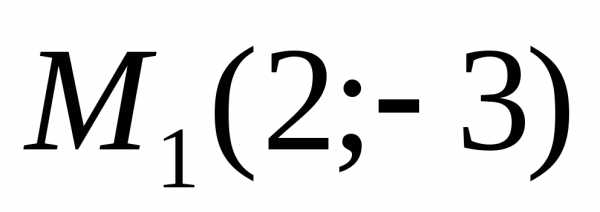 и имеющего большую полуось
и имеющего большую полуось 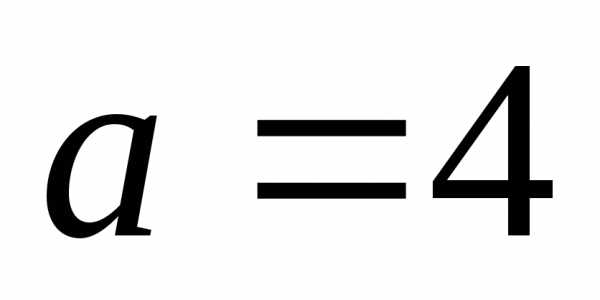 .
.
Решение.
Каноническое уравнение эллипса при 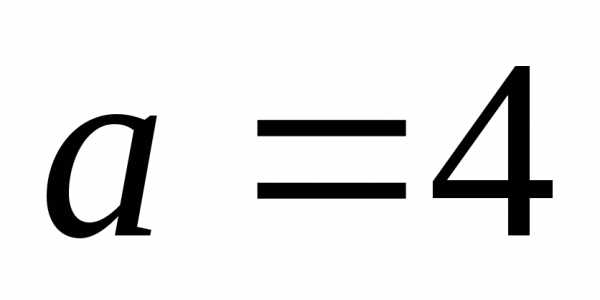 имеет следующий вид:
имеет следующий вид:
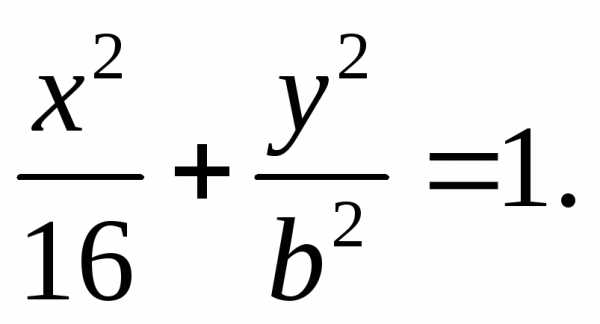
Этому
уравнению должны удовлетворять координаты
точки 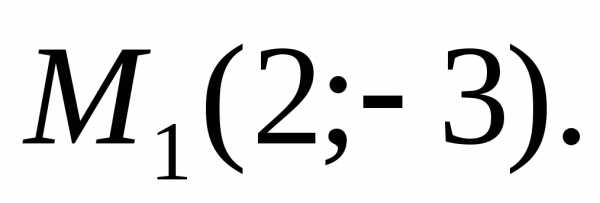
Следовательно,

Найдя
отсюда 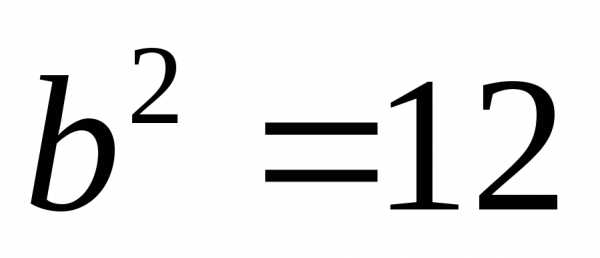 и подставив его в уравнение, получим
искомое каноническое уравнение эллипса:
и подставив его в уравнение, получим
искомое каноническое уравнение эллипса:
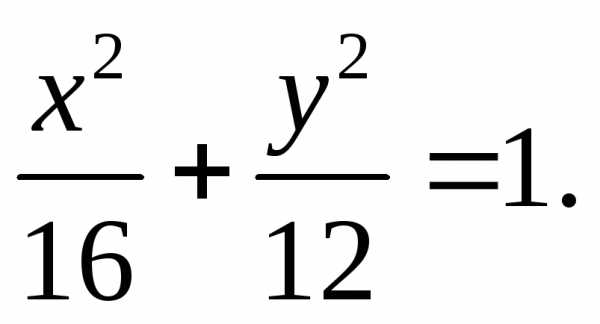
studfiles.net
Кривые второго порядка
В предыдущем разделе было установлено, что уравнению первой степени соответствует одна из плоских прямых. Очевидно, уравнениям более высоких степеней должны соответствовать кривые. Установить это соответствие для уравнения любой степени не представляется возможным из-за бесконечного числа уравнений и кривых. Проведенные исследования показали, что в разделе «Аналитическая геометрия» имеет смысл рассмотреть только уравнение второй степени, поскольку этому уравнению соответствуют только четыре кривые. Исследование уравнений более высоких степеней нецелесообразно. Вместо этого в разделе «Математический анализ» будет предложена схема исследования каждого конкретного уравнения с последующим построением графика функции, соответствующей данному уравнению.
Вначале выведем простейшие (канонические) уравнения каждой из четырех кривых. Затем рассмотрим общее уравнение второй степени и приведение его к каноническому виду.
Окружность
Определение. Окружностью называется множество точек, равноудаленных от некоторой точки, называемой центром окружности.
Построим
уравнение, отражающее это свойство
окружности. Для этого введем декартову
систему координат. Пустькоординаты
центра окружности, а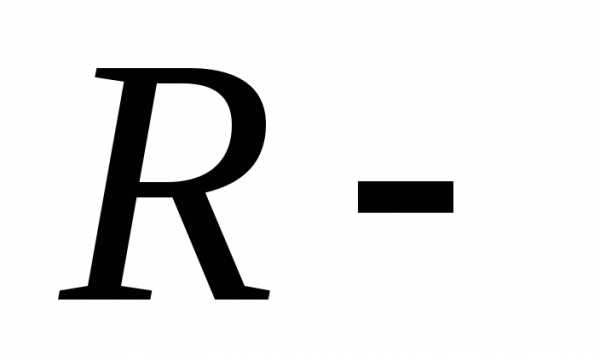 ее
радиус, то есть расстояние от точек
окружности до ее центра. Еслипроизвольная
точка окружности, имеет место формула
ее
радиус, то есть расстояние от точек
окружности до ее центра. Еслипроизвольная
точка окружности, имеет место формула
.
Рисунок 13.
После возведения в квадрат обеих частей уравнения получаем уравнение окружности
.
Это уравнение называется общим уравнением окружности, поскольку никаких ограничений на систему координат не накладывалось.
Раскрывая скобки
,
убеждаемся, что в
самом общем уравнении окружности не
присутствует произведение переменных 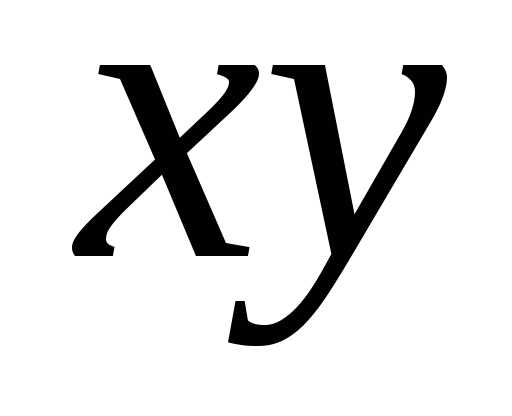 .
.
Можно привести это уравнение к наипростейшему виду, потребовав, чтобы начало координат совпадало с центром окружности. Тогда , и уравнение принимает вид
.
Это уравнение называется каноническим уравнением окружности.
Эллипс
Следующей кривой второго порядка является эллипс. Известно, что его уравнение, хотя и второй степени, но может быть сколь угодно сложным. Поэтому принято выводить его в специально выбранной декартовой системе координат.
Определение. Эллипсом называется множество точек, сумма расстояний от которых до двух заданных точек, называемых фокусами, постоянна.
Из определения
следует, что известны две точки – фокусы
эллипса  и сумма расстояний от точки эллипса до
этих точек
и сумма расстояний от точки эллипса до
этих точек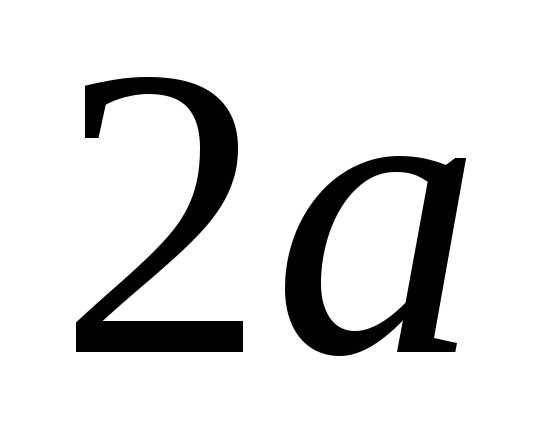 .
Систему координат выбираем следующим
образом. За ось
.
Систему координат выбираем следующим
образом. За ось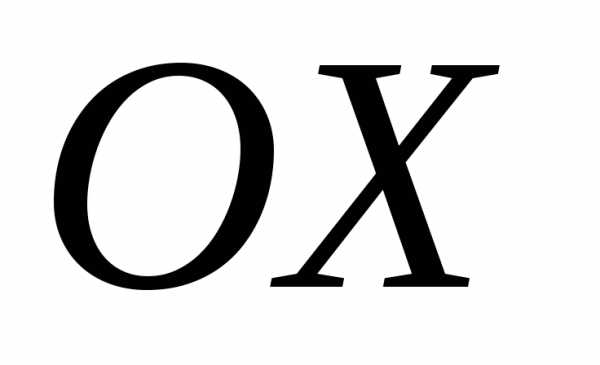 принимаем прямую, проходящую через
фокусы эллипса. Начало координат помещаем
в середину отрезка
принимаем прямую, проходящую через
фокусы эллипса. Начало координат помещаем
в середину отрезка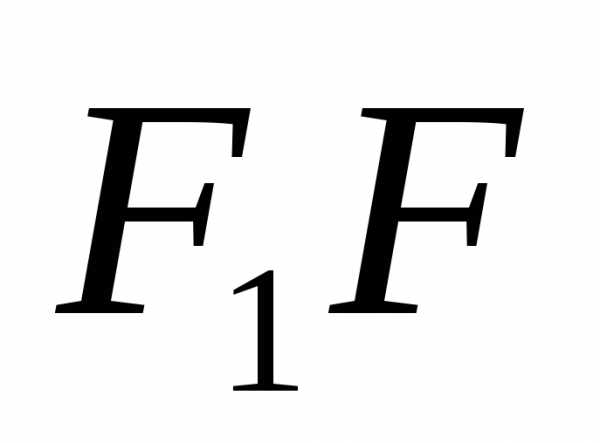 ,
ось
,
ось направляем перпендикулярно оси
направляем перпендикулярно оси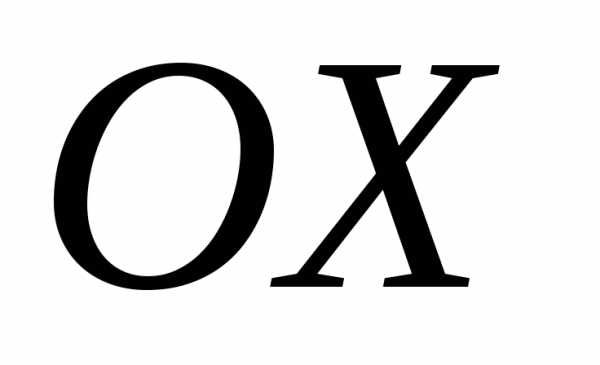 .
.
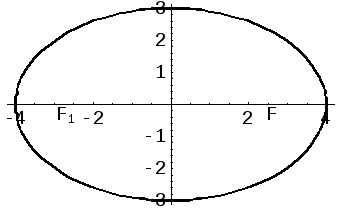
Рисунок 14.
Поскольку фокальные
точки эллипса известны, известно
расстояние между ними, обозначим его
.
Тогда известны координаты фокусови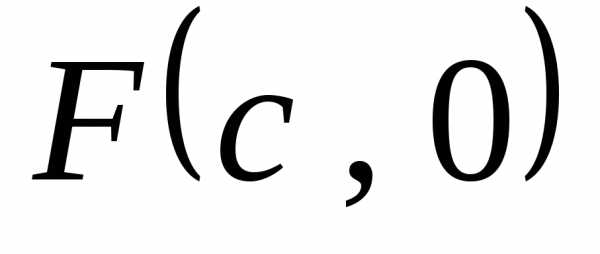 .
.
Зададим произвольную
точку эллипса 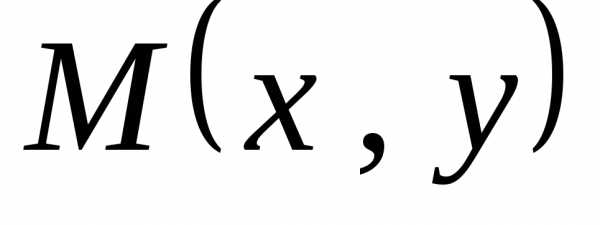 .
Из определения следует
.
Из определения следует
.
Следующей задачей является избавление от корней. Из полученного уравнения имеем
.
Возведем в квадрат обе части уравнения
и раскроем скобки во всех членах уравнения, кроме последнего
После сокращений имеем
.
Еще раз возводим в квадрат обе части уравнения
.
После сокращения подчеркнутых членов получаем
.
Из треугольника 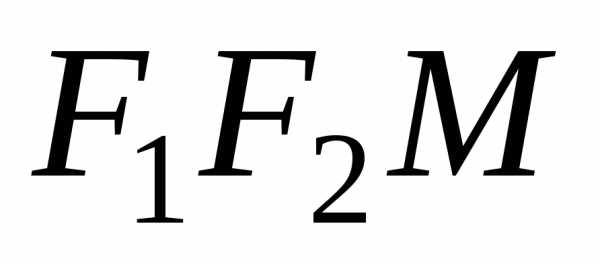 следует, что.
В самом деле
следует, что.
В самом деле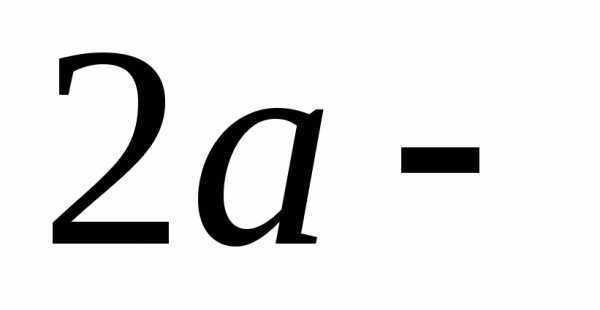 сумма
длин двух сторон треугольника, а
сумма
длин двух сторон треугольника, а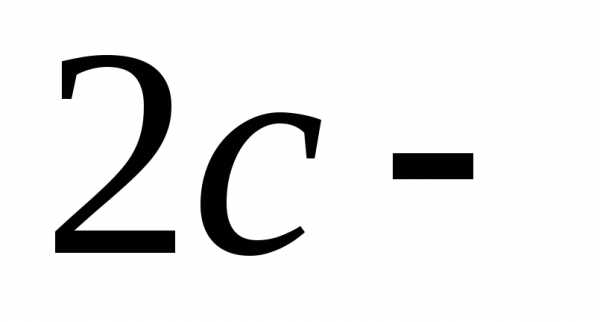 длина
третьей его стороны. Обозначим,
тогда полученное выше уравнение принимает
вид
длина
третьей его стороны. Обозначим,
тогда полученное выше уравнение принимает
вид
 .
.
Это уравнение называется каноническим уравнением эллипса.
Поскольку обе
переменные во второй степени, эллипс
симметричен относительно обеих координат
и расположен между точками 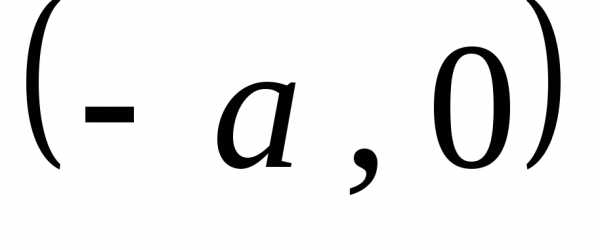 ,
,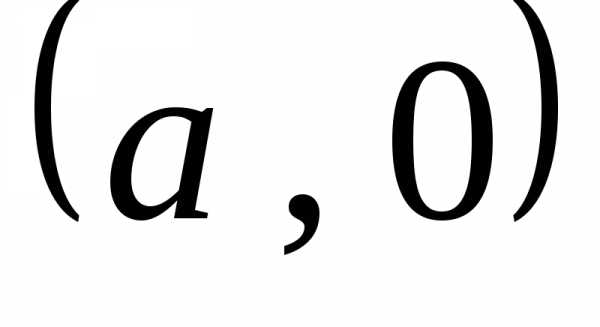 и
и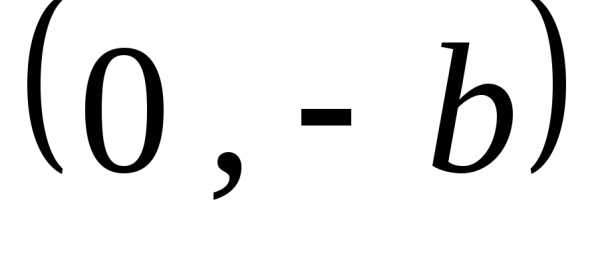 ,
,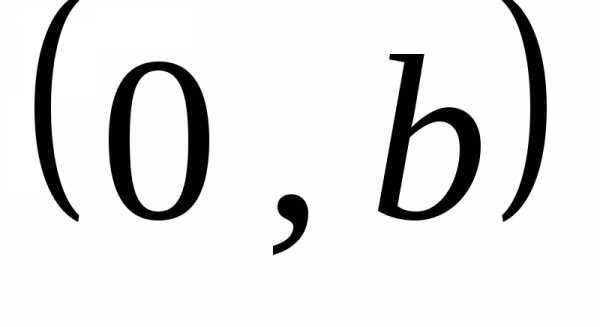 .
Это легко установить, положив в уравнении
вначале
.
Это легко установить, положив в уравнении
вначале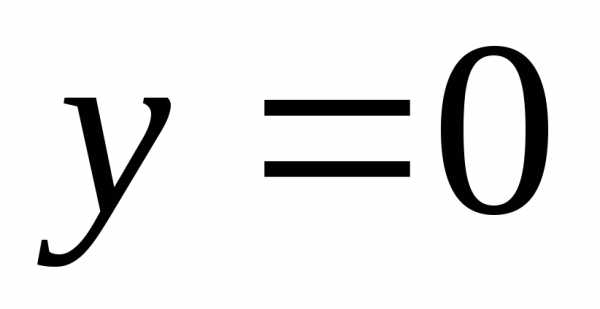 ,
затем
,
затем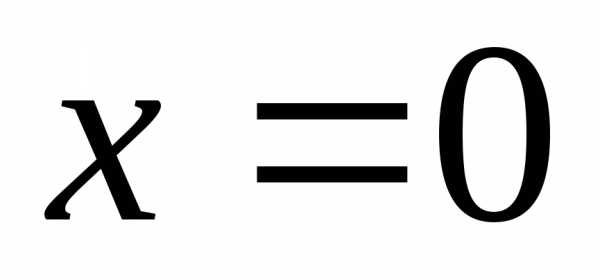 ,
то есть определив точки пересечения
эллипса с осями координат.
,
то есть определив точки пересечения
эллипса с осями координат.
Часто 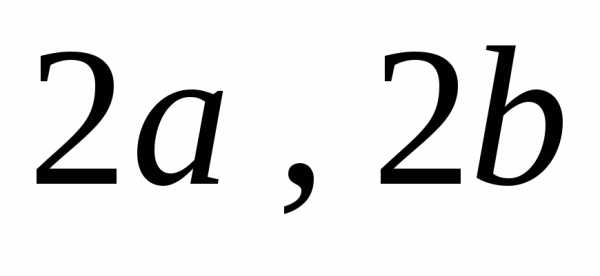 называют горизонтальной и вертикальной
осями эллипса, а
называют горизонтальной и вертикальной
осями эллипса, а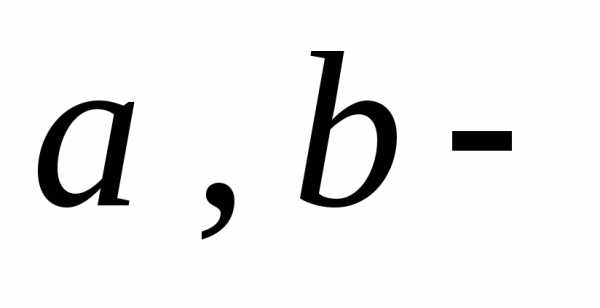 его
полуосями.
его
полуосями.
Кроме трех
параметров, определяющих эллипс, вводят
четвертый — эксцентриситет эллипса,
определяемый формулой 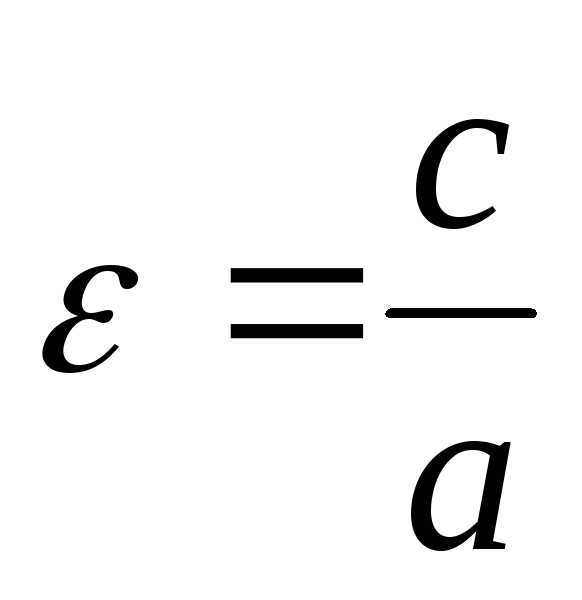 ,
при этом.
При
,
при этом.
При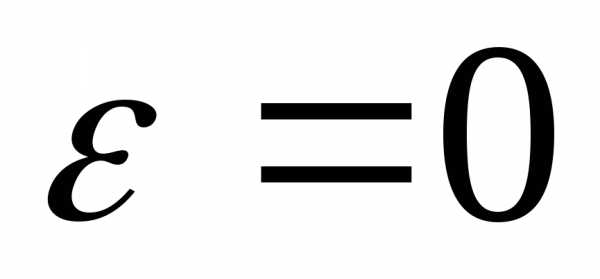 имеем
имеем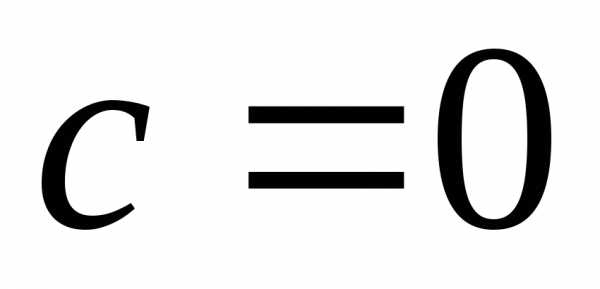 ,
или
,
или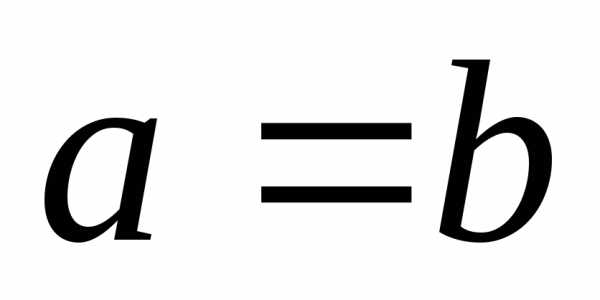 ,
и эллипс превращается в окружность. С
ростом
,
и эллипс превращается в окружность. С
ростом эллипс становится все более «приплюснутым»,
то есть длина его вертикальной оси
уменьшается по сравнению с горизонтальной.
При
эллипс становится все более «приплюснутым»,
то есть длина его вертикальной оси
уменьшается по сравнению с горизонтальной.
При имеем,
и эллипс превращается в разрез.
имеем,
и эллипс превращается в разрез.
Гипербола, асимптоты гиперболы
Определение. Гиперболой называется множество точек, разность между расстояниями от которых до двух заданных точек, называемых фокусами (фокальными точками) гиперболы, постоянна.
Поскольку определения
эллипса и гиперболы очень похожи, систему
координат выбираем так же. Очевидно,
координаты фокусов гиперболы те же.
Разность между расстояниями пусть также 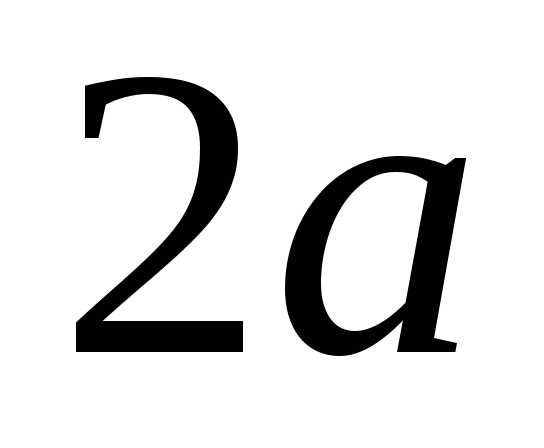 .
Тогда из определения следует формула
.
Тогда из определения следует формула
.
Проделав аналогичные преобразования, получаем
.
Поскольку разность
между длинами двух сторон треугольника
меньше длины его третьей стороны  .
Обозначимили,
в результате получаем каноническое
уравнение гиперболы
.
Обозначимили,
в результате получаем каноническое
уравнение гиперболы
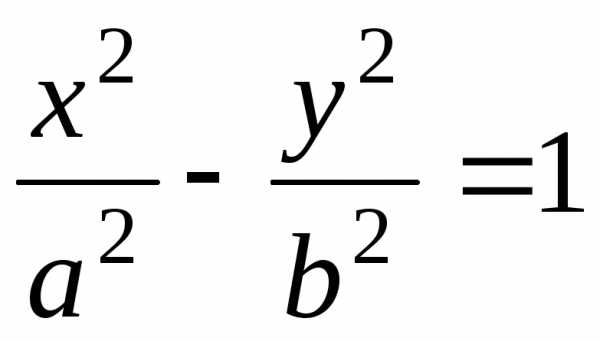 .
.
Определим из
уравнения  .
Область определение кривой
.
Область определение кривой или.
График этой гиперболы симметричен
относительно обеих осей координат, не
пересекает оси
или.
График этой гиперболы симметричен
относительно обеих осей координат, не
пересекает оси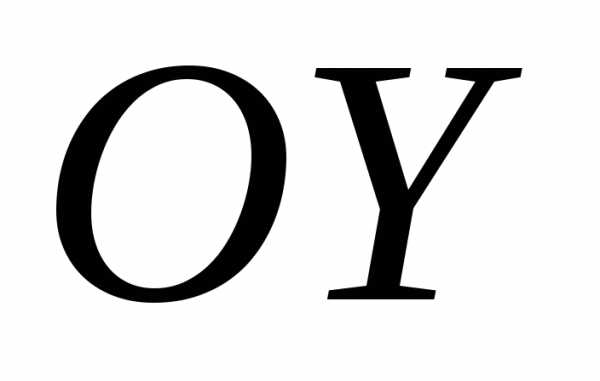 и имеет две ветви. Вершины гиперболы
расположены в точках
и имеет две ветви. Вершины гиперболы
расположены в точках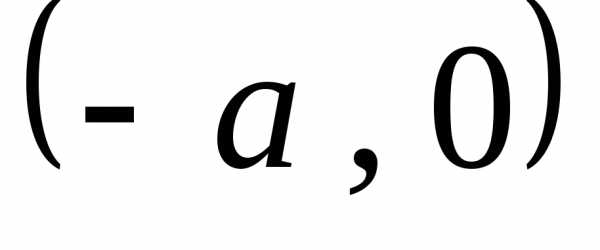 и
и .
.
Эксцентриситет
гиперболы 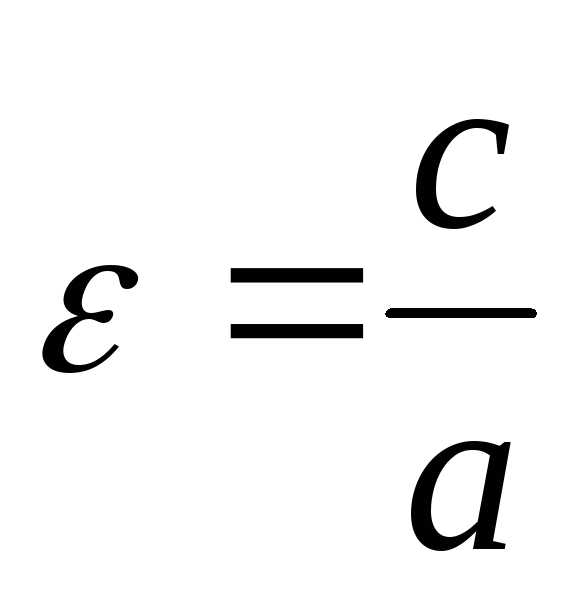 ясно что
ясно что .
.
Известно, что
гипербола является спрямляемой кривой
и имеет асимптоты, то есть пару прямых,
с которыми бесконечно сближается кривая
при
,
не пересекаясь с этими прямыми. Покажем,
что уравнения асимптот гиперболы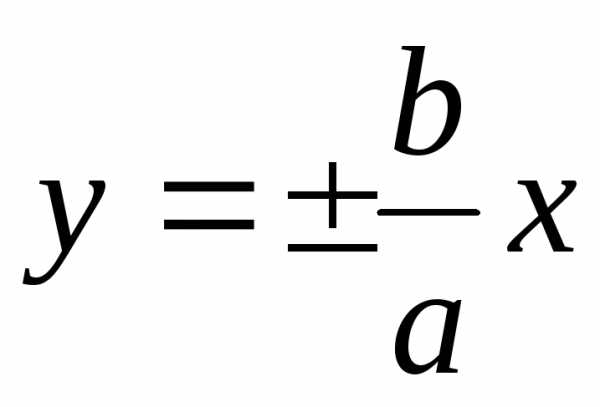 .
Рассмотрим разность,
она определяет расстояние между точками
асимптот и кривой при заданном значении
.
Рассмотрим разность,
она определяет расстояние между точками
асимптот и кривой при заданном значении .
Следует показать, что если, то
.
Следует показать, что если, то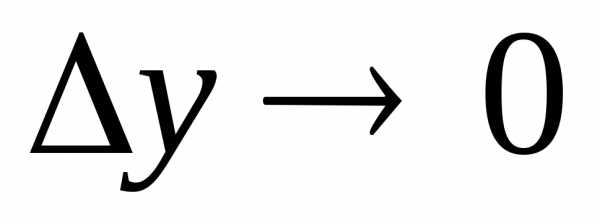 .
.
.
Числитель полученной дроби постоянен, а знаменатель стремится к бесконечности, следовательно, дробь стремится к нулю. Итак, расстояние между кривой и парой прямых, задаваемых вышеприведенными уравнениями, стремится к нулю при . По определению это – асимптоты.
Замечание.
Полученное уравнение соответствует
гиперболе, пересекающей ось 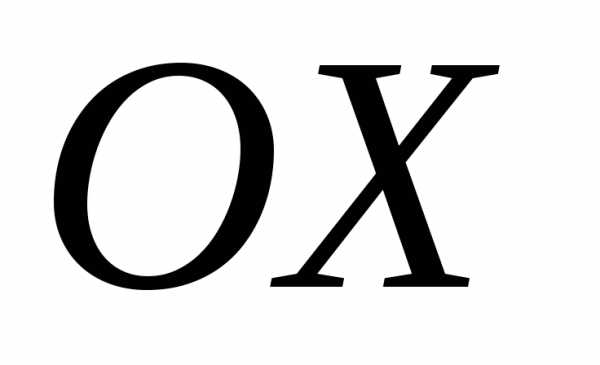 ,
ее ветви идут влево и вправо
,
ее ветви идут влево и вправо

Рисунок 15.
уравнение
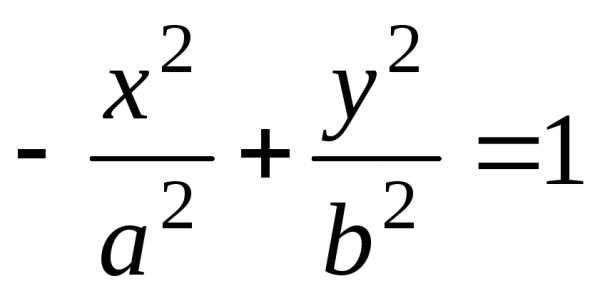 .
.
является уравнением
гиперболы, ветви которой идут вверх и
вниз, вершины ее находятся на оси 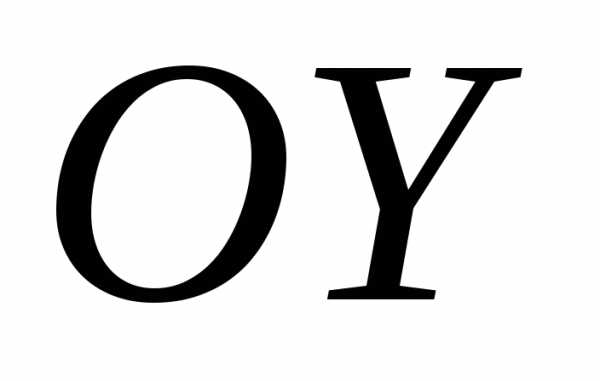
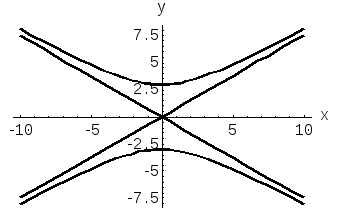
Рисунок 16.
Парабола
Определение. Параболой называется множество точек, равноудаленных от заданной точки, называемой фокусом, и заданной прямой – директрисой параболы.
Установлено, что
наипростейшее уравнение последней из
четырех кривых второго порядка получается
при следующем выборе системы координат.
За ось 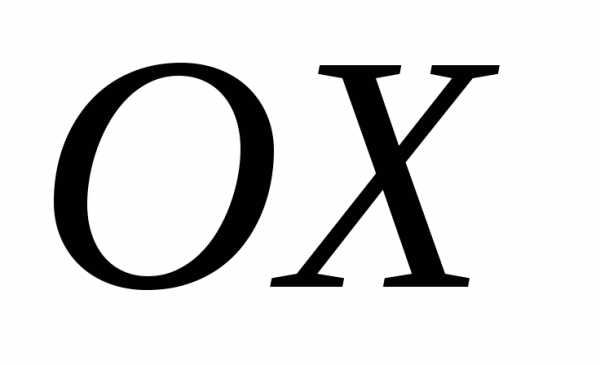 принимается прямая, проходящая через
фокус параболы перпендикулярно
директрисе. Начало координат помещается
в середину отрезка между фокусом и
основанием перпендикуляра, опущенного
на директрису, ось
принимается прямая, проходящая через
фокус параболы перпендикулярно
директрисе. Начало координат помещается
в середину отрезка между фокусом и
основанием перпендикуляра, опущенного
на директрису, ось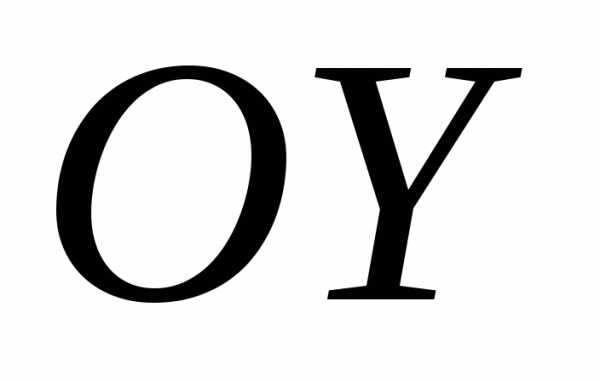 направлена параллельно директрисе.
Поскольку фокус и директриса заданы,
известно кратчайшее расстояние между
ними, обозначим его
направлена параллельно директрисе.
Поскольку фокус и директриса заданы,
известно кратчайшее расстояние между
ними, обозначим его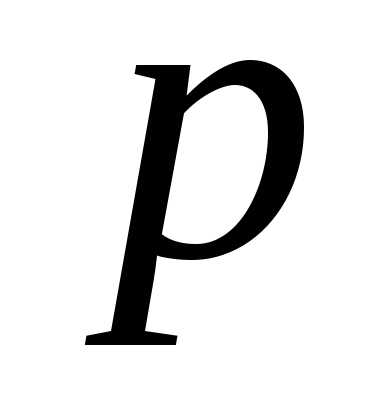 ,
тогда координаты фокуса
,
тогда координаты фокуса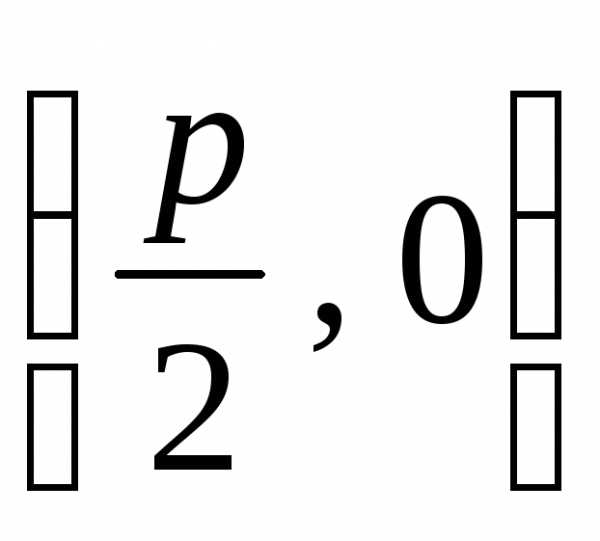 ,
любой точки директрисы
,
любой точки директрисы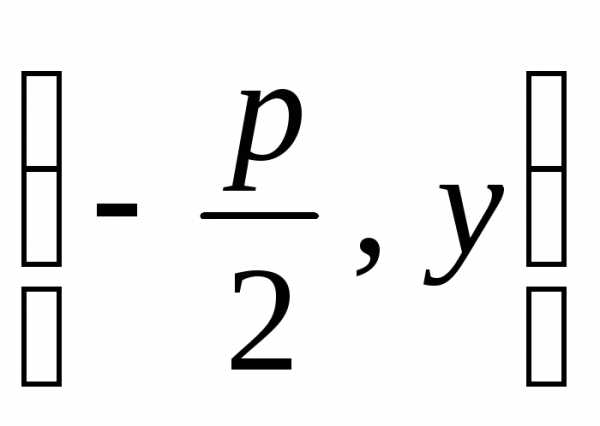 .
Расстояние от произвольной точки
параболы
.
Расстояние от произвольной точки
параболы до директрисы, очевидно,
до директрисы, очевидно,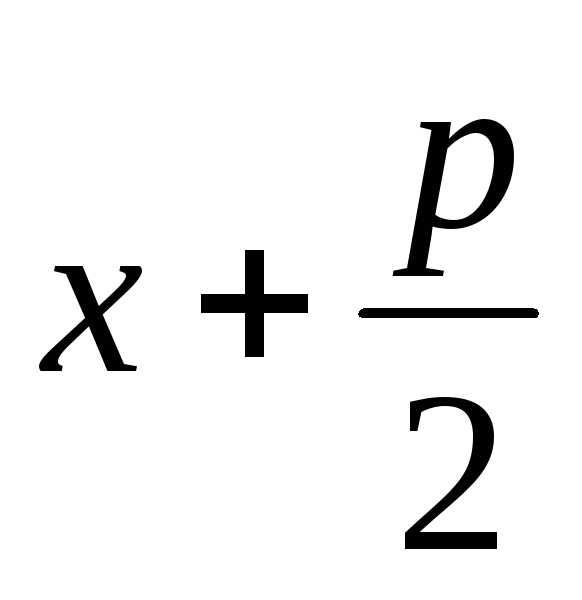 ,
расстояние до фокуса
,
расстояние до фокуса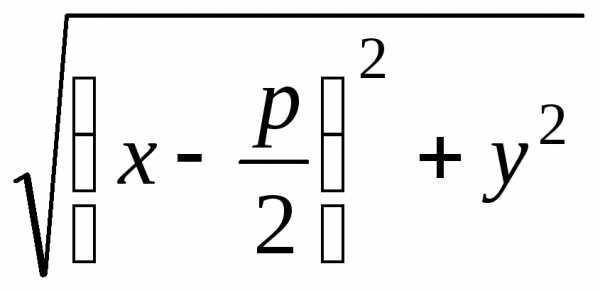 .
Приравнивая квадраты этих величин,
имеем.
После раскрытия скобок получаем
каноническое уравнение рассматриваемой
параболы
.
Приравнивая квадраты этих величин,
имеем.
После раскрытия скобок получаем
каноническое уравнение рассматриваемой
параболы
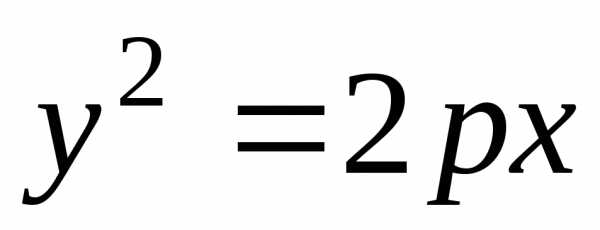 .
.
Она симметрична
относительно оси 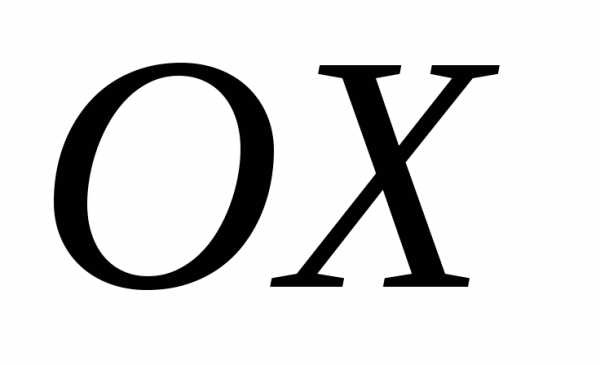 ,
ее вершина в начале координат. Ее график
,
ее вершина в начале координат. Ее график
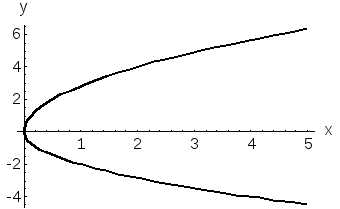
Рисунок 17.
Уравнение  соответствует параболе
соответствует параболе
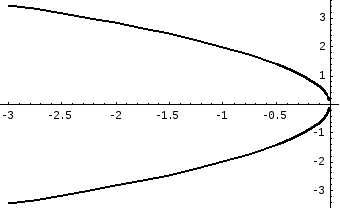
Рисунок 18.
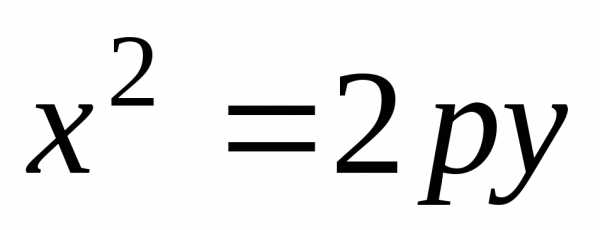 соответствует
параболе, идущей вверх симметрично оси
соответствует
параболе, идущей вверх симметрично оси 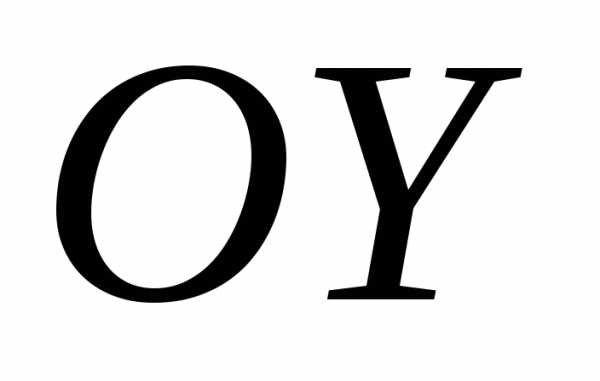 ,
парабола
,
парабола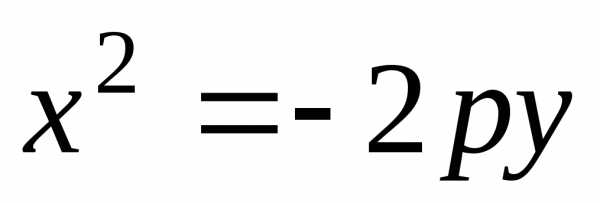 направлена вниз
направлена вниз

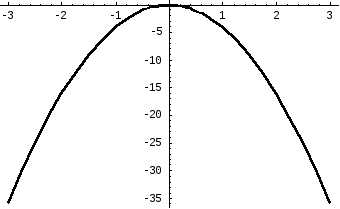
Рисунок 19.
Примеры.
1. Найти точки
пересечения окружности
с прямой .
Решаем систему уравнений
.
Решаем систему уравнений
 .
.
.
Общие точки прямой
и окружности 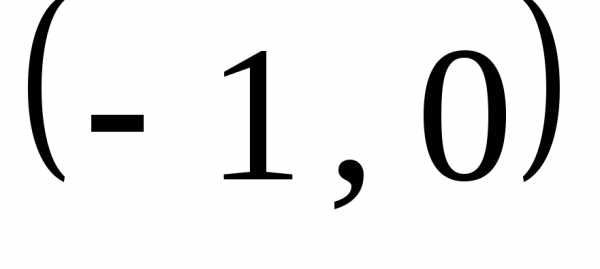 и
и .
.
2. Найти общие точки
окружности
и эллипса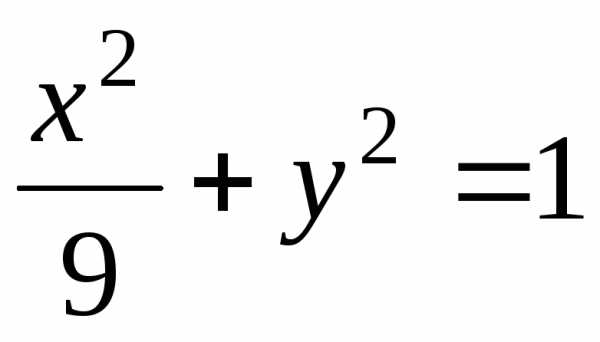 .
.
Решаем систему уравнений
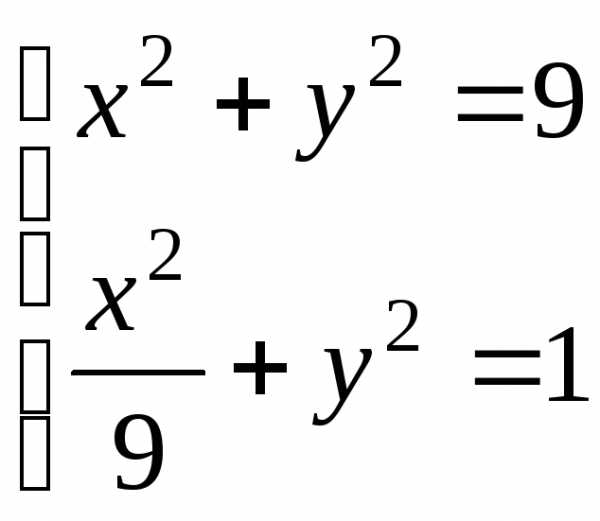 .
.
Вычитаем из первого
уравнения второе 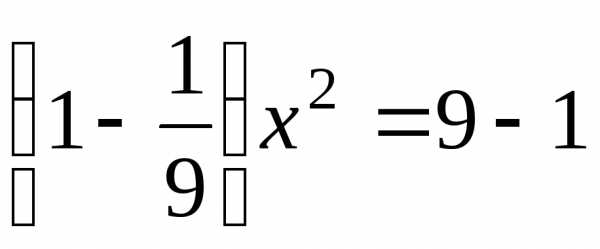 ,
откуда следует
,
откуда следует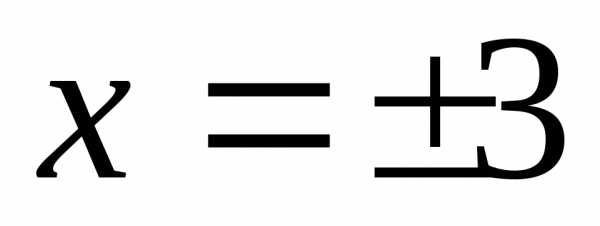 ,
тогда
,
тогда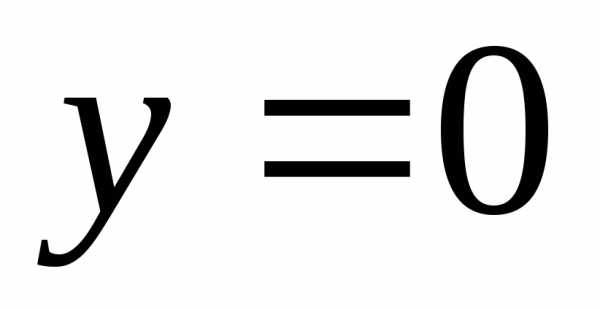 .
Имеем две общие точки
.
Имеем две общие точки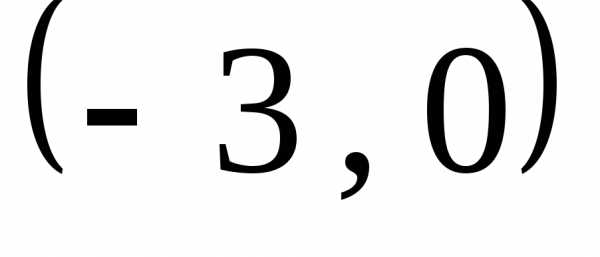 и
и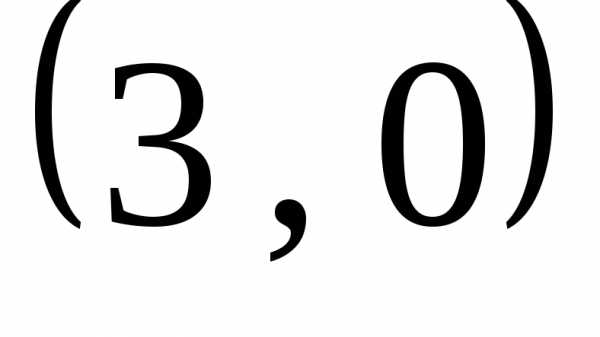 .
.
3. При каком 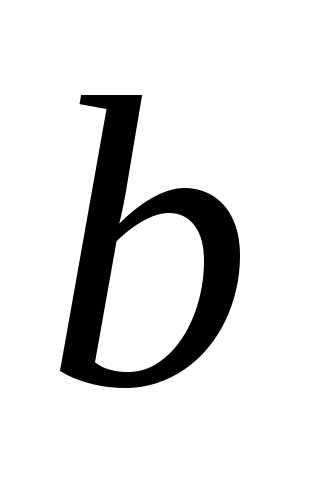 прямая
прямая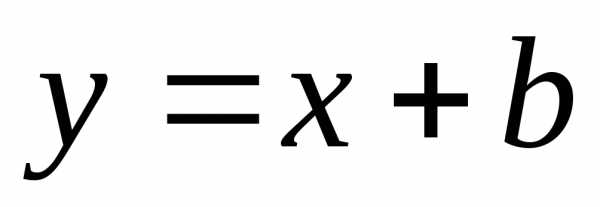 касается параболы
касается параболы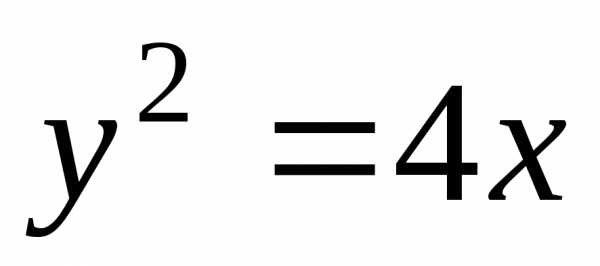 ?
?
Решение.
.
Если прямая касается параболы, имеется
лишь одна их общая точка, следовательно,
дискриминант квадратного уравнения
должен быть равен нулю. Итак,откуда следует,
и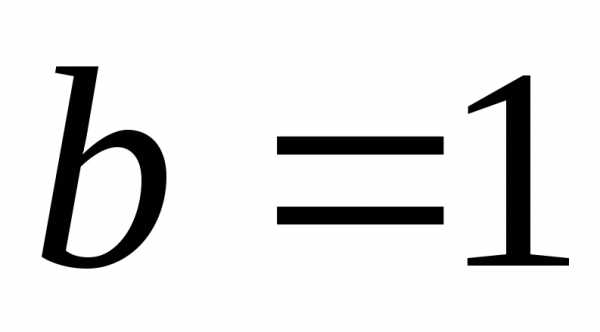 .
.
Общее уравнение второй степени,
приведение его к каноническому виду
Самое полное уравнение второй степени имеет вид
.
В зависимости от
значений коэффициентов  оно соответствует любой из четырех
кривых второго порядка (и не только!).
Однако построение графика и даже
определение вида кривой по этому
уравнению затруднительно, для этой цели
лучше всего привести его к каноническому
виду.
оно соответствует любой из четырех
кривых второго порядка (и не только!).
Однако построение графика и даже
определение вида кривой по этому
уравнению затруднительно, для этой цели
лучше всего привести его к каноническому
виду.
Как было сказано выше, систему координат нужно задавать специальным образом, причем для каждой кривой свою. Это не удобно. Проще всего от одной декартовой системы координат перейти к другой, используя самые общие формулы перехода, затем нужным образом подобрать значения параметров этого перехода (координаты нового центра и ориентацию новых координат на плоскости).
Замена переменных
Выведем общую формулу перехода от одной декартовой системы координат к другой.
Введем две системы
координат – старую с началом в точке O
и векторами ортонормированного базиса 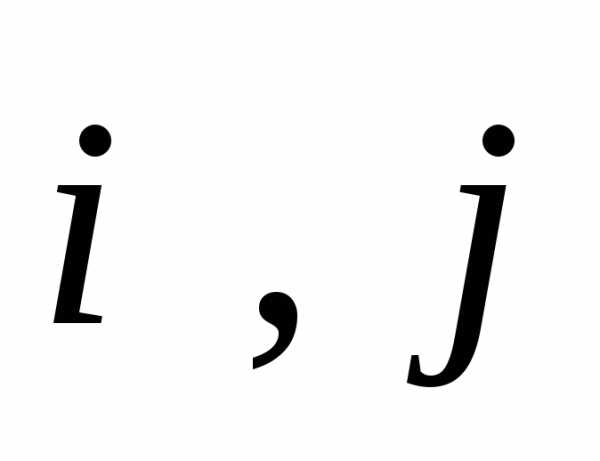 ,
направленными вдоль оси
,
направленными вдоль оси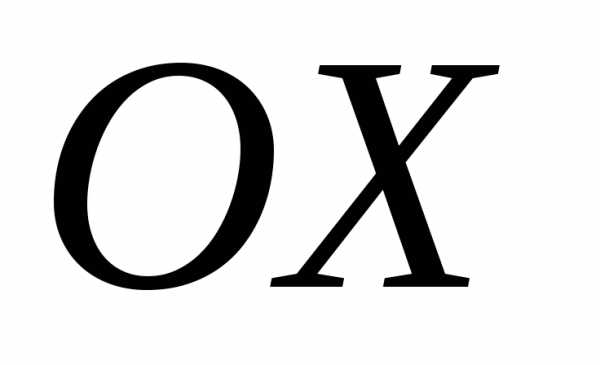 и
и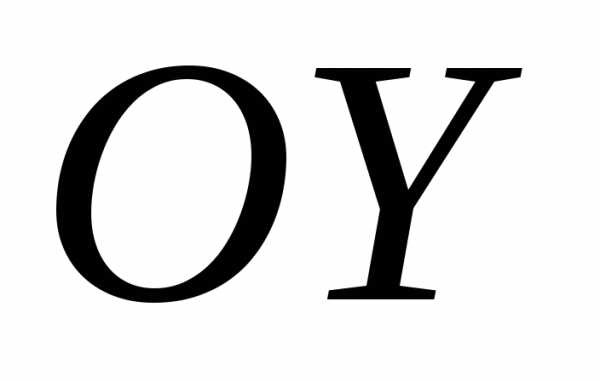 соответственно, и новую с началом в
точке
соответственно, и новую с началом в
точке и векторами ортонормированного базиса
и векторами ортонормированного базиса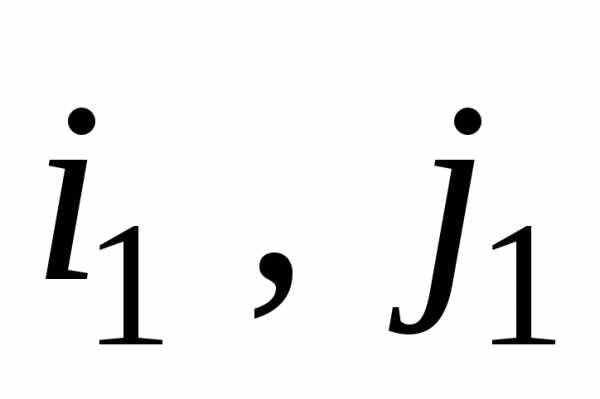 ,
направленными вдоль осей
,
направленными вдоль осей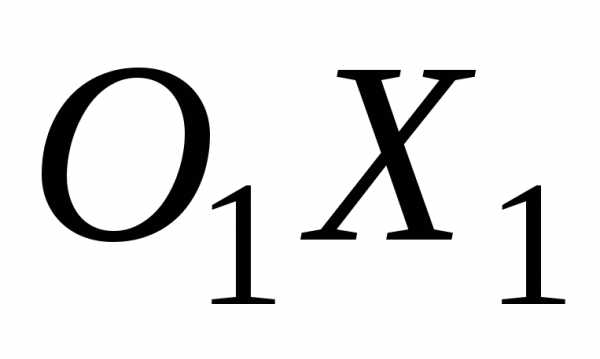 и
и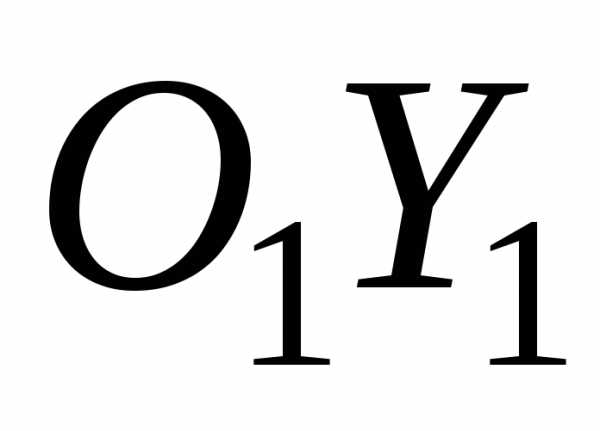 .
.
Пусть угол между
осями 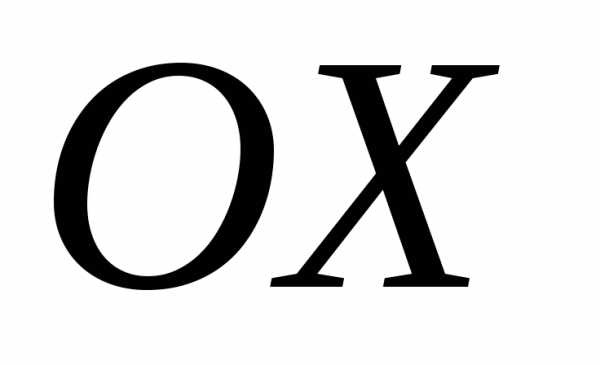 и
и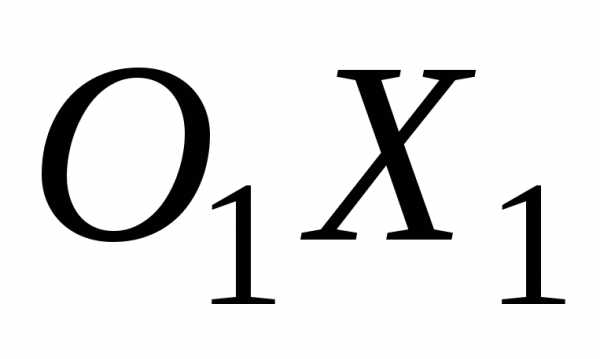 равен
равен ,
координаты начала координат
,
координаты начала координат в старой системе координат
в старой системе координат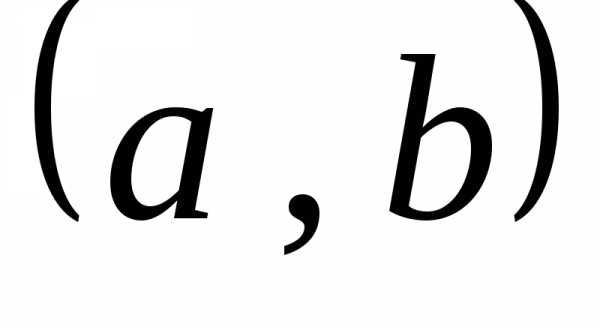 .
Возьмем произвольную точку плоскости
.
Возьмем произвольную точку плоскости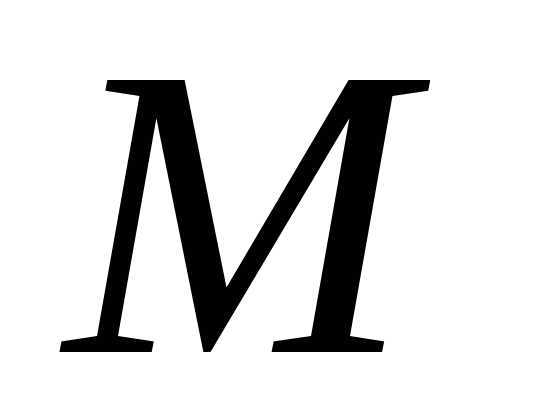 с
координатами в старой системе
с
координатами в старой системе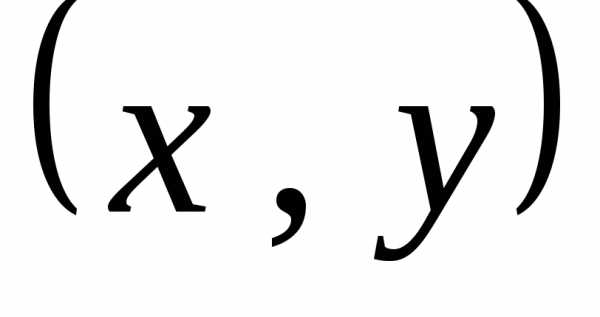 и новой
и новой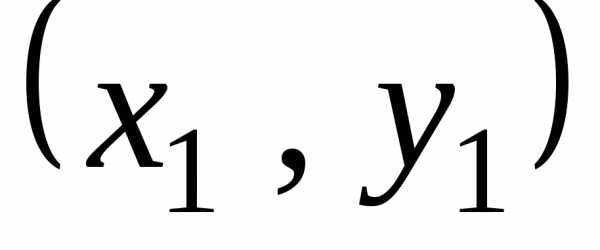 .
.
В дальнейшем нам
понадобятся углы между векторами двух
базисов и скалярные произведения
базисных векторов. Очевидно, угол между 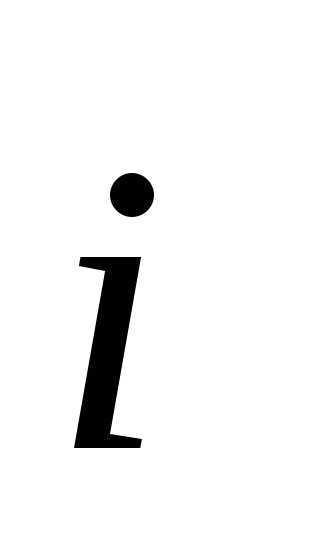 и
и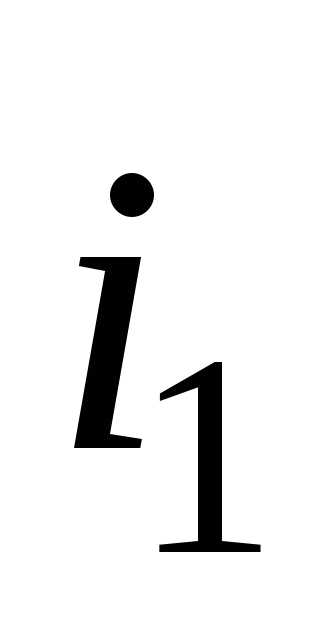 ,
а также
,
а также и
и равен
равен ,
тогда угол между
,
тогда угол между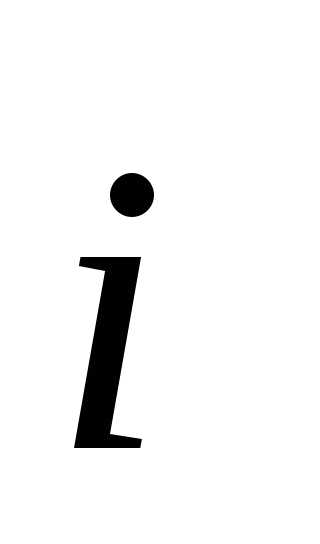 и
и равен
равен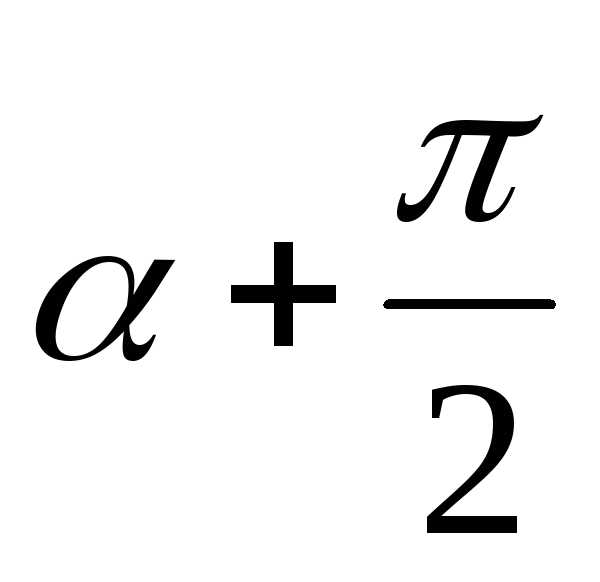 ,
угол между
,
угол между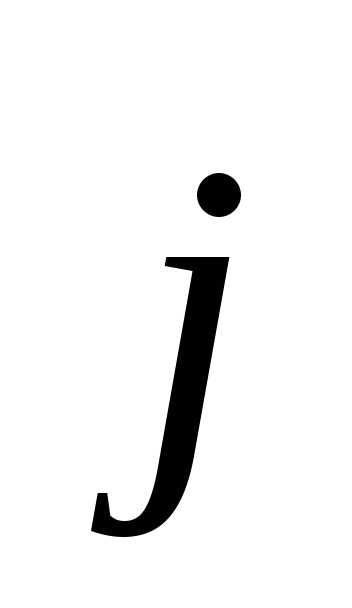 и
и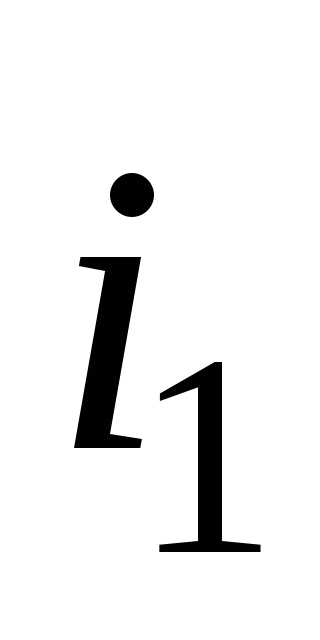 равен
равен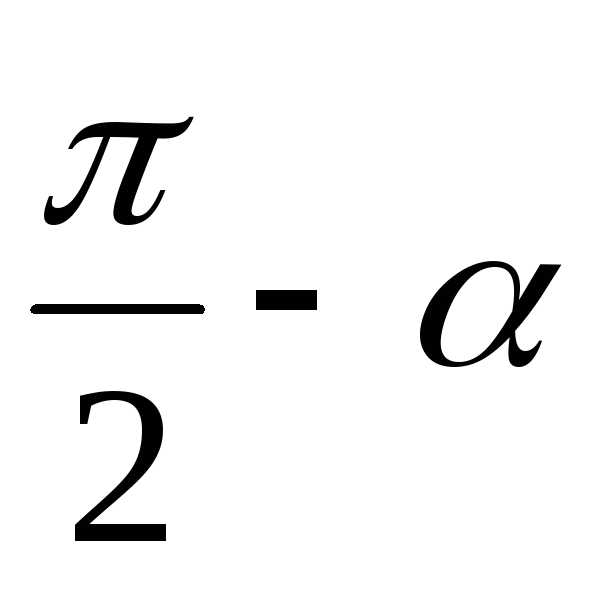 .
.
Подсчитаем скалярные произведения этих векторов. Ясно, что скалярное произведение каждого базисного вектора на самого себя равно 1, скалярное произведение векторов одного базиса равно 0. Остается подсчитать
, ,
, .
Выпишем формулы
для радиусов-векторов точек 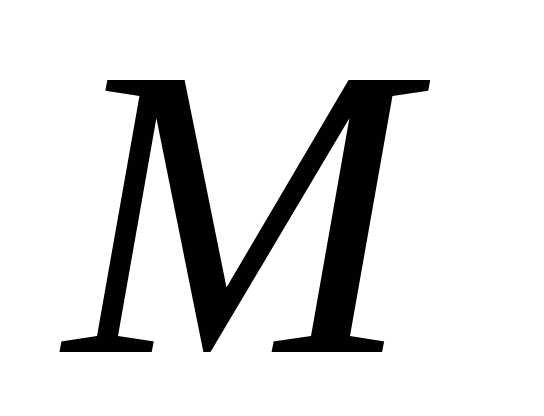 и
и в старой системе координат,.
В то же время в новой системе координат.
Поскольку,
имеем
в старой системе координат,.
В то же время в новой системе координат.
Поскольку,
имеем
.
Умножаем это
векторное равенство скалярно сначала
на 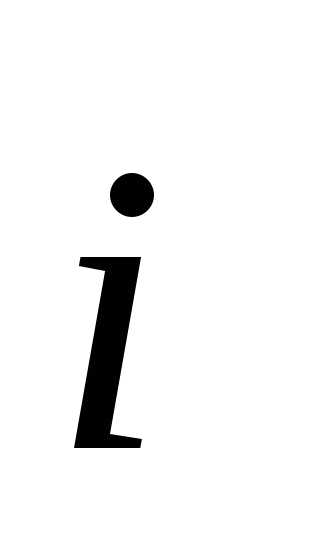 затем на
затем на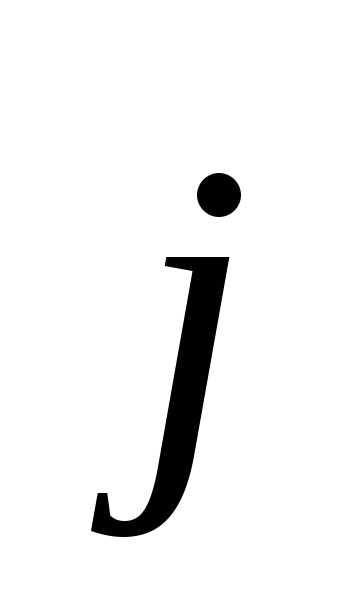 ,
тогда
,
тогда
,
.
Используя вышеприведенные формулы для скалярных произведений, получаем связь между старыми и новыми координатами
.
Если умножить
векторное равенство скалярно сначала
на  затем на
затем на
,
получаем формулы связи между новыми и старыми координатами
или
.
Интересны частные случаи этих формул.
Параллельный перенос системы координат
(перенесение начала координат)
В этом случае 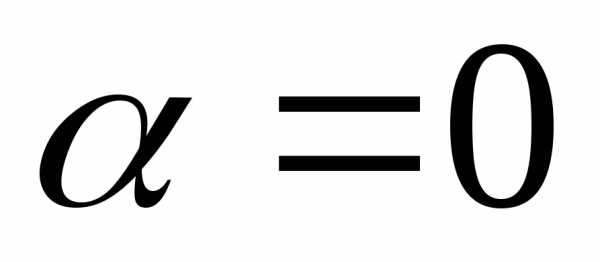 ,
тогда формулы параллельного переноса
координат имеют вид
,
тогда формулы параллельного переноса
координат имеют вид
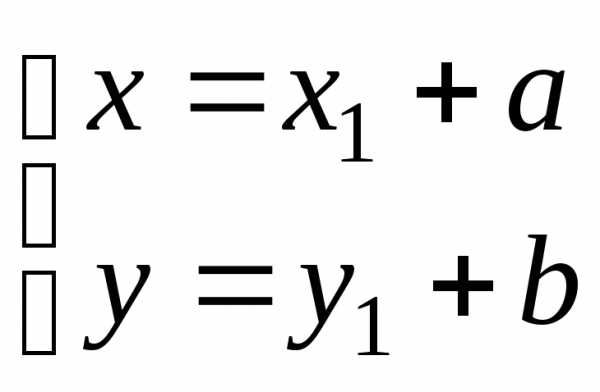 и
и 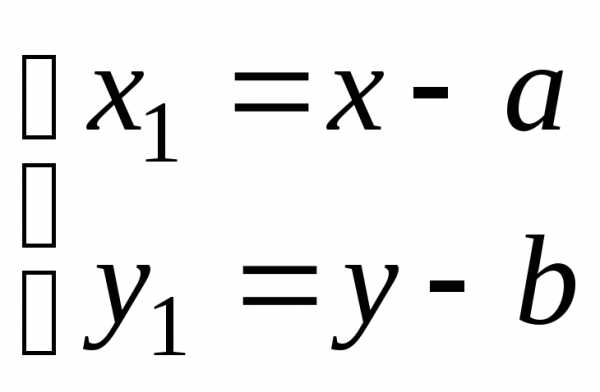 .
.
Поворот системы координат при общем начале
Ясно что , тогда
и .
Приведение общего уравнения к каноническому виду
Рассмотрим два случая преобразований.
I. В общем уравнении отсутствует произведение переменных, то есть
.
Это наиболее простой случай. Он оправдан еще тем, что общее уравнение одной из кривых – окружности – не содержит этого слагаемого. В этом случае достаточно параллельного переноса координат. Покажем, как это делается на примерах.
Пример 1. Изобразить кривую
Решение.
.
Это окружность с центром в точке 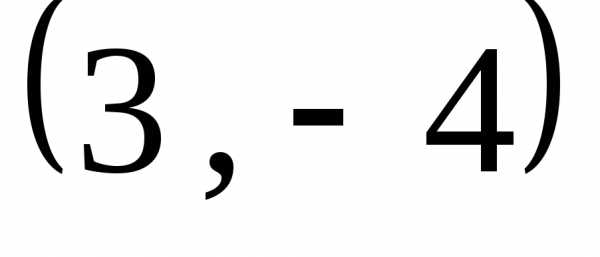 и радиусом 5.
и радиусом 5.
Пример 2. Установить вид кривой .
Решение
.
Введем новые
координаты
.
Это соответствует параллельному переносу
системы координат. Координаты нового
начала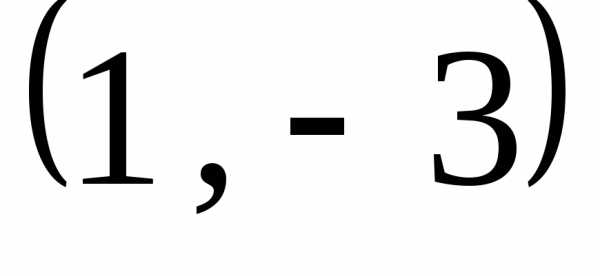 .
Уравнение кривой имеет вид
.
Уравнение кривой имеет вид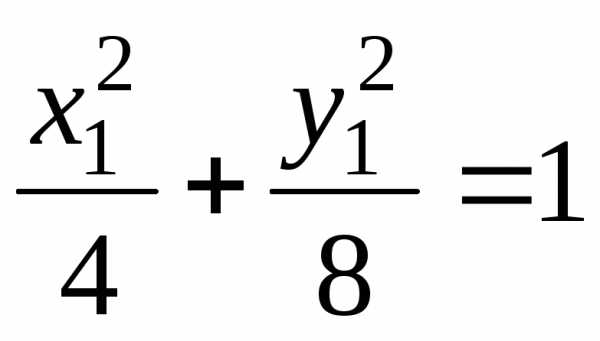 .
Это эллипс.
.
Это эллипс.
II.
Рассматривается общее уравнение
кривой. Возможны два подхода к решению
задачи приведения уравнения к каноническому
виду. В первом используется общая замена,
параметры замены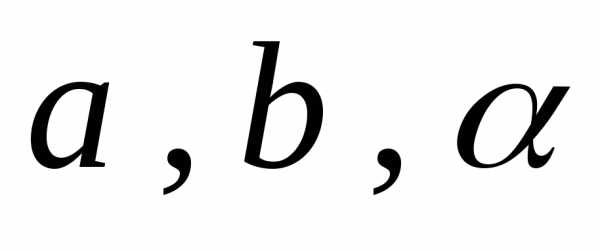 подбираются так, чтобы уравнение стало
наипростейшим.
подбираются так, чтобы уравнение стало
наипростейшим.
Чаще применяется
второй, поэтапный подход. Используя
формулы поворота системы координат,
добиваемся отсутствия в новом уравнении
произведения неизвестных 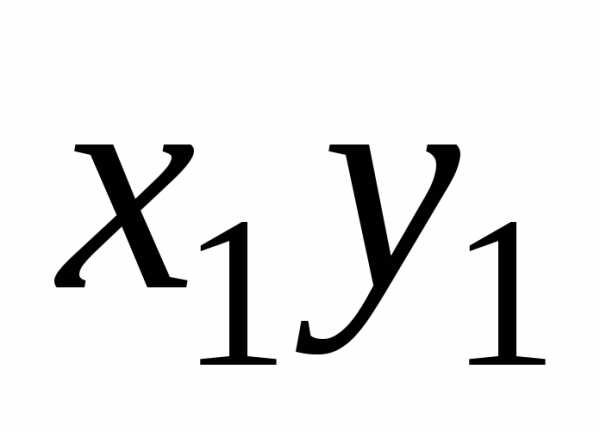 ,
то есть сводим решение к первой задаче.
,
то есть сводим решение к первой задаче.
Пример 3. Преобразовать к каноническому виду и построить кривую
.
Подставляем в уравнение формулы
Откуда следует
После приведения подобных членов имеем
Используя не
заданный пока параметр  ,
потребуем равенства нулю коэффициента
при
,
потребуем равенства нулю коэффициента
при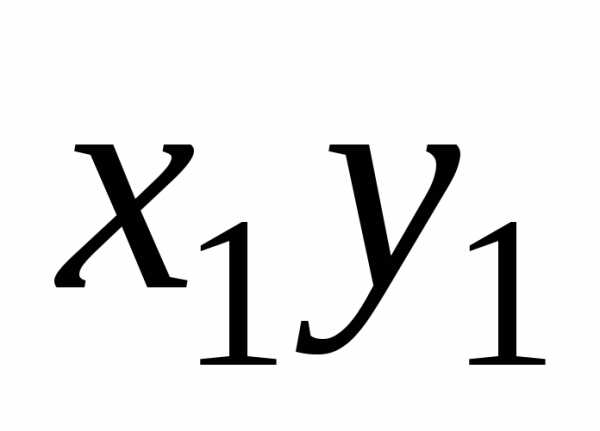 .
Очевидно,или
.
Одним из решений этого уравнения является
.
Очевидно,или
.
Одним из решений этого уравнения является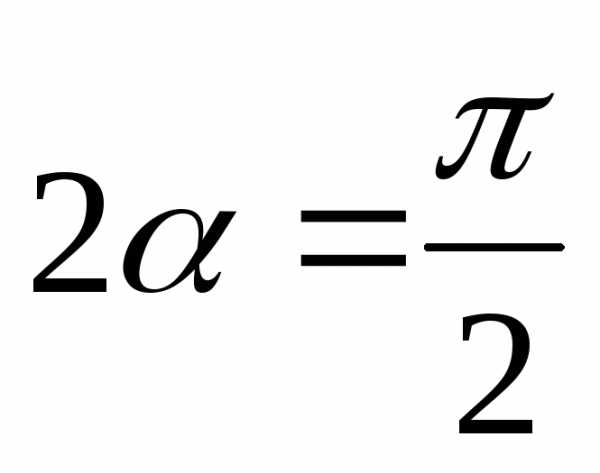 .
Это означает, что в новой системе
координат, повернутой относительно
старой системы на угол
.
Это означает, что в новой системе
координат, повернутой относительно
старой системы на угол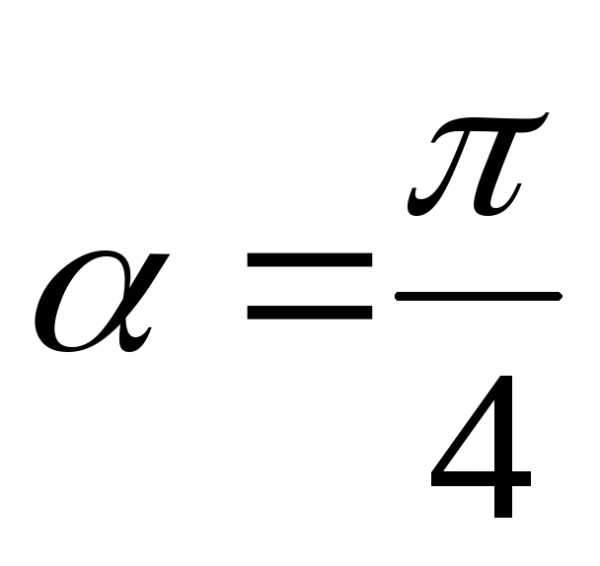 ,
уравнение не содержит произведения
переменных. Подставим в уравнение
найденное значение углаили
,
уравнение не содержит произведения
переменных. Подставим в уравнение
найденное значение углаили
.
Сделаем еще одну замену переменных , после чего получаем следующее уравнение гиперболы
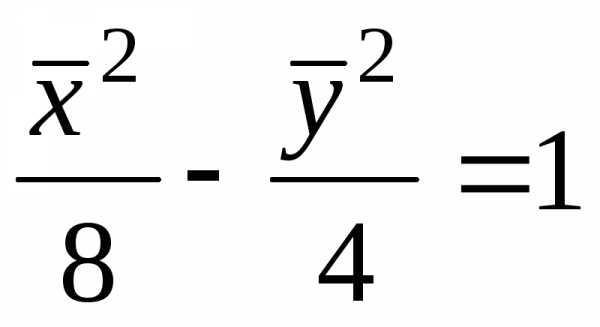 .
.
Для построения
кривой следует повернуть систему
координат на угол 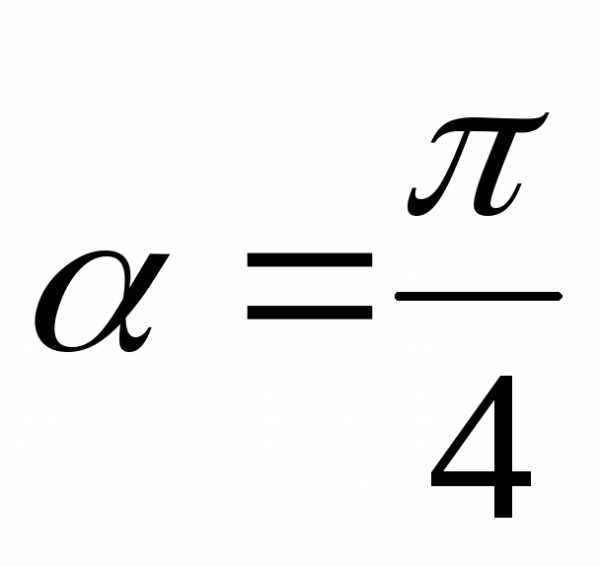 и перенести начало в точку
и перенести начало в точку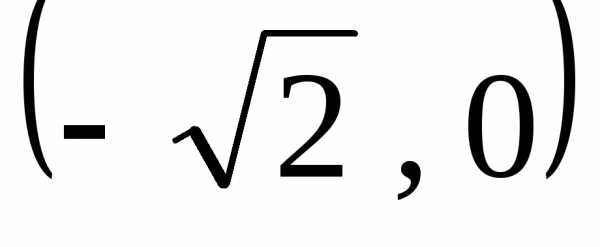 .
.
Замечание.
Уравнение второй степени не обязательно
соответствует одной из кривых второго
порядка. Так,
соответствует точке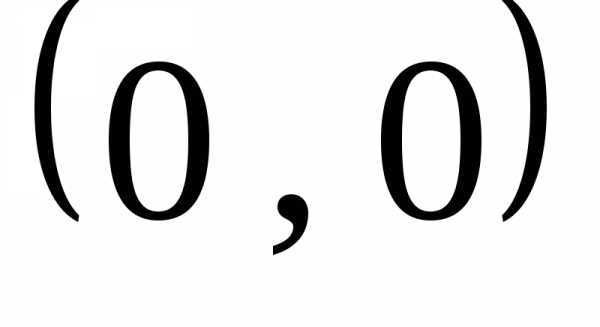 ,дает пустое множество,соответствует паре прямых. В самом деле.
Две прямые.
,дает пустое множество,соответствует паре прямых. В самом деле.
Две прямые.
studfiles.net
§ 3. Кривые второго порядка
Литература: (1, с.135-149; 2, с. 120-138; 3, с. 52-64; 4, с. 52-64)
Определение кривой второго порядка
Кривой второго порядка называется линия, определяемая уравнением второй степени относительно текущих декартовых координат. В общем случае это уравнение имеет вид:
(18)
где коэффициент – действительные числа и хотя бы одно из чисел А, В или С отлично от нуля.
К кривым второго порядка относятся линии: окружность, эллипс, гипербола, парабола.
Окружность
Окружностью называется совокупность точек, равноудалённых от одной и той же точки, называется центром. Уравнение окружности имеет вид:
(19)
где 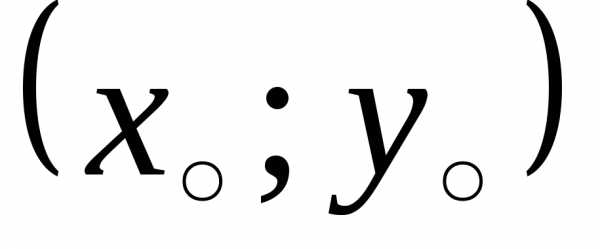 — координаты центра окружности, а
— координаты центра окружности, а — радиус окружности.
— радиус окружности.
Пример 1. Составить
уравнение окружности, которая проходит
через точку 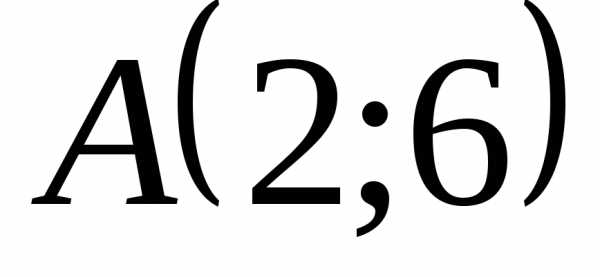 и её центр находится в точке
и её центр находится в точке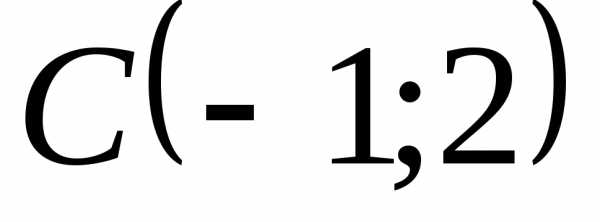 .
.
Решение. Воспользуемся
формулой (19). Имеем  ;
;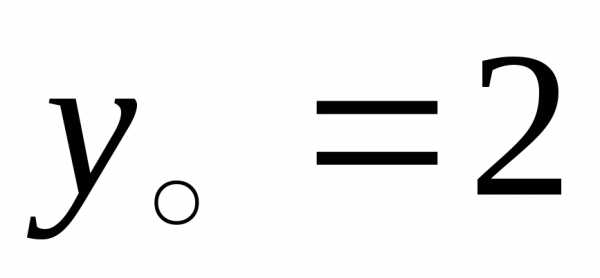 .
Найдём радиус окружности
.
Найдём радиус окружности
. Тогда уравнение окружности имеет вид:
Эллипс
Эллипсом называется совокупность точек, сумма расстояний которых до двух данных точек, называется фокусами, есть величина постоянная. Каноническое (простейшее) уравнение эллипса имеет вид:
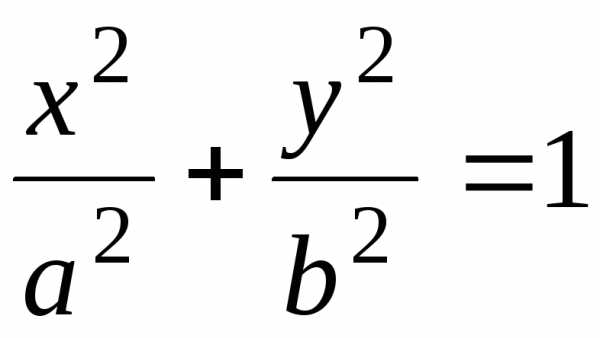 (20)
(20)
где  — большая.
— большая.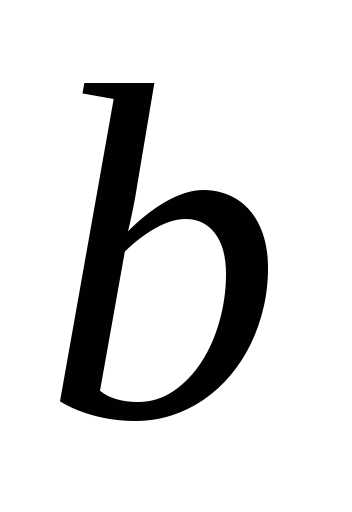 — малая полуоси эллипса (рис. 6)
— малая полуоси эллипса (рис. 6)
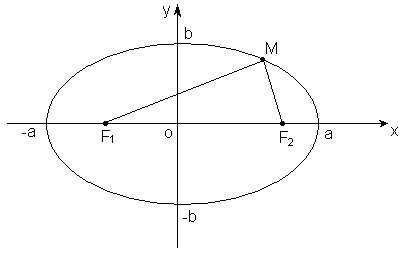
— фокусное расстояние.
Связь между  ,
,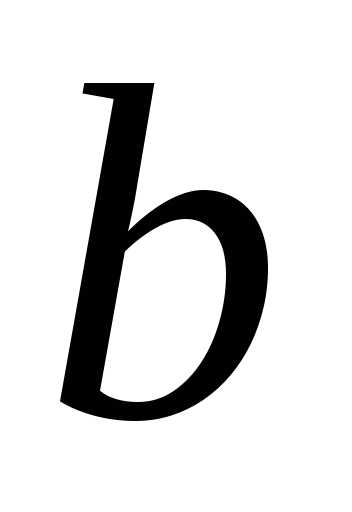 и
и определяется формулой:
определяется формулой:
(21)
Форма эллипса
(мера его сжатия) характеризуется
эксцентриситетом  :
:
 (22)
(22)
Для эллипса 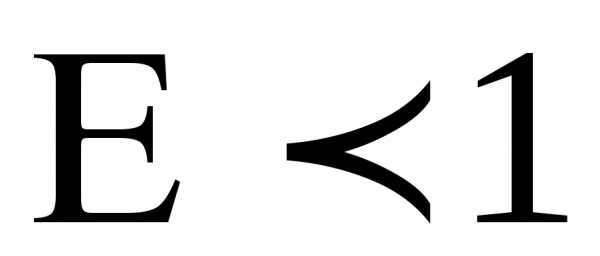 ,
так как
,
так как .
Фокусы эллипса лежат на большой оси.
.
Фокусы эллипса лежат на большой оси.
Пример 2. Составить каноническое уравнение эллипса, проходящего через точки и.
Решение. Каноническое
уравнение эллипса имеет вид (20): 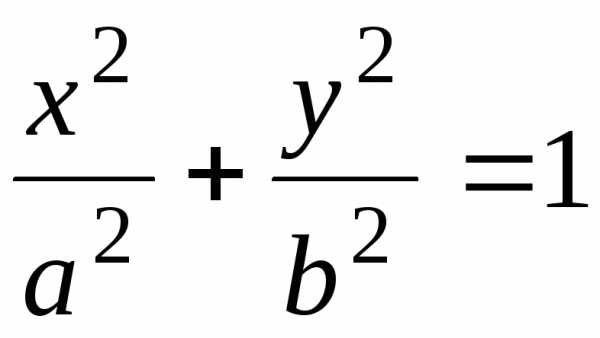 .
Так как точки
.
Так как точки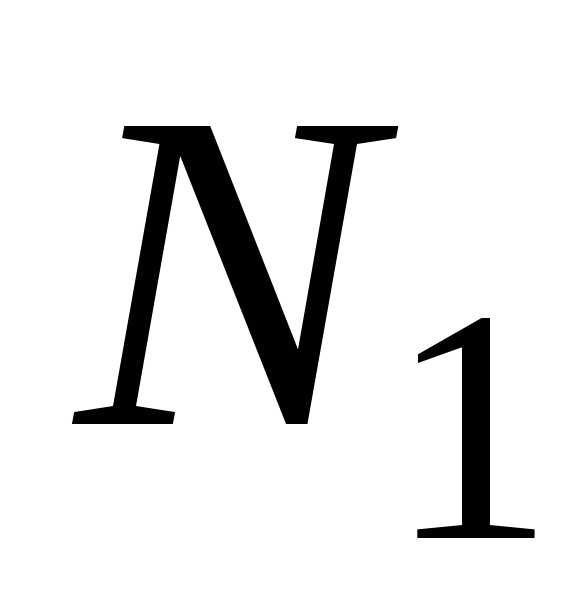 и
и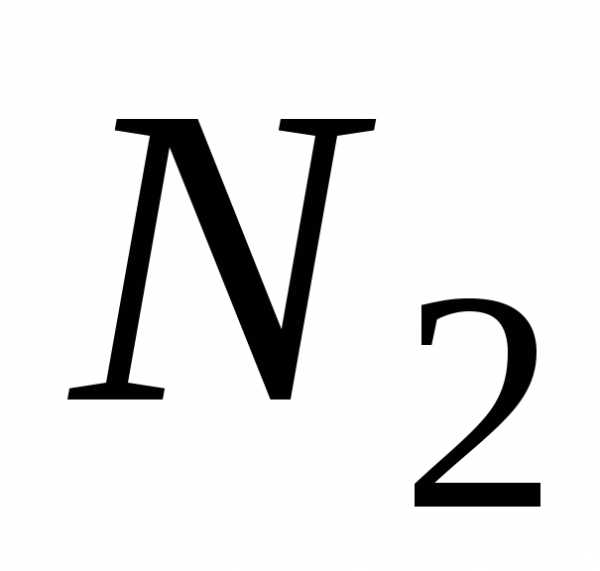 лежат на эллипсе, то их координаты
удовлетворяют уравнению (20).
лежат на эллипсе, то их координаты
удовлетворяют уравнению (20).
Имеем:

Решая систему
получим: 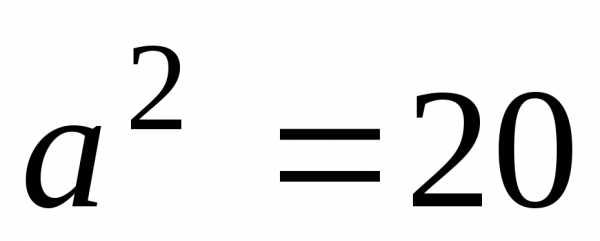 ,
,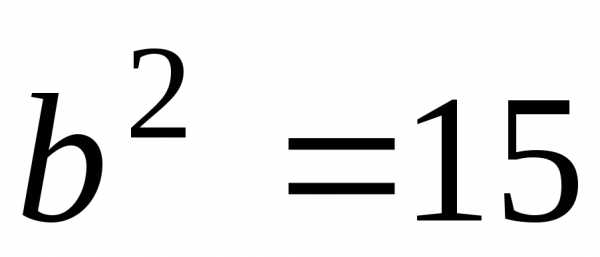 .
Следовательно, уравнение эллипса имеет
вид:
.
Следовательно, уравнение эллипса имеет
вид: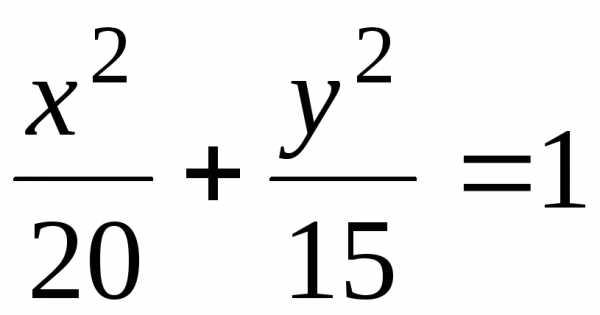 .
.
Гипербола
Гиперболой называется совокупность точек, разность расстояний которых до двух данных точек, называется фокусами, есть величина постоянная.
Каноническое уравнение гиперболы имеет вид:
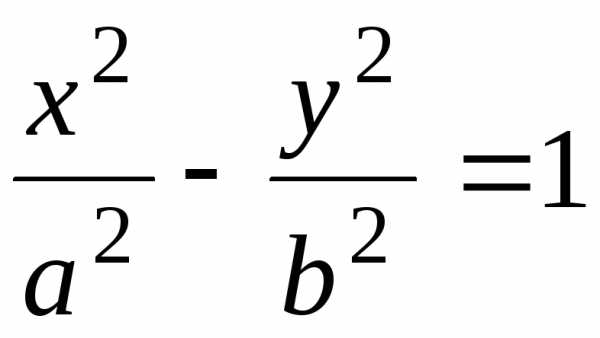 (23)
(23)
где  — вещественная,
— вещественная,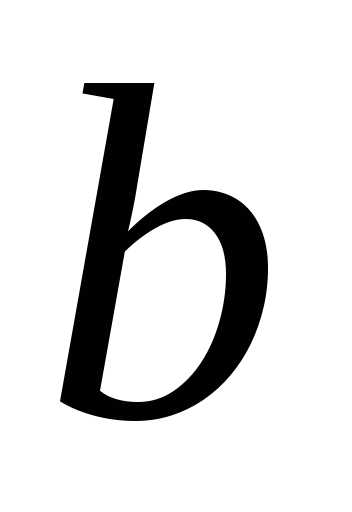 — мнимая полуоси (рис. 7).
— мнимая полуоси (рис. 7).
— фокусное расстояние.
Связь между  ,
,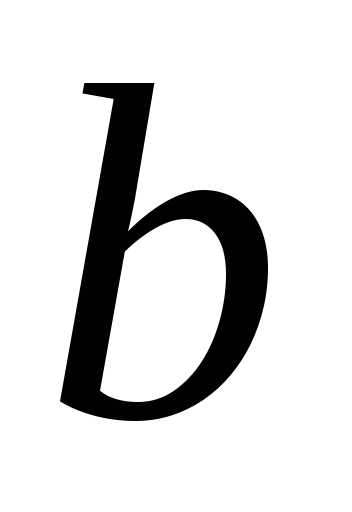 и
и определяется соотношением:
определяется соотношением:
(24)
Гипербола имеет две асимптоты, уравнения которых:
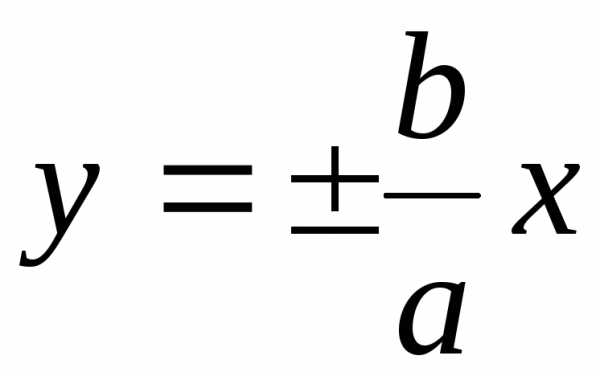 (25)
(25)
Отношение  называется эксцентриситетом гиперболы.
Фокусы гиперболы расположены на
действительной оси.
называется эксцентриситетом гиперболы.
Фокусы гиперболы расположены на
действительной оси.
Пример 3. Составить
каноническое уравнение гиперболы,
проходящей через точку
,
зная, что её эксцентриситет равен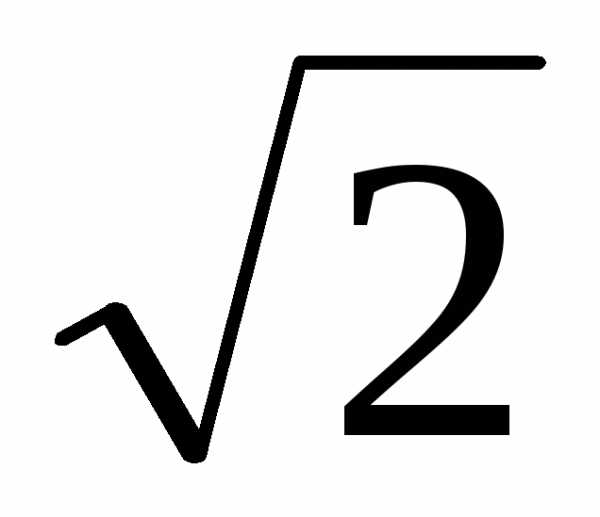 .
.
Решение. Такая
точка М лежит на гиперболе, то её
координаты удовлетворяют уравнению
гиперболы. Подставив 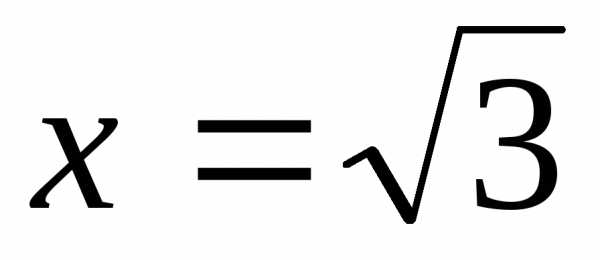 ,
,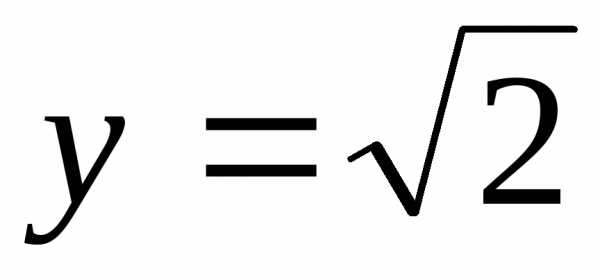 в уравнение (23), получим
в уравнение (23), получим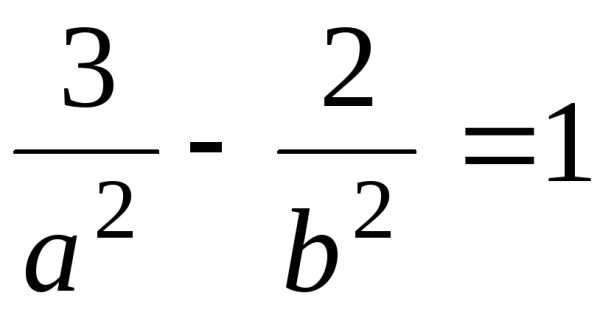 .
Так как эксцентриситет
.
Так как эксцентриситет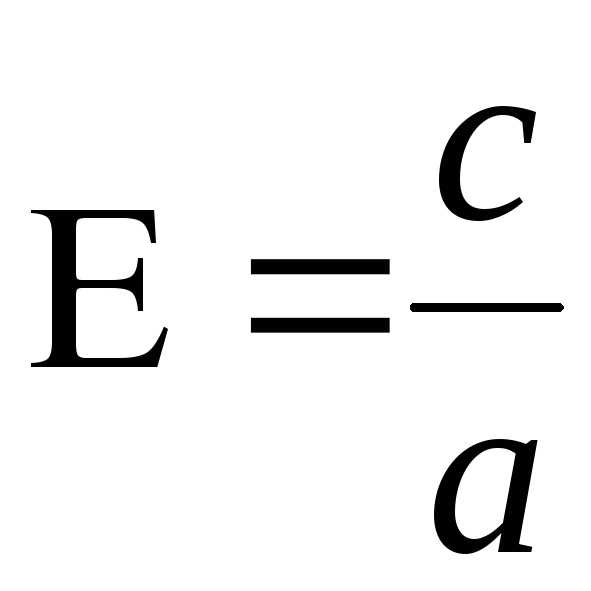 ,
то по условию получим
,
то по условию получим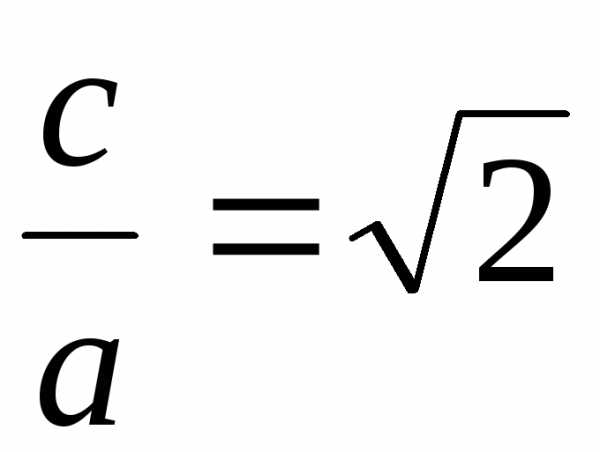 ,
или
,
или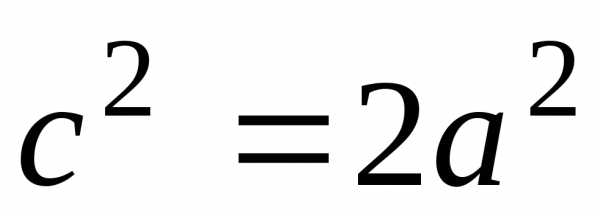 .
Используя формулу (24), имеем.
Следовательно,.
Таким образом, уравнение искомой
гиперболы имеет вид.
.
Используя формулу (24), имеем.
Следовательно,.
Таким образом, уравнение искомой
гиперболы имеет вид.
Парабола
Параболой называется совокупность точек, равноудалённых от данной точки, называемой фокусом, и данной прямой, называемой директрисой.
Каноническое уравнение параболы:
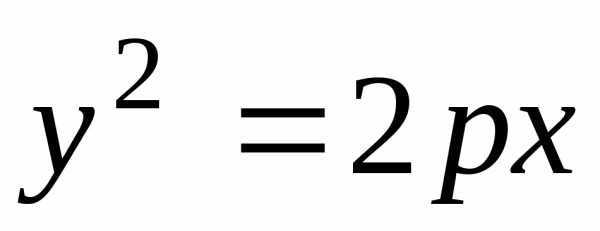 (26)
(26)
где 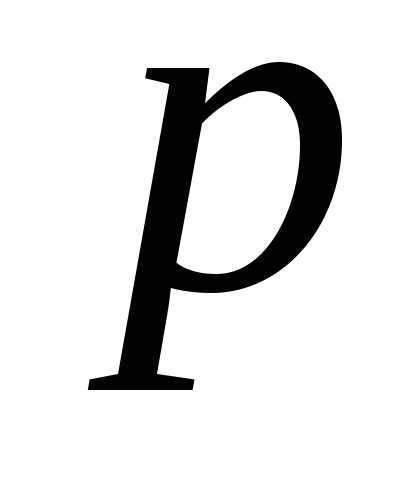 — параметр,
— параметр, ,
определяет расстояние от фокуса
,
определяет расстояние от фокуса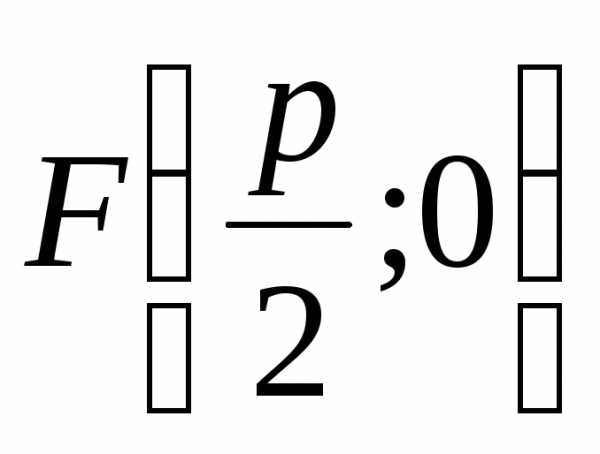 до директрисы
до директрисы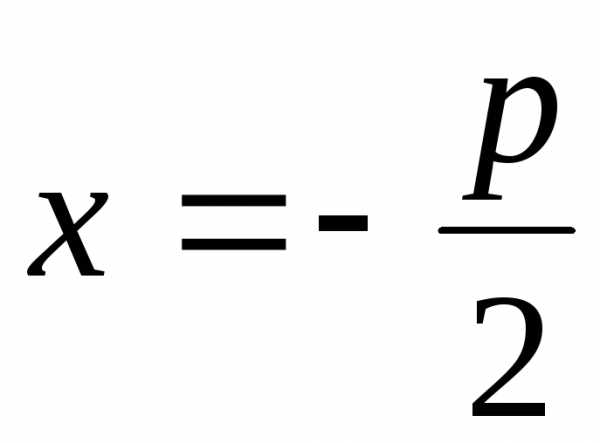 (рис. 8)
(рис. 8)
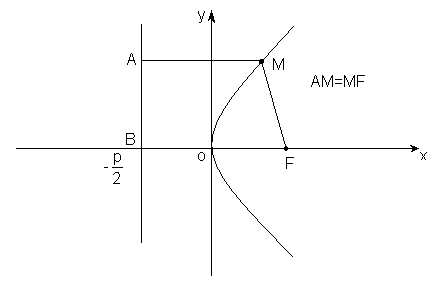
Другие виды уравнений параболы (рис. 9)

Пример 4. Парабола
симметрична оси Ох, проходит через точку  ,
а вершина его лежит в начале координат.
Составить её уравнение.
,
а вершина его лежит в начале координат.
Составить её уравнение.
Решение. Так как
парабола проходит через точку  с положительной абсциссой, а её осью
служит ось Ох, то уравнение параболы
имеет вид
с положительной абсциссой, а её осью
служит ось Ох, то уравнение параболы
имеет вид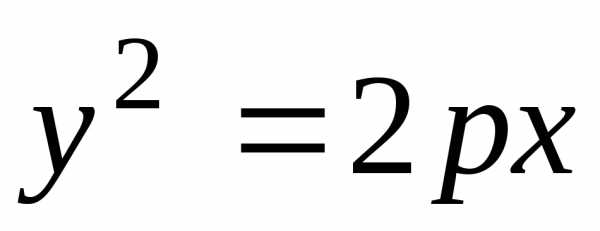 .
Подставив координаты тачки А в это
уравнение, получим
.
Подставив координаты тачки А в это
уравнение, получим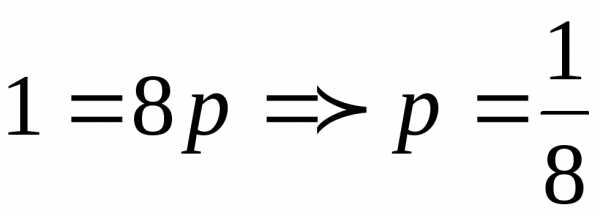 ,.
Следовательно, искомое уравнение имеет
вид
,.
Следовательно, искомое уравнение имеет
вид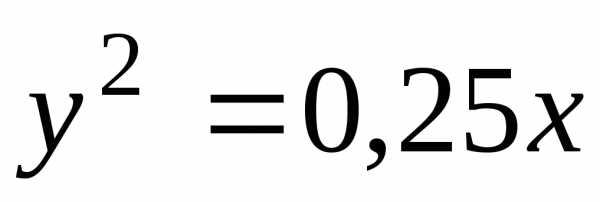 .
.
Приведение общего уравнения кривой второго порядка к каноническому
Общее уравнение линии второго порядка имеет вид (18).
Задача упрощения такого уравнения состоит в том, чтобы в преобразованном уравнении, были устранены: 10 член, содержащий произведение текущих координат, и 2) члены, содержащие первые степени двух координат или, по крайней мере, одной из них.
Рассмотрим случай упрощения уравнения кривой второго порядка, когда оно не содержит произведения текущих координат, т.е. имеет вид: . Путём дополнения до полного квадрата и параллельного переноса такое уравнение сводится к одному из канонических уравнений.
Пример 5. Какую линию определяет уравнение ?
Решение. Преобразуем данное уравнение следующим образом:
,
Обозначим: ,.
Тогда уравнение
в новой системе  с центром в точке
с центром в точке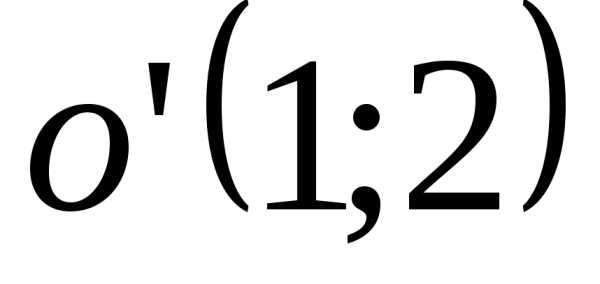 примет вид:,
или
примет вид:,
или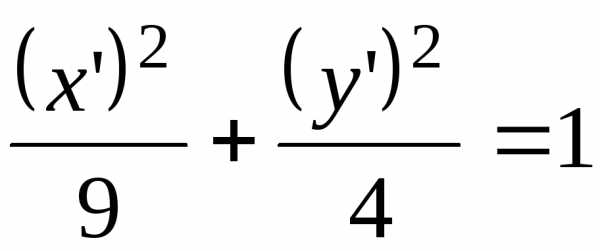 .
.
Т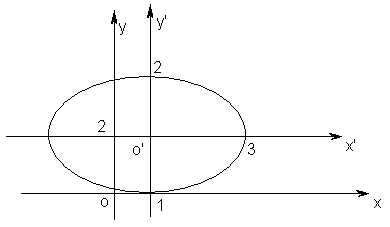 аким
образом, заданная кривая является
эллипсом (рис. 10).
аким
образом, заданная кривая является
эллипсом (рис. 10).
Пример 6. Какую линию определяет уравнение
Решение. Преобразуем данное уравнение следующим образом:
;
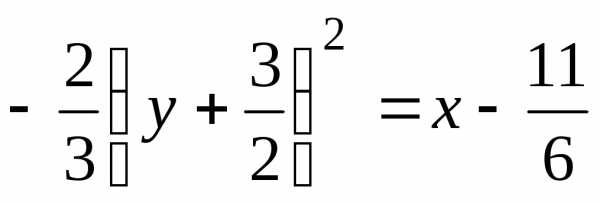 ;
.
;
.
Обозначим: 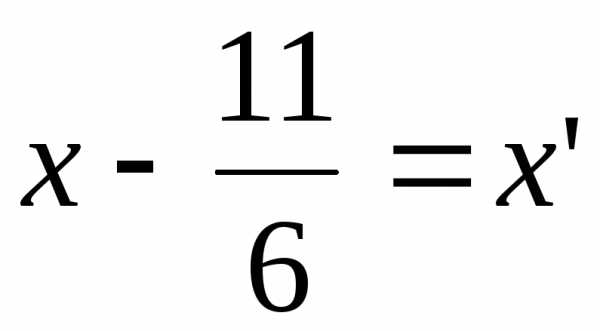 ,
,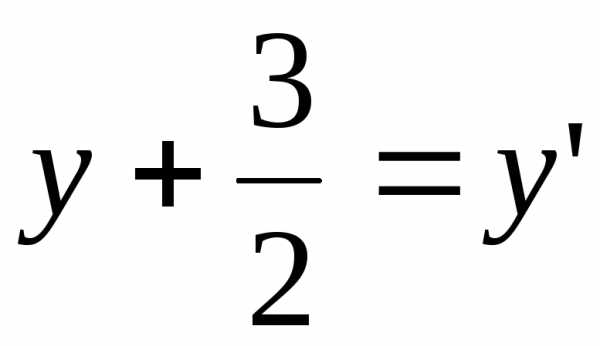 .
.
Тогда уравнение
в системе 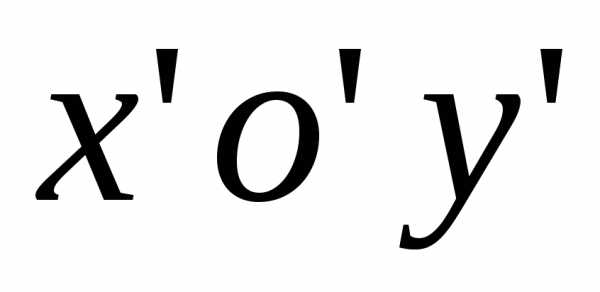 с центром в точке
с центром в точке примет вид
примет вид .
.
Таким образом:
данная кривая – парабола с вершиной в
точке 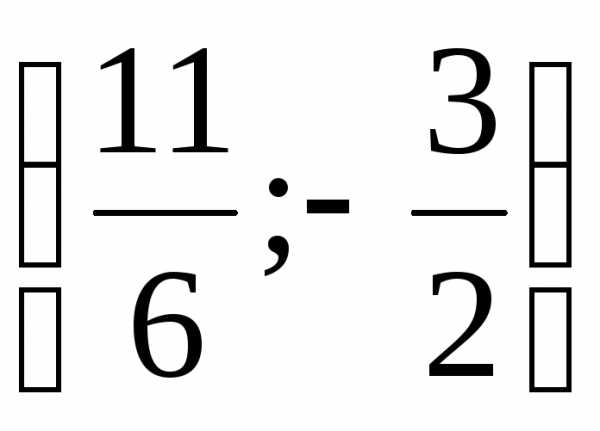 (рис. 11).
(рис. 11).
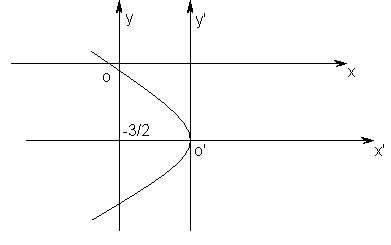
Замечание. Если уравнение линии второго порядка содержит произведение текущих координат, то путём поворота осей и надлежащим выбором угла поворота следует добиться того, чтобы преобразованном уравнении отсутствовало произведение текущих координат.
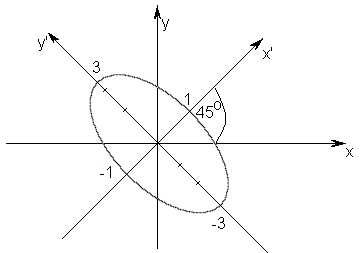
Пример 7. Привести к простейшему виду уравнение кривой
.
Решение. Применим формулы поворота (6).
;
.
Выберем угол  так, чтобы.
так, чтобы.
Тогда .
Следовательно,
уравнение кривой в системе 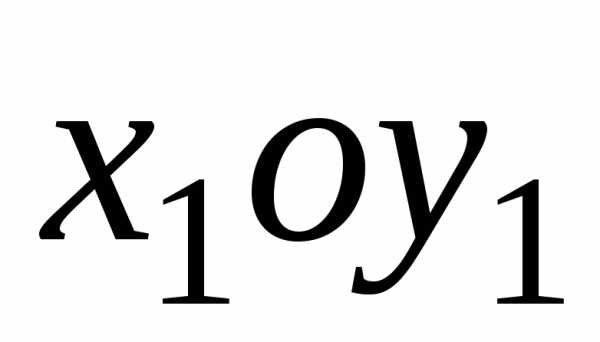 примет вид:или
примет вид:или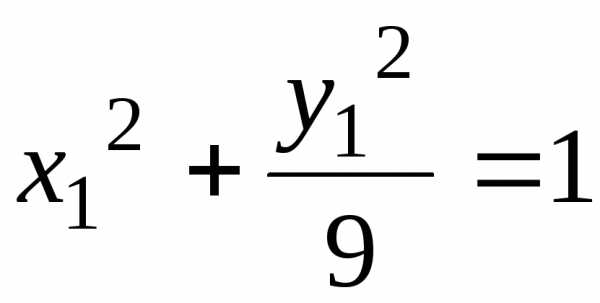 — эллипс (рис. 12).
— эллипс (рис. 12).
Вопросы для самопроверки
Как определяется кривая второго порядка?
Что называется окружностью и как записывается её каноническое уравнение?
Как определяется эллипс и каково его каноническое уравнение?
Определите гиперболу и запишите её каноническое уравнение.
Какая линия называется параболой и какой вид имеет её каноническое уравнение?
Как приводится уравнение кривой второго порядка к каноническому виду?
Примеры для самостоятельного решения
Написать уравнение окружности с центром в точке
 и радиусом, равным 6.
и радиусом, равным 6.Ставить уравнение окружности, проходящей через точки
 и
и ,
если её центр лежит на прямой.
,
если её центр лежит на прямой.Найти длинны осей, координаты фокусов и эксцентриситет эллипса .
Составить уравнение гиперболы, проходящей через точку
 ,
если асимптоты гиперболы имеют
уравнения
,
если асимптоты гиперболы имеют
уравнения .
.Составить простейшее уравнение параболы, если известно, что её фокус находится в точке пересечения прямой с осью Ох.
Определить, какие кривые определяются следующими уравнениями. Построить рисунки.
а) ;
б) ;
в) :
г) ;
д) .
Ответы к примерам
3.8.1. 3.8.2.
3.8.3.
;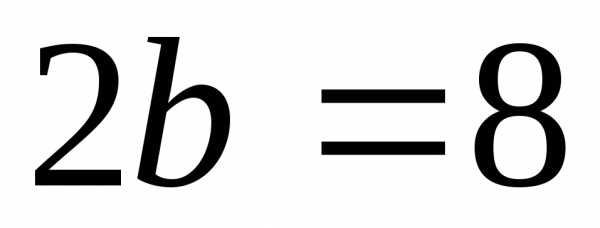 ;
;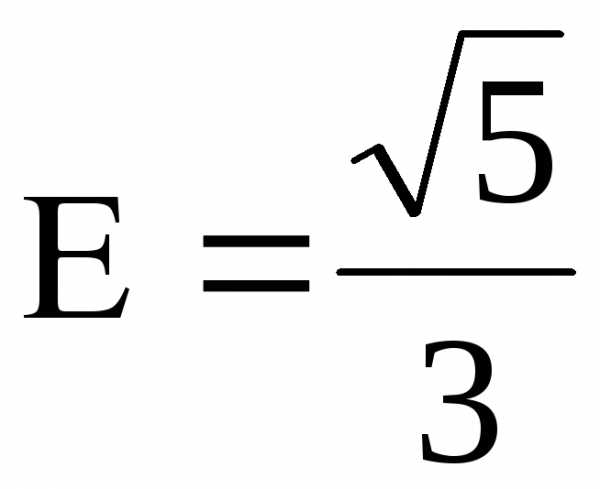 ;;
;;
3.8.4. 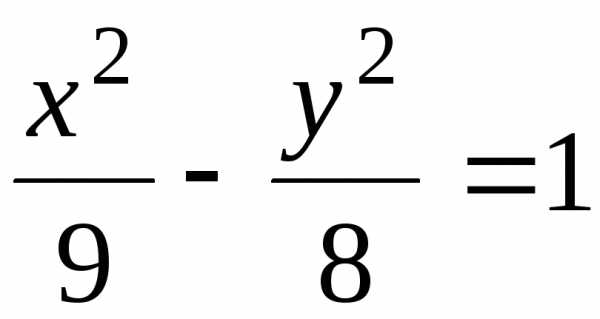 3.8.5.
3.8.5.
3.8.6. а) окружность,
центр в точке 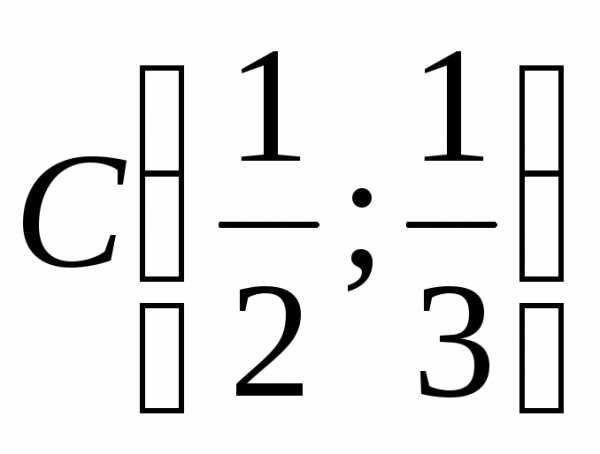 ,
,
б) эллипс 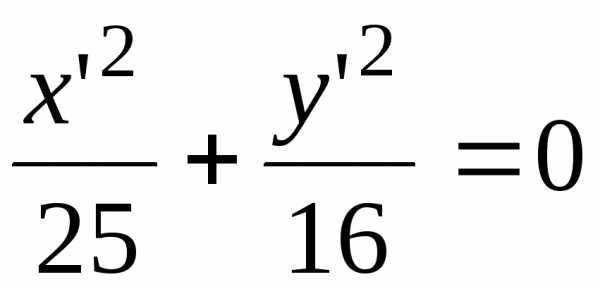 ,
,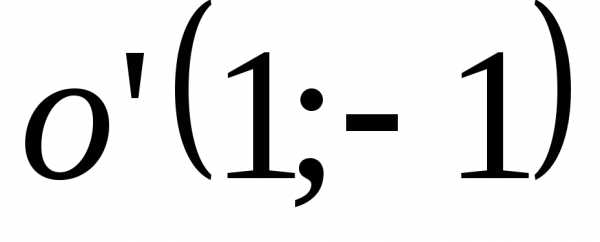
в) гипербола 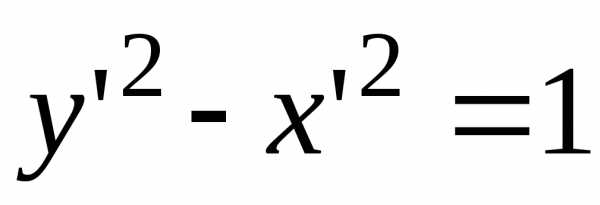 ,
,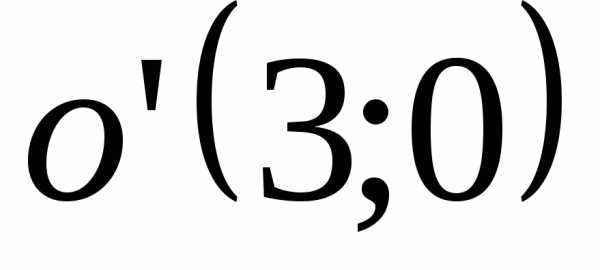
г) парабола 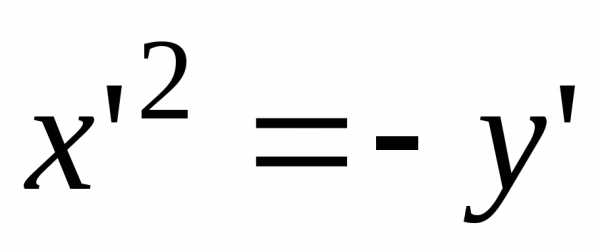 ,
,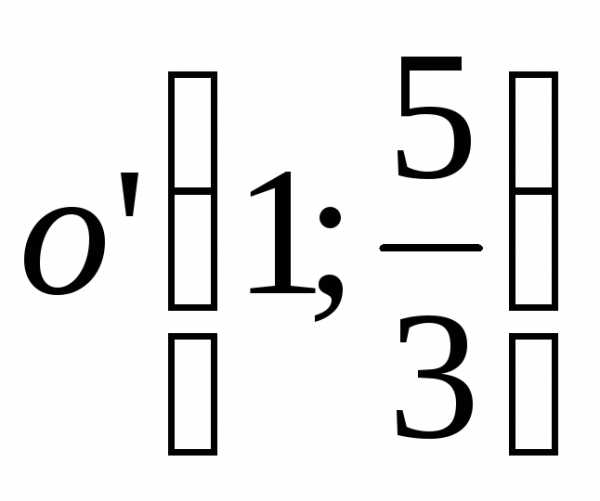
д) эллипс 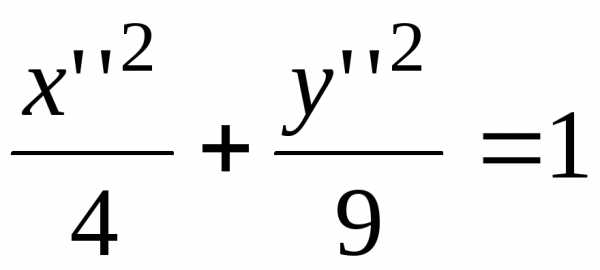 ;
;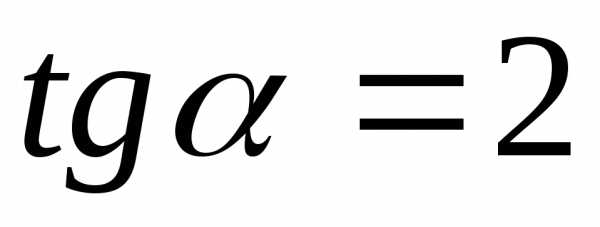 ;
;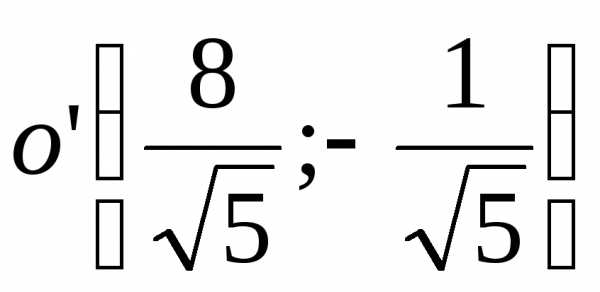 в системе
в системе .
.
studfiles.net
Кривые второго порядка — это… Что такое Кривые второго порядка?
Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида
- a11x2 + a22y2 + 2a12xy + 2a13x + 2a23y + a33 = 0,
в котором по крайней мере один из коэффициентов отличен от нуля.
История
Впервые кривые второго порядка изучались одним из учеников Платона. Его работа заключалась в следующем: если взять две пересекающиеся прямые и провращать их вокруг биссектрисы угла, ими образованного, то получится конусная поверхность. Если же сечь эту поверхность плоскостью, то в сечении получаются различные геометрические фигуры, а именно эллипс, окружность, парабола, гипербола и несколько вырожденных фигур (см. ниже).
Однако эти научные знания нашли применение лишь в XVII, когда стало известно, что планеты движутся по эллиптическим траекториям, а пушечный снаряд летит по параболической. Еще позже стало известно, что если придать телу первую космическую скорость, то оно будет двигаться по окружности вокруг Земли, при увеличении этой скорости — по эллипсу, а по достижению второй космической скорости тело по параболе покинет поле притяжения Земли.
Инварианты
Вид кривой зависит от четырёх инвариантов:
- инварианты относительно поворота и сдвига системы координат:
- инвариант относительно поворота системы координат (полуинвариант):
Характеристическая квадратичная форма и характеристическое уравнение
Многие важные свойства кривых второго порядка могут быть изучены при помощи характеристической квадратичной формы, соответствующей уравнению кривой
F0(x,y) = a11x2 + 2a12xy + a22y2.
Так, например, невырожденная кривая () оказывается действительным эллипсом, мнимым эллипсом, гиперболой или параболой в зависимости от того, будет ли F0(x,y) положительно определённой, отрицательно определённой, неопределённой или полуопределённой квадратичной формой, что устанавливается по корням характеристического уравнения:
или
λ2 − Δλ + D = 0.
Корни этого уравнения являются собственными значениями действительной симметричной матрицы
и, как следствие этого всегда действительны.
Классификация кривых второго порядка
Невырожденные кривые
Кривая второго порядка называется невырожденной, если Могут возникать следующие варианты:
- Невырожденная кривая второго порядка называется центральной если
- эллипс — при условии D > 0 и ΔI < 0;
- частный случай эллипса — окружность — при условии I2 = 4D или a11 = a22,a12 = 0;
- мнимый эллипс (ни одной действительной точки) — при условии ΔI > 0;
- гипербола — при условии D < 0;
- эллипс — при условии D > 0 и ΔI < 0;
- Невырожденная кривая второго порядка называется нецентральной если ΔI = 0
Вырожденные кривые
Кривая второго порядка называется вырожденной, если Δ = 0. Могут возникать следующие варианты:
- действительная точка на пересечении двух мнимых прямых (вырожденный эллипс) — при условии D > 0;
- пара действительная пересекающихся прямых (вырожденная гипербола) — при условии D < 0;
- вырожденная парабола — при условии D = 0:
Диаметры и центр кривой второго порядка
Диаметром кривой второго порядка называется геометрическое место середин параллельных хорд этой кривой. Полученный таким образом диаметр называется сопряжённым этим хордам или их направлению. Диаметр, сопряжённый хордам, образующих угол θ с положительным направлением оси Ox, определяется уравнением:
Если выпоняется условие то все диаметры кривой пересекаются в одной точке — центре, а сама кривая называется центральной. В противном случае (D = 0) все диаметры кривой либо парралельны, либо совпадают.
Координаты центра определяются системой уравнений:
Решая эту систему относительно x0 и y0, получим:
Если кривая центральная, то перенос начала координат в её центр приводит уравнение к виду
где — координаты относительно новой системы.
Главные оси и вершины кривой второго порядка
Главной осью кривой второго порядка называется её диаметр, перпендикулярный к сопряжённым к ним хордам. Этот диаметр является осью симметрии кривой. Каждая центральная кривая либо имеет две взаимно перпендикулярные оси, либо все диаметры являются главными осями. В последнем случае кривая является окружностью. Нецентральные кривые имеют лишь одну главную ось. Точки пересечения главной оси с самой кривой называются её вершинами.
Направляющие косинусы нормалей к главным осям удовлетворяют уравнениям
где λ — отличный от нуля корень характеристического уравнения. Направления главных осей и сопряжённых им хорд называются главными направлениями кривой. Угол между положительным направлением оси Ox и каждым из двух главных направлений определяется формулой
Из всех видов кривых второго порядка только окружность имеет неопределённые главные направления.
Уравнения
Общее уравнение в матричном виде
Общее уравнение кривой можно записать в матричном виде
Канонический вид
Вводом новой системы координат можно привести уравнения кривых второго порядка к стандартному каноническому виду (см. таблицу). Параметры канонических уравнений весьма просто выражаются через инварианты и корни характеристического уравнения (см. выше раздел «Характеристическая квадратичная форма и характеристическое уравнение»).
Для центральной кривой в каноническом виде её центр находится в начале координат.
Через эксцентриситет
Каноническое уравнение любой невырожденной кривой второго порядка при помощи подходящего преобразования начала координат может быть приведено к виду
В этом случае кривая проходит через начало новой системы координат, а ось Ox является осью симметрии кривой. Данное уравнение выражает тот факт, что невырожденная кривая второго порядка является геометрическим местом точек, отношение расстояний которых (эксцентриситет) от данной точки (фокуса) и от данной прямой (директрисы) постоянно. Кроме того, при кривая является окружностью, при — эллипсом, при — параболой, при — гиперболой.
Уравнение директриссы кривой выражается уравнением а координаты фокуса Директрисса перпендикулярна оси симметрии, проходящей через фокус и вершину кривой (фокальная ось). Расстояние между фокусом и директриссой равно
Если кривая второго порядка центральная (эллипс или гипербола), то прямая
является осью симметрии и, следовательно, кривая имеет два фокуса и две директриссы.
Параметр p называется фокальным параметром и равен половине длины хорды, проходящей через фокус и перпендикулярной к фокальной оси (фокальная хорда).
Полярные координаты
Если взять в качестве полюса полярной системы координат фокус невырожденной кривой второго порядка, а в качестве полярной оси — её ось симетрии, то в полярных координатах ρ, φ уравнение кривой будет иметь вид
Кривая, заданная своими пятью точками
Кривая второго порядка вполне определяется пятью своими точками, если никакие четыре из них не лежат на одной прямой. Уравнение кривой, проходящей через точки и
Кривая, заданная пятью точками вырождается в том и только в том случае, когда три из заданных точек лежат на одной прямой.
Касательные и нормали
Уравнение касательной к кривой второго порядка f(x,y) в её точке имеет вид:
Уравнение нормали к кривой второго порядка в точке имеет вид
Полюсы и поляры
Уравнение
помимо касательной опряделяет прямую, называемую полярой точки относительно кривой второго порядка, независимо от того, лежит ли эта точка на кривой или нет. При этом точка называется полюсом этой прямой. Поляра точки кривой есть её касательная в этой точке.
Теоремы о полюсах и полярах:
- Если прямая, проведённая через полюс P, пересекает поляру в точке Q, а кривую второго порядка — в точках R1 и R2, то точки P и Q гармонически разделяют отрезок R1R2, т. е. выполняется условие
- Если точка лежит на некоторой прямой, то её поляра проходит через полюс этой прямой. Если прямая проходит через некоторую точку, то её полюс лежит на поляре этой точки.
- Диаметр кривой второго порядка есть поляра бесконечно удалённой точки, через которую проходят сопряжённые ему хорды, а центр кривой есть полюс бесконечно удалённой прямой.
- Фокус кривой есть центр пучка, обладающего тем свойством, что полюс любой его прямой принадлежит перпендикулярной к ней прямой пучка. Директрисса есть поляра фокуса.
Из этих утверждений, в частности, следует, что:
- если через точку можно провести две касательные к кривой, то то поляра этой точки проходит через точки касания;
- касательные к кривой в концах диаметра параллельны сопряжённым ему хордам;
- точка пересечения касательных к кривой в концах любой её хорды, проходящей через фокус, лежит на директриссе;
- каждая хорда, проходящая через фокус, перпендикулярна к прямой, проведённой через её фокус и точку пересечения касательных в концах хорды.
Теоремы, связанные с кривыми второго порядка
- Теорема Паскаля: точки пересечения противоположных сторон шестиугольника, вписанного в кривую второго порядка, лежат на одной прямой.
- Теорема Брианшона: диагонали, проходящие через противоположные вершины шестиугольника, описанного около кривой второго порядка, пересекаются в одной точке.
См. также
Ссылки
Литература
- Корн Г., Корн Т. Кривые второго порядка (конические сечения) // Справочник по математике. — 4-е издание. — М: Наука, 1978. — С. 64-69.
Wikimedia Foundation. 2010.
dic.academic.ru
Кривые второго порядка

Кривые второго порядка
Черникова Юлия Васильевна
Г. Каменск – Уральский
МБОУ «Средняя общеобразовательная школа №3
имени Героя Советского Союза
лётчика – космонавта П. И. Беляева

Кривая второго порядка —
геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида
в котором по крайней мере один из коэффициентов
отличен от нуля. Иначе говоря

История
Впервые кривые второго порядка изучались одним из учеников Платона. Его работа заключалась в следующем: если взять две пересекающиеся прямые и вращать их вокруг биссектрисы угла, ими образованного, то получится конусная (коническая) поверхность . Если же сечь эту поверхность плоскостью, то в сечении получаются различные геометрические фигуры , а именно эллипс, окружность (пирибола), парабола, гипербола и несколько вырожденных фигур .

Однако эти научные знания нашли применение лишь в XVII.
Стало известно, что планеты движутся по эллиптическим траекториям , а пушечный снаряд летит по параболической . Еще позже стало известно, что если придать телу первую космическую скорость, то оно будет двигаться по окружности вокруг Земли, при увеличении этой скорости — по эллипсу , а по достижению второй космической скорости тело по параболе покинет поле притяжения Земли.
Также, благодаря своим геометрическим свойствам, кривые второго порядка нашли широкое применение в современной технике, например, в создании спутниковых тарелок и прожекторов.

Классификация кривых второго порядка
Невырожденные кривые:
- Эллипс — Окружность (частный случай эллипса) — Мнимый Эллипс (пустое множество) — Гипербола — Парабола —
- Эллипс —
- Окружность (частный случай эллипса) —
- Мнимый Эллипс (пустое множество) —
- Гипербола —
- Парабола —
Вырожденные кривые:
- Точка — Пара пересекающихся прямых — Пара параллельных прямых — Прямая (две слившихся параллельных прямых) — Пара мнимых параллельных прямых —
- Точка —
- Пара пересекающихся прямых —
- Пара параллельных прямых —
- Прямая (две слившихся параллельных прямых) —
- Пара мнимых параллельных прямых —

Эллипс
Эллипс и его фокусы
Э́ллипс (др.-греч. ἔλλειψις — недостаток) — геометрическое место точки M Евклидовой плоскости, для которой сумма расстояний от двух выделенных точек F 1 и F 2 (называемых фокусами ) постоянна, то есть
| F 1 M | + | F 2 M | = 2a.
Окружность является частным случаем эллипса . Наряду с гиперболой и параболой, эллипс является коническим сечением и квадрикой. Эллипс также можно описать как пересечение плоскости и кругового цилиндра или как ортогональную проекцию окружности на плоскость.

Связанные определения
- Отрезок, проходящий через фокусы эллипса, концы которого лежат на эллипсе, называется большой осью данного эллипса . Длина большой оси равна 2a в вышеприведённом уравнении.
- Отрезок, перпендикулярный большой оси эллипса, проходящий через центральную точку большой оси, концы которого лежат на эллипсе, называется малой осью эллипса .
- Точка пересечения большой и малой осей эллипса называется его центром .
- Концы осей эллипса называются его вершинами .

- Отрезки, проведённые из центра эллипса к вершинам на большой и малой осях называются, соответственно, большой полуосью и малой полуосью эллипса.
- Расстояние c = | F 1 F 2 | / 2 называется фокальным расстоянием , а отношение — эксцентриситетом. Эксцентриситет ( также обозначается ε ) характеризует вытянутость эллипса . Чем эксцентриситет ближе к нулю, тем эллипс больше напоминает окружность и наоборот, чем эксцентриситет ближе к единице, тем он более вытянут.
- Отношение длин малой и большой полуосей называется коэффициентом сжатия эллипса или эллиптичностью : , где b — малая полуось, a — большая полуось. Величина, равная называется сжатием эллипса . Для окружности коэффициент сжатия равен единице, сжатие — нулю. Коэффициент и эксцентриситет эллипса связаны соотношением k 2 = 1 − e 2 .

Свойства
- Прямая, проведённая через середины отрезков, отсечённых двумя параллельными прямыми, пересекающими эллипс, всегда будет проходить через центр эллипса . Это позволяет построением с помощью циркуля и линейки легко получить центр эллипса, а в дальнейшем оси, вершины и фокусы.
- Фокальное свойство. Если F 1 и F 2 — фокусы эллипса, то для любой точки X, принадлежащей эллипсу, угол между касательной в этой точке и прямой (F 1 X) равен углу между этой касательной и прямой (F 2 X).

Соотношение между элементами эллипса
- Малая полуось:
- Расстояние от фокуса до ближней вершины:
- Расстояние от фокуса до дальней вершины:
- Связь фокального параметра с полуосями и фокусным расстоянием:
- Связь фокального параметра с удалением вершин от данного фокуса:

Координатное представление
Для любого эллипса можно найти Декартову систему координат такую, что эллипс будет описываться уравнением (каноническое уравнение эллипса):
при 0

Площадь эллипса
- Площадь эллипса вычисляется по формуле
- Где a и b полуоси эллипса.

Окружность и её центр
Окружность
Окружность в Евклидовой геометрии — геометрическое место точек плоскости, равноудаленных от заданной точки, называемой ее центром . Расстояние от центра окружности до ее точек называется радиусом данной окружности .
Окружность является простой плоской кривой второго порядка, частным случаем эллипса и, аналогично другим кривым второго порядка (парабола, гипербола), имеет греческое название — пири́бола .

Связанные определения
— Отрезок, соединяющий центр окружности с какой-либо
её точкой, называется радиусом окружности.
— Часть плоскости, ограниченная окружностью,
называется кругом . Круговым сектором называется часть круга, ограниченная дугой и двумя радиусами.
— Отрезок, соединяющий две точки окружности,
называется её хордой . Хорда, проходящая через центр окружности, называется диаметром .

— Дугой называется часть окружности,
ограниченная двумя точками.
— Сегментом называется часть круга, ограниченная
дугой и стягивающей её хордой.
— Прямая, имеющая с окружностью ровно одну
общую точку, называется касательной к окружности,
а их общая точка называется точкой касания
прямой и окружности.

— Прямая, проходящая через две точки окружности, называтся секущей .
— Центральным углом в окружности называется плоский угол с вершиной в её центре.
— Угол, вершина которого лежит на окружности, а стороны пересекают эту окружность, называется вписанным углом .
— Отношение длины окружности к ее диаметру — число π .

Свойства
- Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.
- Точка касания двух окружностей лежит на линии, соединяющей их центры.
- Длину окружности радиуса R можно вычислить по формуле C = 2πR.
- Площадь круга радиуса R можно вычислить по формуле

Уравнения
Декартовы координаты:
Окружность с центральной точкой и радиусом r описывается следующим уравнением:
если M есть начало координат, то уравнение принимает вид:
В декартовой системе координат окружность не является графиком функции, но она может быть описана как объединение графиков двух следующих функций:
Если , то функции принимают вид:

Гипербола
и её фокус
Гипербола
Гипербола — геометрическое место точек M Евклидовой плоскости, для которых абсолютное значение разности расстояний от M до двух выделенных точек F 1 и F 2 (называемых фокусами ) постоянно и равно | | F 1 M | — | F 2 M | | = C
Расстояние между фокусами называется фокальным расстоянием , а отношение e = | F 1 F 2 | / C —
эксцентриситетом .
Примером гиперболы служит график функции y = 1 / x.
Наряду с эллипсом и параболой, гипербола является коническим сечением и квадрикой. Гипербола может быть определена как коническое сечение с эксцентриситетом, большим единицы.
Термин «гипербола» (греч. ύπερβολή — избыток) был введён Аполлонием Пергским, поскольку задача о построении точки гиперболы сводится к задаче о приложении с избытком.

Уравнение в прямоугольных координатах
Для любой гиперболы можно найти декартову
систему координат такую, что гипербола
будет описываться уравнением:
Числа a и b называются
соответственно вещественной и мнимой полуосями гиперболы . Зная значения полуосей можно вычислить фокальное расстояние и эксцентриситет:
Каждая гипербола имеет пару асимптот: и
Гиперболу, у которой a = b, называют равнобочной.
Гипербола,
её полуоси и асимптоты

Парабола, её фокус
и директриса
Парабола
Пара́бола — (греч. παραβολή — приложение) геометрическое место точек, равноудалённых от прямой (называемой директрисой параболы) и точки (называемой фокусом параболы).
Наряду с эллипсом и гиперболой, парабола является коническим сечением. Парабола может быть определена как коническое сечение с единичным эксцентриситетом.
Для каждой параболы можно найти Декартову систему координат такую, что парабола представляет собой график y = ax².

Свойства
Парабола является антиподерой прямой.
Отражённые лучи от пучка прямых, перпендикулярных к директрисе, собираются в фокусе параболы.
Данное свойство используется в конструкции телескопов-рефлекторов (оптических, инфракрасных, радио…), в конструкции узконаправленных антенн, необходимых для передачи данных на большие расстояния. Параболические антенны (тарелки) собирают пучок параллельных лучей приходящих от удалённого передатчика на приёмнике.
videouroki.net

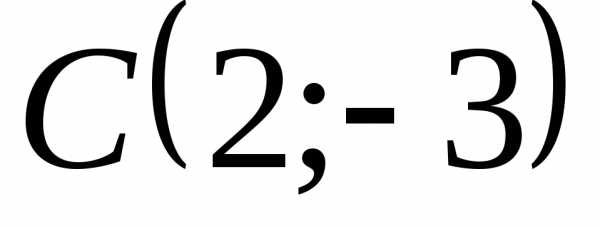 и радиусом, равным 6.
и радиусом, равным 6.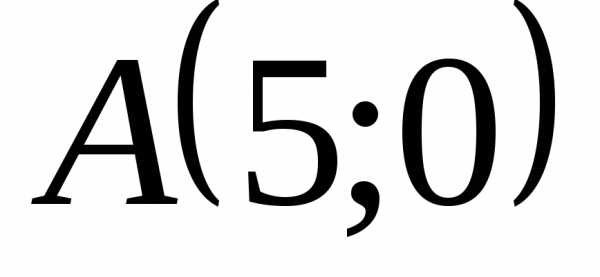 и
и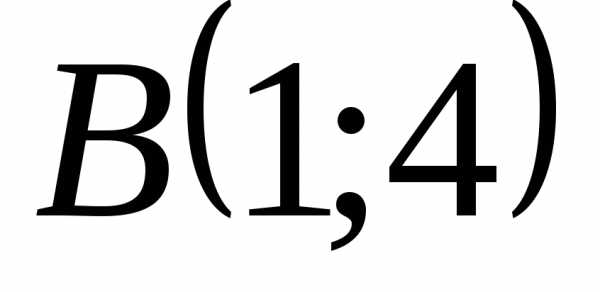 ,
если её центр лежит на прямой.
,
если её центр лежит на прямой. ,
если асимптоты гиперболы имеют
уравнения
,
если асимптоты гиперболы имеют
уравнения .
.