Определители матриц — теория и примеры
Содержание Определитель квадратной матрицы первого порядка Определитель квадратной матрицы второго порядка Схема вычисления определителя второго порядка Примеры вычисления определителей второго порядка Определитель квадратной матрицы третьего порядка Правило треугольников нахождения определителя третьего порядка Примеры вычисления определителей третьего порядка
Используя специальное правило каждой квадратной матрице можно поставить в соответствие число, которое будем называть определителем (детерминантом) и обозначать или или
Определителем квадратной матрицы первого порядка называется число
Заметим, что здесь выражение означает определитель, хоть внешне очень похоже на запись модуля числа Таким образом, определитель матрицы первого порядка равен единственному элементу этой матрицы, например для матриц
и
определители
и
Определителем квадратной матрицы второго порядка
называется число
Таким образом, для того, что вычислить определитель матрицы 2-го порядка нужно умножить элементы главной диагонали матрицы и от полученного произведения вычесть произведение элементов побочной диагонали матрицы. Схема вычисления определителя второго порядка представлена на рис. 1.
Рис. 1
Рассмотрим примеры, где требуется вычислить определитель второго порядка. У матриц
определители
Определителем квадратной матрицы третьего порядка
называется число
Как видим, для того чтобы вычислить определитель матрицы третьего порядка необходимо использовать достаточно сложную для запоминания формулу, однако, заучивать ее вовсе не обязательно. Гораздо легче понять и запомнить схему вычисления определителя третьего порядка
(рис. 2) (ее еще называют правилом треугольников). Используя эту схему решаются задачи на вычисление определителей матриц 3×3, и с ее помощью всегда можно восстановить формулу нахождения определителя 3-го порядка.Рис. 2
Как видно из схемы (рис. 2), для того чтобы найти определитель третьего порядка необходимо вычислить 6 чисел, каждое из которых представляет собой произведение трех чисел. Для нахождения первого числа требуется найти произведение элементов главной диагонали, второе и третье числа представляют собой произведения элементов, находящихся в вершинах равнобедренных треугольников (см. рис. 2), чьи основания параллельны главной диагонали матрицы. Аналогично, четвертое число в схеме есть произведение элементов второй (побочной) диагонали матрицы, а пятое и шестое числа находятся как произведения элементов-вершин равнобедренных треугольников с основаниями параллельными второй диагонали матрицы. Затем следует сложить первые три числа и из этой суммы вычесть сумму чисел с номерами 4 — 6.
Рассмотрим пример вычисления определителя матрицы третьего порядка. Определитель
vmatematika.ru
2.1. Понятие определителя 2-го и 3-го порядков
Рассмотрим квадратную матрицу, состоящую из четырех элементов:
.
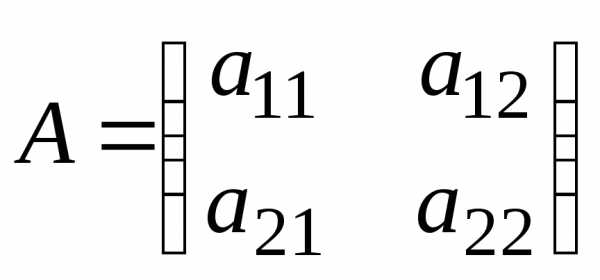(1.1)
Определение
1. Определителем или детерминантом второго порядка, соответствующим матрице (1.1), называется
число, равное разности произведений
элементов стоящих на главной диагонали,
и элементов, стоящих на побочной диагонали
(определитель обозначается 
.
Пример
1.3. 
1),
2).
Рассмотрим
квадратную матрицу, состоящую из девяти
элементов: 
(1.2)
Определение 2. Определителем или детерминантом третьего порядка, соответствующим матрице (1.2), называется число равное
Структура этого выражения помогает понять наглядное правило Саррюса. Припишем к элементам определителя справа первый и второй столбцы определителя. Три произведения, соответствующие прямым, параллельным главной диагонали, надо взять со знаком плюс, а остальные три произведения, соответствующие прямым, параллельным побочной диагонали, надо взять его со знаком минус.
Пример 1.
Свойства определителей
10. Величина определителя не изменится, если его строки и столбцы поменять местами.
,
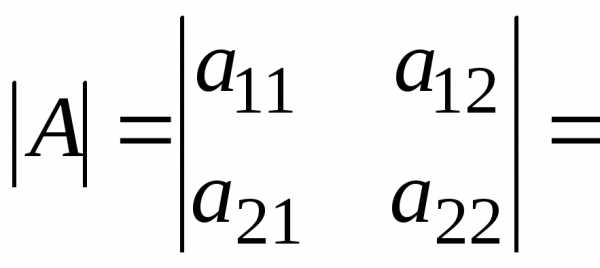
20. Перестановка двух строк или столбцов определителя равносильна умножению его на (-1).
30. Если определитель имеет две одинаковые строки или два одинаковых столбца, то он равен нулю.
40. Умножение всех элементов строки или столбца определителя на любое число равносильно умножению определителя на это число .
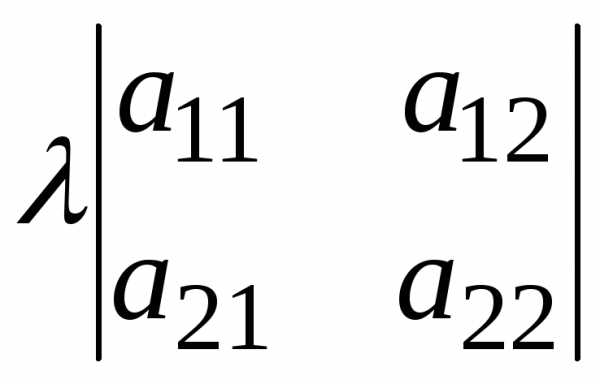
50. Если все элементы некоторого столбца или строки определителя равны нулю, то и сам определитель равен нулю.
60. Если элементы двух строк или двух столбцов определителя пропорциональны, то определитель равен нулю.
70. Если каждый элемент любого столбца или любой строки определителя представлен в виде двух слагаемых, то определитель можно представить в виде суммы двух определителей.
, аналогично для определителей 2-го порядка.
80. Если к элементам некоторой строки или столбца прибавить соответствующие элементы другой строки или столбца, умноженные на любой общий множитель , то величина определителя не изменится.
Определение
3. Минором 
определителя называется определитель,
полученный из данного определителя
вычеркиванием строки и столбца, на
пересечении которых расположен этот
элемент, т.е. i – ой строки и j – го столбца.
Определение 4. Алгебраическим
дополнением 
элемента 
определителя называется минор этого
элемента, умноженный на
,
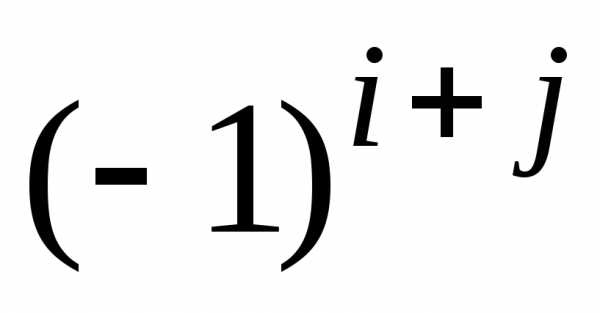т.е..
Для
вычисления алгебраических дополнений
элементов определителей третьего
порядка знаки легко запомнить по
следующей схеме: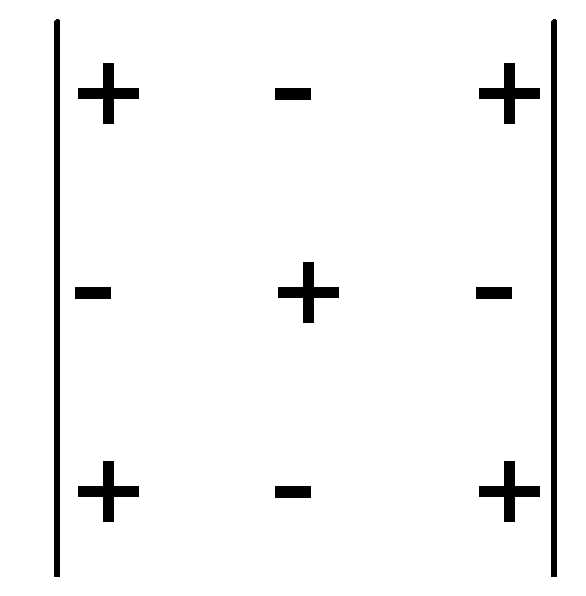 
.
Например: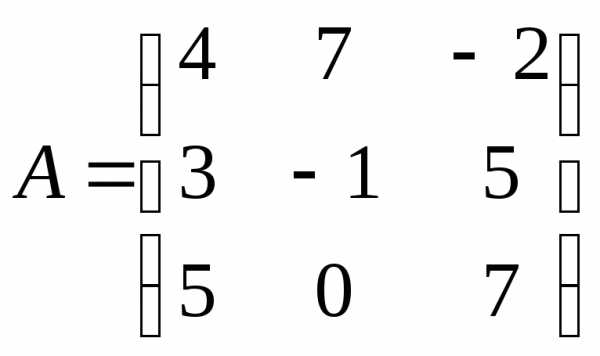 
90. Определитель равен сумме произведений элементов какой-нибудь строки или столбца на их алгебраические дополнения.
Например:
=
.
100. Сумма произведений элементов какого-нибудь столбца или строки определителя на алгебраические дополнения соответствующих элементов другого столбца или строки равна нулю.
Например:
или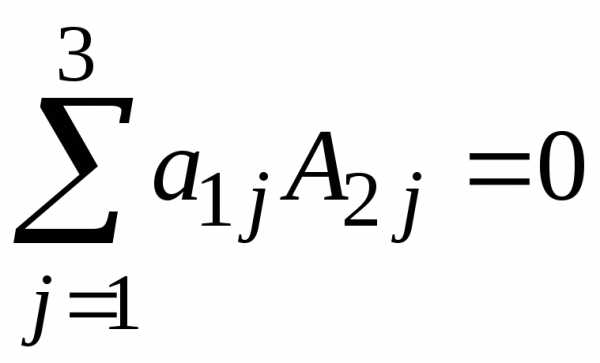
.
Лекция 3. Методы вычисления определителей n – го порядка. Разложение определителя матрицы по элементам строки и столбца.
Примеры вычисления определителей путём разложения по элементам строк или столбцов.
studfiles.net
Определители 2-го и 3-го порядков
Рассмотрим квадратную матрицу 2-го порядка:
Определение. Определителем 2-го порядка, соответствующим матрице А, называется число
.
Числа а11, а12, а21, а22 называются элементами определителя (они же элементы матрицы А).
Элементы а11, а22 составляют главную диагональ, а элементы а21, а12 – побочную диагональ.
Пусть дана квадратная матрица 3-го порядка:
Определение. Определителем 3-го порядка, соответствующим матрице А, называется число D, которое определяется выражением:
Элементы а11, а22, а33 – расположены на главной диагонали, элементы а13, а22, а31 – на побочной диагонали.
Вычисление определителей 2-го и 3-го порядка
Определитель 2-го порядка вычисляется по определению:
.
Пример 1
Для вычисления определителя 3-го порядка можно воспользоваться следующими правилами:
Правило Саррюса: дописать справа к элементам определителя сначала 1-й столбец, затем 2-й (можно внизу дописать первую и вторую строки), (рис.1), произведение элементов, стоящих на главной диагонали определителя, а также произведения элементов, стоящих на двух параллелях к ней, содержащих по 3 элемента – нужно взять со знаком «плюс», а произведение элементов побочной диагонали и двух параллелях к ней, содержащих по 3 элемента – нужно взять со знаком «минус» (рис. 1). Сумма этих шести произведений дает определитель 3-го порядка, соответствующий матрице
,
— — — + + +
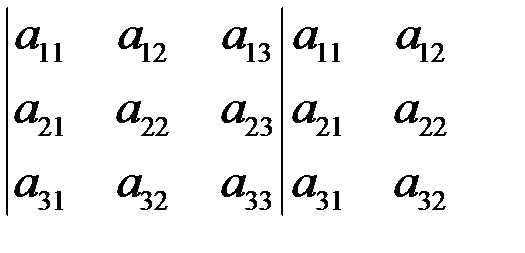Рис. 1
Пример 2
Вычислить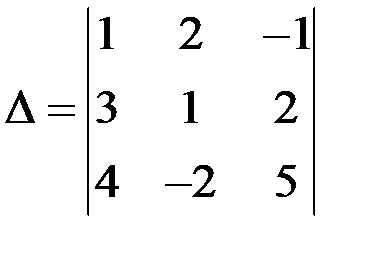 
.
Решение
,
– – – + + +
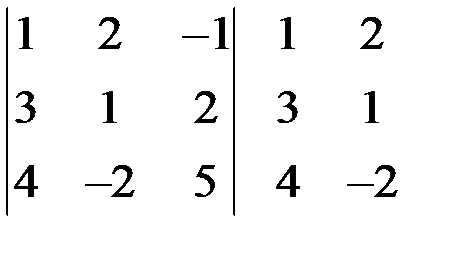таким образом:
Правило треугольника:одно из трех слагаемых, со знаком «плюс» есть произведение элементов главной диагонали определителя, каждое из двух других – произведение элементов, лежащих на параллели к этой диагонали, и элемента из противоположного угла определителя, слагаемые со знаком «минус» строятся так же, но относительно побочной диагонали (рис.2).
(+) (-)
Рис. 2
Пример 3
Вычислить определитель по правилу треугольника: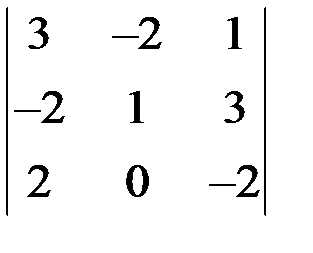 
.
Решение
Свойства определителей
Рассмотрим свойства определителей на примере определителя 3-го порядка.
Рассмотрим определитель:
.
Определение. Минором некоторого элемента определителя называется определитель, полученный из данного путем вычеркивания строки и столбца, на пересечении которых стоит этот элемент. Обозначение минора .
Пример 4
Минор элемента а12: .
Определение. Алгебраическим дополнениемлюбого элемента определителя называется минор этого элемента, взятый со своим знаком, если сумма номеров строки и столбца, на пересечении которых стоит этот элемент, есть число четное, либо с противоположным знаком, если эта сумма есть число нечетное. Обозначение алгебраического дополнения Аij.
Пример 5
Свойство 1.Определитель равен сумме произведений элементов какого-нибудь столбца (или строки) на их алгебраические дополнения.
Пример 6
Вычислим определитель, разложив его по элементам 1-ой строки:
.
Свойство 2. Величина определителя не изменится, если каждую его строку заменить столбцом с тем же номером.
Свойство 3. Перестановка двух столбцов или двух строк определителя равносильна его умножению на (–1).
Свойство 4.Общий множитель всех элементов одного столбца или одной строки определителя можно вынести за знак определителя.
Свойство 5. Если все элементы какой-либо строки или какого-либо столбца равны нулю, то определитель равен нулю.
Свойство 6. Определитель, имеющий два одинаковых столбца или две одинаковых строки, равен нулю.
Свойство 7. Определитель равен нулю, если элементы двух столбцов или двух строк пропорциональны.
Свойство 8. Если каждый элемент некоторой строки (столбца) определителя представлен в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы), кроме данной, прежние, а в данной строке (столбце) в первом определителе стоят первые слагаемые, а во втором – вторые:
.
Свойство 9.Если к элементам некоторого столбца (или строки) определителя прибавить соответствующие элементы другого столбца (или строки), умноженные на общий множитель, то величина определителя не изменится.
Пример 7
Вычислим определитель:
,
при вычислении определителя первую строку умножили на 2 и сложили со второй, затем разложили определитель по 2-й строке.
Свойство 10. Сумма произведений элементов какого-нибудь столбца (или строки) на алгебраические дополнения элементов другого столбца (или строки) определителя равна нулю.
Обратная матрица
Пусть дана квадратная матрица А порядка n.
Обратной матрицей по отношению к данной А называется матрица , которая будучи умноженной, как справа, так и слева на данную матрицу, дает единичную матрицу.
По определению
А · = · А = Е.
Квадратная матрица называется неособенной или невырожденной, если определитель ее отличен от нуля. В противном случае матрица называется особенной или вырожденной.
Всякая неособенная матрица имеет обратную матрицу, которую можно найти по формуле
,
где — определитель матрицы А, — союзная матрица по отношению к данной матрице, в которой элементы каждой строки данной матрицы заменены алгебраическими дополнениями элементов соответствующих столбцов. Например, для квадратной матрицы 2-го порядка союзной является матрица
,
для квадратной матрицы 3-го порядка союзной является матрица
.
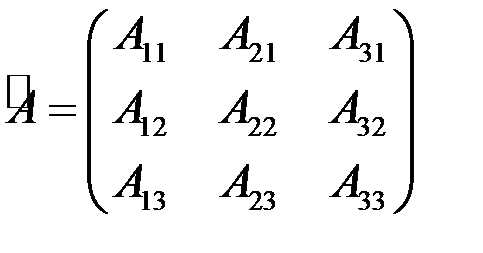Пример
Для матрицы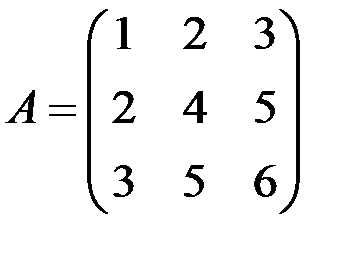 
найти обратную.
Решение
Обратную матрицу находим по формуле
.
Определитель матрицы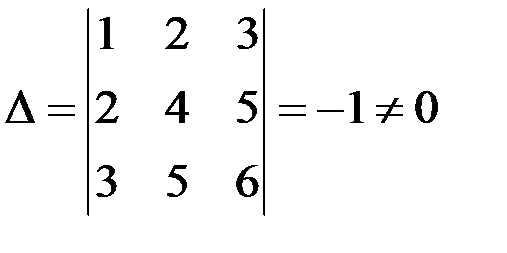 
, следовательно, матрица неособенная и обратная матрица существует. Найдем алгебраические дополнения элементов матрицы:
.
Тогда обратная матрица имеет вид
.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
zdamsam.ru
Вычисление определителей 2-го и 3-го порядков.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Квадратная таблица $$A=\begin{pmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{pmatrix}$$ составленная из четырех действительных или комплексных чисел называется квадратной матрицей 2-го порядка. Определителем 2-го порядка, соответствующим матрице $A$ (или просто определителем матрицы $A$) называется число $$\det A=\begin{vmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{vmatrix}=a_{11}a_{22}-a_{12}a_{21}.$$
Аналогично если $$A=\begin{pmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{pmatrix}$$
— квадратная матрица 3-го порядка, то соответсвующим ей определителем 3-го порядка называется число
$$\det A=\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}=$$ $$a_{11}a_{22}a_{33}+a_{21}a_{32}a_{13}+a_{12}a_{23}a_{31}-a_{13}a_{22}a_{31}-a_{12}a_{21}a_{33}-a_{23}a_{32}a_{11}.$$
Эту формулу называют «правило треугольника»: одно из трех слагаемых, входящих в правую часть со знаком «+», есть произведение элементов главной диагонали матрицы, каждое из двух других — произведение элементов лежащих на параллели к этой диагонали и элемента из противоположного угла матрицы, а слагаемые, входящие в со знаком минус, строятся таким же образом, но относительно второй (побочной) диагонали.
Примеры.
Вычислить определители второго порядка:
3.1. $\begin{vmatrix}-1&4\\-5&2\end{vmatrix}$
Решение.
$\begin{vmatrix}-1&4\\-5&2\end{vmatrix}=-1\cdot 2-(-5)\cdot 4=-2+20=18.$
Ответ: 18.
3.2. $\begin{vmatrix}a+b&a-b\\a-b&a+b\end{vmatrix}$
Решение.
$\begin{vmatrix}a+b&a-b\\a-b&a+b\end{vmatrix}=(a+b)^2-(a-b)^2=a^2+2ab+b^2-a^2+2ab-b^2=4ab.$
Ответ: $4ab.$
3.8. Решить уравнение:
$\begin{vmatrix}x&x+1\\-4&x+1\end{vmatrix}=0.$
Решение.
$\begin{vmatrix}x&x+1\\-4&x+1\end{vmatrix}=x(x+1)-(-4)(x+1)=x^2+x+4x-4=x^2+5x+4.$
Осталось решить квадратное уравнение $x^2+5x+4=0:$
$D=25-16=9$
$x_1=\frac{-5-3}{2}=-4;\qquad x_2=\frac{-5+3}{2}=-1.$
Ответ: $x_1=-4;\,\,\, x_2=-1.$
{jumi[*4]}
3.13. $\begin{vmatrix}3&4&-5\\8&7&-2\\2&-1&8\end{vmatrix}.$
Решение.
$\begin{vmatrix}3&4&-5\\8&7&-2\\2&-1&8\end{vmatrix}=3\cdot 7\cdot8+(-5)\cdot 8\cdot(-1)+4\cdot(-2)\cdot2-(-5)\cdot7\cdot2-$
$-4\cdot8\cdot8-3\cdot(-2)\cdot(-1)=168+40-16+70-256-6=0.$
Ответ: $0.$
3.16. $\begin{vmatrix}\sin\alpha&\cos\alpha&1\\\sin\beta&\cos\beta&1\\\sin\gamma&\cos\gamma&1\end{vmatrix}.$
Решение.
$\begin{vmatrix}\sin\alpha&\cos\alpha&1\\\sin\beta&\cos\beta&1\\\sin\gamma&\cos\gamma&1\end{vmatrix}=\sin\alpha\cos\beta+\sin\beta\cos\gamma+\cos\alpha\sin\gamma-$
$-\cos\beta\sin\gamma-\sin\alpha\cos\gamma-\cos\alpha\sin\beta=$
$=\sin(\alpha-\beta)+\sin(\beta-\gamma)+\sin(\gamma-\alpha).$
Ответ: $\sin(\alpha-\beta)+\sin(\beta-\gamma)+\sin(\gamma-\alpha).$
Свойства определителя:
1) Если матрицу транспонировать, то определитель не изменится: $\det A^T=\det A.$
2) Если все элементы строки (столбца) умножить на одно и тоже число, то определитель умножится на это число.
3) Если поменять местами две строки (столбца), то определитель поменяет знак. В частности, если две строки (столбца) равны, то определитель равен нулю.
4) Если каждый элемент некоторой строки (столбца) определителя представлен в виде суммы двух слагаемых, то определитель равен сумме двух определителей, у которых все строки (столбцы), кроме данной, прежние, а в данной строке (столбце) в первом определителе стоят первые, а во втором — вторые слагаемые.
5) Если одна строка (столбец) является линейной комбинацией других строк (столбцов), то определитель равен нулю.
6) Определитель не меняется если к одной из его строк (столбцов) добавить линейную комбинацию его других строк (столбцов).
Примеры:
3.24. Используя свойства определителя доказать следующее тождество: $\begin{vmatrix}a_1+b_1x&a_1-b_1x&c_1\\a_2+b_2x&a_2-b_2x&c_2\\a_3+b_3x&a_3-b_3x&c_3\end{vmatrix}=$ $-2x\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{vmatrix}.$
Доказательство.
$\begin{vmatrix}a_1+b_1x&a_1-b_1x&c_1\\a_2+b_2x&a_2-b_2x&c_2\\a_3+b_3x&a_3-b_3x&c_3\end{vmatrix}=$
$\begin{vmatrix}a_1&a_1-b_1x&c_1\\a_2&a_2-b_2x&c_2\\a_3&a_3-b_3x&c_3\end{vmatrix}+$ $\begin{vmatrix}b_1x&a_1-b_1x&c_1\\b_2x&a_2-b_2x&c_2\\b_3x&a_3-b_3x&c_3\end{vmatrix}=$
$=\begin{vmatrix}a_1&a_1&c_1\\a_2&a_2&c_2\\a_3&a_3&c_3\end{vmatrix}-$ $\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}+$ $\begin{vmatrix}b_1x&a_1&c_1\\b_2x&a_2&c_2\\b_3x&a_3&c_3\end{vmatrix}-$ $\begin{vmatrix}b_1x&b_1x&c_1\\b_2x&b_2x&c_2\\b_3x&b_3x&c_3\end{vmatrix}=$
$-\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}+$ $\begin{vmatrix}b_1x&a_1&c_1\\b_2x&a_2&c_2\\b_3x&a_3&c_3\end{vmatrix}=$ $-\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}-$ $\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}=$
$-2\begin{vmatrix}a_1&b_1x&c_1\\a_2&b_2x&c_2\\a_3&b_3x&c_3\end{vmatrix}=$ $-2x\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{vmatrix}.$
Что и требовалось доказать.
3.31. Проверить, что определитель $\begin{vmatrix}1&1&1\\x&y&z\\x^2&y^2&z^2\end{vmatrix}$ делится на $x-y, y-z$ и $z-x.$
Проверка.
1) Пользуясь 6-м свойством определителей от первого столбца отнимаем второй, а затем используем 2-е свойство и выносим общий множетель за определитель.
$\begin{vmatrix}1&1&1\\x&y&z\\x^2&y^2&z^2\end{vmatrix}=$ $\begin{vmatrix}0&1&1\\x-y&y&z\\x^2-y^2&y^2&z^2\end{vmatrix}=$ $\begin{vmatrix}0&1&1\\x-y&y&z\\(x-y)(x+y)&y^2&z^2\end{vmatrix}=$
$(x-y)\begin{vmatrix}0&1&1\\1&y&z\\x+y&y^2&z^2\end{vmatrix}.$
Таким образом, мы доказали, что определитель делится на $x-y.$ Совершенно аналогично доказываются и два других случая:
2) $\begin{vmatrix}1&1&1\\x&y&z\\x^2&y^2&z^2\end{vmatrix}=$ $\begin{vmatrix}1&0&1\\x&y-z&z\\x^2&y^2-z^2&z^2\end{vmatrix}=$ $\begin{vmatrix}1&0&1\\x&y-z&z\\x^2&(y-z)(y+z)&z^2\end{vmatrix}=$
$(y-z)\begin{vmatrix}1&0&1\\x&1&z\\x^2&y+z&z^2\end{vmatrix}.$
3) $\begin{vmatrix}1&1&1\\x&y&z\\x^2&y^2&z^2\end{vmatrix}=$ $\begin{vmatrix}1&1&0\\x&y&z-x\\x^2&y^2&z^2-x^2\end{vmatrix}=$ $\begin{vmatrix}1&1&0\\x&y&z-x\\x^2&y^2)&(z-x)(z+x)\end{vmatrix}=$
$(z-x)\begin{vmatrix}1&1&0\\x&y&1\\x^2&y^2&z+x\end{vmatrix}.$
Минором $M_{ij}$ элемента $a_{ij}$ матрицы $A$ $n-$ го порядка называется определитель $n-1-$ го порядка, полученного из исходного определителя вычеркиванием $i-$й строки и $j-$го столбца:
$M_{ij}=$\begin{vmatrix}a_{11}&\cdots&a_{1,j-1}&a_{1,j+1}&\cdots&a_{1n}\\\cdots&\cdots&\cdots&\cdots&\cdots&\cdots\\a_{i-1,1}&\cdots&a_{i-1,j-1}&a_{i-1,j+1}&\cdots&a_{i-1,n}\\a_{i+1,1}&\cdots&a_{i+1,j-1}&a_{i+1,j+1}&\cdots&a_{i+1,n}\\\cdots&\cdots&\cdots&\cdots&\cdots&\cdots\\a_{n1}&\cdots&a_{n,j-1}&a_{n,j+1}&\cdots&a_{nn}\end{vmatrix}
Алгебраическим дополнением $A_{ij}$ элемента $a_{ij}$ матрицы $A$ $n-$ го порядка называется число равное произведению минора $M_{ij}$ на $(-1)^{i+j}:$ $A_{ij}=(-1)^{i+j}M_{ij}.$
Определители $n-$го порядка вычисляются с помощью метода понижения порядка — по формуле $\det A=\sum\limits_{j=1}^na_{ij}A_{ij}$ ($i$ фиксированно) — разложение по $i-$й строке.
Из этой формулы и второго свойства определителей — $\det A^T=\det A,$ следует, что верна также формула разложения по $j$ столбцу $\det A=\sum\limits_{i=1}^na_{ij}A_{ij}$ ($j$ фиксированно).
Метод приведения к треугольному виду заключается в преобразовании определителя, когда все элементы, лежащие по одну сторону одной из ее диагоналей, становятся равными нулю. В этом случае определитель равен произведению диагональных элементов.
Примеры.
Вычислить определители, используя подходящее разложение по строке или столбцу.
3.50. $\begin{vmatrix}1&0&2\\0&2&0\\2&0&3\end{vmatrix}.$
Решение.
Вычислим этот определитель с помощью разложения по второй строке: $\begin{vmatrix}1&0&2\\0&2&0\\2&0&3\end{vmatrix}=$ $0\cdot(-1)^{2+1}\begin{vmatrix}0&2\\0&3\end{vmatrix}+$ $2\cdot(-1)^{2+2}\begin{vmatrix}1&2\\2&3\end{vmatrix}+$ $0\cdot(-1)^{2+3}\begin{vmatrix}1&0\\2&0\end{vmatrix}$ $=2(3-4)=-2.$
3.54. (a) $\begin{vmatrix}2&-3&4&1\\4&-2&3&2\\a&b&c&d\\3&-1&4&3\end{vmatrix}.$
Решение.
Вычислим этот определитель с помощью разложения по третьей строке: $\begin{vmatrix}2&-3&4&1\\4&-2&3&2\\a&b&c&d\\3&-1&4&3\end{vmatrix}=$ $a\cdot(-1)^{3+1}$ $\begin{vmatrix}-3&4&1\\-2&3&2\\-1&4&3\end{vmatrix}+$ $b\cdot(-1)^{3+2}\begin{vmatrix}2&4&1\\4&3&2\\3&4&3\end{vmatrix}+$ $+c\cdot(-1)^{3+3}\begin{vmatrix}2&-3&1\\4&-2&2\\3&-1&3\end{vmatrix}+$ $d\cdot(-1)^{3+4}\begin{vmatrix}2&-3&4\\4&-2&3\\3&-1&4\end{vmatrix}=$
$=a(-27-8-8+3+24+24)-b(18+16+24-9-16-48)+$
$+c(-12-4-18+6+4+36)-d(-16-16-27+24+6+48)=$
$=8a+15b+12c-19d.$
Ответ: $8a+15b+12c-19d.$
{jumi[*4]}
3.61. Вычислить определитель: $\begin{vmatrix}2&1&1&1&1\\1&3&1&1&1\\1&1&4&1&1\\1&1&1&5&1\\1&1&1&1&6\end{vmatrix}.$
Решение.
Вычислим этот определитель с помощью приведения определителя к треугольному виду:
$\begin{vmatrix}2&1&1&1&1\\1&3&1&1&1\\1&1&4&1&1\\1&1&1&5&1\\1&1&1&1&6\end{vmatrix}=$ от каждой из первых четырех строк отнимем пятую $=\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\1&1&1&1&6\end{vmatrix}=$ от пятой строки отнимем первую, затем пятую строку умножим на два
$=\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&1&1&1&11\end{vmatrix}=$ $\frac{1}{2}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&2&2&2&22\end{vmatrix}=$ Далее от пятой строки отнимем вторую, после чего пятую строку умножим на $\frac{3}{2}:$ $=\frac{1}{2}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&2&2&27\end{vmatrix}=$ $\frac{1}{2}\frac{2}{3}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&3&3&40,5\end{vmatrix}=$ Теперь от пятой строки отнимем третью, после чего пятую строку умножим на $\frac{4}{3}:$ $=\frac{1}{3}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&0&3&45,5\end{vmatrix}=$ $\frac{1}{3}\frac{3}{4}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&0&4&\frac{182}{3}\end{vmatrix}=$ Отнимем от пятой строки четвертую и перемножив диагональные элементы получаем ответ: $=\frac{1}{4}\begin{vmatrix}1&0&0&0&-5\\0&2&0&0&-5\\0&0&3&0&-5\\0&0&0&4&-5\\0&0&0&0&\frac{197}{3}\end{vmatrix}=$ $=\frac{1}{4}\cdot2\cdot3\cdot4\cdot\frac{197}{3}=394.$
Ответ: $394.$
Домашнее задание:
Вычислить определители второго порядка:
3.3. $\begin{vmatrix}\cos\alpha&-\sin\alpha\\\sin\alpha&\cos\alpha\end{vmatrix}.$
Ответ: $1.$
3.7. $\begin{vmatrix}\frac{1-t^2}{1+t^2}&\frac{2t}{1+t^2}\\-\frac{2t}{1+t^2}&\frac{1-t^2}{1+t^2}\end{vmatrix}.$
Ответ: $1.$
Решить уравнение:
3.9. $\begin{vmatrix}\cos 8x&-\sin 5x\\\sin 8x&\cos 5x\end{vmatrix}=0.$
Ответ: $x=\frac{\pi}{6}+\frac{\pi k}{3},$ $k\in Z.$
Вычислить определители 3-го порядка:
3.12. $\begin{vmatrix}1&2&3\\4&5&6\\7&8&9\end{vmatrix}.$
Ответ: $0.$
3.15. $\begin{vmatrix}\alpha^2+1&\alpha\beta&\alpha\gamma\\\alpha\beta&\beta^2+1&\beta\gamma\\\alpha\gamma&\beta\gamma&\gamma^2+1\end{vmatrix}.$
Ответ: $\alpha^2+\beta^2+\gamma^2+1.$
3.25. Используя свойства определителя доказать следующее тождество: $\begin{vmatrix}a_1+b_1x&a_1x+b_1&c_1\\a_2+b_2x&a_2x+b_2&c_2\\a_3+b_3x&a_3x+b_3&c_3\end{vmatrix}=$ $(1-x^2)\begin{vmatrix}a_1&b_1&c_1\\a_2&b_2&c_2\\a_3&b_3&c_3\end{vmatrix}.$
3.32. Проверить, что определитель $\begin{vmatrix}x&y&x+y\\y&x+y&x\\x+y&x&y\end{vmatrix}$ делится на $x+y$ и $x^2-xy+y^2.$
Вычислить определители, используя подходящее разложение по строке или столбцу.
3.51. $\begin{vmatrix}-1&5&2\\0&7&0\\1&2&0\end{vmatrix}.$
Ответ: $-14.$
3.52. $\begin{vmatrix}2&1&0\\1&2&1\\0&1&2\end{vmatrix}.$
Ответ: $4.$
3.54. (б) $\begin{vmatrix}5&a&2&-1\\4&b&4&-3\\2&c&3&-2\\4&d&5&-4\end{vmatrix}.$
Ответ: $2a-8b+c+5d.$
3.62. Вычислить определитель: $\begin{vmatrix}5&6&0&0&0\\1&5&6&0&0\\0&1&5&6&0\\0&0&1&5&6\\0&0&0&1&5\end{vmatrix}.$
Ответ: $665.$
{jumi[*4]}
mathportal.net
Определители квадратных матриц
К оглавлению
I. Определитель матрицы первого порядка
Определителем матрицы первого порядка, или определителем первого порядка, называется элемент, называется элемент а11:
.
II. Определитель матрицы второго порядка
Определителем матрицы второго порядка, или определителем второго порядка, называется число, которое вычисляется по формуле:
.
Например, пусть
.
III. Определитель матрицы третьего порядка
Определителем матрицы третьего порядка, или определителем третьего порядка, называется число, которое вычисляется по формуле:
Это число представляет алгебраическую сумму, состоящую из шести слагаемых. В каждое слагаемое входит ровно по одному элементу из каждой строки и каждого столбца матрицы. Каждое слагаемое состоит из произведения трех сомножителей.
Знаки, с которыми члены определителя входят в формулу нахождения определителя третьего порядка можно определить, пользуясь приведенной схемой, которая называется правилом треугольников или правилом Сарруса. Первые три слагаемые берутся со знаком плюс и определяются из левого рисунка, а последующие три слагаемые берутся со знаком минус и определяются из правого рисунка.
Пример. Вычислить определитель третьего порядка:
Решение.
Замечание. Вычисление определителей четвертого и более высокого порядка приводит к большим вычислениям, так как
· для нахождения определителя первого порядка мы находим одно слагаемое, состоящее из одного сомножителя,
· для нахождения определителя второго порядка нужно вычислить алгебраическую сумму из двух слагаемых, где каждое слагаемое состоит из произведения двух сомножителей,
· для нахождения определителя третьего порядка нужно вычислить алгебраическую сумму из шести слагаемых, где каждое слагаемое состоит из произведения трех сомножителей,
· для нахождения определителя четвертого порядка нужно вычислить алгебраическую сумму из двадцати четырех слагаемых, где каждое слагаемое состоит из произведения четырех сомножителей и т.д.
Определить количество слагаемых в алгебраической сумме, можно вычислив факториал:
Вычисление определителя четвертого порядка приводит к большим вычислениям. Поэтому в этом случае используют искусственные методы, о которых мы остановимся позже.
IV. Примеры для самостоятельного решения
А. Вычислить определитель второго порядка:
Б. Вычислить определитель третьего порядка:
В. Решить уравнение:
К оглавлению
miemp-mi-gor.narod.ru
1.2. Определители второго и третьего порядка. Обратная матрица
Определителем второго порядка, соответствующим матрице
называется число .
Этот определитель обозначают или .
Следовательно, согласно определению .
Определителем третьего порядка, соответствующим матрице , называется число, обозначаемое или и определяемое равенством
.
Для запоминания этого определения существует простое правило, которое называется «правилом треугольников». Каждое слагаемое, стоящее в правой части со знаком плюс, представляет собой произведение трех элементов определителя, взятых, как показано на схеме 1. Каждое слагаемое, стоящее со знаком минус, представляет собой произведение трех элементов определителя, взятых, как показано на схеме 2.
Минором элемента (I =1,2,3; J =1,2.3) определителя третьего порядка называется определитель второго порядка, получающийся из данного определителя третьего порядка вычеркиванием I-той строки J-того столбца, на пересечении которых стоит элемент . Минор элемента обозначают .
Алгебраическим дополнением элемента определителя третьего порядка называется произведение минора этого элемента на число , где I — номер строки, J — номер столбца, на пересечении которых стоит элемент . Алгебраическое дополнение элемента обозначают .
Таким образом,
Справедлива следующая теорема.
Определитель равен сумме произведений элементов какой-нибудь строки (или столбца) на их алгебраические дополнения, т. е.
Матрица называется Обратной матрицей по отношению к матрице , если выполняется условие: , где — единичная матрица.
Если определитель матрицы А отличен от нуля, то существует единственная обратная матрица , которая находится по формуле:
,
Где ∆ — определитель матрицы А,, — алгебраические дополнения элементов матрицы А.
Задание 2. Найти матрицу, обратную к данной матрице А.
.
Решение.
1) Вычислим определитель матрицы А:
.
, следовательно, обратная матрица существует и единственна.
2) Находим алгебраические дополнения элементов определителя
Матрицы А.
3) Составим обратную матрицу:
4) Проверим правильность нахождения матрицы , исходя из
Определения обратной матрицы.
Аналогично. Следовательно, обратная матрица найдена верно.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
| Главная > Учебные материалы > Математика: Определители квадратных матриц | ||||
|
1.Определители квадратных матриц. 2.Свойства определителей.
|
||||
| 1 2 3 4 5 6 7 8 9 | ||||
1.Определители квадратных матриц.Как известно из раздела матричной алгебры, матрицы получили широкое распрастранение в экономике. Для того, чтобы как-то характеризовать матрицу, а также решать различные задачи с использованием матриц, в математике введено понятие определитель матрицы. Т.е. определитель матрицы — это число, характеризующее матрицу (параметр). Для каждой квадратной матрицы можно рассчитать число по ее элементам по определенной формуле, которое будет ее характеризовать. |
||||
|
Для матрицы первого порядка определитель равен элементу а11. |
||||
Для матрицы второго порядка определитель равен разности произведений элементов матрицы, рассчитанный по формуле: |
 |
|||
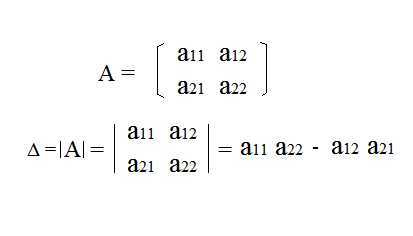Для матрицы третьего порядка определитель равен числу, рассчитанному по формуле: |
 |
|||
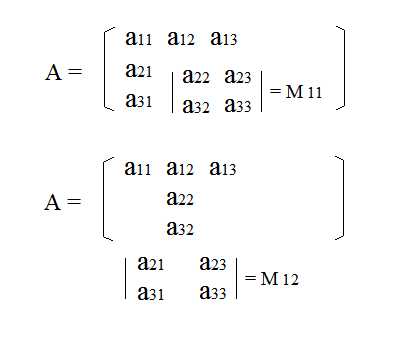
Определители квадратных матриц можно вычислить и другим способом: с помощью разложения элементов матрицы по строке. Для того, чтобы использовать такой способ, предварительно рассчитывают миноры и алгебраические дополнения. Минором Mij элемента аij называется определитель n-1 порядка, а алгебраическое дополнение это произведение Аij = (-1)i+j Mij |
 |
|||
|
Таким образом, определитель третьего порядка можно разложить по элементам первой строки так: |
 |
|||
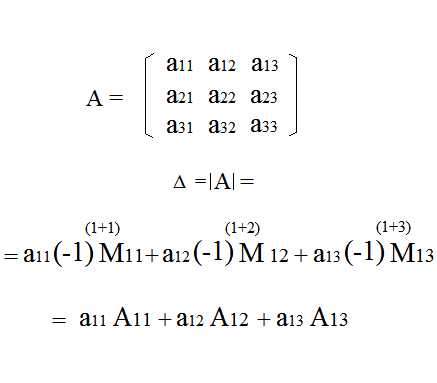2.Свойства определителей. |
||||
1. При транспонировании определитель не меняется. 2. Если поменять местами любые две строки (столбца) матрицы, то определитель поменяет знак на противоположный. 3. Для любой матрицы, определитель равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения. 4. Определитель равен нулю, если матрица содержит две одинаковые строки (столбца). 5. Определитель равен нулю, если все элементы какой-либо строки (столбца) равны нулю. 6. Если суммировать произведения элементов любой строки (столбца) на алгебраические дополнения элементов любой другой строки (столбца), то определитель равен нулю. 7. Общий множитель любой строки (столбца) можно вынести за знак определителя. |
||||
 |
||||
Пример. |
||||
 |
||||
| 1 2 3 4 5 6 7 8 9 | ||||
www.mathtask.ru