Тренажер «Примеры на все действия с рациональными числами»
Примеры на все действия с рациональными числами 6 класс.
Набор примеров широко использую в любом классе после 6-го для корректировки вычислительных навыков учащихся. Особенно в выпускных классах. Набор в двух вариантах: с ответами для учителя и без ответов для учащихся.
1 вариант
№1 (0,4 ∙ 2,38 – 3,452) : 4
— 2
= –3
№ 2 2
— 2
: (0,6 ∙ 3,28 – 5,468) = 3
№ 3 (0,4 ∙ 1,25 – 2,25 ) : 0,5 — = – 4
№ 4 — 2 + 0,54 : ( 0,8 ∙ 22,5 – 22,5) = – 2,37
4 вариант
№ 1 (2
— 5
+1
)∙(0,81 :0,4) = –3,23
№ 2 -1,5:0,5∙( 3
— 4 
— 1
) = 5,27
№ 3 — 3,075 :1,5+0,5∙ ( 0,04–3
) = –3,61
№ 4 (0,0612 : 0,6 — 
) ∙ 0,5 – 0,5 = – 0,649
7 вариант
№ 1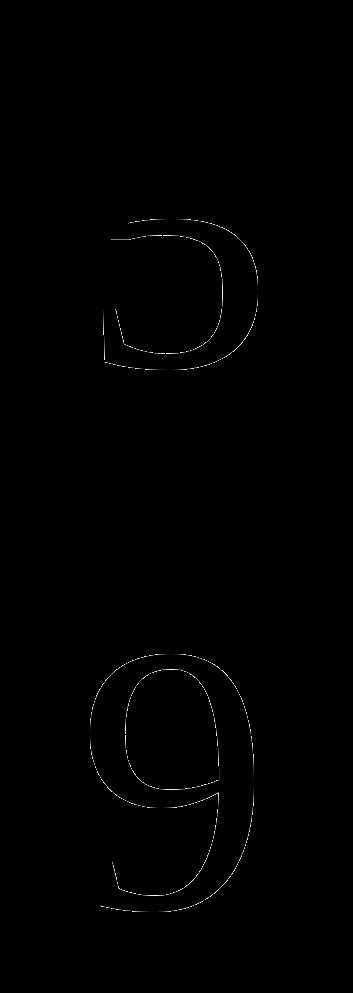 
№ 2 (0,9 – 0,412 : 0,4) ∙ 1,5 +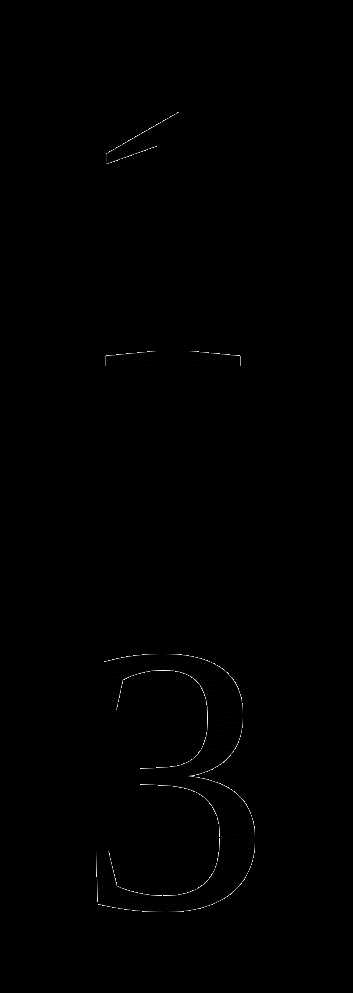 
= 
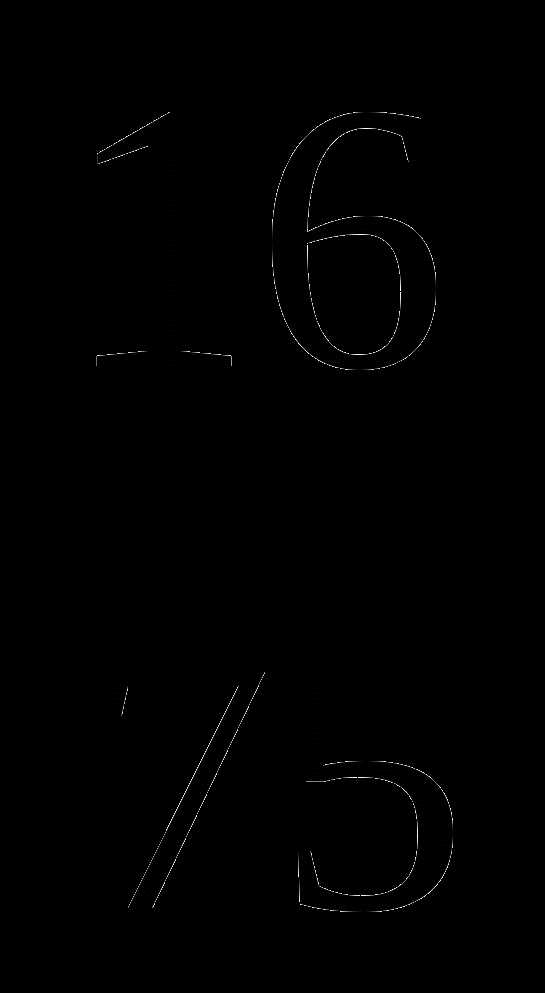
№ 3 ( — 1
∙ 0,5) : — = –
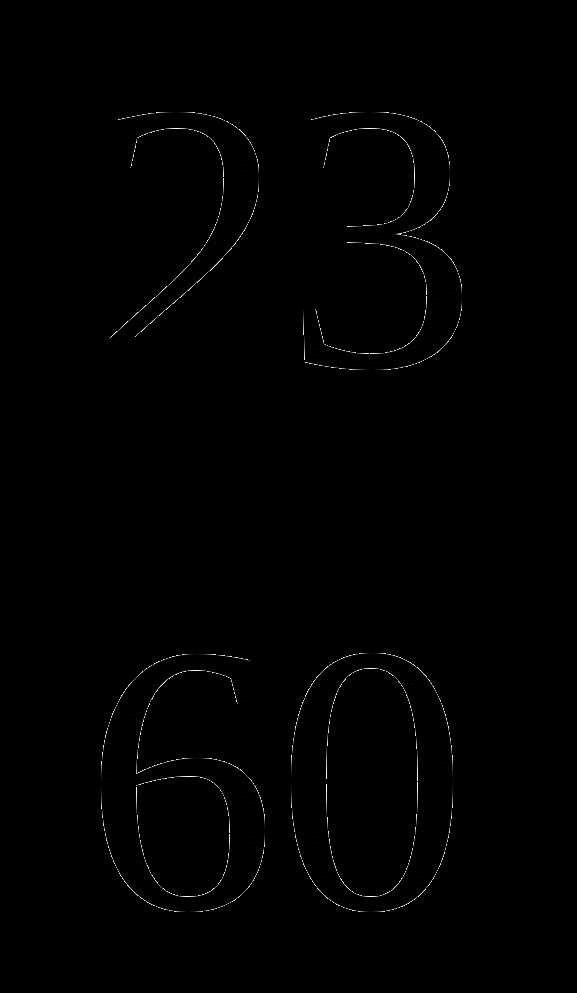
№ 4 — 1,25 + 
: ( ∙ 2,5 — 
2 вариант
№ 1 
+ 2 ∙ ( 0,82 : 0,4 – 2,4 ) = – 
№ 2 (0,005 – 0,041 : 0,2) ∙ 1,25 + = 
№ 3 ( — 
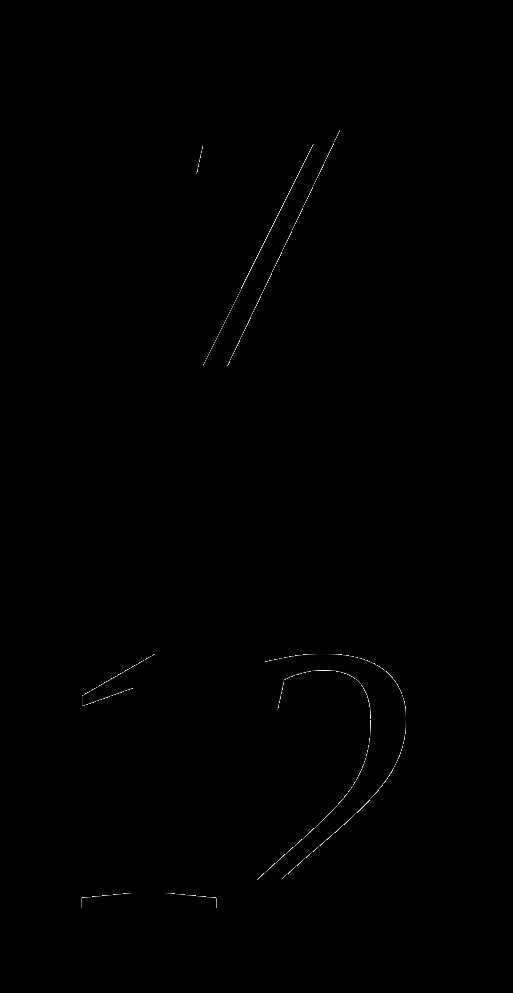∙ 0,5) : — = –
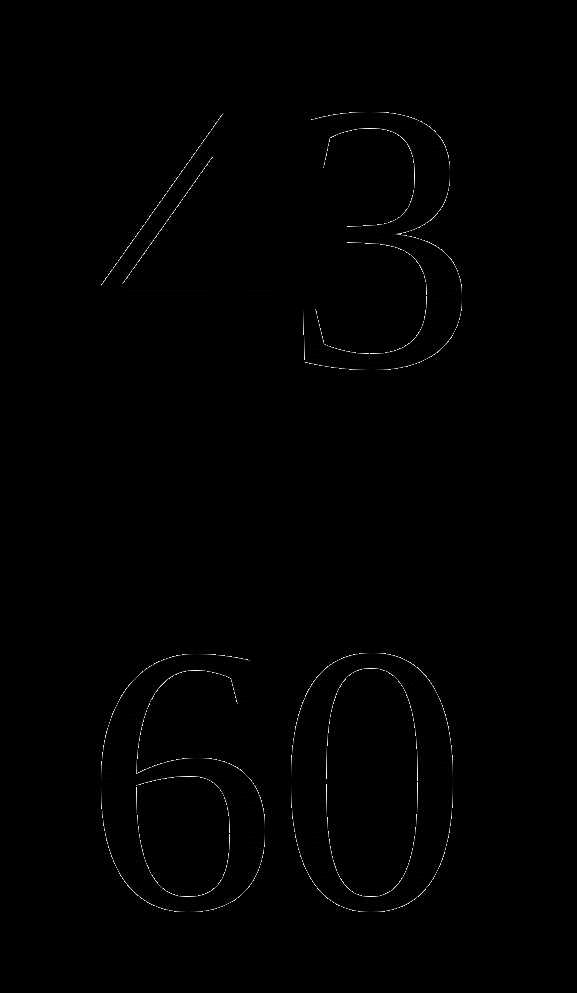
№ 4 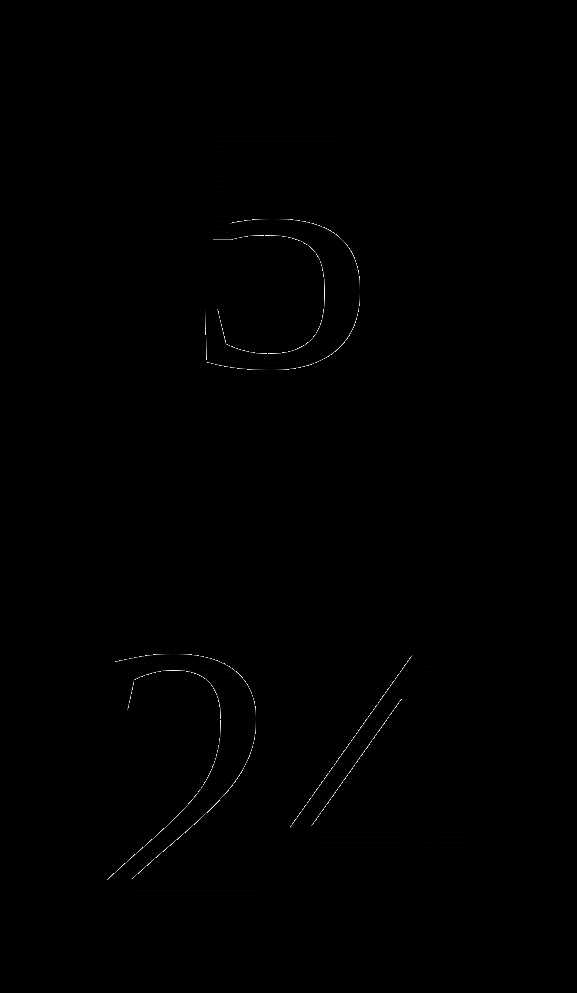— 0,25 + 
: (
) = – 10,255 вариант
№ 1 (0,02 ∙ 0,01–0,01 ):0,25 —
= –0,4142
№ 2 — 
+8,5∙(0,021:0,01– 2,51) = –4,235
№ 3 (0,15–0,15∙6,4):(–+0,175) = 4,05
№ 4 (1,6∙2,15–0,23):(3,45 – 3) = –10,7
8 вариант
№ 1 (
— 2,25 ) ∙ 0,16 – 0,42 : 0,4 = –1,26
№ 2 — 0,168 : 1,6 + 0,2 ∙ (0,45 — 
№ 3 — 0,54∙ ( — 
):(4,59:4,5 — 1,5) — 2 = – 2,125
№ 4 -3 +( 2,94:2,8–1,5)∙( — ) : ( – 0,036)= –4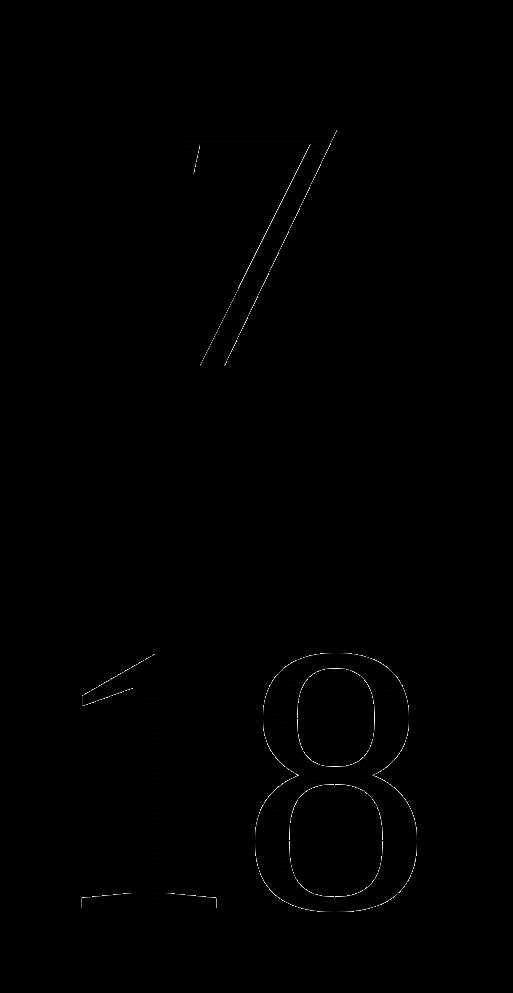
3 вариант
№ 1 (
— 0,45 ) ∙ 0,8 – 0,21 : 0,2 = –1,26
№ 2 0,6 ∙ (0,15 — ) – 0,042 : 0,4 = –0,24
№ 3 — 0,03 ∙ (-) : (1,53:1,5– 1,2) –1 = –1
№ 4 — 2 +(1,47:1,4–1,5) ∙ (-
6 вариант
№ 1 2+2 ∙(0,82:0,4–2,75 ∙ 1,2 = –
№ 2 (4,25∙0,16–2,575:2,5)∙ 6
+
= –
№ 3 (0,8 ∙ 2,25 – 4,5) : 0,25 – = –11,05
№ 4 – 2
+0,3:( 0,8 ∙ 6,75 – 6,25) = –2,44
9 вариант
№ — 7 + 2) ∙ (2,448 : 1,2) = – 3,23
№ 2 — 4,59 : 1,5 ∙ ( 5
— 6 — 1
) = 5,95
№ 3 — 0,615 : 0,3 + 0,2 ∙ (0,2 – 15) = – 5,17
№ 4 (0,1224 : 1,2 — ) ∙ 0,6 – 0,6 = – 0,7788
1 вариант
№1 (0,4 ∙ 2,38 – 3,452) : 4 — 2
№ 2 2 — 2: (0,6 ∙ 3,28 – 5,468)
№ 3 (0,4 ∙ 1,25 – 2,25 ) : 0,5 —
№ 4 — 2 + 0,54 : ( 0,8 ∙ 22,5 – 22,5)
4 вариант
№ 1 (2— 5+1)∙(0,81 :0,4)
№ 2 -1,5:0,5∙( 3 — 4 — 1
№ 3 — 3,075 :1,5+0,5∙ ( 0,04–3)
№ 4 (0,0612 : 0,6 — ) ∙ 0,5 – 0,5
7 вариант
№ 1 + 3 ∙ (15,45 : 1,5 – 11,8)
№ 2 (0,9 – 0,412 : 0,4) ∙ 1,5 +
№ 3 ( — 1 ∙ 0,5) : —
№ 4 — 1,25 +
∙ 2,5 — )2 вариант
№ 1 + 2 ∙ ( 0,82 : 0,4 – 2,4 )
№ 2 (0,005 – 0,041 : 0,2) ∙ 1,25 +
№ 3 ( — ∙ 0,5) : —
№ 4 — 0,25 + : (
)5 вариант
№ 1 (0,02 ∙ 0,01–0,01 ):0,25 —
№ 2 — +8,5∙(0,021:0,01– 2,51)
№ 3 (0,15–0,15∙6,4):(–+0,175)
№ 4 (1,6∙2,15–0,23):(3,45 – 3)
8 вариант
№ 1 ( — 2,25 ) ∙ 0,16 – 0,42 : 0,4
№ 2 — 0,168 : 1,6 + 0,2 ∙ (0,45 — )
№ 3 — 0,54∙ ( — ):(4,59:4,5 — 1,5) — 2
№ 4 -3 +( 2,94:2,8–1,5)∙( — ) : ( – 0,036)
3 вариант
№ 1 ( — 0,45 ) ∙ 0,8 – 0,21 : 0,2
№ 2 0,6 ∙ (0,15 — ) – 0,042 : 0,4
№ 3 — 0,03 ∙ (-) : (1,53:1,5– 1,2) –1
№ 4 — 2 +(1,47:1,4–1,5) ∙ (-):(-0,13)
6 вариант
№ 1 2+2 ∙(0,82:0,4–2,75 ∙ 1,2
№ 2 (4,25∙0,16–2,575:2,5)∙ 6+
№ 3 (0,8 ∙ 2,25 – 4,5) : 0,25 –
№ 4 – 2+0,3:( 0,8 ∙ 6,75 – 6,25)
9 вариант
№ 1 ( 3 — 7 + 2) ∙ (2,448 : 1,2)
№ 2 — 4,59 : 1,5 ∙ ( 5 — 6 — 1)
№ 3 — 0,615 : 0,3 + 0,2 ∙ (0,2 – 15)
№ 4 (0,1224 : 1,2 — ) ∙ 0,6 – 0,6
infourok.ru
Сравнение рациональных чисел, определения и примеры
Чтобы выполнить сравнение рациональных чисел или сравнение дробей, необходимо знать простые правила. Как сравнивать рациональные числа? Рассмотрим подробнее.
Сравнение рациональных чисел с одинаковыми знаменателями.
Если у рациональных чисел одинаковый положительный знаменатель, то переходим к сравнению числителей.
- Если положительные числители у дроби, то та дробь больше у которой числитель больше.
- Если отрицательные числители у дроби, то та дробь больше у которой числитель по модулю меньше.
- Если у числителей разные знаки, то та дробь больше у которой положительный знак.
Рассмотрим пример:
Сравните рациональные числа: а) \(\frac{3}{20}\) и \(\frac{7}{20}\) б) \(\frac{-5}{13}\) и \(\frac{-7}{13}\) в) \(\frac{4}{7}\) и \(\frac{-5}{7}\)
Решение:
а) Знаменатели одинаковые, переходим к сравнению числителей. У первого числителя число 3 у второго 7.
7>3
\(\frac{3}{20}б) При одинаковых знаменателях сравниваем числители.
|-7|=7
|-5|=5
7>5 у отрицательных чисел наоборот правее, а значит больше -7<-5
\(\frac{-5}{13} > \frac{-7}{13}\)в) С дробями у которых разные знаки все просто, всегда больше положительная дробь
\(\frac{4}{7} > \frac{-5}{7}\)Сравнение рациональных чисел с нулем.
Правила сравнения рациональных чисел с нулем.
- Если рациональное число положительно, то оно всегда будет больше нуля.
- Если рациональное число отрицательно, то оно всегда меньше нуля.
Рассмотрим пример:
Сравните с нулем рациональные числа: а) 0 и \(\frac{-1}{33}\) б) \(\frac{3}{4}\) и 0
Решение:
а) Дробь \(\frac{-1}{33}\) отрицательна, поэтому нуль будет больше рационального числа.
б) Дробь положительна \(\frac{3}{4}\), поэтому нуль будет меньше рационального числа.
\(\frac{3}{4} > 0\)Сравнение рациональных чисел с одинаковыми числителями и разными знаменателями.
Правило сравнение рациональных чисел с одинаковыми числителями:
Если у рациональных чисел одинаковые положительные числители и разные положительные знаменатели, та дробь больше у которой знаменатель меньше.
Разберем пример:
Сравните рациональные числа с одинаковыми числителями \(\frac{1}{4}\) и \(\frac{1}{16}\).
Решение:
Рассмотрим рисунок.
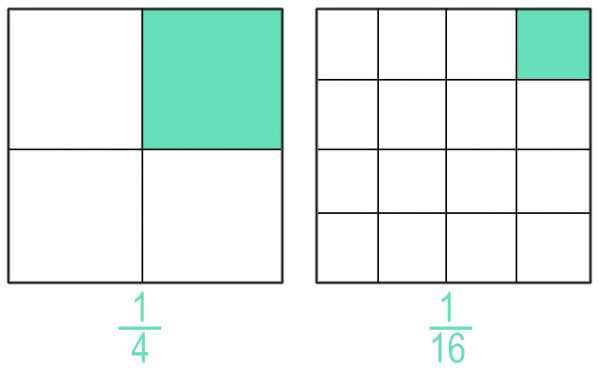
Видно, что взятая одна часть из четырех больше по размеру, чем взятая одна часть из 16. Поэтому, \(\frac{1}{4} > \frac{1}{16}\)
Если у дробей одинаковые отрицательные числители и разные положительные знаменатели, то та дробь больше у которой знаменатель больше.
Рассмотрим тот же пример:
Сравните дроби с одинаковыми отрицательными числителями \(\frac{-1}{4}\) и \(\frac{-1}{16}\).
Решение:
Из выше решенной задачи на рисунке мы видели, что 1 часть из 16 по размеру меньше, а значит и числовое значение имеет меньше, чем 1 часть из 4. Но в отрицательных числах меньшее отрицательное число на числовой прямой лежит ближе, то есть левее к нулю чем большее число.
Поэтому, \(\frac{-1}{4} < \frac{-1}{16}\)
Сравнение рациональных чисел с разными знаменателями.
Для начала ознакомимся с алгоритмом сравнения рациональных чисел:
- Нужно привести дроби к общему положительному знаменателю.
- Потом сравнить числители дробей по правилам сравнения дробей с одинаковыми знаменателями.
Рассмотрим пример:
Выполните сравнение рациональных чисел с разными знаменателями: а) \(\frac{3}{7}\) и \(\frac{2}{9}\) б) \(\frac{-5}{6}\) и \(\frac{-2}{3}\) в) \(\frac{1}{2}\) и \(\frac{-7}{10}\)
Решение:
а) Чтобы сравнить дроби \(\frac{3}{7}\) и \(\frac{2}{9}\) приведем их к общему знаменателю. Общим знаменателем будет число 63.
&\frac{3}{7}=\frac{3 \times 9}{7 \times 9}=\frac{27}{63} \\\\
&\frac{2}{9}=\frac{2 \times 7}{9 \times 7}=\frac{14}{63} \\\\
\end{align}\)
Получили две дроби с одинаковыми знаменателями, теперь сравниваем их числители 27>14.
\(\begin{align}&\frac{27}{63} > \frac{14}{63} \\\\
&\frac{3}{7} > \frac{2}{9} \\\\
\end{align}\)
б) Найдем общий знаменатель дробей \(\frac{-5}{6}\) и \(\frac{-2}{3}\), чтобы сравнить их. Общий знаменатель равен 6.
\(\frac{-2}{3}=\frac{-2 \times 2}{3 \times 2}=\frac{-4}{6}\)У отрицательных числителей больше то число, которое по модулю меньше.
|-5|=5
|-4|=4 это число меньше по модулю, поэтому -5<-4
&\frac{-5}{6} > \frac{-4}{6} \\\\
&\frac{-5}{6} > \frac{-2}{3} \\\\
\end{align}\)
в) Эти дроби \(\frac{1}{2}\) и \(\frac{-7}{10}\) можно не приводить к общему знаменателю, потому что у них разные знаки. Дробь с положительным знаком всегда больше дроби с отрицательным знаком.
\(\begin{align}\frac{1}{2} > \frac{-7}{10}\end{align}\)
Одинаковые рациональные числа.
Рациональные числа равны тогда, когда при одинаковых знаменателях равны их числители. Например:
\(\begin{align}\frac{1}{5} = \frac{1}{5}\end{align}\)
tutomath.ru
Рациональные числа. 8-й класс
Разделы: Математика
Цели урока:
Создать условия, при которых ученик:
- расширит представления учащихся о числе, сформирует понятие «рациональное число»;
- систематизирует знания о числовых множествах;
- познакомится с историей возникновения числовых множеств;
- приобретет навыки перевода рациональных чисел вида, а/n, где а — целое число, а n — натуральное в десятичную (конечную или бесконечную) дробь;
- приобретет навыки перевода бесконечных десятичных периодических дробей в рациональные числа вида а/n, где а — целое число, а n — натуральное;
- выявит различные способы перевода бесконечной десятичной периодической дроби в обыкновенную дробь;
- приобретет умения работать в парах,
- разовьет навыки самостоятельной работы, умения анализировать, сравнивать.
В результате ученик:
- знает, как определить вид числа;
- умеет представлять десятичную дробь в виде дроби a/n, где а — целое число, а n — натуральное;
- умеет представлять рациональное число в виде конечной или бесконечной периодической дроби;
- умеет представлять бесконечную периодическую дробь в виде обыкновенной дроби;
- умеет правильно пользоваться математической символикой в процессе выполнения заданий.
Оборудование к уроку: проектор, компьютер, тетрадь с печатной основой (приложение1), презентация.
Ход урока
I. Мотивационно — ориентировочный этап.
-Проверим домашнее задание (слайд 2),которое поможет нам определить тему урока.
Заполните пропуски в тетради с печатной основой (приложение, слайд 3)
Для счета предметов используются числа, которые называются натуральными. Для обозначения множества натуральных чисел употребляется буква : — первая буква латинского слова 2 : , «естественный», «натуральный». Натуральные числа, числа им противоположные и число нуль, образуют множество целых чисел, которое обозначается : — первой буквой немецкого слова 0 : - «число». Множество чисел, которые можно представить в виде называется множеством рациональных чисел и обозначается : первой буквой французского слова : («отношение».) Название этого множества происходит также от латинского слова : , что также переводится как «отношение»
-Спрогнозируйте тему урока. (Числовые множества)
— Известны ли вам те числовые множества, о которых идет речь в тексте. (Известны, их мы начали изучать в начальной школе, затем продолжили в 5,6 и 7 классах).
-Приведите примеры натуральных, целых и рациональных чисел.
-Вспомните отношения между множествами, назовите самое большое из них. (Множество рациональных чисел)
Уточним тему урока «Рациональные числа« (слайд 4) и запишем ее в тетрадь.
Спрогнозируйте цель урока: систематизировать знания о рациональных числах.
Краткая информация из истории развития числа сопровождается записями в тетради
:N — множество всех натуральных чисел, « n — натуральное число» ,
Z — множество всех целых чисел , » m — целое число» ,
Q — множество всех рациональных чисел, » r — рациональное число».
Историческая справка (слайды 5-18).
Натуральные числа возникли в силу необходимости вести счет любых предметов.
Натуральные числа несут ещё другую функцию: характеристику порядка предметов, расположенных в ряд.
О натуральном в смысле естественном ряде чисел говорится во «Введении в арифметику» греческого математика (неопифагорийца) Никомаха из Геразы.
В современном смысле понятие и термин «Натуральное число» встречается у французского философа и математика Ж.Даламбера(1717-1783)
Сумма и произведение натуральных чисел есть число натуральное.
Дроби естественно возникли при решении задач о разделе имущества, измерении земельных участков, исчислении времени.
Сумма, произведение и частное дробных чисел есть число дробное.
Доли или единичные дроби, у которых числитель единица, знаменателем же может быть любое целое число;
Дроби систематические, у которых числителями могут быть любые числа, знаменателями же - только числа некоторого частного вида, например, степени десяти или шестидесяти;
Дроби общего вида, у которых числители и знаменатели могут быть любыми числами.
Десятичные дроби в XV веке ввел самаркандский ученый ал — Каши. Ничего, не зная об открытии ал - Коши, десятичные дроби открыл второй раз, приблизительно через 150 лет, после него, фламандский ученый математик и инженер Симон Стевин в труде «Децималь» (1585 г).
Понятие отрицательных чисел возникло в практике решения алгебраических уравнений.
Отрицательные числа трактовались так же как долг при финансовых и бартерных расчетах.
Отрицательные числа ввели в математический обиход Михаэль Штифель (1487-1567) в книге «Полная арифметика» (1544), и Никола Шюке (1445-1500)- его работа была обнаружена в 1848 году.
Сумма, произведение и разность целых чисел есть число целое.
Отношения между множествами натуральных, целых и рациональных чисел наглядно демонстрирует геометрическая иллюстрация — круги Эйлера.
Леонард Эйлер жил в России в середине XVIII века и внес большой вклад в развитие математики.
Операционно-исполнительский этап.
Задание 1. (выполняется самостоятельно с последующей проверкой) (слайд 19 — проверка по щелчку)
Вычислите значения числовых выражений и изобразите их на кругах Эйлера числа а, в, с, d, m , если
| а в с d m |
1 : 5+0,8 =_________________________________ (1) 0,6: 0,2- 22 =________________________________ (-1) 17:3 -5 = __________________________________(1/3) (-1) 3 +( -1)2 =_______________________________ (0) 13 :2 +0,5 = _________________________________ (7) Оставшуюся на диаграмме точку обозначьте буквой «к«. |
Задание 2 — интерактивный тест (слайд 20 - триггер) устная работа.
Используя диаграмму, определите, какие из высказываний истинные, а какие ложные.
Нам уже известно, что любое рациональное число можно записать в виде отношения , где .
Выполните следующее задание:
Задание3 (работа в парах » сильный - слабый»)
Представьте в виде , где числа:
— 3; 2; 0; ; ; 0,23; -3,14
(; ; ; ; ; )
Вы также умеете записывать рациональные числа в виде десятичных дробей.
Задание 4 — интерактивный тест (слайд 21- триггер) устная работа.
Замените данные рациональные числа десятичными дробями.
| = (0,5) | = (0,2) | =(0,125) | = (0,(3)) |
| = (0,25) | = (0,4) | = (0,375) | =(0,6)) |
| =(0,75) | = (0,6) | =(0,625) | =(0,1(6)) |
Что замечаем? (Получились конечные и бесконечные десятичные дроби. В записи дробной части каждой бесконечной дроби повторяется одна и та же группа цифр).
Как называем мы такие бесконечные десятичные дроби? (Бесконечные десятичные периодические дроби).
Вспомните, как коротко мы записывали такие дроби. (Мы выделяли повторяющуюся группу цифр и записывали ее в круглые скобки).
Как называют повторяющуюся группу цифр? (Периодом).
Итак, различные рациональные числа представили их в виде десятичных дробей (конечных или бесконечных). Какой можно сделать вывод? (Любое рациональное число можно представить в виде десятичной дроби (конечной или бесконечной).
Вспомните, как записываются и читаются бесконечные десятичные дроби, выполнив следующее задание.
Задание 5 (работа в парах) (слайд 22)
Прочитайте дроби.
1) 0,(2) 2) 2,(21) 3) 1,(1) 4) -3,0(3) 5) -0,0(6) 6) 12,45(7)
Иногда периодические дроби разделяют на «чисто периодические», например. 0,(2) и «смешанные периодические»- 12,45(7).
Задание 6. Докажите, что равенства верны:
а) 0,222:= б) 0,8181:= в) 0,4666 :=
Каким способом мы это можем сделать?
Обыкновенную дробь представить в виде бесконечной десятичной периодической дроби, произведя деление числителя на знаменатель.
Сегодня мы рассмотрим два способа перевода десятичной периодической дроби в обыкновенную дробь (слайд 23, каждый шаг — по щелчку).
| Пусть х = 0,222:. 10 х = 2,222: 10х-х = 2,222:-0,222 9 х = 2 х = Значит, 0,222:= |
Сначала рассмотрим алгоритм перевода
чисто периодической дроби. Нужно умножить х на такое число, чтобы запятая передвинулась вправо ровно на один период. Каково это число? ( В периоде одна цифра, значит, надо умножить на 10). Вычтите из второго уравнение первое и найдите число х. |
По этому алгоритму проверьте второе равенство.
(Учащиеся записывают решение в тетради, один ученик выполняет задание у доски с комментариями)
Наводящий вопрос: на какое число нужно умножить бесконечную периодическую дробь, чтобы запятая передвинулась ровно на одну цифру.
В периоде две цифры, значит, надо умножить на 2.
х = 0,8181:
100 х = 81,8181:
100х—х = 81, 8181:-0,8181:
99 х = 81
х =
х = .
Значит, 0,8181:=
Запишем в виде обыкновенной дроби смешанную периодическую дробь 0,4666:
| х = 0,4666: 10х = 4,666: 100 х = 46,666: 100х -10 х = 46,666:-4,666.. 90 х = 42 х = , значит, 0,4666:= |
Мы с вами изучили правило перевода
чистой периодической дроби в обыкновенную. Как
из смешанной периодической дроби получить
чистую периодическую дробь? Умножить на 10 k ,гдек — число цифр до периода. В нашем случае на 10. Далее ваши действия аналогичны примеру 1. (Выполняются самостоятельно с последующей проверкой) |
Существует еще одно правило перевода чисто периодических и смешанных дробей в обыкновенную дробь. Примем их без доказательства (слайд 25,26, каждый шаг — по щелчку).
Чтобы обратить чисто периодическую десятичную дробь в обыкновенную, нужно в числителе обыкновенной дроби поставить число, образованное из цифр, стоящих в периоде, а в знаменатель — написать цифру 9 столько раз, сколько цифр в периоде.
Запишем дроби 0,222:и 0,8181: вторым способом
1) 0,222:= 2) 0,8181=
Чтобы обратить смешанную периодическую десятичную дробь в обыкновенную, нужно в числителе обыкновенной дроби поставить число, равное разности числа, образованного цифрами, стоящими после запятой до начала второго периода, и числа, образованное из цифр, стоящих после запятой до начала первого периода. Полученную разность взять в качестве числителя дроби; а в знаменателе написать цифру 9 столько раз, сколько цифр в периоде, и со столькими нулями, сколько цифр между запятой и началом периода.
1) 0,4(6) =
Какой способ позволяет быстрее достигнуть результата?
(Второй, но сформулировать правило достаточно сложно).
Задание 7 (взаимопроверка в парах) (слайд 27)
Представьте в виде обыкновенной дроби:
1) 1,(72) 2) 2,9(12) 3) 1,12(8)
Как представить данные десятичные дроби в виде обыкновенной дроби?
(Дробь нужно представить в виде суммы целого числа и бесконечной периодической дроби, бесконечную периодическую дробь перевести в обыкновенную дробь по правилу, затем смешанную дробь представить в виде , где.)
Рефлексивно-оценочный этап.
Итак, подведем итог нашего урока. Какова цель стояла перед нами в начале урока?
(Систематизировать знания о числовых множествах. Научиться переводить бесконечные периодические десятичные дроби в обыкновенные.)
Достигли ли мы этой цели?
(Цель наша достигнута. Мы знаем, что все числа объединены во множество рациональных чисел. На этом множестве выполняются все известные нам действия, кроме деления на ноль. Мы выделили свойства рациональных чисел: любое число может быть представлено в виде в виде дроби , где или в виде бесконечной периодической дроби. Научились переводить бесконечные периодические дроби в обыкновенные двумя способами, заметили, что второй способ трудно формулировать, но его применение ускорит получение результата).
Домашнее задание: по усмотрению учителя.
Графический диктант (проверка — слайд28).
1) 2011
2)
3) любое целое является рациональным.
4)
5)
6) любое целое число является натуральным.
7) любое рациональное число можно записать в виде конечной или бесконечной периодической дроби.
8) сумма, разность, произведение и частное (если делитель не ноль) рациональных чисел есть число рациональное.
9) (- 37,4 — 26,6) : (0,1) — натуральное.
10) Q -обозначение множества рациональных чисел.
Оценка настроения (слайд 29).
27.03.2011
xn--i1abbnckbmcl9fb.xn--p1ai
Рациональные числа
Учебник «Математика 6 класс» автор В.Я.Виленкин, В.И. Жохов.
Тема учебного занятия: «Рациональные числа»
Тип урока: Урок повторения изученного материала.
Цель и ожидаемый результат урока: Систематизировать знания по теме «Рациональные числа». Применять их в упражнениях практического характера.
Задачи урока (деятельность учителя)
1.Подвести обучающихся к совместной формулировке темы урока.
2.Создать условия для постановки учебных задач.
3.Обеспечить решение учебных задач через совместную деятельность по систематизации материала.
4.Организовать самоанализ и самооценку деятельности обучающихся на уроке.
Содержание и технология урока
Вводно-мотивационный этап урока.
Девиз нашего урока: «Чем больше я знаю, тем больше умею».
Ребята, а вы любите путешествовать? Сегодня нам в путешествии будет помогать математика. Выполняя задания, мы соприкоснемся с историей нашей Родины. Сегодня мы познакомимся с городами, в которых много памятников архитектуры, поэтому они стали крупными туристическими центрами.
Целеполагание.
Чтобы узнать тему нашего урока мы должны выполнить следующее задание:
Прочитайте числа. Как называются числа, записанные на доске?
-4; 0; 2,5; — 5; 7; -6; 7,5; 9; -5,5;-7,5;-7; -8; 10; 6,5
Определите тему нашего урока.
Итак, посмотрите на слайд, где записана тема: «Рациональные числа»
В течение всего урока вы должны себя оценивать и отмечать в лист самооценки, а в конце урока подведем итоги.
Применение полученных знаний в упражнениях практического характера.
Первая задача урока: повторить расположение чисел на координатной прямой.
Определим цель нашего путешествия.
3.1.Отметьте числа на координатной прямой:
Обучающимся выдаются карточки:
З (-8), О (-7,5), Л(-7), О(-6), Т(-5,5), О(-5), Е(-4)
К(-1), О(0), Л(1,5), Ь(2,5), Ц(4), О( 0)
Р(6,5), О (7), С( 7,5), С(8), И( 9), И (10)
Назовите точки, имеющие противоположные координаты.
Подведем итог: мы справились с задачей?
Оцените свою работу на данном этапе.
Цель путешествия: «Золотое кольцо России» — один из самых популярных туристических маршрутов, включающих в себя группу древних городов, занимающих особое место в истории русской земли. Города находятся недалеко от Москвы. Какие же это города?
Оцените, сможете ли вы выполнить данное задание?
3.2.Выполните действия:
-4,8 – 5,9 = -7,3 – (-0,3) =
6,2 – (-1,2) = 8,5 – (-3,5) =
7 – 9,3 = — 4,1 – 0,4 =
1,2- 12,3 = 4,1 – 7,1 =
Какую мы задачу выполнили, выполняя это задание?
Подведем итог: мы справились с задачей?
Оцените свою работу на данном этапе. Поднимите руку те, у кого совпала оценка до выполнения задания и после. Молодцы! Но она совпала не у всех, выясним причину.
Следующая наша задача: повторить понятие модуля.
3.3.Назовите модули данных чисел.
Следующая наша задача: сравнение чисел.
3.4.Расположите ответы в порядке возрастания. (1б)
3.5 Учитывая это заполните схему расположения этих городов.
-11.1 – Загорск -3 — Кострома
-10.7 – Переяславль Залесский -2.3 — Иваново
-7 – Ростов Великий 7,4 — Суздаль
-4.5 –Ярославль 12 – Владимир
Назовите, какую задачу мы будем решать, выполняя следующие задания?
3.6.Какой из городов был столицей Северо-Восточной Руси до Москвы?
54* (-2/5)* (-5/9) =
3.7.Узнайте год основания этого города:
-1/2* 3,5 + (-1/2)* (-2,5) =
Учитывается рациональный способ вычисления.
3.8. Определите название самого древнего города «Золотого кольца»:
(-1,5+3,4- 0,5): ( -0,2)=
Подведем небольшой итог: мы справились с данной задачей? Оцените свою работу на данном этапе.
Назовите задачу, которая у нас осталась.
Оцените, сможете ли вы решить данное уравнение?
3.9.В каком году он был образован?
1 вар. -1000+ х = -138
2 вар. – 0,03* х = — 25,86
Подведем итог: мы справились с задачей?
Оцените свою работу на данном этапе.
Поднимите руку те, у кого совпала оценка до решения уравнения и после. Молодцы! Я рада, что она совпала у всех.
Итог урока.
Домашнее задание
Выберите домашнее задание:
1.Узнай герб, какого города изображен?
2.Составьте задание на тему «Рациональные числа», связанное с городами «Золотого кольца»
5.Рефлексия.
videouroki.net
Рациональные числа — урок. Алгебра, 8 класс.
Некоторые символы математического языка
Тебе хорошо известны натуральные числа: \(1\), \(2\), \(3\), \(4…\)
Множество всех натуральных чисел обычно обозначают буквой ℕ.
Если к натуральным числам присоединить число \(0\) и все целые отрицательные числа: \(-1\), \(-2\), \(-3\), \(-4…\) — то получится множество целых чисел. Это множество обычно обозначают буквой ℤ.
Если к множеству целых чисел присоединить все обыкновенные дроби: 23;−12;83 и т. д. — то получится множество рациональных чисел. Это множество обычно обозначают буквой ℚ.
Любое целое число \(m\) можно записать в виде дроби m1, поэтому справедливо утверждение о том, что множество ℚ рациональных чисел — это множество, состоящее из чисел вида mn;−mn, где \(m, n\) — натуральные числа и число \(0\).
Используя введённые обозначения ℕ, ℤ, ℚ, условимся о следующем:
1. вместо фразы «\(n\) — натуральное число» можно писать n∈ℕ (читается: «элемент \(n\) принадлежит множеству ℕ»).
2. Вместо фразы «\(m\) — целое число» можно писать m∈ℤ.
3. Вместо фразы «\(r\) — рациональное число» можно писать r∈ℚ.
Понятно, что ℕ — часть множества ℤ, а ℤ — часть множества ℚ. Для описания этой ситуации в математике также имеется специальное обозначение: ℕ⊂ℤ,ℤ⊂ℚ.
Обрати внимание!
Математический символ ∈ называют знаком принадлежности (элемент принадлежит множеству).
Математический символ ⊂ называют знаком включения (одно множество cодержится в другом).
Вообще, в математике запись x∈X означает, что \(x\) — один из элементов множества \(X\). Запись A⊂B означает, что множество \(A\) представляет собой часть множества \(B\). Математики чаще говорят так: \(A\) — подмножество множества \(B\).Обрати внимание!
Множества в математике обычно обозначают прописными буквами, а элементы множества — строчными буквами.
А как записать, что элемент \(x\) не принадлежит множеству \(X\), или что множество \(A\) не является частью (подмножеством) множества \(B\)? Используют те же символы, но перечёркнутые косой чертой: x∉X;A⊄B.Рациональные числа как бесконечные десятичные периодические дроби
Для всех этих чисел можно использовать один и тот же способ записи, который мы сейчас и обсудим.Рассмотрим, например, целое число \(5\), обыкновенную дробь 722 и десятичную дробь \(8,377\).
Целое число \(5\) можно записать в виде бесконечной десятичной дроби: \(5,0000…\) Десятичную дробь \(8,377\) также можно записать в виде бесконечной десятичной дроби: \(8,377000…\) Для числа 722 воспользуемся методом «деления углом»:
Как видишь, начиная со второй цифры после запятой происходит повторение одной и той же группы цифр: \(18\), \(18\), \(18…\) Таким образом, 722 \(= 0,3181818…\) Короче это записывают так: \(0,3(18)\).
Повторяющуюся группу цифр после запятой называют периодом, а саму десятичную дробь — бесконечной десятичной периодической дробью.
Между прочим, и число \(5\) можно представить в виде бесконечной десятичной дроби. Для этого надо в периоде записать число \(0\):\(5 = 5,00000… = 5,(0)\).
Обрати внимание!
Вообще, любое рациональное число можно записать в виде бесконечной десятичной периодической дроби.
Этот вывод удобен для теории, но не очень удобен для практики. Ведь если дана конечная десятичная дробь \(8,377\), то зачем нужна её запись в виде 8,377(0)?
Поэтому обычно говорят так: любое рациональное число можно записать в виде конечной десятичной дроби или в виде бесконечной десятичной периодической дроби.
Выше мы показали, как обыкновенную дробь представляют в виде бесконечной периодической десятичной дроби. Верно и обратное: любую бесконечную десятичную периодическую дробь можно представить в виде обыкновенной дроби.
Это значит, что любая бесконечная десятичная периодическая дробь есть рациональное число.
www.yaklass.ru
Тест по алгебре (7 класс) на тему: Действия с рациональными числами
По теме: методические разработки, презентации и конспекты
устный счет, математика 6 класс. «Действия с рациональными числами»Не все дети любят считать. Но забавная «Пчелка» поможет проявить интерес даже к такой трудной теме. Эта презентация наверняка понравится вашим ученикам. А может использоваться и родителями….
Сказочное путешествие по теме «Действия с рациональными числами» (6 класс)Разработка урока с презентацией сказочное путешествие по теме: «Действия с рациональными числами» в 6 классе по учебнику Н.Я. Виленкина…
Обобщающий урок по теме «Все действия с рациональными числами» 6 классОбобщающий урок по теме «Все действия с рациональными числами» для 6 класса выполнен с применением игровых технологий. Сюжет урока — путешествие под водой с целью поиска пиратского клада. В данной мет…
Конспект урока по математике в 6 классе «Свойства действий с рациональными числами».Урок,объяснение нового материала на базе знаний 5 класса в виде устной работы,которая позволяет самим учащимся рассказать о свойствах действий с рациональными числами.На уроке ребята отрабатывают пере…
«Действия с рациональными числами», 6 классЦели:повторить действия сложения, вычитания, умножения и деления рациональных чисел; закрепить решений уравнений….
Математика 6 класс. Урок-путешествие «Полет в космос». Урок обобщения и систематизации по теме «Действия с рациональными числами и свойства действий с рациональными числами»В данной статье представлено описание урока обобщения и систематизации знаний по теме «Действия с рациональными числами и свойства действий с рациональными числами». Урок посвящен повторению правил, о…
Контрольная работа по теме «Модуль числа. Действия с рациональными числами» (6 класс)Контрольная работа по теме «Модуль числа. Действия с рациональными числами» (6 класс)…
nsportal.ru
Рациональные числа. Видеоурок. Математика 6 Класс
Мы уже говорили про множества натуральных и целых чисел. Множество натуральных чисел является подмножеством целых чисел .
Теперь мы узнали, что такое дроби, научились с ними работать. Дробь , например, не является целым числом. Значит, нужно описать новое множество чисел, куда будут входить все дроби, и этому множеству нужно название, четкое определение и обозначение.
Начнем с названия. Латинское слово ratio переводится на русский язык как отношение, дробь. Название нового множества «рациональные числа» и происходит от этого слова. То есть «рациональные числа» можно перевести как «дробные числа».
Разберемся, из каких чисел состоит это множество. Можно предположить, что оно состоит из всех дробей. Например, таких – . Но такое определение было бы не совсем корректным. Дробь – это не само число, а форма записи числа. В примере, представленном ниже, две разные дроби обозначают одно и то же число:
Тогда точнее будет сказать, что рациональные числа – это те числа, которые можно представить в виде дроби. И это в самом деле уже почти то самое определение, которое и используют в математике.
Обозначили это множество буквой . А как связаны множества натуральных и целых чисел с новым множеством рациональных чисел? Натуральное число можно записать в виде дроби, причем бесконечным числом способов . А раз его можно представить в виде дроби, то оно тоже является рациональным.
С отрицательными целыми числами аналогичная ситуация. Любое целое отрицательное число можно представить в виде дроби . А можно ли число ноль представить в виде дроби? Конечно, можно, тоже бесконечным числом способов .
Таким образом, все натуральные и все целые числа тоже являются рациональными числами. Множества натуральных и целых чисел являются подмножествами множества рациональных чисел ().
Замкнутость множеств относительно арифметических операций
Необходимость введения новых чисел – целых, затем рациональных – м ожно объяснять не только задачами из реальной жизни. Сами арифметические операции подсказывают нам это. Сложим два натуральных числа: . Получим снова натуральное число.
Говорят, множество натуральных чисел замкнуто относительно операции сложения ( замкнуто относительно сложения). Самостоятельно подумайте, замкнуто ли множество натуральных чисел относительно умножения.
Как только мы пытаемся вычесть из числа равное ему или большее, то натуральных чисел нам не хватает. Введение нуля и отрицательных целых чисел исправляет ситуацию:
Множество целых чисел замкнуто относительно вычитания. Мы можем складывать и вычитать любые целые числа, не опасаясь, что у нас не будет числа, чтобы записать результат ( замкнуто относительно сложения и вычитания).
Замкнуто ли множество целых чисел относительно умножения? Да, произведение любых двух целых чисел дает в результате целое число ( замкнуто относительно сложения, вычитания и умножения).
Осталось еще одно действие – деление. Замкнуто ли множество целых чисел относительно деления? Ответ очевиден: нет. Поделим на . Среди целых чисел нет такого, чтобы записать ответ: .
Но с помощью дробного числа мы почти всегда можем записать результат деления одного целого числа на другое. Почему почти? Вспомним, что, по определению, делить на ноль нельзя.
Таким образом, множество рациональных чисел (которое возникает при введении дробей) претендует на роль множества, замкнутого относительно всех четырех арифметических операций.
Давайте проверим.
- Сумма двух рациональных чисел всегда рациональное число: .
- Разность двух рациональных чисел всегда рациональное число: .
- Произведение двух рациональных чисел всегда рациональное число: .
- Частное двух рациональных чисел – рациональное число, за исключением деления на ноль: .
То есть множество рациональных чисел замкнуто относительно сложения, вычитания, умножения и деления, исключая деление на ноль. В этом смысле можно говорить, что множество рациональных чисел устроено «лучше», чем предшествующие множества натуральных и целых чисел. Означает ли это, что рациональные числа – последнее числовое множество, которое мы изучаем? Нет. Впоследствии у нас появятся другие числа, которые нельзя записать в виде дробей, например иррациональных.
Числа как инструмент
Числа – это инструмент, которые человек создавал по мере необходимости.
Рис. 1. Использование натуральных чисел
Понадобилось считать предметы или нумеровать их – появились натуральные числа () (см. рис. 1).
Дальше, когда понадобилось вести денежные расчеты, перед числом стали ставить знаки плюс или минус, показывая, нужно увеличить или уменьшить исходную величину. Так появились отрицательные и положительные числа. Новое множество назвали множеством целых чисел ().
Рис. 2. Использование дробных чисел
Считать нужно не только целые количества, но и дробные: например, литра воды (см. рис. 2).
Поэтому появляется новый инструмент, новые числа – дроби. Мы их записываем разными эквивалентными способами: обыкновенными и десятичными дробями ().
Все числа – «старые» (целые) и «новые» (дробные) – объединили в одно множество и назвали его множеством рациональных чисел ( – рациональные числа )
Итак, рациональное число – это число, которое можно представить в виде обыкновенной дроби. Но это определение в математике еще немного уточняют. Любое рациональное число можно представить в виде дроби с положительным знаменателем, то есть отношением целого числа к натуральному: .
Тогда получаем определение: число называется рациональным, если его можно представить в виде дроби с целым числителем и натуральным знаменателем ().
Кроме обыкновенных дробей, мы используем и десятичные. Посмотрим, как они связаны с множеством рациональных чисел.
Десятичные дроби бывают трех видов: конечные, периодические и непериодические.
- Конечные десятичные дроби: после запятой стоит конечное количество цифр: .
- Бесконечные периодические дроби: после запятой стоит бесконечное количество цифр, но одна или несколько цифр повторяются. Повторяющиеся цифры называют периодом. Для краткости записи его записывают в скобках. Цифры между запятой и периодом называют предпериодом. В первом числе предпериода нет, во втором он равен :
Бесконечные непериодические дроби: у таких дробей тоже бесконечное количество цифр после запятой, но периода нет. Примером является десятичная запись числа ПИ:
Любая конечная десятичная дробь по определению – это обыкновенная дробь со знаменателем и т.д.
Прочитаем десятичную дробь вслух и запишем в виде обыкновенной: , .
При обратном переходе от записи в виде обыкновенной дроби к десятичной могут получаться конечные десятичные дроби или бесконечные периодические дроби.
Переход от обыкновенной дроби к десятичной
Самый простой случай, когда знаменатель дроби – это степень десятки: и т.д. Тогда мы пользуемся определением десятичной дроби:
Есть дроби, у которых знаменатель легко приводится к такому виду: . Перейти к такой записи возможно, если в разложение знаменателя входят только двойки и пятерки.
Знаменатель состоит из трех двоек и одной пятерки. Каждая
interneturok.ru