Примеры решение слау методом гаусса – Метод Гаусса

Содержание

Метод Гаусса

Метод Гаусса: описание алгоритма решения системы линейных уравнений, примеры, решения.

Метод Гаусса прекрасно подходит для решения систем линейных алгебраических уравнений (СЛАУ). Он обладает рядом преимуществ по сравнению с другими методами:

во-первых, нет необходимости предварительно исследовать систему уравнений на совместность;
во-вторых, методом Гаусса можно решать не только СЛАУ, в которых число уравнений совпадает с количеством неизвестных переменных и основная матрица системы невырожденная, но и системы уравнений, в которых число уравнений не совпадает с количеством неизвестных переменных или определитель основной матрицы равен нулю;
в-третьих, метод Гаусса приводит к результату при сравнительно небольшом количестве вычислительных операций.

Краткий обзор статьи.

Сначала дадим необходимые определения и введем обозначения.

Далее опишем алгоритм метода Гаусса для простейшего случая, то есть, для систем линейных алгебраических уравнений, количество уравнений в которых совпадает с количеством неизвестных переменных и определитель основной матрицы системы не равен нулю. При решении таких систем уравнений наиболее отчетливо видна суть метода Гаусса, которая заключается в последовательном исключении неизвестных переменных. Поэтому метод Гаусса также называют методом последовательного исключения неизвестных. Покажем подробные решения нескольких примеров.

В заключении рассмотрим решение методом Гаусса систем линейных алгебраических уравнений, основная матрица которых либо прямоугольная, либо вырожденная. Решение таких систем имеет некоторые особенности, которые мы подробно разберем на примерах.

Навигация по странице.

Основные определения и обозначения.
Решение систем линейных алгебраических уравнений, в которых число уравнений равно числу неизвестных и основная матрица системы невырожденная, методом Гаусса.
Решение систем линейных алгебраических уравнений, в которых число уравнений не совпадает с числом неизвестных или основная матрица системы вырожденная, методом Гаусса.

Основные определения и обозначения.

Рассмотрим систему из p линейных уравнений с n неизвестными (p может быть равно n): где- неизвестные переменные,- числа (действительные или комплексные),- свободные члены.

Если , то система линейных алгебраических уравнений называетсяоднородной, в противном случае – неоднородной.

Совокупность значения неизвестных переменных , при которых все уравнения системы обращаются в тождества, называетсярешением СЛАУ.

Если существует хотя бы одно решение системы линейных алгебраических уравнений, то она называется

совместной, в противном случае – несовместной.

Если СЛАУ имеет единственное решение, то она называется определенной. Если решений больше одного, то система называется неопределенной.

Говорят, что система записана в координатной форме, если она имеет вид .

Эта система в матричной форме записи имеет вид , где- основная матрица СЛАУ,- матрица столбец неизвестных переменных,- матрица свободных членов.

Если к матрице А добавить в качестве (n+1)-ого столбца матрицу-столбец свободных членов, то получим так называемую расширенную матрицу системы линейных уравнений. Обычно расширенную матрицу обозначают буквой Т, а столбец свободных членов отделяют вертикальной линией от остальных столбцов, то есть,

Квадратная матрица А называется вырожденной, если ее определитель равен нулю. Если , то матрицаА называется невырожденной.

Следует оговорить следующий момент.

Если с системой линейных алгебраических уравнений произвести следующие действия

поменять местами два уравнения,
умножить обе части какого-либо уравнения на произвольное и отличное от нуля действительное (или комплексное) число k,
к обеим частям какого-либо уравнения прибавить соответствующие части другого уравнения, умноженные на произвольное число k,

то получится эквивалентная система, которая имеет такие же решения (или также как и исходная не имеет решений).

Для расширенной матрицы системы линейных алгебраических уравнений эти действия будут означать проведение элементарных преобразований со строками:

перестановку двух строк местами,
умножение всех элементов какой-либо строки матрицы T на отличное от нуля число k,
прибавление к элементам какой-либо строки матрицы соответствующих элементов другой строки, умноженных на произвольное число
k.

Теперь можно переходить к описанию метода Гаусса.

К началу страницы

Решение систем линейных алгебраических уравнений, в которых число уравнений равно числу неизвестных и основная матрица системы невырожденная, методом Гаусса.

Как бы мы поступили в школе, если бы получили задание найти решение системы уравнений .

Некоторые сделали бы так.

Заметим, что прибавив к левой части второго уравнения левую часть первого, а к правой части — правую, можно избавиться от неизвестных переменных x₂ и x₃ и сразу найти x₁:

Подставляем найденное значение x₁=1 в первое и третье уравнение системы:

Если умножить обе части третьего уравнения системы на -1 и прибавить их к соответствующим частям первого уравнения, то мы избавимся от неизвестной переменной

x₃ и сможем найти x₂:

Подставляем полученное значение x₂=2 в третье уравнение и находим оставшуюся неизвестную переменную x₃:

Другие поступили бы иначе.

Разрешим первое уравнение системы относительно неизвестной переменной x₁ и подставим полученное выражение во второе и третье уравнение системы, чтобы исключить из них эту переменную:

Теперь разрешим второе уравнение системы относительно x₂ и подставим полученный результат в третье уравнение, чтобы исключить из него неизвестную переменную x₂: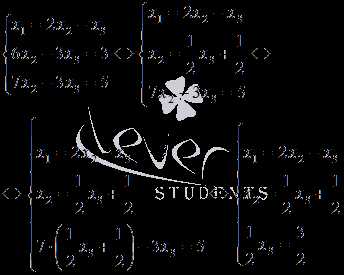

Из третьего уравнения системы видно, что x₃=3. Из второго уравнения находим , а из первого уравнения получаем.

Знакомые способы решения, не правда ли?

Самое интересное здесь то, что второй способ решения по сути и есть метод последовательного исключения неизвестных, то есть, метод Гаусса. Когда мы выражали неизвестные переменные (сначала x₁, на следующем этапе x₂) и подставляли их в остальные уравнения системы, мы тем самым исключали их. Исключение мы проводили до того момента, пока в последнем уравнении не осталась одна единственная неизвестная переменная. Процесс последовательного исключения неизвестных называется прямым ходом метода Гаусса. После завершения прямого хода у нас появляется возможность вычислить неизвестную переменную, находящуюся в последнем уравнении. С ее помощью из предпоследнего уравнения находим следующую неизвестную переменную и так далее. Процесс последовательного нахождения неизвестных переменных при движении от последнего уравнения к первому называется обратным ходом метода Гаусса

Следует заметить, что когда мы выражаем x₁ через x₂ и x₃ в первом уравнении, а затем подставляем полученное выражение во второе и третье уравнения, то к такому же результату приводят следующие действия:

к левой и правой частям второго уравнения прибавляем соответствующие части первого уравнения, умноженные на ,
к левой и правой частям третьего уравнения прибавляем соответствующие части первого уравнения, умноженные на .

Действительно, такая процедура также позволяет исключить неизвестную переменную x₁ из второго и третьего уравнений системы:

Нюансы с исключением неизвестных переменных по методу Гаусса возникают тогда, когда уравнения системы не содержат некоторых переменных.

Например, в СЛАУ в первом уравнении отсутствует неизвестная переменная

x₁ (иными словами, коэффициент перед ней равен нулю). Поэтому мы не можем разрешить первое уравнение системы относительно x₁, чтобы исключить эту неизвестную переменную из остальных уравнений. Выходом из этой ситуации является перестановка местами уравнений системы. Так как мы рассматриваем системы линейных уравнений, определители основных матриц которых отличны от нуля, то всегда существует уравнение, в котором присутствует нужная нам переменная, и мы это уравнение можем переставить на нужную нам позицию. Для нашего примера достаточно поменять местами первое и второе уравнения системы , дальше можно разрешить первое уравнение относительноx₁ и исключить ее из остальных уравнений системы (хотя во втором уравнении x₁ уже отсутствует).

Надеемся, что суть Вы уловили.

Опишем алгоритм метода Гаусса.

Пусть нам требуется решить систему из

n линейных алгебраических уравнений с nнеизвестными переменными вида , и пусть определитель ее основной матрицы отличен от нуля.

Будем считать, что , так как мы всегда можем этого добиться перестановкой местами уравнений системы. Исключим неизвестную переменнуюx₁ из всех уравнений системы, начиная со второго. Для этого ко второму уравнению системы прибавим первое, умноженное на , к третьему уравнению прибавим первое, умноженное на, и так далее, кn-омууравнению прибавим первое, умноженное на . Система уравнений после таких преобразований примет видгде, а.

К такому же результату мы бы пришли, если бы выразили x₁ через другие неизвестные переменные в первом уравнении системы и полученное выражение подставили во все остальные уравнения. Таким образом, переменная x₁ исключена из всех уравнений, начиная со второго.

Далее действуем аналогично, но лишь с частью полученной системы, которая отмечена на рисунке

Будем считать, что (в противном случае мы переставим местами вторую строку сk-ой, где ). Приступаем к исключению неизвестной переменнойx₂ из всех уравнений, начиная с третьего.

Для этого к третьему уравнению системы прибавим второе, умноженное на , к четвертому уравнению прибавим второе, умноженное на, и так далее, кn-омууравнению прибавим второе, умноженное на . Система уравнений после таких преобразований примет видгде, а. Таким образом, переменнаяx₂ исключена из всех уравнений, начиная с третьего.

Далее приступаем к исключению неизвестной x₃, при этом действуем аналогично с отмеченной на рисунке частью системы

Так продолжаем прямой ход метода Гаусса пока система не примет вид

С этого момента начинаем обратный ход метода Гаусса: вычисляем x_n из последнего уравнения как , с помощью полученного значенияx_n находим x_n-1 из предпоследнего уравнения, и так далее, находим x₁ из первого уравнения.

Разберем алгоритм на примере.

Пример.

Найдите решение системы уравнений методом Гаусса.

Решение.

Коэффициент a₁₁ отличен от нуля, так что приступим к прямому ходу метода Гаусса, то есть, к исключению неизвестной переменной x₁ из всех уравнений системы, кроме первого. Для этого к левой и правой частям второго, третьего и четвертого уравнения прибавим левую и правую части первого уравнения, умноженные соответственно на ,и: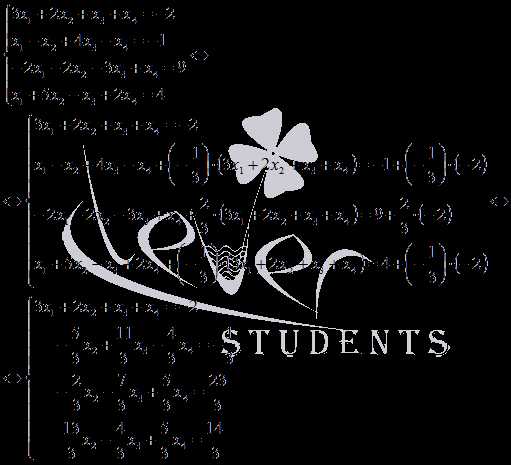

Неизвестную переменную x₁ исключили, переходим к исключению x₂. К левым и правым частям третьего и четвертого уравнений системы прибавляем левую и правую части второго уравнения, умноженные соответственно на и:

Для завершения прямого хода метода Гаусса нам осталось исключить неизвестную переменную x₃ из последнего уравнения системы. Прибавим к левой и правой частям четвертого уравнения соответственно левую и правую часть третьего уравнения, умноженную на :

Можно начинать обратный ход метода Гаусса.

Из последнего уравнения имеем , из третьего уравнения получаем, из второго, из первого.

Для проверки можно подставить полученные значения неизвестных переменных в исходную систему уравнений. Все уравнения обращаются в тождества, что говорит о том, что решение по методу Гаусса найдено верно.

Ответ:

А сейчас приведем решение этого же примера методом Гаусса в матричной форме записи.

Пример.

Найдите решение системы уравнений методом Гаусса.

Решение.

Расширенная матрица системы имеет вид . Сверху над каждым столбцом записаны неизвестные переменные, которым соответствуют элементы матрицы.

Прямой ход метода Гаусса здесь предполагает приведение расширенной матрицы системы к трапецеидальному виду с помощью элементарных преобразований. Этот процесс схож с исключением неизвестных переменных, которое мы проводили с системой в координатной форме. Сейчас Вы в этом убедитесь.

Преобразуем матрицу так, чтобы все элементы в первом столбце, начиная со второго, стали нулевыми. Для этого к элементам второй, третьей и четвертой строк прибавим соответствующие элементы первой строки умноженные на ,и насоответственно:

Далее полученную матрицу преобразуем так, чтобы во втором столбце все элементы, начиная с третьего стали нулевыми. Это будет соответствовать исключению неизвестной переменной x₂. Для этого к элементам третьей и четвертой строк прибавим соответствующие элементы первой строки матрицы, умноженные соответственно на и:

Осталось исключить неизвестную переменную x₃ из последнего уравнения системы. Для этого к элементам последней строки полученной матрицы прибавим соответствующие элементы предпоследней строки, умноженные на :

Следует отметить, что эта матрица соответствует системе линейных уравнений которая была получена ранее после прямого хода.

Пришло время обратного хода. В матричной форме записи обратный ход метода Гаусса предполагает такое преобразование полученной матрицы, чтобы матрица, отмеченная на рисунке стала диагональной, то есть, приняла видгде- некоторые числа.

Эти преобразования аналогичны преобразованиям прямого хода метода Гаусса, но выполняются не от первой строки к последней, а от последней к первой.

Прибавим к элементам третьей, второй и первой строк соответствующие элементы последней строки, умноженные на , наи насоответственно:

Теперь прибавим к элементам второй и первой строк соответствующие элементы третьей строки, умноженные на и насоответственно:

На последнем шаге обратного хода метода Гаусса к элементам первой строки прибавляем соответствующие элементы второй строки, умноженные на :

Полученная матрица соответствует системе уравнений , откуда находим неизвестные переменные.

Ответ:

ОБРАТИТЕ ВНИМАНИЕ.

При использовании метода Гаусса для решения систем линейных алгебраических уравнений следует избегать приближенных вычислений, так как это может привести к абсолютно неверным результатам. Рекомендуем не округлять десятичные дроби. Лучше от десятичных дробей переходить к обыкновенным дробям.

Пример.

Решите систему из трех уравнений методом Гаусса .

Решение.

Отметим, что в этом примере неизвестные переменные имеют другое обозначение (неx₁, x₂, x₃, а x, y, z). Перейдем к обыкновенным дробям:

Исключим неизвестную x из второго и третьего уравнений системы:

В полученной системе во втором уравнении отсутствует неизвестная переменная y, а в третьем уравнении y присутствует, поэтому, переставим местами второе и третье уравнения:

На этом прямой ход метода Гаусса закончен (из третьего уравнения не нужно исключать y, так как этой неизвестной переменной уже нет).

Приступаем к обратному ходу.

Из последнего уравнения находим , из предпоследнегоиз первого уравнения имеем

Ответ:

x = 10, y = 5, z = -20.

К началу страницы

Решение систем линейных алгебраических уравнений, в которых число уравнений не совпадает с числом неизвестных или основная матрица системы вырожденная, методом Гаусса.

Системы уравнений, основная матрица которых прямоугольная или квадратная вырожденная, могут не иметь решений, могут иметь единственное решение, а могут иметь бесконечное множество решений.

Сейчас мы разберемся, как метод Гаусса позволяет установить совместность или несовместность системы линейных уравнений, а в случае ее совместности определить все решения (или одно единственное решение).

В принципе процесс исключения неизвестных переменных в случае таких СЛАУ остается таким же. Однако следует подробно остановиться на некоторых ситуациях, которые могут возникнуть.

На определенном этапе исключения неизвестных переменных некоторые уравнения системы могут обратиться в тождества . Это говорит о том, что такие уравнения излишни, то есть, их можно смело убрать из системы уравнений и продолжить прямой ход метода Гаусса.

К примеру, при исключении x₁ из второго и третьего уравнений системы мы имеем такую ситуацию:

Следовательно, второе уравнение можно удалить из системы и продолжить решение.

При проведении прямого хода метода Гаусса одно (или несколько) уравнений системы могут принять вид , где- некоторое число, отличное от нуля. Это говорит о том, что уравнение, которое обратилось в равенство, не может обратиться в тождество ни при каких значениях неизвестных переменных. Другими словами, система линейных алгебраических уравнений в этом случае несовместна (не имеет решения). Наиболее часто такие ситуации встречаются, когда число уравнений в системе больше числа неизвестных переменных.

Пример.

Найдите решение системы линейных уравнений методом Гаусса.

Решение.

Исключим неизвестную переменную x₁ из всех уравнений системы, начиная со второго. Для этого прибавим к левой и правой частям второго, третьего и четвертого уравнения левую и правую части первого уравнения, умноженные на (-1), (-2) и (-3) соответственно: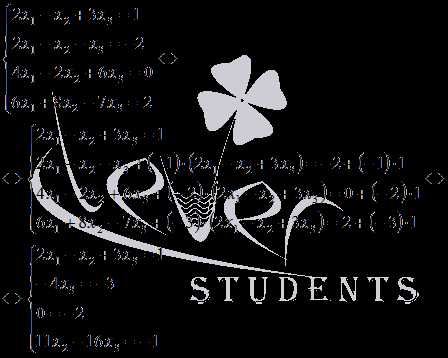

Равенство 0=-2, которое получилось в третьем уравнении системы, не достижимо ни для каких значений неизвестных переменных x₁, x₂ и x₃, поэтому, исходная система уравнений решений не имеет.

Ответ:

система несовместна.

Предположим, что мы выполняем прямой ход метода Гаусса, и мы подошли к моменту исключения неизвестной переменной x_k, а на каком-то предыдущем i-омшаге (i < k) эта переменная уже исключилась вместе с x_i. Как поступать в данном случае? В этом случае следует перейти к исключению неизвестной переменнойx_k+1. Если x_k+1 также уже исключилась, то переходим к x_k+2 и так далее.

К примеру, после исключения неизвестной переменной x₁ система уравнений принимает вид.

Вместе с x₁ исключились x₂ и x₃. Так что прямой ход метода Гаусса продолжаем исключением переменной x₄ из всех уравнений, начиная с третьего:

studfiles.net

описание алгоритма решения системы линейных уравнений, примеры, решения.

во-первых, нет необходимости предварительно исследовать систему уравнений на совместность;
во-вторых, методом Гаусса можно решать не только СЛАУ, в которых число уравнений совпадает с количеством неизвестных переменных и основная матрица системы невырожденная, но и системы уравнений, в которых число уравнений не совпадает с количеством неизвестных переменных или определитель основной матрицы равен нулю;
в-третьих, метод Гаусса приводит к результату при сравнительно небольшом количестве вычислительных операций.

Краткий обзор статьи.

Сначала дадим необходимые определения и введем обозначения.

Навигация по странице.

Основные определения и обозначения.
Решение систем линейных алгебраических уравнений, в которых число уравнений равно числу неизвестных и основная матрица системы невырожденная, методом Гаусса.
Решение систем линейных алгебраических уравнений, в которых число уравнений не совпадает с числом неизвестных или основная матрица системы вырожденная, методом Гаусса.

Основные определения и обозначения.

Рассмотрим систему из p линейных уравнений с n неизвестными (p может быть равно n): где — неизвестные переменные, — числа (действительные или комплексные), — свободные члены.

Если существует хотя бы одно решение системы линейных алгебраических уравнений, то она называется совместной, в противном случае – несовместной.

Говорят, что система записана в координатной форме, если она имеет вид .

Эта система в матричной форме записи имеет вид , где — основная матрица СЛАУ, — матрица столбец неизвестных переменных, — матрица свободных членов.

Квадратная матрица А называется вырожденной, если ее определитель равен нулю. Если , то матрица А называется невырожденной.

Следует оговорить следующий момент.

Если с системой линейных алгебраических уравнений произвести следующие действия

поменять местами два уравнения,
умножить обе части какого-либо уравнения на произвольное и отличное от нуля действительное (или комплексное) число k,
к обеим частям какого-либо уравнения прибавить соответствующие части другого уравнения, умноженные на произвольное число k,

перестановку двух строк местами,
умножение всех элементов какой-либо строки матрицы T на отличное от нуля число k,
прибавление к элементам какой-либо строки матрицы соответствующих элементов другой строки, умноженных на произвольное число k.

Теперь можно переходить к описанию метода Гаусса.

К началу страницы

studfiles.net

Решение СЛАУ 3-его порядка методом Гаусса, пример № 4

СЛАУ 3-его порядка: 1 — 2 — 3 — 4 — 5 — 6 — 7 — 8 — 9 — 10 — 11 — 12
СЛАУ 4-ого порядка: 1 — 2 — 3 — 4 — 5 — 6 — 7 — 8 — 9 — 10 — 11 — 12

Условие

— x ₁	+ x ₂	— 4x ₃	= -11
3x ₁	+ 2x ₂	+ x ₃	= 10
x ₁	— x ₂	+ 2x ₃	= 5

Решение системы линейных алгебраических уравнений методом Гаусс

Для проверки ответов можете воспользоваться нашим онлайн сервисом — Решение системы линейных уравнений методом Гаусса. Все действия описанные в данном разделе не противоречат правилам обращения с матрицами и являются элементарными преобразованиями матрицы. Если после изучения примеров решения задач у Вас останутся вопросы, то Вы всегда можете задать их на форуме, и не забывайте про наши онлайн калькуляторы для решения задач по математике и другим предметам!

Перепишем систему линейных алгебраических уравнений в матричную форму. Получится матрица 3 × 4, слева от разделительной линии стоят коэффициенты при переменных, а справа стоят свободные члены.

Проведём следующие действия:

Поменяем местами строку № 1 и строку № 3

Получим:

Проведём следующие действия:

Из строки № 2 вычтем строку № 1 умноженную на 3 (Строка 2 — 3 × строка 1)
К строке № 3 прибавим строку № 1 (Строка 3 + строка 1)

Получим:

Проведём следующие действия:

Строку № 2 поделим на 5 (Строка 2 = строка 2 / 5)
Строку № 3 поделим на -2 (Строка 3 = строка 3 / -2)

Получим:

Проведём следующие действия:

К строке № 2 прибавим строку № 3 (Строка 2 + строка 3)
Из строки № 1 вычтем строку № 3 умноженную на 2 (Строка 1 — 2 × строка 3)

Получим:

Проведём следующие действия:

К строке № 1 прибавим строку № 2 (Строка 1 + строка 2)

Получим:

В левой части матрицы по главной диагонали остались одни единицы. В правом столбце получаем решение:
х₁ = 1
х₂ = 2
х₃ = 3

Вы поняли, как решать? Нет?

Помощь с решением

www.webmath.ru

Решение систем линейных алгебраических уравнений методом Гаусса — ПриМат

Метод Гаусса

Метод Гаусса — метод последовательного исключения неизвестных, он состоит в приведении данной системы, применяя элементарные преобразования, к ступенчатому виду.

Удобнее всего это делать путем приведения (с помощью элементарных преобразований строк) расширенной матрицы $B$ данной системы к ступенчатой
матрице $B_1$.

Конечная система будет равносильна исходной, так как между элементарными преобразованиями системы и элементарными преобразованиями строк ее расширенной матрицы имеет место быть взаимно однозначное соответствие, а при элементарных преобразованиях системы она переходит в равносильную.

Пример:

Пусть дана система уравнений

$\begin{equation*}
\begin{cases}
2x_1 + x_2 + x_3 = 2\\
x_1 — x_2 = -2\\
3x_1 — x_2 + 2x_3 = 2
\end{cases}
\end{equation*}$

Решение:

Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем эту матрицу к ступенчатому виду, а затем далее выполним обратный ход метода Гаусса (сделаем нули выше главной диагонали). Первым делом поменяем первую и вторую строку, чтобы элемент $a_{11}$ равнялся $1$ (это делается для упрощения вычислений):

$A = \left(\begin{matrix}
2 & 1 & 1 \\
1 & -1 & 0 \\
3 & -1 & 2
\end{matrix}\left|
\begin{matrix}
2 \\ -2 \\ 2
\end{matrix}\right)\right.\
\sim~\
\left(\begin{matrix}
1 & -1 & 0 \\
2 & 1 & 1 \\
3 & -1 & 2
\end{matrix}\left|
\begin{matrix}
-2 \\ 2 \\ 2
\end{matrix}\right)\right.\
$

Затем получаем нули под главной диагональю в первом столбце. Для этого от второй строки отнимаем две первых, от третьей — три первых:
$A = \left(\begin{matrix}
1 & -1 & 0 \\
0 & 3 & 1 \\
0 & 2 & 2
\end{matrix}\left|
\begin{matrix}
-2 \\ 6 \\ 8
\end{matrix}\right)\right.\ $

Все элементы третьей строки делим на два (или, что тоже самое, умножаем на $1/2$):

$A = \left(\begin{matrix}
1 & -1 & 0 \\
0 & 3 & 1 \\
0 & 1 & 1
\end{matrix}\left|
\begin{matrix}
-2 \\ 6 \\ 4
\end{matrix}\right)\right.\ $

Затем получаем нули во втором столбце под главной диагональю, для удобства вычислений меняем местами вторую и третью строки, чтобы диагональный элемент равнялся $1$:

$A = \left(\begin{matrix}
1 & -1 & 0 \\
0 & 1 & 1 \\
0 & 3 & 1
\end{matrix}\left|
\begin{matrix}
-2 \\ 4 \\ 6
\end{matrix}\right)\right.\ $

От третьей строки отнимем вторую, умноженную на $3$:

$A = \left(\begin{matrix}
1 & -1 & 0 \\
0 & 1 & 1 \\
0 & 0 & -2
\end{matrix}\left|
\begin{matrix}
-2 \\ 4 \\ -6
\end{matrix}\right)\right.\ $

После умножения третей строки на $(-1/2)$ , получаем:

$A = \left(\begin{matrix}
1 & -1 & 0 \\
0 & 1 & 1 \\
0 & 0 & 1
\end{matrix}\left|
\begin{matrix}
-2 \\ 4 \\ 3
\end{matrix}\right)\right.\ $

Выполним теперь обратный ход метода Гаусса, то есть сделаем нули над главной диагональю. Начнем с элементов третьего столбца. Обнуляем элемент $a_{23}$, для этого от второй строки отнимем третью:

$A = \left(\begin{matrix}
1 & -1 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{matrix}\left|
\begin{matrix}
-2 \\ 1 \\ 3
\end{matrix}\right)\right.\ $

Следующим действием обнулим недиагональные элементы второго столбца, прибавив к первой строке вторую:

$A = \left(\begin{matrix}
1 & -1 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{matrix}\left|
\begin{matrix}
-2 \\ 1 \\ 3
\end{matrix}\right)\right.\ $

Полученной матрице соответствует система

$\begin{equation*}
\begin{cases}
x_1 = -1\\
x_2 = 1\\
x_3 = 2
\end{cases}
\end{equation*}$

Литература:

Конспект лекций Г.С. Белозерова
Линейная алгебра. Воеводин В.В. М.: Наука. Главная редакция физико-математической литературы, 1980, с.9-13
Лекции по общей алгебре (издание второе). Курош А.Г. М.: Наука. Главная редакция физико-математической литературы, 1973, с.14-17

Тест

Лимит времени: 0

Информация

Решите систему уравнений методом Гаусса

Вы уже проходили тест ранее. Вы не можете запустить его снова.

Тест загружается…

Вы должны войти или зарегистрироваться для того, чтобы начать тест.

Вы должны закончить следующие тесты, чтобы начать этот:

Правильных ответов: 0 из 1

Ваше время:

Время вышло

Вы набрали 0 из 0 баллов (0)

Средний результат
Ваш результат

Ваш результат был записан в таблицу лидеров

С ответом
С отметкой о просмотре

Поделиться ссылкой:

Похожее

ib.mazurok.com

Решение СЛАУ 4-ого порядка методом Гаусса, пример № 7

Условие

x ₁	— x ₂	+ 3x ₃	+ x ₄	= 5
4x ₁	— x ₂	+ 5x ₃	+ 4x ₄	= 4
2x ₁	— 2x ₂	+ 4x ₃	+ x ₄	= 6
x ₁	— 4x ₂	+ 5x ₃	— x ₄	= 3

Решение системы линейных алгебраических уравнений методом Гаусс

Перепишем систему линейных алгебраических уравнений в матричную форму. Получится матрица 4 × 5, слева от разделительной линии стоят коэффициенты при переменных, а справа стоят свободные члены.

Проведём следующие действия:

Из строки № 2 вычтем строку № 1 умноженную на 4 (Строка 2 — 4 × строка 1)
Из строки № 3 вычтем строку № 1 умноженную на 2 (Строка 3 — 2 × строка 1)
Из строки № 4 вычтем строку № 1 (Строка 4 — строка 1)

Получим:

Проведём следующие действия:

К строке № 4 прибавим строку № 2 (Строка 4 + строка 2)
Строку № 3 поделим на -2 (Строка 3 = строка 3 / -2)

Получим:

Проведём следующие действия:

К строке № 4 прибавим строку № 3 умноженную на 5 (Строка 4 + 5 × строка 3)
Строку № 4 умножим на 2 (Строка 4 = строка 4 * 2)

Получим:

Проведём следующие действия:

Из строки № 3 вычтем строку № 4 умноженную на 0.5 (Строка 3 — 0.5 × строка 4)
Из строки № 1 вычтем строку № 4 (Строка 1 — строка 4)

Получим:

Проведём следующие действия:

К строке № 2 прибавим строку № 3 умноженную на 7 (Строка 2 + 7 × строка 3)
Из строки № 1 вычтем строку № 3 умноженную на 3 (Строка 1 — 3 × строка 3)

Получим:

Проведём следующие действия:

Строку № 2 поделим на 3 (Строка 2 = строка 2 / 3)
К строке № 1 прибавим строку № 2 (Строка 1 + строка 2)

Получим:

В левой части матрицы по главной диагонали остались одни единицы. В правом столбце получаем решение:
х₁ = 9
х₂ = 18
х₃ = 10
х₄ = -16

Вы поняли, как решать? Нет?

Помощь с решением

www.webmath.ru

Решение СЛАУ 4-ого порядка методом Гаусса, пример № 2

Условие

3x ₁	+ 3x ₂	+ 6x ₃	+ 3x ₄	= 6
3x ₁	+ x ₂	+ 5x ₃	+ x ₄	= 2
2x ₁	+ x ₂	+ 4x ₃	+ 2x ₄	= 1
x ₁	+ 3x ₂	+ 3x ₃	+ 2x ₄	= 6

Решение системы линейных алгебраических уравнений методом Гаусс

Для проверки ответов можете воспользоваться нашим онлайн сервисом — Решение системы линейных уравнений методом Гаусса. Все действия описанные в данном разделе не противоречат правилам обращения с матрицами и являются элементарными преобразованиями матрицы. Если после изучения примеров решения задач у Вас останутся вопросы, то Вы всегда можете задать их на форуме, и не забывайте про наши онлайн калькуляторы для решения задач по геометрии и другим предметам!

Проведём следующие действия:

Строку № 1 поделим на 3 (Строка 1 = строка 1 / 3)

Получим:

Проведём следующие действия:

Из строки № 2 вычтем строку № 1 умноженную на 3 (Строка 2 — 3 × строка 1)
Из строки № 3 вычтем строку № 1 умноженную на 2 (Строка 3 — 2 × строка 1)
Из строки № 4 вычтем строку № 1 (Строка 4 — строка 1)

Получим:

Проведём следующие действия:

Строку № 3 поделим на -1 (Строка 3 = строка 3 / -1)
Поменяем местами строку № 2 и строку № 3

Получим:

Проведём следующие действия:

К строке № 3 прибавим строку № 2 умноженную на 2 (Строка 3 + 2 × строка 2)
Из строки № 4 вычтем строку № 2 умноженную на 2 (Строка 4 — 2 × строка 2)

Получим:

Проведём следующие действия:

К строке № 4 прибавим строку № 3 (Строка 4 + строка 3)
Строку № 4 умножим на -1 (Строка 4 = строка 4 * -1)

Получим:

Проведём следующие действия:

К строке № 3 прибавим строку № 4 умноженную на 2 (Строка 3 + 2 × строка 4)
Из строки № 1 вычтем строку № 4 (Строка 1 — строка 4)

Получим:

Проведём следующие действия:

К строке № 1 прибавим строку № 3 умноженную на 2 (Строка 1 + 2 × строка 3)
Из строки № 1 вычтем строку № 2 (Строка 1 — строка 2)
Строку № 3 умножим на -1 (Строка 3 = строка 3 * -1)

Получим:

В левой части матрицы по главной диагонали остались одни единицы. В правом столбце получаем решение:
х₁ = 3
х₂ = 3
х₃ = -2
х₄ = 0

Вы поняли, как решать? Нет?

Помощь с решением

www.webmath.ru

Решение СЛАУ 4-ого порядка методом Гаусса, пример № 6

Условие

2x ₁	+ x ₂	+ 3x ₃	+ 2x ₄	= 0
2x ₁	+ x ₂	+ 5x ₃	+ x ₄	= 2
2x ₁	+ x ₂	+ 4x ₃	+ 2x ₄	= 1
x ₁	+ 3x ₂	+ 3x ₃	+ 2x ₄	= 6

Решение системы линейных алгебраических уравнений методом Гаусс

Для проверки ответов можете воспользоваться нашим онлайн сервисом — Решение системы линейных уравнений методом Гаусса. Все действия описанные в данном разделе не противоречат правилам обращения с матрицами и являются элементарными преобразованиями матрицы. Если после изучения примеров решения задач у Вас останутся вопросы, то Вы всегда можете задать их на форуме, и не забывайте про наши онлайн калькуляторы для решения задач по теории вероятности и другим предметам!

Проведём следующие действия:

Поменяем местами строку № 1 и строку № 4

Получим:

Проведём следующие действия:

Из строки № 2 вычтем строку № 1 умноженную на 2 (Строка 2 — 2 × строка 1)
Из строки № 3 вычтем строку № 1 умноженную на 2 (Строка 3 — 2 × строка 1)
Из строки № 4 вычтем строку № 1 умноженную на 2 (Строка 4 — 2 × строка 1)

Получим:

Проведём следующие действия:

Строку № 2 поделим на -5 (Строка 2 = строка 2 / -5)

Получим:

Проведём следующие действия:

К строке № 3 прибавим строку № 2 умноженную на 5 (Строка 3 + 5 × строка 2)
К строке № 4 прибавим строку № 2 умноженную на 5 (Строка 4 + 5 × строка 2)

Получим:

Проведём следующие действия:

Из строки № 4 вычтем строку № 3 умноженную на 2 (Строка 4 — 2 × строка 3)
Строку № 3 умножим на -1 (Строка 3 = строка 3 * -1)

Получим:

Проведём следующие действия:

Из строки № 3 вычтем строку № 4 (Строка 3 — строка 4)
К строке № 2 прибавим строку № 4 умноженную на 0.6 (Строка 2 + 0.6 × строка 4)
К строке № 1 прибавим строку № 4 умноженную на 2 (Строка 1 + 2 × строка 4)
Строку № 4 умножим на -1 (Строка 4 = строка 4 * -1)

Получим:

Проведём следующие действия:

Из строки № 2 вычтем строку № 3 умноженную на 0.2 (Строка 2 — 0.2 × строка 3)
Из строки № 1 вычтем строку № 3 умноженную на 3 (Строка 1 — 3 × строка 3)

Получим:

Проведём следующие действия:

Из строки № 1 вычтем строку № 2 умноженную на 3 (Строка 1 — 3 × строка 2)

Получим:

В левой части матрицы по главной диагонали остались одни единицы. В правом столбце получаем решение:
х₁ = -2.4
х₂ = 1.8
х₃ = 1
х₄ = 0

Вы поняли, как решать? Нет?

Помощь с решением

Метод Гаусса

описание алгоритма решения системы линейных уравнений, примеры, решения.

Основные определения и обозначения.

Решение СЛАУ 3-его порядка методом Гаусса, пример № 4

Решение систем линейных алгебраических уравнений методом Гаусса — ПриМат

Метод Гаусса

Пример:

Решение:

Литература:

Тест

Информация

Поделиться ссылкой:

Похожее

Решение СЛАУ 4-ого порядка методом Гаусса, пример № 7

Решение СЛАУ 4-ого порядка методом Гаусса, пример № 2

Решение СЛАУ 4-ого порядка методом Гаусса, пример № 6

Добавить комментарий Отменить ответ