Примеры с отрицательными числами за 6 класс – «Отрицательные числа в изучении математики» (6 класс)

«Отрицательные числа в изучении математики» (6 класс)

ПОЛОЖИТЕЛЬНЫЕ И ОТРИЦАТЕЛЬНЫЕ ЧИСЛА.

1. История возникновения отрицательных чисел:

Впервые отрицательные числа появились в древнем Китае примерно 2100 лет тому назад. Там умели также складывать и вычитать положительные и отрицательные числа. Отрицательные числа трактовали как долг, а положительные как имущество. Таким же образом смотрели на эти числа и в Индии в VII столетии, но там уже были известны правила умножения и деления. Люди с некоторым недоверием относились к отрицательным числам, считая их не совсем реальными, истолкование их как имущество – долг вызвало недоумение: как можно «складывать» и «вычитать» имущество и долг.

Натуральные числа принято называть положительными целыми числами. Иногда перед положительными числами ставят знак «+».

Например: + 5=5 ; +7=7.

Два положительных или два отрицательных числа-это числа одного знака. Положительное и отрицательное число-это числа разных знаков.

С помощью знака «минус» записывается число, противоположное данному:

Число противоположное а, обозначают — а

Если а=15, то -а = -15;

Если а= -20, то –а = -(-20) = 20;

Если а =0, то –а = 0. Если положительные числа появились еще в древности, и стали использоваться для счета предметов, то отрицательные числа, изобретение недавнее: Отрицательные числа возникали при вычитании. Вначале они представлялись непонятными и бессмысленными, т.к наименьшим количеством было «ничто», то есть, как всегда привыкли считать это нуль. Что может быть меньше нуля?

XVII веке великий французский математик Рене Декарт предложил откладывать отрицательные числа на числовой оси влево от нуля. Отрицательные числа получили реальное истолкование. Их стали признавать наравне с положительными. Наступило полное числовое равноправие.

-7 -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6

О

Если перед числом стоит знак «+», его называют положительным.

Если «-», отрицательным.

Число «0» не является ни положительным , ни отрицательным.

На координатной прямой числа расположенные справа от нуля —положительные;

Числа расположенные слева от нуля — отрицательные.

2. Отрицательные числа.

На уроках математики мы уже познакомились с натуральными , дробными числами и действиями над ними. Однако в жизни мы уже встречались и с отрицательными числами. Примером может быть обыкновенный термометр:

Из рисунка можно наблюдать, что температура может быть как выше нуля, так и ниже нуля. Со знаком «+» и со знаком «-

Любое положительное число больше нуля : 5 > 0;

Любое отрицательное число меньше нуля: — 7 < 0;

Любое отрицательное число < положительного: — 7 < 5

3.Пример применения отрицательных чисел:

— в географии:

Самая большая положительная величина на Земле –вершина

Джомолунгма +8848 м.

Самая большая отрицательная величина—

Марианская впадина — 11034 м.

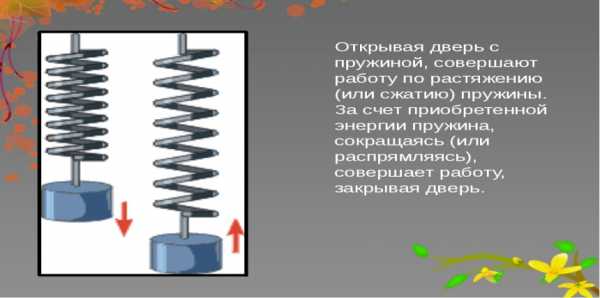
-в физике:

При растяжении пружины:

Если пружину растянуть

, то измерение длины является положительным числом, а если сжать –отрицательным числом.

3. Правила умножения положительных и отрицательных чисел:

При умножении двух чисел с разными знаками в результате получается отрицательное число, модуль которого равен произведению модулей множителей.

«+» * «-» = «-»

«-» * «+» = «-»

При умножении двух чисел с одинаковыми знаками в результате получается положительное число, модуль которого равен произведению модулей множителей.

«-» * «-» = «+»

«+» * «+» = «+»

4.Сравнение отрицательных чисел:

-7 -6 -5 -4 -3 -2 -1 0 1

>

А В О

При сравнении целых отрицательных чисел, можно представить их на координатной прямой. Точка А с координатой -7 левее, чем точка В с координатой -3,

Поэтому: -7 < -3.

Из двух отрицательных чисел больше то, у которых модуль меньше.

5. Практические задачи:

Задача 1. Таня живет на пятом этаже многоэтажного дома, где имеется три подвала для парковки автомобилей (в лифте они указаны числами -1, -2, -3). Выйдя из своей квартиры, смогла бы Таня спуститься на лифте на семь этажей и какую кнопку ей следует нажать.

Ответ: Да, спуститься сможет. Нужно нажать на кнопку второго этажа подвала «-2»

Задача 2. Белые медведи выдерживают температуру до -80⁰ С, моржи – выше этой температуры на 45⁰ С, самые «морозостойкие» гуси и утки – ниже на 30⁰ С. Какую температуру выдерживают моржи и гуси, утки?

Решение: — 80 + 45 = — 35⁰ С выдерживают моржи; — 80 – 30 = — 110⁰ С выдерживают гуси, утки. Ответ: — 35⁰ С, — 110⁰ С.

Задание 3. Попробуйте в тексте найти положительные и отрицательные величины и сделайте выводы об их использовании в жизни.

Площадь Кунгурской Ледяной пещеры составляет 106,5 гектаров. Ее поверхность усеяна многочисленными карстовыми воронками, крупнейшие из которых достигают 50-60 метров в диаметре и 10-12 м в глубине.

В первом Бриллиантовом гроте пещеры зимой температура может достигать -15, -20 градусов, хотя в центре пещеры постоянная весна: +5 °C летом и зимой при 100% влажности.

В каменной нише Полярного грота скрывается массивная ледяная колонна, напоминающая застывший водопад. Ее еще описывал профессор М.Я. Киттара 165 лет назад.

Большое подземное озеро находится в гроте «Титанический» (площадь – 1300 кв.м., ширина 38 м, глубина достигает 3 м., температура воды постоянная +5 °C). В другом гроте – «Романтиков» экскурсанты могут любоваться небольшим озером с так называемым сифоном – подводным каналом, который опускается ниже уровня озера на 4-5 м.

(отрывок из книги Валентина Рапп «Путеводитель по Кунгуру и Ледяной пещере»)

Использованная литература:

1. Выгодский М.Я. Справочник по элементарной математике. – М.: Наука, 1972. – С. 130-136.

2. Едуш О.Ю. Математика. Подсказки на каждый день.

3. Лиман М.М. Школьникам о математике и математиках. – М.: Просвещение, 1981. – С. 26.

4. Новейший полный справочник школьника 5-11 классы. Том 1.– М.: Эксмо, 2014. – С. 224.

5. Рапп В.В. Путеводитель по Кунгуру и Ледяной пещере.– Пермь: Звезда, 1999. – С. 73-87.

6. История возникновения отрицательных чисел [Электронный ресурс]

7. История возникновения цифр. Применение отрицательных чисел.[Электронный ресурс]

infourok.ru

Дидактические материалы по математике для 6 класса по теме «Действия с положительными и отрицательными числами»

Действия с положительными и отрицательными числами

1. Сложение отрицательных чисел

Правило: Чтобы сложить два отрицательных числа, надо:

1. сложить их модули,

2. поставить перед полученным числом знак ( — ).

Примеры: а) — 3,9 + ( — 5,4) = — ( 3,9 + 5,4 ) = — 9,3

б) — 2 + ( — 3 ) = — ( 2 + 3 ) = — 5 = — 5

2. Сложение чисел с разными знаками

Правило: Чтобы сложить два числа с разными знаками, надо:

1. из большего модуля слагаемых вычесть меньший,

2. поставить перед полученным числом знак того слагаемого, модуль которого больше.

Примеры: а) 1,3 + ( — 0,5 ) = 1,3 – 0,5 = 0,8

б) — 3 + 4 = 4 — 3 = 1

в) 2,7 + ( — 3,4 ) = — ( 3,4 – 2,7 ) = — 0,7

г) — 8 + 2 = — ( 8 — 2 ) = — 6 = — 6

д) = = — = —

3. Вычитание

Правило: Чтобы из данного числа вычесть другое, надо к уменьшаемому прибавить

число, противоположное вычитаемому: а – b = а + ( — b ) .

Примеры: а) 15 — 60 = 15 + ( — 60) = — ( 60 – 15 ) = — 45

б) — 15 – 60 = — 15 + (- 60) = — ( 15 + 60 ) = — 75

в)

г)

д)

4. Умножение

А) Умножение чисел с разными знаками

Правило: Чтобы перемножить два числа с разными знаками, надо

перемножить модули этих чисел и поставить перед полученным

числом знак ( — ).

Примеры: а) — 1,2 · 3 = — 3,6

б)

Б) Умножение отрицательных чисел

Правило: Чтобы перемножить два отрицательных числа, надо

перемножить их модули.

Примеры: а) — 6 · (- 15 ) = 90

б)

5. Деление

А) Деление отрицательных чисел

Правило: Чтобы разделить отрицательное число на отрицательное, надо

модуль делимого разделить на модуль делителя.

Примеры: а) — 4,5 : (- 1,5 ) = 4.5 : 1.5 = 3

б)

Б) Деление чисел с разными знаками

Правило: При деление чисел с разными знаками надо:

1. разделить модуль делимого на модуль делителя,

2. поставить перед полученным числом знак ( — ).

Примеры: а) 3,6 : (- 3 ) = — ( 3,6 : 3 ) = — 1,2

б)

Сложение и вычитание положительных и отрицательных чисел

1

А) – 1 + 0

8 + ( — 8 )

0 + (- 3 )

— 5 + 5

Б) – 3 + (- 4 )

— 9 + (- 5 )

— 6 + (- 8 )

— 1 +

В) 1 + (- 4 )

— 3 + 6

— 12 + 8

7 + (- 6 )

— 1 +

Г) 6 – 8

5 – (- 7 )

— 3 – 4

— 2 – (- 9 )

2

А) 0 + 3

— 4 + 4

— 5 + 0

6 + (- 6 )

Б) – 7 + (- 2 )

— 5 + (- 8 )

— 3 + (- 9 )

— 3 +

В) 3 + (- 2 )

— 4 + 9

12 + (- 6 )

— 8 + 4

+ (- 1 )

Г) 7 – 9

6 – (- 8 )

— 5 – 3

— 9 – (- 3 )

3

А) 7 + (- 7 )

— 5 + 0

— 3 + 3

0 + (- 4 )

Б) – 5 + (- 7 )

— 3 + (- 8 )

— 6 + (- 4 )

— 1 +

В) — 2 + 9

— 3 + 5

6 + (- 4 )

7 + (- 10 )

1 +

Г) — 4 – 6

2 – 5

7 – (- 4 )

— 8 – (- 5 )

4

А) 1 + (- 1 )

— 9 + 0

— 2 + 2

0 + (- 7 )

Б) – 8 + (- 2 )

— 4 + (- 9 )

— 5 + (- 3 )

— + (- 3 )

В) — 4 + 7

8 + (- 2 )

— 7 + 3

5 + (- 8 )

+ 1

Г) — 2 – 3

3 – 7

3 – (- 6 )

— 4 – (- 8 )

5

А) – 2 + 0

— 6 + 6

0 + (- 9 )

9 + (- 9 )

Б) – 6 + (- 7 )

— 2 + (- 9 )

— 11 + (- 3 )

— 2 +

В) 9 + (- 5 )

— 8 + 3

— 5 + 6

2 + (- 7 )

— 1 +

Г) 4 – 8

4 – (- 7 )

— 3 – 6

— 5 – (- 9 )

6

А) 0 + (- 7 )

5 + (- 5 )

— 4 + 0

— 7 + 7

Б) – 2 + (- 3 )

— 9 + (- 6 )

— 4 + (- 8 )

— 1 +

В) — 5 + 7

6 + (- 8 )

— 11 + 3

9 + (- 2 )

+ (- 1 )

Г) — 5 – 6

3 – (- 8 )

2 – 5

— 10 – (- 4 )

М – 6 В – 1

Сложение положительных и

отрицательных чисел

Вычислить:

5 + (- 4) = — 6 + (- 4) =

— 3 + 0 = 2 + (- 2) =

— 10 + 6 = 4 + (- 9) =

8 + (- 9) = — 7 + (- 7) =

0 + (- 5) = — 12 + 21 =

М – 6 В – 2

Сложение положительных и

отрицательных чисел

Вычислить:

4 + (- 5) = — 4 + (- 4) =

— 7 + 0 = 3 + (- 3) =

— 12 + 6 = 6 + (- 9) =

8 + (- 5) = — 7 + (- 5) =

0 + (- 4) = — 11 + 31 =

М – 6 В – 3

Сложение положительных и

отрицательных чисел

Вычислить:

5 + (- 9) = — 6 + (- 7) =

— 6 + 0 = 5 + (- 5) =

— 10 + 8 = 4 + (- 9) =

7 + (- 3) = — 4 + (- 7) =

0 + (- 8) = — 12 + 31

М – 6 В – 4

Сложение положительных и

отрицательных чисел

Вычислить:

6 + (- 4) = — 8 + (- 4) =

— 9 + 0 = -7 + 7 =

— 15 + 6 = 2 + (- 9) =

4 + (- 7) = — 6 + (- 6) =

0 + (- 6) = — 13 + 41 =

М – 6 Вычитание

Вариант 1

Вычислить:

а) 48 – 50 =

б) 3,4 – 2,8 =

в) =

г) — 48 – 50 =

д) — 3,4 – (- 2,8 ) =

е) 48 – ( — 50 ) =

ж) — ( — 1 ) =

М – 6 Вычитание

Вариант 2

Вычислить:

а) 37 – 40 =

б) 8,4 – 7,6 =

в)

г) — 37 – 40 =

д) — 8,4 – (- 7,6 ) =

е) 37 – ( — 40 ) =

ж) — ( — 1 ) =

М – 6 Устный счёт В – 1

М – 6 Устный счёт В – 2

М – 6 Устный счёт В – 3

5 – 9 =

— 5 + 9 =

— 5 – 9 =

5 + (- 9) =

— 5 + (- 9) =

5 – (- 9) =

— 5 – (- 9) =

9 + (- 5) =

9 – (- 5) =

— 9 + 5 =

— 9 – 5 =

9 ∙ (- 5) =

— 9 ∙ (- 5) =

12 : (- 2) =

— 12 : (- 2) =

— 12 : 2 =

3 – 7 =

— 3 + 7 =

— 3 – 7 =

3 + (- 7) =

— 3 + (- 7) =

3 – (- 7) =

— 3 – (- 7) =

7 + (- 3) =

7 – (- 3) =

— 7 + 3 =

— 7 – 3 =

7 ∙ (- 3) =

— 7 ∙ (- 3) =

12 : (- 4) =

— 12 : (- 4) =

— 12 : 4 =

2 – 6 =

— 2 + 6 =

— 2 – 6 =

2 + (- 6) =

— 2 + (- 6) =

2 – (- 6) =

— 2 – (- 6) =

6 + (- 2) =

6 – (- 2) =

— 6 + 2 =

— 6 – 2 =

6 ∙ (- 2) =

— 6 ∙ (- 2) =

18 : (- 3) =

— 18 : (- 3) =

— 18 : 3 =

Правила раскрытия скобок

1) Если перед скобками стоит знак «+», то при раскрытии скобок все слагаемые, стоящие в скобках, записываются со своими знаками.

2) Если перед скобками стоит знак « – », то при раскрытии скобок все слагаемые, стоящие в скобках, меняют свои знаки на противоположные.

3) Если у первого слагаемого в скобках нет никакого знака, то это слагаемое пишется с тем знаком, который был перед скобками.

Примеры:

а) a + (- b + c + m) = a – b + c + m

б) a – ( — b + c + m) = a + b – c – m

в) a + (b – c + m) = a + b – c + m

г) a – (b – c + m) = a – b + c – m

д) (a – b) – (c – m) = a – b – c + m

Правила раскрытия скобок

1. Если перед скобками стоит знак «+», то при раскрытии скобок все слагаемые, стоящие вскобках, записываются со своими знаками.

2. Если перед скобками стоит знак « – », то при раскрытии скобок все слагаемые, стоящие в скобках, меняют свои знаки на противоположные.

3. Если у первого слагаемого в скобках нет

никакого знака, то это слагаемое пишется с тем знаком, который был перед скобками.

Примеры:

а) a + (- b + c + m) = a – b + c + m

б) a – ( — b + c + m) = a + b – c – m

в) a + (b – c + m) = a + b – c + m

г) a – (b – c + m) = a – b + c – m

д) (a – b) – (c – m) = a – b – c + m

Вычислить:

а) 4 – 12 = б) – 24 – 31 =

— 5 — 20 = — 7 + 13 =

— 8 + 19 = 45 – 60 =

26 – 30 = — 16 – 34 =

-14 + 14= — 27 + 13 =

Раскрыть скобки:

1) a + ( b – c + m) =

2) a – ( b – c – m) =

3) (a – b ) + (- m + n) =

4) – (a – b) – ( — m + n) =

5) – ( — a + b) + ( m – n) =

Вычислить:

а) 4 – 12 = б) – 24 – 31 =

— 5 — 20 = — 7 + 13 =

— 8 + 19 = 45 – 60 =

26 – 30 = — 16 – 34 =

-14 + 14= — 27 + 13 =

Раскрыть скобки:

1) a + ( b – c + m) =

2) a – ( b – c – m) =

3) (a – b ) + (- m + n) =

4) – (a – b) – ( — m + n) =

5) – ( — a + b) + ( m – n) =

Фамилия _____________________ В – 1

Вычислить:

а) 4 – 15 = б) – 14 – 31 =

— 5 — 5 = — 19 + 13 =

— 8 + 12 = 35 – 50 =

26 – 36 = — 9 – 2 =

-12 + 12 = — 7 + 13 =

Раскрыть скобки:

a + ( b + c — m) =

a – ( b – c + m) =

(a + b ) + (- m + n) =

– (a + b) – ( m — n) =

– ( — a — b) + ( m – n) =

Фамилия _____________________ В – 2

Вычислить:

а) — 4 + 15 = б) – 18 – 32 =

— 8 — 8 = — 23 + 13 =

— 6 + 12 = 25 – 50 =

16 – 30 = — 6 – 4 =

-20 + 20 = 7 — 13 =

Раскрыть скобки:

a + ( b — n — m) =

a – ( b + c — n) =

(a — n ) + ( m — b) =

– (a + n) – ( m — b) =

— ( — a — n) + ( — m – b) =

Фамилия _____________________

В – 3

Вычислить:

а) 3 – 15 = б) – 12 – 41 =

— 15 — 8 = — 29 + 13 =

— 9 + 11 = 55 – 70 =

34 – 48 = — 16 – 16 =

-15 + 15 = -17 + 23 =

Раскрыть скобки:

c — ( b + a — m) =

c + ( b – a + m) =

(c — b ) + (- a + n) =

– (c + b) + ( a — n) =

– ( — c — b) — ( a – n) =

Фамилия _____________________ В – 4

Вычислить:

а) — 14 + 25 = б) – 18 + 18 =

— 7 — 7 = — 28 + 13 =

— 5 + 15 = 49 – 60 =

12 – 40 = — 16 – 25 =

— 20 — 2 = 3 — 17 =

Раскрыть скобки:

b — ( a — n + m) =

b + ( a + c — n) =

(b + n ) — (- m + a) =

– (b + n) + ( m — c) =

— ( — b — n) + ( — m – c) =

infourok.ru

Положительные и отрицательные числа. 6-й класс

Разделы: Математика, Конкурс «Презентация к уроку»

---

Презентация к уроку

Загрузить презентацию (1 МБ)

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

---

Цель: закрепить умения и навыки в действиях с положительными и отрицательными числами.

Задачи:

• Повторить понятия положительных и отрицательных чисел; закрепить навыки выполнения действий с положительными и отрицательными числами.
• Способствовать воспитанию интереса к предмету через нетрадиционную форму проведения урока.
• Развивать логическую смекалку, творческое мышление.

Тип урока: урок повторения и закрепления знаний учащихся с использованием ИТ.

Формы организации учебной деятельности: коллективная, индивидуальная.

Оборудование: компьютер, проектор, презентация PowerPoint, набор индивидуальных карточек (приложение 1, приложение 2), аудиофайлы с музыкой.

Ход урока

I. Организационный момент.

Я рада видеть каждого из вас
И пусть весна прохладой в окна дышит
Нам будет здесь уютно, ведь наш класс
Друг друга любит, чувствует и слышит.

– Сегодня в нашей школе открыт научно-исследовательский институт. На месте кабинетов организованны лаборатории, а все учащиеся школы его научные сотрудники. В кабинете математики открыта лаборатория № 1. Заведующей лабораторией назначили меня. И сегодня мы с вами повторим, обобщим и систематизируем знания, полученные вами на предыдущих занятиях.

– Для работы мне понадобятся помощники – старшие научные сотрудники – которые будут помогать мне в течение урока. Это Рината и Ирина.

– А теперь в ваших журналах наблюдения – рабочих тетрадях – запишем число, классная работа, тема исследования: «Положительные и отрицательные числа».

II. Устная работа.

– В нашу лабораторию поступило сообщение. Прочитайте его.

«В архиве нашего института произошел сбой системы. Потерялись многие сведения. Чтобы их восстановить, нужны специалисты в области положительных и отрицательных чисел. Помогите»

– Мы с вами уже изучили положительные и отрицательные числа, много действий умеем с ними делать. Мы в какой-то мере являемся специалистами в этой области, как вы думаете? {Да}

– Поможем? {Да}

– Раз мы будем помогать восстанавливать утраченные сведения, то мы должны пройти испытания: все ли готовы совершить эту важную миссию.

– Ответим на несколько вопросов.

1. Скажите пожалуйста какое перед нами число? {Число – 32}
2. Как называется это число? {Это число отрицательное}
3. А где расположено это число на координатной прямой? {Это число на координатной прямой расположено слева от нуля}
4. А какие числа называются отрицательными? {Отрицательными числами называются числа, которые расположены на координатной прямой слева от нуля}
5. Мы говорим о координатной прямой. А какая прямая называется координатной? {Координатной прямой называется прямая, на которой есть начало отсчета, единичный отрезок и направление}
6. Назовите два целых соседних с данным числа. {– 31 и – 33}
7. А какое число будет противоположно данному? {Число 32}
8. А какие числа называются противоположными? {Противоположными называются числа, которые отличаются друг от друга только знаками}
9. Чему равен модуль данного числа? {Модуль данного числа равен 32}
10.  А что называется модулем числа? {Модулем числа называется расстояние от начала отсчета до точки на координатной прямой}

– Ну что ж с заданием все справились. Значит, можем продолжить восстанавливать потерянные сведения.

III. Задания на сравнение чисел и выполнение действий с модулями чисел.

– Выполним следующее задание: Расставьте синие числа в порядке возрастания, а красные – в порядке убывания.

2,3		0,1	5
— 7		— 8	— 3,5
	— 4,2	1,4

– А теперь проверим, что у вас получилось. {Синие: — 8; — 7; — 4,2; — 3,5; ; ; Красные: ; 5; ; 2,3; 1,4; 0,1}

– Молодцы. С этим заданием вы справились.

– Теперь возьмите желтые листы. На них вы видите схему, по которой нужно найти значение выражения. I вариант выполняет первое задание, II вариант выполняет второе задание. А так как мы все сотрудники одной лаборатории, то и ответ вы найдете вместе.

– Проверим ваши ответы. {Ответ: 28}

IV. Историческая справка.

– Сейчас сядьте поудобнее, можно немножко расслабится,  подготовится к следующим серьезным заданиям и прослушать небольшую историческую справку.

Понятие об отрицательных числах возникло в практике очень давно, причем при решении таких заданий, где из меньшего числа приходилось вычитать большее число. Египтяне, вавилоняне, а также древние греки не знали отрицательных чисел и для производства вычислений математики того времени пользовались счетной доской. А так как знаков «плюс» и «минус» не существовало, то они на этой доске положительные числа отмечали красными счетными палочками, а отрицательные – синими. И отрицательные числа долгое время назывались словами, которые означали долг, недостача, а положительные трактовались как имущество.

Древнегреческий ученый Диофант вообще не признавал отрицательных чисел, и если при решении у него получался отрицательный корень, то он отбрасывал его как недоступный.

Совершенно по-другому относились к отрицательным числам древнеиндийские математики: они признавали существование отрицательных чисел, но относились к ним с некоторым недоверием, считая их своеобразными, не совсем реальными.

Не одобряли их долго и европейцы, потому что истолкование имущество – долг вызывало недоумение и сомнение. Действительно, можно складывать и вычитать имущество – долг, а как умножать и делить? Это было непонятно и нереально.

Всеобщее признание отрицательные числа получили в первой половине XIX века. Была создана теория, по которой мы сейчас и изучаем отрицательные числа.

– Скажите, пожалуйста, а эти определения отрицательных и положительных чисел как имущество и долг сейчас в нашем современном мире просматриваются? Как вы думаете? {Ответы учащихся}

– Ну вот, мы восстановили еще немного информации об отрицательных числах.

V. Практические задания.

– Все научно-исследовательские институты решают задачи, которые потом применяются на практике. Сейчас мы тоже решим несколько задач, в которых увидим, где применяются отрицательные числа.

Задача 1. Птица клест-еловик несет яйца и высиживает птенцов зимой. Даже при температуре воздуха – 35°С в гнезде температура не ниже 14°С. На сколько температура в гнезде выше температуры воздуха?

Решение.

Чтобы определить на сколько температура в гнезде больше, чем температура воздуха, нужно от 14 отнять – 35.

1) 14 – (- 35) = 14 + 35 = 49°С – температура в гнезде больше.

Ответ: на 49°С.

Задача 2. Шмели выдерживают температуру до – 7,8°С, пчелы – выше этой на 1,4°С. Какую температуру выдерживают пчелы?

Решение.

Чтобы найти на какую температуру выдерживают пчелы, нужно к числу – 7,8 прибавить число 1,4.

1) – 7,8 + 1,4 = — (7,8 – 1,4) = — 6,4 °С выдерживают пчелы.

Ответ: — 6,4°С.

– Молодцы. С этим заданием вы тоже справились.

VI. Релаксация.

– Как и у каждого учреждения у нас перерыв.

– Сядьте посвободнее, закройте глаза, расслабьтесь. На улице весна. Ярче светит солнышко. Звенит капель. Побежали ручейки и стали появляться проталины. На проталинах робко выглядывает и тянется к солнышку зеленая трава. С юга потянулись стаи птиц. Лучик солнца скользит по вашим лицам. От этого вам тепло и уютно, вы чувствуете себя отдохнувшими и полными свежих сил и энергии.

– А теперь откройте глаза. Перерыв окончен.

VII. Тестовая работа.

– Пока вы отдыхали, я узнала, что руководство НИИ решило провести тестирование научных сотрудников.

– Перед вами лежат бланки с тестами. Подпишите их. В этом тестовом задании вам нужно выбрать правильный вариант ответа и обвести его кружочком.

– Все готовы? Тогда начинаем.

Фамилия, имя _____________ Класс 6 Вариант 1	Фамилия, имя _____________ Класс 6 Вариант 2
Сравните числа – 15 и – 12. А) – 15 >  – 12; Б) – 15 <  – 12; В) – 15 =  – 12. Найдите сумму чисел – 1,4 и – 1,8. А) – 0,4; Б) – 3,2; В) 0,4; Г) 3,2. Найдите разность чисел – 0,3 и – 0,7. А) – 0,4; Б) – 1; В) 0,4; Г) 1. Найдите произведение чисел 0,2 и – 0,4. А) – 0,08; Б) – 0,8; В) – 8; Г) 0,8. Найдите неизвестное число . Ответ: ___________	Сравните числа – 17 и – 23. А) – 17 >  – 23; Б) – 17 <  – 23; В) – 17 =  – 23. Найдите сумму чисел – 1,4 и 0,8. А) – 0,6; Б) – 2,2; В) 0,6; Г) 2,2. Найдите разность чисел – 0,9 и 0,7. А) – 0,2; Б) – 1,6; В) 0,2; Г) 1,6. Найдите произведение чисел – 0,5 и — 0,3 А) – 0,15; Б) 0,15; В) – 1,5; Г) 1,5. Найдите неизвестное число . Ответ: ___________

– Время закончилось. Я попрошу старших научных сотрудников собрать бланки с тестами.

VIII. Итог урока.

– Вот и закончился рабочий день в нашем научно-исследовательском институте. Мы помогли восстановить потерянные сведения о положительных и отрицательных числах.

– Придете вы сегодня домой, к своим родителям и что вы скажете? Продолжите, пожалуйста, фразу: «Сегодня на уроке математики я …»

– А я сегодня, когда приду домой скажу своим родственникам, что сегодня на уроке математики я еще раз убедилась какие у меня замечательные, дружные, умные ученики.

– А сегодня у нас урок закончился. Спасибо. До свидания.

5.03.2011

urok.1sept.ru

Тест репетитора по математике на отрицательные числа — 6 класс

Еще один простейший тест по арифметике. Существует множество самых разных учебных материалов, но когда репетитор по математике в 6 классе сталкивается с по-настоящему слабым проблемным учеником – их всегда не хватает. Из учебника уже все решено, но навыки еще не закреплены как следует. Кроме того, нулевые знания, как правило, — следствие низкого интереса к учебе в общем и к математике в частности. Поэтому репетиторам важно разбавлять свои занятия как можно большим количеством разных видов деятельности. Один из них — прохождение тестов. Ниже размещен простейший тест для 6 класса на тему «отрицательные числа». В нем 15 специально отобранных примеров, рассчитанных на 25-30 минут самостоятельной работы школьника. Пользуйтесь на здоровье!

Какова польза от тестов? Многие репетиторы по праву ругают тестовую форму работы. Либо используют ее лишь для промежуточного контроля меры усвоения материала. Мое мнение о тестах неоднозначное. В них есть 2 очевидных минуса, а именно:

1. Возможность угадать ответ
2. Отсутствие оформления и, как следствие, какого-либо обоснования проведенных расчетов

Последний пункт особенно мешает репетитору по математике, так как становится весьма затруднительно разбираться с системными ученическими ошибками и ляпами.

Все это так, но в последнее время я стал замечать, что тесты из интернета какой-то магической силой притягивают учеников. Может быть потому, что современное поколение, вылупившееся из телефона и планшета, уже больше доверяет интернету, а не преподавателю и маниакально вовлекается в ту форму деятельности, в которой можно просто понажимать на кнопки. И если репетитор по математике позволяет это делать на уроке – почему бы к нему не походить? Вот вам и лишний мотив.

Поэтом у я решил развивать систему тестов на своем сайте. Иногда я привлекаю в помощь других репетиторов, изъявивших желание поработать для общего блага. Я надеюсь, что в ближайшее время удастся доработать функционал тестов и любой ученик сможет высылать репетитору по математике результаты своей работы на сайте для соответствующей проверки. Следите за новостями.

Еще одна проблема в организации занятий — распределение умственной нагрузки равномерно по времени всего урока. Для этого нужно стараться по максимуму разнообразить форму заданий. Тесты – один из винтиков механизма, помогающего репетитору получать такое разнообразие.

Активнее используйте тесты сайта. Постепенно я собираюсь их составить по всем основным разделам школьного курса.

Колпаков. А.Н. Услуги репетитора в Строгино (м.Щукинская).

ankolpakov.ru

Урок математики в 6 классе на тему «Действия с положительными и отрицательными числами»

Тема урока «Действия с положительными и отрицательными числами».

Урок – путешествие в страну положительных и отрицательных чисел.

Учитель математики Лоцманова Елена Васильевна, МОУ Жедяевская СШ, Ульяновской области Старомайнского района.

Предмет (направленность): математика.

Возраст детей: 6 класс

Место проведения: класс.

Тип урока: урок обобщения и систематизации знаний, умений, навыков.

Форма урока: урок-путешествие.

Цели: формирование УУД на уроке математики.

Коммуникативные: договариваться и приходить к общему решению совместной деятельности, умение слышать, слушать и понимать партнера, вести диалоги, отстаивать свою точку зрения, взаимно контролировать действия друг друга, правильно выражать свои мысли, оказывать поддержку друг другу и эффективно сотрудничать как с учителем, так и со сверстниками.

Познавательные: выработать навыки сложения и вычитания положительных и отрицательных чисел, умение применять правила сложения и вычитания положительных и отрицательных чисел при выполнении упражнений, применять его творчески, перенося в новые условия, умение логически мыслить, видеть закономерности, рассуждать.

Регулятивные: Самостоятельно обнаружить и формировать учебную проблему, определять цель УД, оценивать правильность выполнения действий, корректировать свои действия, осуществлять оперативный контроль процесса обучения.

Личностные: умение сделать учение осмысленным, применять творческие способности к выполнению заданий.

Методы: объяснительно-иллюстративный (применение знаний с использованием компьютера), репродуктивный (выполнение заданий по образцу с последующей проверкой)

Формы: фронтальная, индивидуальная, парная.

Оборудование: компьютер, презентация, раздаточный материал.

Этапы урока.

I. 1.Проверка домашнего задания.

2. Работа с деформированным текстом (Задание 1).

3. Устный счёт-игра.

4. Решение ситуационных задач (Задание 2 и 3).

II. 1. Историческая справка (Задание 4).

III. 1.Сравнение чисел (Задание 5).

2.Нахождение значений выражений (Задание 6).

3. Решение уравнений (Задание 7).

IV. 1.Анаграммы.

2.Обгонялки.

3.Кроссворд.

V. 1.Лист Мёбиуса.

VI. 1.Тест контроль

2.Подведение итогов.

Подготовительный этап:

Класс заранее разделен на команды, выбран капитан каждой команды, название и девиз.

Ход урока

Учитель. Сегодня необычный урок. Проведём мы его под девизом: математику нельзя изучать, наблюдая, как это делает сосед (презентация слайд 1). Сегодня мы с вами отправимся в путешествие в страну положительных и отрицательных чисел (презентация слайд 2). На этом уроке мы вспомним все теоретические знания и практические умения, которые приобрели при изучении темы «Сложение и вычитание чисел с разными знаками». Вы должны показать умения выполнять действия с положительными и отрицательными числами. За правильно выполненные задания вы получите жетоны. За устные задания 1 жетон, за письменные 2 жетона. Ознакомимся с планом путешествия (презентация слайд 3).

План путешествия.

1. Край математических знаний.

2. Исторический район

3. Салон красоты

4. Кафе «Эврика»

5. Поле математических чудес.

6. Таможня.

1. Край математических знаний (презентация слайд 4).

Начнём урок с самопроверки домашнего задания с использованием презентации (презентация слайд 5).

Задание 1: работа с деформированным текстом, используя раздаточный материал.

Задание №1.

Вставьте пропущенные слова.

1.Числа со значком «-» называют …

2.Ни положительным, ни отрицательным числом является …

3.Число, показывающее положение точки на координатной прямой, называют … этой точки .

4.Положительные числа расположены … от нуля.

5.Координатной прямой называют прямую с выбранными на ней … .

6. Целыми числами называют : …числа, … числа и … .

Устный счёт (выбор правильного ответа).

На этом этапе учащимся даются карточки с примерами на сложение и вычитание чисел с разными знаками по пять примеров на каждой карточке. К каждому примеру написаны четыре варианта ответов. Ученики работают самостоятельно с последующей проверкой правильности выполненных заданий у всех членов команды. На данном этапе дети зарабатывают себе баллы на личную оценку — по одному жетону за каждый правильно решенный пример и для команды (общее количество баллов).

Карточка с примерами на сложение

№1

Примеры

Варианты ответов

Выбран

ный вариант

А

Б

В

Г

1

-27

27

-41

Г

2

-183

-281

183

281

 Б

3

-33,5

33,5

-52,1

-135,8

 В

4

-35,814

-28,754

35,814

35,337

 А

5

104

88

-88

-104

 Б

Решение ситуационных задач.

С математикой мы сталкиваемся везде: в магазине, на транспорте… Каждый может оказаться в ситуации, как герои следующих задач.

Задание №2.

Находясь в походе, туристы оставили пакеты в пунктах К, М, С. Где по отношению к лагерю находятся эти пункты. Указать координаты.

( раздаточный материал).

Вы нашли записку в которой закодировано расположение клада, для этого выполните задание 3.

Задание №3.

Отметьте на координатной прямой точку А(-6) ,приняв за единичный отрезок длину одной клетки тетради. Отметьте на этой прямой точки В, С, Д, если В правее А на 10 клеток, С- середина отрезка АВ ,точка Д левее точки С на 6 клеток .Укажите координату точки Д , где и будет расположен клад.

2. Исторический район (презентация слайд 6).

Задание №4.

Назовите числа противоположные данным и расшифруйте фамилию математика.

-1/2 ; 4,7 ; 0; -6,91; 3/11 ; -9. (презентация слайд 7).

Историческая справка о математике Видмане даётся учащимися.

– Когда и где появились отрицательные числа? Ни египтяне, ни вавилоны, ни даже древние греки чисел этих не знали. Впервые с отрицательными числами столкнулись китайские ученые (2 век до нашей эры) в связи с решением уравнений, однако знаки “ + “ или “ – “ тогда не употребляли, а изображали положительные числа красным цветом, а отрицательные – черным.
Индийские математики Брамагупта (VII век) и Бхаскара (XII век) с помощью положительных чисел выражали имущество, а с помощью отрицательных “долг”. Они составили правила действий для этих чисел. Однако долгое время отрицательные числа считали не настоящими, фиктивными, абсурдными.
В Европе к отрицательным числам обращается итальянский математик Леонардо Фибоначчи, но в учении об отрицательных числах далее продвинулся М.Штифель (XVI век). Отрицательные числа он называл как “меньше чем ничто” и говорил, что нуль находится между истинными и абсурдными числами. И только после работ выдающегося ученого Р.Декарта (XVII век) и других ученых (XVII – XVIII века) отрицательные числа приобрели “права гражданства”. Символы “ + “ и “ – “ как математические знаки ввёл в 15 веке чешский математик Видман.

«Физкультминутка»

Учащиеся выполняют упражнения на мелкую моторику рук: «Цветок», «Бабочка», «Птица» и др.

3. Салон красоты (презентация слайд 7).

Вашему вниманию представляется красивое платье с заданиями.

Задание №5.

Сравните.

А) -4,4 и -4,8.

Б)0,42 и -2,95.

Задание №6.

Найдите значение выражения.

А) -14+19

Б) 16-(-8)

В) 3,5+I-1,5I.

Задание №7.

Решите уравнение.

А) 7,8-х=9,3

Б) Iх-2I=4.

4. Кафе «Эврика» (презентация слайд 7).

Меню:

1.Винегрет из анаграмм.

2.Борщ с математическими обгонялками.

3.Компот из кроссворда:

«И в шутку и всерьез».

А н а г р а м м ы.

Дирокотана

Лумодь

Пирожныевотполо

Обгонялки.

1.Назовите автора учебника «Математика 6».

2.Что тяжелее 1кг ваты или 1 кг железа.

3. I-6I равен

4.На координатной прямой даны точки А(-3) и В (5).Найдите расстояние от А до В.

5.Назовите наименьшее натуральное число.

6.Наибольшее натуральное трёхзначное число.

7.Результат сложения.

8.Количество см в метре.

Кроссворд.

По горизонтали:

1.Название нашего кафе.

По вертикали:

2.Нелюбимая оценка ученика.

3.Число показывающее положение точки на прямой.

4. «Вымирающая» разновидность учеников.

5.Проверка учеников на прочность.

6.Числа, употребляемые при счёте предметов.

Ответы.

Анаграмма:

Координата. Модуль. Противоположные.

Обгонялки:

1) Зубарева. 2) Одинаковые. 3)6. 4) 8. 5) 1. 6) 999. 7) сумма 8)100.

Кроссворд.

По горизонтали:

1.Эврика.

По вертикали:

2.Два.

3. Координата.

4. Отличник.

5.Контрольная

6. Натуральные.

5. Поле математических чудес (презентация слайд 7).

Знакомство с листом Мёбиуса

6. Таможня (презентация слайд 7).

Раздаточный материал тест по теме.

7. Домашнее задание

Индивидуальное на карточках

8.Подведение итогов. Рефлексия.

Список используемой литературы:

1.Барышникова Н. Математика. 5-11 классы. Игровые технологии на уроках, 2007.

2.Данилов И.К. Об игровых моментах на уроках математики // Математика в школе. — 2000. — № 1. — С.95.

3. Рузина М.С. и др. Страна пальчиковых игр. – СПБ: Кристалл, 97.

infourok.ru

Методическая разработка по алгебре (6 класс) по теме: «Страна положительных и отрицательных чисел», урок математики в 6 классе

Шипикова Анастасия Игоревна

Открытый урок.

Тема: «Урок-путешествие в страну положительных и отрицательных чисел»

Цели урока:
образовательные: повторить понятие модуля, правила сравнения чисел, расположение чисел на координатной прямой, закрепить навыки сложения и вычитания отрицательных и положительных чисел, умений переносить свои знания в новую нестандартную ситуацию, овладение математической терминологией;
развивающие: развитие творческой, речевой, мыслительной активности, используя различные формы работы;
воспитательные: воспитание чувства ответственности, солидарности, доброты, интереса к математике, внимательности, активности и настойчивости в достижении цели, привитие навыков самостоятельной работы.

Тип урока: урок обобщения и систематизации знаний.

Форма проведения урока: урок –решения познавательных задач.

Оборудование: компьютер, мультимедийный оборудование, интерактивная доска, карточки для учащихся, рабочие листы, жетоны.

План урока.

1. Организационная часть (3 мин.)
2. Станция «Сигнальная (3 мин.)
3. Станция «Внимательная» (3 мин.)
4. Станция «Вычислительная» (8 мин.)
5. Физкультминутка (1 мин.)
6. Самостоятельная работа (4 мин.)
7. Станция «Конечная» ( 2 мин.)
8. Подведение итогов урока (1 мин.)
9. Рефлексия ( 2 мин.)

Организационный момент.

Здравствуйте, дорогие ребята, уважаемые гости. Я уверена, что каждый из вас любит путешествовать, поэтому сегодня мы с вами отправляемся в путешествие, а именно, в страну положительных и отрицательных чисел. У каждого из вас на столе лежит комплект, который понадобится нам во время путешествия, но об этом чуть позже. Перед путешествием нам необходимо принять ряд правил:

-работаем с места, не вставая, в целях экономии времени;

-сигналом для вопроса или желания ответить на вопрос служит поднятая рука.

Вопросы есть по правилам?

Тогда мы с вами готова, но возникает вопрос, какой вид транспорта мы выберем для нашего путешествия? Это мы узнаем, ответив на несколько вопросов. Возьмите, пожалуйста, лист, который называется выбор транспорта. Прочитайте инструкцию.

Инструкция: Самостоятельно ответить на поставленный вопрос, а в пустое окно под номером вопроса, записать лишь первую букву ответа.

1. Числа, записываемые со знаком минус, называются …
2. Шестая по счету буква в алфавите…
3. Математический символ, используемый для сравнения чисел.
4. Как называются два числа, отличающиеся только знаками?
5. Не любимая оценка ученика?

Получился набор букв:

Ниже, из записанных букв, составить слово, которое определит вид транспорта.

Как мы отправимся в путешествие? Правильно, поездом! На каждой станции вас ожидает задание, для которого имеется свой бланк. Так что всем я желаю плодотворно поработать на каждой станции, удачи, в добрый путь!

Станция «Сигнальная».

Первая наша станция «Сигнальная». Возьмите бланк данной станции и прочитайте инструкцию. В пустое окно поставьте знак +, если согласны с утверждением или знак -, если не согласны. Понятно задание?

1. – 5 – отрицательное число
2. Дана точка А(-6), расстояние от нее до начала отсчета равно -6 единицам.
3.  -7 и 7 – противоположные числа.
4. Модуль – 6 равен 6
5. -15
6. – 12  > — 2
7. Уравнение |x|=7 имеет один корень: 7.

А теперь поменяйтесь бланками с вашим соседом по парте и выполним проверку.

Станция «Внимательная»

Переходим к следующей станции «Внимательная».

Прочитайте инструкцию.

Перед вами ряд чисел. -5,6; 11,8; -0,5; 3,7; 7 ; -19; 0.
Ответьте на вопросы, записав ответ в пустое окно под номером вопроса.
1 Какое число в ряду наибольшее?
2Какое число имеет наибольший модуль?
3Какое число является наименьшим в ряду?
4 Какое число имеет наименьший модуль?
5 Назовите числа в порядке возрастания.

1	2	3	4	5
11,8	-19	-19	0	-19; -5,6; -0,5; 0; 3,7; 7; 11,8

Выполним проверку

Станция «Вычислительная».

Прежде, чем войти на станцию «Вычислительная» повторим теоретические вопросы:

1. Какие числа называются отрицательными?
2. Сумма двух противоположных чисел равна…
3. Ноль — это какое число?
4. Какие числа называются противоположными?
5. Как сравнить противоположные числа?
6. Как сравнить отрицательные числа?
7. Как сравнить отрицательные и положительные числа?
8. Что можно сказать о модулях отрицательных и положительных чисел?
9. Как сложить два отрицательных числа?
10. Как сложить два числа с разными знаками?

Теперь вы готовы к этой станции приступим к решению примеров.

Комментируем свой ответ

1. -2,5+3,6                        1,1
2. -4,7+1,2                       -3,5
3. 3,6-6,7                         -3,1
4. -2,1+(-0,9)                   -3
5. 5,6+(-0,2)                     5,4
6. 3,1+(-3,1)                     0
7. 5,3-(-2,7)                      8

8.-5+7-10                          -8

Станция «Спортивная»
Мы с вами попали на станцию, которой нем в нашем маршруте, но размяться нам нужно.

Все ребята дружно встанем,
Руки кверху поднимаем,
А потом их отпускаем.
А теперь их развернем
И к себе скорей прижмем.

Разотрите все ладошки,
приготовьте для хлопков,
если правда – вы похлопайте,
если ложь потопайте.

Число 5 – положительное число;
27 0 – отрицательное число;
Сумма противоположных чисел равна 0.

Наш урок продолжить нужно.
Подравнялись, сели дружно!

Станция «Самостоятельная»

Вот мы  и попали на станцию самостоятельная. По ее названию понятна, что работаете вы самостоятельно.

Прочитайте инструкцию, всем понятно, что нужно сделать. Приступаем.

Вариант 1		Вариант 2
-5+12	7	-14+7	-7
-13-5	-18	-15-3	-18
-4+6-3	-1	-5+6-4	-3
-3,8+3,8	0	-7,4+7,4	0
8-10+2	0	3-11+8	0

Ребята проверяют друг у друга решение и ответы.

Станция «Конечная».

Наконец мы добрались до конечной станции, она у нас необычная – музыкальная. Закрепим правила сложения чисел с разными знаками, исполнив песню.

1. Числа отрицательные, новые для нас,

Лишь совсем недавно изучил наш класс.

Сразу поприбавилось всем теперь мороки –

Учат-учат правила дети все уроки.

2. Если уж захочется очень всем сложить

Числа отрицательные, нечего тужить:

Надо сумму модулей быстренько узнать,

К ней потом знак « минус» взять да приписать.

3. Если числа с разными знаками дадут,

Чтоб найти их сумму, все мы тут как тут.

Больший модуль быстро очень выбираем

Из него мы меньший модуль вычитаем.

Самое же главное – знак не позабыть!

— Вы какой поставите? – мы хотим спросить.

— Вам секрет откроем. Проще дела нет,

Знак, где модуль больше, запиши в ответ.

Молодцы. Эту песню, она же является и правилом, можете оставить себе на память от нашего урока. На каждой станции у нас были очень активные путешественники, которые заработали заслуженные 5 – это…А остальные путешественники будут оценены по станции самостоятельная.

Ну и напоследок мне хочется узнать понравилась ли вам та или иная станция, поэтому возьмите последний лист,  и ответьте на вопрос, если отвечаете да, то нарисуйте веселый смайлик, если нет грустный. И в 3 столбце отметьте наиболее понравившуюся станцию.

Вопрос Станция	Понравилась ли тебе станция?	Отметь знаком «+» ту станцию, которая понравилась больше.
Сигнальная
Внимательная
Вычислительная
Спортивная
Самостоятельная
Конечная

nsportal.ru

Положительные и отрицательные числа. Координатная прямая. Математика, 6 класс: уроки, тесты, задания.

1.	Положительные и отрицательные числа Сложность: лёгкое	1
2.	Температура воздуха Сложность: лёгкое	1
3.	Расположение двух чисел на координатной прямой Сложность: лёгкое	1
4.	Координата точки Сложность: лёгкое	1
5.	Название точки Сложность: среднее	2
6.	Расстояние до нуля Сложность: среднее	2
7.	Точка, симметричная данной относительно точки 0 Сложность: среднее	2
8.	Расстояние между точками на координатной прямой Сложность: среднее	2
9.	Неотрицательные и неположительные числа Сложность: среднее	2
10.	Координата точки, симметричной данной точке Сложность: сложное	4
11.	Координата центра симметрии Сложность: сложное	4
12.	Координаты трёх точек Сложность: сложное	3

www.yaklass.ru