Системы уравнений. Основные сведения и примеры. Видеоурок. Алгебра 11 Класс
Тема: Уравнения и неравенства. Системы уравнений и неравенств
Урок: Системы уравнений. Основные сведения и примеры
Рассмотрим системы двух уравнений с двумя неизвестными (1) и трех уравнений с тремя неизвестными (2).
Здесь р и q – некоторые выражения, зависящие от х и у.
Здесь р, q и r – некоторые выражения, зависящие от х, у и z.
Частным решением системы 1 называется пара чисел () такая, при подстановке которой в уравнения системы получим верные равенства.
Частным решением системы 2 называется тройка чисел () такая, при подстановке которой в уравнения системы получим верные равенства.
Решить систему уравнений – означает найти множество всех ее решений.
Чтобы найти множество всех решений системы, лучше всего пользоваться эквивалентными или равносильными преобразованиями, то есть такими, которые не искажают множество решений.
Таким образом, процесс решения системы сводится к постепенному переходу от заданной сложной системы к все более простой и так до тех пор, пока не получим ответ.
После получения ответа можно выполнить проверку, подставив найденные решения в исходную систему, но если при решении были применены только равносильные преобразования, то проверку выполнять принципиально не обязательно.
Методы решения систем с помощью эквивалентных преобразований:
-метод подстановки;
-метод алгебраического сложения;
-метод введения новых переменных;
Не всегда удается сохранить равносильность преобразований, в таких случаях приходится прибегать к переходу к следствию. Пусть мы упростили исходную систему (система вида 1) и получили некоторую новую. Если в исходной системе было два решения – две пары чисел х и у, то в новой системе эти решения сохранятся, но добавятся новые – посторонние решения. В таких случаях необходимо выполнить проверку, найти и отбросить посторонние решения и только после этого выписать ответ.
Обратим внимание, что при решении систем недопустима потеря решений. Одной из важных причин таких потерь является сужение ОДЗ при упрощении системы. То есть, например, в исходной системе вида 1 было два решения, а в результате получена система, имеющая единственное решение. Поэтому важно во время преобразований следить за областью допустимых значений.
Пример 1 – решить систему:
В первом уравнении выразим у через х, второе уравнение без изменений:
Подставляем полученное выражение во второе уравнение:
Подставляем найденное значение х в первое уравнение и находим у:
Поскольку при решении мы пользовались эквивалентными преобразованиями, проверку выполнять не нужно.
Ответ: (1;1)
Пример 2 – решить систему:
Данную систему можно решать различными способами, мы перейдем к следствию – воспользуемся свойствами логарифма:
Получили простую систему с двумя неизвестными, решаем ее:
Поскольку не всегда при решении системы применялись равносильные преобразования, обязательна проверка. Второе решение () не удовлетворяет ОДЗ, его следует отбросить.
Ответ: ()
Рассмотрим некоторые формулы и их особенности, которые приводят к потере решений.
1.
Когда n – натуральное число, левое выражение справедливо при любом значении х, кроме нуля, а правое справедливо уже только при положительных х, произошло сужение ОДЗ. Для сохранения равносильности необходимо использовать модуль:
2.
Проанализируем ОДЗ. Для левой части:
Для правой части:
Сужение ОДЗ в данном случае продемонстрировано на рисунке 1:
Рис. 1. Cужение ОДЗ
Чтобы избежать данной ситуации, поставим модуль, при этом произойдет расширение ОДЗ, что не так страшно:
Теперь в правой части и х, и у могут быть любым числом.
Итак, мы рассмотрели основные сведения о системах уравнений с двумя переменными и х решении, далее рассмотрим метод подстановки как метод решения систем уравнений.
Список литературы
1. Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
2. Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
3. Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Xenoid.ru (Источник).
2. Xvatit.com (Источник).
3. Внеклассный урок (Источник).
Домашнее задание
1. Алгебра и начала анализа, 10-11 класс (А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын) 1990, № 180-183 ст. 287-288;
2. Решить систему:
3. Решить систему:
interneturok.ru
| 1. |
Метод сложения (линейные уравнения)
Сложность: лёгкое |
|
| 2. | Метод подстановки (линейные уравнения) Сложность: лёгкое | |
| 3. |
Корни квадратного уравнения, теорема Виета
Сложность: лёгкое |
|
| 4. |
Метод подстановки (линейное и квадратное)
Сложность: лёгкое |
|
| 5. |
Метод алгебраического сложения
Сложность: среднее |
|
| 6. |
Способ сложения
Сложность: среднее |
|
| 7. |
Пары чисел, которые являются решением системы уравнений
|
|
| 8. |
Графический метод (парабола и прямая)
Сложность: среднее |
|
| 9. |
Графический метод (гипербола и прямая)
Сложность: среднее |
|
| 10. |
Графический метод (элементарные функции)
Сложность: среднее | |
| 11. |
Система квадратных уравнений
Сложность: среднее |
|
| 12. |
Система уравнений (линейное и квадратное) I
Сложность: среднее |
|
| 13. |
Система уравнений (линейное и квадратное) II
Сложность: среднее |
|
| 14. |
Система уравнений (линейное и квадратное) III
Сложность: среднее |
|
| 15. |
Задача на составление системы уравнений
Сложность: среднее |
|
| 16. |
Система рациональных уравнений
Сложность: среднее |
|
| 17. |
Система, состоящая из рационального и квадратного уравнений
Сложность: среднее |
|
| 18. |
Система, состоящая из рационального и линейного уравнений
Сложность: среднее |
|
| 19. |
Система рациональных уравнений, вводится одна новая переменная
Сложность: среднее |
|
| 20. |
Система, состоящая из рациональных уравнений
Сложность: среднее |
|
| 21. |
Система, состоящая из квадратного и рационального уравнений
Сложность: среднее |
|
| 22. |
Система линейных уравнений
Сложность: среднее |
|
| 23. |
Система, состоящая из квадратного и рационального уравнений, метод умножения
Сложность: среднее |
|
| 24. |
Пары чисел, которые являются решением системы уравнений
Сложность: среднее |
|
| 25. |
Графический метод (окружность и парабола)
Сложность: сложное |
www.yaklass.ru
Как решать систему уравнений за 7 класс 🚩 как решать систему уравнений методом подстановки 🚩 Школы
Понять сущность этого способа проще всего на примере решения одной из типичных систем, включающей в себя два уравнения и требующей нахождения значений двух неизвестных. Так, в этом качестве может выступить следующая система, состоящая из уравнений x + 2y = 6 и x — 3y = -18. Для того чтобы решить ее методом подстановки, требуется в любом из уравнений выразить один член через другой. Например, это можно сделать, используя первое уравнение: x = 6 — 2y.
Затем необходимо подставить полученное выражение во второе уравнение вместо x. Результатом такой подстановки станет равенство вида 6 — 2y — 3y = -18. Произведя простые арифметические вычисления, это уравнение легко привести к стандартному виду 5y = 24, откуда y = 4,8. После этого полученное значение следует подставить в выражение, использованное для подстановки. Отсюда x = 6 — 2*4,8 = -3,6.
Затем целесообразно осуществить проверку полученных результатов, подставив их в оба уравнения первоначальной системы. Это даст следующие равенства: -3,6 + 2*4,8 = 6 и -3,6 — 3*4,8 = -18. Оба этих равенства являются верными, благодаря чему можно сделать вывод о том, что система решена правильно.
Второй способ решения подобных систем уравнений носит название способа сложения, который можно проиллюстрировать на основании того же примера. Для его использования следует все члены одного из уравнений умножить на определенный коэффициент, в результате чего один из них станет противоположным другому. Выбор такого коэффициента осуществляется методом подбора, причем одну и ту же систему можно правильно решить, используя разные коэффициенты.
В данном случае целесообразно произвести умножение второго уравнения на коэффициент -1. Таким образом, первое уравнение сохранит свой первоначальный вид x + 2y = 6, а второе приобретет вид -x + 3y = 18. Затем необходимо сложить полученные уравнения: x + 2y — x + 3y = 6 + 18.
Произведя простые вычисления, можно получить уравнение вида 5y = 24, которое аналогично уравнению, ставшему результатом решения системы способом подстановки. Соответственно, корни такого уравнения также окажутся теми же величинами: x = -3,6, y = 4,8. Это наглядно демонстрирует, что оба способа являются одинаково применимыми для решения систем подобного рода, и оба дают одинаковые правильные результаты.
Выбор того или иного способа может зависеть от личных предпочтений ученика или от конкретного выражения, в котором проще выразить один член через другой или подобрать коэффициент, который сделает члены двух уравнений противоположными.
Очень часто при решении задач по алгебре для 7 класса сложность представляют примеры с многочленами. При упрощении примеров или приведении их к заданному виду следует знать основные правила преобразования многочленов. Также ученику потребуются основы работы со скобками. Любой пример можно упростить, сократив выражение на общий делитель, выведя общую часть за скобки или выполнив приведение к общему знаменателю. При любом преобразовании многочлена очень важно учитывать знак каждого его слагаемого.

Инструкция
Запишите заданный пример на листке. Если он представляет собой многочлен, выделите в нем общую часть. Для этого найдите все слагаемые с одинаковым основанием. Одинаковое основание имеют члены с одной буквенной частью, а также с одной степенью. Такие слагаемые называют подобными. Сложите подобные члены. При этом учитывайте знаки, стоящие перед ними. Если перед одним из них стоит знак «-», вместо сложения выполните вычитание членов и с учетом знака же запишите результат. Если знак «-» имеют оба члена, следовательно выполняется их сложение и результат записывается также со знаком «-».При наличии дробных значений в коэффициентах многочлена, приведите для упрощения примера дроби к общему знаменателю. Для этого умножьте все коэффициенты выражения на одно и то же число так, чтобы при сокращении дробей осталась лишь целая часть. В самом простом случае общий знаменатель является произведением всех знаменателей в дробных коэффициентах. После умножения всех членов, проведите упрощение подобных слагаемых.
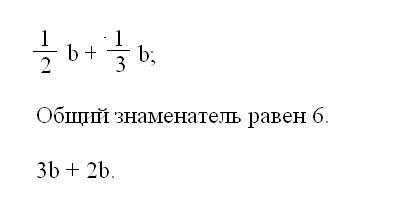
После приведения к общему знаменателю и сложению подобных членов вынесите общие части выражения за скобки. Для этого определите группу членов, где имеется одинаковая часть выражения. Поделите коэффициенты группы на общую часть и запишите ее впереди скобок. В скобках оставьте не весь многочлен, а именно данную группу членов с оставшимися от деления коэффициентами.
Не потеряйте знак при выносе за скобки. Если вы хотите общую часть вынести со знаком «-», то для каждого члена в скобках замените знак на противоположный. Остальные члены, не участвующие в выносе за скобки, запишите до или после скобок с сохранением их знака.
Если за скобки выносится общая часть со степенью, для группы в скобках производится вычитание показателя выносимой степени. При раскрытии скобок степени подобных членов складываются, а коэффициенты умножаются.Выражение можно сократить на целое число, если на него делятся все коэффициенты многочлена. Проверьте, нет или в заданном примере общего делителя. Для этого найдите для всех коэффициентов число, на которое нацело поделится каждый из них. Выполните деление всех коэффициентов многочлена.
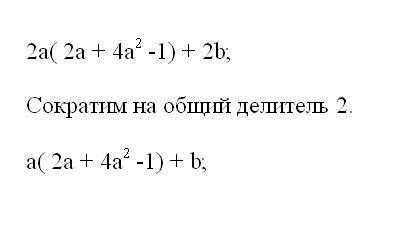
Если для решения примера задано значение буквенной переменной, подставьте ее в преобразованное выражение. Посчитайте результат и запишите. Пример решен.
Система уравнений представляет собой совокупность математических записей, каждая из которых содержит некоторое количество переменных. Существует несколько способов их решения.

Вам понадобится
- -линейка и карандаш;
- -калькулятор.
Инструкция
Решить систему уравнений — означает найти множество всех ее решений, или доказать, что она их не имеет. Её принято записывать с помощью фигурной скобки. Для решения системы уравнений с двумя переменными обычно используют следующие методы: графический способ, способ подстановки и способ сложения. Остановимся подробнее на первом из вышеперечисленных вариантов. Рассмотрим последовательность решения системы, которая состоит из линейных уравнений имеющих вид: a1x + b1y = c1 и a2x + b2y = c2. Где x и y – неизвестные переменные, а b,c – свободные члены. При применении данного способа каждое решение системы представляет собой координаты точек прямых, соответствующих каждому уравнению. Для начала в каждом случае выразите одну переменную через другую. Затем задайте переменной х несколько любых значений. Достаточно два. Подставьте в уравнение и найдите y. Постройте систему координат, отметьте на ней полученные точки и проведите через них прямую. Аналогичные расчеты необходимо провести и для других частей системы.Точка или точки пересечения построенных графиков и будут являться решением данной совокупности уравнений.
Система имеет единственное решение, если построенные прямые пересекаются и имеют одну общую точку. Она несовместна, если графики параллельны друг другу. И имеет бесконечно много решений, когда прямые сливаются друг с другом.
Данный способ считается очень наглядным. Главным недостатком является то, что вычисленные неизвестные имеют приближенные значения. Более точный результат дают так называемые алгебраические методы.
Любое решение системы уравнений стоит проверить. Для этого подставьте вместо переменных полученные значения. Так же можно найти его решение несколькими методами. Если решение системы верное, то все ответы должны получиться одинаковыми.
Уравнение – это запись математического равенства с одним или несколькими аргументами. Решение уравнения заключается в поиске неизвестных значений аргументов – корней, при которых заданное равенство истинно. Уравнения бывают алгебраические, неалгебраические, линейные, квадратные, кубические и др. Для их решения необходимо освоить тождественные преобразования, переносы, подстановки и другие операции, позволяющие упрощать выражение, сохраняя заданное равенство.

Инструкция
Линейное уравнение в общем случае имеет вид: ах + b = 0, причем неизвестная величина х здесь может быть только в первой степени, также она не должна находится в знаменателе дроби. Однако при постановке задачи часто уравнение предстает, например, в таком виде: х+2/4 + х = 3 – 2*х. В этом случае перед вычислением аргумента необходимо привести уравнение к общему виду. Для этого выполняется ряд преобразований.
Перенесите вторую (правую) часть уравнения по другую сторону равенства. При этом каждое слагаемое поменяет свой знак: х+2/4 + х — 3 + 2*х = 0. Проведите сложение аргументов и чисел, упростив выражение: 4*х – 5/2 = 0. Таким образом, получена общая форма записи линейного уравнения, отсюда легко найти х: 4*х = 5/2, х = 5/8. Помимо описанных операций, при решении уравнений следует использовать 1 и 2 тождественные преобразования. Их суть заключается в том, что обе части уравнения можно сложить с одним и тем же или умножить на одно и то же число или выражение. Полученное уравнение будет выглядеть иначе, но его корни останутся неизменными. Решение квадратных уравнений вида ах² + bх +с = 0 сводится к определению коэффициентов а, b, с и их подстановки в известные формулы. Здесь так же, как правило, для получения записи общего вида необходимо предварительно выполнять преобразования и упрощения выражений. Так, в уравнении вида -х² = (6х + 8)/2 раскройте скобки, перенося правую часть за знак равенства. Получится следующая запись: -х² — 3х + 4 = 0. Умножьте обе части равенства на -1 и запишите результат: х² + 3х — 4 = 0.Вычислите дискриминант квадратного уравнения по формуле D = b² – 4*a*c = 3² – 4*1*(-4) = 25. При положительном дискриминанте уравнение имеет два корня, формулы нахождения которых таковы: х1 = -b + √(D)/2*а; х2 = -b — √(D)/2*а. Подставьте значения и вычислите: х1 = (-3+5)/2 = 1 и х2 = (-3-5)/2 = -4. Если бы полученный дискриминант был равен нулю, уравнение имело бы лишь один корень, что следует из приведенных формул, а при D
При нахождении корней кубических уравнений используют метод Виета-Кардано. Более сложные уравнения 4 степени вычисляются с помощью замены, в результате которой понижается степень аргументов, и уравнения решаются в несколько этапов, как квадратные.
www.kakprosto.ru
Внеклассный урок — Система уравнений с двумя переменными. Системы уравнений с двумя переменными. Способы решения.
Система уравнений с двумя переменными. Уравнения первой степени. Способы решения
Уравнение может содержать не одну, а две переменных. Понятно, что такие уравнения называются уравнениями с двумя переменными.
Система уравнений – это два и более уравнений, которыми можно манипулировать для нахождения общих решений. Система из двух уравнений вкючает в себя две переменных, значения которых являются общими для обоих уравнений. С помощью одного уравнения системы решается другое, а в итоге решаются оба уравнения системы.
Способы решения системы уравнений первой степени.
1. Решение методом подстановки.
Суть в том, что в системе уравнений выбираете наиболее простое, в котором одну переменную выражаете через другую. Результат подставляете во второе уравнение, благодаря чему преобразуете его в более простое уравнение с одной переменной. Вычисляете это уравнение и получаете значение одной из переменных. Подставляется его в первое уравнение и получаете значение второй переменной. Так вы решаете всю систему уравнений.
Пример: Решим систему уравнений
│x + y = 1
│2x – y = 2
Решение:
Первое уравнение системы проще второго – его и используем.
Выразим в нем x через у:
x = 1 – y
Подставляем это значение x в наше второе уравнение и находим значение y:
2(1 – y) – y = 2
2 – 2y – y = 2
2 – 3y = 2
3y = 2 – 2
3y = 0
y = 0.
Мы получили значение y. Подставляем его в наше первое уравнение и находим теперь уже значение x:
x + 0 = 1
x = 1
Мы нашли значения обеих переменных.
Ответ:
│x = 1
│y = 0
2. Решение методом сложения.
Этот метод целесообразно применять, если при сложении одно из неизвестных пропадает.
Пример 1: Решим систему уравнений
│x + y = 5
│x – y = 1
Решение.
Сложим (вычтем) почленно оба уравнения системы:
│(x + y) + (x – y) = 5 + 1
│(x + y) – (x – y) = 5 – 1
Раскрываем скобки в обоих уравнениях и сводим подобные члены. В результате в первом уравнении пропадает у, во втором х. Мы получаем уравнения с одной переменной, которые проще решать:
│ x + y + x – y = 6
│ x + y – x + y = 4
↓
│2x = 6
│2y = 4
↓
│x = 6 : 2
│y = 4 : 2
↓
│x = 3
│y = 2
Пример решен.
Необязательно производить взаимное сложение и вычитание двух уравнений системы. Часто достаточно бывает произвести одно из двух действий, чтобы вычислить значение одной из двух переменных. А зная одну переменную, мы уже легко сможем найти и вторую.
Пример 2. Решить систему уравнений
│2х + 4у = 26
│8х + 4у = 44
В обоих уравнениях есть число 4у. Значит, можем применить метод сложения. При этом произвести не взаимное сложение, а совершить лишь одно действие: вычесть из первого уравнения второе, чтобы 4у исчезло и чтобы в результате мы получили уравнение с одной переменной:
2х + 4у – 8х – 4у = 26 – 44.
-6х = -18
х = -18 : (-6)
х = 3
Теперь можем найти и значение у, подставив значение х в любое из двух уравнений системы:
2 · 3 + 4у = 26
6 + 4у = 26
4у = 20
у = 20 : 4
у = 5
Ответ: х = 3, у = 5.
Однако рассмотрим еще один пример.
Пример 3: Решим систему уравнений
│3х + 5у = 21
│8х – 3у = 7
Здесь нет переменных с одинаковыми коэффициентами, чтобы при вычитании они исчезли. Что делать в этом случае? Для таких случаев придумано оригинальное решение: умножим почленно первое уравнение на 3, а второе на 5. От этого истина не пострадает, потому что мы просто получим равносильные уравнения. Зато благодаря этому приему у нас появятся одинаковые переменные 15у:
│(3х + 5у = 21) · 3
│(8х – 3у = 7) · 5
↓
│3 · 3х + 3 · 5у = 3 · 21
│5 · 8х – 5 · 3у = 5 · 7
↓
│9х + 15у = 63
│40х – 15у = 35
Итак, у нас появились одинаковые переменные и мы можем сложить два уравнения, чтобы прийти к уравнению с одной переменной:
9х + 15у + 40х – 15у = 63 + 35
49х = 98
х = 2
Осталось найти значение второй переменной, подставив значение х, например, в первое уравнение системы:
3 · 2 + 5у = 21
6 + 5у = 21
5у = 21 – 6
5у = 15
у = 3.
Ответ: х = 2; у = 3.
Опять же не всегда нужно преобразовывать оба уравнения системы так, как было в предыдущем примере. Бывает и так, что достаточно изменить лишь одно из уравнений.
Пример 4. Решим систему уравнений:
│3х – 4у = 7
│х + 3у = 11
Здесь достаточно второе уравнение умножить на –3. Тогда мы получим число –3х, а при сложении двух уравнений придем к уравнению с одной переменной.
Итак, умножаем второе уравнение на –3:
(х + 3у = 11) · (–3)
–3х – 9у = –33
Теперь складываем два уравнения, приходим к уравнению с одной переменной у и решаем его:
3х – 4у –3х – 9у = 7 – 33
–13у = –26
у = 2.
И находим значение х. Это проще сделать во втором уравнении:
х + 3 · 2 = 11
х + 6 = 11
х = 5.
Ответ: х = 5; у = 2.
3. Решение методом введения новой переменной.
Пример. Решить систему уравнений
│ 2 3
│———— + ———— = 2
│ х – 3у 2х + у
│
│ 8 9
│———— – ———— = 1
│ х – 3у 2х + у
Перед нами система сложных уравнений, осложненных дробными числами. Наша задача – упростить их, чтобы потом решить. Если применить какой-нибудь из первых двух методов, получатся еще более сложные уравнения. Зато хорошо подходит метод введения новой переменной, благодаря которому мы целую дробь можем заменить одной переменной. Как это сделать?
Обратите внимание: у первых чисел обоих уравнений одинаковые знаменатели х – 3у, при этом их числители делятся на 2. У вторых чисел тоже одинаковые знаменатели 2х + у, а их числители делятся на 3. Этим и воспользуемся.
1) Выпишем снова нашу систему уравнений, разложив на множители числители второго уравнения и вынеся их за дробь:
│ 2 3
│———— + ———— = 2
│ х – 3у 2х + у
│
│ 2 3
│4 · ———— – 3 · ———— = 1
│ х – 3у 2х + у
Теперь в обоих уравнениях у нас абсолютно одинаковые первые дроби и абсолютно одинаковые вторые дроби.
2) Заменим эти дроби новыми переменными a и b следующим образом:
2 3
———— = а, ———— = b.
х – 3у 2х + у
Так мы существенно упрощаем уравнения, которые обретают совсем иной вид:
│ а + b = 2
│4а – 3b = 1
3) Применяем уже известный нам метод подстановки.
Первое уравнение проще, поэтому сначала выражаем в нем а через b:
а = 2 – b.
Подставляем полученное значение а во второе уравнение, раскрываем скобки, приводим подобные члены и вычисляем численное значение b:
4 · (2 – b) – 3b = 1
8 – 4b – 3b = 1
8 – 7b = 1
7b = 8 – 1
7b = 7
b = 1
Раз нам известно численное значение b, то мы легко можем найти и численное значение а. Это проще сделать с помощью первого уравнения:
а + b = 2
а + 1 = 2
а = 2 – 1
а = 1.
Итак:
а = 1, b = 1.
Вписываем в дроби эти значения а и b:
│ 2
│———— = 1
│ х – 3у
│
│ 3
│———— = 1
│ 2х + у
4) Преобразуем эти уравнения по известному вам правилу: неизвестные влево, известные вправо:
│ х – 3у = 2 : 1
│2х + у = 3 : 1
↓
│ х – 3у = 2
│2х + у = 3
5) Решаем эту систему уравнений снова с помощью метода подстановки. Для этого в первом уравнении х выражаем через у:
х = 2 + 3у.
Подставляем во второе уравнение и находим у:
2 · (2 + 3у) + у = 3
4 + 6у + у = 3
7у = 3 – 4
7у = –1
у = –1/7
И с помощью первого уравнения находим х:
х – 3у = 2
х – 3 · (–1/7) = 2
х + 3/17 = 2
х = 2 – 3/7
х = 11/7.
Мы нашли значения х и у в нашей исходной системе уравнений – а значит, решили ее.
Ответ: х = 11/7, у = –1/7
ПРИМЕЧАНИЕ.
Как видно из этого примера, нередки случаи, когда при решении системы уравнений надо последовательно применить сразу несколько методов.
raal100.narod.ru
