Умножение комплексных чисел | Математика
Как умножить комплексные числа?
Рассмотрим, как следует выполнять умножение комплексных чисел, в теории и на конкретных примерах.
Произведением комплексных чисел
и
записанными а алгебраической форме, называется комплексное число
На практике умножение комплексных чисел выполняют по правилу умножения двучленов, с последующей заменой i² на -1.
Примеры.
Найти произведение комплексных чисел, записанных в алгебраической форме:
Решение:
Перемножаем комплексные числа, как обыкновенные многочлены:
приводим подобные слагаемые и заменяем i² на -1:
Утверждение.
Произведение комплексно-сопряженных чисел равно квадрату модуля одного из них.
Доказательство:
Что и требовалось доказать.
Соответственно, чтобы умножить комплексно-сопряженные числа, пользуются правилом:
Например,
Умножение комплексных чисел подчиняется коммутативному (переместительному):
ассоциативному (сочетательному):
и дистрибутивному (распределительному относительно сложения)
законам умножения.
www.matematika.uznateshe.ru
Умножение комплексных чисел, формула и примеры
Рассмотрим умножение комплексных чисел записанных в алгебраической, тригонометрической и показательной формах.
Умножение в алгебраической форме
Умножение комплексных чисел и выполняется непосредственным произведением чисел в алгебраической форме, учитывая свойство мнимой единицы :
Умножение в тригонометрической форме
Для произведения комплексных чисел в тригонометрической форме верно равенство:
Умножение в показательной форме
Для произведения комплексных чисел в тригонометрической форме верно равенство:
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Умножение комплексных чисел
Умножение на число и умножение заданных комплексных чисел выполняются для чисел, представленных в любой форме записи.
Определение 1
Произведением заданного комплексного числа $z=a+b\cdot i$ на действительное число $k$ является комплексное число, которое определяется равенством \[k\cdot z=k\cdot (a+b\cdot i)=k\cdot a+k\cdot b\cdot i.\]
Пример 1
Выполнить умножение комплексных чисел на число $k=\sqrt{3} $:
1) $z_{1} =\sqrt{3} +\sqrt{3} \cdot i$; 2) $z_{2} =5-4\cdot i$; 3) $z_{3} =\sqrt{3} \cdot i$.
Решение:
Для умножения комплексных чисел на число воспользуемся определением и получим:
1) $k\cdot z_{1} =\sqrt{3} \cdot z_{1} =\sqrt{3} \cdot \left(\sqrt{3} +\sqrt{3} \cdot i\right)=\sqrt{3} \cdot \sqrt{3} +\sqrt{3} \cdot \sqrt{3} \cdot i=3+3\cdot i$;
2) $k\cdot z_{2} =\sqrt{3} \cdot z_{2} =\sqrt{3} \cdot (5-4\cdot i)=\sqrt{3} \cdot 5-\sqrt{3} \cdot 4\cdot i=5\sqrt{3} -4\sqrt{3} \cdot i$;
3) $k\cdot z_{3} =\sqrt{3} \cdot z_{3} =\sqrt{3} \cdot (0+\sqrt{3} \cdot i)=\sqrt{3} \cdot \sqrt{3} \cdot i=3i$.
Примечание 1
При умножении заданного комплексного числа $z=a+b\cdot i$ на число $k\, \, (|k|>1)$ модуль этого числа увеличивается в $|k|$ раз:
\[|k\cdot z|=|k|\cdot \sqrt{a^{2} +b^{2} } .\]
Примечание 2
При умножении заданного комплексного числа $z=a+b\cdot i$ на число $k\, \, (|k|
\[|k\cdot z|=\frac{\sqrt{a^{2} +b^{2} } }{\left|\frac{1}{k} \right|} .\]
Примечание 3
Графическая интерпретация операции умножения заданного комплексного числа $z=a+b\cdot i$ на число $k\, \, (|k|>1)$: длина радиус-вектора, изображающего исходное комплексное число, увеличивается в $|k|$ раз (радиус-вектор становится длиннее в $|k|$ раз).
Примечание 4
Графическая интерпретация операции умножения заданного комплексного числа $z=a+b\cdot i$ на число $k\, \, (|k|
Иллюстрация примера умножения заданного комплексного числа $z=a+b\cdot i$ на число $k_{1} =2,\, \, k_{2} =\frac{1}{4} $ с использованием комплексной плоскости приведена на рис.1-2.
Рис. 1
Рис. 2
Определение 2
Произведением двух заданных комплексных чисел $z_{1} =a_{1} +b_{1} i$ и $z_{2} =a_{2} +b_{2} i$ является комплексное число, которое получается перемножением данных чисел по правилам алгебры с учетом того, что $i^{2} =-1$.
Пример 2
Вычислить $i^{k} $ для $k=3..7$.
Решение:
\[i^{2} =-1\]
\[i^{3} =i^{2} \cdot i=-1\cdot i=-i\]
\[i^{4} =i^{2} \cdot i^{2} =-1\cdot (-1)=1\]
\[i^{5} =i^{2} \cdot i^{3} =-1\cdot (-i)=i\]
\[i^{6} =(i^{2} )^{3} =(-1)^{3} =-1\]
\[i^{7} =(i^{2} )^{3} \cdot i=(-1)^{3} \cdot i=-1\cdot i=-i\]
Пример 3
Выполнить умножение комплексных чисел:
1) $z_{1} =1+3i$ и $z_{2} =3-5i$; 2) $z_{1} =\sqrt{3} +2i$ и $z_{2} =\sqrt{5} \cdot i$.
Решение:
Для умножения комплексных чисел воспользуемся определением и получим:
1) $z_{1} \cdot z_{2} =(1+3i)\cdot (3-5i)=1\cdot 3+3\cdot 3i+1\cdot (-5i)+3i\cdot (-5i)=3+9i-5i-15i^{2} =3+4i+15=18+4i$
2)\[\begin{array}{l} {z_{1} \cdot z_{2} =(\sqrt{3} +2i)\cdot (0+\sqrt{5} \cdot i)=\sqrt{3} \cdot 0+0\cdot 2i+\sqrt{3} \cdot \sqrt{5} \cdot i+2i\cdot \sqrt{5} \cdot i=0+0+\sqrt{15} \cdot i+2\sqrt{5} \cdot i^{2} =\sqrt{15} \cdot i-2\sqrt{5} =-2\sqrt{5} +\sqrt{15} \cdot i} \end{array}\]
Замечание 1
Произведение комплексно-сопряженных чисел $z=a+b\cdot i$ и $\overline{z}=a-b\cdot i$ определяется равенством
\[z\cdot \overline{z}=a^{2} +b^{2} \]
или
\[z\cdot \overline{z}=|z|^{2} =|\overline{z}|^{2} .\]
Другими словами, произведение комплексно-сопряженных чисел есть квадрат модуля каждого из них.
Пример 4
Выполнить умножение комплексно-сопряженных чисел, используя замечание 1 и определение:
1) $z=1+3i$ и $\overline{z}=1-3i$; 2) $z=\sqrt{3} +2i$ и $\overline{z}=\sqrt{3} -2i$.
Решение:
Для умножения комплексных чисел воспользуемся замечанием 1 и получим:
1) $z\cdot \overline{z}=(1+3i)\cdot (1-3i)=1^{2} +3^{2} =1+9=10$
2) \[z\cdot \overline{z}=(\sqrt{3} +2i)\cdot (\sqrt{3} -2i)=(\sqrt{3} )^{2} +2^{2} =3+4=7\]
Для умножения комплексных чисел воспользуемся определением и получим:
1) $z\cdot \overline{z}=(1+3i)\cdot (1-3i)=1\cdot 1+1\cdot 3i+1\cdot (-3i)+3i\cdot (-3i)=1+3i-3i-9i^{2} =1+9=10$
2) $\begin{array}{l} {z\cdot \overline{z}=(\sqrt{3} +2i)\cdot (\sqrt{3} -2i)=\sqrt{3} \cdot \sqrt{3} +\sqrt{3} \cdot 2i-\sqrt{3} \cdot 2\cdot i+2i\cdot (-2)\cdot i=3+2\sqrt{3} \cdot i-2\sqrt{3} \cdot i-2^{2} \cdot i^{2} =3+4=7} \end{array}$
Результаты выполнения операции умножения комплексных чисел совпадают.
Определение 3
Произведением двух заданных комплексных чисел в тригонометрической форме $z_{1} =r_{1} \cdot (\cos \varphi _{1} +i\sin \varphi _{1} )$ и $z_{2} =r_{2} \cdot (\cos \varphi _{2} +i\sin \varphi _{2} )$ является комплексное число, которое определяется равенством
\[z_{1} \cdot z_{2} =r_{1} \cdot r_{2} \cdot [\cos (\varphi _{1} +\varphi _{2} )+i\sin (\varphi _{1} +\varphi _{2} )].\]
Пример 5
Выполнить умножение комплексных чисел:
1) $z_{1} =\sqrt{3} \cdot (\cos \frac{\pi }{4} +i\cdot \sin \frac{\pi }{4} )$ и $z_{2} =2\cdot (\cos \frac{2\pi }{3} +i\cdot \sin \frac{2\pi }{3} )$;
2) $z_{1} =4\cdot (\cos \pi +i\cdot \sin \pi )$ и $z_{2} =5\cdot (\cos \frac{\pi }{2} +i\cdot \sin \frac{\pi }{2} )$.
Решение:
Для умножения комплексных чисел воспользуемся определением и получим:
1) $\begin{array}{l} {z_{1} \cdot z_{2} =\left(\sqrt{3} \cdot (\cos \frac{\pi }{4} +i\cdot \sin \frac{\pi }{4} )\right)\cdot \left(2\cdot (\cos \frac{2\pi }{3} +i\cdot \sin \frac{2\pi }{3} )\right)=2\cdot \sqrt{3} \cdot [\cos (\frac{\pi }{4} +\frac{2\pi }{3} )+i\cdot \sin (\frac{\pi }{4} +\frac{2\pi }{3} )]=2\sqrt{3} \cdot (\cos \frac{11\pi }{12} +i\cdot \sin \frac{11\pi }{12} )} \end{array}$
2) \[\begin{array}{l} {z_{1} \cdot z_{2} =\left(4\cdot (\cos \pi +i\cdot \sin \pi )\right)\cdot \left(5\cdot (\cos \frac{\pi }{2} +i\cdot \sin \frac{\pi }{2} )\right)=4\cdot 5\cdot [\cos (\pi +\frac{\pi }{2} )+i\cdot \sin (\pi +\frac{\pi }{2} )]=20\cdot (\cos \frac{3\pi }{2} +i\cdot \sin \frac{3\pi }{2} )} \end{array}\]
Определение 4
Произведением двух заданных комплексных чисел в показательной форме $z_{1} =r_{1} \cdot e^{i\varphi _{1} } $ и $z_{2} =r_{2} \cdot e^{i\varphi _{2} } $ является комплексное число, которое определяется равенством
\[z_{1} \cdot z_{2} =r_{1} \cdot e^{i\varphi _{1} } \cdot r_{2} \cdot e^{i\varphi _{2} } =r_{1} \cdot r_{2} \cdot e^{i(\varphi _{1} +\varphi _{2} )} .\]
Пример 6
Выполнить умножение комплексных чисел:
1) $z_{1} =\sqrt{3} \cdot e^{i\cdot \frac{\pi }{4} } $ и $z_{2} =2\cdot e^{i\cdot \frac{\pi }{3} } $; 2) $z_{1} =\sqrt{5} \cdot e^{i\cdot \frac{2\pi }{3} } $ и $z_{2} =2\cdot e^{i\cdot \frac{\pi }{2} } $.
Решение:
Для умножения комплексных чисел воспользуемся определением и получим:
1) \[z_{1} \cdot z_{2} =\left(\sqrt{3} \cdot e^{i\cdot \frac{\pi }{4} } \right)\cdot \left(2\cdot e^{i\cdot \frac{\pi }{3} } \right)=2\cdot \sqrt{3} \cdot e^{i\cdot (\frac{\pi }{4} +\frac{\pi }{3} )} =2\sqrt{3} \cdot e^{i\cdot \frac{7\pi }{12} } \]
2) \[z_{1} \cdot z_{2} =\left(\sqrt{5} \cdot e^{i\cdot \frac{2\pi }{3} } \right)\cdot \left(2\cdot e^{i\cdot \frac{\pi }{2} } \right)=2\cdot \sqrt{5} \cdot e^{i\cdot (\frac{2\pi }{3} +\frac{\pi }{2} )} =2\sqrt{3} \cdot e^{i\cdot \frac{7\pi }{6} } \]
spravochnick.ru
Комплексные числа, примеры решений
Теория про комплексные числа
ОПРЕДЕЛЕНИЕ Комплексным числом называется число вида , где и действительные числа, а – мнимая единица такая, что .При этом такая запись комплексного числа называется алгебраической; является действительной частью комплексного числа, а – мнимою. Каждое комплексное число может быть так же представлено в тригонометрической форме
или показательной форме:
где – модуль комплексного числа, а – аргумент комплексного числа такой, что , где или .
Комплексные числа изображаются на комплексной плоскости. Для них введены операции сложения, умножения, вычитания и деления. Так же их можно возводить в степень и извлекать из них корень, для этого используют формулу Муавра.
Примеры
ПРИМЕР 1| Задание | Представить в показательной и тригонометрической формах комплексное число . |
| Решение | Найдем модуль заданного комплексного числа, по условию действительная часть , а мнимая , тогда подставляя в формулу для нахождения модуля, получим
Вычислим аргумент заданного комплексного числа:
Тогда тригонометрическая форма этого комплексного числа будет иметь вид:
показательная:
|
| Ответ |
| Задание | Найти разность и сумму комплексных чисел и . |
| Решение | Найдем сумму комплексных чисел, при этом отдельно складываем действительные и мнимые части заданных чисел:
Вычислим разность заданных комплексных чисел, при этом действительные и мнимые части чисел вычитаются отдельно:
|
| Ответ |
| Задание | Найти произведение и частное чисел и . |
| Решение | Найдем произведение заданных комплексных чисел:
Учитывая, что , окончательно получим:
Вычислим частное комплексных чисел и :
умножим числитель и знаменатель полученной дроби на сопряженное комплексное число к знаменателю, то есть на , получим:
Учитывая, что , окончательно получим:
|
| Ответ |
| Задание | Возвести комплексное число в степень : а) ; б) . |
| Решение | а) Возведем заданное комплексное число в квадрат, используя формулы сокращенного умножения:
б) Для возведения комплексного числа в шестую степень, воспользуемся формулой Муавра. Чтобы её применить, необходимо представить комплексное число в тригонометрической или показательной формах. Найдем модуль заданного комплексного числа:
Далее находим его аргумент:
Запишем тригонометрическую форму заданного комплексного числа:
По формуле Муавра
Преобразовывая это выражение, получим алгебраическую форму шестой степени заданного комплексного числа :
|
| Ответ |
| Задание | Вычислить и изобразить корни на комплексной плоскости. |
| Решение | Представим число в тригонометрической форме, для этого найдем его модуль и аргумент:
Тогда
Корни четвертой степени найдем, используя формулу Муавра
В нашем случае . Найдем значения этого выражения для каждого :
Полученные корни можно изобразить на комплексной плоскости. Они будут точками, лежащими на окружности с центром в начале координат и радиусом , а центральные углы между радиусами, проведенными в соседние точки, равны (рис. 1). 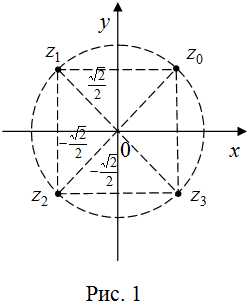
|
| Ответ |
ru.solverbook.com
Умножение комплексных чисел — МегаЛекции
Вопрос 1
Натуральные числа, противоположные им и ноль называют целыми числами. Множество целых чисел обозначают символом Z.
Рациональные числа — это числа вида m/n , где m — целое число, а n — натуральное число.
Множество рациональных чисел принято обозначать буквой Q.
Выполняется соотношение Z⊂Q , поскольку любое число m можно представить в виде m1.
Итак, можно сказать, что
Рациональные числа — это все целые числа, а также положительные и отрицательные обыкновенные дроби.
Действительные числа
Множество всех рациональных и всех иррациональных чисел называется множеством действительных (вещественных) чисел.
Действительные числа обозначаются символом R.
Вопрос 2
Комплексные числа записываются в виде: a+ bi. Здесь a и b – действительные числа, а i – мнимая единица, т.e. i^2 = –1. Число a называется абсциссой, a b – ординатой комплексного числа a+ bi.
Виды комплексных чисел:
1. Алгебраическая форма комплексного числа
Запись комплексного числа в виде z=a+bi , где a и b — действительные числа, называется алгебраической формой комплексного числа.
Например: z=1-i
2. Тригонометрическая форма комплексного числа
Если — модуль комплексного числа z=a+bi , а — его аргумент, то тригонометрической формой комплексного числа z называется выражение:
3. Показательная форма комплексного числа.
Показательной формой комплексного числа называется выражение:
Геометрический смысл комплексных чисел:
Геометрическая интерпретация комплексных чисел заключается в том, что комплексному числу z = х + yi сопоставляется точка на плоскости с координатами х, у. Именно действительная часть числа мыслится как х-координата, а мнимая — как y-координата. Таким образом устанавливается взаимно однозначное соответствие между комплексными числами и точками «числовой плоскости».
Вопрос 3
Сложение комплексных чисел
Сложить два комплексных числа ,
Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:
Таким нехитрым способом можно найти сумму любого количества слагаемых: просуммировать действительные части и просуммировать мнимые части.
Для комплексных чисел справедливо правило первого класса: – от перестановки слагаемых сумма не меняется.
Вычитание комплексных чисел
Пример 2
Найти разности комплексных чисел и , если ,
Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:
Результат не должен смущать, у полученного числа две, а не три части. Просто действительная часть – составная: . Для наглядности ответ можно переписать так: .
Рассчитаем вторую разность:
Здесь действительная часть тоже составная:
Чтобы не было какой-то недосказанности, приведу короткий пример с «нехорошей» мнимой частью: . Вот здесь без скобок уже не обойтись.
Умножение комплексных чисел
Настал момент познакомить вас со знаменитым равенством:
Пример 3
Найти произведение комплексных чисел ,
Очевидно, что произведение следует записать так:
Что напрашивается? Напрашивается раскрыть скобки по правилу умножения многочленов. Так и нужно сделать! Все алгебраические действия вам знакомы, главное, помнить, что и быть внимательным.
Повторим, школьное правило умножения многочленов: Чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена.
Я распишу подробно:
Надеюсь, всем было понятно, что
Внимание, и еще раз внимание, чаще всего ошибку допускают в знаках.
Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство: .
В учебной литературе и на просторах Сети легко найти специальную формулу для вычисления произведения комплексных чисел. Если хотите, пользуйтесь, но мне кажется, что подход с умножением многочленов универсальнее и понятнее. Формулу приводить не буду, считаю, что в данном случае – это забивание головы опилками.
Деление комплексных чисел
Даны комплексные числа , . Найти частное .
Составим частное:
Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.
Вспоминаем бородатую формулу и смотрим на наш знаменатель: . В знаменателе уже есть , поэтому сопряженным выражением в данном случае является , то есть
Согласно правилу, знаменатель нужно умножить на , и, чтобы ничего не изменилось, домножить числитель на то же самое число :
Далее в числителе нужно раскрыть скобки (перемножить два числа по правилу, рассмотренному в предыдущем пункте). А в знаменателе воспользоваться формулой (помним, что и не путаемся в знаках!!!).
Распишу подробно:
Пример я подобрал «хороший», если взять два числа «от балды», то в результате деления почти всегда получатся дроби, что-нибудь вроде .
В ряде случаев перед делением дробь целесообразно упростить, например, рассмотрим частное чисел: . Перед делением избавляемся от лишних минусов: в числителе и в знаменателе выносим минусы за скобки и сокращаем эти минусы: . Для любителей порешать приведу правильный ответ:
Вопрос 4
Степенью называется выражение вида: , где:
§ — основание степени;
§ — показатель степени.
Степень с натуральным показателем {1, 2, 3,…}
Определяем понятие степени, показатель которой — натуральное число (т.е. целое и положительное).
1. По определению: .
2. Возвести число в квадрат — значит умножить его само на себя:
3. Возвести число в куб — значит умножить его само на себя три раза: .
Возвести число в натуральную степень — значит умножить число само на себя раз:
Степень с целым показателем {0, ±1, ±2,…}
Если показателем степени является целое положительное число:
, n > 0
Возведение в нулевую степень:
, a ≠ 0
Если показателем степени является целое отрицательное число:
,a ≠ 0
Прим: выражение не определено, в случае n ≤ 0. Если n > 0, то
Пример 1.
Рекомендуемые страницы:
Воспользуйтесь поиском по сайту:
megalektsii.ru
Сложение комплексных чисел
Пример 1
Сложить два комплексных числа ,
Для того чтобы сложить два комплексных числа нужно сложить их действительные и мнимые части:
Просто, не правда ли? Действие настолько очевидно, что не нуждается в дополнительных комментариях.
Таким нехитрым способом можно найти сумму любого количества слагаемых: просуммировать действительные части и просуммировать мнимые части.
Для комплексных чисел справедливо правило первого класса:
–от перестановки слагаемых сумма не меняется.
Вычитание комплексных чисел
Пример 2
Найти разности комплексных чисел и, если,
Действие аналогично сложению, единственная особенность состоит в том, что вычитаемое нужно взять в скобки, а затем – стандартно раскрыть эти скобки со сменой знака:
Результат не должен смущать, у полученного числа две, а не три части. Просто действительная часть – составная: . Для наглядности ответ можно переписать так:.
Рассчитаем вторую разность:
Здесь действительная часть тоже составная:
Чтобы не было какой-то недосказанности, приведу короткий пример с «нехорошей» мнимой частью: . Вот здесь без скобок уже не обойтись.
Умножение комплексных чисел
Настал момент познакомить вас со знаменитым равенством:
Пример 3
Найти произведение комплексных чисел ,
Очевидно, что произведение следует записать так:
Что напрашивается? Напрашивается раскрыть скобки по правилу умножения многочленов. Так и нужно сделать! Все алгебраические действия вам знакомы, главное, помнить, что и быть внимательным.
Повторим, школьное правило умножения многочленов: Чтобы умножить многочлен на многочлен нужно каждый член одного многочлена умножить на каждый член другого многочлена.
Я распишу подробно:
Надеюсь, всем было понятно, что
Внимание, и еще раз внимание, чаще всего ошибку допускают в знаках.
Как и сумма, произведение комплексных чисел перестановочно, то есть справедливо равенство: .
В учебной литературе и на просторах Сети легко найти специальную формулу для вычисления произведения комплексных чисел. Если хотите, пользуйтесь, но мне кажется, что подход с умножением многочленов универсальнее и понятнее. Формулу приводить не буду, считаю, что в данном случае – это забивание головы опилками.
Деление комплексных чисел
Пример 4
Даны комплексные числа ,. Найти частное.
Составим частное:
Деление чисел осуществляется методом умножения знаменателя и числителя на сопряженное знаменателю выражение.
Вспоминаем бородатую формулу и смотрим на нашзнаменатель: . В знаменателе уже есть, поэтому сопряженным выражением в данном случае является, то есть
Согласно правилу, знаменатель нужно умножить на , и, чтобы ничего не изменилось, домножить числитель на то же самое число:
Далее в числителе нужно раскрыть скобки (перемножить два числа по правилу, рассмотренному в предыдущем пункте). А в знаменателе воспользоваться формулой (помним, чтои не путаемся в знаках!!!).
Распишу подробно:
В ряде случаев перед делением дробь целесообразно упростить, например, рассмотрим частное чисел: . Перед делением избавляемся от лишних минусов: в числителе и в знаменателе выносим минусыза скобки и сокращаем эти минусы: . Для любителей порешать приведу правильный ответ:
Редко, но встречается такое задание:
Пример 5
Приём тот же самый – умножаем знаменатель и числитель на сопряженное Дано комплексное число . Записать данное число в алгебраической форме (т.е. в форме).
знаменателю выражение. Снова смотрим на формулу . В знаменателе уже есть, поэтому знаменатель и числитель нужно домножить на сопряженное выражение, то есть на:
Пример
6
Даны два комплексных числа ,. Найти их сумму, разность, произведение и частное.
studfiles.net
Примеры действий над комплексными числами
Формулы и уравнения с комплексными числами здесь.
Пример. Сумма комплексных чисел.
Дано:
Найти:
Решение:
Исходя из того, что сумма комплексных чисел — это комплексное число, действительная часть которого равна сумме действительных частей, а мнимая часть равна сумме мнимых частей суммируемых комплексных чисел , получим:
.
Ответ: .
Пример. Разность комплексных чисел.
Дано:
Найти:
Решение:
Исходя из того, что разность комплексных чисел — это комплексное число, действительная часть которого равна разности действительных частей, а мнимая часть равна разности мнимых частей вычитаемых комплексных чисел , получим:
.
Ответ: .
Пример. Произведение комплексных чисел.
Дано:
Найти:
Решение:
Исходя из того, что перемножение комплексных чисел выполняется с помощью обычного раскрытия скобок с последующим выделением вещественной и мнимой частей (следует учесть i2=-1)
получим:
Ответ: .
Пример. Деление комплексных чисел.
Дано:
Найти:
Решение:
Исходя из того, что при делении комплексных чисел результат представляют в виде дроби, после чего числитель и знаменатель этой дроби умножают на число, комплексно сопряженное знаменателю:
получим:
Ответ: .
Пример. Возведение комплексного числа в степень.
Дано: .
Найти:
Решение:
Исходя из того, что для возведения комплексного числа в степень его представляют в тригонометрической форме, после чего модуль комплексного числа возводится в эту степень, а аргумент умножается на эту степень:
получим:
Модуль комплексного числа: .
Аргумент: .
Тригонометрическая форма числа: .
В итоге:
Ответ:
Действия над комплексными числами рассмотрены здесь.
matematika.electrichelp.ru
