Проценты математика 5 класс задачи на проценты с – Задачи на проценты. Математика 5 класс.

Содержание

Решение задач на проценты (урок изучения нового материала). 5-й класс

Разделы: Математика, Конкурс «Презентация к уроку»

Презентация к уроку

Загрузить презентацию (2,9 МБ)

Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.

Цели:

научить решать основные задачи на проценты: нахождение процента от величины, нахождение величины по её проценту, нахождение процента одной величины от другой;
способствовать развитию творческой активности учащихся;
развивать познавательный интерес к предмету путем применения информационных технологий;
способствовать развитию математической речи.

етод обучения: лекция, объяснение, устные упражнения, письменные упражнения, самостоятельная работа.

Формы контроля: проверка самостоятельно решенных задач.

Оборудование: мультимедийный проектор (презентация на тему » Проценты»)

Учебник: Математика: Учеб. Для 5 кл. общеобразоват. Учреждений/ Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С. И. Шварцбурд.

Ход урока

I. Актуализация прежних знаний.

1. Устная работа (на закрепление понятия «процент») Предлагаются упражнения по переводу дроби в проценты, а процентов в десятичные дроби.

1. Представьте данные десятичные дроби в процентах: (слайд №2)
0,5= : (50%)	0,01=: (1%)	0,42=: (42%)
123=: (12300%)	0,123=: (12,3%)	7,2=: (720%)
0,045=: (4,5%)	70,5=: (7050%)	1,5=: (150%)
0,6=: (60%)	0,0035=: (0,35%)	10= : (1000%)
2. Представьте проценты десятичными дробями: (слайд №3)
100%=:	1000%=:	72,1%=:
230%=:	3,17%=:	0,5%=:
0,08%=:	133%=:	94,8%=:

3. Заполнить таблицу: (слайд №4)

Обыкновенная дробь	1/2			1/5			4/5
Десятичная дробь		0,25			0,4			0,75
Проценты			10%			60%			100%

II. Изучение нового материала

1). Простейшие задачи на проценты. Существует три типа задач на проценты. Сегодня на уроке вы научитесь их различать и решать, используя определение процента.

1 тип. Нахождение процентов данного числа (дано все и процент, найти часть). (Слайд №5)

В книге 600 страниц. Мальчик прочитал 23% книги. Сколько страниц прочитал мальчик?

2 тип. Нахождение числа по его процентам (дана часть и процент, найти всё). (Слайд №6)

Мальчик прочитал 138 страниц — это 23% всей книги. Сколько страниц в книге?

3 тип. Нахождение процентного отношения чисел (дано два числа, найти процент одного от другого) (слайд №7)

В книге 600 страниц. Мальчик прочитал 138 страниц. Сколько процентов всей книги он прочитал?

(Учащимся раздаются памятки, в которых написаны три типа задач на проценты и их признаки).

Задание 1. Устно определить тип задачи: №1536, №1543, №1544, №1555, №1540 (учебника)

При решении задач на проценты удобно пользоваться следующим алгоритмом (слайд 8):

Попытаться определить тип задачи;
Определить, что принимаем за 100%;
Первым действием находим, сколько приходится на 1%.

Учащиеся вместе с учителем решают задачи 1-3.

Задача 1. (Слайд 9)

Решение. Задача на нахождение процента от числа.

600стр. — 100%

?стр. — 23%

600 : 100 = 6 (стр.) — 1% книги

6 x 23 = 138 (стр.) — прочитал мальчик

Ответ: 138 страниц.

Задача 2. (Слайд 10)

Решение. Задача на нахождение числа по проценту.

?стр. — 100%

138стр. — 23%

138 : 23 = 6 (стр.) — 1% книги.

6 x 100 = 600 (стр.) — в книге.

Ответ: 600 страниц.

Задача 3. (Слайд 11)

Решение. Задача на процентное отношение.

600стр. — 100%

138стр. — ?%

600 : 100 = 6 (стр.) — 1% книги

138 : 6 = 23 % книги прочитал мальчик

Ответ: 23%.

III. Тренировочные упражнения

№1538 (учебника) На поле, площадь которого 620 га, работали хлопкоуборочные машины. За сутки они убрали 15% всего поля. Сколько гектаров поля убрали за сутки?

Решение. Задача на нахождение процента от числа.

620 га — 100%

? га — 15%

620 : 100 = 6,2(га) — 1% поля

6,2^{x 15 = 93 (га) — убрали за сутки.}

Ответ: 93га.

№1548 (учебника) Масса медвежонка составляет 15% массы белого медведя. Найдите массу белого медведя, если масса медвежонка 120 кг.

Решение. Задача на нахождение числа по проценту.

? кг — 100%

120 кг — 15%

120 :15 = 8 (кг)- 1% массы белого медведя.

8 x 100 = 800 (кг) — масса белого медведя.

Ответ: 800 кг.

№1551 (учебника) В школе 700 учащихся. Среди них 357 мальчиков. Сколько процентов учащихся этой школы составляют мальчики?

Решение. Задача на процентное отношение.

700 учащихся — 100%

357 учащихся — ?%

700 : 100 = 7(уч.) — 1 % учащихся школы.

357 : 7 = 51 (%) — составляют мальчики.

Ответ: 51%.

IV. Обучающая самостоятельная работа (7 минут) (Слайд №12)

Вариант №1.

1. Из сахарного тростника получается 18% сахара. Сколько тонн сахара получится из 42,5 т сахарного тростника?

2. Засеяли 65% поля, что составило 325 га. Найдите площадь всего поля.

Вариант №2.

1. Площадь поля 450 га. В первую смену засеяли 270 га. Сколько процентов всей площади засеяли в первую смену?

2. Из овса получается 40% муки. Сколько муки получится из 26,5 т овса?

Работу сдают на проверку.

V. Подведение итогов урока, выставление отметок.

VI. Домашнее задание. п.40; №1571, 1575. (Слайд 13)

15.02.2011

xn--i1abbnckbmcl9fb.xn--p1ai

Задачи на проценты для 5 класса

Задача 1. Первое число составляет 80% от второго. А сколько процентов второе число составляет от первого?

Решение. Обозначим второе число через х. Тогда первое число по равно 0,8х. Найдем, сколько второе число составляет от первого. Для этого разделим второе число на первое, и результат умножим на 100%.

Ответ: второе число составляет 125% от первого.

Задача 2. На сколько процентов увеличится площадь квадрата, если его сторону увеличить на 30%?

Решение. Если сторона квадрата равна а, то площадь квадрата S=а². После увеличения стороны на 30% ее длина составит 130% от а. Это 1,3а. Новая площадь S₁=(1,3a)²=1,69a². Разница составила 0,69а². Обращаем десятичную дробь 0,69 в проценты и получаем 69%. Ответ: Если сторону квадрата увеличить на 30%, то площадь квадрата увеличится на 69%.

Задача 3. Яблоки, содержащие 70% воды, потеряли при сушке 60% своей массы. Сколько процентов воды содержат сушеные яблоки?

Решение. Пусть было х яблок по массе. В них содержится 70% воды, значит, 30% сухого концентрата. 30% от х – это 0,3х. После сушки яблок это количество 0,3х сухого вещества так и остается. Известно, что при сушке яблоки потеряли 60% своей массы. Следовательно, осталось 40% от х, Это 0,4х. То, что осталось, примем за 100%. В этой массе 0,3х сухого вещества. Узнаем, сколько это процентов.

В сушеных яблоках 75% сухого вещества, значит, воды в сушеных яблоках 100%-75%=25%. Ответ: в сушеных яблоках 25% воды.

Задача 4. Свежие грибы содержат 90% влаги, сушеные – 12%. Сколько сушеных грибов получится из 13,2 кг свежих?

Решение. Пусть из 13,2 кг свежих грибов получится х кг сушеных грибов. Тогда сухого вещества в х кг будет содержаться 100%-12%=88%. Получается 0,88х кг. В 13,2 кг свежих грибов сухого вещества содержится 100%-90%=10%. В килограммах получается 0,1∙13,2=1,32 кг. Имеем равенство: 0,88х=1,32, отсюда х=1,32 : 0,88;

х=1,5 кг. Ответ: из 13,2 кг свежих грибов получается 1,5 кг сушеных грибов.

Задача 5. Сколько литров воды нужно разбавить с 300 г соли для получения раствора с концентрацией 15%?

Решение. Пусть нужно х граммов воды разбавить с 300 г соли для получения раствора с концентрацией 15%. Выразим количество соли в х г воды 15%-го раствора. Это 15% от х. Получаем 0,15х г. По условию соли 300 г. Получаем равенство:

0,15х=300, отсюда х=300:0,15=30000:15=2000 г = 2 л воды.

Ответ: нужно разбавить 2 л воды.

Задача 6. В раствор сахарной воды массой 200 г с концентрацией 30% налили 100 г чистой воды. Сколько процентов составляет концентрация сахара в последнем растворе?

Решение. В 200 г сахарной воды с концентрацией 30% содержится 0,3∙200=60 г сахара. После того, как в раствор налили 100 г чистой воды, масса раствора стала равной 300 г, а сахара в нем по-прежнему 60 г. Найдем процентное отношение массы сахара к массе раствора.

Ответ: концентрация сахара в последнем растворе составляет 20%.

Задача 7. В раствор соленой воды массой 600 г с концентрацией 15% добавили раствор соленой воды массой 240 г с концентрацией 50%. Сколько процентов соли в полученной смеси?

Решение. В 600 г соленой воды с концентрацией 15% содержится 15% от 600 г соли. Это 0,15∙600=90 г соли. В 240 г соленой воды с концентрацией 50% содержится 50% от 240 г соли. Это 0,5∙240=120 г соли. Масса полученной смеси равна 600+240=840 г. Соли в этой массе 90+120=210 г. Найдем процент соли в полученной смеси.

Ответ: в полученной смеси содержится 25% соли.

Задача 8. Цену товара сначала снизили на 20%, затем новую цену снизили еще на 25%. На сколько процентов снизили первоначальную цену товара?

Решение. Обозначив первоначальную стоимость товара через х, выразим окончательную стоимость товара и найдем, сколько процентов последняя цена товара будет составлять от первоначальной. После первого снижения на 20% товар стал стоить 80% от первоначальной цены. Это 80% от х или 0,8х Эту цену снизили еще на 25%, стоимость стала составлять 75% от последней цены, равной 0,8х. Тогда последняя цена составит 75% от 0,8х или 0,75∙0,8х=0,6х. Находим, сколько процентов 0,6х (последняя цена товара) составляет от х (первоначальной цены товара).

Получается, что новая цена составляет 60% от первоначальной цены. Это означает, что цена товара после двух снижений уменьшилась на 40%. Ответ: цену товара снизили на 40%.

Задача 9. Число увеличили на 25%. На сколько процентов нужно уменьшить полученное число, чтобы вновь получилось заданное?

Решение. Пусть заданное число было равно х. После увеличения оно составит 1,25х (это 125% от х). Выясним, сколько процентов от числа 1,25х нужно взять, чтобы опять получить х. Получается, что:

Так как х составляет от 1,25х только 80%, то это означает, что, для того, чтобы получить заданное число, нужно полученное число уменьшить на 100%-80%=20%. Ответ: на 20%.

Если вы хотите научиться решать задачи на проценты, то полезной будет эта книга: перейдите по ссылке.

www.mathematics-repetition.com

решить задачу на проценты 5 класс

Записи с меткой «решить задачу на проценты 5 класс»

Задача 1. Первое число составляет 80% от второго. А сколько процентов второе число составляет от первого?

Ответ: второе число составляет 125% от первого.

Задача 2. На сколько процентов увеличится площадь квадрата, если его сторону увеличить на 30%?

В сушеных яблоках 75% сухого вещества, значит, воды в сушеных яблоках 100%-75%=25%. Ответ: в сушеных яблоках 25% воды.

Задача 4. Свежие грибы содержат 90% влаги, сушеные – 12%. Сколько сушеных грибов получится из 13,2 кг свежих?

х=1,5 кг. Ответ: из 13,2 кг свежих грибов получается 1,5 кг сушеных грибов.

Задача 5. Сколько литров воды нужно разбавить с 300 г соли для получения раствора с концентрацией 15%?

0,15х=300, отсюда х=300:0,15=30000:15=2000 г = 2 л воды.

Ответ: нужно разбавить 2 л воды.

Ответ: концентрация сахара в последнем растворе составляет 20%.

Ответ: в полученной смеси содержится 25% соли.

Если вы хотите научиться решать задачи на проценты, то полезной будет эта книга: перейдите по ссылке.

www.mathematics-repetition.com

открытый урок по математике «Решение задач на проценты» (5 класс)

1.Масса медвежонка составляет 15 % массы белого медведя. Найдите массу белого медведя, если масса медвежонка 120 кг.

2.Сливочное мороженое содержит 14 % сахара. На приготовление мороженого израсходовали 35 кг сахара. Сколько сделали порций мороженого, если в каждой порции 100 г?

3.Придумайте задачу на проценты, основанную на реальной ситуации. Определите ее тип.

infourok.ru

Разработка урока математики 5 класса «Решение задач на проценты»

Урок математики по теме: «Решение задач на проценты»

Класс: 5

Формы работы учащихся на уроке: фронтальная — повторение, объяснение нового материала, индивидуальная — проверка знаний, закрепление нового материала, групповая (в парах) – закрепление нового материала.

Конспект урока.

Постановка цели урока (1 минута).

Учитель: Ребята, на прошлом уроке мы познакомились с новым для вас понятием «процент». Вы научились обращать проценты в числа и наоборот. Но как вы считаете для чего необходимо все знать о процентах?

Учащиеся приводят ситуации из бытовой, финансовой и производственной сторон жизни.

Учитель объявляет тему урока «Решение задач на проценты»

Актуализация опорных знаний (5 минут).

Повторение ранее изученного материала, необходимого для изучения темы урока. Форма работы — фронтальная с использованием мультимедийного проектора, используется не только связь «учитель-ученик», но и «ученик-ученик».

На слайдах записаны задания. Первое задание на каждом слайде обсуждается фронтально. Затем учащиеся выполняют оставшиеся задания и обсуждают результаты в парах. Затем заслушивается по одному ответу от пары. Если первая пара ошиблась, то предоставляется возможность второй паре исправить и объяснить правильный ответ. Аналогично по всем слайдам.

Презентация по теме: «Повторение. Проценты» прилагается (Приложение 1).

Проверка знаний (10-11 минут)

Учащиеся разделены на две группы. Первая группа (каждый учащийся индивидуально) выполняет тест на компьютере по теме «Процент» (5 минут). Вторая группа учащихся (каждый учащийся индивидуально) выполняет задания самостоятельной работы по карточкам в тетрадях по теме повторения «Все действия с десятичными дробями»(5 минут). По истечении времени (5 минут) группы учащихся меняют рабочие места: первая группа приступает к выполнению самостоятельной работы в тетрадях, вторая приступает к выполнению теста на компьютерах.

Карточка для выполнения самостоятельной работы на повторение по теме «Все действия с десятичными дробями»:

Выполните действия:

а) 3,785∙1000; б) 2,09:0,1; в) 34,71:10; г) 50,01∙0,01.

2. Найдите значение выражения:

а) 58,78 – 1,38 ∙ (275,4 : 6,8).

Тест по теме «Процент» прилагается (Приложение 2)

Физкультминутка. Гимнастика для глаз. (1 минута)

Рефлексия (2 минуты).

Учитель: Какое на ваш взгляд задание вызвало больше всего затруднений при выполнении теста или при работе по карточкам?

Учащиеся высказывают свои мнения по очереди (обязательно каждый учащийся), учитель фиксирует затруднения учащихся с целью дальнейшей индивидуальной коррекционной работы.

Объяснение нового материала (8 минут).

На доске три схемы (три вида) задач на проценты:

Нахождение А% от числа В

В : 100 = С – число, приходящееся на 1%
С ∙ А = число, соответствующее А%

Нахождение числа М по заданным N%, соответствующих числу Р

Р : N = К – число, приходящееся на 1%
К ∙ 100 = М

Нахождение числа R от числа S в %

R : S = D
D ∙ 100

Учитель читает первую схему и приводит пример задачи. Далее предлагает учащимся привести пример данной задачи, слушает два-три примера, корректировать условия предложенных задач предлагает учащимся. Далее учитель выбирает один из примеров задач и показывает решение задачи согласно первой схемы. Аналогично учитель работает по двум другим видам задач.

Тексты задач:

№1. Завод выпустил 800 телевизоров. Из них 15% были проданы в магазинах города за первую неделю. Сколько телевизоров было продано за первую неделю?

№2. За контрольную работу по математике оценку «4» получили 6 учеников, что составляет 40% всех учеников. Сколько учеников в классе всего?

№3. Из 500га поля в первый день пшеницей засеяли 125га. Какой процент поля засеяли пшеницей в первый день?

VII. Закрепление изученного материала (14 минут)

Первичное закрепление нового материала проходит по методике «Каждый учит каждого». Каждый учащийся получает карточку А, В или С. Каждому номеру карточки соответствует один из трех видов задач на проценты. Карточка оформлена следующим образом: с одной стороны задача, с другой стороны указан номер схемы и решение задачи. Далее учащиеся работают по инструкции (инструкция висит на классной доске):

Прочитайте задачу, определите номер схемы (№1, №2 или №3), решите задачу в тетради.

Проверьте решение задачи, используя готовое решение на обратной стороне карточки (в случае наличия ошибок, исправьте их).

Создай пару с учащимся другой карточки.

Задай свою задачу учащемуся, который должен определить номер схемы и решить ее в тетради.

Проконтролируй решение задачи, в случае ошибок исправь и объясни решение.

Выполни задание учащегося из пары.

После того, как в твоей тетради будет решено две задачи из трех, создай пару с учащимся такой карточки, которая у тебя отсутствует.

Выполни пункты 4,5,6.

Итог работы: в твоей тетради решены задачи на три различные схемы задач на проценты.

Учитель во время работы учащихся по инструкции наблюдает, направляет, корректирует действия учеников. А также фиксирует действия учеников в листе учета, отмечая в ячейках того учащегося, с кем работал ученик в паре (например):

VIII.Подведение итогов работы (1 минута).

Учитель анализирует работу учащихся на уроке, выставляет оценки.

IX. Комментирование домашнего задания (1 минута).

Учитель комментирует домашнее задание из учебника: №1600, №1605 – два вида задач на проценты, №1612(а) – задание на повторение (действия с десятичными дробями).

X. Рефлексия (1 минута).

Учитель: Ребята, чем больше всего вам запомнился урок?

Учащиеся высказывают коротко свое мнение.

Приложение 1.

Презентация по теме: «Повторение. Проценты»

1 слайд

ПОВТОРЕНИЕ.

ПРОЦЕНТЫ.

2 слайд

Умножение на 10, 100, 1000,…Вспомните правило умножения десятичной дроби на 10, 100, 1000, …

— приведите пример умножения десятичной дроби на 100 устно;
— запишите в тетради пример умножения десятичной дроби на 10;
— проверьте друг у друга правильность умножения.

3 слайд

Деление на 10, 100, 1000,…

Вспомните правило деления десятичной дроби на 10, 100, 1000, …

— приведите пример деления десятичной дроби на 100 устно;
— запишите в тетради пример деления десятичной дроби на 10;
— проверьте друг у друга правильность деления.

4 слайд

Чтобы перевести обыкновенную дробь в десятичную, надо…

Переведите обыкновенную дробь в десятичную:
3 18 206

5 20 25

5 слайд

Чтобы перевести десятичную дробь в обыкновенную, надо…

Переведите десятичную дробь в обыкновенную:

0,32 0,09 3,55

6 слайд

Процент – это … часть числа.

1% метра — это ?

1% сотки — это?

1% центнера — это?

1% числа 300 — это?

7 слайд

50% — это . . . числа

20% — это . . . часть числа

10% — это . . . часть числа

25% — это . . . часть числа

5% — это . . . часть числа

8 слайд

НАЙДИТЕ:

50% от 40; 20% от 150;

10% от 80; 5% от 680;

25% от 48.

9 слайд

Чтобы перевести проценты в десятичную дробь, надо…

Запишите в виде десятичной дроби:

48% = … ; 3% = … ;

6,3% = … ; 208% = … .

10 слайд

Чтобы перевести десятичную дробь в проценты, надо…

Запишите в виде процентов:

0,31 = …% ; 0,08 = …%;

0,017 = …% ; 4,35 = …% .

Приложение 2.

Тест по теме «Процент»

1. 1. 1% от числа 2500 – это

А) 100; Б) 250; В) 25; Г)2.

2. Выполните умножение 3,2∙100

А) 32; Б) 320; В) 3200; Г) 0,032.

3. 2% — это

А) пятая часть числа; Б) двадцатая часть числа;

В) десятая часть числа; Г) пятидесятая часть числа.

4. Выполните деление 4,23:10

А) 42,3; Б) 0,423; В) 423; Г) 0,0423.

5. Найдите 25% от числа 800

А) 200; Б) 400; В) 160; Г) 100.

6. Переведите обыкновенную дробь 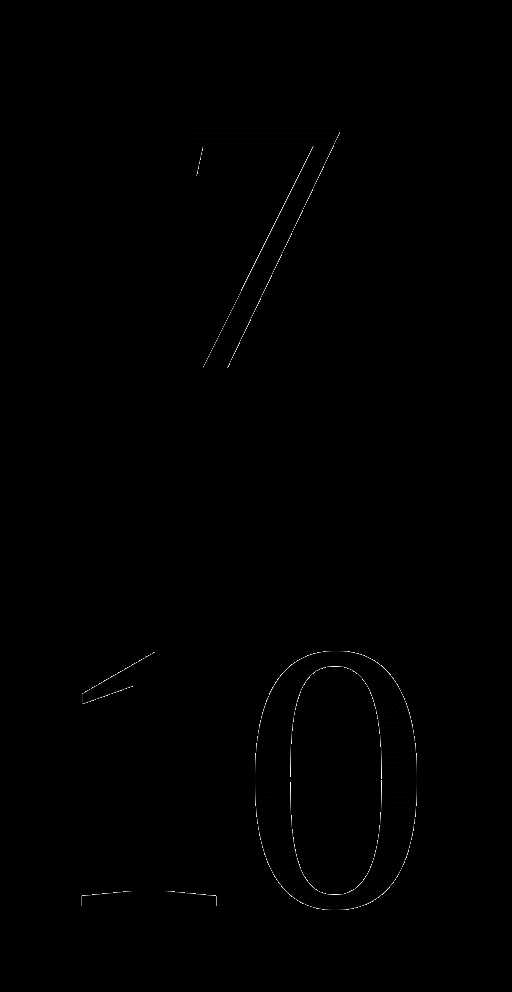в десятичную

А) 0,07; Б) 0,77; В) 0,007; Г) 0,7.

7. Переведите 79% в десятичную дробь

А) 7,09; Б) 0,79; В) 7,9; Г) 0,079.

8. Переведите десятичную дробь 0,13 в обыкновенную дробь

А); Б) ; В) ; Г) .

9. Переведите десятичную дробь 0,07 в проценты

А) 7%; Б) 70%; В) 0,7%; Г) 70,7%.

10. Найдите 10% от 280

А) 2,8; Б) 0,28; В) 14; Г) 28.