Урок-лекция «Свойства функции»
Разделы: Математика, Конкурс «Презентация к уроку»
Презентация к уроку
Загрузить презентацию (919,6 кБ)
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Ключевые слова: функция, область определения, промежутки знакопостоянства, монотонности.
Оборудование: маркерная доска, компьютер, мультимедиа-проектор.
Тип урока: урок-лекция.
Цели урока: образовательные: систематизировать имеющиеся знания, научиться исследовать графики функций по их свойствам.
Метод обучения: объяснительно-иллюстративный.
Формы обучения: фронтальная, индивидуальная.
Ход урока
Изучение новой темы
Сегодня на уроке мы вспомним определения основных свойств функции, их геометрическую интерпретацию, символическую запись и посмотрим, как эти знания использовать при выполнении заданий.
Пусть дан график некоторой функции .
Рассмотрим следующие свойства:
Область определения функции (слайд 2)
Определение: 1. Область определения функции - это множество значений аргумента, при которых функция определена.
Или: это те значения, которые принимает независимая переменная.
На графике: Проекция графика функции на ось ОХ.
Проецируем крайние точки графика на ось ОХ. Заключённый между проекциями числовой промежуток и будет являться областью определения.
Задание (устно): Укажите область определения данной функции
Ответ запишем в виде:
Область значений функции (слайд 3)
Определение: Область значений функции – это множество чисел, состоящее из всех значений функции
Или: это те значения, которые принимает зависимая переменная
На графике: Проекция графика функции на ось ОУ
Задание (устно): Укажите область значений данной функции
Ответ запишем в виде:
Промежутки монотонности, или промежутки возрастания и убывания функции (слайд 4)
Определение: Функцию f называют возрастающей на некотором промежутке, если для любых двух значений аргумента x1и x2 из этого промежутка таких, что x2 > x1, выполняется неравенство f (x2) > f (x1).
Функцию f называют убывающей на некотором промежутке, если для любых двух значений аргумента x1 и x2 из этого промежутка таких, что x2 > x1 , выполняется неравенство f (x2)< f (x1).
Определение можно сформулировать и так: Функция возрастает, если большему значению аргумента соответствует большее значение функции
Функция убывает, если большему значению аргумента соответствует меньшее значение функции.
На графике: это интервалы оси ох, на которых график функции идёт вверх или вниз
Рассмотрим части графика, где он идёт вверх. Спроецируем начало и конец каждой такой части на ось ОХ. Заключённый между проекциями числовой промежуток и будет являться промежутком возрастания.
Задание (устно): Укажите промежутки возрастания и убывания данной функции
Ответ запишем в виде:
Наибольшее и наименьшее значения функции на промежутке (слайд5)
Определение: Наибольшее и наименьшее значения функции на промежутке — это ординаты точек, в которых функция на данном промежутке принимает наибольшее и наименьшее значения
На графике: Ординаты самой высокой и самой низкой точек графика функции.
Задание (устно): Посмотрите на график. Укажите наибольшее и наименьшее значения функции на отрезках:.
Сравним результаты и сделаем вывод: при выполнении этого задания необходимо указать промежуток, на котором рассматривается наибольшее и наименьшее значения функции. Если в условии отрезок не указывается, то наибольшее и наименьшее значения функции рассматриваются на всей области определения. Записывается так:
Нули функции (слайд 6)
Определение: Нули функции — это точки пересечения графика с осью ОХ
На графике: Абсциссы точек пересечения графика с осью ОХ
Задание (устно): Укажите нули данной функции
Ответ запишем в виде:
Точки экстремума (слайд 7)
Определение: Точка х0 называется точкой максимума функции f, если для всех х из некоторой окрестности х0 выполнено неравенство:
Точка х0 называется точкой минимума функции f, если для всех х из некоторой окрестности х0 выполнено неравенство:
Точки минимума и максимума называются точками экстремума
На графике: Точки, около которых график функции выгибается выпуклостью вверх или вниз
Задание (устно): укажите на графике точку минимума и точку максимума
Ответ запишем в виде:
точки экстремума: х = — 2 и х = 2,2
Промежутки постоянного знака функции (слайд 8)
Определение: Промежутки постоянного знака функции — это промежутки, на которых функция принимает положительные (отрицательные) значения
На графике: Интервалы оси ОХ, соответствующие точкам графика, лежащим выше (ниже) этой оси.
Рассмотрим части графика, расположенные выше оси ОХ. На оси абсцисс им соответствуют числовые промежутки, на которых функция принимает положительные значения.
Задание (устно): Укажите промежутки, на которых функция принимает положительные и отрицательные значения.
Ответ запишем в виде:
Значения х на заданном интервале функции (слайд 9)
Укажите значения х, при которых -3< f(x) < 2
Нам нужно указать такие значения х, при которых части графика заключены между прямыми у = -3 и у = 2. Проведём эти прямые. Между ними заключены три части графика. Проецируем каждую на ось ОХ и записываем ответ:
Закрепление:
Укажите значения х, при которых f(x) 1,5
Ответ проверяем по слайду (слайд 10)
Домашнее задание:
Дан график функции .(слайд11)
Перерисуйте его и укажите следующие свойства:
- Область определения функции
- Область значений функции
- Промежутки монотонности, или промежутки возрастания и убывания функции
- Наибольшее и наименьшее значения функции на промежутке
- Нули функции
- Точки экстремума
- Промежутки постоянного знака функции
Список литературы
- Башмаков М.И. Математика: учебник для учреждений нач. и среднего профессионального. Образования/ М.И. Башмаков. – М.: Академия, 2010
- Дорофеев Г.В. Сборник заданий для подготовки и проведения письменного экзамена по математике/ Г.В. Дорофеев. — М.: Дрофа, 2010. – 160 с.
- Колмогоров А.Н. Алгебра и начала анализа: учебник для общеобразовательных учреждений для 10-11 классов/ А.Н. Колмогоров. — М.: Просвещение, 2010. – 383 с.
- Островский C.Л. Как сделать презентацию к уроку?/ С.Л. Островский: Первое сентября, 2010.
1.04.2014
xn--i1abbnckbmcl9fb.xn--p1ai
Исследование графика функции. Минимум и максимум
На рисунке изображен график функции . Посмотрим, как исследовать функцию с помощью графика. Оказывается, глядя на график, можно узнать всё, что нас интересует, а именно:
- область определения функции
- область значений функции
- нули функции
- промежутки возрастания и убывания
- точки максимума и минимума
- наибольшее и наименьшее значение функции на отрезке.
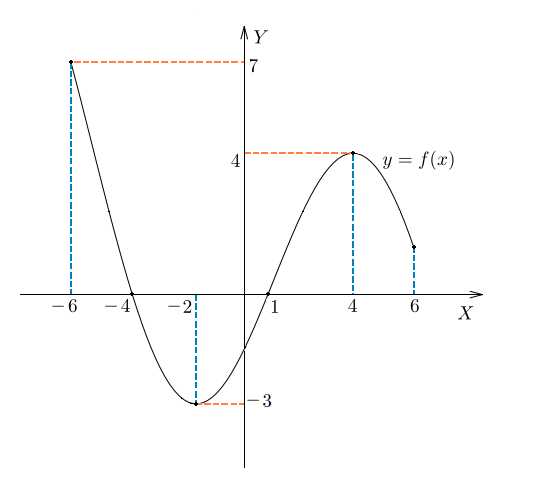
Уточним терминологию:
Абсцисса
Ордината — координата по вертикали.
Ось абсцисс — горизонтальная ось, чаще всего называемая ось .
Ось ординат — вертикальная ось, или ось .
Аргумент — независимая переменная, от которой зависят значения функции. Чаще всего обозначается .
Другими словами, мы сами выбираем , подставляем в формулу функции и получаем .
Область определения функции — множество тех (и только тех) значений аргумента , при которых функция существует.
Обозначается: или .
На нашем рисунке область определения функции — это отрезок . Именно на этом отрезке нарисован график функции. Только здесь данная функция существует.
Область значений функции — это множество значений, которые принимает переменная . На нашем рисунке это отрезок — от самого нижнего до самого верхнего значения .
Нули функции — точки, где значение функции равно нулю, то есть . На нашем рисунке это точки и .
Значения функции положительны там, где . На нашем рисунке это промежутки и .
Значения функции отрицательны там, где . У нас это промежуток (или интервал) от до .
Важнейшие понятия — возрастание и убывание функции на некотором множестве . В качестве множества можно взять отрезок , интервал , объединение промежутков или всю числовую прямую.
Функция возрастает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .
Иными словами, чем больше , тем больше , то есть график идет вправо и вверх.
Функция убывает на множестве , если для любых и , принадлежащих множеству , из неравенства следует неравенство .
Для убывающей функции большему значению соответствует меньшее значение . График идет вправо и вниз.
На нашем рисунке функция возрастает на промежутке и убывает на промежутках и .
Определим, что такое точки максимума и минимума функции.
Точка максимума — это внутренняя точка области определения, такая, что значение функции в ней больше, чем во всех достаточно близких к ней точках.
Другими словами, точка максимума — такая точка, значение функции в которой больше, чем в соседних. Это локальный «холмик» на графике.
На нашем рисунке — точка максимума.
Точка минимума — внутренняя точка области определения, такая, что значение функции в ней меньше, чем во всех достаточно близких к ней точках.
То есть точка минимума — такая, что значение функции в ней меньше, чем в соседних. На графике это локальная «ямка».
На нашем рисунке — точка минимума.
Точка — граничная. Она не является внутренней точкой области определения и потому не подходит под определение точки максимума. Ведь у нее нет соседей слева. Точно так же и на нашем графике не может быть точкой минимума.
Точки максимума и минимума вместе называются точками экстремума функции. В нашем случае это и .
А что делать, если нужно найти, например, минимум функции на отрезке ? В данном случае ответ: . Потому что минимум функции — это ее значение в точке минимума.
Аналогично, максимум нашей функции равен . Он достигается в точке .
Можно сказать, что экстремумы функции равны и .
Иногда в задачах требуется найти наибольшее и наименьшее значения функции на заданном отрезке. Они не обязательно совпадают с экстремумами.
В нашем случае наименьшее значение функции на отрезке равно и совпадает с минимумом функции. А вот наибольшее ее значение на этом отрезке равно . Оно достигается в левом конце отрезка.
В любом случае наибольшее и наименьшее значения непрерывной функции на отрезке достигаются либо в точках экстремума, либо на концах отрезка.
Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России) +7 (495) 984-09-27 (бесплатный звонок по Москве)
Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.
ege-study.ru
11 кл урок 1 алгебра
Учитель Толчева Оксана Николаевна
Предмет Алгебра
Класс 11-Б
Тема №1 Повторение и систематизация учебного материала.
Урок 1
Числовые функции их свойства и графики..
Цель: Обобщить и систематизировать знания учащимися числовых функций, их свойства(область определения, область значений, нули функции, промежутки постоянства знака и монотонности, четности) и графиков.
I. Повторение и анализ фактов
1. Определение числовой функции
Числовой функцией с областью определения D называется соответствие, при которой каждому числу x из множества D ставится в соответствие единственное число у, которая обозначается y=f(x), х-аргумент (независимая переменная), у-функция (зависимая переменная).
2.Свойства числовых функций
Свойства функции | Определение | Геометрическая интерпретация |
Область определения Обозначение:D, D(y). | Множество
тех действительных значений аргумента | Проекция
графика функции на ось абсцисс( |
Множество значений Обозначение: Е, Е(у). | Множество всех значений, которые приобретает функция, при всех значениях аргумента с области определения функции | Проекция
графика функции на ось ординат( |
Нули функции | Значение
аргумента, при котором функция равна
нулю, т.е. корни уравнения | абсциссы
точек пересечения графика функции с
осью |
Промежутки знакопостоянства | Промежутки,
на которых функция положительна или
отрицательна, т.е. решения неравенства | Отрезки
оси |
Промежутки монотонности (промежутки, на которых функция возрастает или убывает) | Функция убывающей, если | Отрезки
оси |
Наибольшее и наименьшее значения функции | Ординаты «самой высокой» и «самой низкой» точек графика | |
Четность и нечетность функции | Если область определения функции
если
, то функция нечетная. | График симметричен относительно оси ординат График симметричен относительно начала координат |
3. Как найти область определения функции
№ | Вид функции | Ограничения | Формулировка |
1 |
|
| Знаменатель дроби не равен нулю. |
2 |
|
| Под знаком квадратного корня может находиться только неотрицательное число. |
4. График функции
Графиком функции у=f(x) называется
множество всех точек плоскости с
координатами  , где первая
координата
, где первая
координата 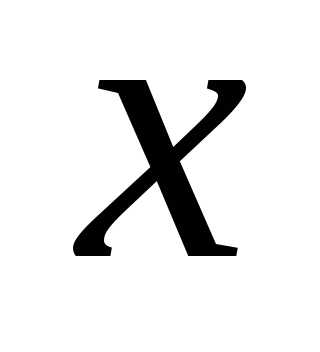 «пробегает» всю область определения
функцииf, а другая–
соответственное значение функции в
точке х.
«пробегает» всю область определения
функцииf, а другая–
соответственное значение функции в
точке х.
5.Основные виды элементарных функций и их графики
Линейная функция | Обратная
пропорциональность | Квадратичная функция |
|
| |
Квадратный корень | Кубическая функция |
|
, |
|
|
II. Усовершенствование умений
Алгоритм исследования функции на четность и нечетность
Найти область определения функции и проверить будет ли она симметричной относительно нуля.
Если область определения симметрична относительно нуля, то найти
 :
:
если , то функция четная;
если , то функция нечетная.
Примеры:
1. Доказать, что функция четная.
Решение.1)  — симметрична относительно нуля;
— симметрична относительно нуля;
2) ,,.
Вывод: функция четная.
2. Доказать, что функция нечетная.
Решение.1) 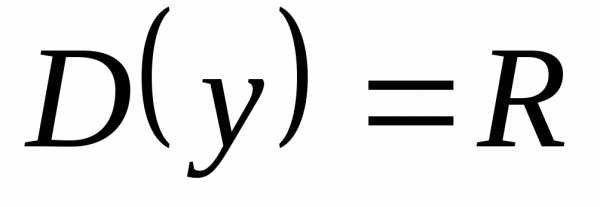 — симметрична относительно нуля;
— симметрична относительно нуля;
2) ,,
, .
Вывод: функция нечетная
3. Исследуйте
функцию 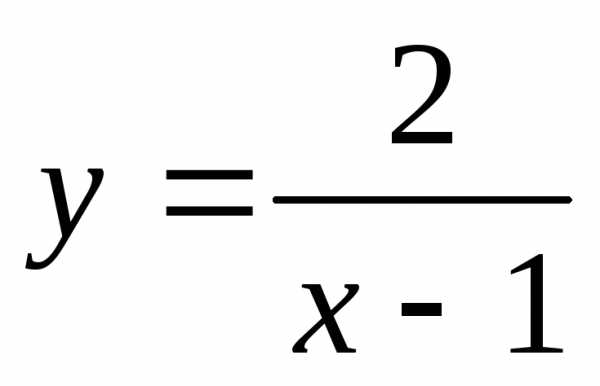 ина четность и нечетность.
ина четность и нечетность.
Решение.1) 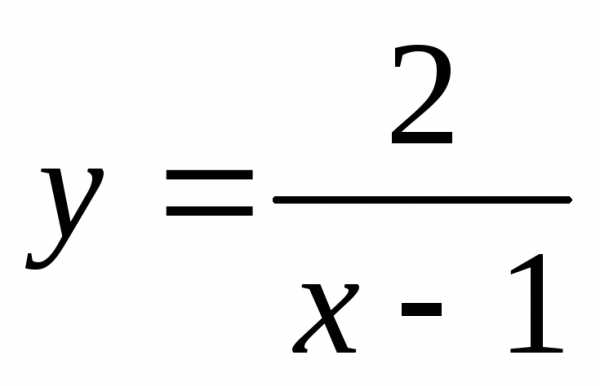 ,не симметрична относительно нуля, значит
функция ни четная, ни нечетная.
,не симметрична относительно нуля, значит
функция ни четная, ни нечетная.
2)
,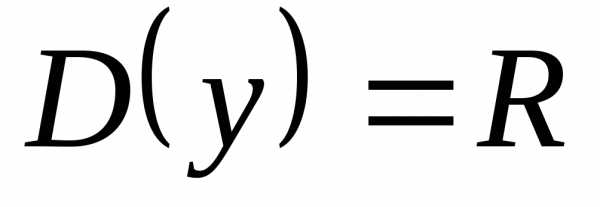 ,,,,
,,,,
, , значит функция ни четная, ни нечетная.
III. Самостоятельное выполнение практических заданий
№1 Найдите значения функции в заданной точке x0.
1),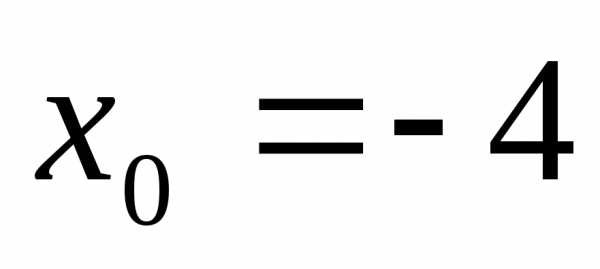 ;
2)
;
2)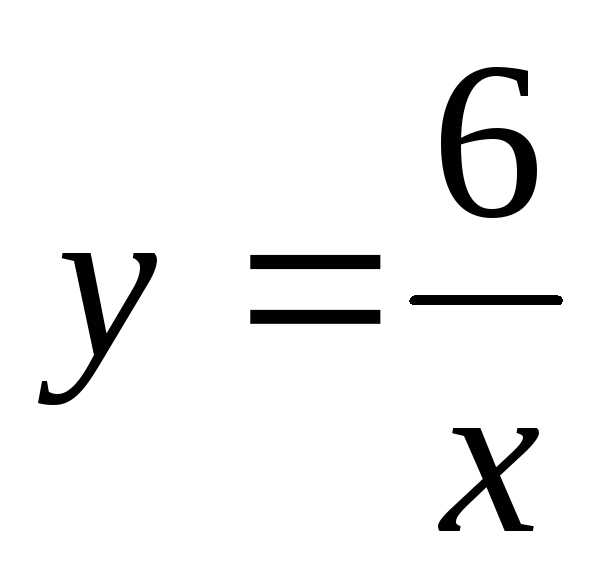 ,
, ;
3),
;
3),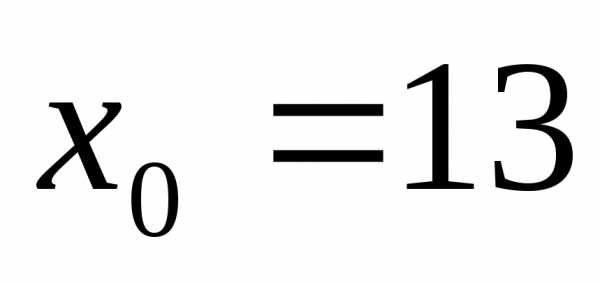 .
.
№2 Найдите область определения функции:
1)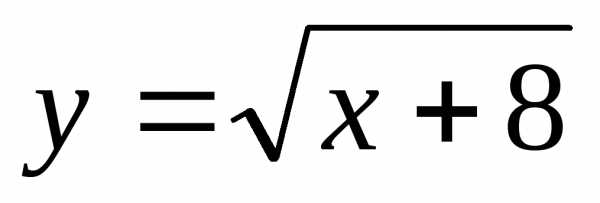 ;
2)
;
2)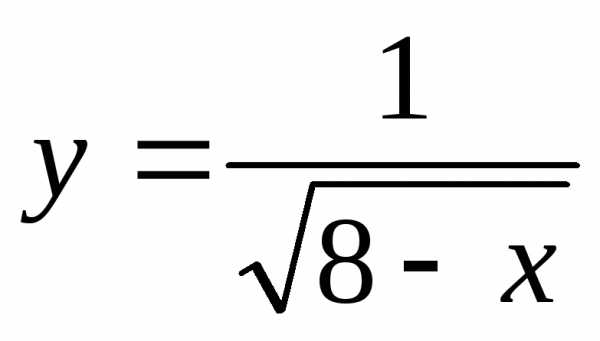 ;
3);
4)
;
3);
4)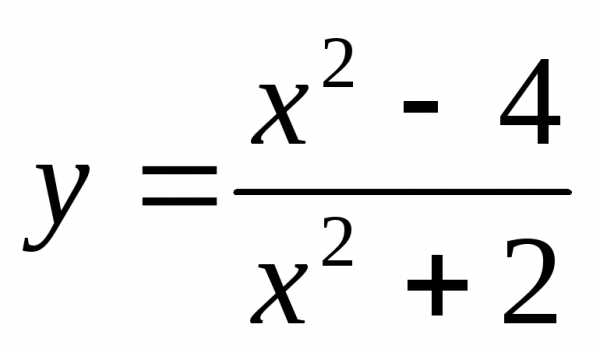 ;
5)
;
5)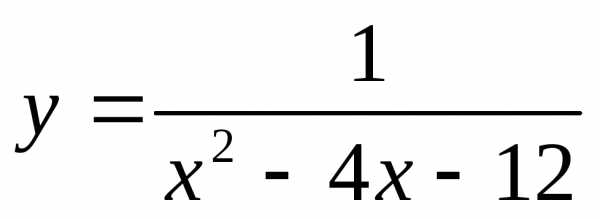 ;
;
№3 Найдите область значения функции:
1); 2);
№4 Исследуйте на четность или нечетность функции, которые заданы формулой:
1);
2)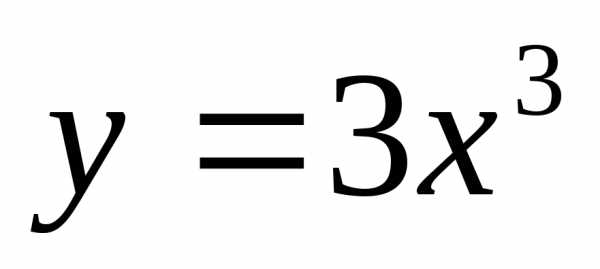 ;
;
№5 Какая из приведенных функций есть убывающей на множестве действительных чисел?
1) 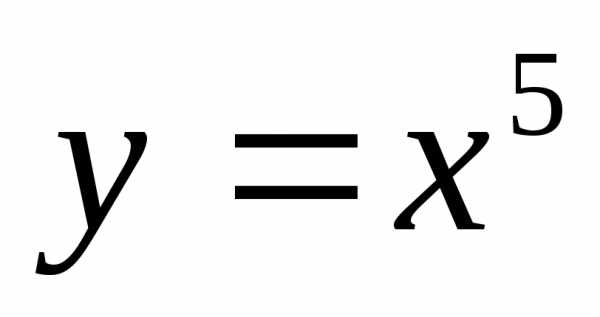 ;
2)
;
2)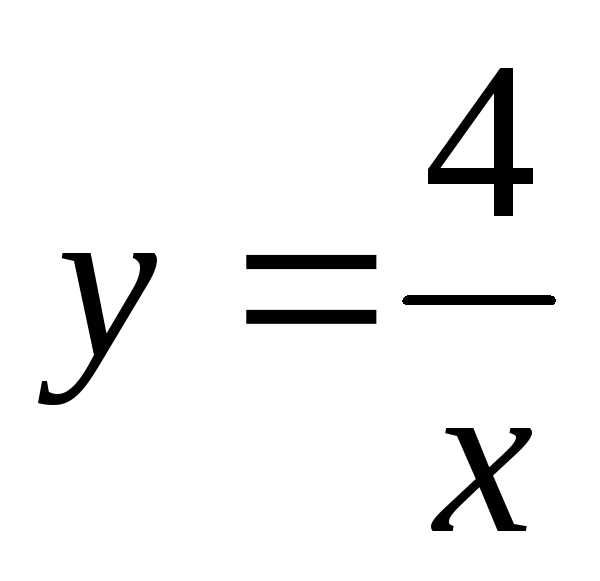 ;
3)
;
3)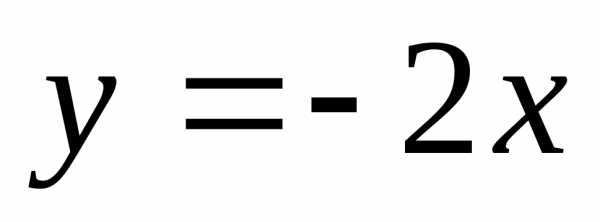 ;
4)
;
4)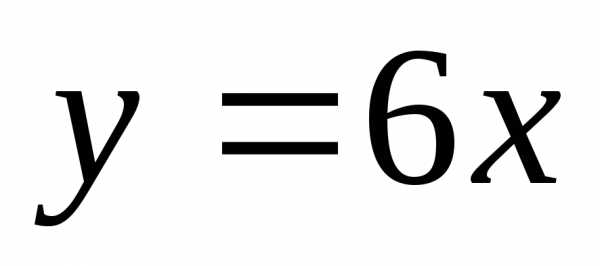 .
.
№6 Какая из линейных функций возрастает?
1) ; 2) ; 3) ; 4) .
3
studfiles.net
Асимптоты графика функции
k = lim | f (x) | , b= lim(f(x)− kx). | ||
x |
| |||
x→∞ | x→∞ | |||
Но если хотя бы один из этих пределов не существует или равен бесконечности, то кривая y =f (x) наклонных асимптот не имеет.
Отметим, что следует отдельно рассмотреть случаи х→ +∞ их → − ∞. Частным случаем
наклонной асимптоты при k = 0 иb = limf (x) будет горизонтальная асимптота. Поэтомуy = b –
x→∞
уравнение горизонтальной асимптоты.
Рассмотрим график функции на рис. 15. Точки х = х2,х = х4 – точки экстремумов функции, точках = х1 – это точка перегиба. Точках = х3 является особенной точкой для функции, в нейf (x) терпит разрыв, а прямаях = х3 является вертикальной асимптотой
графика функции. Прямая y = kx + b тоже будет асимптотой графика, только наклонной, прямаяу = 0 – горизонтальная асимптота графика.
Если точка М (х, у) лежит на графике и неограниченно удаляется от начала координат, то она приближается к одной из этих прямых; расстояние от точкиМ (х, у) до асимптот стремится к нулю.
Общая схема исследования функции и построения графика
Для общего исследования функции и построения графика полезно придерживаться следующего плана.
Найти область определения функции, точки разрыва функции и интервалы непрерывности Найти (если это возможно) точки пересечения графика с осями координат.
Найти интервалы знакопостоянства функции (промежутки, на которых f (x) > 0 илиf (x) < 0). Решить вопрос о чётности, нечётности, симметрии, периодичности функции.
Если есть точки разрыва 2-города, найти вертикальные асимптоты. Найти, если они есть, наклонные и горизонтальные асимптоты.
Спомощью 1-ойпроизводной найти точки экстремума и области возрастания и убывания данной функции. Найти экстремальные значения функции.
Спомощью 2-ойпроизводной найти точки перегиба, области выпуклости и вогнутости. Построить график.
Пример: Исследовать функцию y = | (3− x)2 | и построить её график. | |
1−x | |||
|
|
Функция определена на всей числовой оси за исключением точки х = 1, где знаменатель дроби обращается в нуль. Так как область определения не симметрична относительно начала координат, то не имеет смысла говорить о чётности (нечётности) функции.
Точка х = 1 является точкой разрыва функции. Найдём пределыy = f (x) прих → 1 (слева и справа) (рис. 16).
| (3− x)2 | Рис. 16. | (3− x)2 |
| |
lim | = −∞ lim | = +∞ | |||
1−x | 1−x | ||||
x→1+0 | , x→1−0 |
|
studfiles.net
Функции Область определения и значения Четность и нечетность Периодичность Возрастание, убывание функции Преобразования графиков функций — СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА
Функции
Числовой функцией с областью определения D называется соответствие, при котором каждому числу x из множества D сопоставляется по некоторому правилу единственное число y, зависящее от x.
Обозначение: y = f(x)
Независимая переменная x – аргумент функции f.
Число y, соответствующее x – значение функции f в точке x.
График функции
График функции f – множество всех точек (x; y) координатной плоскости, где y=f(x), а x «пробегает» всю область определения функции f.
Графики элементарных функций
Область определения функции
Область определения функции – множество значений x, для которых выполнимы действия, указанные в правиле f.
Обозначается: ООФ или D(f).
С геометрической точки зрения ООФ есть проекция графика этой функции на ось ОХ.
Область значения функции
Область значений функции – множество значений функции f(x), которые она принимает при изменении x на ООФ.
Обозначается: ОЗФ или E(f).
С геометрической точки зрения ОЗФ – проекция графика на ось OY.
Четность и нечетность функций
Функция f называется четной, если для любых x из ООФ
f(-x) = f(x)
График четной функции симметричен относительно оси OY.
Функция f называется нечетной, если для любых x из ООФ f(-x) = — f(x)
График нечетной функции симметричен относительно начала координат.
Алгоритм определения четности функции одной переменной
Периодичность функций
Функция называется периодической с периодом Т ≠ 0, если для любого x из ООФ
f(x + T) = f(x) = f(x — T).
Для построения графика периодичностью функции с периодом T достаточно провести построение на отрезке длиной T и полученный график параллельно перенести на расстояние nT вправо и влево вдоль оси OX (n – любое натуральное число).
Возрастание, убывание функций
Функция f возрастает на множестве P, если для любых x1 и x2 из множества P, таких, что x2 > x1, выполнено неравенство f(x2) > f(x1).
Функция f убывает на множестве P, если для любых x1 и x2 из множества P, таких, что x2 > x1, выполнено неравенство f(x2) < f(x1).
Преобразования графиков функций
Пусть дан график функции y = f(x)
Тогда:
1 . График функции y = f(–x) получается симметричным отображением графика y = f(x) относительно оси OY:
2 . График функции y = –f(x) получается симметричным отображением графика y = f(x) относительно оси OX:
3 . График функции y = |f(x)| получается следующим образом: обводим ту часть графика функции y = f(x), которая лежит выше оси OX, а часть лежащую ниже отобразить симметрично оси OX:
4 . График функции y =f(|x|) получается следующим образом: отбрасываем часть графика функции y = f(x), лежащую левее оси OY, обводим ту часть графика функции y = f(x), которая лежит правее оси OY и отображаем ее симметрично оси OY:
5 .График функции y =f(x–a) + b получается построением графика функции y = f(x) в новой системе координат X`0`Y`, где 0`(a, b), 0`X` || 0X, 0`Y` || 0Y:
6 . График функции y =f(m*x), m > 0, получается из данного растяжением в 1/m раз (если m < 0) от оси OY (вдоль оси OX) и сжатием в m раз (m > 1) к оси OY:
7 . График функции y =k* f(x), k > 0, получается из данного растяжением в k раз (k > 1) относительно оси OX (вдоль оси OY) и сжатием в 1/k раз (при k < 1) к оси OX:
intellect.icu
параллельный перенос (сдвиг), отображение, растяжение, сжатие, отражение. Курсы по математике
Тестирование онлайн
Преобразование графиков
Параллельный перенос
График функции y=f(x)+B получается параллельным переносом графика функции y=f(x) в положительном направлении вдоль оси Оу на расстояние В, если В>0 и в отрицательном направлении вдоль оси Оу, если B.

График функции y=f(x+b) получается параллельным переносом графика функции y=f(x) в положительном направлении вдоль оси Оx на расстояние b, если b и в отрицательном направлении вдоль оси Оx, если b>0.
Отображение
График функции y=-f(x) получается симметричным отображением графика y=f(x) относительно оси Ох.
График функции y=f(-x) получается симметричным отображением графика y=f(x) относительно оси Оу.
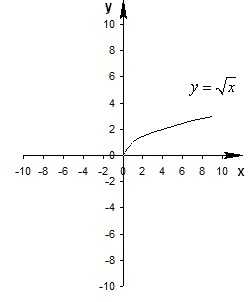
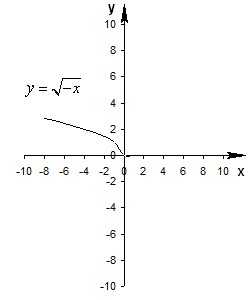
Деформация (растяжение и сжатие) графика
График функции y=Af(x), получается растяжением графика y=f(x) вдоль оси Оу от оси Ох в A раз при A>1 или сжатием вдоль оси Оу к оси Ох в раз при A.
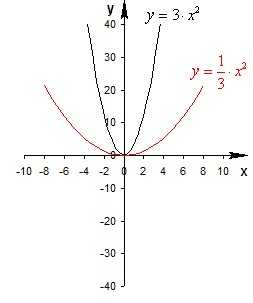
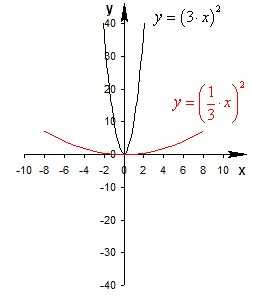
График функции y=f(ax), получается сжатием графика y=f(x) вдоль оси Ох к оси Оу в а раз при а>1 или растяжением вдоль оси Ох к оси Оу в раз при а.
Отражение
График функции получается из графика функции y=f(x) следующим образом: часть графика функции y=f(x), лежащая над осью Ох и на оси, остается без изменений, а часть графика, лежащая под осью Ох, отражается симметрично относительно оси Ох на верхнюю полуплоскость.
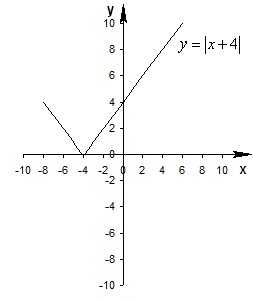
График функции получается из графика функции y=f(x) следующим образом: часть графика функции y=f(x), соответствующая неотрицательным значениям аргумента , остается без изменений, а отрицательным значениям аргумента будет соответствовать график, полученный путем симметричного относительно оси Оy отображения части графика, оставленной без изменений.
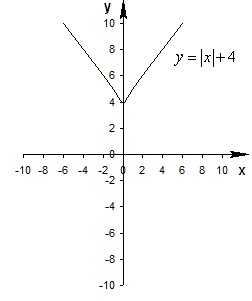
Примеры
fizmat.by

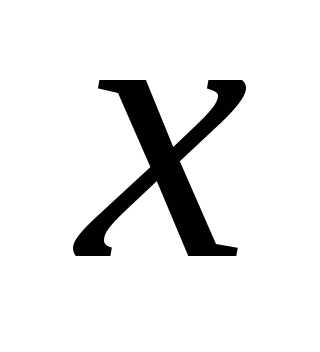 ,
при которых выражение
,
при которых выражение не теряет смысла и приобретает
действительные значения
не теряет смысла и приобретает
действительные значения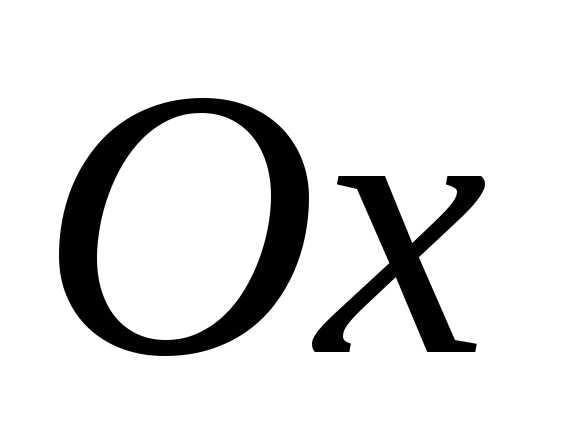 )
)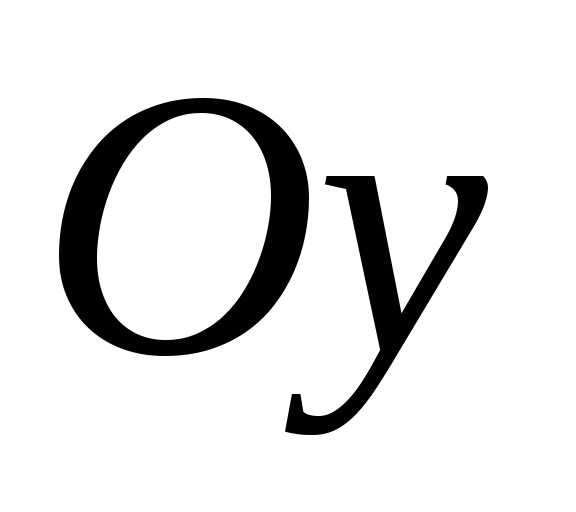 )
)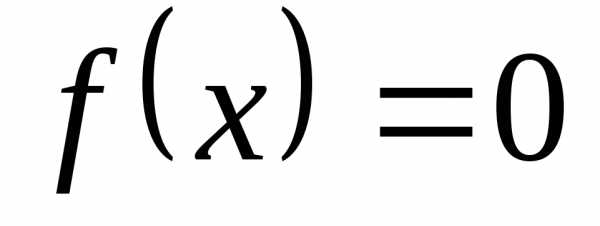
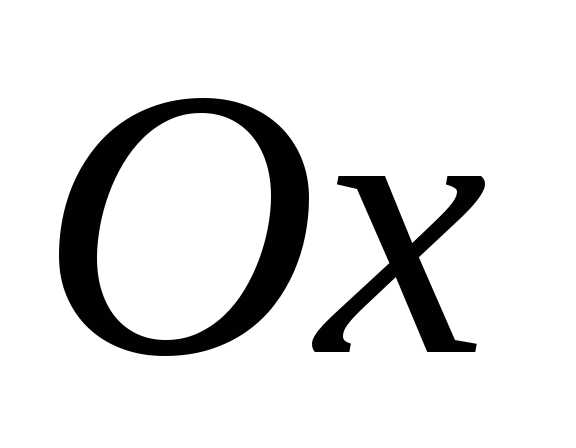 .
.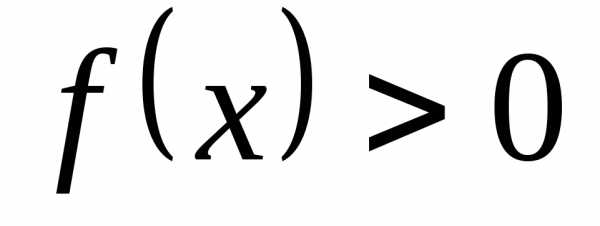 и
и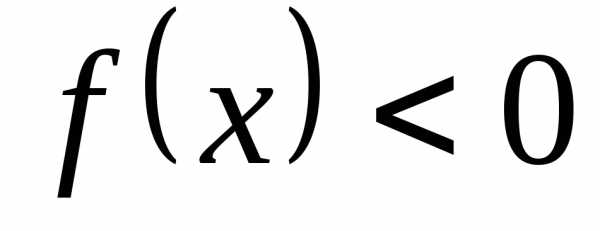
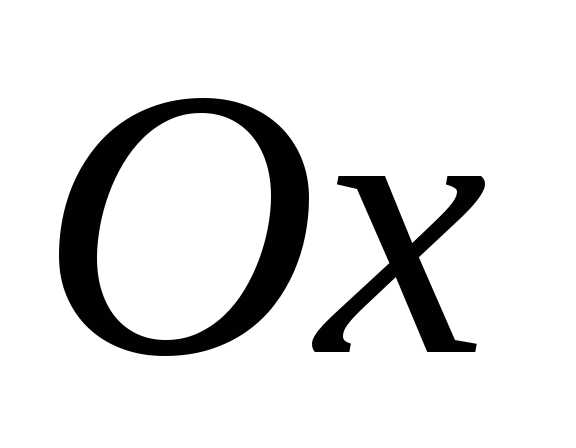 ,
которые соответствуют точкам графика
функции, расположенных выше(ниже) оси
,
которые соответствуют точкам графика
функции, расположенных выше(ниже) оси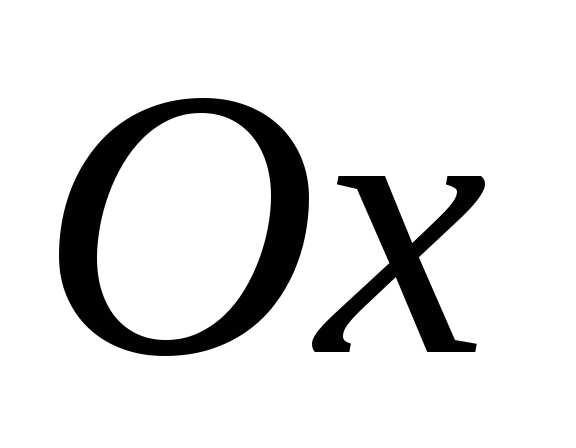
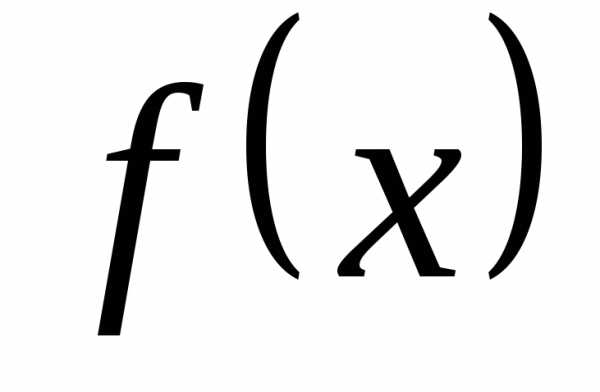 называется возрастающей на множестве
называется возрастающей на множестве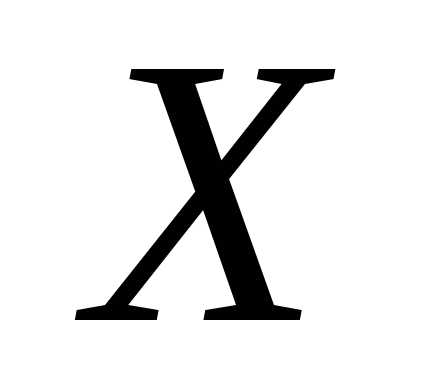 ,
если для любых точек
,
если для любых точек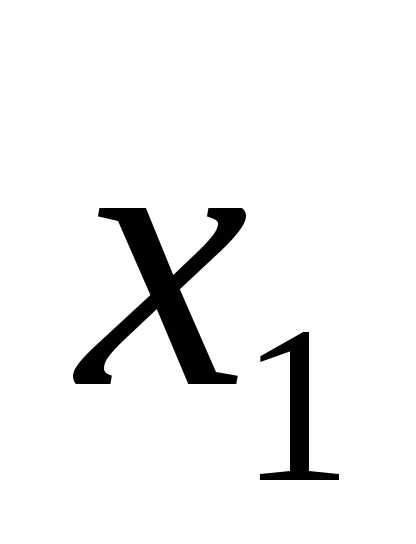 и
и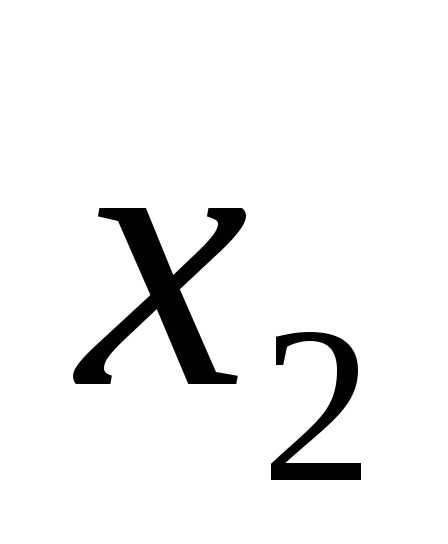 этого множества – таких, что
этого множества – таких, что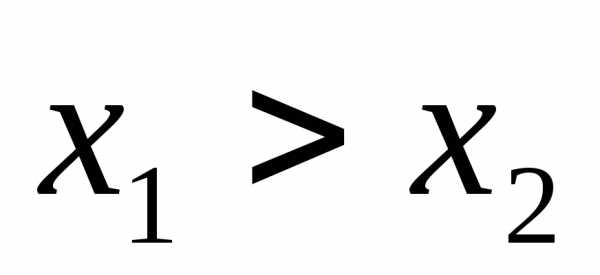 ,
-;
,
-;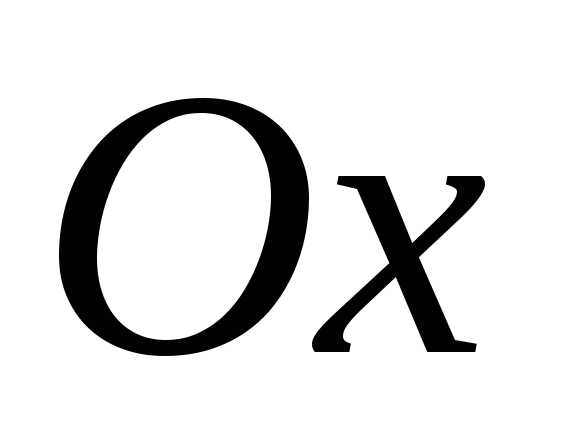 ,
где график «идет вверх» (вниз)
,
где график «идет вверх» (вниз)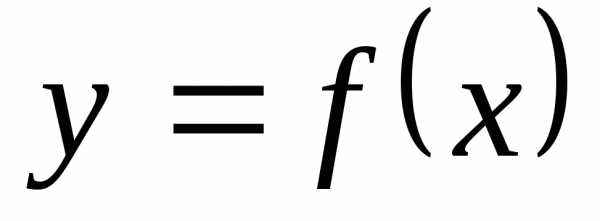 симметрична
относительно нуля и, то функция четная,
симметрична
относительно нуля и, то функция четная,

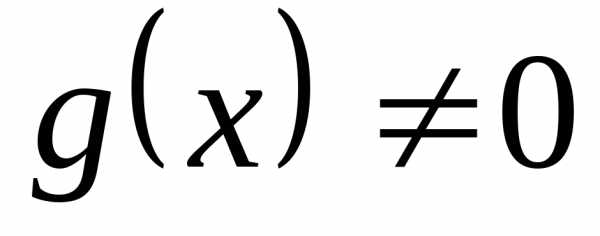
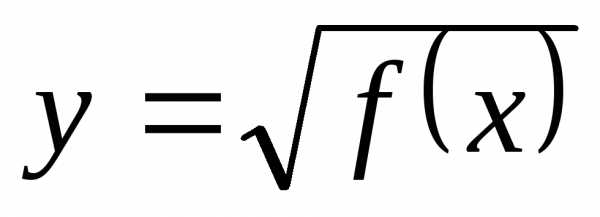
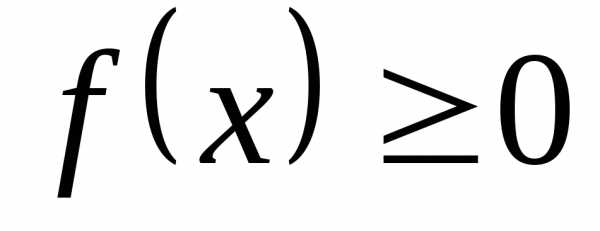
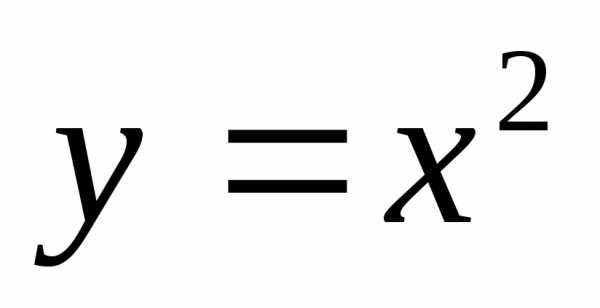
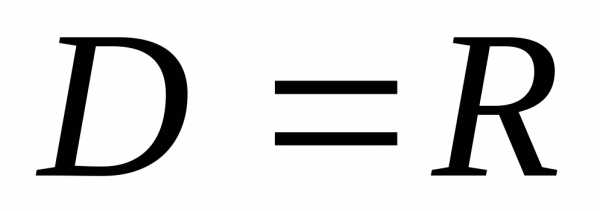 ,
, 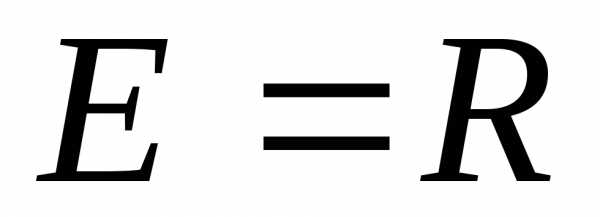
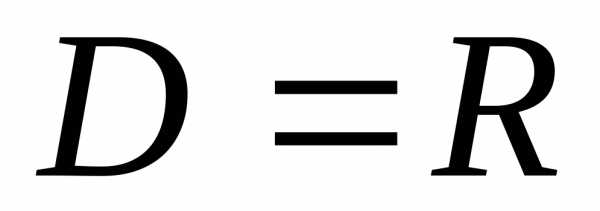
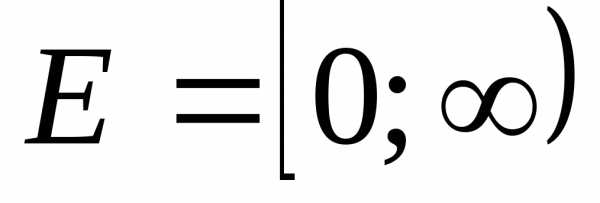

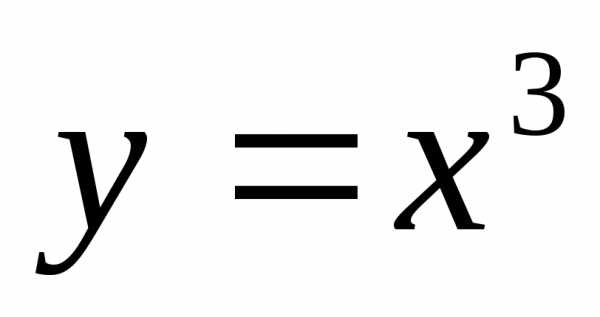

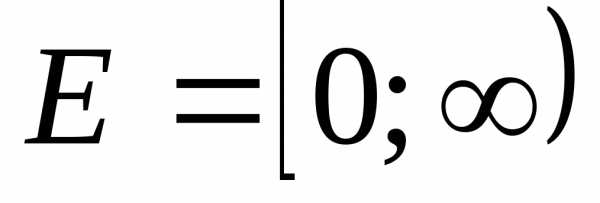
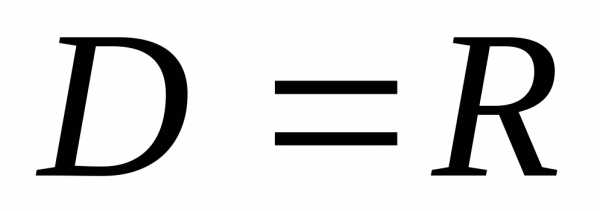 ,
, 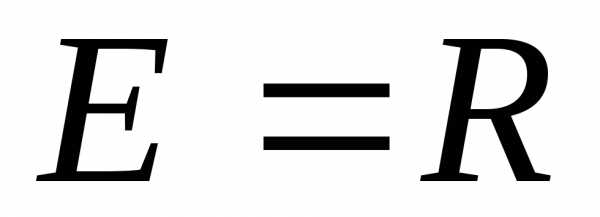
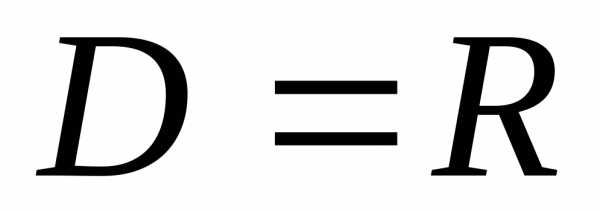 ,
, 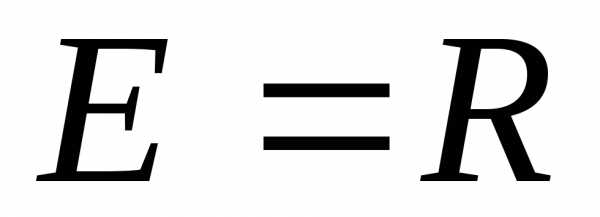
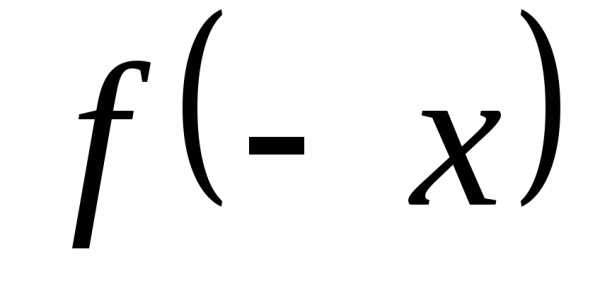 :
: