Матрицы и определители 3
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РЕСПУБЛИКИ КАЗАХСТАН
Рудненский индустриальный институт
ДИСТАНЦИОННОЕ ОБРАЗОВАНИЕ
МАТЕМАТИКА
ЮНИТА № 1
Матрицы и определители.
Рудный 2005
ББК 22.1я73
Рецензент: Т.А.Калдыбиев
Рекомендовано к изданию УМС РИИ
Курс: Математика. Базовый курс.
Юнита 1. Матрицы и определители
Юнита 2 Системы линейных уравнений
Юнита 3 Векторная алгебра
Юнита 4 Аналитическая геометрия на плоскости
Юнита 5 Аналитическая геометрия в пространстве
Юнита 6 Предел функции и непрерывность
Юнита 7 Дифференцирование
Юнита 8 Исследование функций и построение графиков
Юнита 9 Неопределенный интеграл.
Юнита 10 Определенный интеграл
Юнита 11 Дифференциальное исчисление функции многих переменных.
Юнита 12 Диффференциальные уравнения (1 и высших порядков) Юнита 13 Дифференциальные уравнения с постоянными коэффициентами.
Юнита 15 Ряды Фурье
Юнита 16 Кратные интегралы
Юнита 17 Криволинейные интегралы
Юнита 18 Линейное программирование
Юнита 19 Теория вероятностей
Юнита 20 Математическая статистика
ЮНИТА 1
В данном учебном пособии содержится материал, включающий понятия матриц, определителей, их основных свойств, понятие обратной матрицы. Комплектуется файлом материалов.
Для студентов технических специальностей: 050707, 050709, 050726, 050730, 050729, 050724, 050713, 050718, 050702, 050731, 050901, 050703.
Для студентов экономических специальностей: 050506, 050511
Юнита соответствует типовой образовательной программе
Для внутривузовского использования
© Рудненский индустриальный институт 2005
Содержание
Тематический план………………………………………………………..4
Литература…………………………………………………………………5
Тематический обзор……………………………………………………….6
Глава 1. Матрицы………………………………………………………….7
§1. Основные определения………………………………………………..7
§2. Линейные операции над матрицами…………………………………..8
§3. Умножение матриц………….…………………………………………8
Глава 2. Определители……………………………………………………10
§1. Определители второго и более высоких порядков……………………………………………………………………10
§2. Свойства определителей………………………………………………12
Глава 3. Обратная матрица. Существование и структура обратной матрицы…………………………………………………………………….13
Файл материалов….………………………………………………………16
Перечень умений……………………………………………………………21
Тренинг умений…………………………………………………………….23
Задания для самостоятельной работы……………………………………………………………………….30
Глоссарий
Тематический план
Матрицы, действия над матрицами (сложение, умножение на число, умножение матриц).
Определители 2го и 3го порядков.
Правило Саррюса (треугольника).
Свойства определителей. Обратная матрица.
Основная
- И.В. Виленкин, В.М. Гробер Высшая математика. Ростон-на-Дону, 2002
- В.Е. Шнейдер, А.И. Слуцкий, А.С. Шумов Краткий курс высшей математики. Т. 1, М. 1978
Дополнительная
3. П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова Высшая математика в упражнениях и задачах. Ч. 1. М. 1980
Тематический обзор
Широкое применение математических методов в самых различных областях науки, техники, экономики и практической деятельности инженеров предъявляет повышенные требования к изучению математических приемов. Особенно важны методы и приемы линейной алгебры, наиболее простые и важные из которых рассматриваются в этом курсе.
В задачи нашего курса входит ознакомление с действиями над матрицами, изучение вычисления определителей, нахождения обратной матрицы.
Глава 1. Матрицы
§1. Основные определения.
МАТРИЦЕЙ размера m. n называется прямоугольная таблица чисел
,содержащая m строк и n столбцов. Каждый элемент матрицы а ik имеет два индекса: i – номер строки и k – номер столбца. Краткая форма записи матрицы:
А = (а ik )m,n
Матрица называется КВАДРАТНОЙ порядка n , если она состоит из n строк, и n столбцов.
Матрица размера 1 . n называется МАТРИЦЕЙ-СТРОКОЙ , а матрица размера m. 1 — МАТРИЦЕЙ-СТОЛБЦОМ .
НУЛЕВОЙ матрицей заданного размера называется матрица, все элементы которой равны нулю.
ТРЕУГОЛЬНОЙ матрицей n-го порядка называется квадратная матрица, все элементы которой, расположенные ниже главной диагонали, равны нулю:
.ЕДИНИЧНОЙ называется квадратная матрицаn-го порядка, у которой элементы главной диагонали равны единице, а в се остальные элементы – нули:
Матрицы А = (а ik )m,n и В = (в ik )m,n называются РАВНЫМИ , если а ik = в ik i = 1,…,m
k = 1,…,n.
§2. Линейные операции над матрицами.
СУММОЙ матриц А = (а ik )m,n и В = (в ik )m,n называются матрица А + В = (а ik + в ik )m,n .
ПРОИЗВЕДЕНИЕМ матрицы А = (а ik )m,n на число l называется матрица lА = (lа ik )m,n .
Для любых матриц одинакового размера и любых чисел l и m выполняются свойства:
1) А + В = В +А 2) А + (В + С) = (А + В) + С
3) А + 0 = А 4) l(mА) = (lm)А
5) l(А + В) = lА + lВ 6) (l + m)А = lА + mА
Докажем свойство 5):
l(А + В) = (l(а ik + в ik ))m,n = (lа ik + lв ik )m,n = (lа ik )m,n + lв ik )m,n = lА + lВ
Доказательство Остальных свойств читатель проведет самостоятельно.
ТРАНСПОНИРОВАННОЙ для матрицы А называется матрица АТ , строки которой являются столбцами матрицы А, а столбцы – строками матрицы А.
ПРИМЕР 1. Даны матрицы
иПостроить матрицу С = 2А – 3В + АТ .
РЕШЕНИЕ .
-++
=.§3. Умножение матриц.
ПРОИЗВЕДЕНИЕМ матрицы А = (а ik )m,р на матрицу В = (в ik )р,n
Иными словами, для получения элемента, стоящего в i -ой строке результирующей матрицы и в k -ом ее столбце, следует вычислить сумму попарных произведений элементовi -ой строки матрицы А на k -ый столбец матрицы В.
ПРИМЕР 2. Найти произведение матрицы
на матрицу .РЕШЕНИЕ.
т.е.
.В самом определении произведения матриц заложено, что число столбцов первой матрицы равно числу строк второй. Это – условие согласования матриц при умножении. Если оно нарушено, матрицы перемножить нельзя. Поэтому возможна ситуация, когда произведение А*В существует, а произведение В*А – нет. Кроме того, когда существуют оба произведения, то чаще всего они не совпадают, т.е. в большинстве случаев произведение матриц некоммутативно: А*В¹В*А. Если А, В, С – квадратные матрицы одинакового порядка и Е – единичная матрица того же размера, то справедливы тождества:
Свойство 1) оставим без доказательства
mirznanii.com
2.3. Произведение матриц.
Умножение матриц – это специфическая операция, составляющая основу алгебры матриц. Строки и столбцы матрицы можно рассматривать как векторы- строки и векторы-столбцы соответствующих размерностей : иными словами, любую матрицу можно интерпретировать как совокупность векторов-строк и векторов-столбцов.
Пусть
даны матрица А размером 
и матрица В размером
.
Будем рассматривать матрицу А как
совокупность т векторов – строк
размерности
п каждый, а матрицу В – как совокупностьk
векторов – столбцов
Определение
3. Произведением матриц А и В называется
матрица С, элементы которой 
равны скалярным произведениям
векторов-строк
матрицы А на векторы-столбцы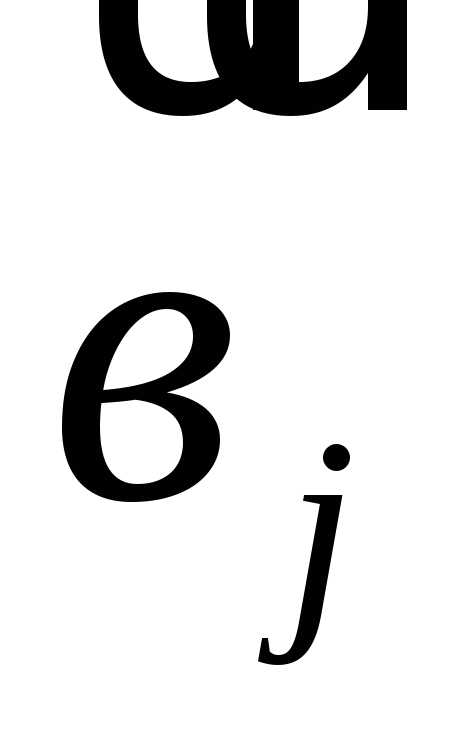
матрицы В:
,
Для
вычисления элементов первой строки
матрицы С необходимо последовательно
получить скалярные произведения первой
строки матрицы А на все столбцы матрицы
В; вторая строка матрицы С получается
как скалярные произведения второй
вектор – строки матрицы А на все вектор
– столбцы матрицы В и так далее. Для
удобства запоминания размера произведения
матриц нужно перемножить отношения
размеров матриц – сомножителей: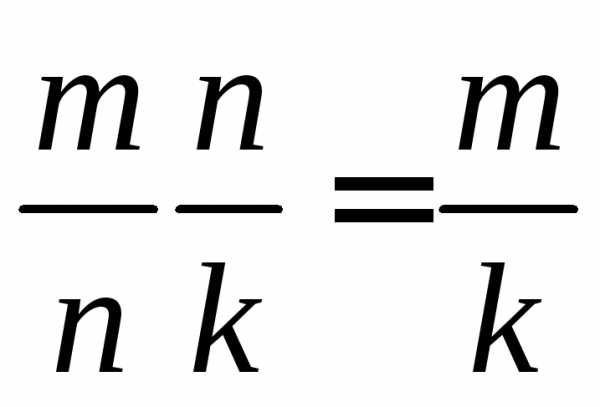
.В операции умножения матриц есть характерная особенность: произведение матриц А и В имеет смысл, если число столбцов в А равно числу строк в В. тогда если А и В – прямоугольные матрицы , то произведение В и А уже не будет иметь смысла, так как в скалярных произведениях, формирующих элементы соответствующей матрицы, должны участвовать векторы с одинаковым числом координат.
Если
матрицы А и В квадратные размером
,
то имеет смысл как произведение матриц
АВ, так и произведение матриц ВА, причем
размер этих матриц такой же, как и у
исходных сомножителей. При этом в общем
случае перемножения матриц правило
перестановочности не соблюдается,
т.е..
Рассмотрим примеры на умножения матриц.
Пример 4.
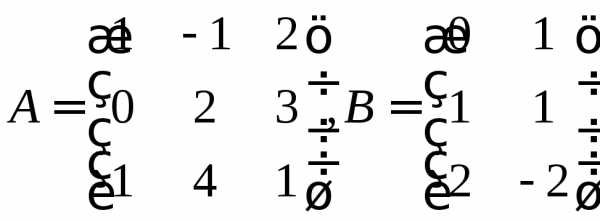
РЕШЕНИЕ.
Поскольку число столбцов матрицы А
равно числу строк матрицы В, то произведение
матриц АВ имеет смысл. По формулам (1.2)
получаем в произведении матрицу размером 
Произведение ВА не имеет смысла, так как число столбцов матрицы В не совпадает с числом строк матрицы А.
Свойства произведения матриц. Пусть А,В, и С – матрицы соответствующих размеров, а – действительное число. Тогда следующие свойства произведения матриц имеют место:
,
,
,
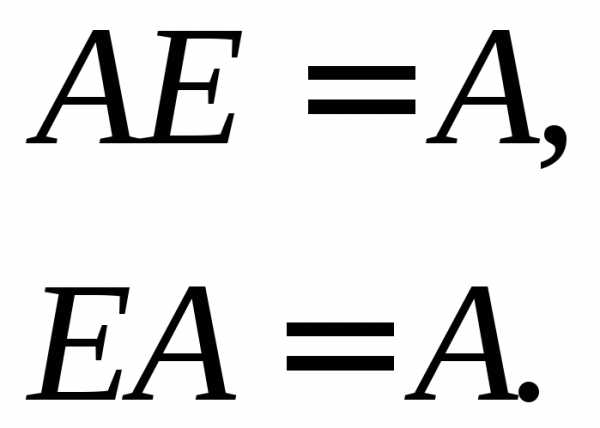
2.4. Ранг матрицы
Рассмотрим
матрицу размера
.
Её можно рассматривать систему, состоящую
из
мерных
векторов. Поскольку любая система
векторов характеризуется рангом, то
естественно встает вопрос о такой же
характеристике для матриц. Так как здесь
имеют место две совокупности векторов
– векторы- строки и векторы- столбцы,
то у матрицы два ранга – строчечный и
столбцовый. Ответ на этот вопрос дает
следующая
Теорема 1. Строчечный и столбцовый ранги любой матрицы равны.
Стало
быть, ранг любой матрицы размера 
можно искать как ранг одной из двух
систем векторов. Для прямоугольной
матрицы максимальный ранг.
Для квадратной матрицы размером
ее максимальный ранг не может превышать
.
studfiles.net
05.3. Произведение матриц. Многочлены от матриц
Произведение определяется для квадратных матриц одного и того же порядка, а также для прямоугольных матриц, у которых число столбцов матрицы множимого равно числу строк матрицы множителя.
Произведением матрицыНа матрицуНазывается та
Кая матрица, для которой
(5.6)
Т. е. элементМатрицы равен — сумме произведений элементов ?-й строки матрицыНа соответствующие элементыСтолбца матрицыМатрица ИмеетСтрок (как и матрица) ИСтолбцов (как и матрица). Произведение матрицыНа матрицуОбозначается
Замечание. Из того, что матрицуМожно умножить на, не следует, что матрицу В можно умножать наОбщем случаеБелиТо
Матрицы А и В называются перестановочными или коммутативными.
При умножении матриц единичная матрица Е играет роль единицы, а нулевая матрица— роль нуля, так как
Умножение матриц обладает следующими свойствами. Если имеют смысл соответствующие действия, то выполняются равенства:
Где- любое действительное число.
Отметим, что, где штрихом обозначена матрица, транспо
Нированная данной.
Целой положительной степеньюКвадратной матрицыНазывается
ПроизкДение к матриц, каждая из которых равна, т. е.. Мат
РицаИмеет тот же порядок, что и матрица. Нулевой степенью квадратной матрицыНазывается единичная матрица того же порядка, что и, т. е.
Первой степеньюМатрицыНазывается сама матрица, т. е. Многочленом (или полиномом) степени(-> целое неотрицательное число) от квадратной матрицыНазывается выражение вида
Где- любые числа, причемОбозначим многочлен от
МатрицыЧерез, тогда по определению
(5.7)
Из определения следует, что многочлен от матрицы можно получить, если в обычный многочленВместоПодставить
Квадратную матрицу (и учесть, что).
Пусть дан многочлен, ЕслиЯвляется нулевой матрицей, т. е.
То матрицаНазывается корнем многочлена, а многочлен
— аннулирующим многочленом для матрицы..
Пример 5.3. Найти произведение,ИМатриц
Обе матрицы являются квадратными матрицамиодного и того же порядка (второго), поэтому можно получить произведенияИПрименяя формулу
(5.6) для случаяПолучаем
Отметим, чтоТ. е. результат умножения зависит от порядка множителей.
Пример S.4. Даны две матрицы
Найти произведение. Можно ли получить произведение?
Число столбцов матрицыРавно числу строк матрицы(ширина матрицы равна высоте матрицы), поэтому произведениеОпределено. Умножая строку матрицыНа столбец матрицы, по формуле (5.6) получаем
ПроизведениеНе определено, так как число столбцов матрицы В не равно числу строк матрицы.
Пример 5.5. Найти многочлен, еслиИ
В соответствии с определением многочлена от матрицы (см. формулу (5.7)) получаемИли
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Транспонирование матриц. Умножение матриц.
К оглавлению
I. Транспонирование матриц
Транспонирование матриц – переход от матрицы А к матрице, в которой строки и столбцы поменялись местами с сохранением порядка.
Пример 1. Составить транспонированную матрицу, полученную из А:
Решение: Поменяем местами строки и столбцы, сохраняя порядок:
Примеры для самостоятельного решения:
Составить из исходной матрицы транспонированную матрицу:
II. Умножение матриц
Пример 1. Рассмотрим для начала простейший пример, когда необходимо найти произведение двух матриц А и В размером 2´2, если
Решение:
Элементы матрицы С находятся по следующему алгоритму:
Элемент матрицы С, стоящий на первой строке, в первом столбце находится как сумма произведений первой строки матрицы А на первый столбец матрицы В.
Элемент матрицы С, стоящий на первой строке, во втором столбце находится как сумма произведений первой строки матрицы А на второй столбец матрицы В.
Элемент матрицы С, стоящий на второй строке, в первом столбце находится как сумма произведений второй строки матрицы А на первый столбец матрицы В.
Элемент матрицы С, стоящий на второй строке, во втором столбце находится как сумма произведений второй строки матрицы А на второй столбец матрицы В.
Таким образом, мы получили
То есть мы получили, что
Пример 2. Найдем результат произведения двух матриц
Решение:
то есть мы должны получить матрицу размера 3´3.
Пример 3. В предыдущем примере мы рассмотрели случай умножения матрицы А на матрицу В, а в данном примере рассмотрим случай произведения матрицы В на А.
Решение:
Пример 4. Найти произведение двух матриц:
Решение: В первом случае найдем произведение:
Во втором случае найдем произведение:
Пример 5. Вычислить значение многочлена от матрицы
Решение. В многочлен подставим вместо х матрицу А, вместо числа 3 используем матрицу 3Е, где Е – единичная матрица 2-го порядка
Теперь получим окончательный результат
III. Примеры для самостоятельного решения
I. Найти произведение матриц:
II. Найти значение многочлена от матрицы А
К оглавлению
miemp-mi-gor.narod.ru