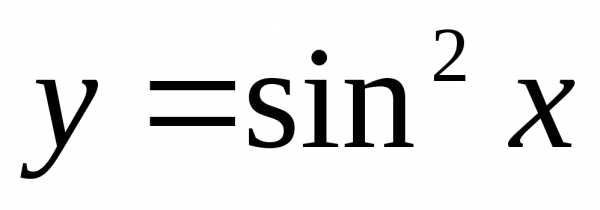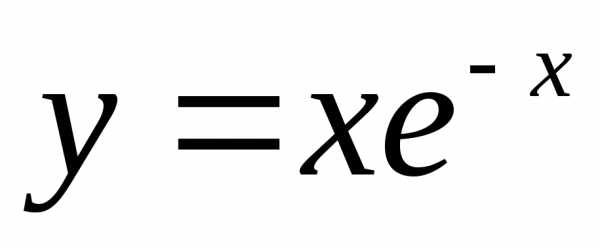Формулы производных функций y (x)
Производные линейной функции.
Производные степенной функции.
Производные показательной функции.
Производные логарифмической функции.
Производные тригонометрической функции.
Производные обратной тригонометрической функции.
- Подробности
- Автор: Administrator
www-formula.ru
Формулы производных
Что такое производная функция — это основное математическое понятие, находится на одном уровне с интегралами, при анализе. Данная функция в определенной точке дает характеристику скорости изменений функции в данной точке.
Такие понятия как дифференцирование и интегрирование, первое расшифровывается как действие поиска производной, второе наоборот, восстанавливает функцию отталкиваясь от данной производной.
Вычислениям производной отводится важная часть в дифференциальных расчетах.
Для наглядного примера, изобразим производную на координатной плоскости.
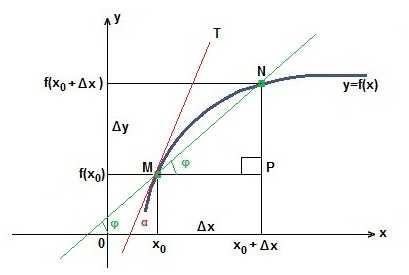
в функции у=f(х) фиксируем точки М в которой (х0; f(X0)) и N f (x0+?x) к каждой абсциссе есть приращение в виде ?x. Приращением называется процесс когда изменяется абсцисса, тогда меняется и ордината. Обозначается как ?у.
tg? = NP/MP = ?у/?x.
При ?x идущем к 0. Пересекающая МN все ближе к касательной МТ и угол ? будет ?. Следовательно, tg ? максимальное значение для tg ?.
tg ? = lim от ?x-0 tg ? = lim от ?x-0 ?у/?x
Таблица производныхЕсли проговаривать формулировку каждой формулы производных. Таблица будет проще запоминаться.
1) Производная от постоянного значения равняется 0.
2) Х со штрихом равняется единице.
3) Если есть постоянный множитель, просто выносим ео за производную.
4) Чтобы найти производную степень, нужно показатель данной степени умножить на степень с таким же основанием, у которого показатель на 1 меньше.
5) Поиск корня равен одному, деленному 2 этих корня.
7) П синус равняется косинусу
8) П косинус равняется синусу со знаком минус.
9) П тангенс равняется одному, деленному на косинус в квадрате.
10) П котангенс равняется одному со знаком минус, деленная на синус в квадрате.
В дифференцировании также существуют правила, которые тоже проще выучить проговаривая их в слух.
1) Очень просто, п. слагаемых равняется их сумме.
2) Производная в умножении равняется умножению первого значения на второе, прибавляя к себе умножение второго значения на первое.
3) Производная в делении равняется умножению первого значения на второе, отнимая от себя умножение второго значения на первое. Дробь деления на второе значение в квадрате.
4) Формулировка является частным случаем третьей формулы.
Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:
reshit.ru
Формулы производной | Формулы с примерами
ФормулыПриращение аргумента
Приращение функции
Производная функции ?(x) в точке x0
Касательная к графику
Геометрический смысл производной
Уравнение касательной к графику ? (x)
Физический смысл производной
Правила дифференцирования

Таблица производных
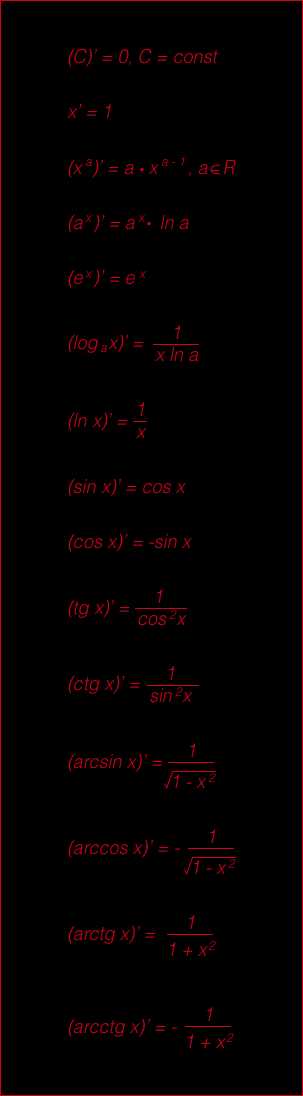
Достаточное условие монотонности функции ? (x)
Экстремумы функции ? (x)
Необходимое условие экстремума ? (x)
Достаточное условие экстремума непрерывной в точке x0 функции ? (x)

formula-xyz.ru
Формулы производных
Производная характеризует скорость изменения функции в определенной точке. На рисунке 1 изображена производная функции на координатной плоскости.
Рисунок 1. Производная функции
2) Производная неизвестной величины равна единице
\[x’=1\]3) Если выражение содержит постоянную величину — ее необходимо вынести за знак предела.
\[y’=\left(c\cdot f\left(x\right)\right)^{{‘} } =c\cdot f’\left(x\right)\]4) Производная степенной функции находится как произведение значения степени на степенное выражение, степень которого уменьшена на 1.
\[y’=\left(x^{n} \right)^{{‘} } =n\cdot x^{n-1} \]5) Производная экспоненты равна самой экспоненте
6) Производная числа в степени х равна произведения данного выражения на логарифм числа:
\[y’=\left(a^{x} \right)^{{‘} } =a^{x} \cdot \log a\]7) Производная sinx равна cosx
8) Производная cosx равна —sinx
9) Производная тангенса равна частному единицы и квадратному косинусу х
\[y’=\left(tgx\right)^{{‘} } =\frac{1}{\cos ^{2} x} \]10) Производная котангенса равна частному минус единицы и квадратному синусу х
\[y’=\left(ctgx\right)^{{‘} } =-\frac{1}{\sin ^{2} x} \]11) Производная арксинуса равна:
\[y’=\left(\arcsin x\right)^{{‘} } =\frac{1}{\sqrt{1-x^{2} } } \]12) Производная арккосинуса равна:
\[y’=\left(\arccos x\right)^{{‘} } =-\frac{1}{1-x^{2} } \]13) Производная арктангенса равна:
\[y’=\left(arctgx\right)^{{‘} } =\frac{1}{1+x^{2} } \]14) Производная арккотангенса противоположна производной арктангенса и равна:
\[y’=\left(arctgx\right)^{{‘} } =-\frac{1}{1+x^{2} } \]15) Производная суммы функций равна сумме их производных:
\[\left(x+y+…+z\right)^{{‘} } =x’+y’+…+z’\]16) Производная произведения нескольких функций равна:
$y’ = (fx1 \cdot fx2 \cdot \dots \cdot fxn) = fx’1fx2fx3\dots fxn + fx1fx’2fx3\dots fxn + \dots + fx1fx2fx3\dots fx’n$
17) Производная частного вычисляется по формуле:
\[y’=\left(\frac{f\left(x\right)}{g\left(x\right)} \right)^{{‘} } =\frac{f\left(x\right)^{{‘} } g\left(x\right)-g\left(x\right)^{{‘} } f\left(x\right)}{g^{2} \left(x\right)} \]spravochnick.ru
7.1. Производная, правила и формулы дифференцирования
Пусть функция y = f(x) определена в промежутке X. Производной функции y = f(x) в точке хo называется предел
= .
Если этот предел конечный, то функция f(x) называется дифференцируемой в точке xo; при этом она оказывается обязательно и непрерывной в этой точке.
Если же рассматриваемый предел равен (или — ), то при условии, что функция в точке хo непрерывна, будем говорить, что функция f(x) имеет в точке хoбесконечную производную.
Производная обозначается символами
y , f (xo), , .
Нахождение производной называется дифференцированием функции. Геометрический смысл производной состоит в том,что производная есть угловой коэффициент касательной к кривой y=f(x) в данной точке хo; физический смысл — в том, что производная от пути по времени есть мгновенная скорость движущейся точки при прямолинейном движении s = s(t) в момент to.
Если с — постоянное число, и u = u(x), v = v(x) — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:
1) (с)‘ = 0, (cu)‘ = cu’;
2) (u+v)’ = u’+v’;
3) (uv)’ = u’v+v’u;
4) (u/v)’ = (u’v-v’u)/v2;
5) если y = f(u), u = (x), т.е. y = f((x)) — сложная функция, или суперпозиция, составленная из дифференцируемых функций и f, то , или
;
6) если для функции y = f(x) существует обратная дифференцируемая функция x = g(y), причем 0, то .
На основе определения производной и правил дифференцирования можно составить список табличных производных основных элементарных функций.
1. (u)’ = u1 u’ ( R).
2. (au)’ = au lna u’.
3. (eu)’ = eu u’.
4. (loga u)’ = u’/(u ln a).
5. (ln u)’ = u’/u.
6. (sin u)’ = cos u u’.
7. (cos u)’ = — sin u u’.
8. (tg u)’ = 1/ cos2u u’.
9. (ctg u)’ = — u’ / sin2u.
10. (arcsin u)’ = u’ /.
11. (arccos u)’ = — u’ /.
12. (arctg u)’ = u’/(1 + u2).
13. (arcctg u)’ = — u’/(1 + u2).
Вычислим производную степенно-показательного выражения y=uv, (u>0), где u и v суть функции от х, имеющие в данной точке производные u’, v’.
Прологарифмировав равенство y=u v, получим ln y = v ln u.
Приравнивая производные по х от обеих частей полученного равенства с помощью правил 3, 5 и формулы для производной логарифмической функции, будем иметь:
y’/y = vu’/u +v’ ln u, откуда y’ = y (vu’/u +v’ ln u).
Итак,
(u v)’=u v (vu’/u+v’ ln u), u > 0.
Например, если y = x sin x, то y’ = x sin x (sin x/x + cos x ln x).
Если функция y = f(x) дифференцируема в точке x, т.е. имеет в этой точке конечную производную y’, то = y’+, где 0 при х 0; отсюда y = y’ х + x.
Главная часть приращения функции, линейная относительно х, называется дифференциалом функции и обозначается dy: dy = y’ х. Если положить в этой формуле y=x, то получим dx = x’х = 1х =х, поэтому dy=y’dx, т. е. символ для обозначения производной можно рассматривать как дробь.
Приращение функции y есть приращение ординаты кривой, а дифференциал dy есть приращение ординаты касательной.
Пусть мы нашли для функции y=f(x) ее производную y = f (x). Производная от этой производной называется производной второго порядка функции f(x), или второй производной, и обозначается .
Аналогично определяются и обозначаются:
производная третьего порядка — ,
производная четвертого порядка —
и вообще производная n-го порядка — .
Пример 3.15. Вычислить производную функции y=(3x3-2x+1)sin x.
Решение. По правилу 3, y’=(3x3-2x+1)’sin x + (3x3-2x+1)(sin x)’ = = (9x2-2)sin x + (3x3-2x+1)cos x.
Пример 3.16. Найти y’, y = tg x +.
Решение. Используя правила дифференцирования суммы и частного, получим: y’=(tgx + )’ = (tgx)’ + ()’ = + = .
Пример 3.17. Найти производную сложной функции y=, u=x4 +1.
Решение. По правилу дифференцирования сложной функции, получим: y’x =y‘u u’x =()’u(x4 +1)’x =(2u +. Так как u=x4 +1,то (2 x4 +2+.
Пример 3.18. Найти производную функции y=.
Решение. Представим функцию y= в виде суперпозиции двух функций: y = eu и u = x2. Имеем: y’x =y‘u u’x = (eu)’u(x2)’x = eu 2x. Подставляя x2 вместо u, получим y=2x.
Пример 3.19.
Решение. Обозначим u=sin x, тогда производная сложной функции y=ln u вычисляется по формуле y’ = (ln u)’u(sin x)’x= .
Пример 3.20. Найти производную функции y=.
Решение. Случай сложной функции, полученной в результате нескольких суперпозиций, исчерпывается последовательным применением правила 5:
.
Пример 3.21. Вычислить производную y=ln .
Решение. Логарифмируя и используя свойства логарифмов, получим:
y=5/3ln(x2+4) +7/3ln(3x-1)-2/3ln(6x3+1)-1/3tg 5x.
Дифференцируя обе части последнего равенства, получим:
.
studfiles.net
Вывод производных основных элементарных функций
Производная логарифма
; ;
; .
См. Вывод производной логарифма тремя способами >>>
Производная степенной и показательной функций
;
;
См. Вывод производной степенной функции >>>
;
;
См. Вывод производной показательной функции и экспоненты тремя способами >>>
Производные тригонометрических функций
См. Вывод производных тригонометрических функций >>>
;
См. Вывод производной синуса >>>
;
См. Вывод производной косинуса >>>
;
См. Вывод производной тангенса >>>
;
См. Вывод производной котангенса >>>
Производные обратных тригонометрических функций
См. Вывод производных обратных тригонометрических функций >>>
;
;
См. Вывод производных арксинуса и арккосинуса двумя способами >>>
;
;
См. Вывод производных арктангенса и арккотангенса двумя способами >>>
Производные гиперболических функций
;
;
;
;
Производные обратных гиперболических функций
;
;
;
.
Обратный гиперболический косинус является многозначной функцией. Он имеет две ветви:
– главное значение;
.
Иногда значения для двух ветвей пишут одной формулой:
.
Тогда его производная имеет вид:
.
Производные высших порядков
.
См. Доказательство методом математической индукции >>>
.
См. Вывод производной степенной функции n-го порядка >>>
.
См. Производные высших порядков показательной функции >>>
Тригонометрические функции
.
См. Доказательство методом математической индукции >>>
.
См. Производные косинуса высших порядков >>>
,
где .
См. Производные тангенса высших порядков >>>.
,
где .
См. Производные котангенса высших порядков >>>.
Обратные тригонометрические функции
Производные арксинуса и арккосинуса
,
где – многочлен степени . Он определяется по формулам:
;
.
Здесь .
.
См. Вывод производных высших порядков арксинуса и арккосинуса >>>.
Производные арктангенса и арккотангенса
;
.
Другой вид производных:
,
где .
,
где .
См. Вывод производных высших порядков арктангенса и арккотангенса >>>.
Автор: Олег Одинцов. Опубликовано: Изменено:
1cov-edu.ru
Правила и формулы нахождения производных. Производная сложной функции.
Основные правила дифференцирования:
Производная постоянной равна нулю, т.е. .
Производная аргумента равна единице, т.е.
 .
.Производная алгебраической суммы конечного числа дифференцируемых функций равна алгебраической сумме производных этих функций, т.е. .
Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго, т.е. .
Следствие 1. Постоянный множитель можно выносить за знак производной: .
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные, например: .
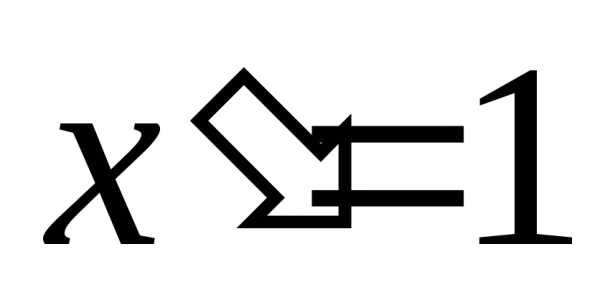
Производная частного двух дифференцируемых функций может быть найдена по формуле
 (при условии,
что
(при условии,
что  ).
).Производная сложной функции. Пусть задана сложная функция .
Теорема. Если 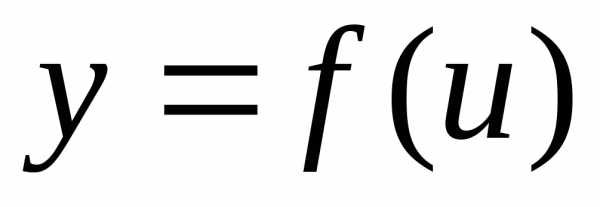 и
и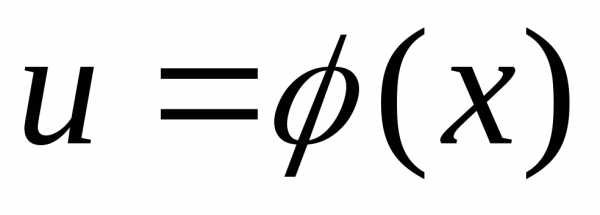
дифференцируемые функции от своих
аргументов, то производная сложной
функции существует и равна производной
данной функции по промежуточному
аргументу и умноженной на производную
промежуточного аргумента по независимой
переменной
дифференцируемые функции от своих
аргументов, то производная сложной
функции существует и равна производной
данной функции по промежуточному
аргументу и умноженной на производную
промежуточного аргумента по независимой
переменной 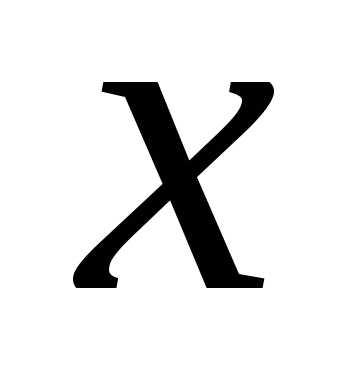
Производные основных элементарных функций (таблица производных):
Производная логарифмической функции.
А) 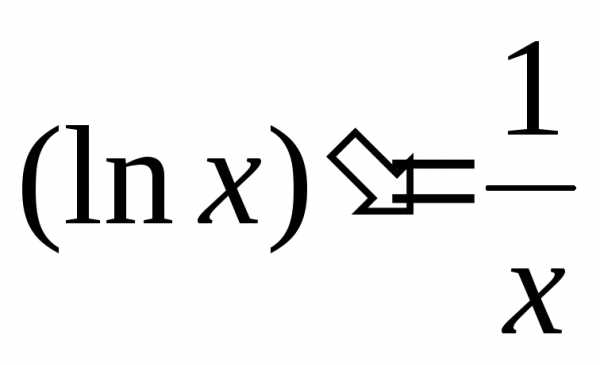 и
и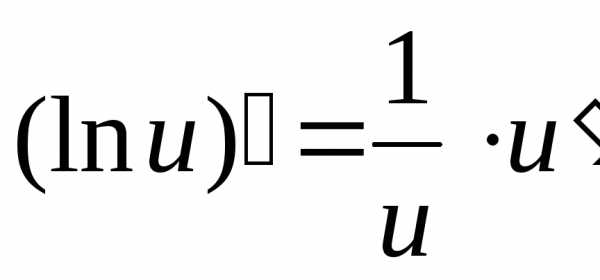 ,
где
,
где
некоторая функция зависящая от
некоторая функция зависящая от 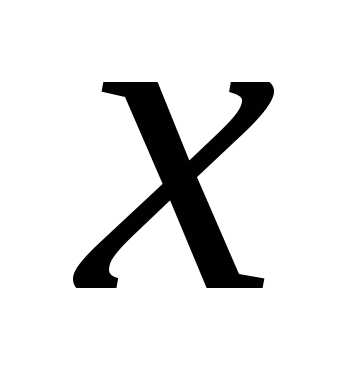 .
.
Б) 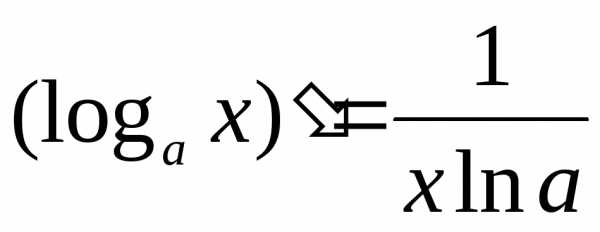 и.
и.
Производная показательной функции.
А) 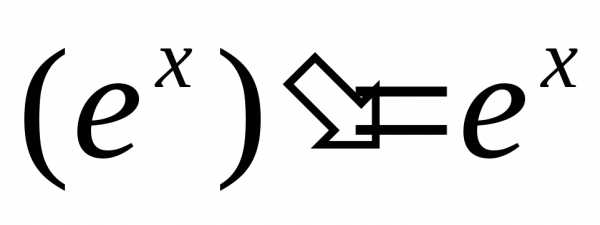 и.
и.
Производная степенной функции.
и .
Производная степенно-показательной функции.
.
Производная тригонометрических функций.
и ;
и ;
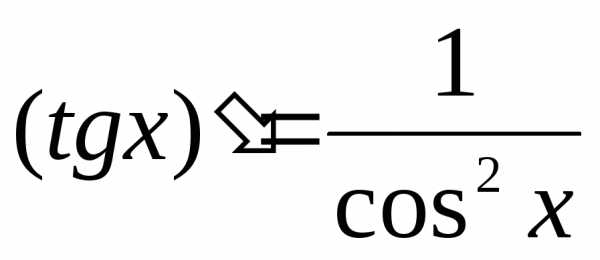 и
и 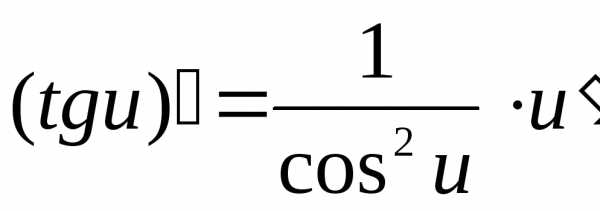 ;
;
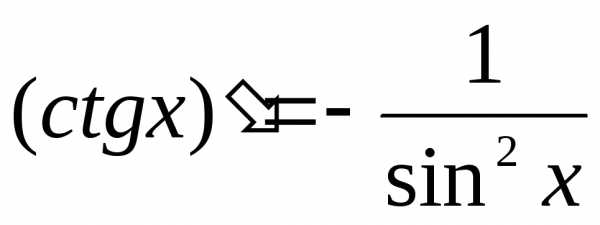 и
.
и
.
Производная обратных тригонометрических функций.
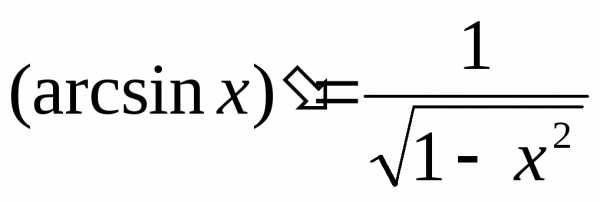 и ;
и ;
и ;
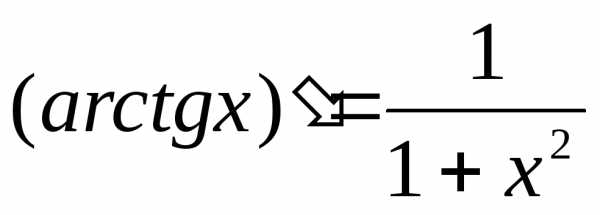 и ;
и ;
и .
Пример. Найти производные следующих функций:
Производные высших порядков.
Производной
второго порядка или второй
производной функции  называется производная от ее первой
производной, т.е.
называется производная от ее первой
производной, т.е. ,
и обозначается
,
и обозначается или
или или
или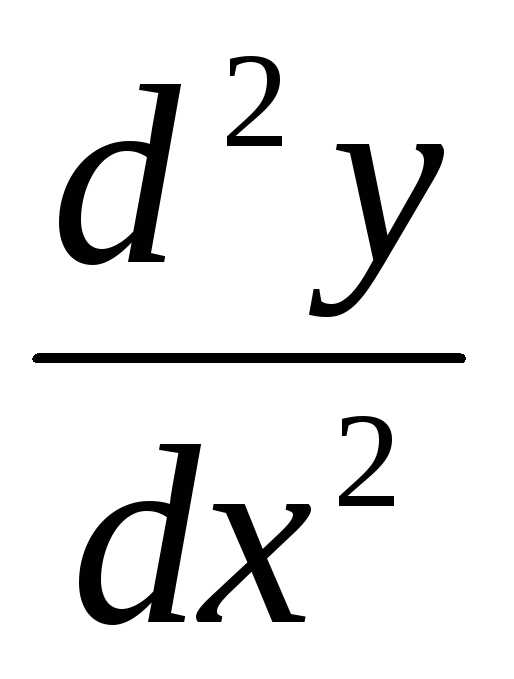 .
.
Аналогично
определяются и обозначаются: производная
3-го порядка 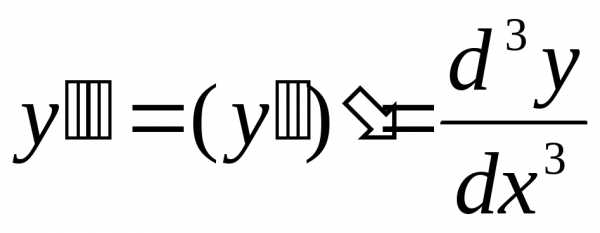 ;
производная 4-го порядка
;
производная 4-го порядка ;
………… производная
;
………… производная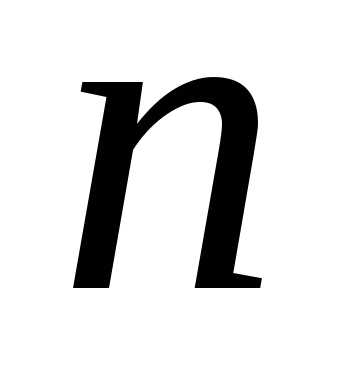 -го
порядка.
-го
порядка.
Пример. Найти производную 2-го и 3-го порядка:
А) | Б) |
Понятие дифференциала и его геометрический смысл.
Пусть функция 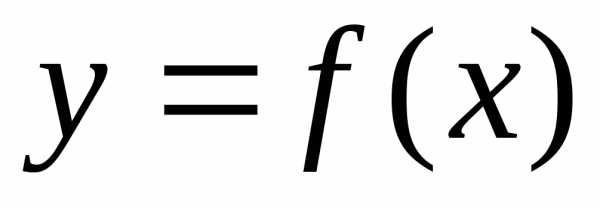 определена на промежутке
определена на промежутке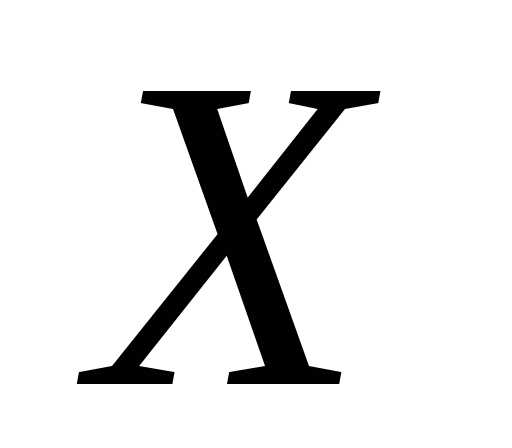 и дифференцируема в окрестности точки
и дифференцируема в окрестности точки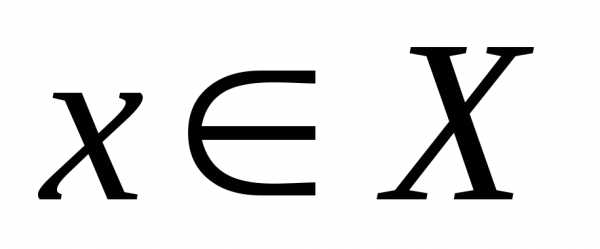 ,тогда
,тогда или по теореме о связи бесконечно малых
с пределами функций имеем,
где
или по теореме о связи бесконечно малых
с пределами функций имеем,
где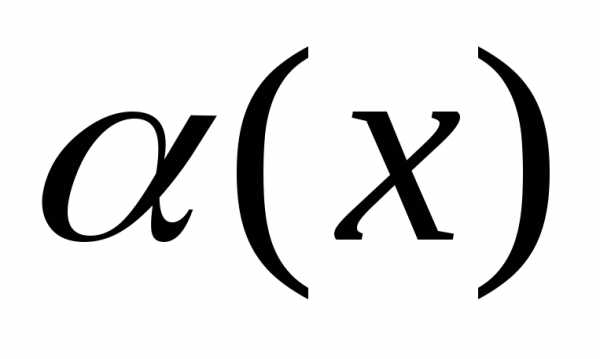
бесконечно малая величина при
.
Отсюда:.
Таким образом, приращение функции
бесконечно малая величина при
.
Отсюда:.
Таким образом, приращение функции состоит из двух слагаемых: 1.
состоит из двух слагаемых: 1.
линейного относительно
линейного относительно 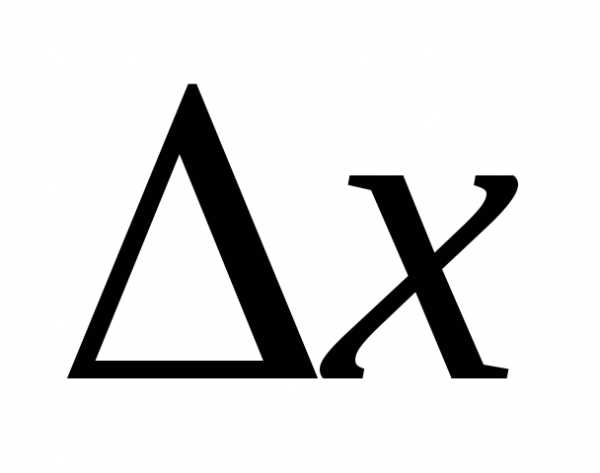 ,
т.к.;
2.
,
т.к.;
2.
нелинейного относительно
нелинейного относительно 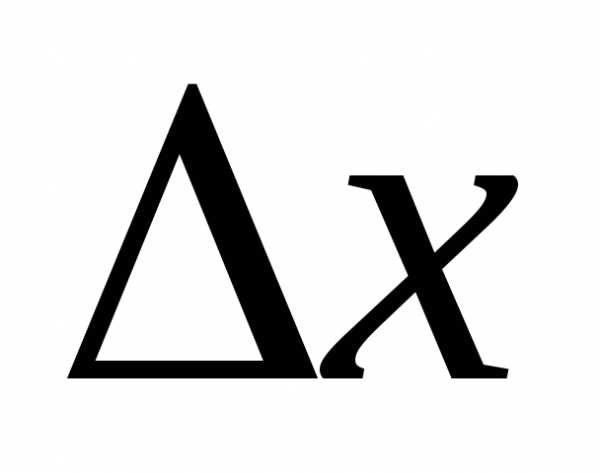 ,
т.к..
,
т.к..
Дифференциалом
функции называется главная, линейная относительно 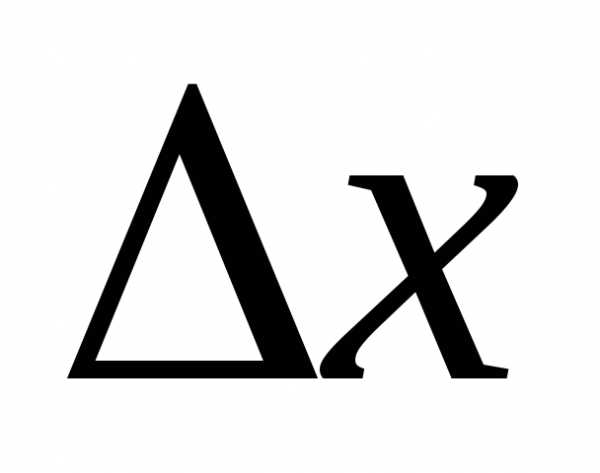 часть приращения функции, равная
произведению производной на приращение
независимой переменной:.
часть приращения функции, равная
произведению производной на приращение
независимой переменной:.
Пример. Найти приращение функции
при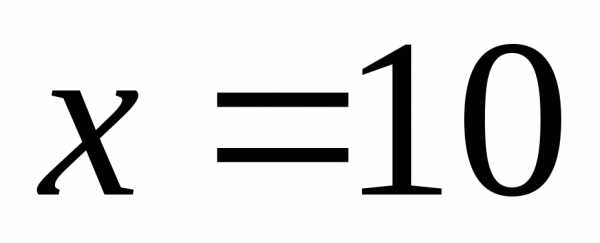 и
и
Пример. Найти дифференциал функции 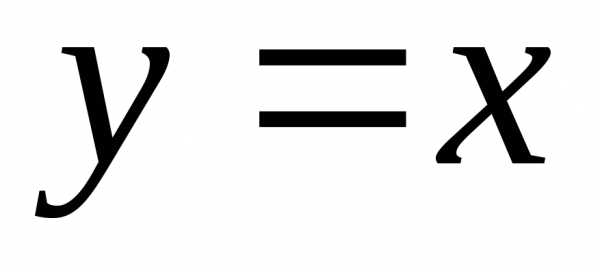 .
.
Дифференциал
независимой переменной 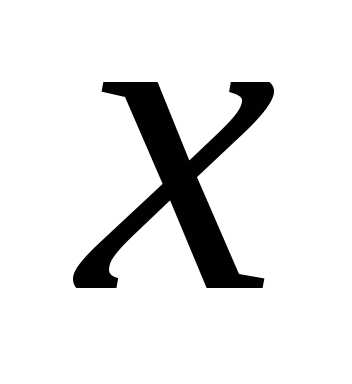 равен приращению этой переменной:.
равен приращению этой переменной:.
Тогда формулу для
дифференциала функции можно записать
в виде:
.
Откуда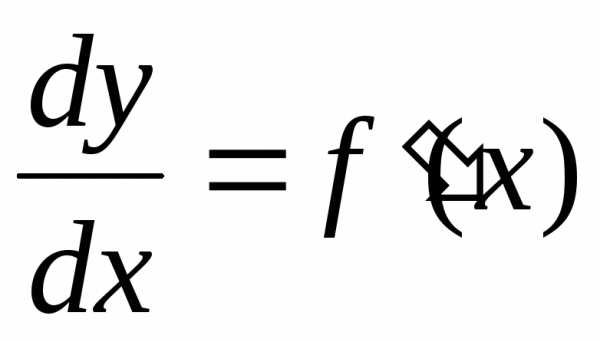 ,
поэтому
,
поэтому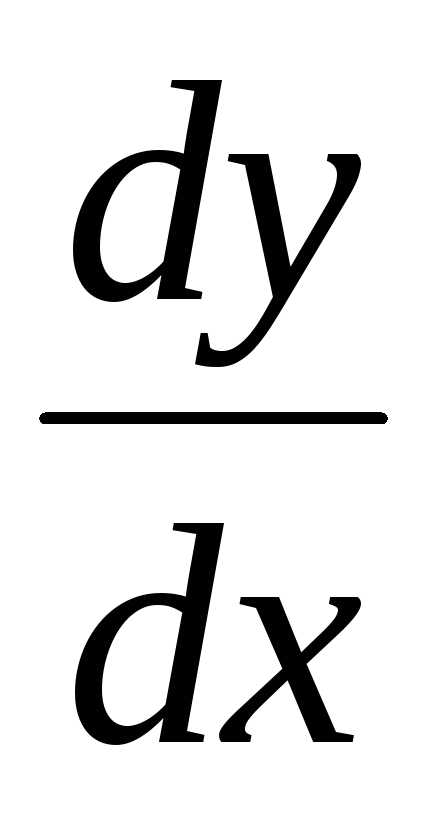 можно рассматривать не только как
символическое обозначение производной,
но и как обычную дробь с числителем
можно рассматривать не только как
символическое обозначение производной,
но и как обычную дробь с числителем и знаменателем
и знаменателем .
.
Геометрический
смысл. На
графике функции 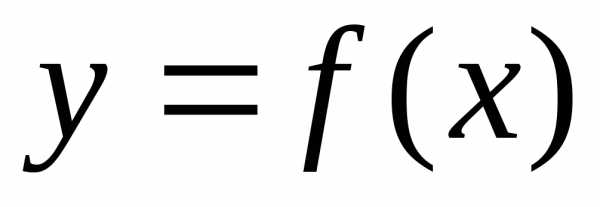 (рис.
5.) возьмем
произвольную точку
(рис.
5.) возьмем
произвольную точку 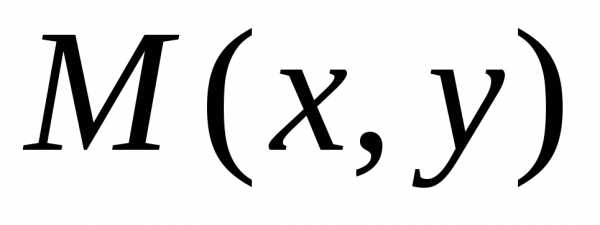 .
Дадим аргументу
.
Дадим аргументу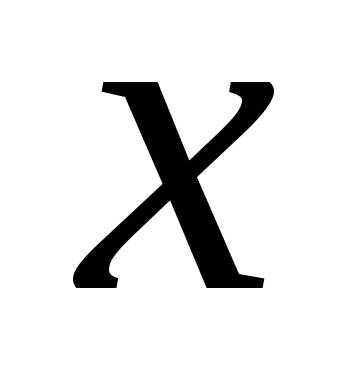 приращение
приращение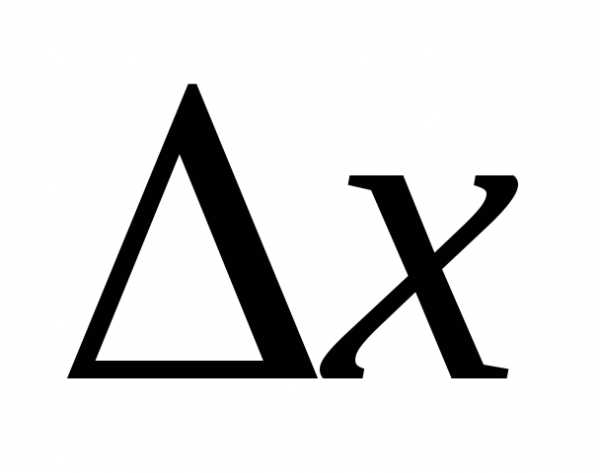 ,
тогда функция получает приращение.
В точке
,
тогда функция получает приращение.
В точке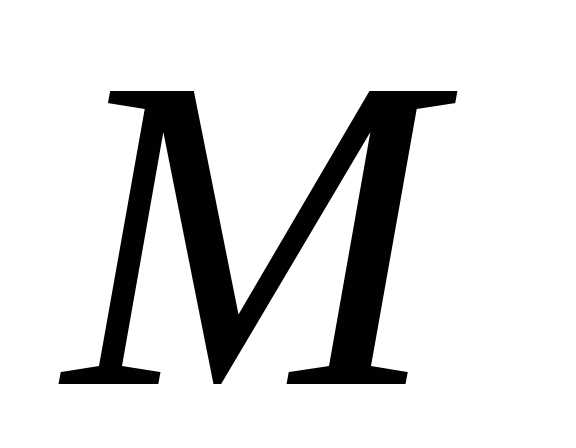 проведем касательную, образующую угол
проведем касательную, образующую угол с осью
с осью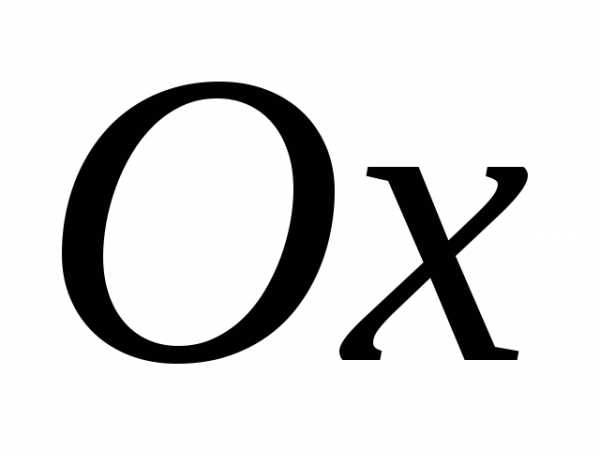 .
Из
.
Из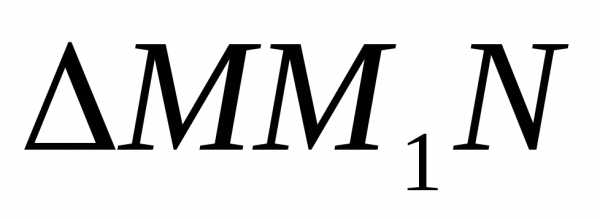 видно,
что.
Из
видно,
что.
Из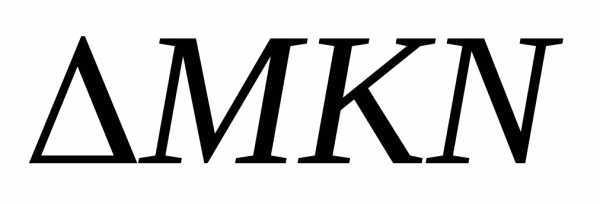 имеем:.
Таким образом,и соответствует формуле.
имеем:.
Таким образом,и соответствует формуле.
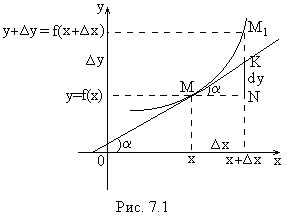
Рис. 5.
Следовательно, с
геометрической точки зрения дифференциал
функции есть приращение ординаты
касательной, проведенной к графику
функции 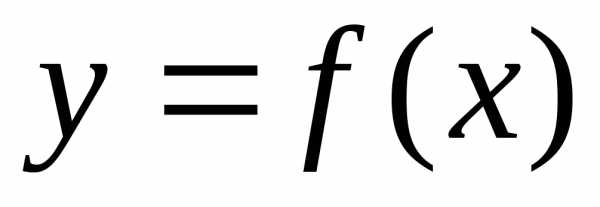 в данной точке, когда
в данной точке, когда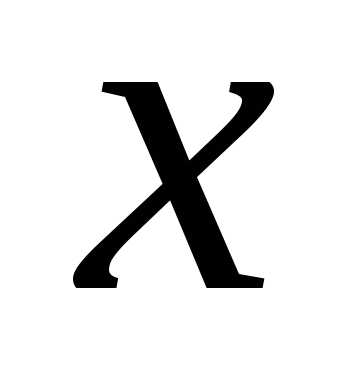 получает приращение
получает приращение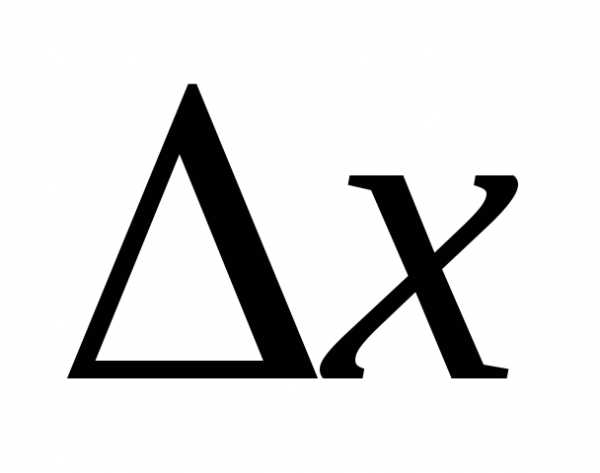 .
.
Свойства дифференциала аналогичны свойствам производной:
Формула дифференциала
не изменится, если вместо функции от
независимой переменной  рассматривать функцию от зависимой
переменной
рассматривать функцию от зависимой
переменной .
Это свойство дифференциала получило
названиеинвариантности (т.е. неизменности) формы дифференциала,
т.е.
.
.
Это свойство дифференциала получило
названиеинвариантности (т.е. неизменности) формы дифференциала,
т.е.
.
Приближенные
вычисления с помощью дифференциала. Согласно
формулы
,
т.е.,
при достаточно малых значениях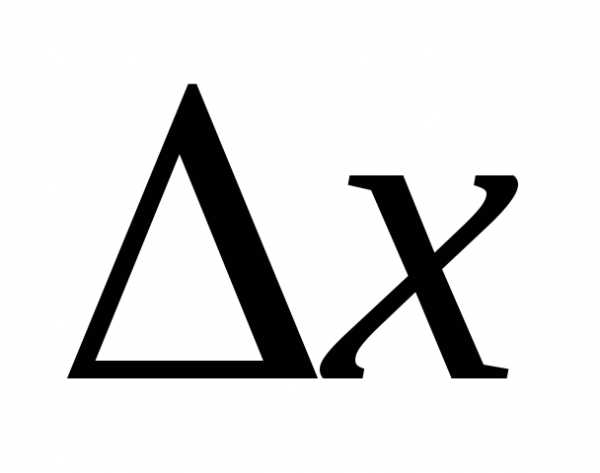 приращение функции
приращение функции приблизительно равно ее дифференциалу
приблизительно равно ее дифференциалу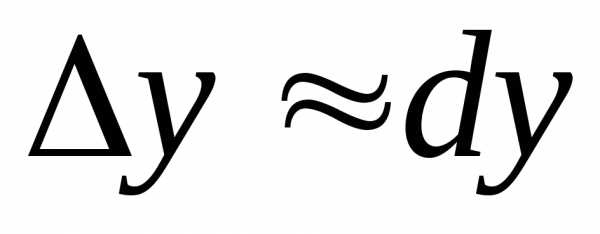 ,.
Эту формулу часто используется в
приближенных вычислениях.
,.
Эту формулу часто используется в
приближенных вычислениях.
Пример. Вычислить  .
.
studfiles.net

 .
.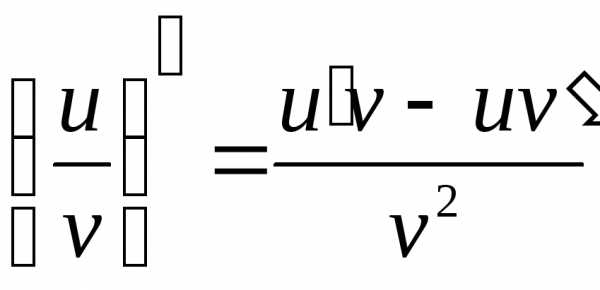 (при условии,
что
(при условии,
что 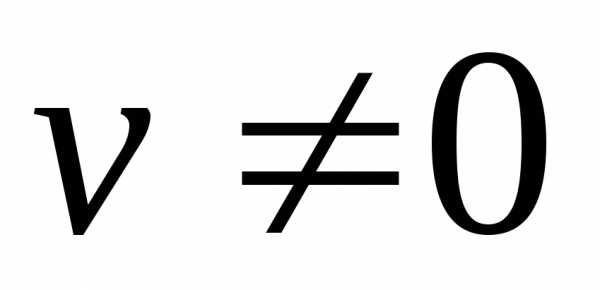 ).
).