Производная синуса – Производная синуса: формулы и примеры решений

Производная синуса — энциклопедический справочник и словарь для студента от А до Я

ОПРЕДЕЛЕНИЕ

Производная синуса равна косинусу того же аргумента.

То есть синус просто «заменяется» на косинус. Заметим, что производная от косинуса равна минус синус того же аргумента:

Чтобы не запутаться, мне принадлежит мнемоническое правило:

Синий косяк

Косяк – синий

Первая строка показывает, что производная от синуса равна косинусу (если вы смотрите на выбранные буквы), а вторая строка дает понять, что производная от косинуса представляет собой минус синус (выбранные буквы и тире) ,

Примеры решения проблем на тему «Синусовая производная»

ПРИМЕР 1

Задача

Найдите производную от функции

Решение

Требуемая производная

Аргумент sine не просто x («X»), поэтому невозможно просто применить приведенную выше формулу, поскольку задана сложная функция. Следовательно, производная от синуса — косинус того же аргумента, найденный по приведенной выше формуле, должна быть умножена на производную от аргумента:

Производная от корня делится на два одинаковых корня. Тогда мы имеем:

Ответ

ПРИМЕР 2

Задача

Найдите производную от функции

Решение

Требуемая производная:

На первом шаге решения мы используем правила дифференцирования, а именно, что константу можно взять из знака производной:

Затем мы найдем производную от синуса — это косинус того же аргумента. И поскольку аргумент является выражением, более сложным, чем просто x, мы имеем дело со сложной функцией и поэтому все еще нужно умножить на производную от аргумента, то есть:

Производная суммы равна сумме производных, тогда:

Производные , как производная от константы, умноженной на х, равны 3; и производная , производная от константы, равна 0.

Таким образом, мы имеем:

Ответ

sciterm.ru

Производные тригонометрических функций: тангенса, синуса, косинуса и других

Из курса геометрии и математики школьники привыкли, что понятие производной доносится до них через площадь фигуры, дифференциалы, пределы функций, а также лимиты. Попробуем посмотреть на понятие производной под другим углом, и определить, как можно увязать производную и тригонометрические функции.

Понятие производной

Итак, рассмотрим некую произвольную кривую, которая описывается абстрактной функцией y = f(x).

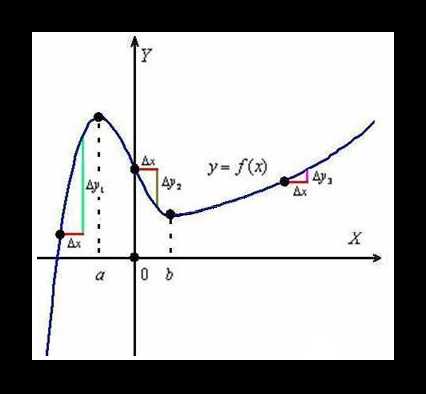
Представим что график — это карта туристического маршрута. Приращение ∆x (дельта икс) на рисунке — это определенный промежуток пути, а ∆y – это изменение высоты тропы над уровнем моря.
Тогда получается, что отношение ∆x/∆y будет характеризовать сложно маршрута на каждом отрезке пути. Узнав это значение можно с уверенностью сказать крутой ли подъем/спуск, понадобится ли альпинистское снаряжение и нужна ли туристам определенная физическая подготовка. Но показатель этот будет справедлив только для одного маленького промежутка ∆x.

Если организатор похода возьмет значения для начальной и конечной точек тропы, то есть ∆x – будет равен длине маршрута, то не сможет получить объективные данные о степени сложности путешествия.  Следовательно, необходимо построить еще один график, который будет характеризовать скорость и «качество» изменений пути, другими словами определять отношение ∆x/∆y для каждого «метра» маршрута.

Этот график и будет являться наглядной производной для конкретной тропы и объективно опишет ее изменения на каждом интересующем интервале. Убедиться в этом очень просто, значение  ∆x/∆y – есть не что иное, как дифференциал, взятый для конкретного значения x и y. Применим же дифференцирование не определенным координатам, а к функции в целом:

Производная и тригонометрические функции

Тригонометрические функции неразрывно связаны с производной. Понять это можно из следующего чертежа. На рисунке координатной оси изображена функция  Y = f (x) – синяя кривая.

K (x0; f (x0)) – произвольная точка, x0 + ∆x – приращение по оси OX, а f (x0 + ∆x) – приращение по оси OY в некой точке L.

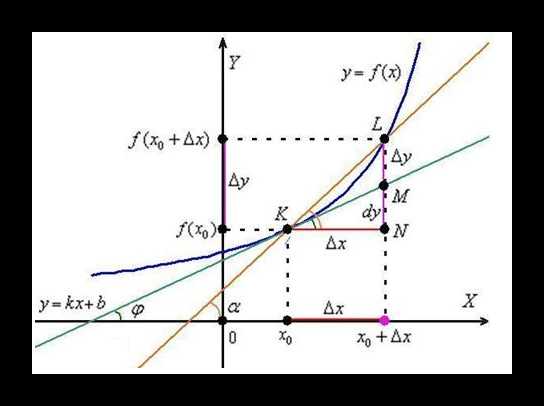
Проведем прямую через точки K и L и построим прямоугольный треугольник KLN. Если мысленно перемещать отрезок LN по графику Y = f (x), то точки L и N будут стремиться к значениям K (x0; f (x0)). Назовем эту точку условным началом графика — лимитом, если же функция бесконечна, хотя бы на одном из промежутков  – это стремление также будет бесконечным, а его предельное значение близким к 0.

Характер данного стремления можно описать касательной к выбранной точке y = kx + b или графиком производной первоначальной функции dy – зеленая прямая.

Но где же здесь тригонометрия?! Все очень просто рассмотрим прямоугольный треугольник KLN. Значение дифференциала для конкретной точки K есть тангенс угла α или ∠K:

Таким образом можно описать геометрический смымсл производной и ее взаимосвязь с тригонометрическими функциями.

Формулы производных для тригонометрических функций

Преобразования синуса, косинуса, тангенса и котангенса при определении производной необходимо заучить наизусть.

Последние две формулы не являются ошибкой, дело в том, что существует разница между определением производной простого аргумента и  функции в том же качестве.

Рассмотрим сравнительную таблицу с формулами производных от синису, косинуса, тангенса и котангенса:

Также выведены формулы для производных арксинуса, арккосинуса, арктангенса и арккотангенса, хотя они применяются крайне редко:

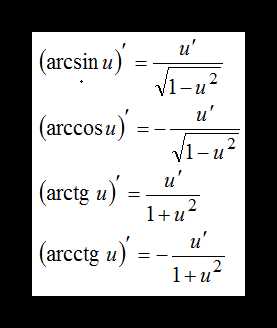
Стоит отметить, что приведенных формул явно недостаточно для успешного решения типовых заданий ЕГЭ, что будет продемонстрированно при решении конкретного примера поиска производной тригонометрического выражения.

Задание: Необходимо найти производную функции и найти ее значение для π/4:

Решение:  Чтобы найти y’ необходимо вспомнить основные формулы преобразования исходной функции в производную, а именно:

Теперь следует приступить к поэтопному преобразованию исходной функции y, сначала применим формулу (1):

Согласно формуле (2) преобразуем числитель выражения:

Избавимся от производным числа 1 по правилу (3) и заменим sin x его производной (4):

Осталось посчитать значение производной для π/4:

Похожие статьи

Рекомендуем почитать:

karate-ege.ru

Производная косинуса — энциклопедический справочник и словарь для студента от А до Я

ОПРЕДЕЛЕНИЕ

Производная косинуса X равна минус синус X.

Чтобы запомнить эту формулу, существует мнемоническое правило:

Синий косяк (производная синуса равна косинусу)

Косяк – синий (производная косинуса равна минус синусу)

Примеры решения задач на «косинусоидальном»

ПРИМЕР 1

Задача

Найти производную функции

Решение

Требуемая производная

Вынимаем константу для знака производной:

Производная косинуса равна минус синус того же аргумента, и поскольку аргумент является более сложным выражением, чем просто х, то мы умножаем все на производную от аргумента. То есть, мы имеем:

Производная от разности равна разности производных:

С первой производной, согласно правилу дифференцирования, мы помещаем три знака производной, а производная от 7 равна нулю как производная от константы:

Производная от независимой переменной х равна единице, поэтому, наконец, мы имеем

Ответ

ПРИМЕР 2

Задача

Найти производную функции

Решение

Требуемая производная

Производная натурального логарифма равна единице, деленной на сублогарифмическую функцию:

Производная косинуса равна минус синус:

В соответствии с тригонометрическими формулами отношение синуса к косинусу равно тангенсу:

Ответ

sciterm.ru

Производная косинуса — cos x

Производная по переменной x от косинуса x равна минус синусу x:
( cos x )′ = – sin x.

Доказательство

Чтобы вывести формулу производной косинуса, воспользуемся определением производной:
.

Преобразуем это выражение, чтобы свести его к известным математическим законам и правилам. Для этого нам нужно знать четыре свойства.
1) Тригонометрические формулы. Нам понадобится следующая формула:
(1)   ;
2) Свойство непрерывности функции синус:
(2)   ;
3) Значение первого замечательного предела:
(3)   ;
4) Свойство предела от произведения двух функций:
Если    и  , то
(4)   .

Применяем эти законы к нашему пределу. Сначала преобразуем алгебраическое выражение
.
Для этого применим формулу
(1)   ;
В нашем случае
; . Тогда
;
;
;
.

Сделаем подстановку . При , . Используем свойство непрерывности (2):
.

Сделаем такую же подстановку и применим первый замечательный предел (3):
.

Поскольку пределы, вычисленные выше, существуют, то применяем свойство (4):

.

Тем самым мы получили формулу производной косинуса.

Примеры

Рассмотрим простые примеры нахождения производных от функций, содержащих косинус. Найдем производные от следующих функций:
y = cos 2x;   y = cos 3x;   y = cos nx;   y = cos ² x;     y = cos ³ x   и   y = cos ⁿ x.

Пример 1

Найти производные от cos 2x, cos 3x и cos nx.

Решение

Исходные функции имеют похожий вид. Поэтому мы найдем производную от функции y = cos nx. Затем, в производную от cos nx, подставим n = 2 и n = 3. И, тем самым, получим формулы для производных от cos 2x и cos 3x.

Итак, находим производную от функции
y = cos nx.
Представим эту функцию от переменной x как сложную функцию, состоящую из двух функций:
1)   Функции , зависящей от переменной : ;
2)   Функции , зависящей от переменной : .
Тогда исходная функция является сложной (составной) функцией, составленной из функций и :
.

Найдем производную от функции по переменной x:
.
Найдем производную от функции по переменной :
.
Применяем формулу производной сложной функции.
.
Подставим :
(П1)   .

Теперь, в формулу (П1) подставим и :
;
.

Ответ

;
;
.

См. также
Все примеры вычисления производных с решениями > > >

Пример 2

Найти производные от косинуса в квадрате, косинуса в кубе и косинуса в степени n:
y = cos ² x;   y = cos ³ x;   y = cos ⁿ x.

Решение

В этом примере также функции имеют похожий вид. Поэтому мы найдем производную от самой общей функции – косинуса в степени n:
y = cos ⁿ x.
Затем подставим n = 2 и n = 3. И, тем самым, получим формулы для производных от косинуса в квадрате и косинуса в кубе.

Итак, нам нужно найти производную от функции
.
Перепишем ее в более понятном виде:
.
Представим эту функцию как сложную функцию, состоящую из двух функций:
1)   Функции , зависящей от переменной : ;
2)   Функции , зависящей от переменной : .
Тогда исходная функция является сложной функцией, составленной из двух функций и :
.

Находим производную от функции по переменной x:
.
Находим производную от функции по переменной :
.
Применяем правило дифференцирования сложной функции.
.
Подставим :
(П2)   .

Теперь подставим и :
;
.

Далее мы можем применить формулу для произведения синуса и косинуса:
.
Тогда
.

Ответ

;
;
.

Производные высших порядков

Заметим, что производную от cos x первого порядка можно выразить через косинус следующим образом:
.

Найдем производную второго порядка, используя формулу производной сложной функции:

.
Здесь  .

Заметим, что дифференцирование cos x приводит к увеличению его аргумента на . Тогда производная n-го порядка имеет вид:
(5)   .

Более строго эту формулу можно доказать с помощью метода математической индукции. Доказательство для n-й производной синуса изложено на странице “Производная синуса”. Для n-й производной косинуса доказательство точно такое. Нужно только во всех формулах заменить sin на cos.

Автор: Олег Одинцов.     Опубликовано: 05-03-2017

1cov-edu.ru

Производная от синуса

Производная от синуса x получается путём стандартной процедуры для вывода производных, а именно, функция $y$, равная $\sin x$ рассматривается как функция $f$ от икс: $f(x)= \sin x$. Рассмотрим функцию $y$ в точке $x$, придав ей приращение, равное $Δx$:

$f(x+ Δx)=\sin(x + Δx)$;

Напишем, чему равно приращение $Δy$ в этом случае:

$Δy=f(x + Δx) — f(x)=\sin(x + Δx)-\sin x\left(1\right)$

Вспомним формулу разности синусов, она выглядит следующим образом:

$\sin α — \sin β = 2 \sin \frac{α-β}{2} \cdot \cos{α + β}$

Применим её для преобразования полученного нами ранее равенства $(1)$:

$\sin(x + Δx)-\sin x=2\sin x \frac{ (x + Δx)-x}{2} \cdot \cos \frac{ (x + Δx)-x}{2} = 2 \sin \frac{Δx}{2} \cdot \cos \frac{2x+Δx}{2}=2 \sin \frac{ Δx}{2} \cos(x+\frac{Δx}{2})$.

Теперь рассмотрим, чему равно отношение приращения $y$ к приращению $x$:

$\frac{Δy}{Δx}=\frac{2 \sin \frac{Δx}{2} \cos(x+\frac{Δx}{2})}{Δx}\left(2\right)$.

Обозначим дробь $\frac{Δx}{2}$ за новую переменную, назовём её $a$ и перепишем выражение $(2)$ с её использованием:

$\frac{Δy}{Δx}=\frac{\sin a \cos (x+a)}{a}\left(2\right)$.

Определим, чему равен предел выражения $(3)$ при $Δx \to 0$:

$\lim_{Δx \to 0} \frac{Δy}{Δx}=\lim_{Δx \to 0}\frac{\sin a \cos (x+a)}{a}\left(3\right)$.

Так как $Δx \to 0$, а $a$ есть не что иное, как $\frac{Δx}{2}$, то $a$ также стремится к нулю. Перепишем выражение $(3)$ в соответствии с этим:

$\lim_{a \to 0} \frac{Δy}{Δx}=\lim_{a \to 0} \frac{\sin a}{a} \cdot \lim_{a \to 0} \cos(x+a)$.

Первый предел в получившемся выражении равен единице, а второй, так как функция косинуса непрерывна, равен $\cos x$.

Таким образом, мы с вами вывели доказательство того, что производная от $\sin x$ равна косинусу

$(\sin x)’= \cos x$.

Пример 1

Найти, чему равны производные функций:

1. y=sin x+ 3

2. y=4sin x+ cos x.

Решение:

1. $ (\sin x+ 3)’=\cos x$

2. $(4sin x+ cosx)’=4\cos x — \sin x$

spravochnick.ru

Производная sin^2 x

Производная sin^2 х находится легко. Необходимо только иметь (или знать) таблицу значений производных от основных функций.
Итак, разберем функцию .
Такая функция называется сложной, потому что состоит она из нескольких функций, в данном случае из двух. Первая функция — степенная (функция в квадрате), а вторая — тригонометрическая (синус х).
Производная от сложной функции находится по определенной правилу:
Сначала находят производную от внешней функции (мы ее назвали первой), в нашем случае от степенной функции, а затем умножают полученное значение на производную от внутренней функции (у нас это вторая), в нашем случае тригонометрической функции.
Распишем аналитически выше проведенные размышления.

   

Производная найдена, но очевидно, что полученное значение можно несколько преобразовать. В результате вычисления производной мы получили значение, которое можно по формуле синуса двойного аргумента записать в следующем виде:

   

Итак, в результате вычислений производной от сложной функции получили:

   

Результат смотрится очень компактно по сравнению с тем, который получили при непосредственном вычислении.

ru.solverbook.com

Таблица производных (логарифм, синус, косинус, экспонента)

Таблица производных (логарифм, синус, косинус, экспонента)

Функция	Производная
const	0
x	1
x2	2x
x3	3x2
xn	nxn-1
ln(x)	1 x
loga(x)	1 xln(a)
ex	ex
ax	axln(a)
xx	(1+ln(x))xx
sin(x)	cos(x)
cos(x)	-sin(x)
tg(x)	1 cos2(x)
ctg(x)	-1 sin2(x)
arcsin(x)	1 √(1-x2)
arccos(x)	-1 √(1-x2)
arcctg(x)	1 1+x2
arcctg(x)	-1 1+x2
sh(x)	ch(x)
ch(x)	sh(x)

— версия для печати

---

Определение

Производная — предел отношения приращения функции функции к приращению аргумента в той же точке. Или, равносильное определение, – предел секущей к графику функции в точке. Либо, формулой:

lim x→x0

f(x) − f(x0) x − x0

Свойства

1. (af+bg)’ = af’+bg’ – производная суммы с коэффициентами (a, b – постоянные).
2. (fg)’ = f’g+g’f – производная произведения.
3. (f/g)’ = (f’g − g’f)/g² – производная частного (g(x) ≠ 0).
4. f(g(x))_x‘ = f’_u(g(x))g_x‘ – производная сложной функции (знак внизу есть переменная, по которой вычисляется производная).

Если у вас есть мысли по поводу данной страницы или предложение по созданию математической (см. раздел «Математика») вспомогательной памятки, мы обязательно рассмотрим ваше предложение. Просто воспользуйтесь обратной связью.

© Школяр. Математика (при поддержке «Ветвистого древа») 2009—2016

scolaire.ru