Таблица производных и интегралов
Таблица производных. Табличные производные.
Производная степенной функции
Производная степенной функции
Производная экспоненциальной функции
Производная экспоненты
Производная сложной экспоненциальной функции
Производная экспоненциальной функции
Производная логарифмической функции
Производная натурального логарифма
Производная натурального логарифма функции
Производная синуса
Производная косинуса
Производная косеканса
Производная секанса
Производная арксинуса
Производная арккосинуса
Производная арксинуса
Производная арккосинуса
Производная тангенса
Производная котангенса
Производная арктангенса
Производная арккотангенса
Производная арктангенса
Производная арккотангенса
Производная арксеканса
Производная арккосеканса
Производная арксеканса
Производная арккосеканса
Производная гиперболического синуса
Производная гиперболического косинуса
Производная гиперболического тангенса
Производная гиперболического котангенса
Производная гиперболического секанса
Производная гиперболического косеканса
Таблица первообразных («интегралов»). Табличные неопределенные интегралы. (Простейшие интегралы и интегралы с параметром).
Интеграл степенной функции.
Интеграл степенной функции.
Интеграл, сводящийся к интегралу степенной функции, если загнать х под знак диффференциала.
Интеграл экспоненциальной функции.
Интеграл экспоненты, где a-постоянное число.
Интеграл сложной экспоненциальной функции.
Интеграл экспоненциальной функции.
Интеграл, равняющийся натуральному логорифму.
Интеграл : «Длинный логарифм».
Интеграл : «Длинный логарифм».
Интеграл : «Высокий логарифм».
Интеграл, где х в числителе заводится под знак дифференциала (константу под знаком можно как прибавлять, так и отнимать), в итоге схож с интегралом, равным натуральному логорифму.
Интеграл : «Высокий логарифм».
Интеграл косинуса.
Интеграл синуса.
Интеграл, равный тангенсу.
Интеграл, равный котангенсу.
Интеграл, равный как арксинусу, так и арккосинусу
Интеграл, равный как арктангенсу, так и арккотангенсу.
Интеграл, равный как арксинусу, так и арккосинусу.
Интеграл, равный как арктангенсу, так и арккотангенсу.
Интеграл равный косекансу.
Интеграл, равный секансу.
Интеграл, равный арксекансу.
Интеграл, равный арккосекансу.
Интеграл, равный арксекансу.
Интеграл, равный арксекансу.
Интеграл, равный гиперболическому синусу.
Интеграл, равный гиперболическому косинусу.
Интеграл, равный гиперболическому тангенсу.
Интеграл, равный гиперболическому котангенсу.
Интеграл, равный гиперболическому тангенсу.
Интеграл, равный гиперболическому котангенсу.
Интеграл, равный гиперболическому секансу.
Интеграл, равный гиперболическому косекансу.
studfiles.net
Найти производную y’ = f'(x) = (tanh(x))^(1/x) ((гиперболический тангенс от (х)) в степени (1 делить на х))
Решение
$$\tanh^{\frac{1}{x}}{\left (x \right )}$$
Подробное решение[LaTeX]
Не могу найти шаги в поиске этой производной.
Но производная
Ответ:
Первая производная[LaTeX]
/ 2 \
x _________ | log(tanh(x)) 1 - tanh (x)|
\/ tanh(x) *|- ------------ + ------------|
| 2 x*tanh(x) |
\ x /$$\left(\frac{- \tanh^{2}{\left (x \right )} + 1}{x \tanh{\left (x \right )}} — \frac{1}{x^{2}} \log{\left (\tanh{\left (x \right )} \right )}\right) \tanh^{\frac{1}{x}}{\left (x \right )}$$
Вторая производная[LaTeX]
/ 2 \
| / 2 \ |
| |log(tanh(x)) -1 + tanh (x)| 2 |
| |------------ + -------------| / 2 \ / 2 \|
x _________ | 2 \ x tanh(x) / \-1 + tanh (x)/ 2*log(tanh(x)) 2*\-1 + tanh (x)/|
\/ tanh(x) *|-2 + 2*tanh (x) + ------------------------------- - ---------------- + -------------- + -----------------|
| x 2 2 x*tanh(x) |
\ tanh (x) x /
-----------------------------------------------------------------------------------------------------------------------
x $$\frac{1}{x} \left(- \frac{\left(\tanh^{2}{\left (x \right )} — 1\right)^{2}}{\tanh^{2}{\left (x \right )}} + 2 \tanh^{2}{\left (x \right )} — 2 + \frac{1}{x} \left(\frac{\tanh^{2}{\left (x \right )} — 1}{\tanh{\left (x \right )}} + \frac{1}{x} \log{\left (\tanh{\left (x \right )} \right )}\right)^{2} + \frac{2 \tanh^{2}{\left (x \right )} — 2}{x \tanh{\left (x \right )}} + \frac{2}{x^{2}} \log{\left (\tanh{\left (x \right )} \right )}\right) \tanh^{\frac{1}{x}}{\left (x \right )}$$
Третья производная[LaTeX]
/ / 2 \ \
| 3 / 2 \ | / 2 \ / 2 \| |
|/ 2 \ |log(tanh(x)) -1 + tanh (x)| | 2 \-1 + tanh (x)/ 2*log(tanh(x)) 2*\-1 + tanh (x)/| |
||log(tanh(x)) -1 + tanh (x)| 2 3 2 3*|------------ + -------------|*|-2 + 2*tanh (x) - ---------------- + -------------- + -----------------| |
||------------ + -------------| / 2 \ / 2 \ / 2 \ / 2 \ \ x tanh(x) / | 2 2 x*tanh(x) | / 2 \|
x _________ |\ x tanh(x) / 4*\-1 + tanh (x)/ 2*\-1 + tanh (x)/ / 2 \ 6*\-1 + tanh (x)/ 6*log(tanh(x)) 3*\-1 + tanh (x)/ \ tanh (x) x / 6*\-1 + tanh (x)/|
-\/ tanh(x) *|------------------------------- - ------------------ + ------------------ + 4*\-1 + tanh (x)/*tanh(x) + ----------------- + -------------- - ------------------ + ---------------------------------------------------------------------------------------------------------- + -----------------|
| 2 tanh(x) 3 x 3 2 x 2 |
\ x tanh (x) x x*tanh (x) x *tanh(x) /
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
x $$- \frac{1}{x} \left(\frac{2 \left(\tanh^{2}{\left (x \right )} — 1\right)^{3}}{\tanh^{3}{\left (x \right )}} — \frac{4 \left(\tanh^{2}{\left (x \right )} — 1\right)^{2}}{\tanh{\left (x \right )}} + 4 \left(\tanh^{2}{\left (x \right )} — 1\right) \tanh{\left (x \right )} + \frac{3}{x} \left(\frac{\tanh^{2}{\left (x \right )} — 1}{\tanh{\left (x \right )}} + \frac{1}{x} \log{\left (\tanh{\left (x \right )} \right )}\right) \left(- \frac{\left(\tanh^{2}{\left (x \right )} — 1\right)^{2}}{\tanh^{2}{\left (x \right )}} + 2 \tanh^{2}{\left (x \right )} — 2 + \frac{2 \tanh^{2}{\left (x \right )} — 2}{x \tanh{\left (x \right )}} + \frac{2}{x^{2}} \log{\left (\tanh{\left (x \right )} \right )}\right) — \frac{3 \left(\tanh^{2}{\left (x \right )} — 1\right)^{2}}{x \tanh^{2}{\left (x \right )}} + \frac{1}{x} \left(6 \tanh^{2}{\left (x \right )} — 6\right) + \frac{1}{x^{2}} \left(\frac{\tanh^{2}{\left (x \right )} — 1}{\tanh{\left (x \right )}} + \frac{1}{x} \log{\left (\tanh{\left (x \right )} \right )}\right)^{3} + \frac{6 \tanh^{2}{\left (x \right )} — 6}{x^{2} \tanh{\left (x \right )}} + \frac{6}{x^{3}} \log{\left (\tanh{\left (x \right )} \right )}\right) \tanh^{\frac{1}{x}}{\left (x \right )}$$
www.kontrolnaya-rabota.ru
Основные свойства гиперболического тангенса — Мегаобучалка
Показательные и логарифмические выражения
Показательная функция, гиперболические функции
Показательной функциейназывается функция
,где .
Основные свойства показательной функции.
1. Область определения: .
2. Множество значений: .
3. Четность и нечетность: не обладает свойством четности.
4. Периодичность: не периодическая.
5. Нули функции: нулей не имеет.
6. Промежутки знакопостоянства:функция положительна для .
7. Наибольшее и наименьшее значения: наибольшего и наименьшего значений функция не имеет.
8. Промежутки возрастания и убывания: если функция возрастает для всех ; если –убывает для .
9. Точки пересечения с осями координат: пересекает ось Оу в точке , ось не пересекает.
10. Асимптоты: прямая y = 0 (ось ) является горизонтальной асимптотой.
11. График функции дляa > 1 изображен на рисунке 1, для –на рис. 2.
Из свойств функции следует: неравенство равносильно неравенству:
1) , если ,
2) , если .
Показательная функция с основанием , где иррациональное число , называется экспонентой, пишут или .
Через показательные выражения с основанием определяются гиперболические функции.
Гиперболическим синусом называется функция
.
Основные свойства гиперболического синуса.
1. Область определения: .
2. Множество значений: .
3. Четность и нечетность: нечётная.
4. Периодичность: не периодическая.
5. Нули функции: .
6. Промежутки знакопостоянства:функция отрицательна для , положительна – для .
7. Наибольшее и наименьшее значения: наибольшего и наименьшего значений функция не имеет.
8. Промежутки возрастания и убывания: функция возрастает для всех .
9. Точки пересечения с осями координат: .
10. Асимптоты: асимптот не имеет.
11. График функции изображен на рисунке 3.
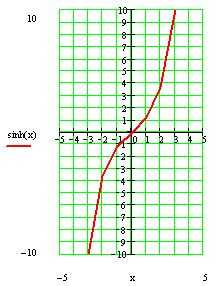
Рис. 3.
Гиперболическим косинусом называется функция
Основные свойства гиперболического косинуса.
1. Область определения: .
2. Множество значений: .
3. Четность и нечетность: чётная.
4. Периодичность: не периодическая.
5. Нули функции: нулей не имеет.
6. Промежутки знакопостоянства:функция положительна для .
7. Наибольшее и наименьшее значения: наименьшее значение, равное 1, функция принимает при .
8. Промежутки возрастания и убывания: функция убывает при ; возрастает – при .
9. Точки пересечения с осями координат: пересекает ось в точке , ось не пересекает.
10. Асимптоты: асимптот не имеет.
11. График функции изображен на рисунке 4.
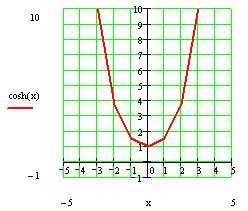
Рис. 4.
Гиперболические тангенс и котангенс определяются через отношение гиперболического синус и косинуса.
Гиперболического тангенсом
называется функция,
.
Основные свойства гиперболического тангенса.
1. Область определения: .
2. Множество значений: .
3. Четность и нечетность: нечётная.
4. Периодичность: не периодическая.
5. Нули функции: .
6. Промежутки знакопостоянства:функция отрицательна для ; положительна – для .
7. Наибольшее и наименьшее значения: наибольшего и наименьшего значений функция не имеет.
8. Промежутки возрастания и убывания: функция возрастает для .
9. Точки пересечения с осями координат: .
10. Асимптоты: имеет горизонтальные асимптоты и .
11. График функции изображен на рисунке 5.
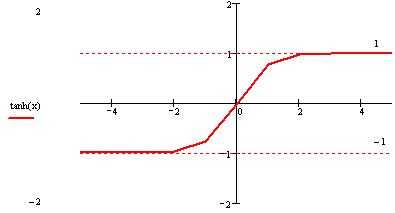
Рис. 5.
Гиперболический котангенсом
, т.е.
.
megaobuchalka.ru
Производная, правила дифференцирования, теоремы о среднем. Логарифмическое дифференцирование. Возрастание и убывание функции, экстремум функции
внутренняя точка, в которой касательная параллельна оси Ох.
Если, в частности, f′(a) = f′(b) = 0, то теорема Ролля означает, что между двумя корнями функции содержится хотя бы один корень ее производной.
Теорема Лагранжа. Если функция f(x) непрерывна на отрезке [a; b], дифференцируема в интервале (a; b), то в этом интервале (a; b) найдется хотя бы одно значение х = с, при котором выполняется равенство:
Геометрический смысл этой теоремы: на дуге АВ непрерывной кривой y = f(x), имеющей в каждой внутренней точке определенную касательную (не параллельную оси Оу), найдется хотя бы одна внутренняя точка, в которой касательная параллельна хорде АВ.
Теорема Коши. Если функции f(x) и g(x) непрерывны на отрезке [a; b] и дифференцируемы в интервале (a; b), причем g'(x) ≠ 0, то в этом интервале найдется хотя бы одно значение х = с, при котором , где a< с < b.
Производная сложной функции
Пусть y = f(u), u = u(x), тогда сложная функция имеет производную, равную , (т.е. производная сложной функции равна произведению производной данной функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной).
Производная обратной функции
Пусть у = f(х) и х = j(у) – взаимно обратные функции. Тогда, если функция у = f(х) имеет не равную нулю производную f ¢(х), то обратная функция имеет производную j¢(у) и или, .
Таблица производных основных элементарных функций:
1. | (C)’= 0 | 7. | |
2. | 8. | ||
В частности: | 9. | ||
10. | |||
3. | 11. | ||
4. | 12. | ||
5. | 13. | ||
6. | 14. |
производные гиперболических функций.
— гиперболический синус
— гиперболический косинус (цепная линия)
и — гиперболический тангенс и котангенс (e – неперово число).
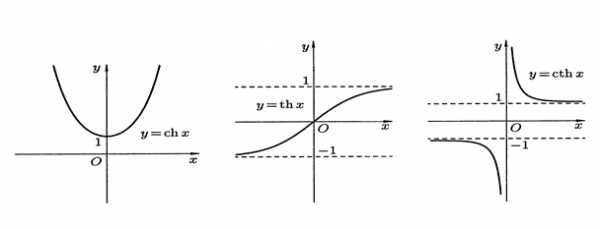
Свойства гиперболических функций:
1) ch2x – sh2x = 1;
2) sh
3) ch(x ± y) = chx·chy ± shx·shy;
4) ;
5) sh3x = 2·shx·chx;
6) ch3x = ch2x + sh2x.
Производные гиперболических функций:
(shx)′ = chx ; (chx)′ = shx ; (thx)′ = ; (cthx)′ = .
дифференциал функции.
Дифференциалом первого порядка функции y= f(x) в точке х называется главная часть приращения функции, равная произведению производной функции на приращение аргумента: dy = f ¢(x)×Dx.
Дифференциал функции вычисляется по формуле: .
Геометрический смысл дифференциала: дифференциал функции в точке х равен приращению ординаты касательной к графику функции в этой точке, когда х получает приращение Dx.
Инвариантная форма дифференциала 1-го порядка: , где y(u) – сложная функция.
Применение дифференциала для приближенных вычислений
Задача 1: Найти дифференциал функции
Дифференциал функции находится по формуле:
Найдем производную:
Тогда дифференциал функции: .
Задача 2: Вычислить приближенно с помощью дифференциалов arctg1,02.
Выбираем х0 = 1, т.к. эта точка ближайшая для 1,02 и значение функции в ней можно вычислить точно: f(x0) = arctg1 = .
Тогда x0 + Δx = 1,02 ÞΔx = 1,02 — 1 = 0,02
Þ
Подставляем в формулу: f (x0 + Δx) ≈
производная неявно заданной функции.
Под неявным заданием функциипонимают задание функции в виде F(x,y) = 0 не разрешенного относительно у.
Для нахождения производной неявно заданной функции нужно продифференцировать это уравнение по х, рассматривая при этом у как функцию х, и полученное затем уравнение разрешить относительно у′. Производная неявно заданной функции выражается через х и функцию у.
Задача 3: Найти производную функции .
Функция задана неявно, т.к. задана уравнением неразрешенным относительно у.
Дифференцируем обе части уравнения:
Выражаем у’:
логарифмическое дифференцирование.
Функция вида y = uv, где u и v – функции от х, называется степенно-показательной функцией.
Для нахождения производной степенно-показательной функции используется метод логарифмического дифференцирования.
Логарифмическое дифференцирование
1) прологарифмируем обе части уравнения функции:
2) дифференцируем обе части:
3) отсюда находим производную у′ :
, т.е. .
производные и дифференциалы высших порядков.
Производной n-го порядка от функции называется производная от производной (n–1)-го порядка .
Дифференциалом n-го порядка функции называется дифференциал от дифференциала (n-1)-го порядка , т.е.
Формула Лейбница
Производные высших порядков неявно заданных функций
Для того чтобы найти производную функции нужно продифференцировать обе части уравнения F(x; y) = 0 и выразить у‘. Затем дифференцируем по х первую производную и выразим . Подставив найденное значение у‘ в выражение второй производной, выразим через х и у.
Аналогично поступаем для нахождения производной 3-го порядка
vunivere.ru
