Высота треугольника Формула
Александр | 2018-02-19
Высота треугольника Формула. Здравствуйте! Также для вас здесь представлены формулы медианы и биссектрисы в треугольнике. Выражены указанные элементы через стороны треугольника.
Стоит отметить, что данные формулы используются при решении задач в курсе геометрии довольно редко. Всё-таки необходимость в них иногда возникает. Поэтому будет хорошо, если вы о их существовании будете знать, может быть и пригодится. Итак! Рассмотрим треугольник:
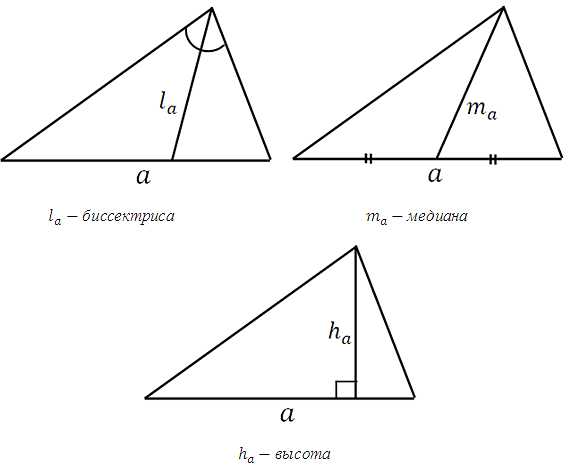
Формула медианы треугольника:
Формула биссектрисы треугольника:
Формула высоты треугольника:
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Категория: Формулы Теория | Формулы
Подготовка к ОГЭ по математике. Полный курс!
Школа репетиторов Анны Малковой!
Онлайн-обучение, подготовка к ЕГЭ и ОГЭ по предметам!
Замучили боль и скованность в мышцах спины?
*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.
matematikalegko.ru
Все формулы высоты прямого угла в прямоугольном треугольнике
В прямоугольном треугольнике катеты, являются высотами. Ортоцентр — точка пересечения высот, совпадает с вершиной прямого угла.
H — высота из прямого угла
a, b — катеты
с — гипотенуза
c1 , c2 — отрезки полученные от деления гипотенузы, высотой
α, β — углы при гипотенузе
Формула длины высоты через стороны, (H):
Формула длины высоты через гипотенузу и острые углы, (H):
Формула длины высоты через катет и угол, (H):
Формула длины высоты через составные отрезки гипотенузы , (H):
- Подробности
- Автор: Administrator
www-formula.ru
Элементы треугольника. Высота | Подготовка к ЕГЭ по математике
Категория: ПланиметрияСправочные материалы
Елена Репина 2013-04-16 2013-07-29Определение
Высотой треугольника называют перпендикуляр, опущенный из вершины треугольника на прямую, содержащую противолежащую сторону треугольника.
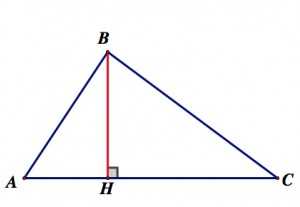
Свойства
1. Если треугольник остроугольный, то все основания высот принадлежат сторонам треугольника, а у тупоугольного треугольника две высоты попадают на продолжение сторон
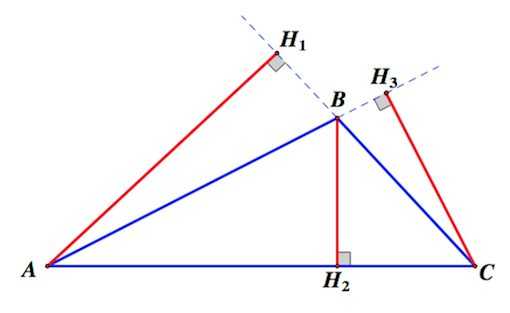
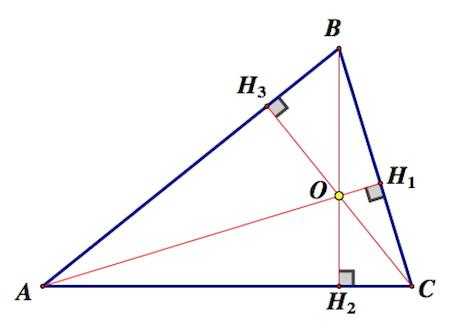
2. Высоты треугольника (или их продолжения) пересекаются в одной точке, называемой ортоцентром
3. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному
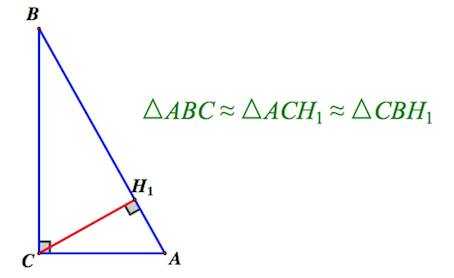
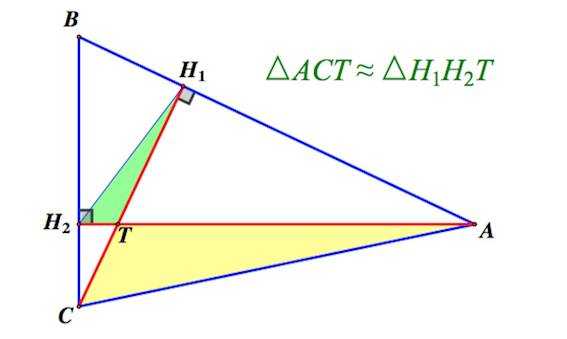
4. В остроугольном треугольнике две его высоты отсекают от него подобные треугольники
Некоторые формулы, связанные с высотой треугольника
где — площадь треугольника, — длина стороны треугольника, на которую опущена высота
- — высота в равностороннем треугольнике
Автор: egeMax | Нет комментариев
egemaximum.ru
Как определить высоту треугольника 🚩 определение высоты треугольника 🚩 Математика
Автор КакПросто!
Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону. Длину высоты можно определить двумя путями. Первый — из площади треугольника. Второй — рассматривая высоту как катет прямоугольного треугольника.

Статьи по теме:
Вам понадобится
- — ручка;
- — бумага для записей;
- — калькулятор.
Инструкция
Первый способ найти высоту – через площадь треугольника. Площадь треугольника вычисляется по формуле: S = 1/2 ah, где (a) – сторона треугольника, h – высота, построенная к стороне (а). Из этого выражения найдите высоту: h = 2S/a. Если в условии даны длины трех сторон треугольника, найдите площадь по формуле Герона: S = (p*(p-a)*(p-b)*(p-c))^1/2, где p – полупериметр треугольника; а, b, с – его стороны. Зная площадь, вы можете определить длину высоты к любой стороне. Например, в задаче указан периметр треугольника, в который вписана окружность с известным радиусом. Рассчитайте площадь из выражения: S = r*p, где r – радиус вписанной окружности; p – полупериметр. Из площади вычислите высоту к стороне, длина которой вам известна. Площадь треугольника также можно определить по формуле: S = 1/2ab*sina, где а, b – стороны треугольника; sina – синус угла между ними.Еще один случай – известны все углы треугольника и одна сторона. Используйте теорему синусов: a/sina = b/sinb = с/sinc = 2R, где a, b, c – стороны треугольника; sina, sinb, sinc – синусы углов, противолежащих этим сторонам; R – радиус окружности, которую можно описать вокруг треугольника. Найдите сторону b из соотношения: a/sina = b/sinb. Затем рассчитайте площадь аналогично шагу 4.
Второй способ вычислить высоту – применить тригонометрические зависимости для прямоугольного треугольника. Высота в остроугольном треугольнике делит его на два прямоугольных. Если известна сторона, противолежащая основанию (а), и угол между ними, примените выражение: h = b*sina. В формула немного меняется: h = b*sin(180-a) или h = — c*sina.
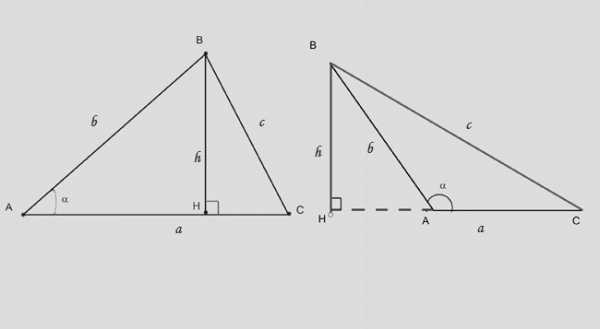
Если вам даны противолежащий высоте угол и длина отрезка AH, который высота отсекает от основания, используйте зависимость: BH = (AH)*tga.
Также, зная длины отрезка AH и стороны АВ, найдите высоту ВН из теоремы Пифагора: BH = (AB^2 – BC^2)^1/2.
Источники:
- найти наибольшую высоту треугольника
- Медианы, биссектрисы и высоты треугольника
Совет полезен?
Статьи по теме:
Не получили ответ на свой вопрос?
Спросите нашего эксперта:
www.kakprosto.ru
Высота прямоугольного треугольника | Треугольники
Высота прямоугольного треугольника, проведенная к гипотенузе, может быть найдена тем или иным способом в зависимости от данных в условии задачи.
Длина высоты прямоугольного треугольника, проведенной к гипотенузе, может быть найдена по формуле
или, в другой записи,
где BK и KC — проекции катетов на гипотенузу (отрезки, на которые высота делит гипотенузу).
Высоту, проведенную к гипотенузе, можно найти через площадь прямоугольного треугольника. Если применить формулу для нахождения площади треугольника
(половина произведения стороны на высоту, проведенную к этой стороне) к гипотенузе и высоте, проведенной к гипотенузе, получим:
Отсюда можем найти высоту как отношение удвоенной площади треугольника к длине гипотенузы:
Так как площадь прямоугольного треугольника равна половине произведения катетов:
То есть длина высоты, проведенной к гипотенузе, равна отношению произведения катетов к гипотенузе. Если обозначить длины катетов через a и b, длину гипотенузы — через с, формулу можно переписать в виде
Так как радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы, длину высоты можно выразить через катеты и радиус описанной окружности:
Поскольку проведенная к гипотенузе высота образует еще два прямоугольных треугольника, ее длину можно найти через соотношения в прямоугольном треугольнике.
Из прямоугольного треугольника ABK
Из прямоугольного треугольника ACK
Длину высоты прямоугольного треугольника можно выразить через длины катетов. Так как
по теореме Пифагора
Если возвести в квадрат обе части равенства:
можно получить еще одну формулу для связи высоты прямоугольного треугольника с катетами:
www.treugolniki.ru
Высота в прямоугольном треугольнике
Определение и формулы высоты в прямоугольном треугольнике
ОПРЕДЕЛЕНИЕ Высотой треугольника называется перпендикуляр, опущенный из вершины треугольника на противоположную сторону.В прямоугольном треугольнике высоты, опущенные из вершин острых углов, совпадают с катетами треугольника, а высота, опущенная из вершины прямого угла на гипотенузу, делит треугольник на два треугольника, подобных исходному и подобных друг другу.
Длина высоты треугольника (рис.1), проведенной к гипотенузе , находится по формуле
где и – проекции катетов на гипотенузу.
Площадь треугольника можно найти по формуле
Примеры решения задач
ПРИМЕР 1| Задание | В прямоугольном треугольнике высота делит гипотенузу на отрезки см и см. Найти катеты треугольника. |
| Решение | Найдем квадрат длины высоты пользуясь формулой
Рассмотрим прямоугольные треугольники и , и найдем в них стороны и : см см |
| Ответ | см см |
| Задание | В прямоугольном треугольнике катеты равны см и см. Найти высоту , опущенную на гипотенузу . |
| Решение | Пусть катет см, а см (рис. 2). Тогда по теореме Пифагора гипотенуза
см Площадь прямоугольного треугольника равна половине произведения катетов, т.е.
Высоту найдем по формуле
|
| Ответ | см |
Медиана в прямоугольном треугольнике
Равенство треугольников
Подобные треугольники
Соотношение между сторонами и углами треугольника
Центр окружности описанной около треугольника
ru.solverbook.com
