Расчет длины хорды окружности – Формула длины хорды окружности

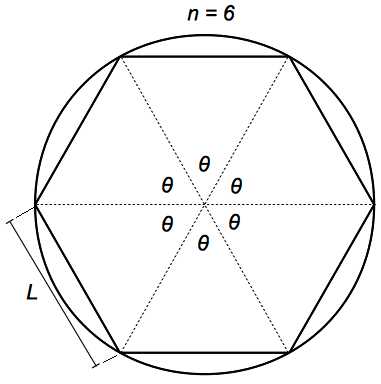
Длина хорды окружности

В элементарной геометрии хордой называют отрезок прямой линии, который соединяет две точки, лежащие на некоторой кривой (окружности, эллипсе, параболе). Хорда, которая проходит через центр окружности, называется ее диаметром.

Определение длины хорды окружности

 

 

Длина хорды окружности может быть определена по формуле:

L = 2r × sin ( α / 2 )

 

L – хорда

r – радиус окружности

O – центр окружности

α – центральный угол

 

Следует заметить, что такую величину, как длина хорды, инженерам, конструкторам различных машин и механизмов, а также архитекторам приходится вычислять не так уж и редко. Чаще всего этот параметр необходим для того, чтобы правильно сконструировать и разметить весьма распространенные в технике фланцевые соединения.

Основные их элементы, фланцы, представляют собой плоские кольца, на которых на одинаковом друг от друга расстоянии располагаются отверстия, куда устанавливаются резьбовые шпильки или болты. Фланцы используются для соединения между собой участков различных трубопроводов и валов, причем применяются они в большинстве случаев попарно. Для того чтобы определить, в каких именно местах при изготовлении этих деталей следует просверлить отверстия, необходимо знать, какова длина хорды окружности, проходящей через их центры. При этом имеется в виду та хорда, которая располагается между центрами соседних отверстий. Зная этот параметр, можно не только составить правильный чертеж, по которому в дальнейшем будут производиться фланцы, но и впоследствии проконтролировать точность их изготовления. С большой точностью определить такой параметр, как длина хорды, требуется и тогда, когда разрабатываются детали машин и механизмов, имеющих форму криволинейных скоб: именно он определяет расстояние между конечными точками этих изделий.

Важную роль длина хорды играет и в баллистике – науке, изучающей движение тел, брошенных в пространстве. Дело в том, что перемещаются они по эллиптической траектории, и для того чтобы определить такой параметр, как, скажем, расстояние по прямой, которое при тех или иных условиях преодолеет пуля или баллистическая ракета, требуется вычислить именно длину хорды. При этом специалистами используются достаточно сложные математические методы и формулы, учитывающие большое количество различных параметров, и для того, чтобы определить такую, казалось бы, простую величину, как длина хорды, в баллистике широко применяется современная высокопроизводительная вычислительная техника.

Что касается хорд в архитектуре, то их чаше всего можно встретить там, где используются различные сводчатые и арочные конструкции. Например, для того, чтобы точно рассчитать ширину дверного проема, верхняя часть которого выполнена в виде арки, требуется вычислить именно такой параметр, как длина хорды. При проектировании строений, которые увенчаны куполами (например, христианские храмы), архитекторам также в обязательном порядке нужно пользоваться

формулами расчета хорд для того, чтобы правильно определить параметры снования этих конструкций (например, требуемые их диаметры).

simple-math.ru

Формула высоты сегмента круга

---

Сегмент — часть круга ABC, отсеченная хордой AC

h —  высота сегмента ABC

L — хорда AC

R — радиус кружности

O — центр окружности

α — центральный угол AOC

 

Формула высоты через радиус и центральный угол, (h):

 

 

Формула высоты через хорду и центральный угол, (h):

 

Формула высоты через радиус и хорду, (h):

---

---

 

Дополнительные формулы для окружности:

Подробности

Автор: Administrator

Опубликовано: 16 октября 2011

Обновлено: 27 сентября 2017

www-formula.ru

Сегмент круга — расчет параметров онлайн

Данный калькулятор считает параметры сегмента круга, а именно:

Перед вами 2 калькулятора, чтобы рассчитать параметры сегмента:

1) сегмент круга решается с помощью радиуса (R) и угла (A).

2) сегмент круга находим с помощью высоты и длины хорды.

The field is not filled.

‘%1’ is not a valid e-mail address.

Please fill in this field.

The field must contain at least% 1 characters.

The value must not be longer than% 1 characters.

Field value does not coincide with the field ‘%1’

An invalid character. Valid characters:’%1′.

Expected number.

It is expected a positive number.

Expected integer.

It is expected a positive integer.

The value should be in the range of [%1 .. %2]

The ‘% 1’ is already present in the set of valid characters.

The field must be less than 1%.

The first character must be a letter of the Latin alphabet.

Su

Mo

Tu

We

Th

Fr

Sa

January

February

March

April

May

June

July

August

September

October

November

December

century

B.C.

%1 century

An error occurred while importing data on line% 1. Value: ‘%2’. Error: %3

Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).

%3.%2.%1%4

%3.%2.%1%4 %6:%7

s.sh.

u.sh.

v.d.

z.d.

yes

no

Wrong file format. Only the following formats: %1

Please leave your phone number and / or email.

hostciti.net

Таблица соотношений между длинами дуг, стрелками, длинами хорд, площадями сегментов при радиусе, равном единице.

	Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса  / / Таблица соотношений между длинами дуг, стрелками, длинами хорд, площадями сегментов при радиусе, равном единице. Таблица соотношений между длинами дуг, стрелками, длинами хорд, площадями сегментов при радиусе, равном единице. При пользовании таблицей при радиусах, не равных 1, следует: умножить l, h и C на величину радиуса, а площадь сегмента умножить на квадрат радиуса. При данной длине дуги l и стрелке h находим r=l:lo, где lo-длина дуги, соответствующая данному отношению l:h при r=1. Если r — радиус круга и α — центральный угол в градусах, то получаем: длина хорды C = 2*r* sin(α/2) = 2*(2*r*h—h2 )1/2 стрелка h = r*(1-cos( α/2)) = (c/2)*tg(α/4) = 2*r*sin2(α/4) = r-(r2—(c2/4))1/2 длина дуги l = π*r*(α/180o) = 0,017453*r*a ≈ (c2+(16/3)*h2)1/2 площадь сегмента = (r2/2)*((π/180o)*αo-sinα) Центральный угол в градусах Длина дуги l Стрелка h 1/h Длина хорды C Площадь сегмента 1 0,0175 0,0000 458,36 0,0175 0,00000 2 0,0349 0,0002 229,19 0,0349 0,00000 3 0,0524 0,0003 152,79 0,0524 0,00001

dpva.ru

Таблица соотношений между длинами дуг, стрелками, длинами хорд, площадями сегментов при радиусе, равном единице.

Таблица соотношений между длинами дуг, стрелками, длинами хорд, площадями сегментов при радиусе, равном единице. При пользовании таблицей при радиусах, не равных 1, следует умножить l, h и C на величину радиуса, а площадь сегмента умножить на квадрат радиуса. При данной длине дуги l и стрелке h находим r=l:lo, где lo-длина дуги, соответствующая данному отношению l:h при r=1. Если r — радиус круга и α — центральный угол в градусах, то получаем: длина хорды с = 2*r* sin(α/2) = 2*(2*r*h—h2 )1/2 стрелка h = r*(1-cos(α/2)) = (c/2)*tg(α/4) = 2*r*sin2(α/4) = r-(r2—(c2/4))1/2 длина дуги l = π*r*(α/180o) = 0,017453*r*a ≈ (c2+(16/3)*h2)1/2 площадь сегмента = (r2/2)*((π/180o)*αo-sinα) Центральный угол в градусах Длина дуги lo Стрелка h 1/h Длина хорды с Площадь сегмента 1 0,0175 0,0000 458,36 0,0175 0,00000 2 0,0349 0,0002 229,19 0,0349 0,00000 3 0,0524 0,0003 152,79 0,0524 0,00001 4 0,0698 0,0006 114,60 0,0698 0,00003 5 0,0873 0,0010 91,69 0,0872 0,00006 6 0,1047 0,0014 76,41 0,1047 0,00010 7 0,1222 0,0019 64,01 0,1221 0,00015 8 0,1396 0,0024 56,01 0,1395 0,00023 9 0,1571 0,0031 50,96 0,1569 0,00032 10 0,1749 0,0038 45,87 0,1743 0,00044 11 0,1920 0,0046 41,70 0,1917 0,00059 12 0,2094 0,0055 38,23 0,2091 0,00076 13 0,2269 0,0064 35,28 0,2264 0,00097 14 0,2443 0,0075 32,78 0,2437 0,00121 15 0,2618 0,0086 30,60 0,2611 0,00149 16 0,2793 0,0097 28,04 0,2783 0,00181 17 0,2967 0,0110 27,01 0,2956 0,00217 18 0,3142 0,0123 25,35 0,3219 0,00257 19 0,3316 0,0137 24,17 0,3301 0,00302 20 0,3491 0,0152 22,98 0,3473 0,00352 21 0,3665 0,0167 21,95 0,3645 0,00408 22 0,3840 0,0184 20,90 0,3816 0,00468 23 0,4014 0,0201 20,00 0,3987 0,00535 24 0,4189 0,0219 19,17 0,4158 0,00607 25 0,4363 0,0237 18,47 0,4329 0,00686 26 0,4538 0,0256 17,71 0,4499 0,00771 27 0,4712 0,0276 17,06 0,4669 0,00862 28 0,4887 0,0297 16,45 0,4838 0,00961 29 0,5061 0,0319 15,89 0,5008 0,01087 30 0,5236 0,0341 15,37 0,5176 0,01180 31 0,5411 0,0364 14,88 0,5345 0,01301 32 0,5585 0,0387 14,42 0,5513 0,01429 33 0,5760 0,0412 13,99 0,5680 0,01566 34 0,5934 0,0437 13,58 0,5847 0,01711 35 0,6109 0,0463 13,20 0,6014 0,01864 36 0,6283 0,0489 12,84 0,6180 0,02027 37 0,6458 0,0517 12,50 0,6346 0,02198 38 0,6632 0,0545 12,17 0,6511 0,02378 39 0,6807 0,0574 11,87 0,6676 0,02568 40 0,6981 0,0603 11,58 0,6840 0,02767 41 0,7156 0,0633 11,30 0,7004 0,02976 42 0,7330 0,0664 11,04 0,7167 0,03195 43 0,7505 0,0696 10,78 0,7330 0,03425 44 0,7679 0,0728 10,55 0,7492 0,03664 45 0,7854 0,0761 10,32 0,7654 0,03915 46 0,8029 0,0795 10,10 0,7815 0,04176 47 0,8203 0,0829 9,80 0,7975 0,04448 48 0,8378 0,0865 9,69 0,8135 0,04731 49 0,8552 0,0900 9,50 0,8294 0,05025 50 0,8727 0,0937 9,31 0,8452 0,05331 51 0,8901 0,0974 9,14 0,8610 0,05649 52 0,9076 0,1012 8,97 0,8767 0,05978 53 0,9250 0,1051 8,80 0,8924 0,06319 54 0,9425 0,1090 8,65 0,9080 0,06673 55 0,9599 0,1130 8,49 0,9235 0,07039 56 0,9774 0,1171 8,35 0,9389 0,07417 57 0,9948 0,1212 8,21 0,9543 0,07808 58 1,0123 0,1254 8,07 0,9696 0,08212 59 1,0297 0,1296 7,94 0,9848 0,08629 60 1,0472 0,1340 7,81 1,0000 0,09059 61 1,0647 0,1384 7,69 1,0151 0,09502 62 1,0821 0,1428 7,56 1,0301 0,09958 63 1,0996 0,1474 7,46 1,0450 0,10428 64 1,1170 0,1520 7,35 1,0598 0,10911 65 1,1345 0,1566 7,24 1,0746 0,11408 66 1,1519 0,1613 7,14 1,0893 0,11919 67 1,1694 0,1661 7,04 1,1039 0,12443 68 1,1868 0,1710 6,94 1,1184 0,12982 69 1,2043 0,1759 6,85 1,1328 0,13535 70 1,2217 0,1808 6,76 1,1472 0,14102 71 1,2392 0,1859 6,67 1,1614 0,14683 72 1,2566 0,1910 6,58 1,1756 0,15270 73 1,2741 0,1961 6,50 1,1896 0,15889 74 1,2915 0,2014 6,41 1,2036 0,15514 75 1,3090 0,2066 6,34 1,2175 0,17154 76 1,3265 0,2120 6,26 1,2312 0,17808 77 1,4339 0,2174 6,18 1,2450 0,18477 78 1,3614 0,2229 6,11 1,2586 0,19160 79 1,3788 0,2284 6,04 1,2722 0,19859 80 1,3963 0,2340 5,97 1,2856 0,20573 81 1,4137 0,2396 5,90 1,2989 0,21301 82 1,4312 0,2453 5,83 1,3221 0,22045 83 1,4486 0,2510 5,77 1,3252 0,22804 84 1,4661 0,2569 5,71 1,3383 0,23578 85 1,4735 0,2627 5,65 1,3512 0,24367 86 1,5010 0,2686 5,59 1,3640 0,25171 87 1,5184 0,2746 5,53 1,3767 0,25990 88 1,5359 0,2807 5,47 1,3893 0,26825 89 1,5553 0,2867 5,42 1,4018 0,27675 90 1,5708 0,2929 5,36 1,4142 0,28540 91 1,5882 0,2991 5,31 1,4265 0,29420 92 1,6057 0,3053 5,26 1,4387 0,30316 93 1,6232 0,3116 5,21 1,4507 0,31226 94 1,6406 0,3180 5,16 1,4627 0,32152 95 1,6580 0,3244 5,11 1,4746 0,33093 96 1,6755 0,3309 5,06 1,4863 0,34050 97 1,6930 0,3374 5,02 1,4979 0,35021 98 1,7104 0,3439 4,97 1,5094 0,36008 99 1,7279 0,3506 4,93 1,5208 0,37009 100 1,7453 0,3572 4,89 1,5321 0,38026 101 1,7628 0,3639 4,84 1,5432 0,39050 102 1,7802 0,3707 4,80 1,5543 0,40104 103 1,7977 0,3775 4,76 1,5652 0,41166 104 1,8151 0,3843 4,72 1,57,60 0,42242 105 1,8326 0,3912 4,68 1,5867 0,43333 106 1,8500 0,3982 4,65 1,5973 0,44439 107 1,8675 0,4052 4,61 1,6077 0,45560 108 1,8850 0,4122 4,57 1,6180 0,46695 109 1,9024 0,4193 4,54 1,6282 0,47845 110 1,9199 0,4264 4,50 1,6383 0,49008 111 1,9373 0,4336 4,47 1,6483 0,50187 112 1,9548 0,4408 4,43 1,6581 0,51379 113 1,9722 0,4481 4,40 1,6678 0,52586 114 1,9897 0,4554 4,37 1,6773 0,53807 115 2,0071 0,4627 4,34 1,6868 0,55041 116 2,0246 0,4701 4,31 1,6961 0,56389 117 2,0420 0,4775 4,28 1,7053 0,57551 118 2,0595 0,4850 4,25 1,7143 0,58827 119 2,0769 0,4925 4,22 1,7233 0,60116 120 2,0944 0,5000 4,19 1,7321 0,61418 121 2,1118 0,5076 4,16 1,7407 0,62734 122 2,1293 0,5152 4,13 1,7492 0,64063 123 2,1468 0,5228 4,11 1,7576 0,65404 124 2,1642 0,5305 4,08 1,7659 0,66759 125 2,1817 0,5387 4,05 1,7740 0,68125 126 2,1991 0,5460 4,03 1,7820 0,69505 127 2,2166 0,5538 4,00 1,7899 0,70897 128 2,2340 0,5616 3,98 1,7976 0,72301 129 2,2515 0,5695 3,95 1,8052 0,73716 130 2,2689 0,5774 3,93 1,8126 0,75144 131 2,2864 0,5853 3,91 1,8199 0,76584 132 2,3038 0,5933 3,88 1,8277 0,78034 133 2,3213 0,6013 3,86 1,8341 0,79497 134 2,3387 0,6093 3,84 1,8410 0,80970 135 2,3562 0,6173 3,82 1,8478 0,82454 136 2,3736 0,6254 3,80 1,8545 0,83949 137 2,3911 0,6335 3,77 1,8608 0,85455 138 2,4086 0,6416 3,75 1,8672 0,86971 139 2,4160 0,6498 3,73 1,8733 0,88497 140 2,4435 0,6580 3,71 1,8794 0,90034 141 2,4609 0,6662 3,69 1,8853 0,91580 142 2,4784 0,6744 3,67 1,8910 0,93135 143 2,4958 0,6827 3,66 1,8966 0,94700 144 2,5133 0,2910 3,64 1,9021 0,96274 145 2,5307 0,6993 3,62 1,9074 0,97858 146 2,5482 0,7076 3,60 1,9126 0,99449 147 2,5656 0,7160 3,58 1,9176 1,01050 148 2,5831 0,7244 3,57 1,9225 1,02658 149 2,6005 0,7328 3,55 1,9273 1,04275 150 2,6180 0,7412 3,53 1,9319 1,05900 151 2,6354 0,7496 3,52 1,9363 1,07532 152 2,6429 0,7581 3,50 1,9406 1,09171 153 2,6704 0,7666 3,48 1,9447 1,10818 154 2,6878 0,7750 3,47 1,9487 1,12472 155 2,7053 0,7836 3,45 1,9526 1,14132 156 2,7227 0,7921 3,44 1,9563 1,15799 157 2,7402 0,8006 3,42 1,9598 1,17472 158 2,7576 0,8092 3,41 1,9633 1,19151 159 2,7752 0,8178 3,39 1,9665 1,20835 160 2,7925 0,8264 3,38 1,9696 1,22525 161 2,8100 0,8350 3,37 1,9726 1,24221 162 2,8274 0,8436 3,35 1,9754 1,25921 163 2,8449 0,8522 3,34 1,9780 1,27626 164 2,8623 0,8608 3,33 1,9805 1,29335 165 2,8798 0,8695 3,31 1,9829 1,31049 166 2,8972 0,8781 3,30 1,9851 1,32766 167 2,9147 0,8868 3,28 1,9871 1,34487 168 2,9322 0,8955 3,27 1,9890 1,36212 169 2,9496 0,9042 3,26 1,9908 1,37940 170 2,9671 0,9128 3,25 1,9924 1,39671 171 2,9845 0,9215 3,24 1,9938 1,41404 172 3,0020 0,9302 3,23 1,9951 1,43140 173 3,0194 0,9390 3,22 1,9963 1,44878 174 3,0369 0,9477 3,20 1,9973 1,46617 175 3,0543 0,9564 3,19 1,9981 1,48359 176 3,0718 0,9651 3,18 1,9988 1,50101 177 3,0892 0,9738 3,17 1,9993 1,51845 178 3,1067 0,9825 3,16 1,9997 1,53589 179 3,1241 0,9913 3,15 1,9999 1,55334 180 3,1416 1,0000 3,14 2,0000 1,57080 Пример 1. Вычислить радиус окружности, у которой при стрелке h=2 мм длина дуги l=10 мм. Находим l/h=10/2=5. Из таблицы определяем lo≈ 1,6930, r=l/ lo=10/1,6930=5,9 мм. Пример 2. Вычислить стрелку h дуги окружности радиусом r=50 мм при центральном угле α=30o Из таблицы находим h=0,0341*50=1,705 мм.

tehtab.ru

Длина хорды, центральный угол в ° (угловых градусах) и радианах при делении окружности единичного диаметра на равные сегменты.

Адрес этой страницы (вложенность) в справочнике dpva.ru:  главная страница  / / Техническая информация / / Математический справочник / / Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Треугольники, Прямоугольники и т.д. Градусы в радианы. / / Плоские фигуры. Свойства, стороны, углы, признаки, периметры, равенства, подобия, хорды, секторы, площади и т.д.  / / Длина хорды, центральный угол в ° (угловых градусах) и радианах при делении окружности единичного диаметра на равные сегменты. Длина хорды, центральный угол в ° (угловых градусах) и радианах при делении окружности единичного диаметра на равные сегменты. Опа-на! Не путаем диаметр и радиус! Длину хорды при делении круга / окружности на равные сегменты вы можете посчитать используя таблицу ниже. Например. Для окружности с диаметром = 4м (радиусом = 2м) надо найти длину хорды при делении на 5 равных сегментов. Берем значение L для n равного 5 и умножаем на 4 м. Ответ:0,587785*4м = 2,351141м Число сегментов n Длина одной хорды L Суммарная длина хорд, L*n 3 120,0000 2,094395 0,866025 2,598076 4 90,0000 1,570796 0,707107 2,828427 5 72,0000 1,256637 0,587785 2,938926 6 60,0000 1,047198 0,500000 3,000000 7 51,4286 0,897598 0,433884 3,037186 8 45,0000 0,785398 0,382683 3,061467 9 40,0000 0,698132 0,342020 3,078181 10 36,0000 0,628319 0,309017 3,090170 11 32,7273 0,571199 0,281733 3,099058 12 30,0000 0,523599 0,258819 3,105829 13 27,6923 0,483322 0,239316 3,111104 14 25,7143 0,448799 0,222521

dpva.ru

Как найти длину хорды окружности

Чтобы разобраться, как найти длину хорды окружности, сначала вспомним — что такое хорда.
Хордой называют отрезок, который соединяет две произвольные точки, расположенные на окружности.
Диаметр также можно назвать хордой, причем самой большой длины для заданной окружности. Отличие диаметра от всех других хорд в окружности в том, что он проходит через ее центр.

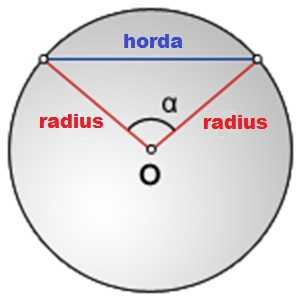
Рассмотрим формулу для вычисления длины хорды:

   

Задача.
Найти длину хорды окружности с радиусом 15 см, если угол между хордой и радиусом равен 45 градусов.

Решение.
Построим окружность с центром в точке О. Проведем в ней хорду АВ и радиусы ОА и ОВ к концам этой хорды.
Треугольник АОВ — равнобедренный с равными сторонами ОА и ОВ (равны длине радиуса):
АО = ВО = radius = 15 см.
Следовательно, углы при основании АВ этого треугольника равны:
Угол ОАВ = ОВА = 45 градусов.
Поскольку сумма углов любого треугольника равна т180 градусов, то:
Угол АОВ = 180 — (ОАВ + ОВА) = 180 — (45 + 45) = 180 — 90 = 90 градусов.
Подставим известные значения в формулу для дины хорды:

   

   

   

   

(см)

Ответ. (см).

ru.solverbook.com

No related posts.