Решение алгебраических: Mathway | Решение химических задач

Содержание

Решение алгебраических уравнений методом эйткена-никипорца Текст научной статьи по специальности «Математика»

ФИЗИКО-МАТЕМАТИЧЕСКИЕ НАУКИ

«НАУКА. ИННОВАЦИИ. ТЕХНОЛОГИИ», № 3, 2014

удк 517.524 Шмойлов В. И. [Shmoylov V. I. ],

Селянкин В. В. [Selyankin V. V.], Кириченко Г. А. [Kirichenko G. A.]

решение алгебраических уравнений методом эйткена-никипорца

Solution of algebraic equations by the method of Aitken-Nikiports

Приводятся аналитические выражения, представляющие все корни произвольного алгебраического уравнения n-й степени через коэффициенты исходного уравнения. Эти формулы состоят из двух отношений бесконечных определителей Теплица, диагональными элементами которых являются коэффициенты алгебраического уравнения.

Такие конструкции были названы непрерывными дробями Никипорца. Для эффективного вычисления значений непрерывных дробей Никипорца используется рекуррентный алгоритм Рутисхаузера. При нахождении корней полинома применяется алгоритм суммирования расходящихся непрерывных дробей (r/ф-алгоритм). Комплексные корни определяются из рассмотрения значений длинной серии подходящих непрерывных дробей. В качестве примера рассмотрено решение алгебраического уравнения 25-й степени.

Ключевые слова: алгебраические уравнения, бесконечные определители Теплица, расходящиеся непрерывные дроби, r/ф-алгоритм.

Presents analytical expressions representing all the roots of a random algebraic equation of the n-th degree through the ratio of the original equation. These formulas consist of two relations infinite Toeplitz determinants, diagonal elements of which are the coefficients of the algebraic equation.

-algorithm.

Введение

Известны разнообразные применения алгебраических уравнений при решении научных и технических задач. Часто алгебраические уравнения появляются в задачах аэродинамики. При расчете устойчивости различных конструкций используют так называемые собственные значения матриц, определяемые из решения алгебраических уравнений, степень которых равна количеству учитываемых гар-

моник. Особенно часто алгебраические уравнения возникают при выполнении различных геометрических расчетов, в частности, при определении точек пересечения и сопряжения криволинейных контуров. Разным аспектам теории и практики алгебраических уравнений посвящены недавно опубликованные монографии [1, 2]. Тем не менее, актуальной является оценка ситуации в разделе математики, которая была дана известным американским специалистом Р. Хеммингом [3]: «Задача нахождения корней многочленов возникает достаточно часто для того, чтобы оправдать тщательное изучение и разработку специальных методов ее решения.

Различным методам нахождения действительных линейных и квадратичных множителей можно посвятить целую книгу. Тот факт, что существует так много методов, показывает, что не сущес -твует ни одного вполне удовлетворительного». В самом деле, известно более сотни алгоритмов и их модификаций, которые используются для нахождения нулей полиномов [4, 5]. В основном, это алгоритмы численного решения алгебраических уравнений.

Ниже будут рассмотрены аналитические выражения, представляющие все корни произвольного алгебраического уравнения п-й степени через коэффициенты исходного уравнения. Эти формулы состоят из двух отношений бесконечных определителей Теплица, диагональными элементами которых являются коэффициенты алгебраического уравнения. Для нахождения комплексных корней дополнительно используется метод суммирования расходящихся непрерывных дробей, именуемый как г/ф-алгоритм [6], нашедший разнообразные применения в вычислительной математике [7-11].

1. Постановка задачи

Имеется алгебраическое уравнение степени п:

х» +а,хп 1 +…+«„_,х + а„ = 0

л-1

(1.1)

Запишем следующую производящую функцию

= 1 + схх + с2х2 +… + стхт +…. (1.2)

1 + ахх + агхг +… + апх

ФИЗИКО-МАТЕМАТИЧЕСКИЕ НАУКИ

_ Решение алгебраических уравнений методом эйткена-никипорца

Коэффициенты ai в (1. 1) и (1.2) совпадают. Коэффициенты ст последовательности (1.2) могут быть найдены из линейного рекуррентного уравнения

Ст = ~(а1Ст-1 + а2Ст-2 + «• + «/„,-„), ¿0 =1 С1 = ««Г (13)

Для определения корней алгебраического уравнения (1.1) Эйткен предложил формулы [12]:

х, — Нт

т >х: Л

т+1

(14)

Ит

т->оо

Ст+1 Ст+2

Ст+2 Ст+3 .Ст+1

Ст Ст+1 С т

Ст+1 Ст+2

л;,

(15)

Нт

т—> оо

Ст+1 Ст+2 Ст+3

Ст+2 Ст+3 Ст+4 Ст+1 Ст+2

Ст+3 Ст+4 Ст+5 Ст+2 Ст+3

С т Ст+1 Ст+2 С т Ст+1

Ст+1 Ст+2 Ст+3 Ст+1 Ст+2

Ст+2 Си+3 Ст+4

Х^Х^Х^

(1. 6)

Корень xi может быть представлен выражением:

хп = Ит

т-> оо

Ст+1 Сш+2 ‘ • Ст+1 Ст+1 Ст+2 • • Ст+1-1

Ст+2 Ст+3 ‘ • Ст+|’+1 Ст+2 Ст+3 ‘ • Ст+<

Ст+1 Ст+г+1 ‘ • Ст+21-1 Ст+г-1 С7я+; • • Ст+2;-3

С т Ст+1 » • Ст+л-1 Ст+1 » Ст+<-2

Ст+1 Ст+2 • • Ст+п Ст+1 Ст+2 » Ст+!-1

Ст+1-1 Ст+г » • Ст+21-2 Ст+1-2 Ст+г-1 ■• Ст+21-4

Очевидно, что используя формулы Эйткена можно непосредственно находить только действительные корни алгебраического уравнения (1. 1). Применим г/ф-алгоритм к определению комплексных корней алгебраического уравнения (1.1).

2. Представление нулей полинома

Запишем формулы Эйткена (1.4) — (1.7) в развернутом виде. В результате преобразований получим конструкции из отношений определителей матриц Теплица, диагональными элементами которых являются коэффициенты исходного уравнения (1.1).

Формулу (1.4) можно представить отношением определителей:

х, — ■

~а1 -а2 — «з -«4 ••• -1 -«1 — а2 — аъ

-1 -а1 -а2 -аъ … 0 -1 -а! -а2

0 -1 -«1 -а2 … 0 0 -1 -«1

0 0 -1 -«! … 0 0 0 -1

-«1 -а2 — а3 .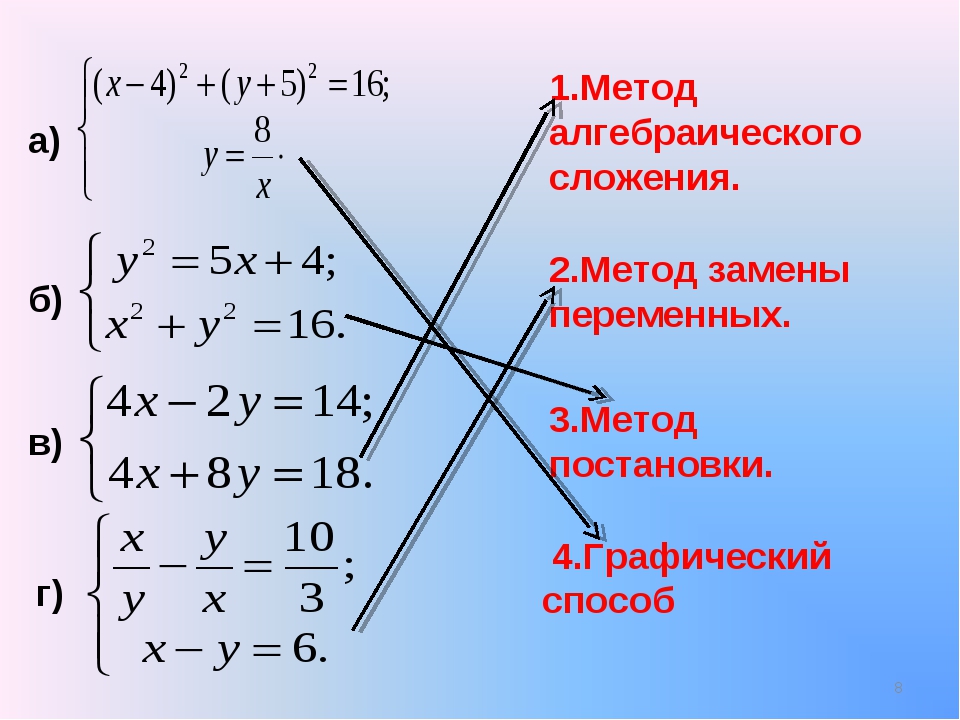 .. -1 -«1 -а2

-1 -ах -а2 … 0 -1 -а!

0 -1 -а! … 0 0 -1

(2.1)

Последующие корни уравнения (1.1) запишутся следующим образом:

х, = —

-а2 -аъ -«4 -а5 … -«1 -а2 — аъ -«4

-а! -а2 -аъ -а4 … -1 -а! -«2 — «з

-1 -а2 — аъ … 0 -1 -а2

0 -1 -а! -а2 … 0 0 -1 -«1

-а2 -«з -а4 … -«1 -а2 -«з

-«1 — а2 -«з … -1 -«1 -а2

-1 -«1 -«2 ••• 0 -1 -«1

(2. 2)

-а,_2 -ам -а, -ам

-а,_ 2 -ам -а, -а,+1

-а,_3 -«,-2 -а,

-а,_2 -«м -а,

х.

(2.3)

-а,_2 -ан -а,

-«м -а,

-«¡-з -«,-2 -«м

Отношения определителей (2.1) — (2.3), выражающие корни алгебраического уравнения (1.1) через его коэффициенты, будем называть функциями N(«). Для функций N1-«» введём обозначение:

уравнений степени выше четвёртой функции N(«) записываются аналогично их записи для алгебраических уравнений степени 2, 3 и 4. «), определяемые выражениями (2.1) — (2.3) будем называть также непрерывными дробями Никипорца. Определение математических конструкций (2.1) — (2.3), как непрерывных дробей особой структуры позволяет естественно ввести такое фундаментальное понятие, как подходящая дробь, что упрощает описание способа решения алгебраических уравнений с использованием функций Ж(«) и г/ф-алгоритма.

Для нахождения комплексных корней уравнения (1.1), определяемых также формулами (2.1) — (2.3), необходимо дополнительно использовать г/ф-алгоритм. Модуль г и модуль аргумента х( — г{е 1<р’ устанавливаются здесь формулами:

Н\п) =Н, (ах,а2,…ап)

Здесь следует подчеркнуть, что для алгебраических

г{ = НттГГ|х,(т) I, г = 1,2,. ‘ л2 ~ \—а2 \-ах

-а2 -аъ -«4 -а! — «з -а3

-ах -а2 — «з -1 -«1 -а2

-1 -«1 -а2 0 -1 -«1

-а2 -аъ ~а\ -«2

-ах -а2 -1 -«1

Для определения подходящих непрерывных дробей, записываемых отношениями определителей Теплица, то есть определителей не общего, а весьма специального вида, может быть использован известный рекуррентный алгоритм частных и разностей, или QD-алгоритм Рутисхаузера [13]. Известны две схемы алгоритма Рутисха-узера. Первая схема алгоритма Рутисхаузера описывается формулами:

■»т-1

_ Л)

(2. 6)

х.

(О _>1)

т+1

х:

‘_т_

Л)

(2.7)

Здесь е0(т). Элементы первой строки х/т) составляют подходящие непрерывной дроби (2.1). QD-алгоритм, определяемый формулами (2.6) и (2.7), представим схемой, показанной на рис. 1.

№3 , 2014

Рисунок 1. Граф первой схемы ОЭ-алгоритма Рутисхаузера.

Вторая схема QD-алгоритма Рутисхаузера строится по формулам:

X(‘+0 = х(‘) + ео) — е0) (2.8)

т т т т-1

( ) ( ) Х +1)

е 0+0 = е О)Лт+1 (2 9)

ет — ет (1+1) . (2.9)

Рисунок 2. Граф второй схемы ОЭ-алгоритма Рутисхаузера.

В качестве начальных условий во второй схеме принимаются величины:

х(0 } = -а, Хт ) = о, (2.10)

е(0)= т = 1,2,3,…, п -1. (2.11)

ат

Кроме того,

х (/+1) = х (/) + е (/) х 0+1)- х О) — е )

х1 — Х1 е1 Лп — Лп ^п-1 ?

На рис. 2 показан граф второй схемы QD-алгоритма Рутисхаузера, описываемой формулами (2.8) — (2.9).

0,5

а) о

0,5 б) О

в)

Г) о

-0,5

Рисунок 3. Распределение подходящих дробей, представляющих

корни алгебраического уравнения (3.1).

3. Пример решения алгебраического уравнения с использованием алгоритма Эйткена-Никипорца

При помощи QD-алгоритма, описываемого формулами (2.8) и (2.9) и г/ф-алгоритма, определяемого формулами (2.4) и (2.5), вычислим корни уравнения:

Таблица 1. ВыЧИСЛЕНИЕ КОРНЯ X ПОЛИНОМА (3.1)

номер звена дроби значения дроби модуль комплексного числа, гдр £г — |Гсп — Гдр| Аргумент комплексного числа, фдр £г — |фсп — фдр

32768 1,299336354881 1,0347662395205 0,000536608578 0,1593265455006 0,0004087497684

65536 0,865755356659 1,0352888473023 0,000014000796 0,1588735170256 0,0000442787066

131072 0,575192287374 1,0352860752943 0,000016772804 0,1588981941309 0,0000196016012

262144 1,281984335003 1,0353012060085 0,000001642090 0,1589190365773 0,0000012408450

524288 0,846468777982 1,0353017233847 0,000001124714 0,1589146624435 0,0000031332886

1048576 0,334897583284 1,0353002609184 0,000002587180 0,1589157722686 0,0000020234635

Таблица 2. вычисление КОРНЯ Х2 ПОЛИНОМА (3.1)

номер звена дроби значения дроби модуль комплексного числа, гдр £г — | Гсп — Гдр| Аргумент комплексного числа, £г — |фсп — фдр|

32768 0,7451778875458 1,0359393947605 0,0006366026760 0,159326545500 0,0004087521972

65536 1,178758885767 1,0353065992655 0,0000038071810 0,158873517025 0,0000442762778

131072 1,4693219550522 1,0353118785096 0,0000090864250 -0,158898194130 0,0000195991724

262144 0,7625299074235 1,0353047625034 0,0000019704188 -0,158919036577 0,0000012432739

524288 1,1980454644447 1,0353032275206 0,0000004354360 -0,158914662443 0,0000031308598

1048576 1,7096166591419 1,0353041305771 0,0000013384925 -0,158915772268 0,0000020210347

х25+ —х24+ —х23+ —х22+. .. + -х + \ = 0. (3.1) 25 24 23 2

На рис. 3 (а, б, в, г) показаны графики значений подходящих непрерывных дробей, которые представляют комплексно-сопряжённые корни хг и х2, а также х23 и х24, алгебраического уравнения (3.1). Из графиков видна «периодичность» в расположении подходящих дробей, представляющих комплексные корни.

Таблица 3. ТАБЛИЦА КОМПЛЕКСНыХ КОРНЕй ПОЛИНОМА (3.1)

номер корня модуль комплексного числа, гдр Ег = | Гсп — Гдр| Аргумент комплексного числа, фдр Ег = |фсп — фдр|

Х1 1,0353024763410 0,0000003717576 0,1589164144872 0,0000013812450

Х2 1,0353029082686 0,0000001161841 -0,158916414487 0,0000013788161

Хз 1,0208971975934 0,0000008189039 0,4048138703132 0,0000013062742

Х4 1,0208929683060 0,0000034066364 -0,404816942111 0,0000017835682

Х5 1,0119546453670 0,0000010606098 0,6539705041609 0,0000006069863

Хб 1,0119525622329 0,0000010224854 -0,653970504160 0,0000006068511

Х7 1,0055905970776 0,0000001204480 0,9032469381432 0,0000007907396

Х8 1,0055896165151 0,0000010592983 -0,903246938143 0,0000008037280

Х9 1,0007367697380 0,0000016010438 1,1523728540076 0,0000002152181

Х10 1,0007353966524 0,0000002521888 -1,152372854007 0,0000002375618

Х11 0,9969117718048 0,0000014100128 1,4013359645609 0,0000005922542

Х12 0,9969113104034 0,0000010021657 -1,401332892762 0,0000024982142

Х13 0,9938588266902 0,0000043215424 1,6501608441892 0,0000000422129

Х14 0,9938596145949 0,0000035334452 -1,6501608441896 0,0000000423559

Х15 0,9914529019847 0,0000090765526 1,8988782108770 0,0000001954571

Х16 0,9914441092771 0,0000003189262 -1,8988782108771 0,0000001770903

Х17 0,9895575261692 0,0000000205123 2,1475126390097 0,0000009182252

Х18 0,9895575692370 0,0000000533751 -2,1475095672112 0,0000021536399

Х19 0,9881385673261 0,0000035211735 2,3960856311753 0,0000026546123

Х20 0,9881416222105 0,0000004660907 -2,3960825593774 0,0000004171151

Х21 0,9871571863949 0,0000006294384 2,6446094745684 0,0000003628114

Х22 0,9871563516141 0,0000001705217 -2,6446094745686 0,0000003313145

Х23 0,9865746589752 0,0000001875744 2,8931087435751 0,0000005178062

Х24 0,9865748432819 0,0000000351984 -2,8931087435750 0,0000005351746

25 -о-

18 о

о 9

О 1

О 2

Рисунок 4.

Расположение корней уравнения (3.1) на комплексной плоскости.

В табл. 1 и табл. 2 приведены результаты вычисления первой пары комплексно-сопряжённых корней уравнения (3.1). В первых колонках табл. 1 и табл. 2 указано число подходящих, которые использовались при определении значений модуля и аргумента комплексных корней.

Во вторых колонках табл. 1 и табл. 2 показаны значения подходящих непрерывных дробей Никипорца, представляющих комплексно-сопряжённые корни уравнения (3.1). В третьих и пятых колонках этих таблиц приведены найденные по г/ф-алгоритму то есть по фор-

мулам (2.4) и (2.5), значения модулей ri и аргументов ф комплексно-сопряжённых корней уравнения (3.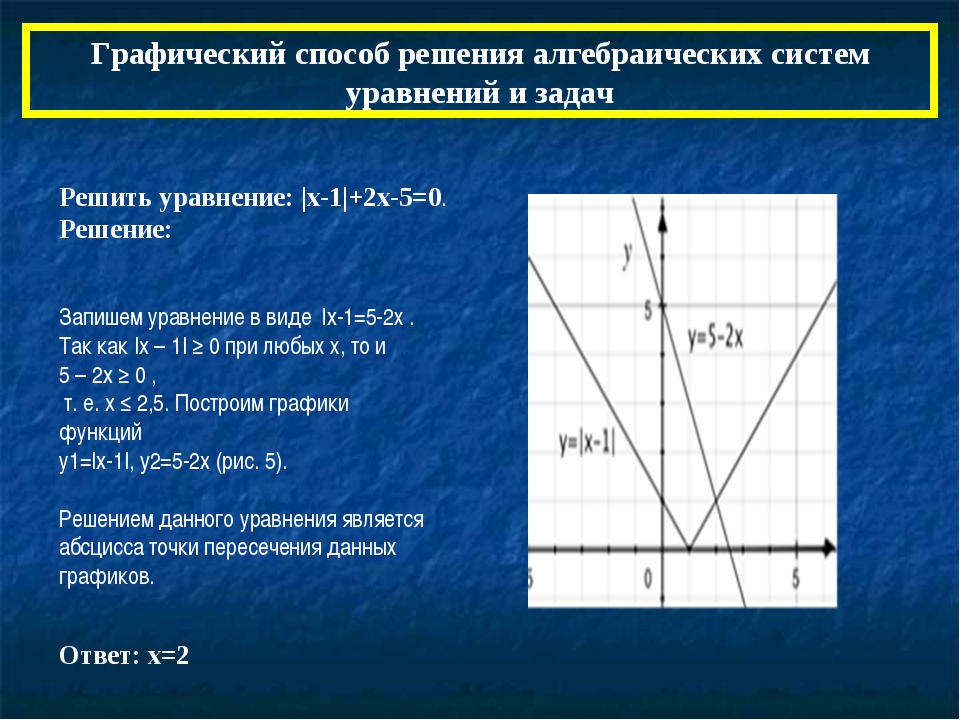 1). В четвёртых и шестых колонках таблиц представлены, соответственно, ег = |гсп — гдр| и ег = |фсп — фдр|, устанавливающие разности между значениями модулей и аргументов комплексных корней, полученных с использованием стандартной программы решения алгебраических уравнений и найденных посредством алгоритма Эйткена-Никипорца. В качестве стандартной программы использовалась функция polyroots, входящая в пакет MathCAD. Комплексные корни х1 и х2, найденные стандартной программой, имеют значения:

X! = 1,035302848098е10 158917795732, х2 = 1,035302792084е-10Д58917793303.

В табл. 3 приведены значения комплексно-сопряжённых корней уравнения (3.1), которые установлены с использованием г/ф-алгоритма.

Значение вещественного корня уравнения (3.1), также установленного при помощи г/ф-алгоритма, равно:

х25 = — 0,9863825764740.

На рис. 4 показано расположение корней уравнения (3.1) на комплексной плоскости.

Заключение

Выше отмечалось, что формулы (2.3)-(2.5) представляют корни полинома п-й степени через его коэффициенты. Используя эти формулы, можно устанавливать различные критерии, связанные с корнями полиномов общего вида. Произвольное алгебраическое уравнение степени п не разрешимо в радикалах, но оно оказалось разрешимо с использованием г/ф-алгоритма, то есть формул (2.4) и (2.5), в функциях Ы((П\ записываемых отношениями определителей Теплица бесконечного порядка (2.3).

Предлагаемый алгоритм нахождения нулей полинома имеет две особенности в сравнении с существующими методами решения ал-

гебраических уравнений. Первая и, пожалуй, принципиально важная особенность: предложен простой аналитический способ записи всех корней уравнения п-й степени по коэффициентам исходного уравнения. Комплексные корни находятся из «расширяющихся» отношений определителей с использованием г/ф-алгоритма. Вторая особенность предложенного алгоритма нахождения нулей полинома п-й степени, -простота и регулярность информационного графа алгоритма, что делает его привлекательным при аппаратной реализации в решающем поле суперкомпьютеров с реконфигурируемой структурой. Следует также отметить, что рассмотренный алгоритм позволяет определять все корни полинома параллельно, то есть одновременно.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Кутищев Г.П. Решение алгебраических уравнений произвольной степени: теория, методы, алгоритмы. М.: Изд-во URRS, 2010. 232 с.

2. Корчагин И.Ф. Алгебраические уравнения. М.: Физматкнига, 2006. 160 с.

3. Хемминг РВ. Численные методы для научных работников и инженеров. М.: Наука, 1972. 400 с.

4. Шмойлов В.И., Тучапский РИ. Алгебраические уравнения. Бесконечные системы линейных алгебраических уравнений // Библиографический указатель. Нац. акад. наук Украины, Ин-т приклад. проблем механики и математики. Львов, 2003. 83 с.

5. Корнеев П.К. Построение итерационных процессов на основе метода наименьшего квадратов для нахождения оптимума функций // Вестник СГУ Ставрополь, 2010. №70. С. 22-26.

6. Шмойлов В.И. Непрерывные дроби. В 3-х т. Т. 2. Расходящиеся непрерывные дроби. Нац. акад. наук Украины, Ин-т приклад. проблем механики и математики. Львов, 2004. 558 с.

7. Шмойлов В.И., Коваленко В.Б. Некоторое применения алгоритма суммирования расходящиеся непрерывных дробей // Вестник Южного научного центра РАН, 2012. № 4 (149). С. 3-13.

8. Шмойлов В. И. Непрерывные дроби и r/j9 / Шмойлов В. И., Савченко Д. И. Об алгоритме суммирования расходящихся непрерывных дробей // Вестник ВГУ. Серия: Физика. Математика. 2013. № 2. С. 258-276.

10. Шмойлов В.И., Редин А.А., Никулин Н.А. Непрерывные дроби в вычислительной математике. Ростов-на-Дону: Изд-во ЮФУ, 2015. 228 с.

11. Кириченко Г.А., Шмойлов В.И. Алгоритмы суммирования расходящихся непрерывных дробей и некоторые его применения. // Журнал вычислительной математики и математической физики. 2015, том 55, №4, С. 12-27.

12. Aitken A.C. On Bernulli’s numerical solution of algebraic equations. Edinburg, Proc. Roy. Soc., (1925/26) P. 289-305.

13. Рутисхаузер Г. Алгоритм частных и разностей. М.: ИИЛ, 1960. 93 с.

ОБ АВТОРАХ

Кириченко Геннадий Анатольевич, аспирант кафедры вычислительной техники Южного федерального университета (Инженерно-технологическая академия). Телефон 89064287987. E-mail: [email protected].

Селянкин Владимир Васильевич, кандидат технических наук, старший научный сотрудник кафедры математического обеспечения и применения ЭВМ Южного федерального университета. Телефон 8-904-346-05-40. E-mail: selyankin@tgn. sfedu.ru.

Шмойлов Владимир Ильич, научный сотрудник Лаборатории цифровой обработки сигналов НИИ многопроцессорных вычислительных систем им. А.В. Каляева Южного федерального университета. Телефон 8 (863-4)318-910. E-mail: [email protected].

Kirichenko Gennadiy Anatol’yevich, graduate student of Computer Engineering Institute of Computer Technology and Information Security Southern Federal University, Engineering and Technology Academy. Phone: 89064287987. E-mail: [email protected].

Selyankin Vladimir Vasil’yevich, Ph. D., Senior Fellow of the software and the use of computers Institute of Computer Technology and Information Security Southern Federal University. Phone: 8-904-34605-40. E-mail: selyankin@ tgn.sfedu.ru.

Shmoylov Vladimir Ilyich, researcher of the Laboratory of Digital Signal Processing, Institute of Research Multiprocessor Computing Systems names A.V. Kaliayeva Southern Federal University. Phone: 8 (863-4) 318-910. E-mail: [email protected].

Конспект урока по Алгебре «Решение алгебраических уравнений»

Тема: Решение алгебраических уравнений.

Цели урока:

систематизировать, обобщить, расширить знания и умения учащихся, связанные с применением методов решения алгебраических уравнений;
содействовать развитию математического мышления учащихся;
побуждать учащихся к преодолению трудностей в процессе умственной деятельности.

План урока.

Организационный момент.
Доведение цели урока до сознания учащихся.
Решение тренировочных упражнений.
Самостоятельная работа(выполнение тестового задания, использовалась локальная сеть)
Историческая справка.
Работа в сети Интернет.
Практическая работа по итогам поиска.
Подведение итогов урока.
Домашнее задание.

Организационный момент.
Доведение цели урока до сознания учащихся.

Цель урока – закрепить алгоритм решения алгебраических уравнений, рассмотреть различные приемы и методы решения таких уравнений.

Мне бы очень хотелось, чтобы каждый ученик, приходя на урок, считал своей основной задачей: понять объяснения учителя и применить их к решению задач.

Решение тренировочных упражнений.

Начнем работу с уравнения, содержащегося в сборнике заданий для проведения экзаменационной работы в 9 классе. Указано, что эти уравнения высокого уровня сложности.

№1. Решите уравнение:

Пусть , тогда:

По теореме, обратной теореме Виета:

t₁ +t₂ = 1 t₁ ∙ t₂ = -2 │ t₁ = 2

2 – 1 = 1 2 ∙ (-1) = -2 │ t₂ = — 1

D = b² -4ac = 9 + 16 = 25, D 0

D = b² — 4ac = 9 — 8 = 1, D 0

Ответ: -1; 1; 2; 4.

Итак, уравнение решено методом введения новой переменной.

. Практическая часть урока.

Далее нам предстоит напряженный этап урока – решить сложное уравнение и выполнить тест (см. приложение).

№ 2. Найти действительные корни уравнения:

Разложим на множители квадратный трехчлен: .

х²– х – 6 = 0

По теореме, обратной теореме Виета:

х₁+х₂ = 1 х₁∙ х₂ = -6 │ х₁ = 3

3 – 2 = 1 3∙ (-2) = -6 │ х₂ = -2

Получаем разложение: х²– х – 6 = (х + 2)(х – 3)

ОДЗ х ≠ 3

х ≠ -2

х²(х-3) + 2х²(х-2)(х+2) = 3х² +19х + 6

х³ – 3х²+2х²(х² – 4) = 3х² + 19х + 6

х³ – 3х²+2х⁴ – 8х² – 3х² – 19х – 6 = 0

2х⁴ + х³ – 14х² – 19х – 6 = 0. Ищем корень уравнения среди делителей свободного члена: ± 1; ± 2; ± 3; ± 6

х₁ = -1, так как 2 – 1 – 14 +19 – 6 = 0

21 – 21 = 0

2х⁴+ х³ – 14х² – 19х – 6 │

2х⁴+ 2х³

— х³ – 14х²

— х³ – х²

— 13х² – 19х

— 13х² – 13х

— 6х – 6

2х³ – х² – 13х – 6 = 0. Ищем корень уравнения среди делителей свободного члена: ± 1; ± 2; ± 3; ± 6

х₂ = — 2, так как — 16 – 4 + 26 – 6 = 0

— 26 + 26 = 0

2х³ – х² – 13х – 6│

2х³ + 4х²

— 5х² – 13х

— 5х² – 10х

— 3х – 6

2х² – 5х – 3 = 0

D = b² – 4ac = 25 +24 = 49, D 0

;

х₃ = 3

х = 3 – посторонний корень

х = — 2 – посторонний корень

Ответ: — 1;

Историческая справка.

При решении уравнения использовался прием отыскания действительных корней алгебраического уравнения среди делителей свободного члена. Однако на практике такой прием не всегда позволяет установить корень уравнения.

Долгое время ученые пытались найти формулу корней уравнения третьей степени.

Дело в том, что формула корней квадратного уравнения была изложена еще в III веке греческим ученым Диафантом. Эта формула позволяет найти корень квадратного уравнения, выполнив действия +, -, ∙,: и √(извлечение корня) над коэффициентами уравнения. А так как знак √ — радикал, то говорят, что квадратное уравнение решено в радикалах.

Задача решения в радикалах уравнения третьей степени была решена только в XVI веке. Формулу корней уравнения третьей степени впервые опубликовал итальянский ученый Кардано в 1545 году. К сожалению, наш учебник только упоминает формулу Кардано, а запись формулы не приводит. Попытаемся найти формулу Кардано в Интернете.

Работа в сети Интернет.

Поиск формулы Кардано.

Практическая работа по итогам поиска.

Итак, мы рассматриваем формулу Кардано для уравнения вида

Решим уравнение с помощью формулы Кардано.

y³ – 3y + 2 = 0 (p = — 3; q = 2)

По формуле Кардано:

y₁ =

y³ – 3y + 2│(y+2)

y³ + 2y²

— 2y² – 3y

— 2y² – 4y

y + 2

y² – 2y+ 1 = 0

(y – 1)² = 0

y₂ = 1 Ответ: — 2; 1.

Подведение итогов урока.

Опубликовав свою формулу, Кардано доказал, что уравнение третьей степени разрешимо в радикалах.

Еще 300 лет ученые будут пытаться решить в радикалах уравнения более высоких степеней. Только в 1826 году норвежец Абель докажет, что эти уравнения в радикалах не разрешимы.

Домашнее задание.

Найти в Интернете историю открытия формулы Кардано.

Тест

I вариант

№1 Найдите корни квадратного уравнения х² – 7х – 8 = 0

1) х₁ = — 8 2) х₁ = 8 3) х₁ = — 1 4) х₁ = 1

х₂ = 1 х₂ = — 1 х₂ = — 8 х₂ = 8

Номер верного ответа:

№2 Числа х₁ = 1 и х₂ = — корни квадратного трехчлена 6х² – 7х + 1. Разложите квадратный трехчлен на множители.

6х² – 7х + 1 = (х – 1) (х — )
6х² – 7х + 1 = (х + 1) (х + )
6х² – 7х + 1 = (х – 1) (6х – 1)
6х² – 7х + 1 =6 (х + 1) (х + )

Номер верного ответа:

№3 Укажите корень уравнения 2х⁴ + х³ – 14х² – 19х – 6 = 0.

1) 5 2) – 1 3) – 4 4) 1

Номер верного ответа:

№4 Решите систему уравнений

1) (- 7; 2) 2) (7; 2) 3) (7; — 2) 4) (- 7; — 2)

(2; — 7) (2; 7) (- 2; 7) (- 2; — 7)

Номер верного ответа:

№5 Решите систему уравнений

1) (8; 5) 2) (64; 25) 3) (- 8; 5) 4) (64; — 25)

(5; 8) (25; 64) (5; — 8) (-25; 64)

Номер верного ответа:

Ваша оценка:

Тест

II вариант

№1 Найдите корни квадратного уравнения х² + 2х – 15 = 0

1) х₁ = — 5 2) х₁ = -3 3) х₁ = — 5 4) х₁ = 3

х₂ = 3 х₂ = 5 х₂ = — 3 х₂ = — 5

Номер верного ответа:

№2 Числа х₁ = — и х₂ = — корни квадратного трехчлена 6х² + х — 1. Разложите квадратный трехчлен на множители.

6х² + х – 1 = (х +) (х — )
6х² + х – 1 = 6 (х — ) (х +)
6х² + х – 1 = (2х + 1) (3х – 1)
6х² + х – 1 = (х — ) (х + )

Номер верного ответа:

№3 Укажите корень уравнения 2х⁴ — 3 х³ – 7х² – 5х – 3 = 0.

1) 5 2) – 1 3) – 4 4) 1

Номер верного ответа:

№4 Решите систему уравнений

1) (- 4; 2) 2) (4; 2) 3) (4; — 2) 4) (- 4; — 2)

(2; — 4) (2; 4) (- 2; 4) (- 2; — 4)

Номер верного ответа:

№5 Решите систему уравнений

1) (7; 5) 2) (49; 25) 3) (- 7; — 5) 4) (- 49; — 25)

(5; 7) (25; 49) (- 5; — 7) (-25; — 49)

Номер верного ответа:

Ваша оценка:

3.

1.6. Алгебраические уравнения

Глава 3. Решение уравнений и неравенств

3.1.

3.1.6.

Теорема Гаусса. Любое алгебраическое уравнение
(*)
имеет на множестве комплексных чисел хотя бы одно решение.

Эту теорему также называют основной теоремой алгебры. Согласно этой теореме, уравнение (*) имеет хотя бы один корень z = z₀. Разделив многочлен, стоящий в левой части (*) на одночлен (z = z₀), мы получим снова уравнение вида (*), которое согласно той же теореме Гаусса имеет хотя бы одно решение. Продолжая так n раз, получим следствие теоремы Гаусса: любое алгебраическое уравнение n-ной степени имеет ровно n, вообще говоря, комплексных, корней (разумеется, некоторые корни могут совпадать).

Пример 1

Решите уравнение z³ + z – 2 = 0.

Очевидно, z = 1 – корень этого уравнения. Разделив многочлен z³ + z – 2 на одночлен (z – 1), например, по схеме Горнера, получим разложение исходного многочлена на множители:

Корни квадратичной функции находим по формуле корней квадратного уравнения:

Ответ. 1,

Рациональные уравнения являются следующим по сложности типом стандартных уравнений.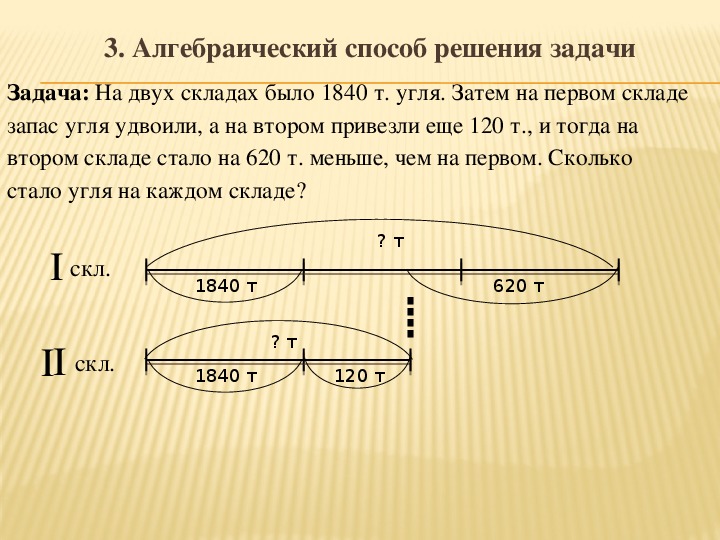

Для решения дробно-рациональных уравнений существует алгоритм.

1. Найти общий знаменатель дробей, входящих в уравнение.

2. Заменить данное уравнение уравнением с целыми коэффициентами, умножив его на общий знаменатель.

3. Попытаться решить полученное уравнение с целыми коэффициентами.

4. Исключить из его корней те, которые обращают в нуль общий знаменатель.

5. Записать ответ.

Пример 2

Решите уравнение

Общий знаменатель дробей, входящих в уравнение, есть (x – 1)(x + 2). Умножая на него обе части уравнения, получим 3x(x + 2) – 2x(x – 1) = 3x + 2. Последнее уравнение сводится к квадратному уравнению x² + 5x + 6 = 0, корни которого x = –3 и x = –2. Подставляя эти числа в общий знаменатель дробей исходного уравнения, убеждаемся, что при x = –2 он обращается в нуль, при x = –3 знаменатель нулю не равен. Значит, x = –2 не является корнем уравнения.

Ответ. x = –3.

Стандартным методом их решения является возведение уравнения в подходящую степень. Однако, как следует из § 3.1.1, возведение уравнения в произвольную степень не всегда приводит к равносильному уравнению.

Действительно, уравнение

(6)

является лишь следствием уравнения f (x) = g (x), то есть содержит все корни этого уравнения, но может иметь и другие корни. Уравнение (6) среди своих корней содержит ещё и корни уравнения f (x) = –g (x) (если таковые существуют), следствием которого оно также является. Итак, у уравнения (6) «больше» корней, чем у уравнения f (x) = g (x), а это как раз и обозначает, что при возведении в чётную степень могут появиться посторонние корни. В этом случае проверка необходима, как составляющий элемент решения. Она необходима даже в тех случаях, когда лишние корни не появились, но ход решения был таков, что они могли появиться. В последнем случае иногда проще сделать проверку, чем доказать, что она не нужна. Именно поэтому проверка здесь является элементом решения.

К тому же, проверка может быть средством контроля правильности проделанных вычислений. Однако проверить полученные корни подстановкой не всегда легко. Лишние корни, которые могли появиться при возведении уравнения, например, в квадрат, могут быть отсеяны на основе следующего соображения.

Рассмотрим уравнение

(7)

Ясно, что если x = x₀ − решение этого уравнения, то обе части этого равенства при x = x₀ должны быть неотрицательны. Следовательно, потребовав дополнительно, чтобы g(x) ≥ 0, уравнение можно возвести в квадрат. Имеем следующее соотношение равносильности:

(8)

Система (8) действительно является равносильной уравнению (7). В самом деле, из системы (8) следует, что функция f (x) равна полному квадрату функции g (x), то есть для решения является неотрицательной.

Пример 3

Решите уравнение

Перейдём сразу к равносильной системе.

Ответ.

Решение системы линейных алгебраических уравнений в параметрическом моделировании

Р. М.Ганеев, А.О.Максименко, А.В.Крючков

Система КОМПАС 3D предназначена для создания моделей (деталей и сборок) и графических документов. Параметрическое моделирование неотъемлемая часть КОМПАС 3D (как и всех современных CAD/CAM-систем), позволяющая быстро получать модели типовых изделий на основе прототипа.

Особенностью системы КОМПАС 3D является использование собственного математического ядра и параметрических технологий.

В этой статье рассматривается построение параметрического двумерного эскиза или чертежа. При этом параметрическая модель состоит из развитого набора геометрических и алгебраических ограничений, заданных на конечном множестве геометрических объектов и переменных. Наиболее распространены такие объекты, как точки, отрезки, окружности и дуги окружностей. А параметрические зависимости описываются с помощью таких геометрических ограничений, как параллельность, перпендикулярность, совпадение, касание, линейные и угловые размеры и прочие отношения. Задачей параметризации в таком случае является решение, благодаря которому все геометрические объекты эскиза (чертежа) приводятся в состояние, удовлетворяющее заданным ограничениям.

На рис. 1 представлен пример параметрического эскиза.

Рис. 1. Пример недоопределенной параметрической модели

Изображение на этом рисунке состоит из четырех прямых, шести точек, одной переменной и описывается системой из 20 ограничений:

где dispp (P1, P2, V) расстояние на величину V между точками P1 и P2, displ (P, L, V ) расстояние от точки P до прямой L, fix (P, c) фиксация координаты c у точки P, ang (L1, L2, V) угол V между прямыми L1, L2, fix (V,const) присвоение переменной V=const, hor (L) горизонтальность прямой.

Каждое из ограничений убирает одну степень свободы объекта. С учетом того, что степень свободы точки и прямой равна 2, а переменной равна 1, вся модель описывается 4*2 + 6*2 + 1 = 21 координатой степеней свобод. Таким образом, недостает ровно одного ограничения, чтобы полностью зафиксировать все объекты модели. Например, точки P2, P3, P4, Pc и прямая L2 имеют одну степень свободы перемещения, и в целом модель недоопределена.

Существуют различные подходы и методы решения задачи параметризации, и все они в основном подразделяются на методы, основанные на графах, на алгебраические и на численные:

• методы, основанные на графах, используют отвлеченную от геометрии эскиза информацию о структуре системы ограничений, например, для разбиения сложной в целом модели на более простые сепаратно решаемые подсистемы;

• алгебраические методы применяют к подсистемам, которые могут быть решены в аналитическом виде;

• численные методы хотя и проигрывают алгебраическим в эффективности, применяются в том случае, если ни один из альтернативных подходов не позволяет решить общую задачу.

Программное средство в составе CAD-системы, которое обеспечивает решение задач параметризации, как правило, применяет все описанные подходы в совокупности.

Для получения численного решения используют итерационные методы, которые, как известно, предполагают некоторое начальное приближение решения системы нелинейных уравнений. Оно уточняется на каждом шаге (итерации), пока не будет достигнута требуемая точность. Широко известный метод Ньютона-Рафсона на каждой итерации отыскивает решение системы линейных алгебраических уравнений (СЛАУ) согласно его итерационной формуле:

(1)

где k номер итерации, pk вектор решения на k-й итерации, Dp вектор направления поиска решения, F вектор значений функций, составляющих правую часть системы нелинейных уравнений, J матрица Якоби , состоящая из частных производных 1-го порядка.

Для привлечения метода Ньютона к решению параметрической модели последняя формулируется в виде системы нелинейных алгебраических уравнений F(p) = 0 из функций в (1) .

Особенность параметрического моделирования состоит в том, что в общем случае система уравнений недоопределена, то есть количество неизвестных превышает количество уравнений. Кроме того, матрица J на некоторой итерации, в том числе и при начальном приближении, может оказаться вырожденной или близкой к таковой, что создает дополнительные трудности применения метода Ньютона.

Согласно (1), на каждом шаге итерационного процесса мы сталкиваемся с решением СЛАУ

(2)

где A Rm,n, m количество строк матрицы (количество уравнений), n количество неизвестных, вектор правых частей c Rm , вектор неизвестных x R .

Вектор x определяет величину в (1). В общем случае rank(A) < m < n . Например, при решении системы нелинейных уравнений, получаемой из модели, показанной на рис. 1, при начальном приближении формируется прямоугольная матрица A R ^20,21. Как оказалось, матрица имеет неполный ранг (rank(A)=18) по причине того, что в СЛАУ присутствуют два уравнения, векторы-строки которых образуют линейную комбинацию с другими уравнениями. В итоге СЛАУ в этом примере имеет бесчисленное множество решений, удовлетворяющих условию минимума

Для обеспечения сходимости процесса (1) в этом множестве выбирают вектор минимальной длины (нормальное решение). Известные алгоритмы решения недоопределенных СЛАУ [1, 2] не учитывают разреженную структуру больших матриц и, как следствие, обладают малой скоростью.

Р.М.Ганеев для повышения скорости решения предложил строить нормальное решение на базе предварительного приведения СЛАУ к треугольной форме.

Пусть ранг матрицы СЛАУ (2) меньше количества неизвестных. Для приведения СЛАУ (2) к треугольной форме используются методы отражений Хаусхолдера или отражений/вращений Гивенса. В случае СЛАУ с разреженной матрицей более эффективны методы Гивенса.

Пусть после приведения к треугольной форме получена совместная СЛАУ:

Rx = b (3)

где R правая треугольная n*n -матрица. При этом считаем, что i -е уравнение отсутствует, то есть в матрице R в i-й строке находятся только нули, и в векторе правой части i-й элемент равен нулю. Таких уравнений может быть несколько.

Коэффициенты дополнительного i -го уравнения вычисляются по формулам:

(4)

Общий алгоритм решения СЛАУ (2) содержит следующие шаги:

1. Параметры СЛАУ (2) необходимо записать в расширенную матрицу: R = [ A Ю ].

Матрица R должна содержать не менее n строк. Если количество уравнений m меньше количества неизвестных (m < n) , то ниже массивов СЛАУ (2) нужно добавить (n-m) строк с нулями:

2. Преобразовать матрицу R к правой треугольной форме.

3. Попробовать решить СЛАУ:

3.1. Если R(n,n) = 0 , то произвести переход в 3.2.

3.1.1. Вычислить n-ю компоненту вектора решения:

x(n) = R(n,n+1) / R(n,n)

3.1.2. Пересчитать правую часть с учетом вычисленного компонента вектора решения и перенести на место n-го столбца:

R(k,n) = R(k,n+1) – R(k,n)*x(n), k = 1,2,. ..,n–1.

3.1.3. Уменьшить счетчик количества неизвестных: n = n–1 .

3.1.4. Если n = 0 , то произвести переход в пункт 4.

3.1.5. Произвести переход в 3.1.

3.2. Построить недостающие уравнения. Возможны два варианта.

3.2.1. В R обязательно есть хотя бы одна строка, в которой элемент r_ii равен нулю, а остальные элементы этой строки не все равны нулю. Обнаружив такую строку с номером i (i = 1,2,3…) , нужно переместить ее в первую же свободную строку ниже (хотя бы одна свободная строка, благодаря пункту 3.1, обязательно есть) и на месте i-й строки построить дополнительное уравнение. Произвести переход в пункт 2.

Рис. 2. График сходимости итерационного процесса на примере модели из параметрического эскиза (рис. 1)

3.2.2. В R нулевые диагональные элементы расположены только в свободных строках. В этом случае построить все недостающие уравнения. Произвести переход в пункт 2.

4. Конец вычислений.

Выводы и результаты

Для испытания предложенного метода был поставлен ряд вычислительных экспериментов с решением различных параметрических моделей. График на рис. 2 показывает сходимость итерационного процесса на примере модели, показанной на рис. 1. Характеристика снята в виде зависимости невязки || F(x_k) || на каждом шаге решения от номера итерации k . В этом примере отрабатывалось решение системы уравнений для изменения угла между L1 и L3 с 15° на 45°.

Из графика видно, что процесс решения по предлагаемому методу имеет устойчивую сходимость.

«САПР и графика» 6’2004

3. Численное решение алгебраических и трансцендентных уравНений

Решение уравнений – это одна из древнейших математических задач. Ещё в Древней Греции умели решать линейные и квадратные алгебраические уравнения. В эпоху Возрождения (XV век) Джироламо Кардано и его ученик Луиджи Феррари получили точные решения для алгебраических многочленов 3 и 4 степени. Позднее много усилий было затрачено на получение точного решения многочленов 5 степени и выше. Но только в 20-х годах XIX века было доказано, что решение алгебраического многочлена n-ой степени
An x n + an-1xn-1 +…+ a0 = 0, где an ¹ 0
При n ³ 5 нельзя выразить через коэффициенты с помощью арифметических действий и операций извлечения корня.
Известно, что алгебраический многочлен n-ой степени имеет n корней, причём они могут быть вещественными и комплексными (теорема Гаусса).
Решение трансцендентных уравнений в явном виде также может быть получено в редких, простейших случаях. Трансцендентные уравнения, включающие алгебраические, тригонометрические, экспоненциальные функции от неизвестного x, как правило, имеют неопределённое число корней. Необходимость решения трансцендентных уравнений возникает, например, при расчёте устойчивости систем, расчете парожидкостного равновесия и т. п.
Достаточно распространенной задачей является так же нахождение некоторых или всех решений системы из n нелинейных алгебраических или трансцендентных уравнений с n неизвестными.
Рассмотрим вначале методы решения нелинейных уравнений с одним неизвестным.
Пусть задана непрерывная функция f(x) и требуется найти корни уравнения
F(x)=0 (3.1)
На всей числовой оси или на некотором интервале .
Всякое значение , удовлетворяющее условию , называется Корнем уравнения (6.1), а способ нахождения этого значения И есть Решение уравнения (3.1).
Методы решения уравнений:
· Прямые (формула Виета для квадратного уравнения и Кардано для кубического и другие)
· Итерационные – для решения любого уравнения
Численное решение уравнения проводится в два этапа:
1 этап. Отделение корней уравнения.
2 этап. Уточнение интересующих корней с заданной точностью ε.

< Предыдущая Следующая >
Решение алгебраических уравнений
Из алгебраических уравнений вида мы научились решать в школе линейные уравнения вида и квадратные уравнения . В обоих случаях коэффициент при старшей степени не должен равняться 0. Мы знаем, что даже квадратное уравнение не всегда имеет корни на множестве действительных чисел. В приложениях, связанных с комплексными числами, очень важно находить корни многочлена от комплексной переменной.

В отличии от этого, алгебраическое уравнение с комплексной переменной степени выше нулевой всегда имеет хотя бы один, вообще говоря, комплексный корень. В этом суть «основной теоремы алгебры», которую мы сформулируем без доказательства.

Теорема 1.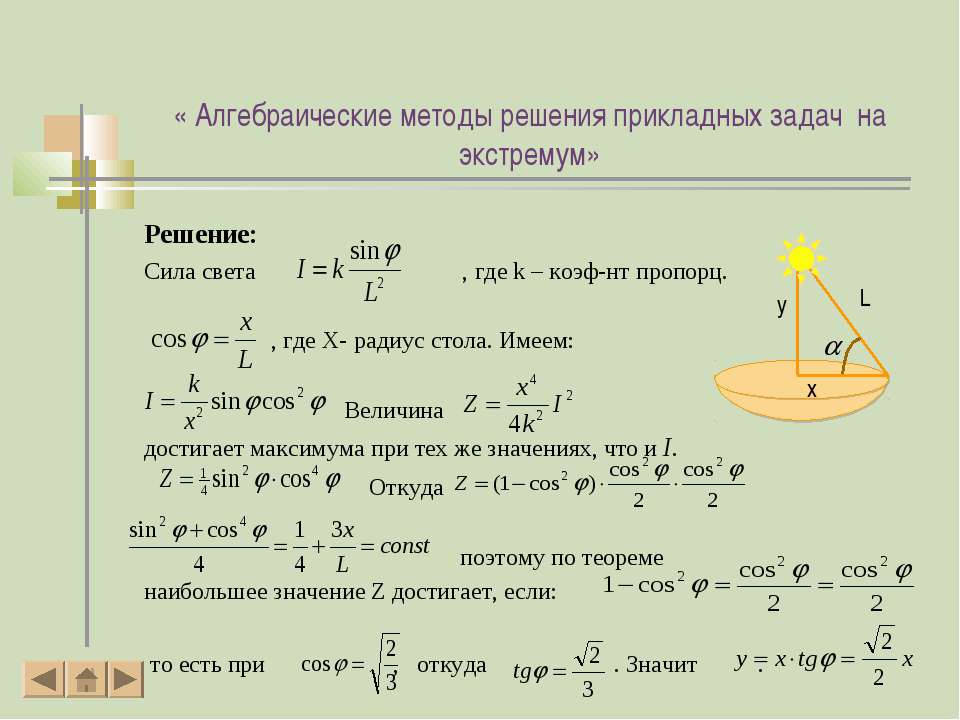 (Основная теорема алгебры) При уравнение имеет хотя один, один, вообще говоря, комплексный корень.

А вот теорема Безу легко доказывается.

Теорема 2. (Теорема Безу) Остаток от деления на двучлен равен .

Доказательство. Пусть , тогда , откуда .

Следствие 1. Многочлен разлагается на линейных множителей, т.е. представляется в виде , где .

Пример 4. Решите уравнение .

Решение. Применим формулу для решения квадратного уравнения с четным коэффициентом при линейном члене. Итак, . Под здесь понимается любое число, квадрат которого равен . Таким числом может быть число , и в итоге .

Ответ. .

Пример 5. Решите уравнение .

Решение. Применим формулу для решения квадратного уравнения с четным коэффициентом при линейном члене. Итак, или . Под здесь понимается любое число, квадрат которого равен . Если число возвести в квадрат и приравнять к , то несложно выяснить, что одним из значений является число . В итоге , и мы приходим к ответу , . Заметим, что можно было «подобрать» эти корни, используя теорему Виета.

Ответ. , .

Узнать еще:
4. Алгебраические решения линейных систем
а. Решение систем уравнений с помощью подстановки
Этот метод включает замену y (или «x», если это проще) из одного уравнения в другое уравнение. Это упрощает второе уравнение, и мы можем легко его решить.
Пример 1
Решите систему
x + y = 3 [1]
3 x — 2 y = 14 [2]
с заменой.
(Числа в квадратных скобках [1] и [2] используются для названия каждого уравнения. Это упрощает обращение к ним в решении.)
Ответ
Из строки [1] мы вычитаем x с обеих сторон и получаем y = −x + 3.
Подставляем это вместо и в строке [2]:
3 x — 2 (- x + 3) = 14
Это дает нам: `3x + 2x — 6 = 14`
Следовательно, `x = 4`.
Теперь, используя строку [1], мы получаем y = −1.
Если у нас есть правильные числа, они также должны работать в другом уравнении.
Проверка в строке [2]:
`3 (4) — 2 (−1) = 14` [OK]
Итак, наше решение `(4, −1)` правильное.
г. Решение систем уравнений методом исключения
Наша цель здесь — исключить одну из переменных. Неважно, какой из них — обычно мы делаем самый простой.
Пример 2
Решите систему с помощью исключения.
3 x + y = 10 [1]
x — 2 y = 1 [2]
Ответ
Если мы вычтем одну строку из другой, мы ничего не удаляем. Однако, если мы умножим одну из строк, мы можем исключить одну из переменных, добавив строки.
Ряд [1] `× 2` дает нам
6 x + 2 y = 20 [3]
x — 2 y = 1 [2] (без изменений)
Если мы сложим строки [3] и [2], мы исключим и .
`7x = 21`
Итак, `x = 3` и используя строку [1],` y = 1`.
Отметьте в строке [2]: `3 — 2 (1) = 1` [OK]
Итак, наше решение — `(3, 1)`.
В следующей главе мы увидим, как решать системы уравнений, используя определителей (хорошо для бумажных решений) и матриц (очень мощный и лучший способ сделать это на компьютерах).
Алгебра — Решения и наборы решений
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметки
Похоже, вы используете устройство с «узкой» шириной экрана ( i. е. вы, вероятно, разговариваете по мобильному телефону). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (должна быть возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 2-1: Решения и наборы решений
Мы начнем эту главу с довольно короткого раздела с некоторой базовой терминологией, которую мы довольно регулярно используем при решении уравнений и неравенств.? 0 \\ 9–9 & = 0 \\ 0 & = 0 \, \, \, \, {\ mbox {OK}} \ end {align *} \]
Итак, мы спрашиваем, равна ли правая сторона левой стороне после того, как мы подключим предложенное решение. В этом смысл «?» над знаком равенства в первой строке.
Поскольку правая и левая части совпадают, мы говорим, что \ (x = 3 \) удовлетворяет уравнению.

b \ (y = 8 \) in \ (3 \ left ({y + 1} \ right) = 4y — 5 \) Показать решение
Итак, мы хотим увидеть, удовлетворяет ли \ (y = 8 \) уравнению.? 4 \ left (8 \ right) — 5 \\ 27 & = 27 \, \, \, \, {\ mbox {OK}} \ end {align *} \]
Итак, \ (y = 8 \) удовлетворяет уравнению и, следовательно, является решением.

c \ (z = 1 \) in \ (2 \ left ({z — 5} \ right) \ le 4z \) Показать решение
В этом случае мы имеем неравенство, и в этом случае «удовлетворить» означает что-то немного другое. В этом случае мы будем говорить, что число будет удовлетворять неравенству, если после его подключения мы получим в результате истинное неравенство.
Давайте проверим \ (z = 1 \).? 4 \ left (1 \ right) \\ — 8 & \ le 4 \, \, \, \, {\ mbox {OK}} \ end {align *} \]
Итак, -8 меньше или равно 4 (на самом деле меньше), и мы имеем истинное неравенство. Следовательно, \ (z = 1 \) будет удовлетворять неравенству и, следовательно, является решением

d \ (z = — 5 \) in \ (2 \ left ({z — 5} \ right) \ le 4z \) Показать решение
Это то же неравенство с другим значением, давайте это проверим. ? 4 \ left ({- 5} \ right) \\ — 20 & \ le — 20 \, \, \, \, {\ mbox {OK}} \ end {align *} \]
В этом случае -20 меньше или равно -20 (в данном случае оно равно), и поэтому мы снова получаем истинное неравенство, и поэтому \ (z = — 5 \) удовлетворяет неравенству и поэтому будет решением.
Мы также должны сделать быстрый пример чисел, которые не являются решением, чтобы мы могли увидеть, как они будут работать.
Пример 2 Покажите, что следующие числа не являются решениями данного уравнения или неравенства.
\ (y = — 2 \) в \ (3 \ left ({y + 1} \ right) = 4y — 5 \)
\ (z = — 12 \) в \ (2 \ left ({z — 5} \ right) \ le 4z \)
Показать все решения Скрыть все решения a \ (y = — 2 \) in \ (3 \ left ({y + 1} \ right) = 4y — 5 \) Показать решение
В этом случае мы делаем то же самое, что и в предыдущем примере.? 4 \ left ({- 2} \ right) — 5 \\ — 3 & \ ne — 13 \, \, \, \, {\ mbox {NOT OK}} \ end {align *} \]
Итак, -3 не то же самое, что -13, и поэтому уравнение не выполняется. ? 4 \ left ({- 12} \ right) \\ — 34 \ require {cancel} & \ bcancel {\ le} — 48 \, \, \, \, {\ mbox {NOT OK}} \ end {align * } \]
В этом случае -34 НЕ меньше или равно -48, поэтому неравенство не выполняется.2} — 9 = 0 \). В этом случае \ (x = — 3 \) также является решением.
Мы называем полный набор всех решений набором решений для уравнения или неравенства. Есть также некоторые формальные обозначения для наборов решений, хотя мы не будем часто их использовать в этом курсе. Несмотря на это, мы все равно должны это признать.
Для уравнений мы обозначаем множество решений, заключая все решения в фигурные скобки, \ (\ left \ {{} \ right \} \). Вот наборы решений для двух уравнений, которые мы рассмотрели выше.2} — 9 & = 0 & \ hspace {0,25 дюйма} & {\ mbox {Набор решений}}: \, \, \, \ left \ {{- 3,3} \ right \} \ end {align *} \]
Для неравенств используются аналогичные обозначения. В зависимости от сложности неравенства набор решений может быть одним числом или диапазоном чисел. Если это одно число, мы используем те же обозначения, что и для уравнений. Если набор решений представляет собой диапазон чисел, как тот, который мы рассмотрели выше, мы будем использовать что-то, называемое нотацией конструктора наборов .Вот набор решений для неравенства, которое мы рассмотрели выше.
\ [\ left \ {{z | z \ ge — 5} \ right \} \]
Это читается как: «Множество всех \ (z \) таких, что \ (z \) больше или равно -5».
Большинство неравенств, которые мы будем рассматривать, будут иметь достаточно простые наборы решений, которые мы часто сокращаем как
\ [z \ ge — 5 \]
Есть еще одна последняя тема, которую мы должны затронуть в отношении наборов решений, прежде чем покинуть этот раздел.2} &
Если мы ограничимся только реальными решениями (что мы не всегда будем делать), тогда у уравнения не будет решения. Возведение в квадрат \ (x \) делает \ (x \) больше нуля, затем добавление 1 к этому означает, что левая часть гарантированно будет не меньше 1. Другими словами, у этого уравнения нет реального решения. По той же основной причине нет решения неравенства. Возведение любого вещественного \ (x \) в квадрат делает его положительным или нулевым, и поэтому никогда не будет отрицательным.
Нам нужен способ обозначить тот факт, что здесь нет решений.В обозначении набора решений мы говорим, что набор решений пустой, и обозначаем его символом: \ (\ emptyset \). Этот символ часто называют пустым набором .
Теперь нам нужно сделать пару заключительных замечаний, прежде чем покинуть этот раздел.
В приведенном выше обсуждении пустых множеств мы предполагали, что ищем только реальные решения. Хотя это то, что мы будем делать с неравенствами, мы не будем ограничиваться реальными решениями с уравнениями.2} + 1 = 0 \) действительно имеет сложные решения.
Наконец, как отмечалось выше, в этом курсе мы не будем часто использовать нотацию набора решений. Это хорошее обозначение, которое иногда может использоваться, особенно для сложных решений. Однако для подавляющего большинства уравнений и неравенств, которые мы будем рассматривать, будут достаточно простые наборы решений, так что их будет проще записать и отпустить. Следовательно, это то, что мы не будем использовать для обозначений наших наборов решений.Однако вы должны знать обозначения и понимать, что они означают.
Алгебраические методы решения систем
Цели обучения
Используйте метод замены
Решите систему уравнений, используя метод подстановки.
Распознавать системы уравнений, не имеющие решения или бесконечное число решений
Используйте метод исключения без умножения
Решите систему уравнений, когда умножение не требуется для исключения переменной
Используйте метод исключения с умножением
Используйте умножение в сочетании с методом исключения для решения системы линейных уравнений
Распознать, когда решение системы линейных уравнений подразумевает, что существует бесконечное число решений
Решите систему уравнений методом подстановки
В последних парах разделов мы проверили, что упорядоченные пары являются решениями систем, и использовали графики, чтобы классифицировать, сколько решений имеет система двух линейных уравнений.Что, если нам не дана точка пересечения или она не очевидна из графика? Можем ли мы еще найти решение этой системы? Конечно, можно, используя алгебру!
В этом разделе мы изучим метод подстановки для нахождения решения системы линейных уравнений с двумя переменными. На протяжении всего курса мы использовали подстановку по-разному, например, когда мы использовали формулы для площади треугольника и простых процентов. Мы подставили значения, которые мы знали, в формулу, чтобы найти значения, которые мы не знали.Идея аналогична применительно к решению систем, в этом процессе всего несколько этапов. Сначала вы решите одну переменную, а затем подставите это выражение в другое уравнение. Чтобы понять, что это означает, давайте начнем с примера.
Пример
Найдите значение x для этой системы.
Уравнение A: [латекс] 4x + 3y = −14 [/ латекс]
Уравнение B: [латекс] y = 2 [/ латекс]
Показать решение Задачу просит решить для x .Уравнение B дает вам значение y , [latex] y = 2 [/ latex], поэтому вы можете подставить 2 в уравнение A для y.
[латекс] \ begin {array} {r} 4x + 3y = −14 \\ y = 2 \, \, \, \, \, \, \, \ end {array} [/ latex]
Подставьте [латекс] y = 2 [/ латекс] в уравнение A.
[латекс] 4x + 3 \ влево (2 \ вправо) = — 14 [/ латекс]
Упростите и решите уравнение для x.
[латекс] \ begin {array} {r} 4x + 6 = −14 \\ 4x = −20 \\ x = −5 \, \, \, \ end {array} [/ latex]
Ответ
[латекс] x = −5 [/ латекс]
Вы можете заменить значение переменной, даже если это выражение.Вот пример.
Пример
Решите для x и y .
Уравнение A: [латекс] y + x = 3 [/ латекс]
Уравнение B: [латекс] x = y + 5 [/ латекс]
Показать решение Цель метода подстановки — переписать одно из уравнений в терминах одной переменной. Уравнение B говорит нам, что [latex] x = y + 5 [/ latex], поэтому имеет смысл заменить [latex] y + 5 [/ latex] в уравнение A для x .
[латекс] \ begin {array} {l} y + x = 3 \\ x = y + 5 \ end {array} [/ latex]
Замените [латекс] y + 5 [/ латекс] в уравнение A для x .
[латекс] \ begin {array} {r} y + x = 3 \\ y + \ left (y + 5 \ right) = 3 \ end {array} [/ latex]
Упростите и решите уравнение для y.
[латекс] \ begin {array} {r} 2y + 5 = \, \, \, \, 3 \\\ подчеркивание {−5 \, \, \, \, \, — 5} \\ 2y = — 2 \\ y = −1 \ end {array} [/ latex]
Теперь найдите x , подставив это значение для y в любое уравнение, и решите для x . Здесь мы будем использовать уравнение A.
[латекс] \ begin {array} {r} y + x = 3 \\ — 1 + x = 3 \\\ подчеркивание {+1 \, \, \, \, \, \, \, \, \, +1} \\ x = 4 \ end {array} [/ latex]
Наконец, проверьте решение [latex] x = 4 [/ latex], [latex] y = −1 [/ latex], подставив эти значения в каждое из исходных уравнений.
[латекс] \ begin {массив} {r} y + x = 3 \\ — 1 + 4 = 3 \\ 3 = 3 \\\ text {TRUE} \ end {array} [/ latex]
[латекс] \ begin {массив} {l} x = y + 5 \\ 4 = −1 + 5 \\ 4 = 4 \\\ text {TRUE} \ end {array} [/ latex]
Ответ
[латекс] x = 4 [/ латекс] и [латекс] y = -1 [/ латекс]
Решение — [латекс] (4, -1) [/ латекс].
Помните, решение системы уравнений должно быть решением каждого из уравнений внутри системы. Упорядоченная пара [latex] (4, −1) [/ latex] действительно работает для обоих уравнений, поэтому вы знаете, что это также решение системы.
Давайте посмотрим на другой пример, замена которого включает свойство распределения.
Пример
Решите для x и y .
[латекс] \ begin {array} {l} y = 3x + 6 \\ — 2x + 4y = 4 \ end {array} [/ latex]
Показать решение Выберите уравнение для замены.
Первое уравнение говорит вам, как выразить y через x , поэтому имеет смысл подставить 3 x + 6 во второе уравнение для y .
[латекс] \ begin {array} {l} y = 3x + 6 \\ — 2x + 4y = 4 \ end {array} [/ latex]
Замените [латекс] 3x + 6 [/ латекс] на y во втором уравнении.
[латекс] \ begin {array} {r} −2x + 4y = 4 \\ — 2x + 4 \ left (3x + 6 \ right) = 4 \ end {array} [/ latex]
Упростите и решите уравнение для x.
[латекс] \ begin {array} {r} −2x + 12x + 24 = 4 \, \, \, \, \, \, \, \\ 10x + 24 = 4 \, \, \, \, \ , \, \, \\\ подчеркивание {−24 \, \, — 24 \, \, \, \,} \\ 10x = −20 \\ x = −2 \, \, \, \ end {array} [/ латекс]
Чтобы найти y , подставьте это значение вместо x обратно в одно из исходных уравнений.
[латекс] \ begin {array} {l} y = 3x + 6 \\ y = 3 \ left (−2 \ right) +6 \\ y = −6 + 6 \\ y = 0 \ end {array} [/ латекс]
Проверьте решение [latex] x = −2 [/ latex], [latex] y = 0 [/ latex], подставив их в каждое из исходных уравнений.
[латекс] \ begin {array} {l} y = 3x + 6 \\ 0 = 3 \ left (−2 \ right) +6 \\ 0 = −6 + 6 \\ 0 = 0 \\\ text { ИСТИНА} \ end {array} [/ latex]
[латекс] \ begin {array} {r} −2x + 4y = 4 \\ — 2 \ left (-2 \ right) +4 \ left (0 \ right) = 4 \\ 4 + 0 = 4 \\ 4 = 4 \\\ текст {ИСТИНА} \ end {array} [/ latex]
Ответ
[латекс] x = -2 [/ латекс] и [латекс] y = 0 [/ латекс]
Решение (−2, 0).
В приведенных выше примерах одно из уравнений уже было дано нам в терминах переменной x или y . Это позволило нам быстро подставить это значение в другое уравнение и найти одно из неизвестных.
Иногда вам, возможно, придется сначала переписать одно из уравнений в терминах одной из переменных, прежде чем вы сможете произвести замену. В приведенном ниже примере вам сначала нужно изолировать одну из переменных, прежде чем вы сможете заменить ее в другое уравнение.
Пример
Решите для x и y .
[латекс] \ begin {array} {r} 2x + 3y = 22 \\ 3x + y = 19 \ end {array} [/ latex]
Показать решение Выберите уравнение для замены. Второе уравнение,
[latex] 3x + y = 19 [/ latex], может быть легко переписан в терминах y , поэтому имеет смысл начать с этого.
[латекс] \ begin {array} 2x + 3y = 22 \\ 3x + y = 19 \ end {array} [/ latex]
Перепишите [латекс] 3x + y = 19 [/ latex] в виде y .
[латекс] \ begin {array} 3x + y = 19 \\ y = 19–3x \ end {array} [/ latex]
Замените [латекс] 19–3x [/ латекс] на y в другом уравнении.
[латекс] \ begin {array} {r} 2x + 3y = 22 \\ 2x + 3 (19–3x) = 22 \ end {array} [/ latex]
Упростите и решите уравнение для x.
[латекс] \ begin {array} {r} 2x + 57–9x = 22 \, \, \, \, \\ — 7x + 57 = 22 \, \, \, \, \\ — 7x = −35 \\ x = 5 \, \, \, \, \, \, \, \ end {array} [/ latex]
Подставьте [latex] x = 5 [/ latex] обратно в одно из исходных уравнений, чтобы найти y.
[латекс] \ begin {array} {r} 3x + y = 19 \, \, \, \, \, \, \, \, \, \, \, \, \\ 3 \ left (5 \ right ) + y = 19 \, \, \, \, \, \, \, \, \, \, \, \, \\ 15 + y = 19 \, \, \, \, \, \, \, \, \, \, \, \, \\ y = 19−15 \\ y = 4 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ end {array} [/ latex]
Проверьте оба решения, подставив их в каждое из исходных уравнений.
[латекс] \ begin {array} {r} 2x + 3y = 22 \\ 2 (5) +3 \ left (4 \ right) = 22 \\ 10 + 12 = 22 \\ 22 = 22 \\\ текст {ИСТИНА} \\\\ 3x + y = 19 \\ 3 \ left (5 \ right) + 4 = 19 \\ 19 = 19 \\\ текст {TRUE} \ end {array} [/ latex]
Ответ
[латекс] x = 5 [/ латекс] и [латекс] y = 4 [/ латекс]
Решение: (5, 4).
В следующем видео вам будет показан пример решения системы двух уравнений с использованием метода подстановки.

Если бы вы выбрали другое уравнение для начала в предыдущем примере, вы все равно смогли бы найти такое же решение. Это действительно вопрос предпочтений, потому что иногда решение для переменной приводит к необходимости работать с дробями. По мере того, как вы приобретете больше опыта в алгебре, вы сможете предвидеть, какой выбор приведет к более желаемым результатам.
Распознавать системы уравнений, не имеющие решения или бесконечное количество решений
Когда мы изучили методы решения линейных уравнений с одной переменной, мы обнаружили, что некоторые уравнения не имеют решений, а другие имеют бесконечное количество решений. Мы снова увидели это поведение, когда начали описывать решения систем уравнений с двумя переменными.
Вспомните этот пример из модуля 1 для решения линейных уравнений с одной переменной:
Решите для x .[латекс] 12 + 2x – 8 = 7x + 5–5x [/ латекс]
[латекс] \ displaystyle \ begin {array} {l} 12 + 2x-8 = 7x + 5-5x \\\, \, \, \, \, \, \, \, \, \, \, \ , \, \, 2x + 4 = 2x + 5 \ end {array} [/ latex]
[латекс] \ begin {array} {l} \, \, \, \, \, \, \, \, \, \, \, \, 2x + 4 = 2x + 5 \\\, \, \ , \, \, \, \, \, \ underline {-2x \, \, \, \, \, \, \, \, \, \, — 2x \, \, \, \, \, \, \, \,} \\\, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \ , \, \, 4 = \, 5 \ end {array} [/ latex]
Это ложное утверждение подразумевает, что не существует решений этого уравнения. Таким же образом вы можете увидеть такой результат, когда используете метод подстановки, чтобы найти решение системы линейных уравнений с двумя переменными.В следующем примере вы увидите пример системы двух уравнений, не имеющей решения.
Пример
Решите для x и y .
[латекс] \ begin {array} {l} y = 5x + 4 \\ 10x − 2y = 4 \ end {array} [/ latex]
Показать решение Поскольку первое уравнение [латекс] y = 5x + 4 [/ latex], вы можете заменить [latex] 5x + 4 [/ latex] на y во втором уравнении.
[латекс] \ begin {array} {r} y = 5x + 4 \\ 10x − 2y = 4 \, \, \, \, \, \, \, \, \, \, \, \, \\ 10x – 2 \ left (5x + 4 \ right) = 4 \, \, \, \, \, \, \, \, \, \, \, \, \ end {array} [/ latex]
Разверните выражение слева.
[латекс] 10x – 10x – 8 = 4 [/ латекс]
Объедините похожие члены в левой части уравнения.
[латекс] 10x – 10x = 0 [/ latex], поэтому у вас остается [latex] −8 = 4 [/ latex].
[латекс] \ begin {array} {r} 0–8 = 4 \\ — 8 = 4 \ end {array} [/ latex]
Ответ
Утверждение [latex] −8 = 4 [/ latex] неверно, поэтому решения нет.
Вы получаете ложное утверждение [латекс] −8 = 4 [/ латекс]. Что это значит? График этой системы проливает свет на то, что происходит.
Прямые параллельны, они никогда не пересекаются, и у этой системы линейных уравнений нет решения. Обратите внимание, что результат [latex] −8 = 4 [/ latex] — это , а не как решение. Это просто ложное утверждение, и оно указывает на то, что не существует решения .
Мы также видели линейные уравнения с одной переменной и системы уравнений с двумя переменными, которые имеют бесконечное количество решений. В следующем примере вы увидите, что происходит, когда вы применяете метод подстановки к системе с бесконечным числом решений.
Пример
Решите относительно x и y.
[латекс] \ begin {массив} {l} \, \, \, y = −0,5x \\ 9y = −4,5x \ end {array} [/ latex]
Показать решение
Подставляя -0,5 x вместо y во втором уравнении, вы получаете следующее:
[латекс] \ begin {array} {r} 9y = −4.5x \\ 9 (−0.5x) = — 4.5 \, \, \, \\ — 4.5x = −4.5x \ end {array} [/ латекс]
На этот раз вы получите верное утверждение: [латекс] −4,5x = −4,5x [/ latex]. Но что означает такой ответ? Опять же, построение графиков может помочь вам разобраться в этой системе.
Эта система состоит из двух уравнений, которые представляют одну и ту же линию; две линии коллинеарны. Каждая точка на линии будет решением системы, и поэтому метод подстановки дает верное утверждение. В этом случае существует бесконечное количество решений.
В следующем видео вы увидите пример решения системы, имеющей бесконечное количество решений.

В следующем видео вы увидите пример решения системы уравнений, не имеющей решений.

Решите систему уравнений методом исключения
Метод исключения для решения систем линейных уравнений использует добавочное свойство равенства. Вы можете добавить одно и то же значение к каждой стороне уравнения, чтобы исключить один из переменных членов. В этом методе вам может потребоваться, а может и не потребоваться сначала умножить члены в одном уравнении на число. Сначала мы рассмотрим примеры, в которых умножение не требуется для использования метода исключения.В следующем разделе вы увидите примеры использования умножения после того, как познакомитесь с идеей метода исключения.
С помощью этого метода легче показать, чем рассказать, поэтому давайте сразу же рассмотрим несколько примеров.
Если сложить два уравнения,
[латекс] x – y = −6 [/ latex] и [latex] x + y = 8 [/ latex] вместе, смотрите, что происходит.
[латекс] \ displaystyle \ begin {array} {l} \, \, \, \, \, xy = \, — 6 \\\ подчеркивание {+ \, x + y = \, \, \, 8} \\\, 2x + 0 \, = \, \, \, \, 2 \ end {array} [/ latex]
Вы исключили член y , и это уравнение можно решить, используя методы решения уравнений с одной переменной.
Давайте посмотрим, как эта система решается методом исключения.
Пример
Используйте устранение, чтобы решить систему.
[латекс] \ begin {array} {r} x – y = −6 \\ x + y = \, \, \, \, 8 \ end {array} [/ latex]
Показать решение Добавьте уравнения.
[латекс] \ displaystyle \ begin {array} {r} xy = \, \, — 6 \\ + \ underline {\, \, x + y = \, \, \, \, \, 8} \\ \, \, \, \, \, \, 2x \, \, \, \, \, = \, \, \, \, \, \, 2 \ end {array} [/ latex]
Решите для x .
[латекс] \ begin {array} {r} 2x = 2 \\ x = 1 \ end {array} [/ latex]
Подставьте [latex] x = 1 [/ latex] в одно из исходных уравнений и решите относительно y .
[латекс] \ begin {array} {l} x + y = 8 \\ 1 + y = 8 \\\, \, \, \, \, \, \, \, \, \, y = 8– 1 \\\, \, \, \, \, \, \, \, \, \, y = 7 \ end {array} [/ latex]
Обязательно проверьте свой ответ в обоих уравнениях!
[латекс] \ begin {array} {r} x – y = −6 \\ 1–7 = −6 \\ — 6 = −6 \\\ text {TRUE} \\\\ x + y = 8 \ \ 1 + 7 = 8 \\ 8 = 8 \\\ текст {ИСТИНА} \ end {array} [/ latex]
Проверяйте ответы.
Ответ
Решение (1, 7).
К сожалению, не все системы справляются с этим легко. Как насчет такой системы, как [латекс] 2x + y = 12 [/ latex] и [latex] −3x + y = 2 [/ latex].Если вы сложите эти два уравнения вместе, никакие переменные не будут исключены.
[латекс] \ displaystyle \ begin {array} {l} \, \, \, \, 2x + y = 12 \\\ подчеркивание {-3x + y = \, \, \, 2} \\ — x + 2y = 14 \ end {array} [/ latex]
Но вы хотите исключить переменную. Итак, давайте добавим противоположность одного из уравнений к другому уравнению. Это означает умножение каждого члена в одном из уравнений на -1, чтобы знак каждого члена был противоположным.
[латекс] \ begin {array} {l} \, \, \, \, 2x + \, \, y \, = 12 \ rightarrow2x + y = 12 \ rightarrow2x + y = 12 \\ — 3x + \, \, y \, = 2 \ rightarrow− \ left (−3x + y \ right) = — (2) \ rightarrow3x – y = −2 \\\, \, \, \, 5x + 0y = 10 \ end {array} [/ латекс]
Вы удалили переменную y , и теперь проблема может быть решена.
В следующем видео описывается аналогичная проблема, при которой можно исключить одну переменную, сложив два уравнения вместе.

Осторожность! Когда вы добавляете противоположность одного целого уравнения к другому, не забудьте изменить знак КАЖДОГО члена с обеих сторон уравнения. Это очень распространенная ошибка.
Пример
Используйте устранение, чтобы решить систему.
[латекс] \ begin {array} {r} 2x + y = 12 \\ — 3x + y = 2 \, \, \, \ end {array} [/ latex]
Показать решение Вы можете исключить переменную y , добавив противоположность одного из уравнений к другому уравнению.
[латекс] \ begin {array} {r} 2x + y = 12 \\ — 3x + y = 2 \, \, \, \ end {array} [/ latex]
Перепишите второе уравнение как противоположное.
Доп. Решите для x .
[латекс] \ begin {array} {r} 2x + y = 12 \, \\ 3x – y = −2 \\ 5x = 10 \, \\ x = 2 \, \, \, \, \ end { array} [/ latex]
Подставьте [latex] y = 2 [/ latex] в одно из исходных уравнений и решите относительно y .
[латекс] \ begin {array} {r} 2 \ left (2 \ right) + y = 12 \\ 4 + y = 12 \\ y = 8 \, \, \, \ end {array} [/ latex ]
Обязательно проверьте свой ответ в обоих уравнениях!
[латекс] \ begin {array} {r} 2x + y = 12 \\ 2 \ left (2 \ right) + 8 = 12 \\ 4 + 8 = 12 \\ 12 = 12 \\\ текст {TRUE} \\\\ — 3x + y = 2 \\ — 3 \ left (2 \ right) + 8 = 2 \\ — 6 + 8 = 2 \\ 2 = 2 \\\ текст {ИСТИНА} \ end {array} [/ латекс]
Проверяйте ответы.
Ответ
Решение (2, 8).
Ниже приведены еще два примера, показывающих, как решать линейные системы уравнений с использованием исключения.
Пример
Используйте устранение, чтобы решить систему.
[латекс] \ begin {array} {r} −2x + 3y = −1 \\ 2x + 5y = \, 25 \ end {array} [/ latex]
Показать решение Обратите внимание на коэффициенты каждой переменной в каждом уравнении. Если вы сложите эти два уравнения, член x будет удален, поскольку [latex] −2x + 2x = 0 [/ latex].
[латекс] \ begin {array} {r} −2x + 3y = −1 \\ 2x + 5y = \, 25 \ end {array} [/ latex]
Складываем и решаем и .
[латекс] \ begin {array} {r} −2x + 3y = −1 \\ 2x + 5y = 25 \, \\ 8y = 24 \, \\ y = 3 \, \, \, \, \ end {array} [/ latex]
Подставьте [латекс] y = 3 [/ latex] в одно из исходных уравнений.
[латекс] \ begin {array} {r} 2x + 5y = 25 \\ 2x + 5 \ left (3 \ right) = 25 \\ 2x + 15 = 25 \ 2x = 10 \ x = 5 \, \, \, \ end {array} [/ latex]
Проверить решения.
[латекс] \ begin {array} {r} −2x + 3y = −1 \\ — 2 \ left (5 \ right) +3 \ left (3 \ right) = — 1 \\ — 10 + 9 = — 1 \\ — 1 = −1 \\\ текст {ИСТИНА} \\\\ 2x + 5y = 25 \\ 2 \ left (5 \ right) +5 \ left (3 \ right) = 25 \\ 10 + 15 = 25 \\ 25 = 25 \\\ текст {ИСТИНА} \ end {array} [/ latex]
Проверяйте ответы.
Ответ
Решение: (5, 3).
Пример
Используйте исключение, чтобы найти x и y.
[латекс] \ begin {array} {r} 4x + 2y = 14 \\ 5x + 2y = 16 \ end {array} [/ latex]
Показать решение Обратите внимание на коэффициенты каждой переменной в каждом уравнении. Вам нужно будет добавить противоположное одному из уравнений, чтобы исключить переменную y , так как [latex] 2y + 2y = 4y [/ latex], но [latex] 2y + \ left (−2y \ right) = 0 [ /латекс].
[латекс] \ begin {array} {r} 4x + 2y = 14 \\ 5x + 2y = 16 \ end {array} [/ latex]
Замените одно из уравнений на противоположное, сложите и решите для x .
[латекс] \ begin {array} {r} 4x + 2y = 14 \, \, \, \, \\ — 5x – 2y = −16 \\ — x = −2 \, \, \, \\ x = 2 \, \, \, \, \, \, \, \ end {array} [/ latex]
Подставьте [latex] x = 2 [/ latex] в одно из исходных уравнений и решите относительно y .
[латекс] \ begin {array} {r} 4x + 2y = 14 \\ 4 \ left (2 \ right) + 2y = 14 \\ 8 + 2y = 14 \\ 2y = 6 \, \, \, \ \ y = 3 \, \, \, \ end {array} [/ latex]
Ответ
Решение: (2, 3).
Проверьте последний пример — подставьте (2, 3) в оба уравнения. Получается два верных утверждения: 14 = 14 и 16 = 16!
Обратите внимание, что вы могли бы использовать противоположное первому уравнению, а не второе уравнение, и получить тот же результат.
Распознавать системы, у которых нет решения или бесконечное количество решений
Как и в случае с методом подстановки, метод исключения иногда удаляет как v ariables, и вы получаете либо истинное, либо ложное утверждение. Напомним, ложное утверждение означает, что решения нет.
Давайте посмотрим на пример.
Пример
Решите для x и y.
[латекс] \ begin {массив} {r} -x – y = -4 \\ x + y = 2 \, \, \, \, \ end {array} [/ latex]
Показать решение Добавьте уравнения, чтобы исключить член x .
[латекс] \ begin {array} {r} -x – y = -4 \\\ подчеркивание {x + y = 2 \, \, \,} \\ 0 = −2 \ end {array} [/ latex ]
Ответ
Нет решения.
Построение этих линий показывает, что они являются параллельными линиями и как таковые не имеют общих точек, подтверждая отсутствие решения.
Если обе переменные исключены и у вас осталось истинное утверждение, это означает, что существует бесконечное количество упорядоченных пар, удовлетворяющих обоим уравнениям. По сути, уравнения — это одна и та же линия.
Пример
Решите для x и y .
[латекс] \ begin {array} {r} x + y = 2 \, \, \, \, \\ — x − y = -2 \ end {array} [/ latex]
Показать решение Добавьте уравнения, чтобы исключить член x .
[латекс] \ begin {array} {r} x + y = 2 \, \, \, \, \\\ underline {-x − y = -2} \\ 0 = 0 \, \, \, \ , \, \ end {array} [/ latex]
Ответ
Существует бесконечное количество решений.
Построение этих двух уравнений поможет проиллюстрировать, что происходит.

В следующем видео система уравнений, не имеющая решений, решается методом исключения.

Решите систему уравнений, когда необходимо умножение, чтобы исключить переменную
Много раз сложение уравнений или добавление противоположности одного из уравнений не приведет к удалению переменной. Посмотрите на систему ниже.
[латекс] \ begin {array} {r} 3x + 4y = 52 \\ 5x + y = 30 \ end {array} [/ latex]
Если вы сложите приведенные выше уравнения или сложите противоположное одному из уравнений, вы получите уравнение, в котором по-прежнему есть две переменные.Итак, давайте теперь сначала воспользуемся свойством умножения равенства. Вы можете умножить обе части одного уравнения на число, которое позволит вам исключить ту же переменную из другого уравнения.
Мы делаем это с умножением. Обратите внимание, что первое уравнение содержит член 4 y , а второе уравнение содержит член y . Если вы умножите второе уравнение на −4, то при сложении обоих уравнений сумма переменных y составит 0.
В следующем примере показаны все шаги по поиску решения для этой системы.
Пример
Решите для x и y .
Уравнение A: [латекс] 3x + 4y = 52 [/ латекс]
Уравнение B: [латекс] 5x + y = 30 [/ латекс]
Показать решение Ищите термины, которые можно исключить. В уравнениях нет членов x или y с одинаковыми коэффициентами.
[латекс] \ begin {array} {r} 3x + 4y = 52 \\ 5x + y = 30 \ end {array} [/ latex]
Умножьте второе уравнение на [латекс] −4 [/ латекс], чтобы получить одинаковый коэффициент.
[латекс] \ begin {array} {l} \, \, \, \, \, \, \, \, \, 3x + 4y = 52 \\ — 4 \ left (5x + y \ right) = — 4 \ влево (30 \ вправо) \ end {array} [/ latex]
Перепишите систему и добавьте уравнения.
[латекс] \ begin {array} {r} 3x + 4y = 52 \, \, \, \, \, \, \, \\ — 20x – 4y = −120 \ end {array} [/ latex]
Решите для x .
[латекс] \ begin {array} {l} −17x = -68 \\\, \, \, \, \, \, \, \, \, \, \, x = 4 \ end {array} [/ latex ]
Подставьте [latex] x = 4 [/ latex] в одно из исходных уравнений, чтобы найти y .
[латекс] \ begin {array} {r} 3x + 4y = 52 \\ 3 \ left (4 \ right) + 4y = 52 \\ 12 + 4y = 52 \\ 4y = 40 \\ y = 10 \ end {array} [/ latex]
Проверьте свой ответ.
[латекс] \ begin {array} {r} 3x + 4y = 52 \\ 3 \ left (4 \ right) +4 \ left (10 \ right) = 52 \\ 12 + 40 = 52 \\ 52 = 52 \\\ текст {ИСТИНА} \\\\ 5x + y = 30 \\ 5 \ влево (4 \ вправо) + 10 = 30 \\ 20 + 10 = 30 \\ 30 = 30 \\\ текст {ИСТИНА} \ конец {array} [/ latex]
Проверяйте ответы.
Ответ
Решение (4, 10).
Осторожность! Когда вы используете умножение для исключения переменной, вы должны умножить КАЖДЫЙ член в уравнении на выбранное вами число.Забыть умножить каждый член — распространенная ошибка.
Есть и другие способы решить эту систему. Вместо умножения одного уравнения с целью исключения переменной при добавлении уравнений вы могли бы умножить и уравнений на разные числа.
На этот раз удалим переменную x . Умножьте уравнение A на 5 и уравнение B на [латекс] -3 [/ латекс].
Пример
Найдите x и y .
[латекс] \ begin {array} {r} 3x + 4y = 52 \\ 5x + y = 30 \ end {array} [/ latex]
Показать решение Ищите термины, которые можно исключить.В уравнениях нет членов x или y с одинаковым коэффициентом.
[латекс] \ begin {array} {r} 3x + 4y = 52 \\ 5x + y = 30 \ end {array} [/ latex]
Чтобы использовать метод исключения, вы должны создать переменные с одинаковым коэффициентом — тогда вы можете их исключить. Умножьте верхнее уравнение на 5.
[латекс] \ begin {array} {r} 5 \ left (3x + 4y \ right) = 5 \ left (52 \ right) \\ 5x + y = 30 \, \, \, \, \, \, \, \, \, \, \, \, \\ 15x + 20y = 260 \, \, \, \, \, \, \\ 5x + y = 30 \, \, \, \, \, \, \, \, \, \ end {array} [/ latex]
Теперь умножьте нижнее уравнение на −3.
[латекс] \ begin {array} {r} 15x + 20y = 260 \, \, \, \, \, \, \, \, \\ — 3 (5x + y) = — 3 (30) \\ 15x + 20y = 260 \, \, \, \, \, \, \, \, \\ — 15x – 3y = −90 \, \, \, \, \, \, \, \ end {array} [ / латекс]
Затем сложите уравнения и решите относительно y .
[латекс] \ begin {array} {r} 15x + 20y = 260 \\ — 15x – 3y = \, — 90 \\ 17y = 170 \\ y = \, \, \, 10 \ end {array} [ / латекс]
Подставьте [latex] y = 10 [/ latex] в одно из исходных уравнений, чтобы найти x .
[латекс] \ begin {array} {r} 3x + 4y = 52 \\ 3x + 4 \ left (10 \ right) = 52 \\ 3x + 40 = 52 \\ 3x = 12 \ x = 4 \, \, \, \ end {array} [/ latex]
Вы пришли к тому же решению, что и раньше.
Ответ
Решение (4, 10).
Эти уравнения были умножены на 5 и [латекс] −3 [/ латекс] соответственно, потому что это дало вам члены, которые в сумме дают 0. Не забудьте умножить все члены уравнения.
В следующем видео вы увидите пример использования метода исключения для решения системы уравнений.

Можно использовать метод исключения с умножением и получить результат, который не указывает решений или бесконечно много решений, точно так же, как с другими методами, которые мы изучили для поиска решений систем.В следующем примере вы увидите систему, которая имеет бесконечно много решений.
Пример
Решите для x и y .
Уравнение A: [латекс] x-3y = -2 [/ латекс]
Уравнение B: [латекс] -2x + 6y = 4 [/ латекс]
Показать решение Ищите термины, которые можно исключить. В уравнениях нет членов x или y с одинаковыми коэффициентами.
[латекс] \ begin {array} {r} x-3y = -2 \\ — 2x + 6y = 4 \ end {array} [/ latex]
Умножьте первое уравнение на [latex] 2 [/ latex] так, чтобы члены x уравнялись.
[латекс] \ begin {array} {l} \, \, \, \, \, \, \, \, \, 2 \ left (x-3y \ right) = 2 \ left (-2 \ right) \\ — 2x + 6y = 4 \ end {array} [/ latex]
Перепишите систему и добавьте уравнения.
[латекс] \ begin {array} {r} 2x-6y = -4 \\ — 2x + 6y = 4 \\ 0x + 0y = 0 \\\, \, \, \, \, \, \, \ , 0 = 0 \ end {array} [/ latex]
Вам знакомо такое решение? Это представляет собой решение всех действительных чисел для линейных уравнений, и это представляет то же самое, когда вы получаете такой результат с системами. Если мы решим оба этих уравнения относительно y, вы увидите, что это одно и то же уравнение.
Решите уравнение A относительно y:
[латекс] \ begin {array} {r} x-3y = -2 \\ — 3y = -x-2 \\ y = \ frac {1} {3} x + \ frac {2} {3} \ end {array} [/ latex]
Решите уравнение B относительно y:
[латекс] \ begin {array} -2x + 6y = 4 \\ 6y = 2x + 4 \\ y = \ frac {2} {6} x + \ frac {4} {6} \ end {array} [/ латекс]
Уменьшите дроби, разделив числитель и знаменатель обеих дробей на 2:
[латекс] y = \ frac {1} {3} + \ frac {2} {3} [/ latex]
Оба уравнения одинаковы, если записаны в форме пересечения наклона, и поэтому набором решений для системы являются все действительные числа.
Ответ
Решение: x и y могут быть действительными числами.
В следующем видео метод исключения используется для решения системы уравнений. Обратите внимание, что сначала нужно умножить одно из уравнений на отрицательное. Кроме того, у этой системы есть бесконечное количество решений.

Сводка
Метод подстановки — это один из способов решения систем уравнений. Чтобы использовать метод подстановки, используйте одно уравнение, чтобы найти выражение для одной из переменных в терминах другой переменной.Затем замените это выражение этой переменной во втором уравнении. Затем вы можете решить это уравнение, поскольку теперь оно будет иметь только одну переменную. Решение с использованием метода подстановки даст один из трех результатов: одно значение для каждой переменной в системе (с указанием одного решения), неверное утверждение (с указанием отсутствия решений) или истинное утверждение (с указанием бесконечного числа решений).
Объединение уравнений — мощный инструмент для решения системы уравнений.Сложение или вычитание двух уравнений для исключения общей переменной называется методом исключения (или добавления). Как только одна переменная исключена, становится намного проще найти другую.
Умножение можно использовать для создания условий соответствия в уравнениях перед их объединением, чтобы помочь в поиске решения системы. При использовании метода умножения важно умножить все члены с обеих сторон уравнения, а не только один член, который вы пытаетесь исключить.
Решайте уравнения и упрощайте выражения с помощью программы «Пошаговое решение математических задач»
Алгебра
Раздел алгебры QuickMath позволяет вам манипулировать математическими выражениями всевозможными полезными способами. На данный момент QuickMath может расширять, разлагать на множители или упрощать практически любое выражение, отменять общие множители в дробях, разбивать дроби на более мелкие («частичные») дроби и объединять две или более дроби в одну дробь. На подходе более специализированные команды.
Что такое алгебра?
Термин «алгебра» используется для обозначения многих вещей в математике, но в этом разделе мы будем говорить только о том типе алгебры, с которым вы сталкиваетесь в старшей школе.
Алгебра — это раздел элементарной математики, в котором символы используются для обозначения неизвестных величин. В более общем смысле он состоит из решения уравнений или манипулирования выражениями, которые содержат символы (обычно буквы, такие как x, y или z), а также числа и функции. Хотя решение уравнений на самом деле является частью алгебры, это настолько большая область, что для нее есть отдельный раздел в QuickMath.
Эта часть QuickMath имеет дело только с алгебраическими выражениями. Это математические утверждения, которые содержат буквы, числа и функции, но не содержат знаков равенства. Вот несколько примеров простых алгебраических выражений:
х ²-1
х ² -2x + 1
ab ² + 3a ³ b-5ab
х ³ +1
Развернуть
Команда расширения используется в основном для перезаписи многочленов с умножением всех скобок и целых числовых степеней, а также всех подобных терминов, собранных вместе.В расширенном разделе у вас также есть возможность развернуть тригонометрические функции, развернуть по модулю любого целого числа и оставить нетронутыми определенные части выражения, а остальные развернуть.
Перейти на страницу «Развернуть»
Фактор
Команда factor попытается переписать выражение как произведение меньших выражений. Он заботится о таких вещах, как вычитание общих множителей, факторизация по парам, квадратичные трехчлены, разности двух квадратов, суммы и разности двух кубов и многое другое.Расширенный раздел включает в себя варианты факторизации тригонометрических функций, факторизации по модулю любого целого числа, факторизации по полю гауссовских целых чисел (как раз то, что нужно для этих сложных сумм квадратов) и даже расширения поля, по которому факторизация происходит с вашими собственными расширениями.
Перейти на страницу Фактора
Упростить
Упрощение, пожалуй, самая сложная из всех команд для описания. Способ выполнения упрощения в QuickMath заключается в рассмотрении множества различных комбинаций преобразований выражения и выборе того, которое имеет наименьшее количество частей.Помимо прочего, команда «Упростить» позаботится об отмене общих множителей сверху и снизу дроби и сборе похожих терминов. Расширенные параметры позволяют упростить тригонометрические функции или указать QuickMath усерднее пытаться найти упрощенное выражение.
Перейти на страницу упрощения
Отмена
Команда отмены позволяет исключить общие множители в знаменателе и числителе любой дроби, встречающейся в выражении.Эта команда отменяет наибольший общий делитель знаменателя и числителя.
Перейти на страницу отмены
Неполные дроби
Команда частичных дробей позволяет разбить рациональную функцию на сумму или разность дробей. Рациональная функция — это просто частное двух многочленов. Любую рациональную функцию можно записать в виде суммы дробей, где знаменатели дробей являются степенями множителей знаменателя исходного выражения.Эта команда особенно полезна, если вам нужно интегрировать рациональную функцию. Разделив его сначала на частичные фракции, часто можно значительно упростить интеграцию.
Перейти на страницу с неполными дробями
Объединить дроби
Команда объединения дробей по существу выполняет обратную операцию по сравнению с командой частичных дробей. Он перепишет ряд дробей, которые будут добавлены или вычтены как одна дробь. Знаменателем этой единственной дроби обычно будет наименьшее общее кратное знаменателей всех добавляемых или вычитаемых дробей.Все общие множители в числителе и знаменателе ответа автоматически исключаются.
Перейти на страницу Объединить фракции
Понятие корреспонденции часто встречается в повседневной жизни. Для Например, каждой книге в библиотеке соответствует количество страниц в книга. Другой пример: каждому человеку соответствует дата рождения. К приведите третий пример, если температура воздуха регистрируется на протяжении всего день, то в каждый момент времени есть соответствующая температура.
Приведенные нами примеры соответствий включают два множества X и Y. В нашем первом примере X обозначает набор книг в библиотеке, а Y — набор положительные целые числа. Каждой книге x в X соответствует положительное целое число y, а именно количество страниц в книге. Во втором примере, если мы положим X обозначить множество всех людей и Y множество всех возможных дат, затем каждому человеку x в X соответствует дата рождения y.
Иногда мы представляем соответствия диаграммами типа, показанного на Фигура 1.17, где множества X и Y представлены точками внутри областей в самолет. Изогнутая стрелка указывает, что элемент y из Y соответствует элемент x из X. Мы изобразили X и Y как разные множества. Однако X и Y могут имеют общие элементы. На самом деле, мы часто имеем X = Y.
Наши примеры показывают, что каждому x в X соответствует один и только один у в Y; то есть y уникален для данного x. Однако тот же элемент Y может соответствуют различным элементам X.Например, две разные книги могут иметь одинаковое количество страниц, два разных человека могут иметь один и тот же день рождения, и скоро.
В большей части нашей работы X и Y будут наборами действительных чисел. Для иллюстрации пусть X и Y оба обозначают множество R действительных чисел, и для каждого действительного числа x обозначим назначьте его квадрат x ². Таким образом, к 3 мы присваиваем 9, к — 5 мы назначаем 25, и скоро. Это дает нам соответствие от R до R. Все примеры Приведенные нами соответствия являются функциями, как определено ниже.
Определение
Функция f из множества X в множество Y — это соответствие, которое присваивается каждому element x of X уникальный элемент y из Y. Элемент y называется изображением x. под f и обозначается f (x). Множество X называется областью определения функции. Диапазон функции состоит из всех изображений элементов X.
Ранее мы ввели обозначение f (x) для элемента Y, который соответствует x. Обычно это читается как «е из х». Мы также называем f (x) значением f в x.С точки зрения графического представления, данного ранее, теперь мы можем набросайте диаграмму, как на рисунке 1.18. Изогнутые стрелки указывают на то, что элементы f (x), f (w), f (z) и f (a) из Y соответствуют элементам x, y, z и a из X. Повторим тот важный факт, что каждому x из X соответствует ровно одно изображение f (x) в Y; однако различные элементы X, такие как w и z на рисунке 1.18 может иметь такое же изображение в Y.
Начинающих студентов иногда путают символы f и f (x).Помнить что f используется для представления функции. Его нет ни в X, ни в Y. Однако f (x) — это элемент Y, а именно элемент, который f присваивает x. Две функции Говорят, что f и g от X до Y равны, записывается
для каждого x в X.
Пример 1 Пусть f будет функцией с областью определения R, такой что f (x) = x ² для каждого x в R. Найдите f (-6) и f (a), где a — любое действительное число. Что это диапазон f?
Решение Значения f (или изображения под f) можно найти, заменив x в уравнение f (x) = x ².Таким образом:
Если T обозначает отключенный диапазон, то по предыдущему определению T состоит из всех числа вида f (a), где a находится в R . Следовательно, T — это множество всех квадраты ², где а — действительное число. Поскольку квадрат любого реального число неотрицательно. T содержится во множестве всех неотрицательных действительных числа. Более того, каждое неотрицательное действительное число c является изображением под символом f, так как . Следовательно, диапазон f — это набор всех неотрицательных действительных чисел.
Если функция определена, как в предыдущем примере, символ, используемый для переменная несущественна; то есть такие выражения, как:
и так далее, все определяют одну и ту же функцию.Это правда, потому что если a есть число в области f, то получается такое же изображение a ² no имеет значение, какое выражение используется.
Пример 2 Пусть X обозначает набор неотрицательных действительных чисел и пусть f будет функция от X до R определяется для каждого x из X. Найдите f (4) и f (пи). Если b и c находятся в X, найдите f (b + c) и f (b) + f (c).
Решение Как и в Примере 1, поиск изображений под f — это просто вопрос подставив соответствующее число вместо x в выражение для f (x).Таким образом:
Многие формулы, встречающиеся в математике и естественных науках, определяют функции. В качестве иллюстрации формула A = pi * r ² для площади A круга радиуса r присваивает каждому положительному действительному числу r уникальное значение A. Это определяет функцию f, где f (r) = pi * r ², и мы можем написать А = f (r). Буква r, обозначающая произвольное число из выключенного домена, часто называют независимой переменной. Буква А, обозначающая число из диапазона off, называется зависимой переменной, так как ее значение зависит от номер, присвоенный tor.Когда две переменные r и A связаны таким образом, принято использовать фразу A — это функция от r. Приведу еще один пример: если автомобиль едет со скоростью 50 миль в час, то расстояние d (мили), пройденное за время t (часы), определяется как d = 50t и, следовательно, расстояние d зависит от времени t.
Мы видели, что разные элементы в области определения функции могут иметь тот же образ. Если изображения всегда разные, то, как в следующем определении, функция называется однозначной.
Определение алгебраического метода
Что такое алгебраический метод?
Алгебраический метод относится к различным методам решения пары линейных уравнений, включая построение графиков, замену и исключение.
Что вам говорит алгебраический метод?
Метод построения графиков включает построение графиков двух уравнений. Пересечение двух линий будет координатой x, y, которая является решением.
Используя метод подстановки, переставьте уравнения, чтобы выразить значение переменных x или y в терминах другой переменной.Затем замените этим выражением значение этой переменной в другом уравнении.
Например, чтобы решить:
Взаимодействие с другими людьми 8 Икс + 6 у знак равно 1 6 — 8 Икс — 4 у знак равно — 8 \ begin {выровнен} & 8x + 6y = 16 \\ & {- 8} x-4y = -8 \\ \ end {выровнен} 8x + 6y = 16−8x − 4y = −8
Во-первых, используйте второе уравнение, чтобы выразить x через y:
Взаимодействие с другими людьми — 8 Икс знак равно — 8 + 4 у Икс знак равно — 8 + 4 у — 8 Икс знак равно 1 — 0 . 5 у {-8} x = -8 + 4yx = \ frac {-8 + 4y} {{- 8} x} = 1-0,5y −8x = −8 + 4yx = −8x − 8 + 4y = 1−0.5лет
Затем замените 1 — 0,5y на x в первом уравнении:
Взаимодействие с другими людьми 8 ( 1 — 0 . 5 у ) + 6 у знак равно 1 6 8 — 4 у + 6 у знак равно 1 6 8 + 2 у знак равно 1 6 2 у знак равно 8 у знак равно 4 \ begin {align} & 8 \ left (1-0,5y \ right) + 6y = 16 \\ & 8-4y + 6y = 16 \\ & 8 + 2y = 16 \\ & 2y = 8 \\ & y = 4 \\ \ end {выровнено} 8 (1−0,5y) + 6y = 168−4y + 6y = 168 + 2y = 162y = 8y = 4
Затем замените y во втором уравнении на 4, чтобы найти x:
Взаимодействие с другими людьми 8 Икс + 6 ( 4 ) знак равно 1 6 8 Икс + 2 4 знак равно 1 6 8 Икс знак равно — 8 Икс знак равно — 1 \ begin {align} & 8x + 6 \ left (4 \ right) = 16 \\ & 8x + 24 = 16 \\ & 8x = -8 \\ & x = -1 \\ \ end {align} 8x + 6 (4) = 168x + 24 = 168x = −8x = −1
Второй метод — метод исключения.Он используется, когда одна из переменных может быть исключена путем сложения или вычитания двух уравнений. В случае этих двух уравнений мы можем сложить их вместе, чтобы исключить x:
Взаимодействие с другими людьми 8 Икс + 6 у знак равно 1 6 — 8 Икс — 4 у знак равно — 8 0 + 2 у знак равно 8 у знак равно 4 \ begin {align} & 8x + 6y = 16 \\ & {- 8} x-4y = -8 \\ & 0 + 2y = 8 \\ & y = 4 \\ \ end {align} 8x + 6y = 16−8x − 4y = −80 + 2y = 8y = 4
Теперь, чтобы найти x, подставьте значение y в любое уравнение:
Взаимодействие с другими людьми 8 Икс + 6 у знак равно 1 6 8 Икс + 6 ( 4 ) знак равно 1 6 8 Икс + 2 4 знак равно 1 6 8 Икс + 2 4 — 2 4 знак равно 1 6 — 2 4 8 Икс знак равно — 8 Икс знак равно — 1 \ begin {align} & 8x + 6y = 16 \\ & 8x + 6 \ left (4 \ right) = 16 \\ & 8x + 24 = 16 \\ & 8x + 24-24 = 16-24 \\ & 8x = -8 \\ & x = -1 \\ \ end {выровнено} 8x + 6y = 168x + 6 (4) = 168x + 24 = 168x + 24−24 = 16−248x = −8x = −1
Ключевые выводы
Алгебраический метод — это набор из нескольких методов, используемых для решения пары линейных уравнений с двумя переменными.
Наиболее часто используемые алгебраические методы включают метод подстановки, метод исключения и метод построения графиков.
Решайте уравнения и упрощайте выражения (Алгебра 2, Уравнения и неравенства) — Mathplanet
В алгебре 1 нас учат, что два правила решения уравнений — это правило сложения и правило умножения / деления.
Правило сложения для уравнений говорит нам, что одна и та же величина может быть добавлена к обеим сторонам уравнения без изменения набора решений уравнения.
Пример
$$ \ begin {array} {lcl} 4x-12 & = & 0 \\ 4x-12 + 12 & = & 0 + 12 \\ 4x & = & 12 \\ \ end {array} $$
Добавление 12 к каждой стороне уравнения в первой строке примера — это первый шаг в решении уравнения. Мы не меняли решение, добавляя по 12 с каждой стороны, поскольку и второе, и третье уравнения имеют одно и то же решение. Уравнения с одинаковыми наборами решений называются эквивалентными уравнениями.
Правило умножения / деления для уравнений говорит нам, что каждый член в обеих частях уравнения может быть умножен или разделен на один и тот же член (кроме нуля) без изменения набора решений уравнения.
Пример
$$ \ begin {array} {lcl} 4x-12 & = & 0 \\ 4x-12 + 12 & = & 0 + 12 \\ 4x & = & 12 \\ \ frac {4x} {4} & = & \ frac {12} {4} \\ x & = & 3 \\ \ end {array} $$
Когда мы упрощаем выражение, мы действуем в следующем порядке:
Упростите выражения внутри скобок, скобок, фигурных скобок и дробей.
Оцените все силы.
Все умножения и деления делайте слева направо.{2} -2)} {\ sqrt {2}} $$
Сначала мы упрощаем выражение в круглых скобках, вычисляя степени, а затем выполняем вычитание внутри него.
$$ \ frac {(4-2)} {\ sqrt {2}} $$
$$ \ frac {(2)} {\ sqrt {2}} $$
Затем мы убираем скобки и умножаем знаменатель и числитель на √2.
$$ \ frac {2 \ cdot \ sqrt {2}} {\ sqrt {2} \ cdot \ sqrt {2}} $$
В качестве последнего шага мы делаем все умножения и деления слева направо.
$$ \ frac {2 \ cdot \ sqrt {2}} {2} $$
$$ \ sqrt {2} $$
Видеоурок
Решите данное уравнение
$$ 12 (\ frac {3b-b} {4a}) = 36 $$

Решение уравнения — методы решения простых уравнений — правило, пример, упрощение и свойство
Уравнение — это алгебраическое выражение, которое обычно связывает неизвестные переменные с другими переменными или константами.Например, x + 2 = 15 — это уравнение, как и y ² = 4. Решение или корень уравнения — это любое значение или набор значений, которые можно подставить в уравнение, чтобы сделать его верное утверждение. В нашем первом примере решение для x равно 13. Во втором примере есть два значения, которые сделают утверждение истинным, а именно 2 и -2. Эти значения составляют набор решений уравнения.
Используя два основных правила алгебры, можно получить решения многих простых уравнений.Первое правило гласит, что одна и та же величина может быть добавлена к обеим сторонам уравнения без изменения решения уравнения. Например, уравнение x + 4 = 7 имеет решение x = 3. Согласно первому правилу, мы можем добавить любое число к обеим сторонам уравнения и при этом получить то же решение. При добавлении 4 к обеим частям уравнение становится x + 8 = 11, но решение остается x = 3. Это правило известно как аддитивное свойство равенства. Чтобы использовать это свойство для поиска решения уравнения, все, что требуется, — это выбрать правильное число для добавления.Решение нашего предыдущего примера x + 4 = 7 можно найти, прибавив -4 к обеим сторонам уравнения. Если это сделано, уравнение упрощается до x + 4-4 = 7-4 или x = 3, и уравнение решается.
Второе фундаментальное правило, известное как мультипликативное свойство равенства, гласит, что каждый член в обеих частях уравнения может быть умножен или разделен на одно и то же число без изменения решения уравнения. Например, решение уравнения y — 2 = 10 — y = 12.Используя мультипликативное правило, мы можем получить эквивалентное уравнение с тем же множеством решений, умножив обе части на любое число, например 2. Таким образом, уравнение принимает вид 2y — 4 = 20, но решение остается y = 12. Это свойство также можно использовать для решения алгебраических уравнений. В случае уравнения 2x = 14 решение получается делением обеих частей на 2. Когда это делается 2x / 2 = 14/2, уравнение упрощается до x = 7.
Часто оба этих правила необходимо использовать для решения одного уравнения, например уравнения 4x + 7 = 23.В этом уравнении к обеим сторонам уравнения добавляется -7, и оно упрощается до 4x = 16. Обе части этого уравнения затем делятся на 4, и это упрощается до решения, x = 4.
.
No related posts.