Расчет площади многоугольника онлайн
Калькулятор считает площадь многоугольника по введенным вами сторонами и диагоналям, главное чтобы диагонали делили многоугольник на несколько треугольников, которые в свою очередь не пересекались бы между собой.
И так, глядя на рисунок, можно сразу представить, что площадь данного многоугольника будет равна сумме площади трех треугольников, расположенных внутри многоугольника.
Для начала расчетов вам придется внимательно внести в таблицу значения сторон ваших треугольников.
Все остальное калькулятор сделает за вас. Пользуйтесь.
The field is not filled.
‘%1’ is not a valid e-mail address.
Please fill in this field.
The field must contain at least% 1 characters.
The value must not be longer than% 1 characters.
Field value does not coincide with the field ‘%1’
An invalid character. Valid characters:’%1′.
Expected number.
It is expected a positive number.
Expected integer.
It is expected a positive integer.
The value should be in the range of [%1 .. %2]
The ‘% 1’ is already present in the set of valid characters.
The field must be less than 1%.
The first character must be a letter of the Latin alphabet.
Su
Mo
Tu
We
Th
Fr
Sa
January
February
March
April
May
June
July
August
September
October
November
December
century
B.C.
%1 century
An error occurred while importing data on line% 1. Value: ‘%2’. Error: %3
Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).
%3.%2.%1%4
%3.%2.%1%4 %6:%7
s.sh.
u.sh.
v.d.
z.d.
yes
no
Wrong file format. Only the following formats: %1
Please leave your phone number and / or email.
hostciti.net
Калькулятор многоугольника
Расчет площади по длине стороны:
Площадь Многоугольника = ((side)² * N) / (4Tan(π / N))
Периметр Многоугольника = N * (side)
Расчет площади по радиусу описанной окружности :
Площадь Многоугольника = ½ * R² * Sin(2π / N)
Расчет площади по радиусу вписанного круга :
Площадь Многоугольника = A² * N * Tan(π / N)
где, A = R * Cos(π / N)
По радиусу вписанного круга и длине стороны :
Площадь Многоугольника = (A * P) / 2
где A = сторона / (2 * Tan(π / N))
где,
- N = Количество сторон,
- A = Радиус вписанного круга,
- R = Радиус описанной окрудности,
- P = Периметр
Примеры:
Задача 1: Найдите площадь и периметр многоугольника, если длина стороны = 2 и количество сторон = 4.
Шаг 1: Найдем площадь.
Площадь = ((длина стороны)² * N) / (4Tan(π / N))
= ((2)² * 4) / (4 * Tan(3.14 / 4))
= (4 * 4) / 4 * Tan(0.785)
= 16 / 4 * 0.999
= 16 / 3.996
Площадь = 4.
Шаг 2: Найдем периметр.
Периметр = (N * (длина стороны) = 4 * 2 = 8
Задача 2: Найдите площадь и периметр многоугольника, если радиус описанной окружности = 2, количество сторон многоугольника = 5.
Шаг 1: Найдем площадь.
Площадь = ½ * R² * Sin(2π / N)
= (0.5) * 2² * Sin(2 * 3.14 / 5)
= 0.5 * 4 * Sin(6.28 / 5)
= 2 * 0.95
Площадь = 1.9.
Задача 3:Найдите площадь многоугольника с радиусом описанной окружности равному 2 и количеству сторон 5, используя радиус вписанного круга.
Шаг 1: Найдем радиус вписанного круга.
А = R * Cos(π / N)
= 2 * Cos(3.14 / 5)
= 2 * Cos(0.63)
= 2 * 0.81
Апофема (радиус вписанного круга) = 1.62.
Шаг 2: Найдем площадь.
Площадь = A² * N * Tan(π / N)
= 1.62² * 5 * Tan(3.14 / 5)
= 2.62 * 5 * Tan(0.63)
= 13.1 * 0.73
Площадь = 9.5.
Задача 4: Найти площадь многоугольника используя Апофему (радиус вписанного круга), если длина стороны равна 2, а количество сторон 5.
Step 1: Найдем Апофему.
Апофема = длина стороны / (2 * Tan(π / N))
= 2 / (2 * Tan(π / 4))
= 2 / (2 * Tan(0.785))
= 2 / (2 * 0.999)
= 2 / 1.998
Апофема (А) = 1.
Шаг 2: Найдем периметр.
Периметр (P) = (N * (длина стороны) = 4 * 2 = 8
Шаг 3: Найдем площадь.
Площадь = (A * P) / 2
= (1 * 8) / 2
= 8 / 2
Площадь = 4.
Приведенные выше примеры показывают, как вычислить площадь и периметр многоугольника вручную.
wpcalc.com
Вычисление площади выпуклого многоугольника по координатам вершин на плоскости
Калькулятор ниже был написан для решения частной задачи расчета площади выпуклого четырехугольника по координатам его вершин. Он только обобщает эту задачу до задачи расчета площади любого выпуклого многоугольника вообще. Собственно, на сайте уже был подобный калькулятор Площадь многоугольника, но там требовалось вводить длины сторон и диагоналей, а это несколько труднее, чем вводить только координаты вершин.
Принцип работы остается таким же — многоугольник разбивается на непересекающиеся треугольники, подсчитывается площадь всех треугольников (это легко сделать зная длины всех трех сторон — Расчет площади треугольника по формуле Герона), затем площади суммируются. Основная проблема была в том, чтобы сделать его устойчивым к ситуации, когда точки вводят не по порядку. Предположим, сначала вводят первые четыре точки получая фигуру на рисунке ниже
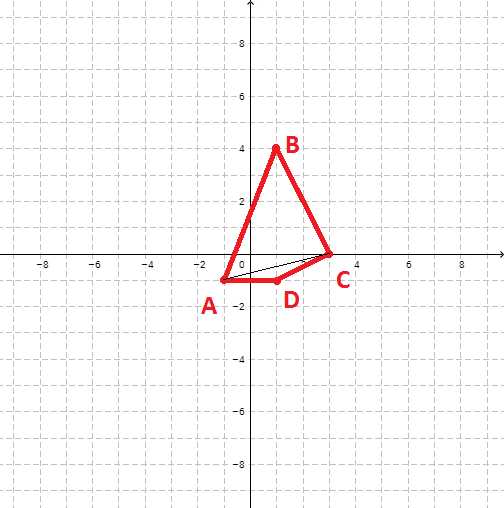 Четырехугольник
ЧетырехугольникПри добавлении следующей точки, например, так, как на следующем рисунке
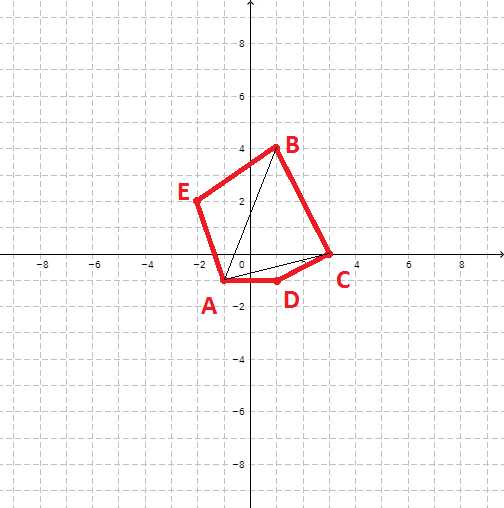 Пятиугольник
Пятиугольникдолжен уже получиться многоугольник ADCBE, а не ABCDE, разбитый на треугольники ADC, ACB и ABE, соответственно.
Чтобы получить правильный многоугольник, фактически требуется получить оболочку введенных точек. Для этого калькулятор использует алгоритм Джарвиса (или алгоритм обхода Джарвиса, или алгоритм заворачивания подарка), который определяет последовательность элементов множества, образующих выпуклую оболочку для этого множества. Метод можно представить как обтягивание верёвкой множества вбитых в доску гвоздей.
Алгоритм работает за время , где n — общее число точек на плоскости, h — число точек в выпуклой оболочке. Для выпуклого многоугольник соответственно будет . Не самый оптимальный алгоритм, зато очень простой, и для этого калькулятора вполне производительный.
Как пользоваться калькулятором: начинаете вводить координаты точек выпуклого многоугольника. Начиная с трех точек алгоритм Джарвиса будет стоить обтягивающий контур, затем контур будет разбиваться треугольники и подсчитываться общая площадь. Для справки также будут выводиться площади всех треугольников.
addimport_exportmode_editdeleteТочки многоугольника
Размер страницы: 5102050100chevron_leftchevron_rightДля разделения полей можно использовать один из этих символов: Tab, «;» или «,» Пример: Lorem ipsum;-50.5;-50.5
Точность вычисленияЗнаков после запятой: 2
Выпуклый многоугольник
Общая площадь
Сохранить share extension
planetcalc.ru
Площадь многоугольника по координатам онлайн
| Вы ввели следующие координаты многоугольника |
| Площадь заданного многоугольника (в условных единицах) |
Описание
Сервис позволяет высчитывать по заданным координатам вершин площадь многоугольника (треугольника, трапеции, паралеллограмма, пятиугольника и т.д) а также любых других непересекающихся многоугольников.
Используется метод трапеций, суть которого заключается в том, что многоугольник представляет собой сумму трапеций, две вершины из которого это две соседние вершины многоугольника, а две другие вершины трапеции, есть абсциссы координат двух вершин многоугольника.
Такой метод позволяет рассчитывать не только выпусклые многоугольники, но и любые другие, главное, что бы линии этого многоугольника не пересекались.
Есть еще два подобных сервиса: Площадь пересечения окружностей и Прямая линия
Кроме этого стоит обратить внимание на такие материалы как: Касательная к кривой второго порядка
Пересечение прямой и кривой второго порядка
Расчет кривых второго порядка на плоскости
Синтаксис
Кто использует XMPP клиента: mnog <координаты вершин>
Кто вводит данные через этот сайт: <координаты вершин>
Координаты вершин задаются в общей строке вида x1:y1 x2:y2 x3:y3 ….xn:yn
Координаты вершин являются действительные числа.
Координата каждой точки (абсцисса и ордината) записывается через двоеточие(без пробелов!)
Координаты вершин вводятся ПОСЛЕДОВАТЕЛЬНО по часовой или(!) против часовой стрелки.
Каждая координата вида x:y должен быть отделена пробелами от другой.
Нет никаких ограничений на количество координат вершин.
Примеры
mnog 5:7 9:7 10:2 2:2
Площадь многоугольника заданный координатами 5:7 9:7 10:2 2:2
равен 30
- Площадь пересечения окружностей на плоскости >>
abakbot.ru
онлайн калькулятор, формулы, примеры решений
Цель:
- закрепить понятие площади.
- вывести формулу площади правильного многоугольника.
- провести лабораторно-исследовательскую работу на тему: “Какой многоугольник имеет наибольшую площадь”.
Ход урока
Устно(5-7 минут). 1. Какая фигура изображена на рисунке? (многоугольник)
Обсуждается с классом, что уже известно о многоугольниках:
а) какая фигура называется многоугольником;
б) виды многоугольников (выпуклый, невыпуклый, правильный, неправильные)
Определить на каждом рисунке вид многоугольника.
- В какую фигуру обычно вписывают многоугольники? (0кружность).
- Какой многоугольник называется вписанным? (Если все его вершины являются точками окружности).
- Какой многоугольник называется описанным? (Если все стороны многоугольника касаются окружности).
Мы уже на протяжении нескольких уроков изучаем площади различных четырехугольников и треугольника, а на этом уроке рассмотрим общий случай.
Как вычислить площадь произвольного многоугольника? Как вы думаете, площадь какого многоугольника проще всего посчитать?
Предлагаю изобразить невыпуклый, выпуклый неправильный, выпуклый правильный пятиугольник.
Невыпуклый пятиугольник разбили на два разных треугольника, надо считать площадь каждого треугольника и складывать.
Выпуклый неправильный пятиугольник Аналогичное решение.
Правильный пятиугольник разбивается на равные треугольники. Достаточно найти площадь одного треугольника и умножить на их количество.
Значит проще всего находить площадь правильного многоугольника.
Но ученые не остановились на этом, они вывели формулу площади для правильного многоугольника. Эту теорему мы сейчас докажем.
Теорема. Площадь правильного многоугольника равна половине произведения периметра многоугольника на радиус вписанной окружности.
Дано: А 1 …….А n — многоугольник правильный,
А 1 А 2 =А 2 А 3 =………=А n-1 А n ,
Все углы равны.
Доказать: S = Pr
Доказательство:
Правильный многоугольник делится на равные равнобедренные треугольники.
Рассмотрим треугольник A 1 OA 2: угол А 1 ОА 2 — центральный (как его вычислить?) .
Все треугольники равны по двум сторонам и углу между ними. Найдем площадь треугольника. Для этого проведем высоту. Эта высота будет радиусом вписанной окружности. Так как треугольники равнобедренные, то высота является медианой и биссектрисой.
S= h A 1 A n. Всего треугольников N штук.
S= hА 1 А 2 n=Pr. Что и требовалось доказать
Вопросом о вычислении площади люди заинтересовались ещё с древнейших времен. Наиболее известная задача — это задача Дидоны.
Финикийская царица Дидона спасалась от своего брата, тирана Пигмалиона. Она отплыла из города Тира в 825 году до нашей эры. После долгого путешествия корабль пристал к берегам Африки. Дидоне понравилась земля. Она обратилась к местному предводителю нумидийцев Ярбу с просьбой продать кусок земли. Ярб заломил баснословную цену за клочок земли, который можно окружить бычьей шкурой. Но Дидона не растерялась и согласилась. Она расплатилась и отправилась отмерять землю. Сначала она разрезала шкуру так, что получился тонкий кожаный ремешок. Этим ремешком она окружила солидный участок земли, на котором обосновала впоследствии великий город Карфаген. Ярб был в ярости, так как его одурачили, но он был честным человеком и сдержал слово. Так гласит легенда. Но к
pedkolledj.ru
Площадь многоугольника по координатам онлайн
| Вы ввели следующие координаты многоугольника |
| Площадь заданного многоугольника (в условных единицах) |
Описание
Сервис позволяет высчитывать по заданным координатам вершин площадь многоугольника (треугольника, трапеции, паралеллограмма, пятиугольника и т.д) а также любых других непересекающихся многоугольников.
Используется метод трапеций, суть которого заключается в том, что многоугольник представляет собой сумму трапеций, две вершины из которого это две соседние вершины многоугольника, а две другие вершины трапеции, есть абсциссы координат двух вершин многоугольника.
Такой метод позволяет рассчитывать не только выпусклые многоугольники, но и любые другие, главное, что бы линии этого многоугольника не пересекались.
Есть еще два подобных сервиса: Площадь пересечения окружностей и Прямая линия
Кроме этого стоит обратить внимание на такие материалы как: Касательная к кривой второго порядка
Пересечение прямой и кривой второго порядка
Расчет кривых второго порядка на плоскости
Синтаксис
Кто использует XMPP клиента: mnog <координаты вершин>
Кто вводит данные через этот сайт: <координаты вершин>
Координаты вершин задаются в общей строке вида x1:y1 x2:y2 x3:y3 ….xn:yn
Координаты вершин являются действительные числа.
Координата каждой точки (абсцисса и ордината) записывается через двоеточие(без пробелов!)
Координаты вершин вводятся ПОСЛЕДОВАТЕЛЬНО по часовой или(!) против часовой стрелки.
Каждая координата вида x:y должен быть отделена пробелами от другой.
Нет никаких ограничений на количество координат вершин.
Примеры
mnog 5:7 9:7 10:2 2:2
Площадь многоугольника заданный координатами 5:7 9:7 10:2 2:2
равен 30
abakbot.ru
Расчет площади правильного многоугольника онлайн
Данный калькулятор считает площадь правильного многоугольника, которая всегда равна сумме площадей всех треугольников, на которые данный многоугольник можно поделить.
S = ½*a*b*sinλ — формула площади 1-го треугольника.
Дальше не трудно догадаться как калькулятор высчитывает суммарную площадь правильного многоугольника.
The field is not filled.
‘%1’ is not a valid e-mail address.
Please fill in this field.
The field must contain at least% 1 characters.
The value must not be longer than% 1 characters.
Field value does not coincide with the field ‘%1’
An invalid character. Valid characters:’%1′.
Expected number.
It is expected a positive number.
Expected integer.
It is expected a positive integer.
The value should be in the range of [%1 .. %2]
The ‘% 1’ is already present in the set of valid characters.
The field must be less than 1%.
The first character must be a letter of the Latin alphabet.
Su
Mo
Tu
We
Th
Fr
Sa
January
February
March
April
May
June
July
August
September
October
November
December
century
B.C.
%1 century
An error occurred while importing data on line% 1. Value: ‘%2’. Error: %3
Unable to determine the field separator. To separate fields, you can use the following characters: Tab, semicolon (;) or comma (,).
%3.%2.%1%4
%3.%2.%1%4 %6:%7
s.sh.
u.sh.
v.d.
z.d.
yes
no
Wrong file format. Only the following formats: %1
Please leave your phone number and / or email.
hostciti.net
