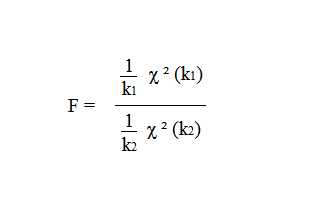| Главная > Учебные материалы > Математика: Основные законы распределения | ||||
|
1.Биномиальный закон распределения. 2.Геометрическое распределение. 3.Гипергеометрическое распределение. 4.Закон распределения Пуассона. 5.Равномерный закон распределения. 6.Нормальный закон распределения (закон Гаусса). 7.Показательный закон распределения. 8.Логарифмически-нормальное распределение. 10.Распределение Стьюдента (t — распределение). 11.Распределение Фишера-Снедекора.
|
||||
| 22 23 24 25 26 27 28 29 30 | ||||
1.Биномиальный закон распределения.Биномиальный закон распределения описывает вероятность наступления события А m раз в n независимых испытаниях, при условии, что вероятность р наступления события А в каждом испытании постоянна.
|
||||
Например, отдел продаж магазина бытовой техники в среднем получает один заказ на покупку телевизоров из 10 звонков. Составить закон распределения вероятностей на покупку m телевизоров. Построить полигон распределения вероятностей. |
||||
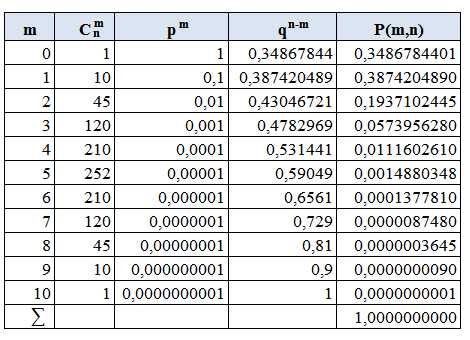 |
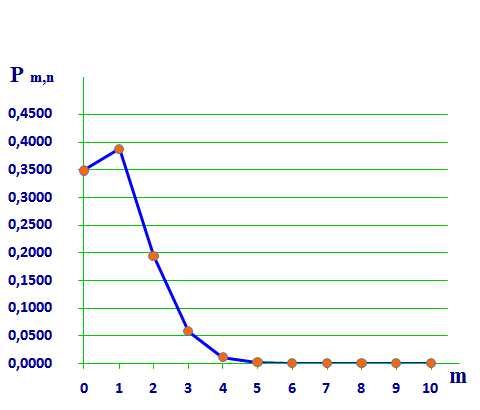 Рис.1 |
|||
|
В таблице m — число заказов, полученных компанией на покупку телевизора. Сnm — число сочетаний m телевизоров по n, p — вероятность наступления события А, т.е. заказа телевизора, q — вероятность не наступления события А, т.е. не заказа телевизора, P m,n — вероятность заказа m телевизоров из n. На рисунке 1 изображен полигон распределения вероятностей.
|
||||
2.Геометрическое распределение. |
||||
Геометрическое распределение случайной величины имеет следующий вид: где Pm — вероятность наступления события А в испытание под номером m. Пример. В компанию по ремонту бытовой техники поступила партия из 10 запасных блоков для стиральных машин. Бывают случаи, что в партии оказывается 1 блок бракованный. Проводится проверка до обнаружения бракованного блока. Необходимо составить закон распределения числа проверенных блоков. Вероятность того, что блок может оказаться бракованным равна 0,1. Построить полигон распределения вероятностей. |
||||
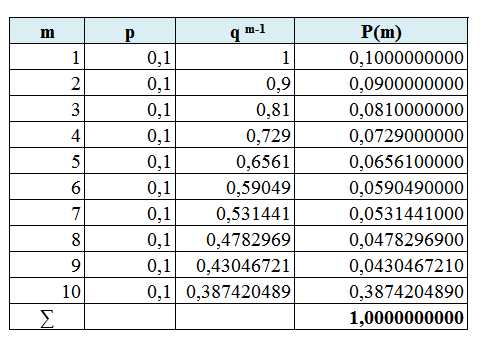 |
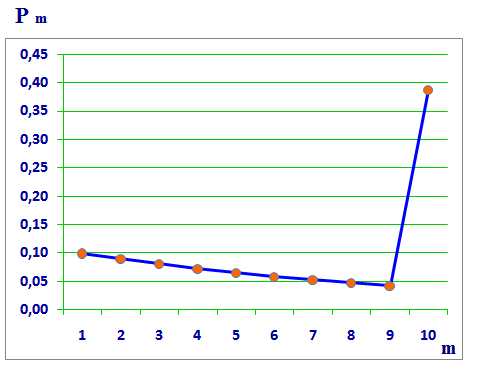 Рис.2 |
|||
|
Из таблицы видно, что с увеличением числа m, вероятность того, что будет обнаружен бракованный блок, снижается. Последняя строчка (m=10) объединяет две вероятности: 1 — что десятый блок оказался неисправным — 0,038742049 , 2 — что все проверяемые блоки оказались исправными — 0,34867844. Так как вероятность того, что блок окажется неисправным относительно низкая (р=0,1), то вероятность последнего события Pm (10 проверенных блоков) относительно высокая. Рис.2.
|
||||
3.Гипергеометрическое распределение. |
||||
Гипергеометрическое распределение случайной величины имеет следующий вид: где Например, составить закон распределения 7-ми угаданных чисел из 49. В данном примере всего чисел N=49, изъяли n=7 чисел, M — всего чисел, которые обладают заданным свойством, т.е. правильно угаданных чисел, m — число правильно угаданных чисел среди изъятых. |
||||
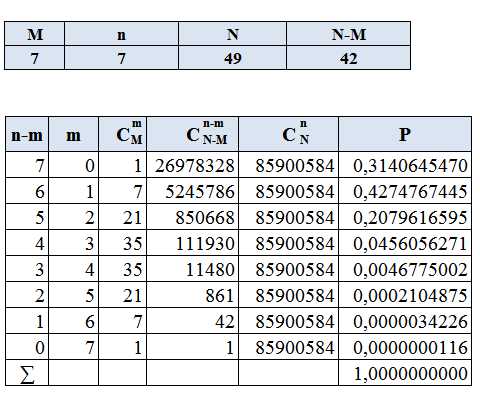 |
 Рис.3 |
|||
|
Из таблицы видно, что вероятность угадывания одного числа m=1 выше, чем при m=0. Однако затем вероятность начинает быстро снижаться. Таким образом, вероятность угадывания 4-х чисел уже составляет менее 0,005, а 5-ти ничтожно мала.
|
||||
4.Закон распределения Пуассона. |
||||
Случайная величина Х имеет распределение Пуассона, если закон ее распределения имеет вид: где λ = np = const
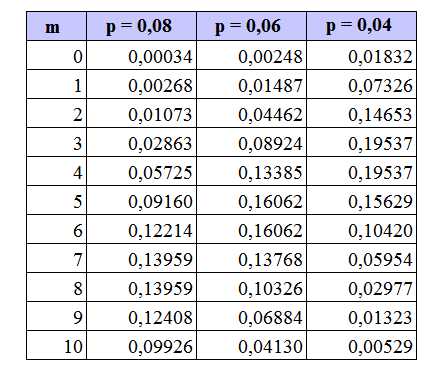
Например, в среднем за день в компанию по продаже телевизоров поступает около 100 звонков. Вероятность заказа телевизора марки А равна 0,08; B — 0,06 и C — 0,04. Составить закон распределения заказов на покупку телевизоров марок А,В и С. Построить полигон распределения вероятностей. Из условия имеем: m=100, λ1=8, λ2=6, λ3=4 ( ≤10 ) |
||||
(таблица дана не полностью) |
 Рис.4 |
|||
Если n достаточно большое и стремится к бесконечности, а значение p стремится к нулю, так что произведение np стремится к постоянному числу, то данный закон является приближением к биномиальному закону распределения. Из графика видно, что чем больше вероятность р, тем ближе кривая расположена к оси m, т.е. более пологая. (Рис.4) |
||||
|
Необходимо отметить, что биномиальный, геометрический, гипергеометрический и закон распределения Пуассона выражают распределение вероятностей дискретной случайной величины.
|
||||
5.Равномерный закон распределения. |
||||
Если плотность вероятности ϕ(х) есть величина постоянная на определенном промежутке [a,b], то закон распределения называется равномерным. На рис.5 изображены графики функции распределения вероятностей и плотность вероятности равномерного закона распределения. |
||||
|
 Рис.5 |
|||
6.Нормальный закон распределения (закон Гаусса). |
||||
Среди законов распределения непрерывных случайных величин наиболее распрастраненным является нормальный закон распределения. Случайная величина распределена по нормальному закону распределения, если ее плотность вероятности имеет вид: где |
||||
|
График плотности вероятности случайной величины, имеющей нормальный закон распределения, симметричен относительно прямой х=а, т.е х равному математическому ожиданию. Таким образом, если х=а, то кривая имеет максимум равный: При изменении величины математического ожидания кривая будет смещаться вдоль оси Ох. На графике (Рис.6) видно, что при х=3 кривая имеет максимум, т.к. математическое ожидание равно 3. Если математическое ожидание примет другое значение, например а=6, то кривая будет иметь максимум при х=6. Говоря о среднем квадратическом отклонении, как можно увидеть из графика, чем больше среднее квадратическое отклонение, тем меньше максимальное значение плотности вероятности случайной величины. |
 Рис.6 |
|||
Функция, которая выражает распределение случайной величины на интервале (-∞,х), и имеющая нормальный закон распределения, выражается через функцию Лапласа по следующей формуле:
|
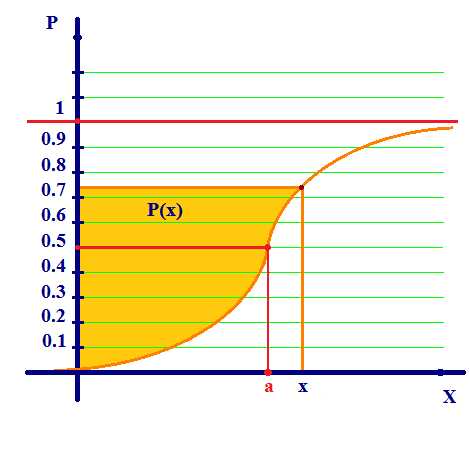 Рис.7 |
|||
Т.е. вероятность случайной величины Х состоит из двух частей: вероятности где x принимает значения от минус бесконечности до а, равная 0,5 и вторая часть — от а до х. (Рис.7)
|
||||
7.Показательный закон распределения. |
||||
Закон распределения случайной величины Х называется показательным (или экспоненциальным), если плотность вероятности имеет вид: где λ — параметр обратно-пропорциональный математическому ожиданию. График плотности вероятности с параметрами |
 Рис.8 |
|||
Функция распределения случайной величины Х, которая имеет показательное распределение, имеет вид: График функции изображен на рис.9 Если функцию распределения случайной величины выразить через плотность вероятности при х ≥ а, то она примет вид:
|
 Рис.9 |
|||
8.Логарифмически-нормальное распределение. |
||||
Если логарифм непрерывной случайной величины изменяется по нормальному закону, то случайная величина имеет логарифмически-нормальное распределение. Функция логаривмически-нормального распределения имеет вид. |
||||
 |
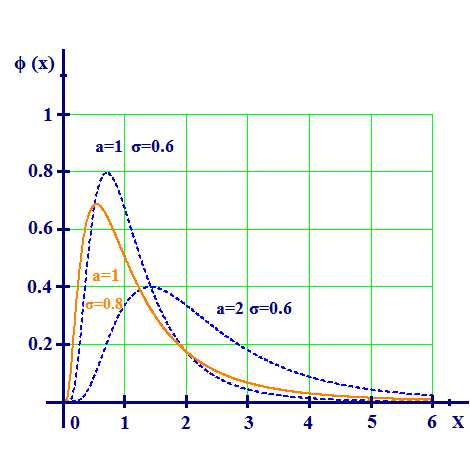 Рис.10 |
|||
|
Из графика видно, что чем меньше σ и больше математическое ожидание а, тем кривая становится более пологая и больше стремится к симметрии. Данный закон, чаще всего, используется для описания распределения поступления денежных средств (доходов), банковских вкладов, износа основных средств и т.д. (Рис.10)
|
||||
9. χ ² распределение |
||||
|
Сумма квадратов k независимых случайных величин, которые распределены по нормальному закону, называется χ ² распределением. χ ² распределение имеет вид: где Аi — i-ая случайная величина, распределенная по нормальному закону (i = 1,2,3,…k).
|
||||
|
Плотность вероятности случайной величины, распределенной по распределению χ ² имеет вид:
|
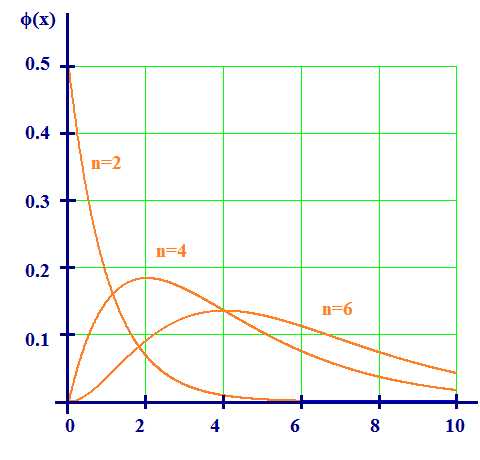 Рис.11 |
|||
|
Из графика видно, что чем больше n=k, тем кривая стремиться к нормальному распределению. Рис.11.
|
||||
10.Распределение Стьюдента (t — распределение) |
||||
Распределение непрерывной случайной величины называется распределением Стьюдента, если оно имеет вид: где Z — случайная величина, распределенная по нормальному закону.
|
||||
Плотность вероятности распределения Стьюдента имеет вид:
|
 Рис.12 |
|||
|
На рис.12 изображена плотность вероятности распределения Стьюдента. Из графика можно увидеть, что чем больше k, тем больше кривая приближается к нормальному распределению.
|
||||
 |
||||
11. Распределение Фишера-Снедекора. |
||||
|
Распределение случайной величины Фишера-Снедекора имеет вид:
|
||||
Плотность вероятности случайной величины имеет вид:
|
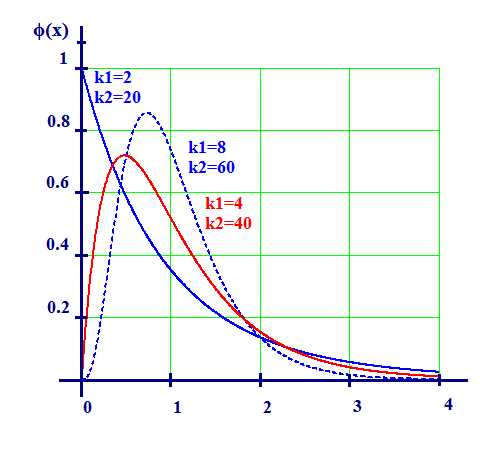 Рис.13 |
|||
|
При стремлении n к бесконечности распределение Фишера-Снедекора стремится к нормальному закону распределения.(Рис.13)
|
||||
| 22 23 24 25 26 27 28 29 30 | ||||
www.mathtask.ru
Законы распределения случайных величин
Биномиальный закон распределения
Среди законов распределения для дискретных случайных величин наиболее распространенным является биномиальный закон распределения. Биномиальное распределение имеет место в следующих условиях. Пусть случайная величина — число появлений некоторого событиявнезависимых испытаниях, вероятность появления в отдельном испытании равна. Данная случайная величина является дискретной случайной величиной, ее возможные значения. Вероятность того, что случайная величинапримет значениевычисляется по формуле Бернулли:.
Определение 15. Закон распределения дискретной случайной величины называетсябиномиальным законом распределения, если вероятности значений случайной величины вычисляются по формуле Бернулли. Ряд распределения будет иметь вид:
Убедимся, что сумма вероятностей различных значений случайной величины равна 1. Действительно,
Так как при данных вычислениях получилась биномиальная формула Ньютона, поэтому закон распределения называется биномиальным. Если случайная величина имеет биномиальное распределение , то ее числовые характеристики находятся по формулам:
(41)
(42)(43)
Пример 15.Имеется партия из 50 деталей. Вероятность брака для одной детали . Пусть случайная величина- число бракованных деталей в данной партии. Найти математическое ожидание, дисперсию и среднее квадратичное отклонение данной случайной величины. Решение. Случайная величина имеет биномиальное распределение, так как вероятность того, что она примет значениевычисляется по формуле Бернулли. Тогда ее математическое ожидание находится по формуле (41), а именно,; дисперсию находим по формуле (42):. Тогда среднее квадратичное отклонение будет равно.Вопрос. Приобретено 200 лотерейных билетов, вероятность выигрыша одного билета равна 0,01. Тогда среднее число лотерейных билетов, на которые выпадут выигрыши, равно: а) 10; б) 2; в) 20; г) 1.
в)
а)
г)
б)
Закон распределения Пуассона
При решении многих практических задач приходится иметь дело с дискретными случайными величинами, которые подчиняются закону распределения Пуассона. Типичными примерами случайной величины, имеющей распределение Пуассона, являются: число вызовов на телефонной станции за некоторое время ; число отказов сложной аппаратуры за время, если известно, что отказы независимы друг от друга и в среднем на единицу времени приходитсяотказов.Ряд распределения будет иметь вид:
То есть вероятность того, что случайная величина примет значениевычисляется по формуле Пуассона:поэтому данный закон и называется законом распределения Пуассона. Случайная величина, распределенной по закону Пуассона, имеет следующие числовые характеристики:
(44) (45)
(46)
Распределение Пуассона зависит от одного параметра , который является математическим ожиданием случайной величины. На рисунке 14 показан общий вид многоугольника распределения Пуассона при различных значениях параметра.
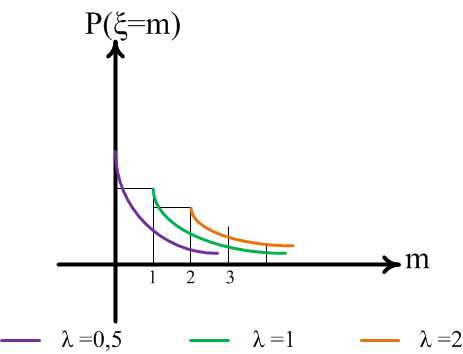
Рис.14
Распределение Пуассона может быть использовано как приближенное в тех случаях, когда точным распределением случайной величины является биномиальное распределение, при этом число испытаний велико, а вероятность появления события в отдельном испытании мала, поэтому закон распределения Пуассона называютзаконом редких событий. А еще, если математическое ожидание мало отличается от дисперсии, то есть когда . В связи с этим распределение Пуассона имеет большое количество различных приложений.Пример 16. Завод отправляет на базу 500 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,002. Найти математическое ожидание числа поврежденных при перевозке деталей. Решение. Случайная величина имеет распределение Пуассона, поэтому.Вопрос. Вероятность искажения символа при передаче сообщения равна 0,004. Чтобы среднее число искаженных символов было равно 4, надо передать 100 символов.
верно
неверно
Равномерное распределение
Определение 16.Непрерывная случайная величина имеетравномерное распределение на отрезке [a;b], если на этом отрезке плотность распределения данной случайной величины постоянна, а вне его равна нулю, то есть
(45)
График плотности для равномерного распределения изображен на рисунке 15:
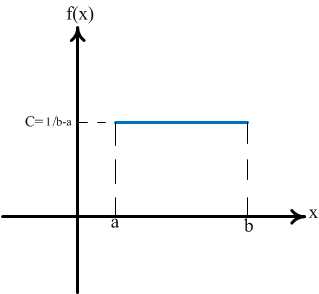
Рис.15
Так как площадь под кривой распределения должна равняться 1, то и следовательно, плотность распределения имеет вид:
(46)
Непрерывная случайная величина подчиняется закону равномерного распределения, если ее возможные значения лежат в пределах некоторого определенного интервала, кроме того, в пределах этого интервала все значения случайной величины одинаково вероятны. Случайные величины, имеющие равномерное распределение часто встречаются в измерительной практике при округлении отсчетов измерительных приборов до целых делений шкал. Ошибка при округлении отсчета до ближайшего целого деления является случайной величиной, которая может принимать с постоянной плотностью вероятности любое значение между двумя соседними целыми делениями. Числовые характеристики случайной величины, имеющей равномерное распределение, вычисляются по формулам:
(47) (48)(49)
Функция распределения вероятностей случайной величины, равномерно распределенной на промежутке имеет вид:
(50)
График данной функции представлен на рисунке 16:
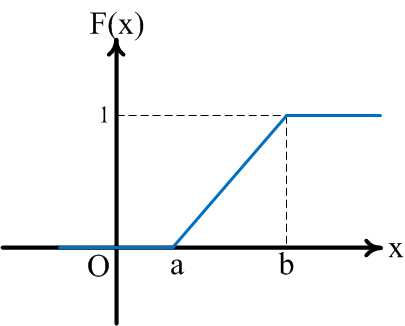
Рис.16
Пример 17. Цена деления шкалы измерительного прибора равна 0,1. Показания прибора округляют до ближайшего деления. Найти математическое ожидание случайной величины — ошибки округления.Решение. Случайная величина — ошибка округления имеет равномерное распределение на промежутке от 0 до 0,1, ее математическое ожидание вычисляется по формуле (47):.Вопрос. Непрерывная случайная величина имеет плотность распределения вероятностей
Тогда ее дисперсия равна:
а); б); в); г).
г)
а)
в)
б)
Нормальное распределение
Среди распределений непрерывных случайных величин центральное место занимает нормальный закон , плотность распределения которого имеет вид:
(51)
где — математическое ожидание, а- среднее квадратичное отклонение данной случайной величины. График плотности распределения нормального закона называюткривой Гаусса, он приведен на рисунке 17:
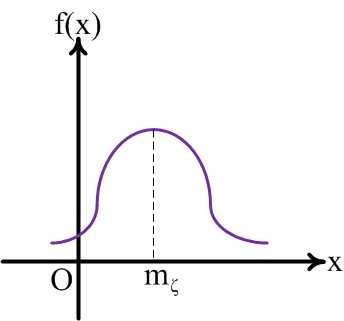
Рис.17
Отметим некоторые свойства кривой Гаусса. 1. Кривая распределения симметрична относительно ординаты, проходящей через точку . 2. Кривая имеет один максимум при, равный. 3. Приветви кривой асимптотически приближаются к оси. 4. Изменение математического ожиданияприприводит к смещению кривой распределения вдоль оси. При этом кривая распределения сохраняет свой вид. При изменении среднего квадратичного отклонения прикривая распределения изменяет свой вид. На рисунке 18 показана зависимость кривой распределения от среднего квадратичного отклонения.

Рис.18
Функция распределения вероятностей для нормального закона имеет вид:
(52)
где — функция Лапласа. Нормальный закон распределения очень широко распространен в задачах практики. Он проявляется во всех тех
случаях, когда случайная величина является результатом действия большого числа различных факторов. Каждый фактор в отдельности на величинувлияет незначительно и нельзя указать, какой именно в большей степени, чем остальные. Примерами случайных величин, имеющих нормальное распределение, могут служить: отклонение действительных размеров деталей, обработанных на станке, от номинальных размеров; ошибки при измерении; отклонения при стрельбе и другие. Основной особенностью, выделяющей нормальный закон среди других законов, служит то, что он является предельным законом для других законов распределения. Вероятность того, что случайная величина, распределенная по нормальному закону, попадет на промежутоквычисляется по формуле:
(53)
Вероятность того, что случайная величина отклонится от своего математического ожидания на величину по модулю меньшуювычисляется по формуле:
(54)
Пример18.Ошибка радиодальномера подчинена нормальному закону. Математическое ожидание этой ошибки равно 5 м, а среднее квадратичное отклонение равно 10 м. Найти вероятность того, что измеренное значение дальности будет отклоняться от истинного не более чем на 20 м. Решение. По условию надо найти вероятность попадания случайной величины — ошибки радиодальномера на промежуток. По формуле (53) находим:.Вопрос. Нормальное распределение характеризуется одним параметром.
неверно
верно
Показательное распределение
В практических приложениях теории вероятностей, особенно в теории массового обслуживания, исследовании операций, в физике, биологии, вопросах надежности и других приложениях, часто имеют дело со случайными величинами, имеющими показательное распределение. Определение 17. Непрерывная случайная величина распределена попоказательному закону, если ее плотность вероятности имеет вид:
(55)
Кривая распределения изображена на рисунке 19:

Рис.19
Функция распределения задается следующим образом:
(56)
Ее график показан на рисунке 20:
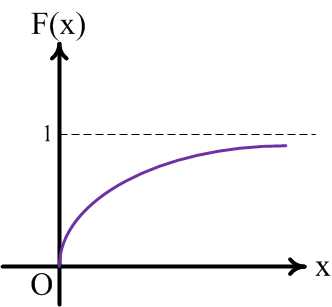
Рис.20
Числовые характеристики случайной величины, имеющей показательное распределение вычисляются по формулам:
(57) (58)(59)
Пример 19. Случайная величина — время работы радиолампы- имеет показательное распределение. Найти вероятность того, что время работы радиолампы будет не меньше 600 часов, если среднее время работы радиолампы 400 часов.Решение. По условию задачи математическое ожидание данной случайной величины равно 400, тогда . Искомая вероятность :.Вопрос. Случайная величина распределена по показательному закону с параметром. Тогда ее математическое ожидание равно 2,5.
неверно
верно
studfiles.net
1. Понятие случайной величины.
Тема 4
ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Понятие случайной величины. Дискретные и непрерывные случайные величины. Функция распределения вероятностей и ее свойства. Плотность распределения вероятности и ее свойства. Числовые характеристики случайных величин: математическое ожидание, дисперсия и их свойства, среднее квадратическое отклонение, мода и медиана; начальные и центральные моменты, асимметрия и эксцесс.
Случайной называется величина, которая принимает в результате испытаний то или иное (но при этом только одно) возможное значение, заранее известное, меняющееся от испытания к испытанию и зависящее от случайных обстоятельств. В отличие от случайного события, являющегося качественной характеристикой случайного результата испытания, случайная величина характеризует результат испытания количественно. Примерами случайной величины могут служить размер обрабатываемой детали, погрешность результата измерения какого-либо параметра изделия или среды. Среди случайных величин, с которыми приходится встречаться на практике, можно выделить два основных типа: дискретные величины и непрерывные.
Дискретной называется такая случайная величина, которая принимает конечное или бесконечное счетное множество значений. Например, частота попаданий при трех выстрелах; число дефектных изделий в партии из штук; число вызовов, поступающих на телефонную станцию в течение суток; число отказов элементов прибора за определенный промежуток времени при испытании его на надежность; число выстрелов до первого попадания в цель и т. д.
Непрерывной называется такая случайная величина, которая может принимать любые значения из некоторого конечного или бесконечного интервала. Очевидно, число возможных значений непрерывной случайной величины бесконечно. Например, ошибка при измерении дальности радиолокатора; время безотказной работы микросхемы; погрешность изготовления деталей; концентрация соли в морской воде и т. д.
Случайные величины обычно обозначают буквами ,и т. д., а их возможные значения -,и т. д. Для задания случайной величины недостаточно перечислить все ее возможные значения. Необходимо также знать, как часто могут появиться те или иные ее значения в результате испытаний при одних и тех же условиях, т. е. нужно задать вероятности их появления. Совокупность всех возможных значений случайной величины и соответствующих им вероятностей составляет распределение случайной величины.
2. Законы распределения случайной величины.
Законом распределения случайной величины называется всякое соответствие между возможными значениями случайной величины и соответствующими им вероятностями. Про случайную величину говорят, что она подчиняется данному закону распределения. Две случайные величины называются независимыми, если закон распределения одной из них не зависит то того, какие возможные значения приняла другая величина. В противном случае случайные величины называются зависимыми. Несколько случайных величин называются взаимно независимыми, если законы распределения любого числа из них не зависит от того, какие возможные значения приняли остальные величины.
Закон распределения случайной величины может быть задан в виде таблицы, в виде функции распределения, в виде плотности распределения. Таблица, содержащая возможные значения случайной величины и соответствующие вероятности, является простейшей формой задания закона распределения случайной величины:
Табличное задание закона распределения может быть использовано только для дискретной случайной величины с конечным числом возможных значений. Табличная форма задания закона случайной величины называется также рядом распределения.
Для наглядности ряд распределения представляют графически. При графическом изображении в прямоугольной системе координат по оси абсцисс откладывают все возможные значения случайной величины, а по оси ординат — соответствующие вероятности. Затем строят точки и соединяют их прямолинейными отрезками. Полученная фигура называетсямногоугольником распределения (рис. 5). Следует помнить, что соединение вершин ординат делается только в целях наглядности, так как в промежутках между и,и, и т. д. случайная величиназначений принять не может, поэтому вероятности ее появления в этих промежутках равны нулю.
Рис. 5.
Многоугольник распределения, как и ряд распределения, является одной из форм задания закона распределения дискретной случайной величины. Они могут иметь самую различную форму, однако все обладают одним общим свойством: сумма ординат вершин многоугольника распределения, представляющая собой сумму вероятностей всех возможных значений случайной величины, всегда равна единице. Это свойство вытекает из того, что все возможные значения случайной величины образуют полную группу несовместных событий, сумма вероятностей которых равна единице.
studfiles.net
Распределение случайной величины — это… Что такое Распределение случайной величины?
Распределение вероятностей — это закон, описывающий область значений случайной величины и вероятности их принятия.
Определение
Определение 1. Пусть задано вероятностное пространство , и на нём определена случайная величина . В частности, по определению, X является измеримым отображением измеримого пространства в измеримое пространство , где обозначает борелевскую сигма-алгебру на . Тогда случайная величина X индуцирует вероятностную меру на следующим образом:
Мера называется распределением случайной величины X.
Способы задания распределений
Определение 2. Функция называется (кумулятивной) функцией распределения случайной величины X. Из свойств вероятности вытекает
Теорема 1. Функция распределения FX(x) любой случайной величины удовлетворяет следующим трем свойствам:
- FX — функция неубывающая;
- ;
- FX непрерывна справа.
Из того факта, что борелевская сигма-алгебра на вещественной прямой порождается семейством интервалов вида , вытекает
Теорема 2. Любая функция F(x), удовлетворяющая трём свойствам, перечисленным выше, является функцией распределения для какого-то распределения .
Для вероятностных распределений, обладающих определенными свойствами, существуют более удобные способы его задания.
Дискретные распределения
Определение 2. Случайная величина называется простой или дискретной, если она принимает не более, чем счётное число значений. То есть , где — разбиение Ω.
Распределение простой случайной величины тогда по определению задаётся: . Введя обозначение , можно задать функцию p(ai) = pi. Очевидно, что . Используя счётную аддитивность , легко показать, что эта функция однозначно определяет распределение X.
Определение 3. Функция p(ai) = pi, где часто называется дискретным распределением.
Пример 1. Пусть функция p задана таким образом, что и . Эта функция задаёт распределение случайной величины X такой, что .
Теорема 3. Дискретное распределение обладает следующими свойствами:
- ;
- .
Непрерывные распределения
Непрерывное распределение — распределение вероятностей, не имеющее атомов. Любое распределение вероятностей есть смесь дискретного и непрерывного.
Абсолютно непрерывные распределения
Определение 4. Распределение случайной величины X называется абсолютно непрерывным, если существует неотрицательная функция , такая что . Функция fX тогда называется плотностью распределения случайной величины X.
Пример 2. Пусть f(x) = 1, когда , и 0 иначе. Тогда , если .
Очевидно, что для любой плотности распределения fX верно равенство . Верна и обратная
Теорема 4. Если функция такая, что:
- ;
- ,
то существует распределение такое, что f(x) является его плотностью.
Просто применение формулы Ньютона-Лейбница приводит к простому соотношению между кумулятивной функцией и плотностью абсолютно непрерывного распределения.
Теорема 5. Если f(x) — непрерывная плотность распределения, а F(x) — его кумулятивная функция, то
- .
Wikimedia Foundation. 2010.
dic.academic.ru
14. Функция распределения случайной величины, ее определение, свойства и график. Примеры.
Числовая величина, принимающая то или иное значение в результате реализации испытания случайным образом, называется случайной величиной.
Если x — дискретная случайная величина, принимающая значения x1 < x2 < … < xi < … с вероятностями p1 < p2 < … < pi < …, то таблица вида
x1 | x2 | … | xi | … |
p1 | p2 | … | pi | … |
называется распределением дискретной случайной величины.
Функция распределения случайной величины, с таким распределением, имеет вид
Свойства функции распределения.
1. .
Доказательство: Это утверждение следует из того, что функция распределения – это вероятность, а как известно,.
2.Функция распределения случайной величины есть неубывающая функция на всей числовой оси.
Доказательство:Пусть х1<x2. Докажем, чтоF(x1)F(x2). Пусть событие А=(Х<x1),B=(x1Х<x2). Тогда А+В=(Х<x2). События А и В несовместны, следовательно по теореме сложения Р(А+В)=P(А)+P(В). То есть Р(Х<x2) =Р(Х<x1)+Р(x1Х<x2). Другими словамиF(x2)=F(x1)+ Р(x1Х<x2).(3)
Так как Р(x1Х<x2)как вероятность невозможного события Х.как вероятность достовероного события Х.
4. Р(х1Х<x2)=F(x2)-F(x1).(4)
Доказательство: это непосредственно следует из формулы (3).
Пример: Найти вероятность того, что случайная величина Х примет значение в интервале [2; 5).
Решение: По формуле Р(х1Х<x2)=F(x2)-F(x1).(4)
Р(2Х<5)=F(5)-F(2)=1-2/3=1/3.(4).
Ответ :1/3.
15. Функция распределения дискретной случайной величины. Примеры.
если — дискретная случайная величина, принимающая значения x1 < x2 < … < xi < … с вероятностями p1 < p2 < … < pi < …, то таблица вида
x1 | x2 | … | xi | … |
p1 | p2 | … | pi | … |
называется распределением дискретной случайной величины.
Функция распределения случайной величины, с таким распределением, имеет вид
У дискретной случайной величины функция распределения ступенчатая. Например, для случайного числа очков, выпавших при одном бросании игральной кости, распределение, функция распределения и график функции распределения имеют вид:
1 | 2 | 3 | 4 | 5 | 6 |
1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |

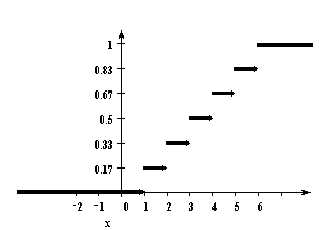
16. Теорема о существовании случайной величины с заданной функцией распределения. Непрерывная случайная величина. Вероятность отдельно взятого значения непрерывной случайной величины. Примеры.
Как известно, случайной величиной называется переменная величина, которая может принимать те или иные значения в зависимости от случая. Случайные величины обозначают заглавными буквами латинского алфавита (X, Y, Z), а их значения – соответствующими строчными буквами (x, y, z). различают непрерывные и дискретные случайные величины.
Непрерывной случайной величиной называется случайная величина Х, если ее функция распределения (интегральная функция распределения) представима в виде:
где f(x) – некоторая неотрицательная функция, такая что
Функция f(x) называется плотностью распределения вероятностей случайной величины X (дифференциальной функцией распределения).
Вероятность того, что непрерывная случайная величина X принимает значение в заданном промежутке, вычисляется следующим образом:
Примеры распределений вероятностей непрерывной случайной величины Х:
равномерное распределение вероятностей непрерывной случайной величины;
показательное распределение вероятностей непрерывной случайной величины;
нормальное распределение вероятностей непрерывной случайной величины.
17. Абсолютно непрерывная случайная величина. Плотность вероятности абсолютно непрерывной случайной величины, ее определение, свойства, и график.
Важный класс непрерывных случайных величин — абсолютно непрерывные случайные величины. Это случайные величины, распределение которых имеет плотность.
Определение 3.7 Случайная величина называетсяабсолютно непрерывной, если существует функция такая, что
,
,
имеет место равенство:
Функция , обладающая вышеперечисленными свойствами, называетсяплотностью распределения случайной величины .
Следствие 3.1 Если — абсолютно непрерывная случайная величина, то
Наглядный смысл плотности можно проиллюстрировать следующим рисунком.
Замечание 3.5 Если плотность непрерывна в точке, то из Следствия3.1вытекает следующее представление:
Следствие 3.2 Если — точка непрерывности функции, то
Примеры абсолютно непрерывных распределений
1) Равномерное распределение в отрезке
2) Показательное распределение с параметром
Показательное распределение называют также экспоненциальным.
3) Нормальное (или гауссовское) распределение ,,:
Стандартное нормальное распределение — :
Плотность распределения удовлетворяет свойствам:
и .
И наоборот, любая интегрируемая функция , удовлетворяющая этим свойствам, может быть взята в качестве плотности распределения некоторой случайной величины.
Поскольку функция распределения является функцией верхнего предела от плотности, то последняя восстанавливается по ней дифференцированием:
.
studfiles.net
Характеристики распределения случайных величин
Для изучения распределений случайных величин в математической статистике пользуются рядом числовых характеристик, определяющих положение центра группирования случайной величины и ее рассеивание около этого центра.
Числовые характеристики положения центра группирования носят общее название мер положения, а числовые характеристики рассеивания — мер рассеивания.
В качестве статистических оценок мер положения используются при теоретическом распределении: математическое ожидание E(Х); при эмпирическом распределении: среднее арифметическое значение, среднее арифметическое взвешенное, среднее гармоническое, среднее геометрическое, среднее геометрическое взвешенное,среднее квадратическое, среднее квадратическое взвешенное, середина размаха, медиана и мода.
В качестве статистических оценок мер рассеивания используются при теоретическом распределении: дисперсия, коэффициент вариации, квантиль; при эмпирическом распределении: стандартное отклонение и размах.
Математическим ожиданием E(Х) дискретной случайной величины Х называется сумма произведений возможных ее значений на соответствующие вероятности:
,
где n — число возможных значений случайной величины Х.
Математическое ожидание E(Х) непрерывной случайной величины Х, имеющей плотность вероятности f(Х), рассчитывается как
,
если интеграл сходится абсолютно.
Пример.Случайная величина имеет следующее распределение
Таблица. Распределение случайной величины
X | 0 | 1 | 2 | 3 | |
р(X) | 0,1 | 0,2 | 0,5 | 0,2 |
Математическое ожидание E(X) равно
E(X) = 0∙0,1 + 1∙0,2 + 2∙0,5 + 3∙0,2 = 1,8
Математическое ожидание непрерывной случайной величины определяется значительно сложнее с использованием интегрального исчисления.
Cреднее арифметическое значение , среднее гармоническое, среднее геометрическое, и среднее квадратическое можно рассчитать по формуле среднего степенного
,
где z – показатель степени, позволяющий определить вид среднего;
n — общее число значений Xi.
Cреднее арифметическое взвешенное , среднее геометрическое взвешенное, среднее квадратическое взвешенное можно рассчитать по формуле среднего взвешенного
,
где z – показатель степени, позволяющий определить вид среднего;
fi — частота значений Xi;
n — общее число значений Xi.
Средним арифметическим значением случайной величины называется отношение суммы всех значений случайной величины, полученных в результате конечного числа испытаний, к числу испытаний (согласно СТБ ГОСТ Р 50779.10 среднее арифметическое – сумма значений, деленная на их число):
Среднее арифметическое получают путем подстановки в формулу среднего степенного показателя степени z, равного 1.
Вышеприведенные формулы справедливы при контроле показателей по количественному признаку.
При контроле показателя по альтернативному признаку оцениваемый показатель может принимать только два взаимоисключающих значения, которым сопоставляются два количественных значения: 1 и 0.Частостью варианта 1 (как правило, обозначается p) является доля единиц, обладающих данным признаком в общей статистической совокупности. Разность 1 – p = q является частостью варианта 0. Таким образом, среднее арифметическое при контроле по альтернативному признаку вычисляется как:
.
Средним арифметическим взвешенным значением случайной величины называется сумма произведений значений случайной величины на их частости (согласно СТБ ГОСТ Р 50779.10 взвешенное среднее арифметическое – сумма произведений каждого значения на его вес, деленная на сумму весов, где веса – неотрицательные коэффициенты, связанные с каждым значением):
,
где fi— частота значений Xi;
n — общее число значений Xi.
m — число дискретных значений Xi.
Для непрерывных случайных величин в качестве Хi принимают середину равных интервалов, на которые разбивается ряд значений Х.
Среднее арифметическое взвешенное получают путем подстановки в формулу среднего взвешенного показателя степени z, равного 1.
Довольно часто под средним арифметическим подразумевают среднее арифметическое взвешенное значение.
Среднее гармоническое рассчитывают как
Среднее гармоническое получают путем подстановки в формулу среднего степенного показателя степени z, равного -1.
Средним геометрическим называют корень n-ой степени из произведения значений случайной величины:
Среднее геометрическое получают путем подстановки в формулу среднего степенного показателя степени z, равного 0.
Среднее геометрическое взвешенное рассчитывают как
Среднее геометрическое используется для анализа динамики явлений и позволяет определить средний коэффициент роста. При расчете среднего геометрического индивидуальные значения случайной величины представляют собой относительные показатели динамики, полученные как отношения каждого уровня ряда к предыдущему уровню.
Среднее геометрическое взвешенное получают путем подстановки в формулу среднего взвешенного показателя степени z, равного 0.
Средним квадратическим называют корень n-ой степени из произведения значений случайной величины:
Среднее квадратическое получают путем подстановки в формулу среднего степенного показателя степени z, равного 2.
Среднее квадратическое взвешенное рассчитывают как
Среднее квадратическое и среднее квадратическое взвешенное применяются при изучении вариации наблюдаемой величины.
Среднее квадратическое взвешенное получают путем подстановки в формулу среднего взвешенного показателя степени z, равного 2.
Согласно правилу мажорантности средних А.Я.Боярского для единой статистической совокупности среднее арифметическое , среднее гармоническое, среднее геометрическое, и среднее квадратическоесвязаны между собой следующей зависимостью:
< < <
Таким образом, численные значения средних возрастают с ростом показателя степени z.
Серединой размаха называют полусумму наибольшего и наименьшего значений (согласно СТБ ГОСТ Р 50779.10 середина размаха – это среднее арифметическое между наибольшим и наименьшим наблюденными значениями количественного признака).
Если n значений измеряемой величины расположить в порядке их возрастания, то значение, находящееся в самом центре, называют медианой (согласно СТБ ГОСТ Р 50779.10 медиана – это квантиль порядка р = 0,5). Если n является нечетным числом, медианой будет значение, которое находится на 1/2(n +1) месте.
Пример. Со станка взято 5 деталей с размерами, в мм: 32,10; 32,05; 31,98; 32,08; 32,03. Расположим полученные размеры в порядке возрастания, в мм: 31,98; 32,03; 32,05; 32,08; 32,10. Так как n = 5, то в качестве медианы берут число, занимающее 1/2(5+1) = 3 место, = 32,05 мм.
Если n является четным числом, то медианой будет значение, являющееся средним арифметическим из двух соседних значений, находящихся в центре последовательности и занимающих соответственно серединное положение.
Например, если взять 4 детали с размерами, в мм: 32,10; 32,05; 31,98; 32,08 и расположить в порядке возрастания, в мм: 31,98; 32,05; 32,08; 32,10, то
= (Х2 + Х3)/2 = (32,05 + 32,08)/2 = 32,065 мм
Модой называется наиболее часто встречающееся значение в статистической совокупности(согласно СТБ ГОСТ Р 50779.10 мода – это значение случайной величины, при котором функция распределения вероятностей масс или плотность распределения вероятностей имеет максимум).
Для эмпирических распределений дискретной случайной величины мода находится непосредственно по классическому определению. Для эмпирических распределений непрерывной случайной величины сначала определяют модальный интервал hk = xk – xk-1, которому соответствует максимальная частота fk. Значение моды внутри модального интервала определяют по интерполяционной формуле Р.М.Орженцкого:
,
где xk-1 – нижняя граница модального интервала;
hk – длина модального интервала;
— частота интервала, соответственно предшествующего модальному, модальному и следующему за модальным.
Математическое ожидание обычно используется в качестве меры положения для теоретических распределений, в которых возможные значения Х оцениваются при помощи вероятностей. В эмпирических распределениях, где наблюдаемые значения Х оцениваются при помощи частот или частостей, в качестве меры положения используется среднее арифметическое, среднее арифметическое взвешенное, среднее гармоническое, среднее геометрическое, среднее геометрическое взвешенное, среднее квадратическое, среднее квадратическое взвешенное, середина размаха, медиана и мода.
Дисперсией дискретной случайной величины называется сумма произведений квадратов отклонений случайной величины Х от ее математического ожидания на соответствующие вероятности
Дисперсия непрерывной случайной величины, имеющей плотность вероятности p(Х), рассчитывается как
,
если этот интеграл сходится.
Эта величина применяется в качестве меры рассеивания теоретического распределения, а для эмпирического распределения используется аналогичная величина σ2, которая определяется как сумма произведений квадратов отклонений значений случайной величины Хi от ее среднего арифметического значения Х на соответствующее частости fi/(n-1). Тогда σ2 при различных случаях определяется из следующих зависимостей
Вышеприведенные формулы справедливы при контроле показателей по количественному признаку.
При контроле показателя по альтернативному признаку оцениваемый показатель может принимать только два взаимоисключающих значения, которым сопоставляются два количественных значения: 1 и 0.Частостью варианта 1 (как правило, обозначается p) является доля единиц, обладающих данным признаком в общей статистической совокупности. Разность 1 – p = q является частостью варианта 0. Таким образом, дисперсия эмпирического распределения при контроле по альтернативному признаку вычисляется как:
.
Таким образом, дисперсия эмпирического распределения случайной величины, контролируемой по альтернативному признаку, равна произведению доли единиц, обладающих данным признаком, на долю единиц, не обладающих этим признаком.
Дисперсия эмпирического распределения случайной величины, контролируемой по альтернативному признаку, принимает наибольшее значение pq = 0,25 при условии равнозначности p и q, то есть когда p = q = 0,5.
На практике используют не саму дисперсию, а квадратный корень из нее, называемый стандартным отклонением (средним квадратическим отклонением).
Размерность σ совпадает с размерностью самой случайной величины Х.
Коэффициентом вариации называют отношение стандартного отклонения случайной величины к ее математическому ожиданию
Квантилем z случайной величины Х называется такое значение случайной величины, которому соответствует значение интегральной функции распределения, равное z.(согласноСТБ ГОСТ Р 50779.10 квантиль – это значение случайной величины Хр, для которого функция распределения принимает значение р (0 < р < 1) или ее значение изменяется скачком от меньшего р до превышающего р).
Размахом называется разность между наибольшим и наименьшим наблюдаемыми значениями случайной величины.
R = Xmax — Xmin
Размахом пользуются как мерой рассеивания в эмпирических распределениях при малом числе наблюдений (когда n ≤ 10).
Дл более подробного описания особенностей распределения П.Л.Чебышевым были предложены начальный и центральный моменты n-го порядка.
Начальный момент n-го порядка определяется как
Центральный момент n-го порядка определяется как
studfiles.net
Распределение случайной величины — это… Что такое Распределение случайной величины?
Распределение вероятностей — это закон, описывающий область значений случайной величины и вероятности их принятия.
Определение
Определение 1. Пусть задано вероятностное пространство , и на нём определена случайная величина . В частности, по определению, X является измеримым отображением измеримого пространства в измеримое пространство , где обозначает борелевскую сигма-алгебру на . Тогда случайная величина X индуцирует вероятностную меру на следующим образом:
Мера называется распределением случайной величины X.
Способы задания распределений
Определение 2. Функция называется (кумулятивной) функцией распределения случайной величины X. Из свойств вероятности вытекает
Теорема 1. Функция распределения FX(x) любой случайной величины удовлетворяет следующим трем свойствам:
- FX — функция неубывающая;
- ;
- FX непрерывна справа.
Из того факта, что борелевская сигма-алгебра на вещественной прямой порождается семейством интервалов вида , вытекает
Теорема 2. Любая функция F(x), удовлетворяющая трём свойствам, перечисленным выше, является функцией распределения для какого-то распределения .
Для вероятностных распределений, обладающих определенными свойствами, существуют более удобные способы его задания.
Дискретные распределения
Определение 2. Случайная величина называется простой или дискретной, если она принимает не более, чем счётное число значений. То есть , где — разбиение Ω.
Распределение простой случайной величины тогда по определению задаётся: . Введя обозначение , можно задать функцию p(ai) = pi. Очевидно, что . Используя счётную аддитивность , легко показать, что эта функция однозначно определяет распределение X.
Определение 3. Функция p(ai) = pi, где часто называется дискретным распределением.
Пример 1. Пусть функция p задана таким образом, что и . Эта функция задаёт распределение случайной величины X такой, что .
Теорема 3. Дискретное распределение обладает следующими свойствами:
- ;
- .
Непрерывные распределения
Непрерывное распределение — распределение вероятностей, не имеющее атомов. Любое распределение вероятностей есть смесь дискретного и непрерывного.
Абсолютно непрерывные распределения
Определение 4. Распределение случайной величины X называется абсолютно непрерывным, если существует неотрицательная функция , такая что . Функция fX тогда называется плотностью распределения случайной величины X.
Пример 2. Пусть f(x) = 1, когда , и 0 иначе. Тогда , если .
Очевидно, что для любой плотности распределения fX верно равенство . Верна и обратная
Теорема 4. Если функция такая, что:
- ;
- ,
то существует распределение такое, что f(x) является его плотностью.
Просто применение формулы Ньютона-Лейбница приводит к простому соотношению между кумулятивной функцией и плотностью абсолютно непрерывного распределения.
Теорема 5. Если f(x) — непрерывная плотность распределения, а F(x) — его кумулятивная функция, то
- .
Wikimedia Foundation. 2010.
3dic.academic.ru