Разложить в ряд тейлора функцию – .

Разложение в ряд Тейлора основных элементарных функций — ПриМат

Перед тем прочтением данной статьи следует просмотреть следующий материал определение многочлена Тейлора, Остатки формулы Тейлора, Коэффициенты Тейлора, ряд Тейлора.

Запишем разложения основных элементарных функций в ряд Тейлора в окрестности точки $x_{0}=0$, т.е. в ряд вида $f(x)=$$\sum\limits _{ n=0 }^{ \infty }{ \frac { { f }^{ (n) }(0) }{ n! } } { x }^{ n }$ (1), который называется рядом Маклорена.

Показательная и гиперболические функции

Пусть $f(x)=e^{x}$. Найдем производные функции: ${f}'(x)= e^{x}$, $f^{\prime\prime}( x )=e^{x}$,$\ldots$,$f^{(n)}(x)=e^{x}$. Тогда $0 < f(x) < e^{\rho }$, $0 < f^{(n)}(x) < e^{\rho }$ для любого $x\in(-\rho ,\rho )$, где $\rho > 0$ и для любого $n\in \mathbb{N}$.

Из теоремы о представлении функции в виде ее ряда Тейлора (Курс математического анализа, ст.437) следует, что ряд (1) для $f(x)=e^{x}$ сходится к этой функции на интервале $(-\rho ,\rho )$ при любом $\rho > 0$. Так как для функции $f(x)=e^{x}$ выполняются $f(0)=1$, $f^{(n)}(0)=1$ для всех $n\in \mathbb{N}$, то, по формуле (1), получаем разложение в ряд Маклорена показательной функции:
$$e^{x}=1+x+\frac{x^{2}}{2!}+ \ldots +\frac{x^{n}}{n!}+ \ldots = \sum_{n=0}^{\infty }\frac{x^{n}}{n!}, x\in \mathbb{R} (2)$$

Используя разложение (2), синус и косинус $\text{sh} \, x=\frac{e ^{x}-e ^{-x}}{2}$, $\text{ch} \, x=\frac{e ^{x}+e ^{-x}}{2}$, находим:
$$\text{sh} \, x=x+\frac{x^{3}}{3!}+ \ldots +\frac{x^{2n+1}}{(2n+1)!}+ \ldots =$$ $$=\sum_{n=0}^{\infty }\frac{x^{2n+1}}{(2n+1)!}, x\in \mathbb{R} (3)$$
$$\text{ch} \, x=1+\frac{x^{2}}{2!}+ \ldots +\frac{x^{2n}}{(2n)!}+ \ldots =$$ $$=\sum_{n=0}^{\infty }\frac{x^{2n}}{(2n)!}, x\in \mathbb{R} (4)$$
Радиус сходимости $R=+\infty $.

Тригонометрические функции

Пусть $f(x)=\sin x$. Найдем производные функции: ${f}'(x)= \cos x$, $f^{\prime\prime}(x)= -\sin x$,$\ldots$,$f^{(n)}(x)=\sin x$ при $n$ — четное. Тогда $\left | f^{(n)}(x) \right | \leq 1$, для любого $n\in \mathbb{N}$ и для любого $x\in \mathbb{R}$.

Из теоремы о представлении функции в виде ее ряда Тейлора (Курс математического анализа, ст.437) ряд (1) для $f(x)=\sin x$ сходится для любого $x\in (-\infty , \infty )$. Радиус сходимости $R=+\infty$.

Если $f(x)=\sin x$, то $f(0)=0$, $f^{(2n)}(0)=0$, ${f}'(0)=1$, $f^{(2n+1)}(0)=(-1)^{n}$ для любого $n\in \mathbb{N}$, и, по формуле (1), получаем разложение в ряд Маклорена:
$$\sin x =x-\frac{x^{3}}{3!}+ \ldots +(-1)^{n}\frac{x^{2n+1}}{(2n+1)!}+ \ldots =$$ $$=\sum_{n=0}^{\infty }(-1)^{n}\frac{x^{2n+1}}{(2n+1)!}, x\in \mathbb{R} (5)$$

Пусть $f(x)=\cos x$. Найдем производные функции: ${f}'(x)= -\sin x$, $f^{\prime\prime}(x)= -\cos x$,$\ldots$,$f^{(n)}(x)=\cos x$ при $n$ — четное. Тогда $\left | f^{(n)}(x) \right | \leq 1$, для всех $x\in \mathbb{R}$, $n\in \mathbb{N}$, $f(0)=1$, ${f}'(0)=0$, $f^{(2n)}(0)=(-1)$, $f^{(2n+1)}(0)=0$ для всех $n\in \mathbb{N}$. По формуле (1):
$$\cos x =1-\frac{x^{2}}{2!}+ \ldots +(-1)^{n}\frac{x^{2n}}{(2n)!}+ \ldots =$$ $$=\sum_{n=0}^{\infty }(-1)^{n}\frac{x^{2n}}{(2n)!}, x\in \mathbb{R} (6)$$

Радиус сходимости $R=+\infty$.

Логарифмическая функция

Пусть $f(x)=\ln(1+x)$. Тогда $$f^{(n)}(x)=\frac{(-1)^{(n-1)}(n-1)!}{(1+x)^{n}} (7),$$ откуда находим $$\frac{f^{(n)}(0)}{n!}=\frac{(-1)^{(n-1)}}{n}.$$

Оценим остаток по формуле остаточного члена в интегральной форме: $$r_{n}=\frac{1}{n!}\int\limits_{0}^{x}(x-t)^{n}f^{(n+1)}(t)dt=\frac{x^{(n+1)}}{n!}\int\limits_{0}^{1}(1-\tau )^{n}f^{(n+1)}(\tau x)d\tau.$$ Используя равенство (7), получаем $$r_{n}=(-1)^{n}x^{n+1}\int\limits_{0}^{1}\frac{(1-\tau )^{n}}{(1+\tau x)^{n+1}}d\tau.$$ Пусть $\left | x \right |

Пусть $x=1$. Тогда $\left | r_{n}(1) \right |=$$\int\limits_{0}^{1}\frac{(1-\tau )^{n}}{(1+\tau )^{n+1}}d\tau$$ \leq \int\limits_{0}^{1}(1-\tau )^{n}d\tau$$ =\frac{1}{n+1}$ $\rightarrow 0.$

Если $x\in (-1,1]$, то остаточный член $r_{n}(x)$ для функции $f(x)=\ln(1+x)$ стремится к нулю при $n\rightarrow \infty.$

В итоге получаем разложение в ряд Маклорена

$$\ln(1+x)=x-\frac{x^{2}}{2}+ \ldots +(-1)^{n+1}\frac{x^{n}}{n}+ \ldots =$$ $$=\sum_{n=1}^{\infty }(-1)^{n+1}\frac{x^{n}}{n}, x\in \mathbb{R} (8)$$
Радиус сходимости $R=1.$

Степенная функция

Пусть $f(x)=(1+x)^{\alpha }$. Если $\alpha =0$, то $f(x)=1$, а если $\alpha =n$, где $n\in \mathbb{N}$, то $f(x)$-многочлен степени $n$, который можно представить в форме бинома Ньютона в форме конечной суммы:
$$f(x)=\sum\limits_{k=0}^{n}C_{n}^{k}x^{k}.$$ Покажем, что если $\alpha \neq 0$ и $\alpha \notin \mathbb{N}$, то функция $f(x)=(1+x)^{\alpha }$ представляется при каждом $x\in (-1,1)$ сходящимся к ней рядом Маклорена $$(1+x)^{\alpha }=\sum\limits_{n=0}^{\infty }C_{\alpha }^{n}x^{n} (9),$$ где $C_{\alpha }^{0}=1$, $C_{\alpha }^{n}=\frac{\alpha (\alpha -1) \ldots (\alpha -n+1))}{n!}$.

Так как $f^{(n+1)}(x)=\alpha (\alpha -1) \ldots (\alpha -n)(1+x)^{\alpha -n-1}$, то по формуле $r_{n}(x)=\frac{x^{(n+1)}}{n!}\int\limits_{0}^{1}(1-\tau )f^{(n+1)}(\tau x)d\tau$ получаем $$r_{n}(x)=A_{n}x^{n+1}\int\limits_{0}^{1}\left ( \frac{1-\tau}{1+\tau x} \right )^{n}(1+\tau x)^{\alpha -1}d\tau,$$ где $C_{n }=\frac{\alpha (\alpha -1) \ldots (\alpha -n)}{n!}.$

Выберем $m\in \mathbb{N}$ такое, чтобы выполнялось условие $\left | \alpha \right |\leq m$. Тогда для всех $n\geq m$ справедливо $\left | A_{n} \right |$$\leq \frac{m(m+1) \ldots (m+n)}{n!}$$\leq \frac{(m+n)!}{n!}=(n+1) \ldots (n+m)\leq (2n)^{m}$. Используя неравенства $\left | 1+\tau x \right |\geq 1-\tau \left | x \right |\geq 1-\tau$, $\left | 1+\tau x \right |\geq 1-\left | x \right |$, а также неравенство $\left | 1+\tau x \right |\leq 1+\left | x \right |$, получаем $0\leq \frac{1-\tau }{1+\tau x}\leq 1$.

Так как $\lim\limits_{t\rightarrow \infty }\frac{t^{m}}{a^{t}}=0$ при $\alpha > 1$, то $\lim\limits_{n\rightarrow \infty }\frac{n^{m}}{\left ( \frac{1}{\left | x \right |} \right )^{n+1}}=0$. Поэтому справедливо равенство $(1+x)^{\alpha }=\sum\limits_{n=0}^{\infty }C_{\alpha }^{n}x^{n}$. Радиус сходимости этого ряда $R=1$ при $\alpha \neq 0$ и $\alpha \notin \mathbb{N}.$

$$(1+x)^{\alpha }=$$ $$1+\alpha x+\frac{\alpha (\alpha -1)}{2!}x^{2}+ \ldots +\frac{\alpha (\alpha -1) \ldots (\alpha -n+1)}{n!}x^{n}+\ldots=$$$$1+\sum_{n=1}^{\infty }\frac{\alpha (\alpha -1) \ldots (\alpha -n+1)}{n!}x^{n}+\ldots, x\in \mathbb{R} (10)$$

Частные случаи формулы (9):
• $\frac{1}{1+x}=1-x+x^{2}-\ldots=\sum\limits_{n=0}^{\infty }(-1)^{n}x^{n}, x\in \mathbb{R}$
• $\frac{1}{1-x}=\sum\limits_{n=0}^{\infty }x^{n}, x\in \mathbb{R}$

Спойлер

Разложить функцию в ряд Маклорена.

$$f(x)=x\cos 3x$$

$\cos 3x=1-\frac{(3x)^2}{2!}+\frac{(3x)^4}{4!}-\ldots+(-1)^{n}\frac{(3x)^{2n}}{(2n)!}+\ldots$

Раскрывая скобки, получим

$\cos 3x=1-\frac{3^{2}x^{2}}{2!}+\frac{3^{4}x^{4}}{4!}-\ldots+(-1)^{n}\frac{3^{(2n)}x^{(2n)}}{(2n)!}+ \ldots $

Умножая левую и правую часть на $x$, получим

$x\cos 3x=x(1-\frac{3^{2}x^{2}}{2!}+\frac{3^{4}x^{4}}{4!}-\ldots+(-1)^{n}\frac{3^{(2n)}x^{(2n)}}{(2n)!}+\ldots)$

Таким образом:

$f(x)=x\cos x=x-\frac{3^{2}x^{3}}{2!}+\frac{3^{4}x^{5}}{4!}-\ldots+(-1)^{n}\frac{3^{(2n)}x^{(2n+1)}}{(2n)!}$

[свернуть]

Литература

Конспект З.М.Лысенко по математическому анализу

А.М.Тер-Крикоров, М.И.Шабунин «Курс математического анализа«, ст. 435-441, 158-165

Разложение в ряд Тейлора основных элементарных функций

Лимит времени: 0

Информация

Для закрепления материала рекомендуется пройти этот тест

Вы уже проходили тест ранее. Вы не можете запустить его снова.

Тест загружается…

Вы должны войти или зарегистрироваться для того, чтобы начать тест.

Вы должны закончить следующие тесты, чтобы начать этот:

Правильных ответов: 0 из 4

Ваше время:

Время вышло

Вы набрали 0 из 0 баллов (0)

Средний результат
Ваш результат

Рубрики

1. Математический анализ 0%

1. С ответом
2. С отметкой о просмотре

Поделиться ссылкой:

Похожее

ib.mazurok.com

1.5. Разложение функции в ряд Тейлора

Если функция f(x) имеет производные всех порядков в окрестности точки x=a, то для нее можно написать ряд по степеням (x—a):

Этот ряд называется рядом Тейлора функции f(x) в точке x=a.

Теорема 6. Если функция f(x) и все ее производные ограничены на интервале (a—R, a+R) одним и тем же числом, т.е. существует постоянная M>0 такая, что выполняется неравенство , то функция f(x) представляется сходящимся к ней рядом Тейлора:

. (13)

Равенство (13) верно и в случае, когда остаточный член ряда Тейлора стремится к нулю при n. Остаточный член R_n(x) можно вычислить по формуле:

. (14)

Если , то ряд не сходится к данной функции.

Если в ряде Тейлора положим

a=0, получим частный случай ряда Тейлора, который называют рядом Маклорена: .

Приведем разложения в ряд Маклорена некоторых элементарных функций:

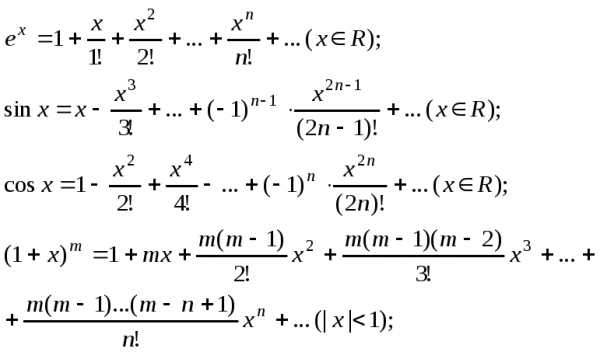
Пример 1. Разложить функцию в ряд Тейлора в окрестности точки x=0.

Решение. Имеем . Вычисляем , т.е. . Далее последовательно получаем: Отметим, что . Записываем ряд Тейлора:

Пример 2. Разложить функцию в ряд по степеням x, используя разложения основных элементарных функций. Воспользуемся приведенным выше биномиальным разложением . (15)

Преобразуем исходную функцию: . Подставим в формулу (15) , а вместо

x выражение . Получим следующее разложение:

Разложение имеет место при , т.е. при |x|<3.

1.6. Применение степенных рядов в приближенных вычислениях

1. Приближенное вычисление значений функций.

Пусть функция f(x) в окрестности точки a разлагается в ряд Тейлора. Тогда приближенное значение функции f(x) в любой точке этой окрестности может быть вычислено как частичная сумма этого ряда.

Пример 1. Вычислить с точностью до 0,001.

Решение. . Воспользуемся биномиальным рядом (15) при . Получаем:

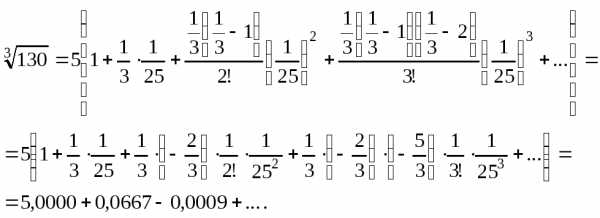
Полученный ряд является знакочередующимся рядом. Третий член по модулю меньше 0,001, поэтому его и следующие за ним члены можно отбросить. С указанной точностью получим .

Пример 2. Вычислить с точностью до 0,001.

Решение.

Воспользуемся разложением

,

где . При x=0,1 получаем: Определим, сколько надо слагаемых для достижения требуемой точности. Так как 0,1[0,0,5], то . Тогда ; . При x=0,1 имеем неравенство: . Полагая n=2, получим . Значит, достаточно взять три слагаемых: .

Пример 3. Вычислить ln2 с точностью до .

Решение. Применим разложение . Этот ряд сходится при x(-1,1). Если , то x=1/3. Возьмем n-ю частичную сумму . Погрешность этого равенства выражается остатком ряда . Для его оценки все множители в знаменателях, стоящие перед степенью 3, заменим на 2n+3. Получим Решая неравенство , находим, что n=4: . Итак,

2. Приближенное вычисление определенных интегралов.

Если подынтегральная функция разлагается в степенной ряд, а пределы интегрирования принадлежат области сходимости этого ряда, то соответствующий определенный интеграл можно вычислить с заданной точностью.

Пример 4. Вычислить интеграл с точностью до 0,00001.

Решение. Разделив почленно ряд для sinx на x, получим . Этот ряд сходится приxR. Интегрируем его почленно.

Получили знакочередующийся ряд. Третий член по модулю меньше заданной точности. Значит, достаточно взять два слагаемых: .

studfiles.net

§8 Методы разложения функций в ряд Тейлора

Разложение функций в ряд Тейлора, по определению, часто связано с громоздкими вычислениями при нахождении производных и сложностью исследования его сходимости. Приведем несколько методов, когда этого можно избежать

Использование формулы суммы бесконечной убывающей геометрической прогрессии

Разложить в ряд Тейлора в окрестности точки 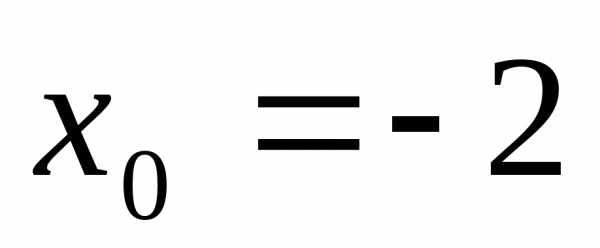функцию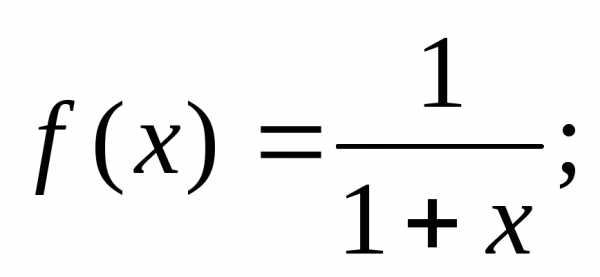Решение т.к.

то при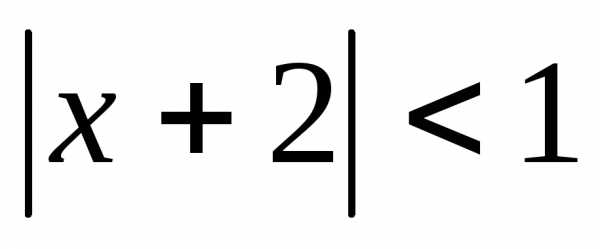

Метод подстановки

Разложить функцию по степеням.

Решение : Запишем следующую цепочку равенств

Возвращаясь к старой переменной х по формуле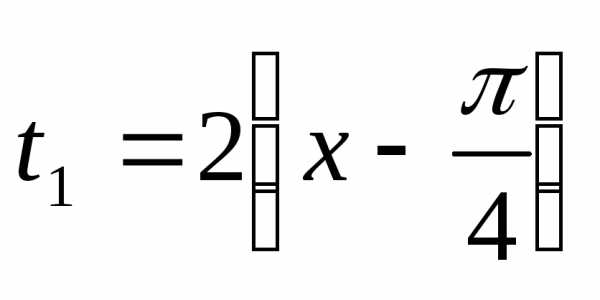

, получаем

.

Метод интегрирования

Разложить в ряд Маклорена функцию

Решение т.к. , то

;

Метод дифференцирования

Разложить в ряд Маклорена функцию

Решение. Так как , то

Для разложения используются и другие методы.

§ 9. Приложения рядов

Приближенное вычисление значений функций.

Для нахождения приближенного значения функции f(x) в точке

с заданной точностью поступим следующим образом. Разложим функцию f(x) в ряд по степеням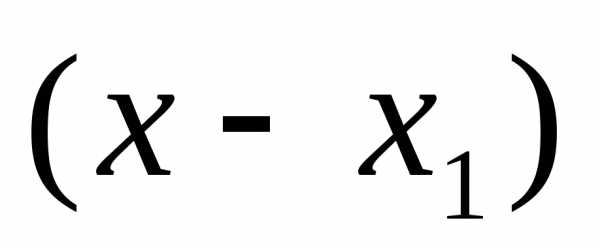

с интервалом сходимости, содержащим точку, где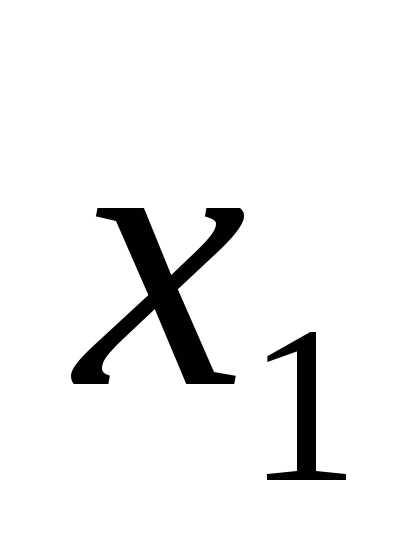— точка , в которой значение функции и ее производных вычисляются легко и точно. Переменной х придадим значение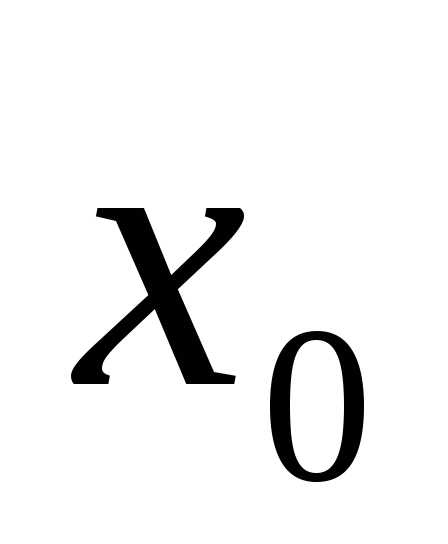и в полученном числовом рядуоставим только члены, гарантирующие только заданную точность вычислений. Минимаьное числотаких членов определим из соответствующей оценки либо остатка формулы Тейлора , либо остатка ряда.

Пример. Вычислить с точностью число е.

Решение. Так как

то из оценки

следует, что , т.е. необходимо взять пять слагаемых .

Пример 2. Вычислить с точностью 0,0001.

Решение Так как и ряд

является рядом Лейбница, то из оценки

получаем . Таким образом

Приближенное вычисление интегралов

Пример Вычислить 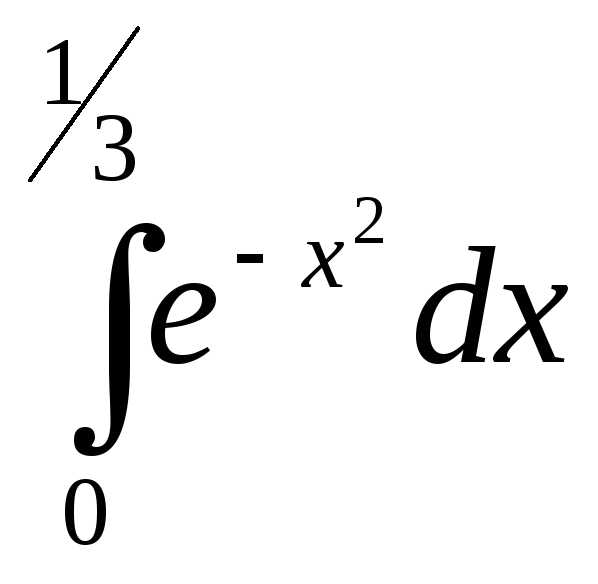c точностью 0,001

Решение. Имеем :

Оценим погрешность

тогда

Интегрирование дифференциальных уравнений

Степенные ряды могут применяться для нахождения приближенного решения дифференциального уравнения, если его решение не удается найти в элементарных функциях.

Пример. Найти решение дифференциального уравнения

удовлетворяющее начальному условию

Решение. Уравнение допускает разделение переменных :

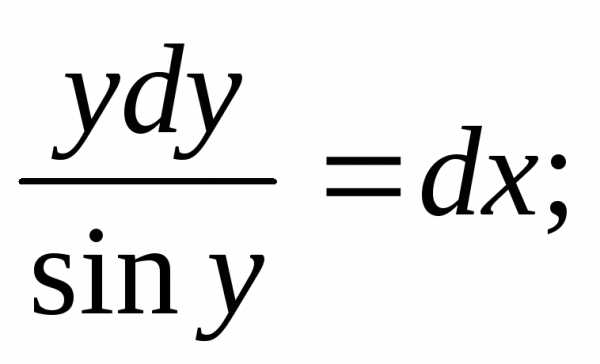
однако интеграл от левой части уравнения не выражается в элементарных функциях. Будем искать решение в виде ряда Маклорена

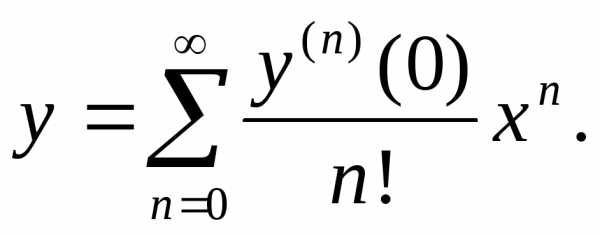
Так как 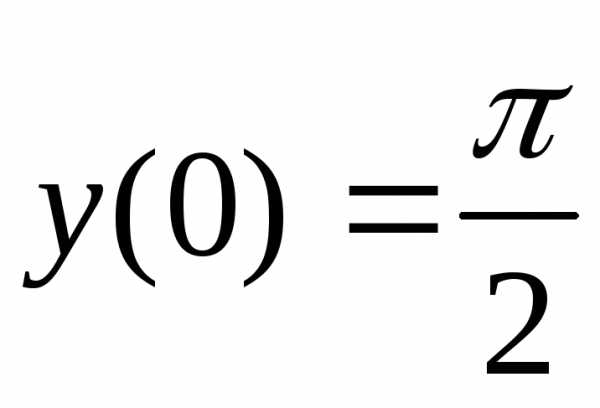, а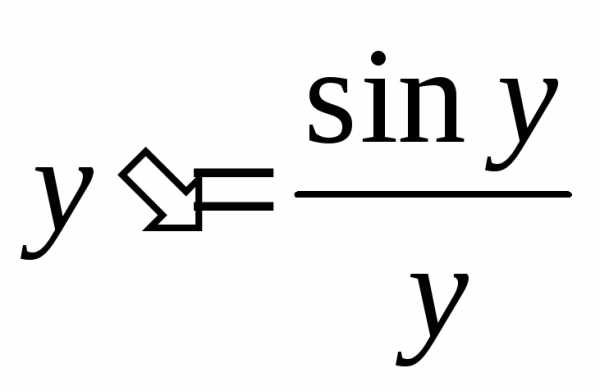(*) то.

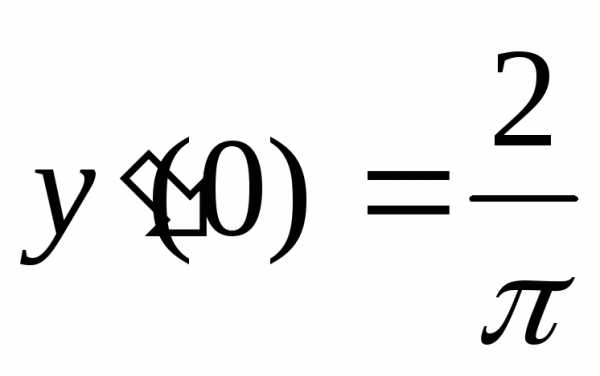Дифференцируя по х обе части равенства (*), находим

; (**)

откуда

;

Дифференцируя обе части равенства (**) , находим 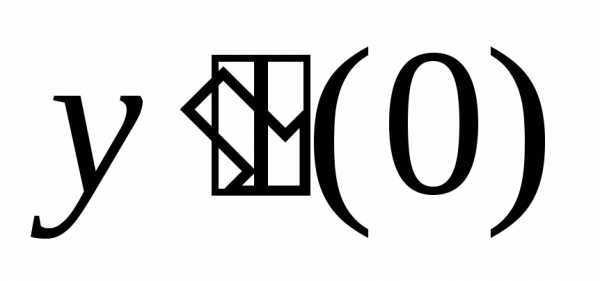. Продолжая этот процесс, можно получить любое число членов разложения в ряд Маклорена искомого решения

Глава 16 Ряды Фурье

§1.Ортонормированные системы.

Определение: Евклидовым пространством называют линейное пространство L, в котором задано скалярное умножение, т.е. отображение f:LR, ставящее упорядоченной паре элементов пространства L в соответствие число и удовлетворяющее аксиомам скалярного умножения :

1.(x,y)=(y,x), x,y_L;

2.(x+y,z)=(x,z)+(y,z), x,y,zL;

3.(x,y)=(x,y), x,yL, R;

4.(x,x)_ 0, и (x,x)=0  x=0.

Определение: Линейное (евклидово) пространство бесконечномерное, если в нем можно выбрать любое количество линейно независимых элементов.

Определение: Функция называется кусочно -непрерывной на отрезке [a;b], если она непрерывна всюду на отрезке [a;b] за исключением конечного числа точек, в которых эта функция имеет разрывы первого рода.

Так функция

f(x)=

является кусочно-непрерывной на отрезке [0;4].

Множество всех кусочно-непрерывных на [a;b] функций образует линейное пространство. При этом под сложением элементов линейного пространства и умножением элемента на число понимают обычные операции сложения функций и умножения функции на число. Нулевым элементом в этом линейном пространстве является функция, тождественно равная нулю.

Произведение любых двух функций f и g из рассматриваемого линейного пространства является кусочно-непрерывной функцией, и, следовательно, интегрируемой на отрезке [a;b] функцией. Значит в этом линейном пространстве определено отображение, которое любым двум функциям f и g ставит в соответствие действительное число (f,g):

(f, g)= (1)

Формула (1) задает скалярное умножение в рассматриваемом линейном векторном пространстве кусочно-непрерывных функций.

Легко проверить, что данное отображение удовлетворяет первым трем аксиомам скалярного умножения. Аксиома (4) не выполняется, действительно:

(f, f)==0

Для любой функции f(x), равной нулю на [a;b] всюду, кроме некоторого конечного числа точек. Такая функция кусочно-непрерывна на [a; b], но не является нулевым элементом линейного пространства, т.к. она не равна тождественно нулю на всем отрезке [a; b] .

Чтобы четвертая аксиома скалярного умножения для введенного отображения выполнялась, будем рассматривать только те кусочно-непрерывные на отрезке [a;b] функции f(x), значения которых в каждой внутренней точке их разрыва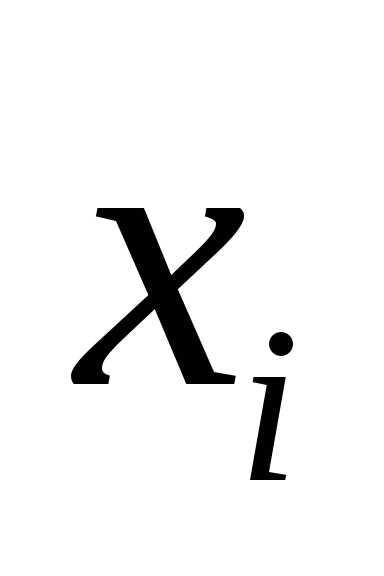равны полусумме правого и левого пределов в этой точке:

(2)

Значения на границах отрезка [a;b] одинаковы и равны полусумме односторонних пределов функции в этих точках:

(3)

Докажем, что для суженного линейного пространства кусочно-непрерывных функций введенное отображение (f,g) удовлетворяет аксиоме (4) скалярного умножения.

Пусть (f,f)==0 и точка -произвольная точка непрерывности функцииf, в которой f(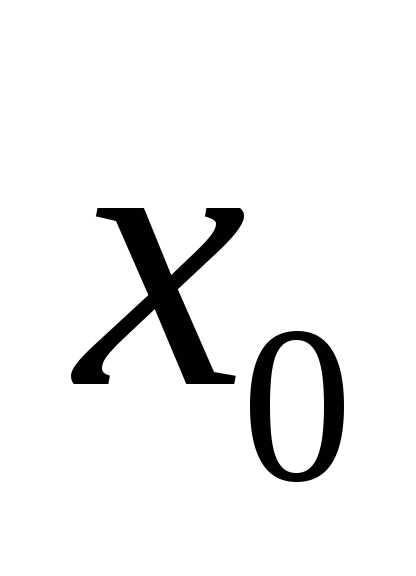) 0. Тогда на [a,b], непрерывна ви .

По свойствам определенного интеграла , что противоречит предположениям.

Следовательно, в любой точке x непрерывности функции f выполняется равенство f(x)=0.

Пусть теперь -точка разрыва функцииf(x). Т.к. точек разрыва у функции конечное число, то для любой точки разрыва найдется ее проколотая окрестность, в которой функция f(x), будет непрерывна и, значит, равна нулю. Поэтому

, ,

т.к. f(x)=0 в точках непрерывности. Тогда, согласно условию (2), имеем равенство . Аналогично для точекa и b найдутся интервалы, в которых функция f(x) непрерывна. Следовательно, f(a+0)=0 и f(b-0)=0. В силу (3) получаем f(a)=f(b)=0.

Т.е.линейное пространство всех кусочно-непрерывных на отрезке [a,b] функций, удовлетворяющих условиям (2) и (3), является евклидовым пространством со скалярным произведением (1).

Определение: Неотрицательное число:

,

называется нормой функции f(x) в евклидовом пространстве. Учитывая, что

,

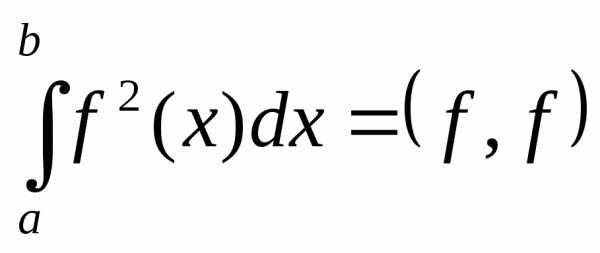то норму функции можно записать в виде: .

Функция называется нормированной, если ее норма равна 1.

Определение: Две функции f(x) и g(x) называются ортогональными на [a,b], если их скалярное произведение равно нулю, т.е.

Пример: Функции f(x)=x и g(x)=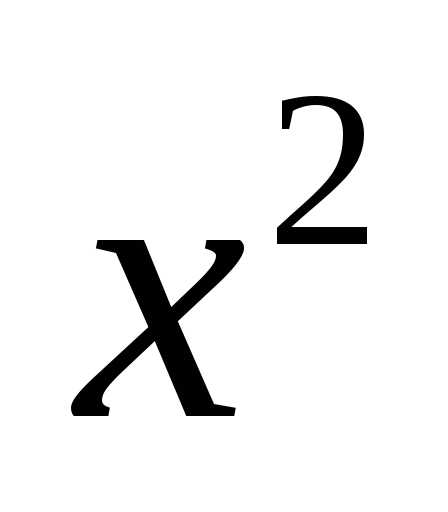 являются ортогональными на отрезке [-1,1].

Вычислим скалярное произведение:

.

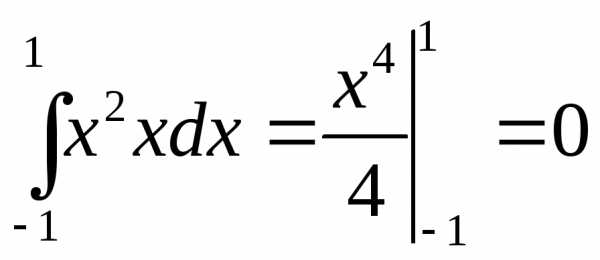Пусть в евклидовом пространстве задана некоторая бесконечная последовательность элементов Эту последовательность называют ортонормированной системой, если для любых натуральныхi и j,

,

т.е. элементы этой последовательности попарно ортогональны и все имеют единичную норму.

studfiles.net

Разложение в ряд Маклорена на примерах

«Найти разложение в ряд Маклорена функци f(x)» — именно так звучит задание по высшей математике, которое одним студентам по силам, а другие не могут справиться с примерами. Есть несколько способов разложения ряда по степенях, здесь будет дана методика разложения функций в ряд Маклорена. При развитии функции в ряд нужно хорошо уметь вычислять производные.

Пример 4.7 Разложить функцию в ряд по степеням x

Вычисления: Выполняем разложение функции согласно формуле Маклорена. Сначала разложим в ряд знаменатель функции

напоследок умножим разложение на числитель.
Первое слагаемое — значение функции в нуле f (0) = 1/3.
Найдем производные функции первого и высших порядков f (x) и значение этих производных в точке x=0




Далее с закономерности изменения значения производных в 0 записываем формулу для n-й производной

Итак, знаменатель представим в виде разложения в ряд Маклорена

Умножаем на числитель и получаем искомое разложение функции в ряд по степеням х

Как видите ничего сложного здесь нет.
Все ключевые моменты базируются на умении вычислять производные и быстрому обобщении значение производной старших порядков в нуле. Следующие примеры помогут Вам научиться быстро раскладывать функцию в ряд.

Пример 4.10 Найти разложение в ряд Маклорена функции

Вычисления: Как Вы возможно догадались раскладывать в ряд будем косинус в числителе. Для этого можете использовать формулы для бесконечно малых величин, или же вывести разложение косинуса через производные. В результате придем к следующему ряду по степеням x

Как видите имеем минимум вычислений и компактную запись разложения в ряд.

Пример 4.16 Разложить функцию в ряд по степеням x:
7/(12-x-x^2)
Вычисления: В подобного рода примерах необходимо дробь разложить через сумму простейших дробей.
Как это делать мы сейчас не будем показывать, но с помощью неопределенных коэффициентов придем к сумме дох дробей.
Далее записываем знаменатели в показательной форме

Осталось разложить слагаемые с помощью формулы Маклорена. Подытоживая слагаемые при одинаковых степенях «икс» составляем формулу общего члена разложения функции в ряд



Последнюю часть перехода к ряду в начале трудно реализовать, поскольку сложно объединить формулы для парных и непарных индексов (степеней), но с практикой у Вас это будет получаться все лучше.

Пример 4.18 Найти разложение в ряд Маклорена функции

Вычисления: Найдем производную этой функции:

Разложим функцию в ряд, воспользовавшись одной из формул Макларена: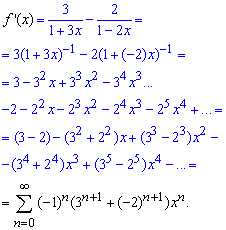

Ряды почленно суммируем на основе того, что оба абсолютно совпадающие. Проинтегрировав почленно весь ряд получим разложение функции в ряд по степеням x

Между последними двумя строками разложения имеется переход который в начале у Вас будет забирать много времени. Обобщение формулы ряда не всем дается легко, поэтому не переживайте по поводу того что не можете достать красивой и компактной формулы.

Пример 4.28 Найти разложение в ряд Маклорена функции:

Запишем логарифм следующим образом

По формуле Маклорена раскладываем в ряд по степеням x логарифм функцию

Конечное свертывания на первый взгляд сложное, однако при чередовании знаков Вы всегда получите нечто подобное. Входной урок по теме расписания функций в ряд завершено. Другие не менее интересные схемы разложения будут подробно рассмотрены в следующих материалах.

yukhym.com