Задачи на условную вероятность – .

Замечание 2. В отличие от условной вероятности, рассматривается и “безусловная” вероятность, когда какие-либо условия наступления некоторого события В отсутствуют.

Пример. В урне 5 шаров, среди которых 3 красных и 2 синих. Поочерёдно из неё извлекают по одному шару с возвратом и без возврата. Найти условную вероятность извлечения во второй раз красного шара при условии, что в первый раз извлечён: а) красный шар; б) синий шар.

Пусть событие А – извлечение красного шара в первый раз, а событие В – извлечение красного шара во второй раз. Очевидно, что р(А) = 3 / 5; тогда в случае, когда вынутый 1-й раз шар возвращается в урну, р(В)=3/5. В случае же когда вынутый шар не возвращается, вероятность извлечения красного шара р(В) зависит от того, какой шар был извлечён в первый раз – красный (событие А) или синий (событие ). Тогда в первом случае

Теорема умножения вероятностей событий, одно из которых совершается при условии совершения другого

Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событие произошло:

р(А ∙ В) = р(А) ∙ р_А(В) . (1.7)

Доказательство. Действительно, пусть n – общее число равновозможных и несовместных (элементарных) исходов испытания. И пусть n₁ – число исходов, благоприятствующих событию А, которое наступает вначале, а m – число исходов, в которых наступает событие В в предположении, что событие А наступило. Таким образом, m – это число исходов, благоприятствующих событию В. Тогда получим:

р(А ∙ В) = = ∙ = ∙ = р(А) ∙ р_А(В).

Если события А и В поменять ролями в отношении первичного и вторичного совершения, то получим:

р(В ∙ А) = р(В) ∙ р_В(А).

Таким образом, в общем случае будем иметь:

р(А ∙ В) = р(А) ∙ р_А(В) = р(В) ∙ р_В(А). ч. и т. д. (1.8)

Теорема умножения (формула (1.7)) для произвольного числа событий обобщается и имеет вид:

Т.е. вероятность произведения нескольких событий равна произведению вероятности одного из этих событий на условные вероятности других, причём условная вероятность каждого последующего события вычисляется в предположении, что все предыдущие события произошли.

Пример. В команде из 10 спортсменов 4 мастера спорта. По жеребьёвке из команды выбирают 3-х спортсменов. Какова вероятность того, что все выбранные спортсмены – мастера спорта?

Решение. Приведём задачу к “урновой” модели, т.е. будем считать, что в урне, содержащей 10 шаров, имеется 4 красных шара и 6 белых. Из этой урны наудачу извлекаются 3 шара ( выборка

Первый способ, основанный на формуле комбинаторики:

р(А) = = = .

Второй способ (по формуле (1.9)). Из урны последовательно без возвращения извлекаются 3 шара. Пусть А₁ – первый извлечённый шар красный, А₂ – второй извлечённый шар красный, А₃ – третий извлечённый шар красный. Пусть также событие А означает, что все 3 извлечённых шара – красные. Тогда: А = А₁ ∙ (А₂ / А₁) ∙ А₃ / (А₁ ∙ А₂), т.е.

Пример. Пусть из совокупности карточек а, а, р, б, о, т последовательно извлекаются карточки по одной. Какова вероятность получения слова “

Пусть В – событие, при котором получается заявленное слово. Тогда по формуле (1.9) получим:

р( В ) = 1/6 ∙ 2/5 ∙ 1/4 ∙ 1/3 ∙ 1/2 ∙ 1/1 = 1/360.

Теорема умножения вероятностей приобретает наиболее простой вид, когда произведение образуется независимыми друг от друга событиями.

Определение. Событие В называется независимым от события А, если его вероятность не меняется от того, произошло событие А или нет. Два события называются независимыми ( зависимыми ), если появление одного из них не изменяет (изменяет) вероятность появления другого. Таким образом, для независимых событий р(В/A) = р(В) или = р(В), а для зависимых событий р(В/A) р(В) или р(В).

Утверждение. Если событие В

Действительно, если по условию событие В не зависит от А, то р(В/A) = р(В). Запишем теорему умножения вероятностей (1.8) в двух формах:

р(А ∙ В) = р(А) ∙ р(В/A) = р(В) ∙ р(А/B).

Заменяя р(В/A) на р(В), получим р(А) ∙ р(В) = р(В) ∙ р(А/B), откуда, предполагая р(В) 0, получим р(А/B) = р(А), т.е. событие А не зависит от В, ч. и т. д.

Таким образом, независимость и зависимость событий всегда взаимны. Поэтому справедливо следующее определение независимости (зависимости) событий.

условная вероятность — 4 Сентября 2013 — Примеры решений задач

www.reshim.su

Задачи на условную вероятность и независимость событий

3.11. Игральную кость подбрасываем один раз. Пусть событие А – выпало нечетное число очков, событие В – выпало число очков большее двух. Вычислить вероятность наступления а) события А при условии наступления события В; б) события В при условии наступления события А.

3.12. Из полной колоды случайным образом вынимается карта. Найти вероятность того, что вытащили туза, если а) вынутая карта масти треф; вынутая карта не масти треф.

3.13. Из полной колоды случайным образом вынимаются одна за другой две карты. Найти вероятности того что обе карты короли, если вытащили карты красной масти.

3.14. Подбрасываем игральную кость. Предположим событие А – выпало четное число, событие В – выпало число кратное 3. Найдем вероятность того, что выпадет четное число, если выпало число кратное 3, т.е. P(В/А).

3.15. Пусть вероятность рождения мальчика 0,5. Известно, что в семье двое детей, причем как минимум один ребенок — мальчик. С какой вероятностью можно утверждать, что оба ребенка – мальчики.

3.16. Проводится олимпиада среди студентов по истории. Подготовлено 12 вопросов. Вопросы достаются произвольно. Среди них 3 по новой истории, 2 по древней и 7 по истории России. Студенту достается три вопроса. Какова вероятность, что: а) первые два вопроса будут по истории России, а третий по древней; б) достанутся вопросы по разным темам.

3.17. Три стрелка стреляют по мишеням. Вероятность попадания первого – 0,8 , для второго – 0,9 и третьего – 0,6. С какой вероятностью в мишени будет а) ровно три пробоины; б) только две пробоины; в) все стрелки промажут.

3.18. Дорожный пост проверяет документы водителя на перевозимый груз. Вероятность того, что документы в порядке, равна 0,9. Найти вероятность того, что из двух проверенных только у одного документы не в порядке.

3.19. В магазин поступают мясные продукты с трех ферм. Из партии изделий менеджер отбирает продукцию высшего сорта. Вероятность того, что наудачу взятый продукт окажется высшего сорта, равна 0,8. Найти вероятность того, что из трех проверенных продуктов только два продукта высшего сорта.

3.20. Из колоды в 36 карт вытаскивается карта черной масти. Из оставшихся 35 карт случайным образом выбираются 9 карт, причем оказывается, что все они одного цвета. С какой вероятностью можно утверждать, что они красной масти?

3.21. Среди 100 студентов 1 курса есть 5 отличников. Зачетки лежат в деканате. Найти вероятность того, что 2 наудачу выбранные зачетки окажутся зачетками отличников.

3.22. На озеленении территории университета работают семь женщин и три мужчины. Наудачу отобраны три человека. Найти вероятность того, что все отобранные окажутся женщинами.

3.23. В коробке 10 кубиков, среди которых шесть красных, остальные белые. Ребенок достает последовательно четыре кубика. Найти вероятность того, что все извлеченные кубики окажутся красными.

3.24. В корзине лежат 6 яблок красного и 4 зеленого сорта. Наудачу извлекают последовательно по одному три яблока. Найти вероятность того, что все три яблока красного сорта: а) выбор производится без возвращения; б) взятое яблоко после осмотра, возвращается обратно.

3.25. Для поражения воздушной цели произведен запуск двух ракет земля-воздух. Найти вероятность того, что а) цель будет поражена; б) не будет поражена, если вероятность поражения цели одной ракетой равна 0,96.

3.26. Вероятность сдать каждый из трех экзаменов сессии на «отлично» для студента равны соответственно 0,8; 0,7 и 0,75. Найти вероятность того, что студент сдал на «отлично»: а) все три экзамена, б) два экзамена, в) ни одного экзамена.

3.27. В столе 12 дефектных и 5 годных микросхем. Извлекаются наудачу 2 микросхемы и если надо ремонтируются и возвращаются в стол. После этого вновь наудачу извлекаются 2 микросхемы. Определить вероятность того, что а) обе микросхемы дефектные; б) одна микросхема дефектная; в) обе микросхемы годные.

3.28. В 2-х корзинах находится соответственно m₁ и m₂ белых и n₁ и n₂ красных яблока. Из каждой корзины наудачу извлекается одно яблоко, а затем из этих 2-х яблок наудачу берется одно. Определить вероятность того, что это яблоко а) белое; б) красное.

3.29. Только один из n ключей подходит к данной двери. Найти вероятность того, что для открывания двери придется опробовать ровно k (k ≤ n) ключей.

3.30. В урне имеется два шара – белый и черный. Производятся извлечения по одному шару до тех пор, пока не появится черный шар, причем при извлечении белого шара в урну возвращается этот шар, и добавляются еще два белых шара. Определить вероятность того, что при первых пятидесяти опытах черный шар не будет извлечен.

3.31. Игра между А и В ведется на следующих условиях: в результате первого хода, который всегда делает А, он может выиграть с вероятностью 0,3; если первым ходом А не выигрывает, то ход делает В и может выиграть с вероятностью 0,5; если в результате этого хода В не выигрывает, то А делает второй ход, который может привести его к выигрышу с вероятностью 0,4. Определить вероятности выигрыша для А и В.

3.32. Игрок А поочередно играет с игроками В и С, имея вероятность выигрыша в каждой партии 0,25, и прекращает игру после первого проигрыша или после двух партий, сыгранных с каждым игроком. Определить вероятности выигрыша В и С.

3.33. Найти вероятность того, что дни рождения 12 человек придутся на разные месяцы года.

3.34. Найти вероятность того, что дни рождения 6 человек придутся на разные месяцы года.

studfiles.net

1.4 Условная вероятность

Случайное событие определено как событие, которое при осуществлении совокупности условий эксперимента может произойти или не произойти. Если при вычислении вероятности события никаких других ограничений, кроме условий эксперимента, не налагается, то такую вероятность называют безусловной; если же налагаются и другие дополнительные условия, то вероятность события называют условной. Например, часто вычисляют вероятность события В при дополнительном условии, что произошло событие А.

Условной вероятностью (два обозначения) называют вероятность событияВ, вычисленную в предположении, что событие А уже наступило.

Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло, т.е.

.

В частности, отсюда получаем .

Пример. В урне находятся 3 белых шара и 2 черных. Из урны вынимается один шар, а затем второй. Событие В – появление белого шара при первом вынимании. Событие А – появление белого шара при втором вынимании.

Решение. Очевидно, что вероятность события А, если событие В произошло, будет . Вероятность событияА при условии, что событие В не произошло, будет .

Пример. В урне 3 белых и 3 черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Найти вероятность появления белого шара при втором испытании (событие В), если при первом испытании был извлечен черный шар (событие А).

Решение. После первого испытания в урне осталось 5 шаров, из них 3 белых. Искомая условная вероятность .

Этот же результат можно получить по формуле.

Действительно, вероятность появления белого шара при первом испытании.

Найдем вероятность того, что в первом испытании появится черный шар, а во втором — белый. Общее число исходов — совместного появления двух шаров, безразлично какого цвета, равно числу размещений. Из этого числа исходов событиюблагоприятствуютисходов. Следовательно,.

Искомая условная вероятность

Результаты совпали.

Пример. В трамвайном парке имеются 15 трамваев маршрута №1 и 10 трамваев маршрута №2. Какова вероятность того, что вторым по счету на линию выйдет трамвай маршрута №1?

Решение. Пусть А — событие, состоящее в том, что на линию вышел трамвай маршрута №1, В — маршрута №2.

Рассмотрим все события, которые могут при этом быть (в условиях нашей задачи): . Из них нас будут интересовать только первое и третье, когда вторым выйдет трамвай маршрута №1.

Так как все эти события совместны, то:

;

;

отсюда искомая вероятность

Пример. Какова вероятность того, что 2 карты, вынутые из колоды в 36 карт, окажутся одной масти?

Решение. Сначала подсчитаем вероятность того, что две карты окажутся одной определенной масти (например «пики»). Пусть А — появление первой карты такой масти, В — появление второй карты той же масти. Событие В зависит от события А, т.к. его вероятность меняется от того, произошло или нет событие А. Поэтому придется воспользоваться теоремой умножения в ее общей форме:

, где (после вынимания первой карты осталось 35 карт, из них той же масти, что и первая — 8).

Получаем .

События, состоящие в том, что будут вынуты две карты масти «пики», масти «треф» и т.д., несовместны друг с другом. Следовательно, для нахождения вероятности их объединения воспользуемся теоремой сложения:.

studfiles.net

1.5. Условная вероятность

Случайное событие определено как событие, которое при осуществлении совокупности условий эксперимента может произойти или не произойти. Если при вычислении вероятности события никаких других ограничений, кроме условий эксперимента, не налагается, то такую вероятность называют безусловной; если же налагаются и другие дополнительные условия, то вероятность события называют условной. Например, часто вычисляют вероятность события В при дополнительном условии, что произошло событие А.

Условной вероятностью (два обозначения) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.

Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло, т.е.

.

В частности, отсюда получаем  .

Пример. В урне находятся 3 белых шара и 2 черных. Из урны вынимается один шар, а затем второй. Событие В – появление белого шара при первом вынимании. Событие А – появление белого шара при втором вынимании.

Решение. Очевидно, что вероятность события А, если событие В произошло, будет  .  Вероятность события А при условии, что событие В не произошло, будет  .

Пример. В урне 3 белых и 3 черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Найти вероятность появления белого шара при втором испытании (событие В), если при первом испытании был извлечен черный шар (событие А).

Решение. После первого испытания в урне осталось 5 шаров, из них 3 белых. Искомая условная вероятность .

Этот же результат можно получить по формуле .

Действительно, вероятность появления белого шара при первом испытании .

Найдем вероятность того, что в первом испытании появится черный шар, а во втором — белый. Общее число исходов — совместного появления двух шаров, безразлично какого цвета, равно числу размещений . Из этого числа исходов событию благоприятствуют исходов. Следовательно, .

Искомая условная вероятность 

Результаты совпали.

Пример. В трамвайном парке имеются 15 трамваев маршрута №1 и 10 трамваев маршрута №2. Какова вероятность того, что вторым по счету на линию выйдет трамвай маршрута №1?

Решение. Пусть А — событие, состоящее в том, что на линию вышел трамвай маршрута №1, В — маршрута №2.

Рассмотрим все события, которые могут при этом быть (в условиях нашей задачи): . Из них нас будут интересовать только первое и третье, когда вторым выйдет трамвай маршрута №1.

Так как все эти события совместны, то:

;

;

отсюда искомая вероятность

Пример. Какова вероятность того, что 2 карты, вынутые из колоды в 36 карт, окажутся одной масти?

Решение. Сначала подсчитаем вероятность того, что две карты окажутся одной определенной масти (например «пики»). Пусть А — появление первой карты такой масти, В— появление второй карты той же масти. Событие В зависит от события А, т.к. его вероятность меняется от того, произошло или нет событие А. Поэтому придется воспользоваться теоремой умножения в ее общей форме:

,  где (после вынимания первой карты осталось 35 карт, из них той же масти, что и первая — 8).

Получаем  .

События, состоящие в том, что будут вынуты две карты масти «пики», масти «треф» и т.д., несовместны друг с другом. Следовательно, для нахождения вероятности их объединения воспользуемся теоремой сложения: .

studfiles.net

Задачи на схему Бернулли

Задача 30. Случайное блуждание по прямой. Частица движется по целым точкам вещественной прямой, перемещаясь каждую секунду либо на единицу вправо, либо на единицу влево с вероятностями, равными 1/2. Найти вероятность того, что через n секунд частица вернется в точку 0.

Решение. Очевидно, вернуться в 0 частица может только за четное число секунд. Поэтому считаем, что n=2k. Считая, успехом движение частицы вправо, заметим, что для возвращения за n секунд должно быть ровно k успехов. Поэтому из формулы Бернулли следует, что вероятность возвращения равна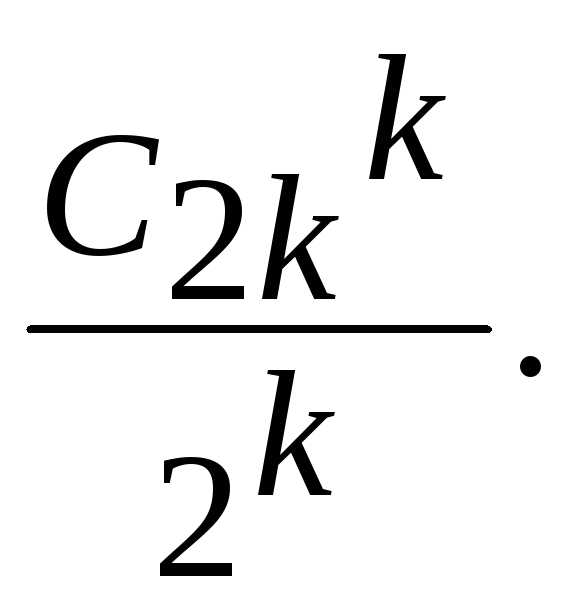

Задача 31. Имеется 5 студенческих групп по 25 человек, в каждой из которых по 5 отличников. Из каждой группы выбирается случайным образом по одному студенту. Найти вероятность того, что среди выбранных студентов будет 3 отличника.

Решение. Вероятность выбрать отличника в одной группе равна p=1/5.Выбор отличника будем считать успехом. Тогда число успехов среди n=5 испытаний должно равняться m=3. Таким образом, по основной формуле схемы Бернулли искомая вероятность равна (1/5)³(4/5)²= (32/625).

Задача 32. Задача Банаха. У рассеянного курильщика в правом и левом кармане пиджака находится по коробку спичек. В каждом коробке по n спичек. Каждый раз, когда ему требуется закурить, курильщик вынимает новую сигарету либо из левого, либо из правого кармана с вероятностями, равными по 1/2. Найти вероятность того, что в тот момент, когда окажется пустым один из коробков, во втором коробке останется k спичек.

Решение. Пусть A – это событие, стоящее в вопросе задачи. Будем считать испытанием Бернулли вытаскивание спичек, причем вытаскивание спички из правого кармана будем считать успехом, а из левого – неудачей. Очевидно, вероятность успеха равна 1/2. Поскольку к моменту окончания «эксперимента» из одного коробка вытащили n спичек, а из другого – (n—k) спичек, то общее число испытаний Бернулли можно считать равным (2n—k), причем событие A реализуется, если число успехов равно n или k. Поэтому

Задача 33. Монета бросается 100 раз. Найти приближенно вероятность того, что герб выпадет 40 раз. (Воспользоваться таблицей )

Решение. Если считать успехом выпадение герба, то вероятность успеха равна 1/2. Поэтому используя предельную локальную теорему Муавра-Лапласа, получим

, где

Таким образом, используя таблицы для плотности нормального распределения, получим P(A)=0.0108.

Задача 34. Город ежедневно посещают 1000 туристов, которые днем идут обедать. Каждый из них выбирает для обеда один из двух городских ресторанов с равными вероятностями и независимо друг от друга. Владелец одного из ресторанов желает, чтобы с вероятностью, приближенно равной 0.99, все пришедшие в ресторан туристы смогли бы там одновременно пообедать. Сколько мест должно быть для этого в ресторане?

Решение. Обозначим через A_i событие, состоящее в том, что i-ый турист пообедал у заинтересованного владельца ресторана, i=1,2,…,1000. Наступление события A_iбудем называть успехом в i-ом испытании. Вероятность успеха P(A_i)=p=1/2. Пусть m – общее число успехов, событие A состоит в переполнении ресторана, k – общее число мест в ресторане. Тогда нам надо подобрать k таким образом, чтобы выполнялось приближенное равенство

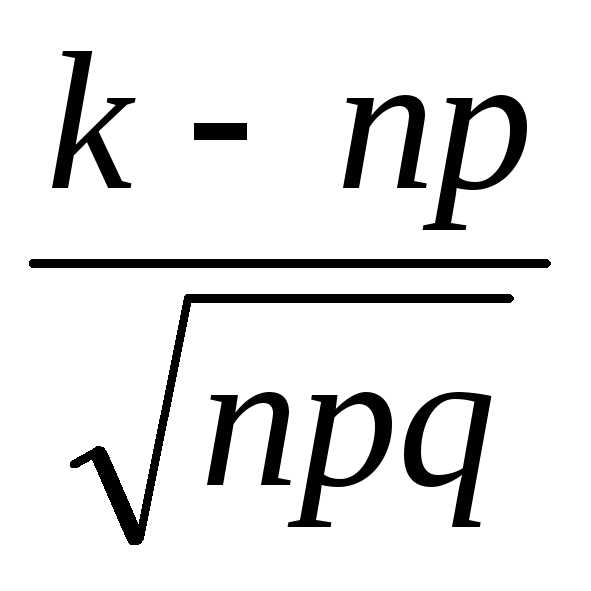P(>) =P(>) =1- 0.99=0.01.

Из интегральной теоремы Муавра-Лапласа Следует, что для этого достаточно, чтобы выполнялось равенство Ф(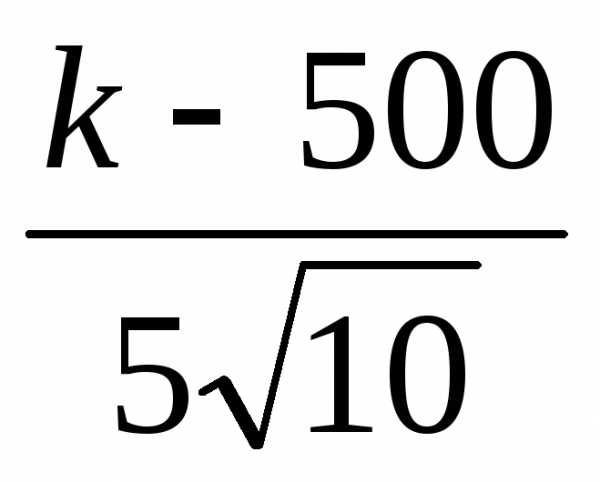) = 0.99.

Обращаясь к таблице значений функции Φ(x), получим уравнение для нахождения числа k:

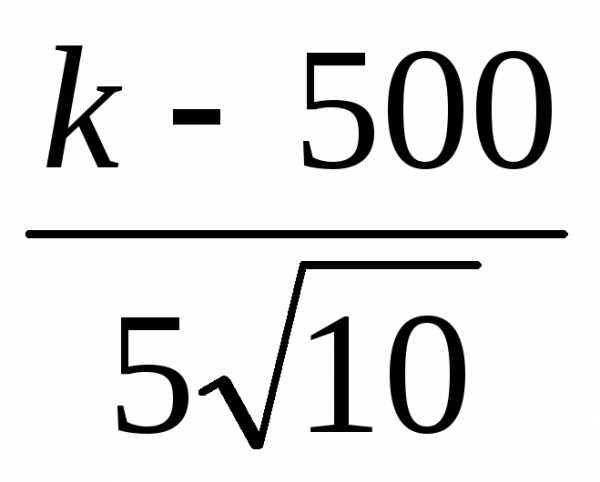= 2.33.

Решение этого уравнения k=500+2.33∙ 5√10=536.8. Поскольку k должно быть целым числом, то следует окончательно выбрать k=537.

Задача 35. Машинистка печатает текст, который содержит 20000 знаков. Каждый знак может быть напечатан неправильно с вероятностью 0.0004. Какова вероятность того, что в тексте не менее 3 опечаток?

Решение. Если опечатку считать успехом, то к этой задаче применима схема Бернулли при p=0.0004, n=20000. Поскольку λ=np=8, то можно использовать предельную теорему Пуассона. Поэтому, искомая вероятность равна 1-P_n⁰— P_n¹— P_n²=1-e^-8— 8 e^-8-(64/2) e^-8= 1-41 e^-8=0.986.

Задача 36. При рождении ребенка вероятность рождения мальчика равна 0.512. Найти вероятность того, что среди 1000 новорожденных мальчиков родится больше, чем девочек.

Решение. Пусть A – это событие, соответствующее вопросу задачи, m – это число рожденных мальчиков. Нетрудно видеть, что P(A) = P(m>500). Поскольку n=1000 можно считать достаточно большим, то применим интегральную теорему Муавра-Лапласа, согласно которой

P(A)=P(

studfiles.net