Решение простейших тригонометрических уравнений с подробным решением – Тригонометрические уравнения. Подготовка к ЕГЭ по математике.

“Не делай никогда того, чего не знаешь, но научись всему, что следует знать”. (Пифагор)

Сегодня на уроке мы научимся решать с вами простейшие тригонометрические уравнения.

1. Актуализация опорных знаний (устная работа).

В результате выполнения задания мы повторим определения арккосинуса, арксинуса, арктангенса и арккотангенса.

1. Сформулировать определение арксинуса числа.

2. Сформулировать определение арккосинуса числа.

3. Сформулировать определение арктангенса числа.

5. С помощью тригонометрической окружности найти все значения из промежутка [-2 которые соответствуют числам , , , , arcsin 0, arcsin (Приложение 1)

6. Проверить, верно ли равенство:

7. Имеет ли смысл выражение:

2. Объяснение новой темы. Простейшие тригонометрические уравнения.

Определение. Уравнения вида f(x) = а, где а – данное число, а f(x) – одна из тригонометрических функций, называются простейшими тригонометрическими уравнениями.

1. Пусть дано простейшее уравнение cos t = a.

Данное уравнение:

a) при -1< t < 1 имеет две серии корней

t₁ = arсcos a + 2k, k Z

t ₂ = — arсcos a + 2m, m Z.

Эти серии можно записать так

t = ± arсcos a + 2n, n Z ;

б) при а = 1 имеет одну серию решений

t = 2n, n Z ;

в) при а = -1 имеет одну серию решений

t = + 2n, n Z ;

г) при а = 0 имеет две серии корней

t₁ = + 2k, k Z

t ₂ = — + 2m, m Z. Обе серии можно записать в одну серию

t_{= + n, n Z.}

д) при а > 1 и a < -1 уравнение не имеет корней.

Задание 1. Решить уравнения:

1) cos х = ;

2) cos х = — ;

3) cos 4x = 1

4x = 2n, n Z

.

4)

,

.

5)

,

,

.

6) Решите уравнение ; укажите корни, принадлежащие промежутку [-; -2].

а)

б) сделаем выборку корней, принадлежащих промежутку [-2; -].

1) с помощью окружности

2) с помощью графика функции

Ответ: а) ; б) .

Задание 2. Найти корни уравнения:

1) a) cos x =1 б) cos x = — 1 в) cos x = 0 г) cos x =1,2 д)

2) а) б) в) г)

2. Пусть дано простейшее уравнение sin t = a.

Данное уравнение :

a) при -1< t < 1 имеет две серии корней

t₁ = arсsin a + 2n, n Z

t ₂ = — arсcsin a + 2n, n Z.

Эти серии можно записать так

t = ( -1)^karсsin a + k, k Z ;

б) при а = 1 имеет одну серию решений

t_{= + 2n, n Z}

в) при а = -1 имеет одну серию решений

t = — + 2n, n Z;

г) при а = 0 имеет две серии корней

t₁ = 2k, k Z,

t₂ = + 2m, m Z.

Обе серии можно записать в одну серию

t = n, n Z ;

д) при а > 1 и a < -1 уравнение не имеет корней.

Задание 3. Решить уравнения:

1) sin х = ;

Запишем ответ в виде одной серии x_{= ( -1)^k+ k, k Z .}

2) sin х = -;

Запишем ответ в виде одной серии x_{= ( -1)^k ( — + k, k Z или x= ( -1)^k+1+ k, k Z .}

Задание 3. Найти корни уравнения :

1) a) sin x =1 б) sin x = — 1 в) sin x

2) а) б) в) г)

3. Пусть дано простейшее уравнение tg t = a.

Данное уравнение при любом а R имеет одну серию решений

х = аrctg a + n, n Z.

1) tg х =

х = аrctg + n, n Z.

x = + n, n Z.

2) tg х = ,

х = аrctg + n, n Z,

x = + n, n Z.

4. Пусть дано простейшее уравнение ctg t = a.

Данное уравнение при любом а R имеет одну серию решений

х = аrcctg a + n, n Z.

1) ctg x = 1

х = аrcctg 1 + n, n Z,

х = + n, n Z.

х = аrcctg ( -1) + n, n Z,

х = — аrcctg 1 + n, n Z

х = + n, n Z.

5. Итог урока

Продолжите фразу :

• Сегодня на уроке я повторил …
• Сегодня на уроке я узнал …
• Сегодня на уроке я научился …

Вы молодцы! Каждый из вас “научись тому, что следует знать”. Формулы для решения тригонометрических уравнений записаны на карточке — информаторе. (Приложение 2)

6. Домашнее задание: п.9, пример 1-9, № 137, 139, 141, 142.

Спасибо за урок!

Литература.

1. А.Н.Колмогоров Алгебра и начала анализа. 10–11 классы
2. С.М. Никольский, М.К. Потапов и др “Алгебра и начала анализа 10”

20.03.2013

Решения простейших тригонометрических уравнений

Министерство образования и молодежной политики Чувашской Республики

Решения простейших тригонометрических уравнений

Преподаватель: Дмитриева М.В.

Введение.

В настоящее время основной задачей перестройки школьного образования является переориентация на приоритет развивающей функции обучения. Это означает, что на первый план выходит задача интеллектуального развития личности, т.е. развитие учебно-познавательной деятельности. Пожалуй, ни один школьный предмет не может конкурировать с возможностями математики в воспитании мыслящей личности. Уже несколько десятилетий тригонометрия, как отдельная дисциплина школьного курса математики не существует, она плавно растеклась не только в геометрию и алгебру основной школы, но и в алгебру и начала анализа.

Цель: Обобщить знания обучающихся об алгоритмах решения простейших тригонометрических уравнений, систематизировать знания, формировать умение их применять при решении профессионально значимых задач; создать условия для более глубокого усвоения обучающимися знаний по указанной теме урока с помощью инновационных компьютерных технологий; развивать у обучающихся умение самостоятельной деятельности, логического мышления.

Задачи:
1.Обобщение и распространение собственного педагогического опыта.

2. Классифицировать уравнения по методам решения;

3. Решать тригонометрические уравнения, выбирая для каждого соответствующий метод решения.

Актуальность темы: Анализ материала, посвященного решению тригонометрических уравнений в учебных пособиях «Алгебра и начала анализа» для 10 – 11 классов разных авторов, учет целей изучения тригонометрических уравнений, а так же обязательных результатов обучения, связанных с рассматриваемой темой, свидетельствует о том, что перед учителем стоит задача – формировать у обучающихся умения решать уравнения каждого вида, развивая тем самым общие тригонометрические представления.

Дидактическая структура урока:

Этапы урока

1. Организационный этап.

2. Постановка цели и задач урока. Мотивация учебной деятельности учащихся.

3. Этап актуализации необходимых знаний и умений, включая

4. Проверка домашнего задания;

5. Этап усвоения новых знаний. (Объяснение нового материала).

6. Этап закрепления новых знаний.

7. Контроль усвоенного на уроке материала.

8. Подведение итогов.

9. Этап информации учащихся о домашнем задании, инструктаж по его выполнению.

1. Организационный этап Показатели выполнения психологической задачи этапа:

— доброжелательный настрой учителя и учащихся;

— быстрое включение класса в деловой ритм;

— организация внимания всех учащихся;

— полная готовность класса и оборудования к работе.

2. Постановка цели. Мотивация Постановка цели может проводится с помощью иллюстрации, анимации, презентации или картографической карты.

3. Этап проверки ранее усвоенных знаний Опрос должен быть интересен ученикам, а для этого известный фактический материал должен рассматриваться в новом свете, теоретические знания применяться на практике. На этапе актуализации знаний возможно использование ПК для организации разных видов устного счета, проведения автоматизированных математических диктантов, что способствует развитию внимания, дисциплинированности т.к. учащиеся понимают, что задания дает машина, а она не может повторяться или останавливаться по чьей-либо просьбе. Возможно создание проблемной ситуации. Даются задания, которые обучающиеся решают с легкостью, а затем предлагается задача, с которой ребята не знакомы.

4. Этап приобретения новых знаний. На этапе приобретения новых знаний компьютер выступает в роли мощного демонстрационного средства, обеспечивая высокий уровень наглядности. Сочетание рассказа учителя с демонстрацией презентации позволяет акцентировать внимание учащихся на особо значимых моментах учебного материала. Возможна демонстрация пошагового решения задачи. На этом этапе один из действенных способов повышения интереса – это использование на уроке сведений из истории математики. К тому же это несет воспитательный характер, служит развитию эстетического вкуса учеников, а также привитию нравственных качеств.

5. Этап первичного закрепления. На этапе первичного закрепления можно давать схемы, чертежи, таблицы, опорные конспекты, алгоритмы и т.д., помогающие находить решение задачи. Контроль знаний и умений обучающихся является одним из важнейших элементов учебного процесса. Другая форма проведения контроля знаний и умений – это тестирование. Тесты могут быть различными: контролирующие т.е. проверяющие уровень усвоения ЗУН обучающимися или обучающее — корректирующие, т.е. имеющие справочный материал, к которому ученик может обратиться в случае затруднения или неверного ответа. Я считаю, что тесты незаменимы для проведения контроля, т.к. помогают быстро определить типичные ошибки, что позволяет сразу же устранить пробелы в знаниях. Конечно, использовать для проверки уровня усвоения учебного материала только тесты, нецелесообразно. Можно проводить самостоятельные работы по вариантам. Рассмотрим конкретный пример урока на тему «Методы решения простейших тригонометрических уравнений».

Тема урока: Методы решения простейших тригонометрических уравнений.

Цели урока:

Образовательные: ознакомление с новым математическим понятием; формирование новых ЗУН; научить решать простейшие тригонометрические уравнения, используя ранее приобретенные знания; учить умению анализировать, творчески подходить к поставленной задаче; помочь учащимся подготовиться к экзаменам.

Развивающие: развитие самостоятельного мышления учащихся, развитие навыков правильной речи школьников.

Воспитывающие: воспитывать аккуратность, четкое оформление решений задач, положительный интерес к изучению математики, самостоятельности, инициативности учащихся на уроке. Воспитать уважительного отношения друг к другу.

Оборудование: экран, компьютер, мультимедиа, рабочая карта для подведения итогов урока, презентация, задачи для домашней работы, справочники.

Тип урока: комбинированный.

Вид урока: урок смешанный.

Метод обучения: проблемно-поисковый, беседа.

Основные вопросы:

1. Формулы решения простейших тригонометрических уравнений.

2. Алгоритм решения.

3. Решение тригонометрических уравнений, выбирая для каждого соответствующий метод решения.

План урока

1) Организационный момент.

2) Проверка домашней работы.

3) Актуализация опорных знаний, умений и навыков.

4) Изучение нового материала.

5) Усвоение навыков и умений.

6) Физ.минутка.

7) Подведение итогов урока.

8) Этап рефлексии

9). Домашнее задание.

Ход урок

1. Организационный момент.

Взаимное приветствие учителя и студентов, фиксация отсутствующих, проверка готовности учащихся к уроку. Студентам сообщается  план урока. Записывают в тетрадях: число, классная работа, тема урока.

Учитель формулирует тему и цели урока. Сегодня на уроке мы с вами изучим тригонометрические уравнения. Научимся решать простейшие тригонометрические уравнения, выбирая для каждого соответствующий метод решения.

2.Проверка домашней работы.

Проверка теоретических знаний проводится в виде теста.

Учитель раздаёт листы с заданиями, оказывает консультации студентам по заполнению листов с ответами. Обучающиеся знакомятся с тестом, решают задания, заносят ответы в карточки.

3)Актуализация опорных знаний, умений и навыков.

Проводится фронтальный опрос учащихся по теме домашнего задания.

1. Сформулировать определение арксинуса числа.

2. Сформулировать определение арккосинуса числа.

3. Сформулировать определение арктангенса числа.

4. Сформулировать определение арккотангенса числа.

3. Проверить, верно ли равенство:

4) Изучение нового материала.

Объяснение новой темы. Простейшие тригонометрические уравнения. Определение. Уравнения вида , где – данное число, а – одна из тригонометрических функций, называются простейшими тригонометрическими уравнениями.

Пусть дано простейшее уравнение .

Данное уравнение:

При имеет две серии корней

б) при имеет одну серию решений

, ;

в) при имеет одну серию решений

, ;

г) при имеет две серии корней

,

, .

Обе серии можно записать в одну серию ,

д) при и уравнение не имеет корней.

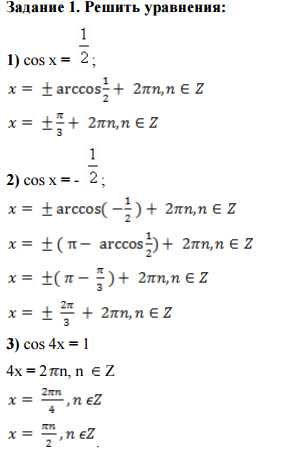
5) Усвоение навыков и умений

Упражнения по образцу.

6) Физкультминутка. Перед закреплением теоретического материала проводится

7. Итог урока.

Итак, подводим итог урока. Что нового узнали? Как решать простейшие тригонометрические уравнения?

Сегодня вы научились решать простейшие тригонометрические уравнения, которые попробуйте использовать.

8) Рефлексия:

Продолжите фразу:

Сегодня на уроке я повторил …

Сегодня на уроке я узнал …

Сегодня на уроке я научился …

Спасибо за работу!

9) Задание на дом:

Решить простейшие тригонометрические уравнения:

1) 2) 3)

4) 5) 6)

7) 8) 9)

10) 11) 12)

13) 14) 15)

16) 17) 18)

19) 20)

ТЕСТ

Заключение.

Решение любых тригонометрических уравнений сводится к решению рассмотренных выше простейших тригонометрических уравнений. Для этого применяются тождественные преобразования, изученные Вами ранее: различные тригонометрические формулы, различные способы решения алгебраических уравнений, формулы сокращенного умножения и т.д..

Литература

Алгебра и начала анализа: дидактические материалы для 10 класса / М.К.Потапов, А.В.Шевкин.-2-е изд.-М.:Просвещение,2007.

Алгебра и начала анализа: дидактические материалы для 11 класса: базовый и профильные уровни / М.К.Потапов, А.В.Шевкин.-2-е изд.-М.:Просвещение,2007.

Единый государственный экзамен: Математика: контрольные измерительные материалы: 2006-2007.-М.:Просвещение: СПб.: Просвещение,2007.

ЕГЭ-2009.Математика: Сдаём без проблем!/ О.А.Креславская, В.В.Крылов, В.И.Снегурова, В.Е.Ярмолюк.-М.:Эксмо.2008.

ЕГЭ. Репетитор. Математика.Эффективная методика./ Л.Д.Лаппо, А.В.Морозов, М.А.Попов.-М.:Издательство «Экзамен»,2007.

Панчишкин А.А.. Шавгулидзе Е.Т. Тригонометрические функции в задачах — М.:Наука. Главная редакция физико – математической литературы,1986.

xn--j1ahfl.xn--p1ai

Решение простейших тригонометрических уравнений

Пуртова Елена Дмитриевна,

учитель математики

Решение простейших

тригонометрических уравнений

Аннотация к уроку: Урок алгебры в 10 классе по теме: «Решение простейших тригонометрических уравнений» соответствует программе общеобразовательных учреждений. Первый урок по теме «Решение тригонометрических уравнений».

Учебник для общеобразовательных учреждений – УМК: Мордкович А. Г. Алгебра и начала математического анализа. 10 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. – 6-е изд., стер. – М.: Мнемозина, 2009.

Тип урока: изучение нового материала.

Мотивация изучения данной темы обеспечивается за счет применения ИКТ, использования различных видов заданий. Приоритетная цель на уроке применение полученных знаний, отработка умений, решение тригонометрических уравнений.

Основой дидактический метод: проблемно-поисковый.

Частые методы: метод эвристической беседы, методы организации и осуществления учебно-познавательной деятельности, методы контроля и самоконтроля за эффективностью учебно-познавательной деятельности.

Формы работы: фронтальная. групповая, индивидуальная.

Дидактические средства: мультимедиапроектор, компьютеры на каждого ученика, макеты числовой окружности на координатной плоскости у учащихся, таблица значений тригонометрических функций у учащихся (составлены на предыдущих уроках), презентация по теме «Простейшие тригонометрические уравнения».

Программное обеспечение: среда Stratum 2000 — приложение для Windows

Введение:

Цель урока: изучить решение простейших тригонометрических уравнений.

Задачи к уроку:

1. Образовательные:

1.1.Создать условия для осознанного понимания решения простейших тригонометрических уравнений;

1.2. Вывести формулы решения простейших тригонометрических уравнений;

1.3. Сформировать у учащихся первичные умения и навыки его решения.

2. Развивающие:

2.1. Развивать познавательный интерес учащихся

2.2. Развивать и совершенствовать у учащихся умение применять знания в изменённой ситуации;

2.3. Развивать логическое мышление, умение делать выводы и обобщения;

2.4. Развивать умения сравнивать, систематизировать, обобщать; навыки контроля и самоконтроля.

3. Воспитательные:

3.1. Формировать научное мировоззрение у учащихся, культуру математической речи,

3.2. Формировать информационную, коммуникативную культуру учащихся;

3.3. Формировать повышение мотивации учащихся за счет компьютерных технологий;

3.4. Формировать воспитание дружелюбного отношения друг другу, умение работать в коллективе.

Универсальные учебные действия:

1. Познавательные УУД:

— Самостоятельное выделение, анализ и формулирование познавательной цели и учебной задачи;

— обучение работе с источниками знаний: Интернет-ресурсами, книгой;

— формулируют ответы на вопросы учителя в устной форме.

— формирование умений решения простейших тригонометрических уравнений;

— формировать умение излагать материал по плану;

— развитие умения формулировать тему и задачи урока.

2. Коммуникативные УУД:

— установление обучающимися связи между учебной деятельностью и ее мотивом, между результатом учения и тем, что побуждает к деятельности, ради чего она осуществляется;

— инициативное сотрудничество в поиске и сборе информации;

— формируют умение слушать партнера и понимать речь других учащихся класса;

— выявление, идентификация проблемы;

— умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации;

— формирование умения строить речевые высказывания в соответствии с поставленными задачами урока;

— умение слушать партнера и понимать речь других учащихся класса.

3. Регулятивные УУД:

— прогнозирование, контроль, коррекция, оценка, саморегуляция.

— формирование умение прогнозировать свою работу;

— формировать умение осуществлять познавательную и личностную рефлексию.

4. Личностные УУД:

— установление обучающимися связи между учебной деятельностью и ее мотивом, между результатом учения и тем, что побуждает к деятельности, ради чего она осуществляется;

— формировать умение проявлять дружелюбность, внимательность, взаимопомощь.

Основная часть

Этапы урока

Содержание учебного материала

Формирование УУД

Деятельность учителя

Деятельность обучающихся

1.Организационный этап. Слайд 1.

Учитель проверяет готовность к уроку.

«Не делай никогда того, чего не знаешь, но научись всему, что следует знать»

Пифагор.

Обучающиеся настраиваются на урок, приветствуют гостей и друг друга, быстрое включение в деловой ритм, уста­новка внимания всего класса.

Установление учащимися связи между учебной деятельностью и ее мотивом, между результатом учения и тем, что побуждает к деятельности, ради чего она осуществляется (К)

2.Актуализация знаний, умений и навыков.

Сайды 2-6.

Проверка знаний по теме «Обратные тригонометрические функции». (Приложение 1).

Проводит фронтальный опрос учащихся по теме домашнего задания

Дают устно определения понятиям arcsina, arccosa, arctga, arcctga.

Выполняют тест «Значения обратных тригонометрических функций» с взаимопроверкой и оценкой результатов.

Формулируют ответы на вопросы учителя в устной форме. (П).

Формируют умение слушать партнера и понимать речь других учащихся класса (К).

Коррекция знаний, обучающихся (Р)

3.Этап подготовки учащихся к активному и созна­тельному усвоению нового материала

Слайд 7, 8. Видеофрагмент фильма.

На экране высвечивается тема урока «Решение простейших тригонометрических уравнений». Аналитический способ решения уравнений.

Выбирают уравнения, те которые не умеют пока решать.

Формулируют тему урока «Решение простейших тригонометрических уравнений».

Раскрывают подробно, о чем пойдет речь на уроке.

Просматривают видеофрагмент фильма «Простейшие тригонометрические уравнения» и формулируют задачи на урок.

Самостоятельное выделение, анализ и формулирование познавательной цели и учебной задачи. (П) Развитие умения формулировать тему и задачи урока (П). Прогнозирование результатов (Р). Формирование умения прогнозировать свою работу. (Р)

4.Этап усвоения новых знаний.

Флеш — презентации

Каждая группа получила маршрутный лист, где указан путь следование.

(Приложение 2). Согласного данного маршрутного листа вы проходите весь путь, заполняя план-конспект.

(Приложение 3)

Делятся и рассаживаются по группам. Знакомятся с маршрутным листом. Выполняют задания по поиску необходимой информации для опорного конспекта. Работают с флеш-презентациями.

Заполняют опорный план-конспект по группам.

1. http://school-collection.edu.ru/catalog/res/9d08983e-a2c7-455c-b5fd-fb6ea6c091bd/view/

2. http://school-collection.edu.ru/catalog/res/0d94ac0b-0762-4d74-a468-75a0071ea9f0/view/

3. http://school-collection.edu.ru/catalog/res/d05654ef-fae6-4ca1-8c1e-5160f82eed23/view/

4. http://www.resolventa.ru/spr/trig/equation.htm

Обучение работе с источниками знаний: Интернет-ресурсами, книгой; (П)

— формирование умений решения простейших тригонометрических уравнений; (П) Выявление, идентификация проблемы (К)

Самостоятельное создание алгоритмов деятельности при решении проблем поискового характера (Р). Инициативное сотрудничество в поиске и сборе информации (К)

5.Этап проверки понимания учащимися нового материала

Слайды 9-12

Сбор информации с групп в единый план-конспект

Защита опорных планов-конспектов представителями каждой группы. Каждый учащийся формирует опорный конспект

Формирование умения излагать материал по плану. (П) Умение с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации. (К) Умение слушать партнера (К)

6.Этап закрепления нового материала Первичная проверка понимания.

Контроль и самопроверка знаний. Слайд 13

Консультация, контроль за выполнением теста в интерактивном кабинете.

Выполняют электронные задания по решению простейших тригонометрических уравнений. Каждый учащийся самостоятельно проверяет полученные знания и отрабатывает навыки решения уравнений в личном кабинете на сайте http://uztest.ru/quiz

Умение применять полученные знания в конкретной ситуации. (Р)

Контроль, самооценка, оценка. (Р)

7. Подведение итогов занятий

Подведем итоги нашего урока. Обсуждение и выставление оценок за урок. А теперь оцените свою деятельность на уроке, выведите средний балл за урок, оценив свою деятельность на уроке.

(Приложение 4).

Вспоминают, что изучали на данном уроке. Оценивают свою деятельность и ставя баллы в оценочный лист.

Формирование умения строить речевые высказывания в соответствии с поставленными задачами урока. (К)

Оценивают свою деятельность на уроке (Л)

8.Рефлексия

Слайд 14

Сделайте «выстрел в рефлексивную мишень».

Оставляют пометки на рефлексивной мишени, высказывают свое мнение по уроку.

Формировать умение осуществлять познавательную и личностную рефлексию. (Р)

9.Домашнее задание

Слайд 15

Выучить составленный опорный план-конспект, выполнить задание с карточки, решить №

Запись домашнего задания в дневник

Само регуляция, как способность к мобилизации сил и энергии, к волевому усилию (к выбору в ситуации мотивационного конфликта) и преодоления препятствий (Р)

10.Логическое завершение урока.

Слайд 16

Вы молодцы!

Каждый из вас «научился тому, что следует знать».

Спасибо за урок!

Психологический настрой на окончание урока

Формирование положительной мотивации, развитие коммуникативных умений (Р)

Заключение. Планируемый результат урока: формирование положительной мотивации, знания определения термина «тригонометрическое уравнение», запись формул решения простейших тригонометрических уравнений, формирование у учащихся первичные умения и навыки решения простейших тригонометрических уравнений; развитие коммуникативных умений.

Список используемых источников:

1. УМК: Мордкович А. Г. Алгебра и начала математического анализа. 10 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. – 6-е изд., стер. – М.: Мнемозина, 2009.

2. УМК: Мордкович А. Г. Алгебра и начала математического анализа. 10 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. – 6-е изд., стер. – М.: Мнемозина, 2009.

Ссылки на цифровые образовательные ресурсы:

1. Сайт с личным кабинетом учителя http://uztest.ru/quiz

2. Флеш-презентация cosx = a http://school—collection.edu.ru/catalog/res/9d08983e—a2c7-455c—b5fd—b6ea6c091bd/view/

3. Флеш-презентация sinx = a http://school-collection.edu.ru/catalog/res/0d94ac0b-0762-4d74-a468-a0071ea9f0/view/

4. Флеш-презентация tgx = a, ctgx = a http://school-collection.edu.ru/catalog/res/d05654ef-fae6-4ca1-8c1e-160f82eed23/view/

5. Сайт учебного центра «Резольвента» http://www.resolventa.ru/spr/trig/equation.htm

Приложение 1

Тест «Обратные тригонометрические функции»

Ф.И. ____________________________________________________________________

arcsin

arccos =

arctg 1 =

arcsin

arccos =

arctg =

arcsin

arccos =

arcctg =

arcsin

arccos =

arctg(- )=

arcsin

arccos =

arcctg =

Решите уравнения:

; 2) ; 3) ; 4) ; 5) .

Приложение 2

Задание 1 группа cos x = a 8 мин

1. Просмотреть флеш-презентацию cos x (теорию), проанализировать информацию.

2. В опорный конспект (1 часть) выписать общую формулу решения простейшего тригонометрического уравнения, формулы для частных случаев.

3. Рассмотреть и оформить в опорном конспекте (1 часть) решение тригонометрических уравнений.

4. Выполнить практическую часть данной презентации.

5. Записать в опорный конспект не менее 3-х примеров

6. Подготовить защиту своего опорного конспекта (общая формула, частные формулы, три примера).

Задание 2 группа sin x = a 8 мин

1. Просмотреть флеш-презентацию sin x (теорию), проанализировать информацию.

2. В опорный конспект (2 часть) выписать общую формулу решения простейшего тригонометрического уравнения, формулы для частных случаев.

3. Рассмотреть и оформить в опорном конспекте (2 часть) решение тригонометрических уравнений.

4. Выполнить практическую часть данной презентации.

5. Записать в опорный конспект не менее 3-х примеров

6. Подготовить защиту своего опорного конспекта (общая формула, частные формулы, три примера).

Задание 3 группа tg x = a ctg x = a 8 мин

1. Выйти по ссылке http://www.resolventa.ru/spr/trig/equation.htm, прочитать и

проанализировать информацию соответствующую заданию.

2. В опорный конспект (3 часть) выписать общую формулу решения простейшего тригонометрического уравнения.

3. Рассмотреть и оформить в опорном конспекте (3 часть) решение тригонометрических уравнений.

4. Выполнить практическую часть флеш-презентации tg x и ctg x

5. Записать в опорный конспект не менее 3-х примеров.

Подготовить защиту своего опорного конспекта (общая формула, три примера).

Приложение 3

Решение простейших тригонометрических уравнений

(опорный конспект)

1группа cos x = a

cos a = 1

cos a = 0

cos a = — 1

2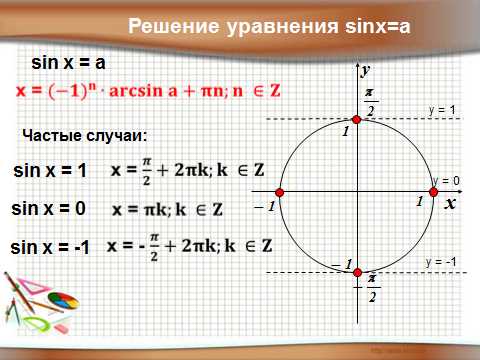группа sinx = a

sin a = 1

sin a = 0

sin a = — 1

3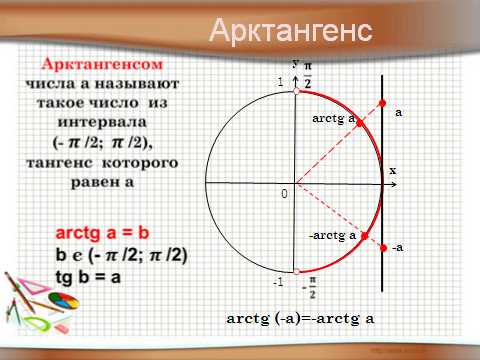группа tg x = a

ctg x = a

Примеры решения

простейших тригонометрических функций

cos x = a

sinx = a

tg x = a

ctg x = a

Приложение 4

Оценочный лист

Ф.И. (ученика) ___________________________________________ 10 класс

Дата оценивать в 5-ти бальной системе

№ п/п

Критерий

Отметка

1

Знание единичной окружности

2

Теоретический опрос по определениям

3

Тест «Значение обратных тригонометрических функций»

4

Поиск информации, ее представление

5

Тест «Простейшие тригонометрические уравнения»

Итого (средний балл)

infourok.ru

Решение простейших тригонометрических уравнений

Разделы: Математика

Цели и задачи урока:

Образовательные:

• закрепить навык решения простейших тригонометрических уравнений вида cos x = a, sin x = a, расширить и углубить знания по данной теме.

Развивающие:

• развитие логического мышления учащихся, развитие памяти, внимания, умения рассуждать, выделять главное, самостоятельно приобретать знания, навыки и применять их на практике.

Воспитательные:

• воспитание уважительного отношения к одноклассникам;
• формирование самостоятельности;
• развитие аккуратности, внимательности, создание успеха.

Оборудование:

• мультимедийный проектор и экран,
• таблицы с заданиями,
• материалы – карточки.

1. Орг. момент:

Взаимное приветствие учителя и учащихся, фиксация отсутствующих, проверка готовности учащихся к уроку. Учитель объявляет о рейтинговой системе оценки на уроке, формулирует тему и цель урока.

Цель урока: закрепить навык решения простейших тригонометрических уравнений вида cos x = a, sin x = a и научиться применять известные формулы для решения более сложных уравнений.

Проверка теоретических знаний по материалу §§ 33-34 проводится в виде теста.

(Учитель раздаёт листы с заданиями, оказывает консультации учащимся по заполнению листов с ответами)

Тест

Вариант – I

1) Все корни уравнения находятся по формуле:

А) x = (-1)ⁿ arccos a + 2k; kZ
Б) x = ± arccos a + 2k; kZ
В) x = (-1)ⁿ arccos a + k; kZ
Г) x = ± arccos a + k; kZ

2) Решить уравнение

А)
Б)
В)
Г)

3) Найдите корни уравнения

А)
Б)
В)
Г)

4) Дополните формулу

А)
Б)
В)
Г)

5) Укажите решение уравнения:

А)
Б)
В) ,
Г)

6) Вычислите

А) 0
Б) 3 — 2
В) -3
Г) 3

Вариант – II

1) Все корни уравнения находятся по формуле

А) x = ± arcsin a + 2k; kZ
Б) x = ± arcsin a + k; kZ
В) x = (-1)ⁿ arcsin a + k; kZ
Г) x = (-1)ⁿ arcsin a + 2k; kZ

2) Решить уравнение

А)
Б)
В)
Г)

3) Найдите корни уравнения

А)
Б)
В)
Г)

4) Дополните формулу

А)
Б)
В)
Г)

5) Укажите решение уравнения:

А)
Б)
В)
Г)

6) Вычислите

А)
Б)
В)
Г)

(Учащиеся знакомятся с тестом, прорешивают задания, заносят ответы в две одинаковые карточки, одну сдают для проверки учителю, вторую оставляют для самопроверки.)

(Учитель организует самопроверку. Ответы на мультимедийном экране. Учащиеся выставляют оценку.)

Работа проводится по трём группам.

Учитель даёт задания каждой группе, организует работу на местах, вызывает к доске.

1 группа выполняет №591(1,3,5),№592(1).

2 группа выполняет №594,№595(1),№596(1) в тетрадях и по одному человеку решение записывают на доске.

3 группа выполняет №597,№598 в тетрадях.

( Учащиеся выполняют предложенные задания).

1 и 2 варианты раздаются “слабым” и “средним” учащимся, 3 вариант получают “сильные” ученики. Учитель оказывает консультацию, раздаёт материалы, учитывает внутриклассную дифференциацию.

Вариант I

Решить уравнения

1)
2)
3)
4)
5)

Вариант II

Решить уравнения

1)
2)
3)
4)
5)

Вариант III

Решить уравнения

1)
2)
3)
4)
5)

6. Подведение итога урока:

Учитель анализирует работу каждого ученика на уроке отдельно и в составе групп и комментирует работу учеников на уроке, выставляет оценки за работу у доски, за работу в группах.

7. Информация о домашнем задании:

На “3” — №591(2,4,6),№592(2)

На “4” и “5” — №595(2), №596(2) и предлагается тренажёр для отработки навыков решения простейших тригонометрических уравнений.

Учитель комментирует домашнее задание, и учащиеся записывают задание в дневник.

Тренажер по теме
“Простейшие тригонометрические уравнения”

27.03.2012

Поделиться страницей:

xn--i1abbnckbmcl9fb.xn--p1ai

Решение тригонометрических уравнений

РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ

Учитель: Копеина

Наталья Васильевна

10 класс

МОУ «Киришский лицей»

ЦЕЛЬ :

• Повторить решение тригонометрических

уравнений.

• 1. Знать формулы для решения простейших тригонометрических уравнений.
• 2. Различать типы тригонометрических уравнений и знать способы их решений.
• 3. Уметь решать тригонометрические уравнения любых типов.

• Выделение основных проблем при решении

этих уравнений:

• Потеря корней.
• Посторонние корни.
• Отбор корней.

Содержание .

• Вводная часть, повторение теоретического материала.

• Решение тригонометрических уравнений.

3. Виды тригонометрических уравнений.

4. Проблемы, возникающие при решении

тригонометрических уравнений.

Устная работа.

• Решите уравнения
• А) 3 х – 5 = 7
• Б) х 2 – 8 х + 15 = 0
• В) 4 х 2 – 4 х + 1= 0
• Г) х 4 – 5 х 2 + 4 = 0
• Д) 3 х 2 – 12 = 0

• Ответы
• 4
• 3; 5
• 0,5
• -2; -1; 1; 2
• -2; 2

• Упростите выражения
• А ) (sin a – 1) (sin a + 1)
• Б ) sin 2 a – 1 + cos 2 a
• В ) sin 2 a + tg a ctg a + cos 2 a
• Г)

• Ответы
• — cos 2 a
• 0
• 2

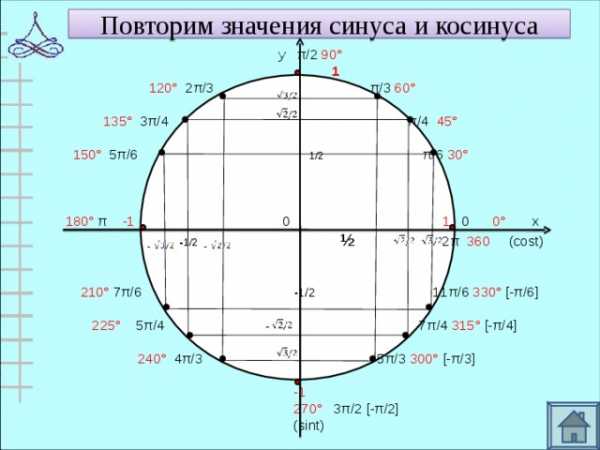
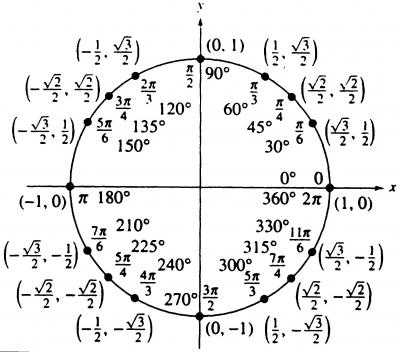
Повторим значения синуса и косинуса

у π /2 90°

1

120° 2 π /3 π /3 60°

135° 3 π /4 π /4 45°

150° 5 π /6 1/2 π /6 30°

180° π -1 0 1 0 0° x

— 1/2 ½ 2 π 360 (cost)

210° 7 π /6 — 1/2 11 π /6 330° [- π /6]

225° 5 π /4 7 π /4 315° [- π /4]

240° 4 π /3 5 π /3 300° [- π /3]

-1

270° 3 π /2 [- π /2]

(sint)

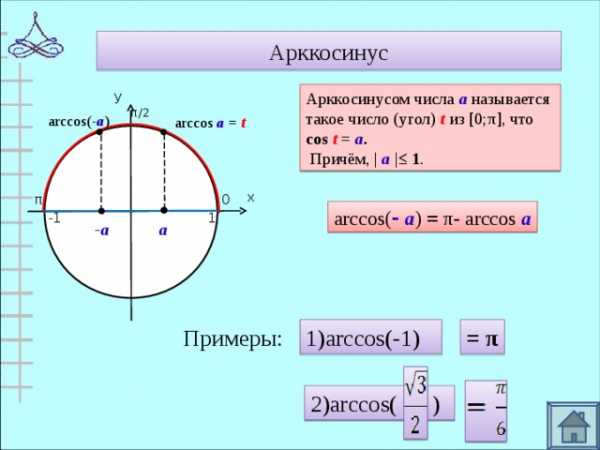
Арккосинус

Арккосинусом числа а называется

такое число (угол) t из [0; π ], что

cos t = а .

Причём, | а |≤ 1 .

у

π/2

arccos( — а )

arccos а = t

х

π

0

arccos( — а ) = π — arccos а

-1

1

а

-а

Примеры:

1) arccos(-1)

= π

2)arccos( )

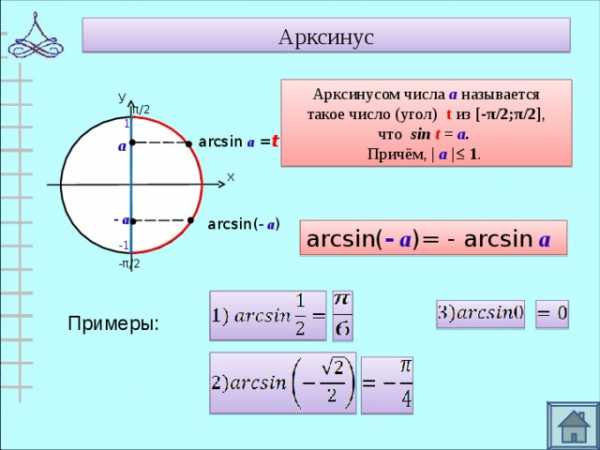
Арксинус

Примеры:

Арксинусом числа а называется

такое число (угол) t из [- π/2 ; π/2 ] ,

что sin t = а .

Причём, | а |≤ 1 .

у

π/2

1

arcsin а = t

а

х

— а

arcsin( — а )

arcsin( — а )= — arcsin а

-1

— π/2

Арктангенс

а

у

Арктангенсом числа а называется

такое число (угол) t из (- π/2;π/2 ),

что tg t = а .

Причём, а Є R .

π/2

arctg а = t

arctg( — а ) = — arctg а

arctg( — а )

— π/2

— а

1) arctg√3/3 =

π/6

Примеры:

2) arctg(-1) =

— π/4

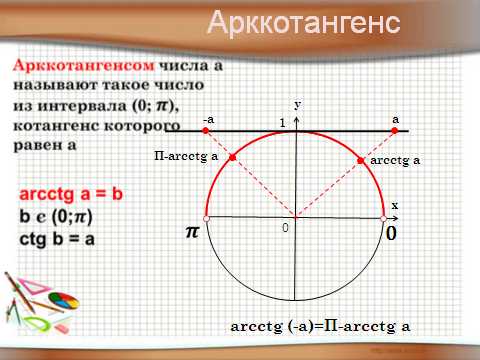
Арккотангенс

у

Арккотангенсом числа а называется

такое число (угол) t из (0; π ),

что c tg t = а .

Причём, а Є R .

— а

а

arcctg а = t

arcctg( — а )

π

х

arcctg( — а ) = π – arcctg а

Примеры:

1) arcctg(-1) =

3 π/4

2) arcctg√3 =

π/6

Повторение

2 вариант

• cos (-π/4 )
• sin π/3
• ctg π/6
• tg π/4
• sin (-π/6)
• cos 5π/6
• arccos √2/2
• arcsin 1
• arccos (- 1 /2)
• arcsin (- √ 3 /2)
• arctg √ 3 / 3

1 вариант

• sin (-π/3)
• cos 2π/3
• tg π/6
• ctg π/4
• cos (-π/6)
• sin 3 π /4
• arcsin √2/2
• arccos 1
• arcsin (- 1/2 )
• arccos (- √3/2 )
• arctg √ 3

Повторение

Ответы 1 вариант

Ответы 2 вариант

• — √ 3/2
• — 1/2
• √ 3/3
• 1
• √ 3/2
• √ 2/2
• π/4
• 0
• — π/ 6
• 5 π/ 6
• π/ 3

• √ 3/2
• √ 3
• 1
• — 1/2
• — √3/2
• π/4
• π/ 2
• 2 π/ 3
• — π/ 3
• π/ 6

Формулы корней простейших тригонометрических уравнений

1 .cost = а , где | а| ≤ 1

или

1) cost=0

t = π/2+π k‚ k Є Z

Частные случаи

2) cost=1

t = 2 π k‚ k Є Z

3) cost = -1

t = π+2π k‚ k Є Z

Формулы корней простейших тригонометрических уравнений

2. sint = а , где | а |≤ 1

или

Частные случаи

1) sint=0

t = π k‚ k Є Z

2) sint=1

t = π/2+2π k‚ k Є Z

3) sint = — 1

t = — π/2+2π k‚ k Є Z

Формулы корней простейших тригонометрических уравнений

3. tgt = а, а Є R

t = arctg а + π k‚ k Є Z

4. ctgt = а, а Є R

t = arcctg а + π k‚ k Є Z

При каких значениях х имеет смысл выражение:

1. arcsin(2x+1)

2.arccos(5-2x)

1) -1≤ 2х+1 ≤1

-2≤ 2х ≤0

-1≤ х ≤0

Ответ: [-1;0]

2) -1≤ 5-2х ≤1

-6≤ -2х ≤ -4

2≤ х ≤3

Ответ: [2;3]

3.arccos(x²-1)

4.arcsin(4x²-3x)

-1≤ х²-1 ≤ 1

0 ≤ х² ≤2

Ответ:

Примеры:

2) sint = 0;

Частный случай:

t = π k, k Є Z

t= ±arccos(-1/2)+2 π k, k Є Z

t= ± + 2 π k, k Є Z

3) tgt = 1;

t = arcctg( ) + π k, k Є Z

t = + π k, k Є Z.

t = arctg1+ π k, k Є Z

t = + π k, k Є Z.

Решение простейших уравнений

2) cos(x+ π /3) = ½

x+ π /3 = ±arccos1/2 + 2 π k, k Є Z

x+ π /3 = ± π /3 + 2 π k, k Є Z

x = — π /3 ± π /3 + 2 π k, k Є Z

Ответ: — π /3 ± π /3 + 2 π k, k Є Z

2x = arctg (-1) + π k, k Є Z

2x = — π /4 + π k, k Є Z

x = — π /8 + π k/2, k Є Z

Ответ: — π /8 + π k/2, k Є Z .

3) sin( π – x/3) = 0

упростим по формулам приведения

sin ( x/3 ) = 0

частный случай

x/3 = π k, k Є Z

x = 3 π k, k Є Z.

Ответ: 3 π k, k Є Z.

Виды тригонометрических уравнений

1.Сводимые к квадратным

Решаются методом введения новой переменной

a∙sin²x + b∙sinx + c=0

Пусть sinx = p, где |p| ≤1 , тогда a∙p² + b∙p + c = 0

Найти корни, вернуться к замене и решить простые уравнения.

Виды тригонометрических уравнений

2. Однородные

1)Первой степени:

Решаются делением на cos х (или sinx ) и методом введения новой переменной .

a∙sinx + b∙cosx = 0

Т.к. sinx и cosx одновременно не равны нулю, то разделим обе части уравнения на cosx (или на sinx ). Получим: простое уравнение

a∙tgx + b = 0 или tgx = m

Пример. Решите уравнение sinx + 2cosx = 0.

Решение: Разделим обе части уравнения на cosx .

Получим

Ответ:

Виды тригонометрических уравнений

2) Однородные уравнения второй степени:

Решаются делением на cos² х (или sin²x ) и методом введения новой переменной .

a∙sin²x + b∙sinx∙cosx + c∙cos²x = 0

Разделим обе части на cos²x . Получим квадратное уравнение:

a∙tg²x + b∙tgx + c = 0 .

П р и м е р .   Решить уравнение:  3sin  2   x  + 4 sin  x  · cos  x  + 5 cos  2  x  = 2.

 

    Р е ш е н и е .  3sin  2   x  + 4 sin  x  · cos  x  + 5 cos  2   x  = 2sin  2   x  + 2cos  2   x  ,

 

                              sin  2   x  + 4 sin  x  · cos  x  + 3 cos  2   x  = 0 ,

 

                             t g 2   x  + 4 t g   x  + 3 = 0 ,  отсюда   y   2  + 4 y  +3 = 0 ,

 

                             корни этого уравнения:   y 1  =   1,   y 2  =   3,  отсюда

                             1)   t g   x  = –1,  2)   t g   x  = –3,

Ответ:

Виды тригонометрических уравнений

3. Уравнение вида:

А sinx + B cosx = C . А, В, С  0

   sin  x  + cos  x  = 1 .

    Р е ш е н и е .   Перенесём все члены уравнения

влево:  

                        sin  x  + cos  x  – 1 = 0 ,

Виды тригонометрических уравнений

4 . Решение тригонометрических уравнений с помощью универсальной

тригонометрической подстановки

Решаются с помощью введения вспомогательного аргумента.

А sinx + B cosx = C

Проверка

Если ,

— не верно, значит

, не является корнями исходного уравнения

Ответ:

При переходе от уравнения (1) к уравнению (2), могла произойти потеря корней, значит необходимо проверить, являются ли корни уравнения  корнями данного уровнения.

Формулы .

Универсальная подстановка.

х   + 2  n ; Проверка обязательна!

Понижение степени.

= (1 + cos2x ) : 2

= (1 – cos 2x) : 2

Метод вспомогательного аргумента.

a cosx + b sinx заменим на C sin ( x +  ), где

 — вспомогательный аргумент .

cos  =

sin  =

Правила.

• Увидел квадрат – понижай степень.

• Увидел произведение – делай сумму.

• Увидел сумму – делай произведение.

1.Потеря корней:

• делим на g (х).
• опасные формулы (универсальная подстановка).

Этими операциями мы сужаем область определения.

2. Лишние корни:

• возводим в четную степень.
• умножаем на g (х) (избавляемся от знаменателя).

Этими операциями мы расширяем область определения.

Потеря корней, лишние корни.

Решение тригонометрических уравнений по известным алгоритмам

Вариант 1.

На «3»

Вариант 2.

На «3»

• 3 sin x+ 5 cos x = 0
• 5 sin 2 х — 3 sin х cos х — 2 cos 2 х =0

• cos x+ 3 sin x = 0
• 6 sin 2 х — 5 sin х cos х + cos 2 х =0

На «4»

На «4»

• 3 cos 2 х + 2 sin х cos х =0
• 5 sin 2 х + 2 sin х cos х — cos 2 х =1

• 2 sin 2 x – sin x cosx =0
• 4 sin 2 х — 2 sin х cos х – 4 cos 2 х =1

На «5»

На «5»

• 2 sin x — 5 cos x = 3
• 1- 4 sin 2 x + 6 cos 2 х = 0

• 2 sin x — 3 cos x = 4
• 2 sin 2 х — 2sin 2х +1 =0

compedu.ru

Урок на тему «Простейшие тригонометрические уравнения»

Тема урока: Простейшие тригонометрические уравнения

Вид занятия: Урок

Тип занятия: изучение нового материала

Цели урока:

Дидактическая: ввести понятия простейших тригонометрических уравнений, формул их корней; закрепить умение находить значения обратных тригонометрических функций

Развивающая: формировать умение анализировать, искать аналоги и различные варианты решения.

Воспитательная: воспитывать внимательность, уверенность; активность, наблюдательность; стремление в взаимовыручке, умение работать в группе и самостоятельно.

Межпредметные связи: физика

Форма проведения: работа в группах, индивидуальная, самостоятельная

Формы контроля: текущий

Оборудование: презентация «Простейшие тригонометрические уравнения», проектор, экран; доска, цветной мел; листы отчета работы в группах; карточки-тесты, индивидуальные задания на карточках; листы.

В результате изучения новой темы студенты должны:

• знать: понятия простейших тригонометрических уравнений и формулы их корней; частные случаи простейших тригонометрических уравнений;

• уметь: применять формулы корней уравнений при решении упражнений; находить значения обратных тригонометрических функций на единичной окружности.

План проведения занятия

1. Организационный момент

2. Проверка знаний, воспроизведение и коррекция опорных знаний.

Тест с выбором ответа (по 2 вариантам)

3. Изучение нового материала

4. Первичное применение приобретенных знаний

5. Рефлексия

6. Итог занятия

Структура занятия

1. Организационный момент

(Приветствие, перекличка)

2. Проверка знаний, воспроизведение и коррекция опорных знаний.

Тест с выбором ответа (по 2 вариантам на карточках)

(См. 1. Приложение)

3. Изучение нового материала

   1. Мотивация обучения

(Сообщение темы урока, постановка цели и задач урока) (См. 2. Приложение \ слайды № 1- 2)

1. 2. Объяснение темы

      • Определение Простейшие тригонометрические уравнения – уравнения вида Sin x = a, Cos x = a, tg x = a, ctg x = a.

      • Решить простейшее тригонометрическое уравнение – значит найти множество всех значений аргумента, при котором данная тригонометрическая функция принимает значение а.

Рассмотрим решения данных уравнений

Т.к. функция у = Cos x имеет смысл при , то рассмотрим основные случаи решения данного уравнения.

(См. слайды № 3, 4 презентации \ Приложение)

Рассмотрим ещё несколько случаев решения данного уравнения, при решении которых используется единичная окружность.

Частные случаи

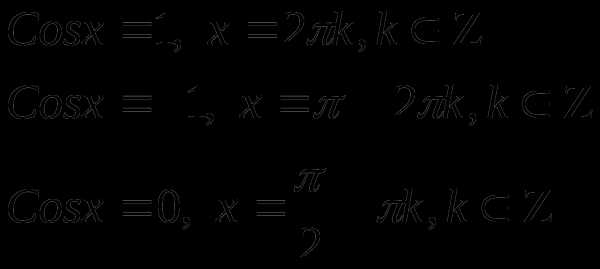
(См. слайды № 5 – 6 презентации \ Приложение)

Рассмотрим примеры

1) 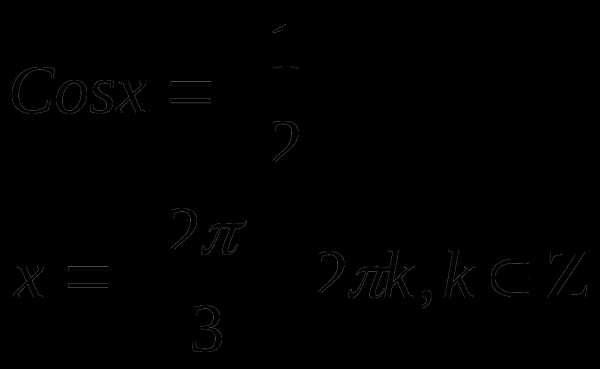(разбираем решение на доске).

2) (разбираем решение по презентации)

Т.к. функция у = Sin x также имеет смысл при , то аналогично рассмотрим основные случаи решения данного уравнения.

(См. слайды № 8, 9 презентации \ Приложение)

Замечание:

при .

Рассмотрим также несколько случаев решения данного уравнения, при решении которых используется единичная окружность.

Частные случаи

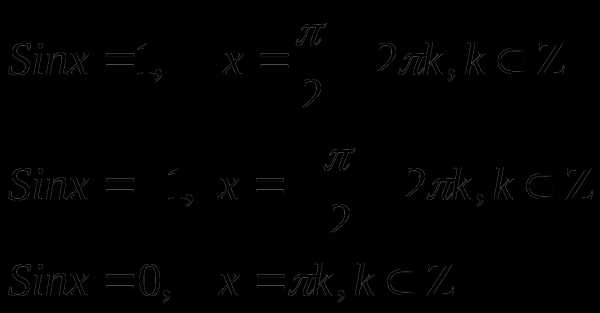
(См. слайды № 10 – 11 презентации \ Приложение)

Рассмотрим пример

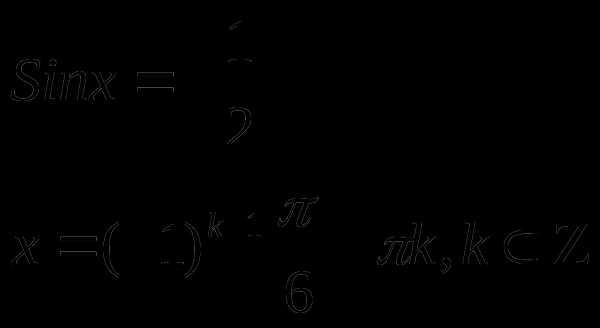(разбираем решение на доске).

.

Т.о.

(См. слайд № 12 презентации \ Приложение)

Аналогично рассматривается

(См. слайд № 13 презентации \ Приложение)

Рассмотрим пример

(разбираем решение на доске).

4. Первичное применение приобретенных знаний

№ 1. Решить уравнения:

а)

б)

Разделяю студентов на группы, выдаю листы отчета работы в группах

№ 2. Решить уравнения (задание в презентации – слайд № 14 презентации \ Приложение.

Далее проводим проверку и разбор решения по ответам на экране (См. слайд № 15 презентации \ Приложение)

5. Рефлексия

Проводится в трех вариантах + Работа по индивидуальным заданиям – карточкам

Задания по вариантам – слайд № 16 презентации \ Приложение

Задания по карточкам – См. 3 Приложение

Проверку и оценивание самостоятельной работы и оценок по карточкам проводится во время записи домашнего задания студентами

6. Итог занятия

   1. Записываем д/з:

а) теория – учебник Н.В. Богомолова «Математика» (п. 39, конспект)

б) № 3. Решить уравнения.

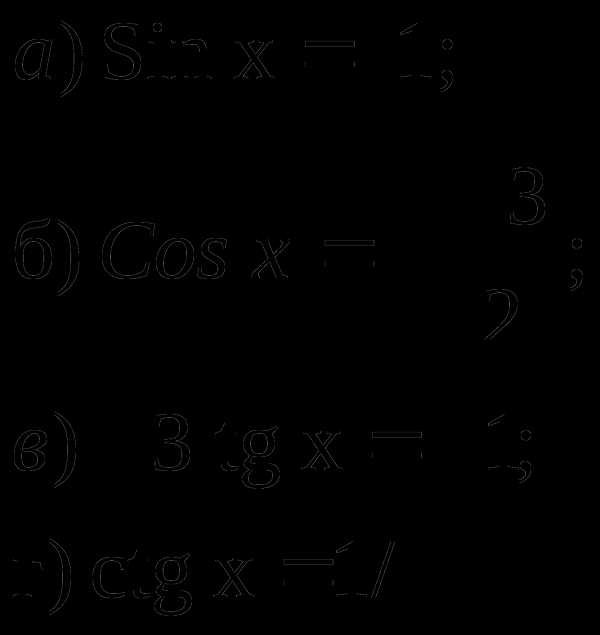
1. 2. Подведение итогов, опрос по изученному, выставление оценок.

Мною проведен урок по теме «Простейшие тригонометрические уравнения», который соответствует п.1 лекции № 5 данного курса. Дидактической целью данного урока было познакомить студентов с понятием простейших тригонометрических уравнений и формулами их решения. Стояла задача – закрепить умение находить значения обратных тригонометрических функций с помощью единичной окружности (это прослеживается во втором этапе урока, т.е. проверка, воспроизведение и коррекция опорных знаний в форме теста с выбором ответа в двух вариантах по теме «Обратные тригонометрические функции»), затем научиться решать простейшие тригонометрические уравнений и уравнения к ним сводящиеся. При этом мною использовался объяснительно-иллюстративный метод обучения в форме объяснения с помощью презентации по данной теме, при этом изложение учебного материала носило диалогически построенный характер при помощи продуманной системы вопросов студентам в ходе объяснения, что способствовало повышению понимания и восприятия научной информации, развитию аналитического мышления, а также обучению студентов переносить знания в другие условия и применять их на практике.

Первичное применение приобретенных навыков студентами учебного материала проводилось в два этапа: 1 этап – работа под руководством учителя с помощью доски и комментировано с места: данный метод используется с целью освоения, закрепления и совершенствования умения решать уравнения данного типа, способствует формированию навыка обучаемых искать аналоги и различные варианты решения; 2 этап – работа в группах применялась мною для развития умения работать в коллективе, группе и воспитания внимательности, уверенности в своих силах, стремления к взаимовыручке. Студенты провели самопроверку решения по готовым ответам на экране, провели разбор недочетов и ошибок для лучшего усвоения изученного.

В качестве закрепления изученного на уроке, т.е. ретроспективная рефлексия, проводилась в виде самостоятельной работы студентов по вариантам, а также применялись индивидуальные задания для более слабых студентов на карточках, что помогло оценить уровень первичного усвоения материала, разобранного на уроке, формировать у обучаемых умения и навыки познавательной деятельности по пройденной теме.

Данное занятие рассчитано на студентов 1 курса с достаточной математической подготовкой. Умение находить значения тригонометрических и обратных тригонометрических функций с помощью единичной окружности способствует в дальнейшем лучшему усвоению материала по физике и технической механике. В ходе применения выбранных мною форм обучения студентов прослеживался рост познавательной активности обучаемых, здесь же был заметен рост усвоения материала у более слабых учащихся. Ребята добивались не только автоматического решения задач по образцам, но и осмысления сущности заданий. Результатом работы может послужить анализ самостоятельной работы, послужившей рефлексией к данному уроку.

Группа

Кол-во студентов в группе

Кол-во выполнявших студентов

Получили оценки

Средний балл

Качество знаний, %

Успеваемость, %

«5»

«4»

«3»

«2»

12Г

27

24

5

8

10

—

3,63

54

100

infourok.ru

No related posts.