Тема 7. Решение транспортной задачи средствами табличного процессора ms Excel .
Требуется решить следующую транспортную задачу. Известны три поставщика с имеющимися у них запасами продукции, четыре потребителя, нуждающиеся в данной продукции и транспортные затраты на поставку продукции от поставщиков к потребителям. Данные представлены в таблице:
Таблица 7.1
Поставщики | Потребители | Запасы | |||
B1 В1 | B3 | В4 | |||
А1 | 4 | 5 | 2 | 3 | 60 |
А2 | 1 | 3 | 6 | 2 | 100 |
A3 | 6 | 2 | 7 | 4 | 120 |
Потребность | 30 | 100 | 40 | 110 | |
Необходимо прикрепить поставщиков к потребителям с учетом минимальных транспортных затрат.
Решение задачи в Excel состоит из следующих шагов:
создание формы для ввода условий задачи;
ввод исходных данных;
ввод ограничений и граничных условий;
проведение расчетов
1. Создание формы для ввода условий задачи, ввод исходных данных и определение целевой функции.
Создаем матрицу перевозок, которая имеет изменяемые ячейки (В14:Е16). После проведения расчетов на ее месте будет записан оптимальный план перевозок. По каждой строке и столбцу матрицы перевозок записываем соответствующую формулу:
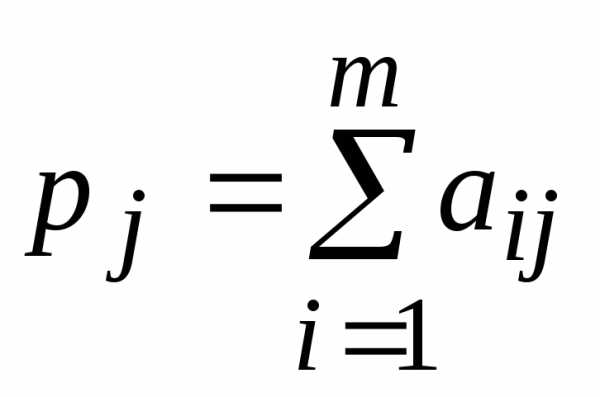
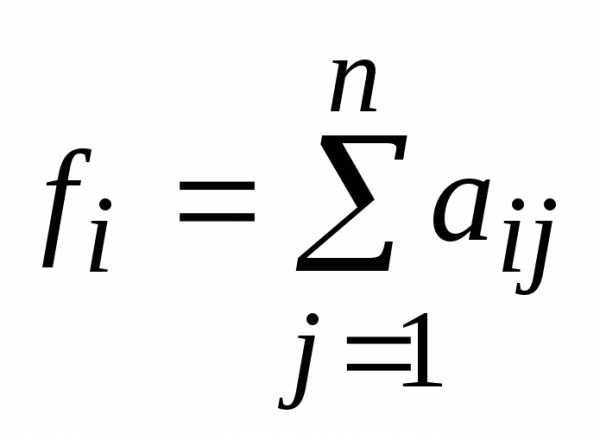
В ячейки A5:F10 введем исходные данные задачи, а в ячейке С18 запишем значение целевой функции, используя функцию –СУММПРОИЗВ(В2:Е5;В11:Е13). Тем самым получим таблицы, как показано на рис. 7.1.
2. Ввод ограничений и граничных условий
Устанавливаем курсор на ячейку C18, в которой записано значение целевой функции, и вызываем операцию Поиск решения: Сервис → Поиск решения в Excel 2003 или Данные→ Анализ→ Поиск решения в Excel 2007. В появившемся окне «Поиск решения» в поле Установить целевую функцию следует внести адрес ячейки C18, в которой записано значение целевой функции (см. рис. 7.2).
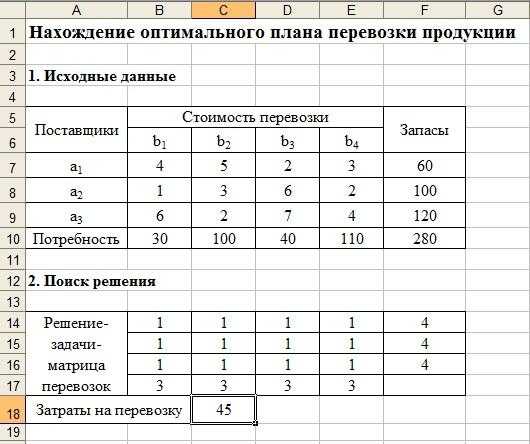
рис. 7.1
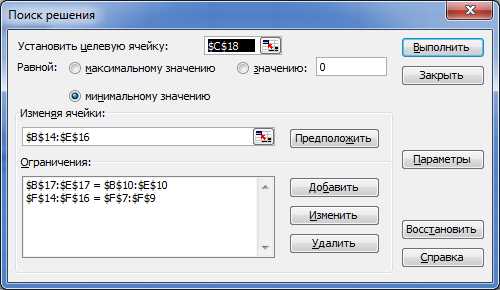
Рис. 7.2
После этого следует
Рис. 7.3
Все потребности должны быть удовлетворены, и все запасы должны быть распределены.
После ввода последнего ограничения вместо нажатия клавиши Добавить необходимо нажать клавишу ОК. На экране появится окно «Поиск решения».
3. Решение задачи
Перед тем как выполнить решение задачи, которое проводится и том же окне «Поиск решения», следует выполнить некоторые назначения, нажав на клавишу Параметры. Например, следует установить флажок Неотрицательные значения и флажок Линейная модель (см. рис. 7.4).
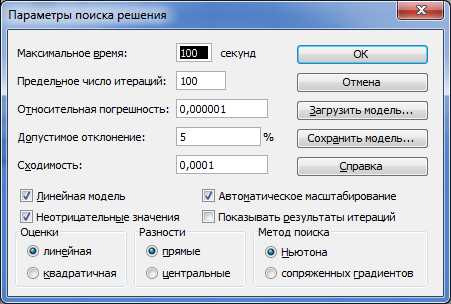
Рис. 7.4
После проведения всех необходимых установок надо нажать клавишу ОК, что приведет к возврату на окно «Поиск решения». В этом окне следует нажать на клавишу Выполнить, после чего на рабочем поле Excel будет выдан оптимальный план поставок и диалоговое окно «Результаты поиска решения», а в ячейке C18 будет выдан результат целевой функции для данной задачи, равный 590 (см. рис. 7.5). 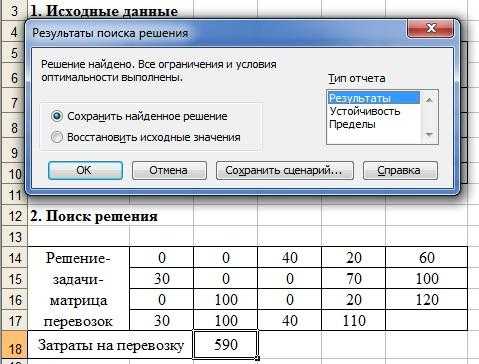
Рис. 7.5
studfiles.net
Решение транспортной задачи с применением электронных таблиц.
Цель:
Получить практические навыки использования функций “Поиск решения” в электронной таблице Excel.
Ход выполнения:
В результате выполнения лабораторной работы студент должен:
• получить навыки решения оптимизационных задач, приводимых к табличным формам;
• научиться использовать средства электронной таблицы в задачах поиска нужного решения при условии изменения только одного параметра некоторой функции.
Использование функции “Поиск решения” при решении “Транспортной задачи”.
Постановка задачи:
Классическая формулировка задачи состоит в следующем. Имеется несколько пунктов производства и пунктов потребления некоторого продукта. Для каждого из пунктов производства задан объем производства, а для каждого пункта потребления – объем потребления. Известна стоимость перевозки из каждого пункта производства в каждый пункт потребления единицы продукта. Требуется составить план перевозок продукта, в котором все пункты потребления были бы обеспечены необходимыми продуктами, ни из какого пункта производства не вывозилось бы продуктов больше, чем там производится, а стоимость перевозки была бы минимальной.
В построенной при помощи Microsoft Excel модели представлена такая задача (см. рис.1). Товары могут доставляться из пункта производства (Белоруссия, Урал, Украина) в любой пункт потребления (Казань, Рига, Воронеж, Курск, Москва). Очевидно, что стоимость доставки на большее расстояние будет большей. Требуется определить объемы перевозок между каждым пунктом производства и пунктом потребления в соответствии с потребностями пунктов потребления и производственными возможностями пунктов производства, при которых транспортные расходы минимальны. Таким образом, цель задачи – уменьшение всех транспортных расходов.
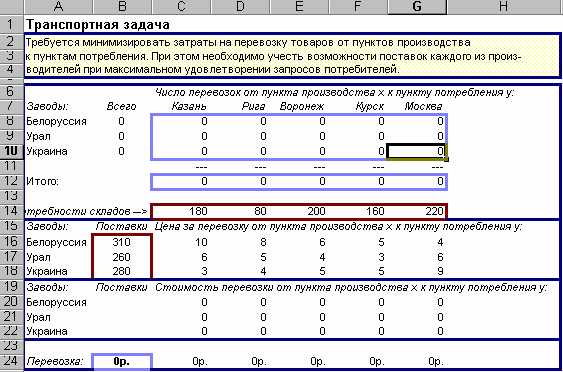
Рис. 1. Таблица для решения “Транспортной задачи”.
Порядок выполнения.
Первый этап — ввод исходных данных:
1. Ввести на рабочем листе необходимые исходные данные и определить их взаимосвязи с результирующими данными:
1.1. Построить таблицы для ввода количества перевозок, цены перевозки и стоимости перевозки из пункта производства “Х” в пункт потребления “Y”, как показано на Рис.1 (количество перевозок для каждого пункта в начале решения задачи будет равно 0).
1.2. Ввести в ячейки С14-G14 потребности складов в товаре, а в ячейки В16-В18 – производственные возможности пунктов производства.
1.3. Ввести в ячейки С16-G18 цены на перевозку товара из пункта производства Х в пункт потребления Y.
2. Ввести формулы в вычисляемые ячейки:
2.1. В ячейки В8:В10 ввести формулы вычисления общего количества перевезенного товара для каждого из пунктов производства (например, формула для ячейки В8=СУММ(С8:G8), т.е. количество перевезенного товара для Белоруссии).
2.2. В ячейки С12:G12 ввести формулы вычисления общего количества перевезенного товара в каждый из пунктов потребления (например, формула для ячейки С12=СУММ(С8:С10), т.е. количество перевезенного товара в Казань).
2.3. В ячейки С20:G22 ввести формулы вычисления общей цены за перевозку товара из каждого пункта производства в каждый пункт потребления, умножив цену перевозки единицы товара (ячейки С16-G18) на общее количество перевезенного товара (ячейки С8-G10) (например, формула для ячейки С20 – общая цена перевозки товара из Белоруссии в Казань – =С8*С16).
2.4. В ячейки С24:G24 ввести формулы вычисления стоимости всех перевозок по каждому из пунктов потребления (например, для Казани в ячейку С24 вводится формула =СУММ(С20:С22)).
2.5. В ячейку В24 ввести формулу подсчета всей стоимости перевозок – результат суммирования значений ячеек С24:G24.
3. Выполнить форматирование ячеек рабочего листа, и выделить ячейки с результатами и изменяемыми данными – синим цветом, а ячейки с исходными данными – красным цветом.
Второй этап – поиск решения:
1. При помощи команды “Сервис” – “Поиск решения…” вызвать диалоговое окно задания данных для решения задачи (Рис.2).
2. Задать целевую ячейку
В качестве целевой ячейки выбрать ячейку (аналогичную ячейке В24 на рис. 1), в которой будет подсчитана общая цена всех перевозок.
По условию задачи целевую ячейку следует установить равной минимальному значению.
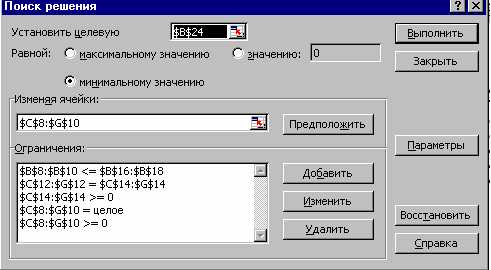
Рис. 2. Диалоговое окно ввода данных для решения задачи.
3. Задать изменяемые ячейки
Минимальное значение целевой ячейки будет определяться путем изменения данных в ячейках, задающих объемы перевозок от каждого из пунктов производства к каждому пункту потребления (ячейки C8:G10 на рис. 1).
4. Наложить требования (ограничения), которые будут предъявляться к результатам задачи:
4.1. Количество перевезенных грузов не может превышать производственных возможностей заводов (на рис. 1 значения ячеек B8:B10 должны быть меньше или равны значениям ячеек B16:B18).
4.2. Количество доставляемых грузов должно быть равно потребностям складов (т.е. на рис. 1 значения ячеек C12:G12 должны быть равны значениям ячеек С14:G14).
4.3. Число перевозок не может быть отрицательным и не целым (т.е. на рис. 1 значения ячеек C8:G10 должны быть больше или равны нулю и должны быть целыми).
5. Ввести значения в окно “Поиск решения”. Для ввода значений в диалоговое окно “Поиск решений” можно использовать выделение ячеек и интервалов мышью (при заполнении соответствующих полей ввода). Кроме того, в некоторых случаях удобно пользоваться для определения изменяемых ячеек кнопкой “Предположить” – в этом случае в качестве изменяемых ячеек предлагается использовать все влияющие ячейки для ранее определенной целевой ячейки.
Для ввода ограничений необходимо нажать кнопку “Добавить”.
На экране появится диалоговое окно, показанное на Рис.3.
Рис. 3. Окно ввода ограничений.
При помощи этого диалогового окна ввести ранее заданные ограничения. Для ввода значений в области “Ссылка на ячейку” и “Ограничение” можно также пользоваться возможностями Microsoft Excel по выделению интервалов мышью.
6. Инициировать «Поиск решения»
Решение задачи начинается после нажатия кнопки “Выполнить” в диалоговом окне “Поиск решения”. После того, как вычисления закончатся, открывается диалоговое окно “Результаты поиска решения” (Рис.4), в котором выводится сообщение о том, найдено или нет решение поставленной задачи. Если найденное решение устраивает пользователя, он может сохранить его на рабочем листе, нажав кнопку «ОК».
Можно также сохранить найденное решение в качестве сценария с помощью кнопки “Сохранить сценарий” (обычно так поступают в том случае, когда требуется сохранить результаты нескольких различных решений, полученных при изменении нескольких ограничений).
Рис. 4. Окно “Результаты поиска решения”.
Оптимальное количество поставок, которое приведет к минимизации транспортных расходов в соответствии с заданными исходными данных, представлено в таблице на Рис.5.
7. Составить отчет о проделанной работе.
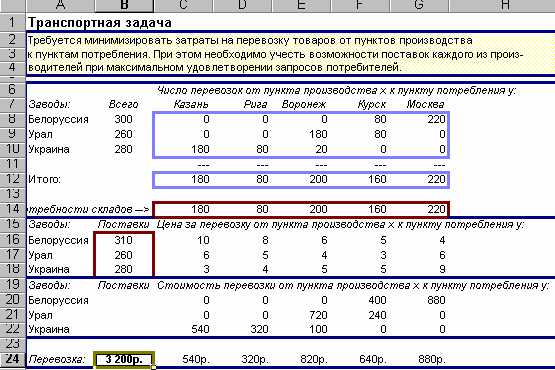
Рис.5. Результаты вычислений.
Отправить его преподавателю по электронной почте в виде вложенного файла или переписать файл преподавателю со своего носителя (флэш-накопителя, компакт-диска) или сдать работу преподавателю в распечатанном и скреплённом виде.
Лабораторное занятие № 4.
studlib.info
«Транспортная задача». Практическая работа по информатике
Тема. Решение оптимизационных задач
Теоретический материал
Классы задач оптимизации
Исходные данные | Исходные переменные | Зависимости | Классы задач |
Детерминированные | Непрерывные | Линейные | Линейное программирование |
Детерминированные | Целочисленные | Линейные | Целочисленное программирование |
Детерминированные | Непрерывные и целочисленные | Нелинейные | Нелинейное программирование |
Случайные | Непрерывные | Линейные | Стохастическое программирование |
Основные этапы работы
Выбор задачи
Содержательная постановка задачи
Составление материальной модели
Сбор исходных данных
Решение задачи
Анализ решения
Принятие оптимального решения
Графическое представление результата
Блок-схема решения задачи линейного программирования
Составить материальную модель
Графическое представление результата
Анализ оптимального решения
Представление результата
Вариантный анализ
Введение дополнительных ограничений
Значения целевой ячейки не сходятся
Поиск не может найти подходящее решение
Корректировка модели, исходных данных
Решение найдено
Есть оптимальное решение
Есть допустимое решение
Ввести условия задачи
Практическая работа.
Транспортная задача
Пусть имеется М складов и N – потребителей.
Хi,j – количество продукции, доставляемой со склада с номером i
Рi,j – издержки доставки единицы продукции со склада i потребителю j
Ci= количество продукции, находящееся на складе с номером i
-количество продукции необходимое ()
Исходные данные приведены в таблице.
Издержки, доставка | Наличие на складе | ||||||
Потребители | 1 | 2 | 3 | 4 | 5 | ||
Склад 1 | 3,2 | 2,7 | 2,9 | 2,5 | 2,8 | 250 | |
Склад 2 | 2,9 | 2,9 | 3,1 | 2,7 | 2,9 | 220 | |
Склад 3 | 2,7 | 2,6 | 2,8 | 2,4 | 2,7 | 280 | |
Склад 4 | 3,1 | 2,8 | 2,8 | 2,9 | 250 | ||
Требуемая сумма | 190 | 210 | 220 | 230 | 150 | ||
Решение.
1) В электронной таблице заполняем данные:
Для подписания массива Р выделяем диапазон C7:G10, вызываем контекстное меню, выбираем команду Имя диапазона, присваиваем имя «Р» и ОК.
2) Заполняем вторую таблицу исходя из условия задачи
3) В ячейку О11 заносим формулу =ЕСЛИ(P11=O12;»совпадает»;»не совпадает»)
4) Даём имена массивам:
выделяем диапазон J7:N10, вызываем контекстное меню, команда Имя диапазона, вводим имя «Х» и ОК.
выделяем диапазон O6:P10, вызываем контекстное меню, выбираем команду Выбрать из раскрывающегося списка, выбрать имя в строке выше и ОК.
выделяем диапазон I11:N12, вызываем контекстное меню, выбираем команду Выбрать из раскрывающегося списка, выбрать имя в столбце слева и ОК.
5) В ячейку I13 заносим целевую функцию =СУММПРОИЗВ(P;Х).
6) В ячейку J11 заносим формулу =СУММ(J7:J10) и копируем протягиванием в ячейки с К11 по N11.
7) В ячейку О7 заносим формулу =СУММ(J7:N7) и копируем протягиванием в ячейки с О8 по О10.
8) Приступаем к решению. На вкладке Данные, пункт меню Анализ, Поиск решения.
Целевая ячейка I13.
Переключатель «равный минимальному значению»
Изменяемые ячейки Х.
Команда Добавить, переходим в окно добавление ограничений
а)
б)
в)
г)
9) Окно Поиск решения, Выполнить.
10) В окне Результаты поиска решений сохранить сценарий «ТЗ1»
11)Результат поиска решения.
12)В окне Диспетчер сценариев (Вкладка Данные, пункт меню Анализ что-если?) выбрать команду Отчёт
ввести адрес целевой функции и ОК.
13) Построить диаграмму
videouroki.net
Тема: Решение транспортной задачи с применением электронных таблиц.
Цель:
Получить практические навыки использования функций “Поиск решения” в электронной таблице Excel.
Ход выполнения:
В результате выполнения лабораторной работы студент должен:
• получить навыки решения оптимизационных задач, приводимых к табличным формам;
• научиться использовать средства электронной таблицы в задачах поиска нужного решения при условии изменения только одного параметра некоторой функции.
Использование функции “Поиск решения” при решении “Транспортной задачи”.
Постановка задачи:
Классическая формулировка задачи состоит в следующем. Имеется несколько пунктов производства и пунктов потребления некоторого продукта. Для каждого из пунктов производства задан объем производства, а для каждого пункта потребления – объем потребления. Известна стоимость перевозки из каждого пункта производства в каждый пункт потребления единицы продукта. Требуется составить план перевозок продукта, в котором все пункты потребления были бы обеспечены необходимыми продуктами, ни из какого пункта производства не вывозилось бы продуктов больше, чем там производится, а стоимость перевозки была бы минимальной.
В построенной при помощи Microsoft Excel модели представлена такая задача (см. рис.1). Товары могут доставляться из пункта производства (Белоруссия, Урал, Украина) в любой пункт потребления (Казань, Рига, Воронеж, Курск, Москва). Очевидно, что стоимость доставки на большее расстояние будет большей. Требуется определить объемы перевозок между каждым пунктом производства и пунктом потребления в соответствии с потребностями пунктов потребления и производственными возможностями пунктов производства, при которых транспортные расходы минимальны. Таким образом, цель задачи – уменьшение всех транспортных расходов.
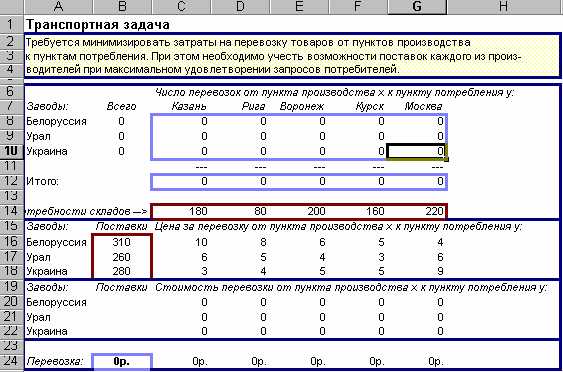
Рис. 1. Таблица для решения “Транспортной задачи”.
Порядок выполнения.
Первый этап — ввод исходных данных:
1. Ввести на рабочем листе необходимые исходные данные и определить их взаимосвязи с результирующими данными:
1.1. Построить таблицы для ввода количества перевозок, цены перевозки и стоимости перевозки из пункта производства “Х” в пункт потребления “Y”, как показано на Рис.1 (количество перевозок для каждого пункта в начале решения задачи будет равно 0).
1.2. Ввести в ячейки С14-G14 потребности складов в товаре, а в ячейки В16-В18 – производственные возможности пунктов производства.
1.3. Ввести в ячейки С16-G18 цены на перевозку товара из пункта производства Х в пункт потребления Y.
2. Ввести формулы в вычисляемые ячейки:
2.1. В ячейки В8:В10 ввести формулы вычисления общего количества перевезенного товара для каждого из пунктов производства (например, формула для ячейки В8=СУММ(С8:G8), т.е. количество перевезенного товара для Белоруссии).
2.2. В ячейки С12:G12 ввести формулы вычисления общего количества перевезенного товара в каждый из пунктов потребления (например, формула для ячейки С12=СУММ(С8:С10), т.е. количество перевезенного товара в Казань).
2.3. В ячейки С20:G22 ввести формулы вычисления общей цены за перевозку товара из каждого пункта производства в каждый пункт потребления, умножив цену перевозки единицы товара (ячейки С16-G18) на общее количество перевезенного товара (ячейки С8-G10) (например, формула для ячейки С20 – общая цена перевозки товара из Белоруссии в Казань – =С8*С16).
2.4. В ячейки С24:G24 ввести формулы вычисления стоимости всех перевозок по каждому из пунктов потребления (например, для Казани в ячейку С24 вводится формула =СУММ(С20:С22)).
2.5. В ячейку В24 ввести формулу подсчета всей стоимости перевозок – результат суммирования значений ячеек С24:G24.
3. Выполнить форматирование ячеек рабочего листа, и выделить ячейки с результатами и изменяемыми данными – синим цветом, а ячейки с исходными данными – красным цветом.
Второй этап – поиск решения:
1. При помощи команды “Сервис” – “Поиск решения…” вызвать диалоговое окно задания данных для решения задачи (Рис.2).
2. Задать целевую ячейку
В качестве целевой ячейки выбрать ячейку (аналогичную ячейке В24 на рис. 1), в которой будет подсчитана общая цена всех перевозок.
По условию задачи целевую ячейку следует установить равной минимальному значению.
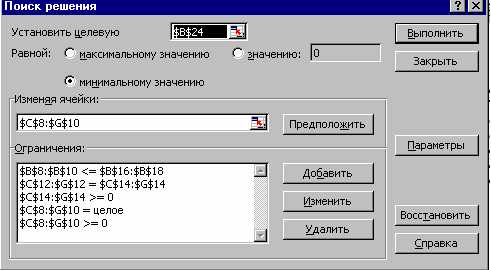
Рис. 2. Диалоговое окно ввода данных для решения задачи.
3. Задать изменяемые ячейки
Минимальное значение целевой ячейки будет определяться путем изменения данных в ячейках, задающих объемы перевозок от каждого из пунктов производства к каждому пункту потребления (ячейки C8:G10 на рис. 1).
4. Наложить требования (ограничения), которые будут предъявляться к результатам задачи:
4.1. Количество перевезенных грузов не может превышать производственных возможностей заводов (на рис. 1 значения ячеек B8:B10 должны быть меньше или равны значениям ячеек B16:B18).
4.2. Количество доставляемых грузов должно быть равно потребностям складов (т.е. на рис. 1 значения ячеек C12:G12 должны быть равны значениям ячеек С14:G14).
4.3. Число перевозок не может быть отрицательным и не целым (т.е. на рис. 1 значения ячеек C8:G10 должны быть больше или равны нулю и должны быть целыми).
5. Ввести значения в окно “Поиск решения”. Для ввода значений в диалоговое окно “Поиск решений” можно использовать выделение ячеек и интервалов мышью (при заполнении соответствующих полей ввода). Кроме того, в некоторых случаях удобно пользоваться для определения изменяемых ячеек кнопкой “Предположить” – в этом случае в качестве изменяемых ячеек предлагается использовать все влияющие ячейки для ранее определенной целевой ячейки.
Для ввода ограничений необходимо нажать кнопку “Добавить”.
На экране появится диалоговое окно, показанное на Рис.3.
Рис. 3. Окно ввода ограничений.
При помощи этого диалогового окна ввести ранее заданные ограничения. Для ввода значений в области “Ссылка на ячейку” и “Ограничение” можно также пользоваться возможностями Microsoft Excel по выделению интервалов мышью.
6. Инициировать «Поиск решения»
Решение задачи начинается после нажатия кнопки “Выполнить” в диалоговом окне “Поиск решения”. После того, как вычисления закончатся, открывается диалоговое окно “Результаты поиска решения” (Рис.4), в котором выводится сообщение о том, найдено или нет решение поставленной задачи. Если найденное решение устраивает пользователя, он может сохранить его на рабочем листе, нажав кнопку «ОК».
Можно также сохранить найденное решение в качестве сценария с помощью кнопки “Сохранить сценарий” (обычно так поступают в том случае, когда требуется сохранить результаты нескольких различных решений, полученных при изменении нескольких ограничений).
Рис. 4. Окно “Результаты поиска решения”.
Оптимальное количество поставок, которое приведет к минимизации транспортных расходов в соответствии с заданными исходными данных, представлено в таблице на Рис.5.
7. Составить отчет о проделанной работе.
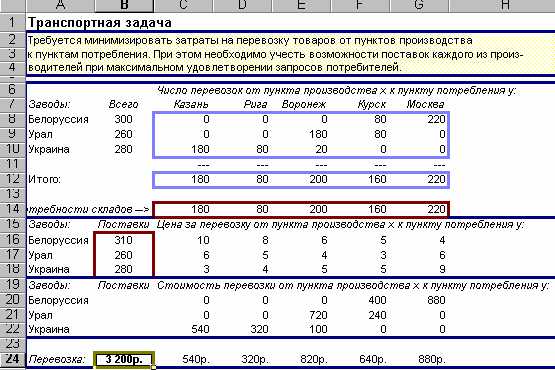
Рис.5. Результаты вычислений.
Отправить его преподавателю по электронной почте в виде вложенного файла или переписать файл преподавателю со своего носителя (флэш-накопителя, компакт-диска) или сдать работу преподавателю в распечатанном и скреплённом виде.
Лабораторное занятие № 4.
student2.ru
Решение транспортной задачи с помощью программного обеспечения
Библиографическое описание:
Шульгина-Таращук А. С. Решение транспортной задачи с помощью программного обеспечения // Молодой ученый. 2016. №12. С. 67-70. URL https://moluch.ru/archive/116/31916/ (дата обращения: 24.06.2019).
Цель работы — научиться составлять оптимальный план для транспортных средств на производстве с учетом ограничений, используя материальные запасы для транспортной задачи, получив оптимизацию планов математическими компьютерными методами линейного программирования посредством применения Solver из программы Microsoft Excel [1].
План транспортных средств представляется в табличной форме, включая количество производственных запасов на складах поставщиков и необходимое количество для потребителя в естественном выражении. При разработке плана производственная цель определена: минимизация расходов транспортировки [2].
Математическая модель для алгоритма оптимизации
Общее утверждение транспортной проблемы включает определение оптимального плана транспортных средств некоторого груза от пунктов отправления до мест назначения . Как критерий оптимальности мы берем или минимальную стоимость транспортных средств всего груза, или минимальное время его поставки [3].
Пусть () — тарифы транспортировки единицы груза от пункта отправления до места назначения; () — груз пункта; () — требование для груза в месте назначения; () — количество единиц груза, транспортируемых от пункта отправления до места назначения. Тогда экономико-математическая постановка задачи заключается в определении минимального значения функции:
(1)
с условиями
(2)
Если потребности в грузовых пунктах назначения равны грузовым резервам в пунктах отправления, т. е.
(3)
тогда модель транспортной задачи называют закрытой, иначе — открытая.
Постановка задачи
Однородный груз в количестве 50, 30 и 10 единиц поступил на три базы . Этот груз требуется доставить в четыре места назначения соответственно в количествах 30, 20, 10 и 20 единиц. Тарифы транспортных средств единицы груза даны в таблице 1. Найти оптимальный план транспортных средств транспортной задачи.
Табличная модель
Оформим план в форме таблицы:
Таблица 1
Транспортные тарифы
A | B | C | D | E | F | |
1 | Транспортная задача (minimum) | |||||
2 | Поставщики | Потребители | Запас | |||
3 | ||||||
4 | 1 | 2 | 4 | 1 | 50 | |
5 | 2 | 3 | 1 | 5 | 30 | |
6 | 3 | 2 | 4 | 4 | 10 | |
7 | Потребность | 30 | 20 | 10 | 20 | |
После того, чтобы получить таблицу плана, необходимо составить формулы для вычислений (таблицы 2 и 3).
Таблица 2
Представление формул ивходных данных
… | A | B | C | D |
8 | ||||
9 | ||||
10 | ||||
11 | ||||
12 | ||||
13 | Импортировано | =SUM(B10:B12) | =SUM(С10:С12) | =SUM(D10:D12) |
Таблица 3
Продолжение таблицы 2
E | F | G |
Экспортировано | Остатки | |
= SUM (B10:E10) | ||
= SUM (B11:E11) | ||
= SUM (B12:E12) | ||
= SUM (E10:E12) |
На первых уроках нецелесообразно автоматизировать работу для планирования экспериментов и обработки результатов, поскольку студент получает готовые результаты, не показав действий, творчества. После ручного контроля эксперимента, когда понимание и знание объекта исследования улучшились, возможно начать автоматизацию планирования и управление экспериментом: изменяя число доставок в ячейках , сокращая расходы в ячейке . В то же время визуально управлять расходом запасов в колонке . Расход не должен превышать резервы на складе (колонка ).
Посредством программы оптимизации мы можем облегчить реализацию этой задачи. После выбора Поиск Решения в MSExsell появится диалоговое окно, в котором мы установим следующие условия, показанные на рисунке 1:
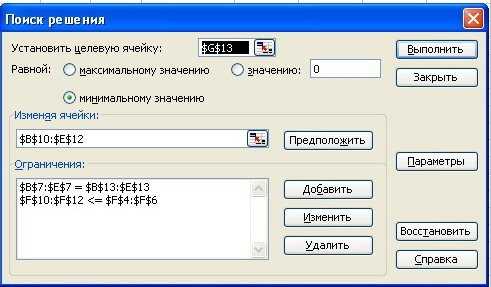
Рис. 1. Диалоговое окно Поиск решения
Мы принимаем модель как линейную, Рисунок 2:
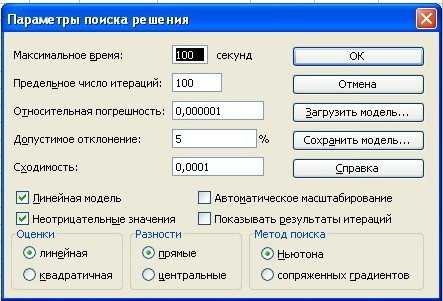
Рис. 2. Диалоговое окно «Параметры Поиска решения»
После нажатия на кнопку «Выполнить», получаем результат, приведенный в таблице 4.
Таблица 4
Полученные результаты
A | B | C | D | F | G | ||
8 | |||||||
9 | Экспортировано | Остатки | |||||
10 | 20 | 10 | 0 | 20 | 50 | 0 | |
11 | 10 | 0 | 10 | 0 | 20 | 10 | |
12 | 0 | 10 | 0 | 0 | 10 | 0 | |
13 | Импортировано | 30 | 20 | 10 | 20 | Об затраты | 110 |
Таким образом, достигнуты минимальные расходы при ограничениях запасов на складах поставщиков. Упростить и ускорить поиск прибыли помогла программа Solver, которая рационализировала решение этой экономической задачи [4].
Литература:
- Горчаков A. A. Компьютерные экономико-математические модели. M.: ЮНИТИ, 1995. — 201 с.
- Додж M. Эффективная работа с MicrosoftExcel 2000. SPb.: Питер, 2001. — 161 с.
- Замков О. О., Толстопятенко А. В., Черемных Ю. Н. Математические методы в экономике. — M.: Изд. «ДИС», 2001. — 368 с.
- Шелобаев С. И. Математические методы и модели в экономике, финансах, бизнесе. Изд. Юнити, 2001. — 367 с.
- Бережная Е. В., Бережной В. И. Математические методы моделирования экономических систем. — 2-е изд., перераб. и доп. — М.: Финансы и статистика, 2006. — 432 с.
Основные термины (генерируются автоматически): SUM, место назначения, пункт отправления, транспортная задача, оптимальный план, диалоговое окно, груз, склад поставщиков, средство, Поиск решения.
moluch.ru
Практическая работа по информатике на тему «Транспортная задача. Решение с помощью ЭТ» 11 класс
Транспортная задача.
Решение с помощью ЭТ.
Подготовим данные:
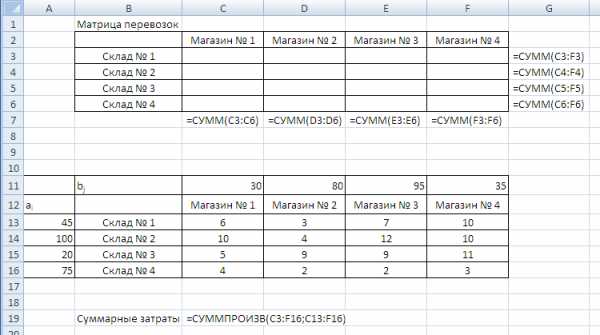
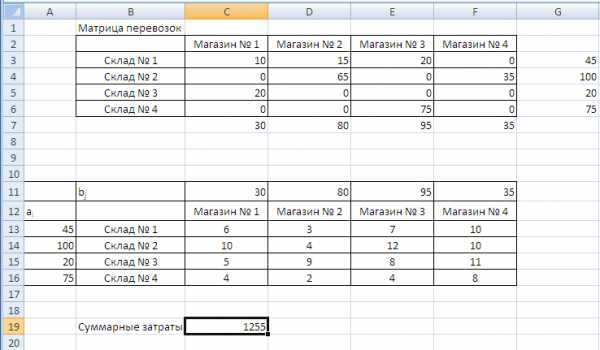
Исходными данными являются удельные затраты на перевозки (диапазон ячеек С13:F16), запасы муки на складах (диапазон ячеек А13:А16), потребности магазинов в муке (диапазон ячеек С11:F11)
Диапазон ячеек С3:F6 предназначен для получения искомого решения – объемов перевозок груза. Суммируя объемы перевозок в каждой строке, задаем левые части уравнений-ограничений, обеспечивающих вывоз всего груза с каждого склада. Суммированием объемов перевозок по столбцам задаются левые части уравнений-ограничений, удовлетворяющих спрос каждого магазина в муке.
Формула =СУММПРОИЗВ(С3:F16;C13:F16), вычисляющая целевую функцию (суммарные затраты) Z, размещена в ячейке С19. Данная формула равносильна формуле: =А1*А3+В1*В3+А2*А4+В2*В4.
Установим курсор в ячейку С19. Выполним команду Поиск решения из меню Сервис.
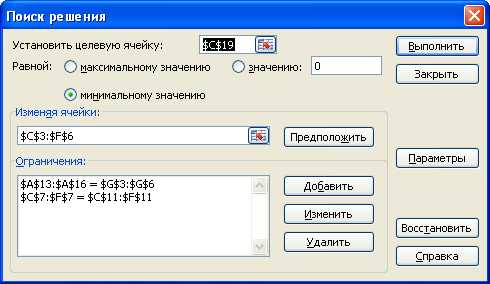
Установим параметры поиска решения – неотрицательные значения (в нашем случае это объемы перевозок) и линейную модель вычислений, воспользовавшись кнопкой Параметры
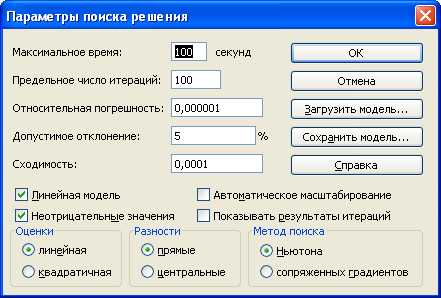
После того, как все установки сделаны, следует нажать на кнопку Выполнить. Искомые объемы перевозок представлены в ячейках С3:F6. Минимальные затраты на перевозки – в ячейке С19
Задания для самостоятельного выполнения:
Постройте математическую модель и решите с помощью табличного процессора Excel, используя инструмент Посик решения.
На складах имеются запасы груза, который необходимо доставить в магазины в определенном объеме:
Запасы груза на складах:
Потребность в грузе в магазинах:
Удельные стоимости перевозки:
infourok.ru
Решение транспортной задачи в среде Excel
математическая модель сводится к минимизации целевой функции, выражающей суммарные затраты на перевозку всего грузапри ограничениях
Пример. Задача организации оптимального снабжения .
ТаблицаЭкономико-математическая модель задачи.
Функциональные ограничения:
1) Указать адреса ячеек, в которые будет помещен результат решения задачи, т. е. изменяемые ячейки . Эти ячейки можно размещать либо в первых строках массива, либо в нижних, как в нашей задаче.2)Ввести исходные данные , как в транспортной таблице.
,где -запас поставщика. Количество потребителей равно 5.Поместим курсор в ячейку G11.Выберем функцию СУММ.Выделим для суммирования ячейки B11:F11.
Теперь введем условия по потребителям:
Выберем функцию сумм.Выделим для суммирования ячейки В11:В13, где находятся запасы молока. Нажмем кнопку ОК.Эту же последовательность действий повторим для ячеек С14, D14,Е14,F14.
Запустим мастер функций .Выберем СУММПРОИЗВ.Нажмем ОК.
В поле Массив1 укажем адреса B3:F5, поместив курсор в указанные ячейки.В поле Массив2 укажем адреса B11:F13, поместив курсор в эти ячейки.Нажмем ОК.В данной задаче в ячейке G14 появится число 0.
6) Назначить ячейку для целевой функции. Для этого поместить курсор в целевую ячейку. Адрес $G$14 введется при этом сам.Ввести тип целевой функции –отметить –Минимальное значение
Первое ограничение –по уровню потребления:B14:F14=B6:F6второе –по уровню запасовG11:G13≤G3:G5После ввода ограничений нажмем кнопку ОК.
Установить Неотрицательные значения и Линейная модельНажмем ОК.В появившемся окне Поиск решения нажать Выполнить.
Общие затраты на перевозку продукции составят 785 д.е.Спрос торговых точек удовлетворен полностью — они получат 150ц молока. У первого фермерского хозяйства останется нереализованным 20ц молока.Пример. Закрепление самолетов за воздушными линиями.
Экономико-математическая модель задачи.
Ограничения:
Ограничения:
Вид электронной таблицыРешение задачи.
Ответ
|
hnu.docdat.com
