Решение уравнений методом подстановки – Решение систем уравнений способом подстановки

Примеры решения систем методом подстановки

Рассмотрим конкретные примеры решения систем линейных уравнений методом подстановки.

   

В данном случае удобно из второго уравнения системы выразить x через y и подставить полученное выражение вместо x в первое уравнение:

   

Первое уравнение — уравнение с одной переменной y. Решаем его:

5(7-3y)-2y = -16

35-15y-2y= -16

-17y= -51

y=3.

Полученное значение y подставляем в выражение для x:

   

Ответ: (-2; 3).

   

В данной системе проще из первого уравнения выразить y через x и подставить полученное выражение вместо y во второе уравнение:

   

   

Второе уравнение — уравнение с одной переменной x. Решим его:

3x-4(-1,5-3,5x)=23

3x+6+14x=23

17x=17

x=1.

В выражение для y вместо x подставляем x=1 и находим y:

   

Ответ: (1; -5).

   

Здесь удобнее из второго уравнения выразить y через x (поскольку делить на 10 проще, чем на 4, -9 или 3):

   

   

Решаем первое уравнение:

4x-9(1,6-0,3x)= -1

4x-14,4+2,7x= -1

6,7x=13,4

x=2.

Подставляем x=2 и находим y:

   

Ответ: (2; 1).

   

Прежде чем применить метод подстановки, эту систему следует упростить. Обе части первого уравнения можно умножить на наименьший общий знаменатель, во втором уравнении раскрываем скобки и приводим подобные слагаемые:

   

   

Получили систему линейных уравнений с двумя переменными. Теперь применим подстановку. Удобно из второго уравнения выразить a через b:

   

   

Решаем первое уравнение системы:

3(21,5 + 2,5b) — 7b = 63

64,5+7,5b-7b=63

0,5b= -1,5

b= -3.

Осталось найти значение a:

   

Согласно правилам оформления, ответ записываем в круглых скобках через точку с запятой в алфавитном порядке.

Ответ: (14; -3).

 

Выражая одну переменную через другую, иногда удобнее оставлять её с некоторым коэффициентом.

   

В данном случае удобно выразить y через x из второго уравнения. При этом лучше не делить обе части уравнения на 3, а оставить коэффициент 3 рядом с y, поскольку в первом уравнении 12y кратно 3:

   

   

9x-4(43-4x)=78

9x-172+16x=78

25x=250

x=10.

   

   

Ответ: (10;1).

 

Из всех способов решения систем уравнений метод подстановки в алгебре используется чаще других. С помощью этого метода могут быть решены не только системы линейных уравнений, но и системы уравнений других видов.

www.algebraclass.ru

Системы уравнений. Метод подстановки. Видеоурок. Алгебра 11 Класс

Тема: Системы уравнений_Основные сведения и примеры

Урок:

Системы уравнений. Метод подстановки

Рассмотрим системы двух уравнений с двумя неизвестными (1) и трех уравнений с тремя неизвестными (2).

Здесь р и q – некоторые выражения, зависящие от пары переменных х и у.

Здесь р, q и r – некоторые выражения, зависящие от тройки переменных х, у и z.

Частным решением системы 1 называется пара чисел () такая, при подстановке которой в уравнения системы получим верные равенства.

Частным решением системы 2 называется тройка чисел () такая, при подстановке которой в уравнения системы получим верные равенства.

Решить систему уравнений означает найти множество всех ее решений.

Чтобы найти множество всех решений системы, лучше всего пользоваться эквивалентными или равносильными преобразованиями, то есть такими, которые не искажают множество решений. В результате таких преобразований мы получаем равносильные системы, то есть имеющие одно и то же множество решений

Таким образом, процесс решения системы сводится к постепенному переходу от заданной сложной системы к все более простой и так до тех пор, пока не получим ответ.

Методы решения систем с помощью эквивалентных преобразований:

-метод подстановки;           

-метод алгебраического сложения;

-метод введения новых переменных;

Повторим метод подстановки. Напомним суть данного метода. Мы рассматриваем заданную систему вида 1 и замечаем, что в одном из уравнений, пусть во втором, легко выразить одну переменную через другую, пусть у через х:

Полученное выражение подставляем в первое уравнение системы:

Таким образом мы получаем одно уравнение (в данном случае первое) только относительно х. решаем это уравнение, находим все значения х, подставляем их в выражение для у и находим соответствующие значения у.

Пример 1 – решить систему методом подстановки:

В данном случае удобно из первого уравнения выразить у:

Подставим полученное выражение во второе уравнение:

Находим соответствующие значения у:

Ответ: (2;-1), (-1;2)

Пример 2 – решить систему методом подстановки:

В данном случае удобно из первого уравнения выразить х:

Подставим полученное выражение во второе уравнение:

Находим соответствующее значение х:

Ответ: (3;1)

В следующей системе важно обратить внимание на ОДЗ.

Пример 3 – решить систему методом подстановки:

Укажем ОДЗ для первого уравнения:

При соблюдении ОДЗ первое уравнение можно преобразовать:

Имеем систему:

В данном случае удобно из первого уравнения выразить у:

Подставим полученное выражение во второе уравнение:

Находим соответствующие значения у:

Сверившись с ОДЗ, выписываем ответ.

Ответ: (5;4), (-1;0)

Пример 4 – решить систему методом подстановки:

В данном случае удобно из первого уравнения выразить у:

Подставим полученное выражение во второе уравнение:

Находим соответствующие значения у:

Ответ: (), ()

Обратим внимание, что n здесь пробегает все целочисленные значения

Пример 5 – решить систему методом подстановки:

Рассмотрим первое уравнение:

ОДЗ соблюдено

Получили равносильную систему:

В данном случае удобно из первого уравнения выразить у:

Подставим полученное выражение во второе уравнение:

Находим соответствующие значения у:

Ответ: (2;6)

Итак, мы рассмотрели метод подстановки при решении систем двух уравнений с двумя неизвестными, далее рассмотрим метод алгебраического сложения.

 

Список рекомендованной литературы

1. Мордкович А.Г. Алгебра и начала математического анализа. М.: Мнемозина

2. Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. М.: Дрофа. 

3. Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. М.: Просвещение.

 

Рекомендованные ссылки на ресурсы интернет

1. Xvatit.com (Источник).

2. Школьный помощник (Источник).

3. Nado5.ru (Источник).

 

Рекомендованное домашнее задание

1. Алгебра и начала анализа, 10—11 класс (А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын) 1990, №190(б,г), 191(б,г) ст.289;

2. Решить систему методом подстановки:

3. Решить систему методом подстановки:

 

interneturok.ru

Решение уравнений методом подстановки

Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Метод подстановки позволяет легко решить системы линейных уравнений любой сложности. Суть метода заключается в том, что, используя первое выражение системы, мы выражаем «у», а далее производим подстановку полученного выражения во второе уравнение системы вместо «у». Поскольку уравнение уже содержит не два неизвестных, а только одно, то мы легко находим значение этой переменной, а затем с ее помощью определяем значение второй.

Допустим, дана система линейных уравнений следующего вида:

\[\left\{\begin{matrix} 3x-y-10=0\\ x+4y-12=0 \end{matrix}\right.\]

Так же читайте нашу статью «Решить алгебраическое уравнение онлайн решатель»

Выразим \[y:\]

\[\left\{\begin{matrix} 3x-10=y\\ x+4y-12=0 \end{matrix}\right.\]

Выполним подстановку полученного выражения во 2 уравнение:

\[\left\{\begin{matrix} y=3x-10\\ x+4(3x-10)-12=0 \end{matrix}\right.\]

Найдем значение \[x:\]

\[x + 4 (3x — 10) — 12 = 0\]

Упростим и решим уравнение с помощью открытия скобок и учета правил переноса членов:

\[x + 12x — 40 -12 = 0\]

\[13х — 52 = 0\]

\[13x = 52\]

\[х = 4\]

Теперь нам известно значение \[x.\] Используем это для нахождения значения \[y:\]

\[y = 3x — 10\]

\[y = 3\cdot 4 — 10\]

\[y = 2\]

Ответ: \[(4;2).\]

Где можно решить систему уравнений онлайн методом подстановки?

Решить систему уравнений вы можете на нашем сайте pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте: pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

www.pocketteacher.ru

Методы решения уравнений: замены, подстановки, примеры, тесты

Тестирование онлайн

Потерянные и посторонние корни

К потере корней может привести сокращение обеих частей уравнения на общий множитель.

Посторонние корни могут появится при умножении обеих частей уравнения на множитель, содержащий неизвестное.

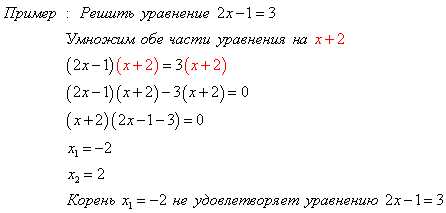
При возведении обеих частей уравнения в квадрат (или любую четную степень) могут появляться посторонние корни.

Посторонние корни могут появляться при решении иррационального уравнения, поэтому лучше выполнять проверку.

Метод замены переменной

В ряде случаев решение уравнения можно упростить введением новой переменной (нового неизвестного).

Например, уравнение вида

где a, b, c — числа, называется биквадратным. Решается введением замены x²=t

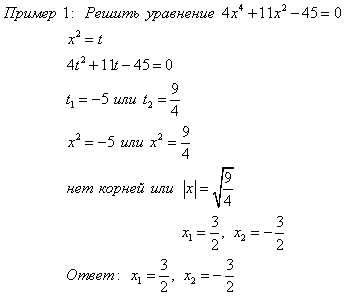
Метод замены используют не только при решении биквадратных уравнений.

Сложные замены переменной

Основная трудность решения задач методом подстановки заключается в том, что иногда трудно угадать вид самой подстановки и вид уравнений, где подстановку можно использовать.

Очень сложные замены переменной

Графический способ решения уравнений

Графический способ решения уравнений f(x)=g(x) заключается в следующем: строят в одной системе координат графики двух функций y=f(x) и y=g(x) и находят абсциссы точек пересечения графиков. Абсциссы точек пересечения графиков и являются корнями уравнения.

Преобразуем выражение a⁴+b⁴=(a+b)⁴:

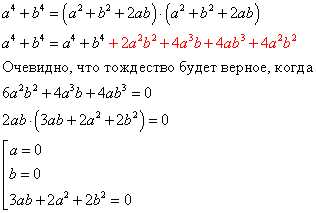
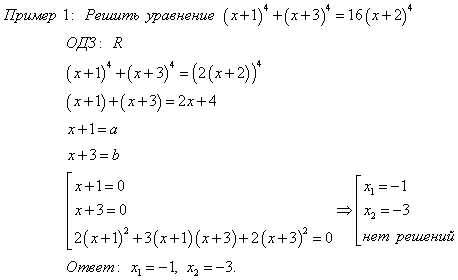
При решении уравнения f(x)=g(x) можно исследовать функции y=f(x) и y=g(x) на монотонность. Если одна из этих функций на промежутке монотонно убывает, а другая функция монотонно возрастает, то уравнение или имеет один корень, или вообще не имеет корней. Корень уравнения можно найти методом подбора или графическим методом.

Если функция y=f(x) возрастает, а y=g(x) убывает на промежутке , и при этом f(a)>g(a), то корней нет.

Примеры уравнений вида f(f(x))=x, где f(x) — некоторая функция:

1. Любой корень уравнения f(x)=x является корнем уравнения f(f(x))=x;
2. Если функция f(x) возрастает на некотором множестве и значения x и значения функции f(x) принадлежат этому множеству, то уравнения f(x)=x и f(f(x))=x равносильны на этом множестве.

Для убывающей функции f(x) правило 2 применить нельзя.

Суть метода состоит в замене переменной х тригонометрической функцией, например . Решение исходного уравнения сводится к решению тригонометрического уравнения. Но тригонометрическое уравнение обычно имеет бесконечное множество решений, а исходное — конечное.

Неравенство Коши.

Неравенство Бернулли.

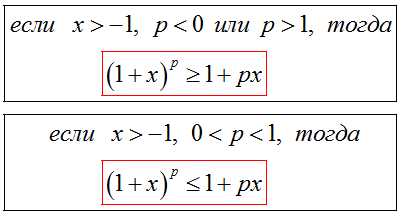
Равенство достигается при x=0 или n=1.

Неравенство Коши-Буняковского.

Равенство достигается в том и только в том случае, когда существует положительная константа a такая, что x₁=ay₁, x₂=ay₂,…,x_n=ay_n.

fizmat.by

Решение системы линейных уравнений. Метод подстановки, сложения, графический. Особые случаи, тесты

Тестирование онлайн

• Система линейных уравнений

Система линейных уравнений

Обычно уравнения системы записывают в столбик одно под другим и объединяют фигурной скобкой

Система уравнений такого вида, где a, b, c — числа, а x, y — переменные, называется системой линейных уравнений.

При решении системы уравнений используют свойства, справедливые для решения уравнений.

Решение системы линейных уравнений способом подстановки

Рассмотрим пример

1) Выразить в одном из уравнений переменную. Например, выразим y в первом уравнении, получим систему:

2) Подставляем во второе уравнение системы вместо y выражение 3х-7:

3) Решаем полученное второе уравнение:

4) Полученное решение подставляем в первое уравнение системы:

Система уравнений имеет единственное решение: пару чисел x=1, y=-4. Ответ: (1; -4), записывается в скобках, на первой позиции значение x, на второй — y.

Решение системы линейных уравнений способом сложения

Решим систему уравнений из предыдущего примера методом сложения.

1) Преобразовать систему таким образом, чтобы коэффициенты при одной из переменных стали противоположными. Умножим первое уравнение системы на «3».

2) Складываем почленно уравнения системы. Второе уравнение системы (любое) переписываем без изменений.

3) Полученное решение подставляем в первое уравнение системы:

Решение системы линейных уравнений графическим способом

Графическое решение системы уравнений с двумя переменными сводится к отыскиванию координат общих точек графиков уравнений.

Графиком линейной функции является прямая. Две прямые на плоскости могут пересекаться в одной точке, быть параллельными или совпадать. Соответственно система уравнений может: а) иметь единственное решение; б) не иметь решений; в) иметь бесконечное множество решений.

2) Решением системы уравнений является точка (если уравнения являются линейными) пересечения графиков.

Графическое решение системы

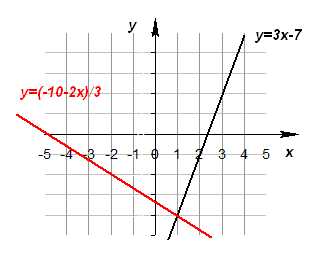
Метод введения новых переменных

Замена переменных может привести к решению более простой системы уравнений, чем исходная.

Рассмотрим решение системы

Введем замену , тогда

Переходим к первоначальным переменным

Особые случаи

Не решая системы линейных уравнений, можно определить число ее решений по коэффициентам при соответствующих переменных.

Пусть дана система

1) Если , то система имеет единственное решение.

2) Если , то система решений не имеет. В этом случае прямые, являющиеся графиками уравнений системы, параллельны и не совпадают.

3) Если , то система имеет бесконечное множество решений. В этом случае прямые совпадают друг с другом.

Суть метода в последовательном исключении неизвестных, приводя систему линейных уравнений к ступенчатой форме.

fizmat.by

Метод подстановки | Алгебра

Метод подстановки решения систем линейных уравнений первый раз изучается в курсе алгебры 7 класса. В дальнейшем этот метод встречается ещё не раз, поскольку с помощью подстановки можно решать и другие виды систем уравнений.

 

Алгоритм решения систем линейных уравнений методом подстановки

1) В одном из уравнений выражаем одну переменную через другую.

2) Полученное выражение подставляем вместо этой переменной в другое уравнение системы и решаем уравнение с одной переменной.

3) Найденное значение переменной подставляем в выражение и вычисляем значение другой переменной.

Ответ системы записывают в круглых скобках через точку с запятой в алфавитном порядке. Для системы уравнений из двух переменных ответ схематически выглядит так:

(x; y),

из трёх — (x; y; z).

 

Как определить, из какого уравнения выразить одну переменную через другую?

При решении систем линейных уравнений способом подстановки выразить одну переменную через другую можно из любого уравнения, но желательно лучше выбирать для этого путь, который проще.

• Как правило, удобнее всего брать переменную, коэффициент при которой равен единице. В этом случае, чтобы выразить такую переменную через другую, нужно просто перенести остальные слагаемые в правую часть, изменив при переносе их знаки на противоположные.

Например, в системе

   

во втором уравнении коэффициент при переменной y равен 1 (b₂=1), поэтому удобно выразить из второго уравнения y через x:

y=с₂ — a₂x

и подставить получившееся выражение вместо y в первое уравнение:

a₁x+b₁(с₂ — a₂x)=с₁.

Записывают эти действия коротко:

   

   

 

• Следующий по удобству вариант — коэффициент -1 перед переменной.

Например, в системе

   

коэффициент при y в первом уравнении равен -1, поэтому удобно выразить из первого уравнения y через x.

Это можно сделать так: оставив y со знаком «-«в левой части, первое слагаемое перенести в правую часть

-y=с₁ -a₁x,

после чего умножить обе части уравнения на -1:

y= a₁x — с₁ .

Также можно y перенести в правую часть, изменив его знак на «+», а a₁x  — в левую, изменив знак на «-«:

a₁x — с₁=y.

Можно сразу же поменять местами правую и левую части:

y= a₁x — с₁ .

Записывают эти действия кратко:

   

   

 

• Поскольку удобно делить на 2, 5, 10, при наличии одного из таких коэффициентов перед переменной удобно выразить такую переменную через другую.

Например, в системе

   

можно выразить из первого уравнения x через y:

   

   

 

• В общем виде план решение систем линейных уравнений способом подстановки можно записать, например, так:

   

   

   

Из второго уравнения находим значение x. Подставив это значение в 1-е уравнение, находим y.

 

В следующий раз рассмотрим решение систем линейных уравнений методом подстановки на конкретных примерах.

www.algebraclass.ru

Решение уравнений методом подстановки онлайн

Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Одним из удобных алгебраических способов решения систем линейных уравнений является метод подстановки, который довольно часто используется для решения уравнений различной сложности. Суть метода заключается в том, что на основе первого выражения мы выражаем \[у\] и подставляем полученное выражение во второе уравнение системы. Определив значение \[у\] можно найти значение \[х.\]

Так же читайте нашу статью «Решить уравнения с модулем онлайн»

Допустим, дана следующая система уравнений:

\[\left\{\begin{matrix} x-2y=3\\ 5x+y=4 \end{matrix}\right.\]

Выразим в первом уравнении \[х:\]

\[x= 3+ 2y\]

Выполним подстановку полученного выражения во второе уравнение:

\[5(3+2y)+y=4\]

Осталось решить простое линейное уравнение с одной неизвестной. Упростим уравнение, открыв скобки, и перенесем целые числа в правую часть, а неизвестные в левую:

\[15+10у+у=4\]

\[10у+у= 4-15\]

\[11у=-11\]

\[y = — 1\]

Если подставить полученный результат \[у\] в полученное на первом этапе уравнение вместо \[у\] и найдем значение \[х:\]

\[x= 3+2y\]

\[x=3+2(-1)\]

\[x=3-2\]

\[x=1\]

Ответ: \[(1;-1)\]

Где можно решить уравнение методом подстановки онлайн?

Решить уравнение вы можете на нашем сайте https://pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

www.pocketteacher.ru

No related posts.