Как сложить два вектора: Как складывать вектора по координатам, формулы, примеры

длина суммы векторов и теорема косинусов

Сложение векторов, заданных координатами (при сложении одноимённые координаты складываются) даёт возможность узнать, как расположен относительно начала координат вектор, являющийся суммой слагаемых векторов. Подробно эти две операции разбирались на уроке «Векторы и операции над векторами».

Теперь же нам предстоит узнать, как найти длину вектора, являющегося результатом сложения векторов. Для этого потребуется использовать теорему косинусов. Такую задачу приходится решать, например, когда дорога из пункта A в пункт С — не прямая, а отклоняется от прямой, чтобы пройти ещё через какой-то пункт B, а нужно узнать длину предполагаемой прямой дороги. Кстати, геодезия — одна из тех сфер деятельности, где тригонометрические функции применяются во всех их полноте.

Поэтому для сложения векторов и определения длины суммы векторов нужно извлечь квадратный корень из каждой части равенства, тогда получится формула длины:

.

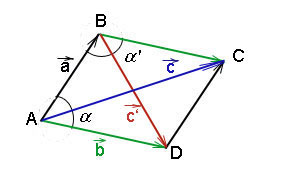
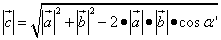Перейдём к примерам.

Проверить решение можно на Калькуляторе онлайн.

Выполнить сложение и вычитание векторов самостоятельно, а затем посмотреть решение

---

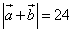Пример 3. Даны длины векторов и длина их суммы . Найти длину их разности .

Решение.

Шаг 1. По теореме косинусов составляем уравнение, чтобы найти косинус угла, смежного с углом между векторами и находим его:

Не забываем, что косинус смежного угла получился со знаком минус. Это значит, что косинус «изначального» угла будет со знаком плюс.

Шаг 2. Выполняем вычитание векторов. Находим длину разности векторов, подставляя в формулу косинус «изначального» угла:

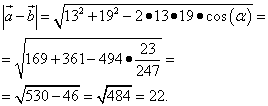
Проверить решение можно на Калькуляторе онлайн.

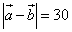Пример 4. Даны длины векторов и длина их разности . Найти длину их суммы .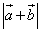

Решение.

Шаг 1. По теореме косинусов составляем уравнение, чтобы найти косинус «изначального» угла (задача обратная по отношению к примеру 1) и находим его:

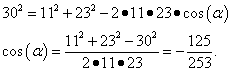
Шаг 2. Меняем знак косинуса и получаем косинус смежного угла между 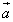и :

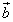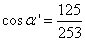
Шаг 3. Выполняем сложение векторов. Находим длину суммы векторов, подставляя в формулу косинус смежного угла:

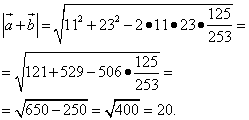
Проверить решение можно на Калькуляторе онлайн.

Пример 6. Какому условию должны удовлетворять векторы 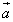и 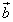, чтобы имели место слелующие соотношения:

1) длина суммы векторов равна длине разности векторов, т. е. ,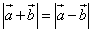

2) длина суммы векторов больше длины разности векторов, т. е. ,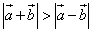

3) длина суммы векторов меньше длины разности векторов, т. е. ?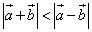

Решение.

Находим условие для первого соотношения. Для этого решаем следующее уравнение:

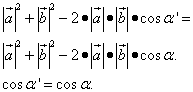
То есть, для того, чтобы длина суммы векторов была равна длине их разности, необходимы, чтобы косинус угла между ними и косинус смежного ему угла были равны. Это условие выполняется, когда углы образуют прямой угол.

Находим условие для второго соотношения. Решаем уравнение:

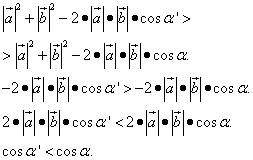
Найденное условие выполняется, когда косинус угла между векторами меньше косинуса смежных углов. То есть, чтобы длина суммы векторов была больше длины разности векторов, необходимо, чтобы углы образовали острый угол (пример 1).

Находим условие для третьего соотношения. Решаем уравнение:

Найденное условие выполняется, когда косинус угла между векторами больше косинуса смежных углов. То есть, чтобы длина суммы векторов была меньше длины разности векторов, необходимо, чтобы углы образовали тупой угол.

Проверить решение можно на Калькуляторе онлайн.

Поделиться с друзьями

Начало темы «Векторы»

Продолжение темы «Векторы»

Вектор. Правило сложение векторов | Подготовка к ЕГЭ по математике

Здесь рассматриваем вектора на плоскости.

Основные определения

 

Вектором называется направленный отрезок , где точка  – начало, точка  – конец вектора.

Нулевым вектором   

 называется вектор, у которого начало совпадает с концом.

Векторы  и  называются одинаково направленными или сонаправленными, если лучи AB и CD одинаково направлены.

Если лучи AB и CD противоположно направлены, векторы  и

называются противоположно направленными.

 

Два вектора называются коллинеарными , если они лежат на одной прямой или на параллельных прямых.

  

Абсолютной величиной (или модулем) вектора называется длина отрезка, изображающего вектор. Абсолютную величину вектора  обозначают 

.

Два вектора называются равными, если они одинаково направлены и равны по абсолютной величине.

Два вектора с равными модулями, лежащие на параллельных прямых, но противоположно направленные, называются противоположными. Вектор, противоположный вектору , обозначается как .

Сложение векторов

 

Сложение векторов

  и   по правилу треугольника

Суммой   двух векторов   и  называют такой третий вектор

, начало которого совпадает с началом , а конец – с концом   при условии, что конец вектора   и начало вектора   совпадают.

Сложение векторов   и   по правилу параллелограмма

Если два неколлинеарных вектора   и   привести к общему началу, то вектор   совпадает с диагональю параллелограмма, построенного на векторах   и . Причем начало вектора  совпадает с началом заданных векторов.

Разностью  векторов  и  называется вектор   такой, что выполняется условие: .

 

Смотрите также «Вектора. Часть 2».

Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор.

Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор В механике существуют два типа величин: скалярные величины, задающие некоторое числовое значение — время, температура, масса и т.д. векторные величины, которые вместе с некоторым числовым значением задают направление — скорость, сила и т.д.. Рассмотрим сначала алгебраический подход к сложению векторов. Покоординатное сложение векторов. Пусть даны два вектора, заданные покоординатно ( чтобы вычислить координаты вектора, нужно вычесть из соответствующих координат его конца соответствующие координаты его начала, т.е. из первой координаты — первую, из второй — вторую и т.д.): Тогда координаты вектора, получившегося при сложении этих двух векторов вычисляются по формуле: В двумерном случае все абсолютно анологично, просто отбрасываем третью координату. Теперь перейдем к геометрическому смыслу сложения двух векторов: . При сложении векторов нужно учитывать и их числовые значения, и направления. Есть несколько широко используемых методов сложения: правило параллелограмма правило треугольника тригонометрический способ Правило параллелограмма. Процедура сложения векторов по правилу параллелограмма заключается в следующем: нарисовать первый вектор, учитывая его величину и направление от начала первого вектора нарисовать второй вектор, также используя и его величину, и его направление дополнить рисунок до параллелограмма, считая, что два нарисованных вектора — это его стороны результирующим вектором будет диагональ параллелограмма, причем его начало будет совпадать с началом первого (а, значит, и второго) вектора.   Правило треугольника Сложение векторов по правилу треугольника заключается в следующем: нарисовать первый вектор, используя данные о его длине ( числовой величине) и направлении от конца первого вектора нарисовать второй вектор, также учитывая и его размер, и его направление результирующим вектором будет вектор, начало которого совпадает с началом первого вектора, а конец — с концом второго.   Тригонометрический способ

Сложение векторов — PhysBook

Скаляры можно складывать, умножать и делить так же, как обычные числа.

Поскольку вектор характеризуется не только числовым значение, но и направлением, сложение векторов не подчиняется правилам сложения чисел. Например, пусть длины векторов a = 3 м, b = 4 м, тогда a + b = 3 м + 4 м = 7 м. Но длина вектора \(\vec c = \vec a + \vec b\) не будет равна 7 м (рис. 1).

Рис. 1.

Для того, чтобы построить вектор \(\vec c = \vec a + \vec b\) (рис. 2), применяются специальные правила сложения векторов.

Рис. 2.

А длину вектора суммы \(\vec c = \vec a + \vec b\) определяют по теореме косинусов \(c = \sqrt{a^2+b^2-2a\cdot b\cdot \cos \alpha}\), где \(\alpha\,\) – угол между векторами \(\vec a\) и \(\vec b\).

Правило треугольника

В зарубежной литературе этот метод называют «хвост к голове».

Для того чтобы сложить два вектора \(\vec a\) и \(\vec b\) (рис. 3, а) нужно переместить вектор \(\vec b\) параллельно самому себе так, чтобы его начало совпадало с концом вектора \(\vec a\) (рис. 3, б). Тогда их суммой будет вектор \(\vec c\), начало которого совпадает с началом вектора \(\vec a\), а конец — с концом вектора \(\vec b\) (рис. 3, в).

      а                                         б                                                    в       Рис. 3.

Результат не поменяется, если перемещать вместо вектора \(\vec b\) вектор \(\vec a\) (рис. 4), т.е. \(\vec b + \vec a = \vec a + \vec b\) (свойство коммутативности векторов).

      а                                         б                                                    в       Рис. 4. <swf age=»13″ bgcolor=»#F8F8FF» dummy=»Dummy_pic1.jpg»>vector-treug-1.swf</swf> «Правило треугольников» Пример 1 Увеличить Flash <swf age=»13″ bgcolor=»#F8F8FF» dummy=»Dummy_pic1.jpg»>vector-treug-2.swf</swf> «Правило треугольников» Пример 2 Увеличить Flash Рис. 5.

При помощи правила треугольника можно сложить два параллельных вектора \(\vec a\) и \(\vec b\) (рис. 6, а) и \(\vec a\) и \(\vec d\) (рис. 7, а). Суммы этих векторов \(\vec c = \vec a + \vec b\) и \(\vec f = \vec a + \vec d\) изображены на рис. 6, б и 7, б. Причем, модули векторов \(c = a + b\) и \(f=\left|a-d\right|\).

   а                                         б Рис. 6.    а                                         б Рис. 7.

Правило треугольника можно применять при сложении трех и более векторов. Например, \(\vec c = \vec a_1 + \vec a_2 +\vec a_3 +\vec a_4\) (рис. 8).

Рис. 8.

Правило параллелограмма

Для того чтобы сложить два вектора \(\vec a\) и \(\vec b\) (рис. 9, а) нужно переместить их параллельно самим себе так, чтобы начала векторов \(\vec a\) и \(\vec b\) находились в одной точке (рис. 9, б). Затем построить параллелограмм, сторонами которого будут эти вектора (рис. 9, в). Тогда суммой \(\vec a+ \vec b\) будет вектор \(\vec c\), начало которого совпадает с общим началом векторов, а конец — с противоположной вершиной параллелограмма (рис. 9, г).

   а                                         б    в                                         г Рис. 9. <swf age=»13″ bgcolor=»#F8F8FF» dummy=»Dummy_pic1.jpg»>vector-paral-1.swf</swf> «Правило параллепипеда» Увеличить Flash Рис. 10.

Вычитание векторов

Для того чтобы найти разность двух векторов \(\vec a\) и \(\vec b\) (рис. 11) нужно найти вектор \(\vec c = \vec a + \left(-\vec b \right)\) (см. Умножение вектора на скаляр) по правилу треугольника (рис. 12) или по правилу параллелограмма (рис. 13).

Рис. 11       а                                       б                                       в Рис. 12.    а                                            б        б                                            в     Рис. 13.

Как сложить два вектора

Вектор представляет собой направленный отрезок. Сложение двух векторов производится как с помощью геометрического или аналитического метода. В первом случае результат сложения измеряется после построения, во втором – рассчитывается. Результатом сложения двух векторов является новый вектор.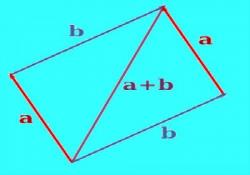Вам понадобится

Чтобы построить сумму двух векторов, при помощи параллельного переноса совместите их так, чтобы они исходили из одной точки. Через конец одного из векторов проведите прямую, параллельную второму вектору. Через конец второго вектора проведите прямую, параллельную первому вектору. Построенные прямые пересекутся в некоторой точке. При правильном построении, вектора и отрезки прямых между концами векторов и точкой пересечения дадут параллелограмм. Постройте вектор, начало которого будет в точке совмещения векторов, а конец в точке пересечения построенных прямых. Это будет сумма двух данных векторов. Измерьте длину полученного вектора линейкой.

Если вектора параллельны и направлены в одну сторону, то измерьте их длины. Отложите параллельный им отрезок, длина которого равна сумме длин данных векторов. Направьте его в ту же сторону, что и исходные вектора. Это и будет их сумма. Если вектора направлены в противоположные стороны, отнимите их длины. Постройте отрезок, параллельно векторам, направьте его в сторону большего вектора. Это будет сумма противоположно направленных параллельных векторов.

Если известны длины двух векторов и угол между ними, найдите модуль (абсолютную величину) их суммы не производя построения. Подсчитайте сумму квадратов длин векторов a и b, и прибавьте к ней их удвоенное произведение, умноженное на косинус угла α между ними. Из полученного числа извлеките корень квадратный c=√(a²+b²+a∙b∙cos(α)). Это будет длина вектора, равного сумме векторов a и b.

Если вектора заданы координатами, найдите их сумму, сложив соответствующие координаты. Например, если вектор a имеет координаты (x1; y1; z1), вектор b (x2; y2; z2), то сложив почленно координаты, получите вектор c, координаты которого (x1+x2; y1+y2; z1+z2). Этот вектор и будет суммой векторов a и b. В случае когда вектора находятся на плоскости, координату z не учитывайте.

Как складывать векторы вместе

2. Образование
3. Наука
4. Физика
5. Как складывать векторы вместе

Стивен Хольцнер

При решении физических задач вас часто просят добавить векторы. Чтобы сложить два вектора, вы помещаете их головой к хвосту, а затем находите длину и величину результата. Порядок, в котором вы добавляете два вектора, не имеет значения.

Например, предположим, что вы направляетесь на большой съезд физиков, и вам сказали, что вам нужно пройти 20 миль на север, а затем 20 миль на восток, чтобы попасть туда.Под каким углом находится конференц-центр от вашего нынешнего местоположения и как далеко он находится?

Вы можете записать эти два вектора следующим образом (где восток расположен вдоль положительной оси x ):

(0, 20)

(20, 0)

В этом случае вам нужно сложить эти два вектора, и вы можете сделать это, просто добавив их компоненты x и y по отдельности:

Посчитайте, и ваш результирующий вектор будет (20, 20).Вы только что завершили векторное сложение. Но вопрос задает вектор в терминах величины / угла, а не в терминах координат. Итак, какова величина вектора от вас к физическому соглашению? Вы можете увидеть ситуацию на следующем рисунке, где у вас есть x и y и вы хотите найти v .

Найти против не так сложно, потому что вы можете использовать теорему Пифагора:

Вставьте числа, чтобы получить

Итак, условное обозначение — 28.3 миль. А как насчет угла тета? Вы знаете

тета = загар ^–1 ( y / x ) = загар ^–1 (20/20) = 45 градусов

Вот и все — теперь вы знаете, что расстояние до съезда составляет 28,3 мили под углом 45 градусов.

Пример вопроса

1. Добавьте два вектора на следующем рисунке. Один имеет звездную величину 5,0 и угол 45 градусов, а другой — 7,0 звездной величины и угол 35 градусов.

   Правильный ответ — 12 б.0, угол 39 градусов.

   1. Разложите два вектора на их компоненты. Для первого вектора примените уравнение v _x = v cos theta, чтобы найти координату x . Это 5,0 cos 45 градусов = 3,5.

   2. Примените уравнение v _y = v sin theta, чтобы найти координату y первого вектора. Это 5.0 sin 45 градусов, или 3.5. Итак, первый вектор (3.5, 3.5) в координатной форме.

   3. Для второго вектора примените уравнение v _x = v cos theta, чтобы найти координату x . Это 7,0 cos 35 градусов = 5,7.

   4. Примените уравнение v _y = v sin theta, чтобы найти координату y второго вектора. Это 7,0 греха 35 градусов = 4.0. Итак, второй вектор (5.7, 4.0) в координатной форме.

   5. Чтобы сложить два вектора, сложите их в виде координат: (3.5, 3.5) + (5.7, 4.0) = (9.2, 7.5).

   6. Преобразуйте (9,2, 7,5) в форму величины / угла. Примените уравнение theta = tan ^–1 ( y / x ), чтобы найти угол, который равен tan ^–1 (7,5 / 9,2) = tan ^–1 (0,82) = 39 градусов.

   7. Примените уравнение

      , чтобы найти звездную величину, которая составляет

      Преобразование в две значащие цифры дает 12.

Практические вопросы

1. Добавьте вектор с величиной 13,0 и углом 27 градусов к вектору с величиной 11,0 и углом 45 градусов.

2. Добавьте вектор с величиной 16,0 и углом 56 градусов к вектору с величиной 10,0 и углом 25 градусов.

3. Сложите два вектора: первый вектор имеет величину 22,0 и угол 19 градусов, а второй вектор имеет величину 19,0 и угол 48 градусов.

4. Добавьте вектор с величиной 10,0 и углом 257 градусов к вектору с величиной 11,0 и углом 105 градусов.

Ниже приведены ответы на вопросы практики:

1. Величина 23,7, угол 35 градусов

   1. Для первого вектора используйте уравнение v _x = v cos theta , чтобы найти координату x : 13,0 x cos 27 градусов = 11.6.

   2. Используйте уравнение v _y = v sin theta , чтобы найти координату y первого вектора: 13,0 x sin 27 градусов или 5,90. Итак, первый вектор (11.6, 5.90) ​​в координатной форме.

   3. Для второго вектора используйте уравнение v _x = v cos theta , чтобы найти координату x : 11,0 x cos 45 градусов = 7.78.

   4. Используйте уравнение v _y = v sin theta , чтобы найти координату y второго вектора: 11,0 x sin 45 градусов = 7,78. Итак, второй вектор (7,78, 7,78) в координатной форме.

   5. Сложите два вектора в виде координат: (11,6, 5,90) + (7,78, 7,78) = (19,4, 13,7).

   6. Преобразуйте (19,4, 13,7) в форму величины / угла. Используйте уравнение theta = tan ^–1 ( y / x ), чтобы найти угол: tan ^–1 (13.7 / 19,4) = загар ^–1 (0,71) = 35 градусов.

   7. Примените уравнение

      , чтобы найти звездную величину, которая составляет

2. Величина 25,1, угол 44 градуса

   1. Для первого вектора используйте уравнение v _x = v cos theta , чтобы найти координату x : 16,0 x cos 56 градусов = 8,95.

   2. Используйте уравнение v _y = v sin theta , чтобы найти координату y первого вектора: 16.0 x sin 56 градусов, или 13,3. Итак, первый вектор (8.95, 13.3) в координатной форме.

   3. Для второго вектора используйте уравнение v _x = v cos theta , чтобы найти координату x : 10,0 x cos 25 градусов = 9,06.

   4. Используйте уравнение v _y = v sin theta , чтобы найти координату y второго вектора: 10.0 x sin 25 градусов = 4,23. Итак, второй вектор (9.06, 4.23) в координатной форме.

   5. Сложите два вектора в виде координат: (8.95, 13.3) + (9.06, 4.23) = (18.0, 17.5).

   6. Преобразуйте вектор (18,0, 17,5) в форму величины / угла. Используйте уравнение theta = tan ^–1 ( y / x ), чтобы найти угол: tan ^–1 (17,5 / 18,0) = tan ^–1 (0,97) = 44 градуса.

   7. Примените уравнение

      , чтобы найти звездную величину, которая составляет

3. Звездная величина 39.7, угол 32 градуса

   1. Для первого вектора используйте уравнение v _x = v cos theta , чтобы найти координату x : 22,0 x cos 19 градусов = 20,8.

   2. Используйте уравнение v _y = v sin theta , чтобы найти координату y первого вектора: 22,0 x sin 19 градусов, или 7,16. Итак, первый вектор (20,8, 7.16) в координатной форме.

   3. Для второго вектора используйте уравнение v _x = v cos theta , чтобы найти координату x : 19,0 x cos 48 градусов = 12,7.

   4. Используйте уравнение v _y = v sin theta , чтобы найти координату y второго вектора: 19,0 x sin 48 градусов = 14,1. Итак, второй вектор (12.7, 14.1) в координатной форме.

   5. Сложите два вектора в виде координат: (20,8, 7,16) + (12,7, 14,1) = (33,5, 21,3).

   6. Преобразуйте вектор (33,5, 21,3) в форму величины / угла. Используйте уравнение theta = tan ^–1 ( y / x ), чтобы найти угол: tan ^–1 (21,3 / 33,5) = tan ^–1 (0,64) = 32 градуса.

   7. Примените уравнение

      , чтобы найти звездную величину, которая составляет

4. звездная величина 5.2, угол 170 градусов

   1. 1. Для первого вектора используйте уравнение v _x = v cos theta , чтобы найти координату x : 10,0 x cos 257 градусов = –2,25.

   2. Используйте уравнение v _y = v sin theta , чтобы найти координату y первого вектора: 10,0 x sin 257 градусов или –9,74. Итак, первый вектор (–2.25, –9.74) в координатной форме.

   3. Для второго вектора используйте уравнение v _x = v cos theta , чтобы найти координату x : 11,0 x cos 105 градусов = –2,85.

   4. Используйте уравнение v _y = v sin theta , чтобы найти координату y второго вектора: 11,0 x sin 105 градусов = 10,6. Итак, второй вектор (–2.85, 10.6) в координатной форме.

   5. Сложите два вектора в виде координат: (–2,25, –9,74) + (–2,85, 10,6) = (–5,10, 0,86).

   6. Преобразуйте вектор (–5,10, 0,86) в форму величины / угла. Используйте уравнение theta = tan ^–1 ( y / x ), чтобы найти угол: tan ^–1 (0,86 / –5,10) = tan ^–1 (–0,17) = 170 градусов. Поскольку x отрицательно, а y положительно, этот вектор должен находиться во втором квадранте.

   7. Примените уравнение

   8. , чтобы найти звездную величину, которая составляет

Об авторе книги

Стивен Хольцнер, доктор философии, был преподавателем и редактором журнала PC Magazine .

,

r — Склеивание двух векторов комбинациями элементов всех векторов

Переполнение стека

1. Около
2. Товары
3. Для команд

1. Переполнение стека Общественные вопросы и ответы
2. Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
3. работы Программирование и связанные с ним технические возможности карьерного роста
4. Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
5. реклама Обратитесь к разработчикам и технологам со всего мира
6. О компании

Загрузка…

2. Авторизоваться зарегистрироваться

.

Как отсортировать два вектора вместе в R?

Переполнение стека

1. Около
2. Товары
3. Для команд

1. Переполнение стека Общественные вопросы и ответы
2. Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
3. работы Программирование и связанные с ним технические возможности карьерного роста
4. Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
5. реклама Обратитесь к разработчикам и технологам со всего мира
6. О компании

,

No related posts.