Как пользоваться | уравнение
Вы можете решать здесь все виды трансцендентых уравнений с помощью онлайн калькулятора с подробным решением!
Приведём примеры трансцедентых уравнений, решаемых данным сервисом:
Дано …
Тэги: уравнение
Калькулятор с буквами умеет упрощать выражения, решать уравнения с применением дробей, степеней и цифр, для некоторых задач можно получить …
Тэги: дробь степень уравнение
Рассмотрим пример решения тригонометрического уравнения онлайн на сайте Контрольная Работа РУ.
Этот сайт даёт полное решение тригонометрического уравнения.
Плюс …
Тэги: уравнение тригонометрия
Используя данный калькулятор онлайн, вы можете решать любые логарифмические уравнения, для большинства получите подробное решение.
Давайте рассмотрим пример уравнения …
Тэги: уравнение логарифм
Вы можете решать уравнения с дробями с помощью онлайн калькулятора, только есть одна проблема, которая возникает у учеников 5, 6, 7, 8 классов школы, а именно, как же вводить собственно дробь в форму калькулятора.
Приведём …
Тэги: уравнение дробь
Биполярные квадратные уравнения являются простыми уравнениями, т.к. они есть аналоги квадратных уравнений, в которых сделана замена x^2 (икс в квадрате) на новую переменную.
Рассмотрим пример, как использовать калькулятор уравнений, чтобы решать биполярные уравнения онлайн:
…Тэги: уравнение
Иррациональные уравнения бывают от простых до сложных — и всех их можно решить онлайн и с подробным решением с помощью калькулятора онлайн.
Итак:
Тэги: уравнение
www.kontrolnaya-rabota.ru
Решение систем линейных уравнений графическим способом
data-ad-client=»ca-pub-8602906481123293″
data-ad-slot=»2890988705″>
- Способ заключается в построении графика каждого уравнения, входящего в данную систему, в одной координатной плоскости и нахождении точки пересечения этих графиков. Координаты этой точки (x; y) и будут являться решением данной системы уравнений.
- Если прямые, являющиеся графиками уравнений системы, пересекаются, то система уравнений имеет единственное решение.
- Если прямые, являющиеся графиками уравнений системы, параллельны, то система уравнений не имеет решений.
- Если прямые, являющиеся графиками уравнений системы, совпадают, то система уравнений имеет бесконечное множество решений.
Примеры. Решить графическим способом систему уравнений.
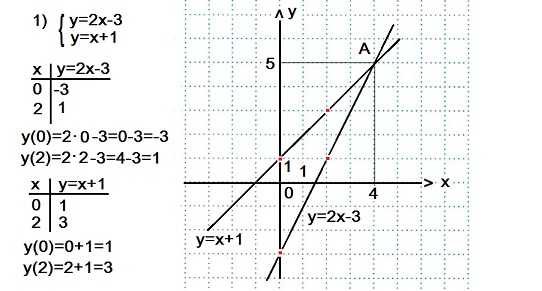Графиком каждого уравнения служит прямая линия, для построения которой достаточно знать координаты двух точек. Мы составили таблицы значений х и у для каждого из уравнений системы.
Прямую y=2x-3 провели через точки (0; -3) и (2; 1).
Прямую y=x+1 провели через точки (0; 1) и (2; 3).
Графики данных уравнений системы 1) пересекаются в точке А(4; 5). Это и есть единственное решение данной системы.
Ответ: (4; 5).
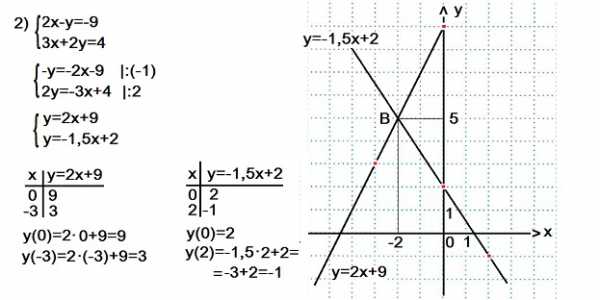Выражаем у через х из каждого уравнения системы 2), а затем составим таблицу значений переменных х и у для каждого из полученных уравнений.
Прямую y=2x+9 проводим через точки (0; 9) и (-3; 3). Прямую y=-1,5x+2 проводим через точки (0; 2) и (2; -1).
Наши прямые пересеклись в точке В(-2; 5).
www.mathematics-repetition.com
Графический метод решения системы уравнений. Видеоурок. Алгебра 9 Класс
Тема: Системы уравнений
Урок: Графический метод решения системы уравнений
Рассмотрим систему
Пару чисел которая одновременно является решением и первого и второго уравнения системы, называют решением системы уравнений.
Решить систему уравнений – это значит найти все её решения, или установить, что решений нет. Мы рассмотрели графики основных уравнений, перейдем к рассмотрению систем.
Пример 1. Решить систему
Решение:
Это линейные уравнения, графиком каждого из них является прямая. График первого уравнения проходит через точки (0; 1) и (-1; 0). График второго уравнения проходит через точки (0; -1) и (-1; 0). Прямые пересекаются в точке (-1; 0), это и есть решение системы уравнений (Рис. 1).
Решением системы является пара чисел Подставив эту пару чисел в каждое уравнение, получим верное равенство.
Мы получили единственное решение линейной системы.
Ответ:
Вспомним, что при решении линейной системы возможны следующие случаи:
cистема имеет единственное решение – прямые пересекаются,
система не имеет решений – прямые параллельны,
система имеет бесчисленное множество решений – прямые совпадают.
Мы рассмотрели частный случай системы, когда p(x; y) и q(x; y) – линейные выражения от x и y.
Пример 2. Решить систему уравнений
Решение:
График первого уравнения – прямая, график второго уравнения – окружность. Построим первый график по точкам (Рис. 2).
|
x |
0 |
-1 |
|
y |
1 |
0 |
Центр окружности в точке О(0; 0), радиус равен 1.
Графики пересекаются в т. А(0; 1) и т. В(-1; 0).
Ответ:
Пример 3. Решить систему графически
Решение: Построим график первого уравнения – это окружность с центром в т.О(0; 0) и радиусом 2. График второго уравнения – парабола. Она сдвинута относительно начала координат на 2 вверх, т.е. ее вершина – точка (0; 2) (Рис. 3).
Графики имеют одну общую точку – т. А(0; 2). Она и является решением системы. Подставим пару чисел в уравнение, чтобы проверить правильность.
Ответ:
Пример 4. Решить систему
Решение: Построим график первого уравнения – это окружность с центром в т.О(0; 0) и радиусом 1 (Рис. 4).
Построим график функции Это ломаная (Рис. 5).
Теперь сдвинем ее на 1 вниз по оси oy. Это и будет график функции
Поместим оба графика в одну систему координат (Рис. 6).
Получаем три точки пересечения – т. А(1; 0), т. В(-1; 0), т. С(0; -1).
Ответ:
Мы рассмотрели графический метод решения систем. Если можно построить график каждого уравнения и найти координаты точек пересечения, то этого метода вполне достаточно.
Но часто графический метод даёт возможность найти только приближенное решение системы или ответить на вопрос о количестве решений. Поэтому нужны и другие методы, более точные, и ими мы займемся на следующих уроках.
Список рекомендованной литературы
1. Мордкович А.Г. и др. Алгебра 9 кл.: Учеб. Для общеобразоват. Учреждений.- 4-е изд. – М.: Мнемозина, 2002.-192 с.: ил.
2. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М.: Мнемозина, 2002.-143 с.: ил.
3. Макарычев Ю. Н. Алгебра. 9 класс : учеб. для учащихся общеобразоват. учреждений / Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, И. Е. Феоктистов. — 7-е изд., испр. и доп. — М.: Мнемозина, 2008.
4. Алимов Ш.А., Колягин Ю.М., Сидоров Ю.В. Алгебра. 9 класс. 16-е изд. — М., 2011. — 287 с.
5. Мордкович А. Г. Алгебра. 9 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович, П. В. Семенов. — 12-е изд., стер. — М.: 2010. — 224 с.: ил.
6. Алгебра. 9 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Л. А. Александрова, Т. Н. Мишустина и др.; Под ред. А. Г. Мордковича. — 12-е изд., испр. — М.: 2010.-223 с.: ил.
Рекомендованные ссылки на интернет-ресурсы
1. Раздел College.ru по математике (Источник).
2. Интернет-проект «Задачи» (Источник).
3. Образовательный портал «РЕШУ ЕГЭ» (Источник).
Рекомендованное домашнее задание
1. Мордкович А.Г. и др. Алгебра 9 кл.: Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович, Т. Н. Мишустина и др. — 4-е изд. — М. : Мнемозина, 2002.-143 с.: ил. № 105, 107, 114, 115.
interneturok.ru
Решите графически уравнение – x^2 = 2x
Задание.
Решить графически уравнение:
— x^2 = 2x
Решение.
Графическое решение уравнений сводится к тому, что нужно построить функции, которые стоят по обе стороны от знака равенства в уравнении, и найти их точки пересечения. Абсциссы этих точек и будут являться корнями заданного уравнения.
Итак, имеем уравнение:
Данное уравнение состоит из двух функций, равных между собой:
Построим первую функцию. Для этого проведем небольшой ее анализ.
Функция квадратичная, следовательно, графиком ее будет парабола. Перед квадратом х стоит знак минус, значит, функция направлена ветвями вниз. Функция четная, так как она квадратичная. Никаких коэффициентов и свободных членов у функции нет, значит, вершина ее будет в начале координат.
Найдем несколько точек, через которые проходит функция. Для этого вместо переменной х подставим значения 1, —1, 2 и —2.
, — точка (—1; —1)
, — точка (1; —1)
, — точка (—2; —4)
, — точка (2; —4)
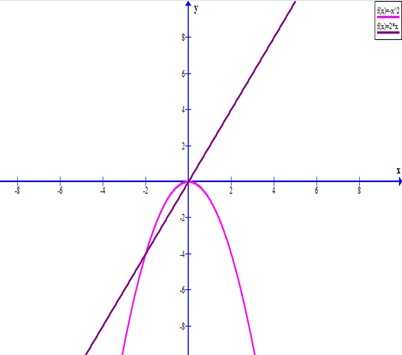
Нанесем все точки на плоскость и проведем через них плавную кривую.
Построим вторую функцию. Функция является линейной, следовательно, для ее построения достаточно двух точек. Найдем эти точки как точки пересечения функции с осями координат.
С осью Ох: у = 0. Подставим значение у в уравнение:
С осью Оу: х = 0.
Получили только одну точку (0; 0). Чтобы найти вторую, подставим вместо переменно х произвольное значение, например, 1.
Вторая точка — (1; 2)
Нанесем эти две точки на ту же координатную плоскость и проведем через них прямую.
Теперь нужно из точек пересечения графиков функций опустить перпендикуляры на ось Ох и получим точки 0 и —2.
Эти значения и являются результатом графического решения исходного уравнения.
Ответ. 0 и —2.
ru.solverbook.com
Графический способ решения уравнений: алгоритм и примеры графиков
Одним из способов решения уравнений является графический способ. Он основан на построении графиков функции и определения точек их пересечения. Рассмотрим графический способ решения квадратного уравнения a*x^2+b*x+c=0.
Первый способ решения
Преобразуем уравнение a*x^2+b*x+c=0 к виду a*x^2 =-b*x-c. Строим графики двух функций y= a*x^2 (парабола) и y=-b*x-c (прямая). Ищем точки пересечения. Абсциссы точек пересечения и будут являться решением уравнения.
Покажем на примере: решить уравнение x^2-2*x-3=0.
Преобразуем его в x^2 =2*x+3. Строим в одной системе координат графики функции y= x^2 и y=2*x+3.
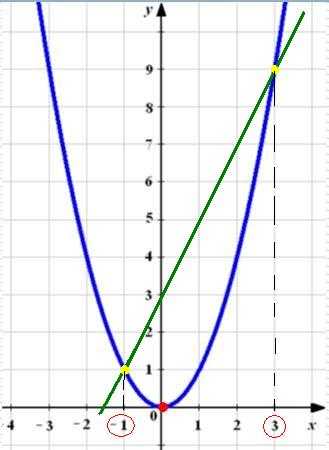
Графики пересекаются в двух точках. Их абсциссы будут являться корнями нашего уравнения.
Решение по формуле
Для убедительности проверим это решение аналитическим путем. Решим квадратное уравнение по формуле:
D = 4-4*1*(-3) = 16.
X1= (2+4)/2*1 = 3.
X2 = (2-4)/2*1 = -1.
Значит, решения совпадают.
Графический способ решения уравнений имеет и свой недостаток, с помощью него не всегда можно получить точное решение уравнения. Попробуем решить уравнение x^2=3+x.
Построим в одной системе координат параболу y=x^2 и прямую y=3+x.
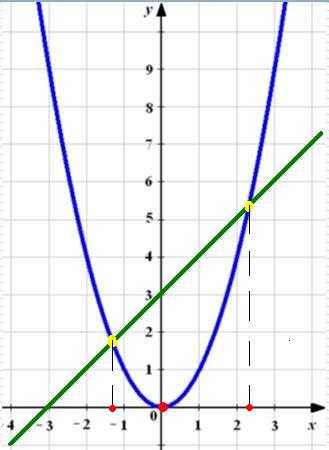
Опять получили похожий рисунок. Прямая и парабола пересекаются в двух точках. Но точные значения абсцисс этих точек мы сказать не можем, только лишь приближенные: x≈-1,3 x≈2,3.
Если нас устраивают ответы такой точности, то можно воспользоваться этим методом, но такое бывает редко. Обычно нужны точные решения. Поэтому графический способ используют редко, и в основном для проверки уже имеющихся решений.
Нужна помощь в учебе?
Предыдущая тема: Решение задач с помощью рациональных уравнений: схема и примеры
Следующая тема:   Функция: область определения и область значений функций + ПРИМЕРЫ
Все неприличные комментарии будут удаляться.
www.nado5.ru