Решение уравнения степенного – Показательные уравнения — что это такое и как решать

Задание 8.

Решите уравнение   В ответе укажите наименьший из корней, если их несколько.

Решение: + показать

Вы можете пройти тест №3 по теме «Задачи №5».

egemaximum.ru

49. Показательные уравнения, показательно-степенные уравнения

Показательным уравнением называется уравнение, которое содержит неизвестную величину в показателе степени при постоянном основании A (A > 0).

Типы показательных уравнений и способы их решения

Всюду далее F(X), G(X) – некоторые выражения с неизвестной величиной X.

I тип: уравнение вида

где (6.2)

Имеет решение, если B > 0. Его решают логарифмированием по основанию A:

Тогда

(6.3)

Решение уравнения (6.3) производят соответственно типу этого уравнения.

II тип: Уравнение вида

где (6.4)

По свойству равенства степеней равносильно уравнению

Последнее уравнение решают в зависимости от его типа.

III тип: уравнение вида

(6.5)

Где F – некоторое выражение относительно

Производят замену переменной и решают уравнение F(Y) = 0.

Если – корни уравнения, то после возвращения к старой переменной решение уравнения (6.5) сводится к решению равносильной ему совокупности уравнений

IV тип: уравнения, решаемые графическим методом.

Для таких уравнений строят соответствующие графики для левой и правой частей уравнения. Определяют, для каких значений X графики имеют общую ординату. Используют также иные функциональные свойства, в частности, монотонность функции (возрастание, убывание).

Показательно-степенным уравнением называется уравнение, в котором неизвестная величина содержится и в основании степени, и в показателе. Такие уравнения принято решать при условии, что основания степени положительны (ОДЗ уравнения).

Типы показательно-степенных уравнений

И способы их решения

Всюду далее F(X), G(X), H(X) – Некоторые выражения с неизвестной X, F(X) > 0.

I тип: уравнение вида

(6.6)

Решение уравнения (6.6) на ОДЗ сводится к решению совокупности

II тип: уравнение вида

(6.7)

Решение уравнения (6.7) на ОДЗ сводится к решению совокупности

Пример 1. Решить уравнение

Решение. 1-й способ. Имеем уравнение I типа (формула (6.2)). Решаем логарифмированием по основанию 3. Получаем:

т. е.

Приходим к линейному уравнению

Откуда

2-й способ. Преобразуем правую часть при помощи основного логарифмического тождества:

Получили уравнение II типа (формула (6.4)), которое решаем по свойству равенства степеней:

Пришли к ответу:

Пример 2. Решить уравнение

Решение. Выполним необходимые преобразования, сведем показательные выражения к одному и тому же основанию 3:

По свойству степеней:

Получаем ответ: Х = 0.

Пример 3. Решить уравнение

Решение. Преобразуем уравнение

Имеем квадратное уравнение относительно 2Х. Решаем при помощи замены Получаем:

Корнями последнего уравнения являются значения

Возвращаясь к неизвестной X, имеем совокупность:

Первое уравнение совокупности решений не имеет. Решаем второе уравнение:

т. е.

Получили ответ: Х = 3.

Пример 4. Решить уравнение

Решение. Выполним необходимые преобразования:

Имеем однородное уравнение. Разделим обе части уравнения на 92Х (92Х ¹ 0). Получим:

Т. е. получили квадратное уравнение относительно Вводим замену Тогда

Откуда

Возвращаемся к старой переменной:

Получили ответ:

Пример 5. Решить уравнение

Решение. 1-й способ. Подбором убеждаемся, что Х = 2– корень уравнения. Функции (т. е. ) и монотонно возрастают (рис. 6.12). Они имеют единственную общую точку.

Рис. 6.12

2-й способ. Разделим обе части уравнения на 2Х. Получим:

или

Заменим Получим

При Х = 2 получим основное тригонометрическое тождество, т. е. Х = 2 является корнем исходного уравнения.

Получили ответ: Х = 2.

Пример 6. Решить уравнение

Решение. ОДЗ: X = 2, 3, …, N, … .

Перепишем уравнение в виде

Разделим обе части уравнения на (так как ). Получим:

Вводим замену

Получаем квадратное уравнение откуда

Возвращаемся к старой переменной:

Но ни один из корней не подходит по ОДЗ. Следовательно, уравнение корней не имеет.

Пример 7. Решить уравнение

Решение. ОДЗ: X ¹ 2.

Решением является совокупность

Корень X = 2 не подходит по ОДЗ.

Получили ответ: X = 1, X = 3.

matica.org.ua

Методы решения уравнений высших степеней

Методы решения уравнений высших степеней.

I) Решение уравнений с помощью деления в столбик.

Очевидно 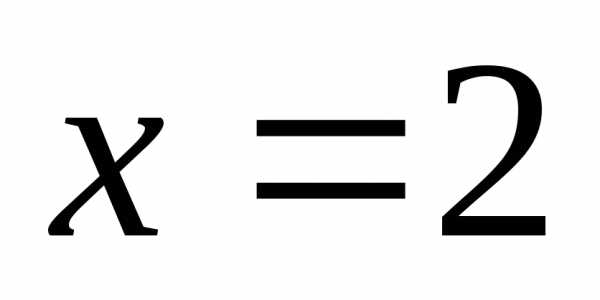— корень уравнения

Очевидно 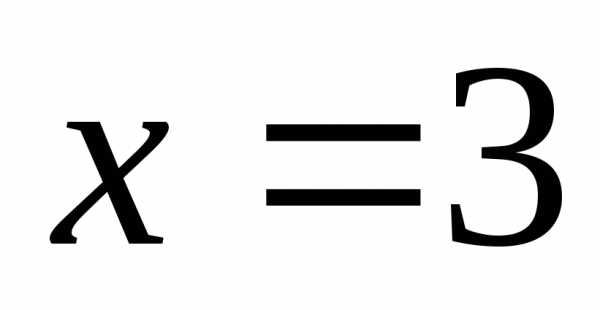— корень уравнения

Ответ: -5;2;3;4

II) Возвратные уравнения и к ним сводящиеся.

Уравнение называется возвратным, если в нем коэффициенты равноудаленные от концов совпадают, т.е. ,,

1) Возвратные уравнения четной степени.

т.к. 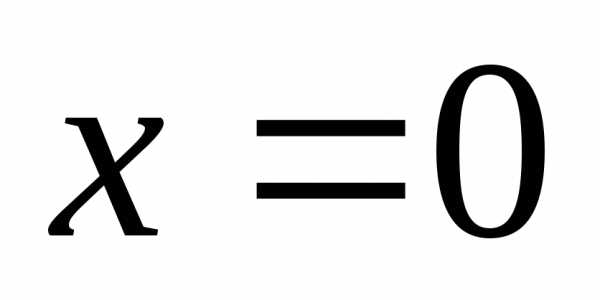— не является корнем уравнения, то разделим обе части уравнения на.

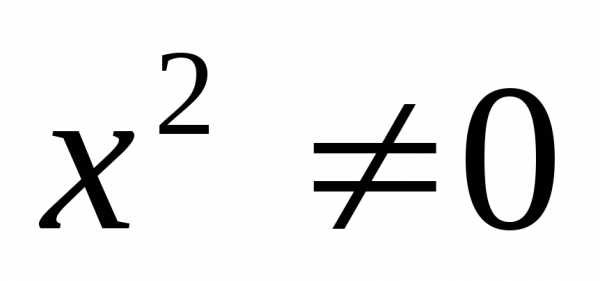Введем замену.

Пусть 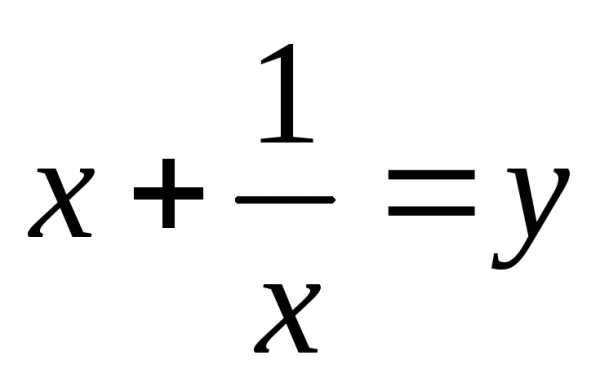,,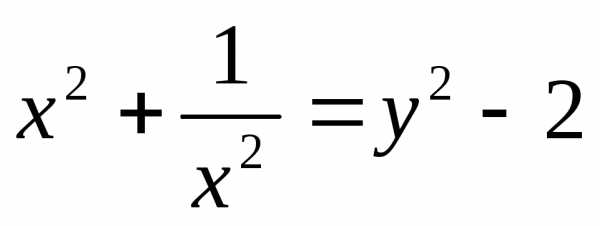 получим

;

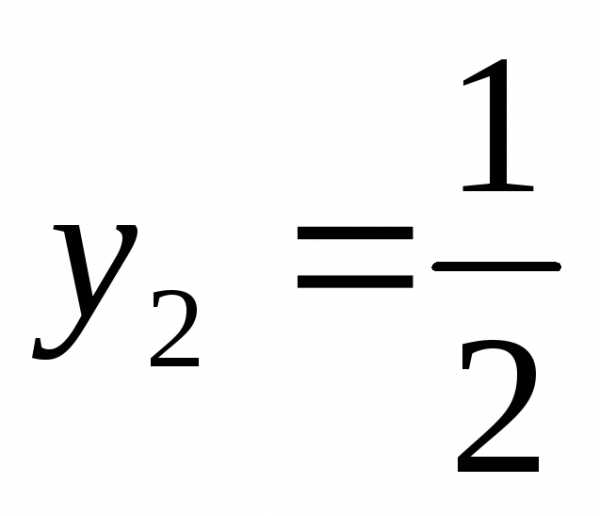
Вернемся к замене.

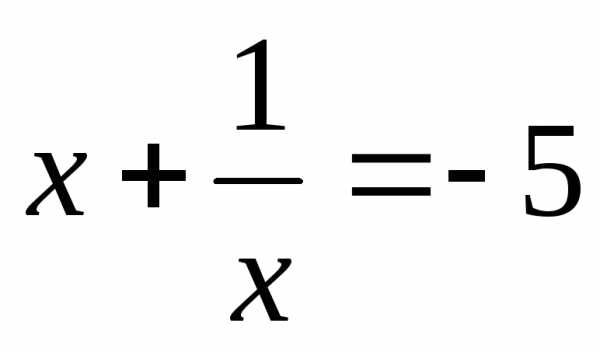или

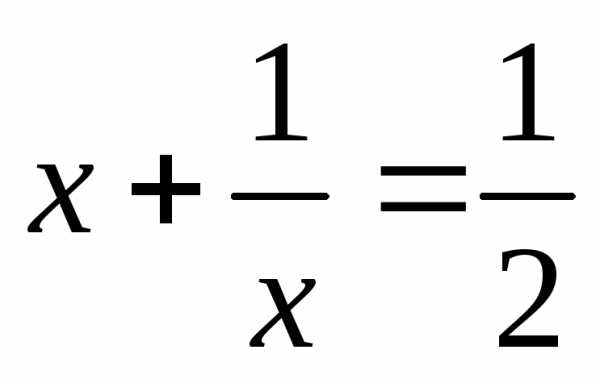
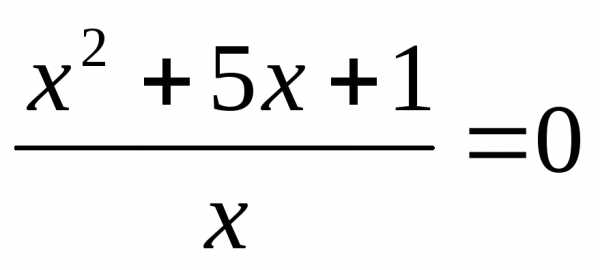
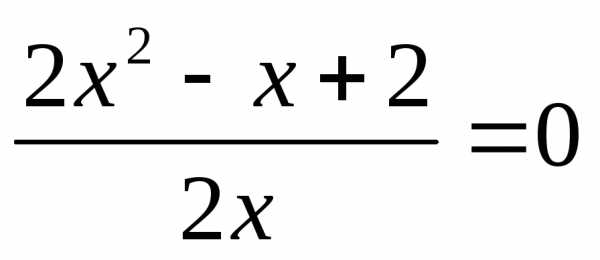
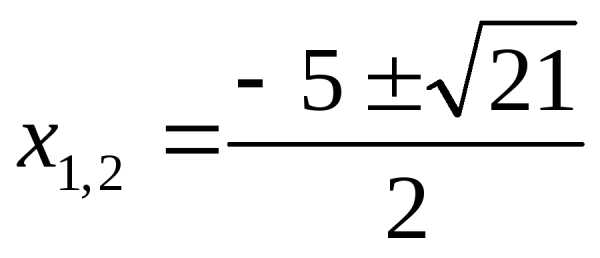корней нет

Ответ: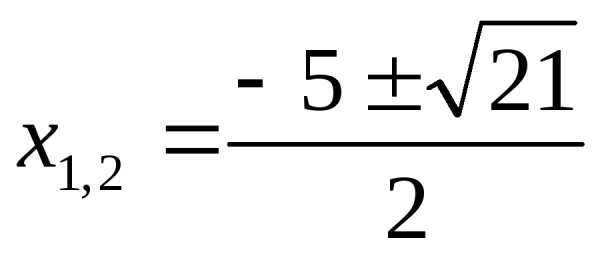

2) Возвратные уравнения нечетной степени.

Любое возвратное уравнение нечетной степени сводится к квадратному уравнению четной степени, т.к у любого возвратного ур–ия нечетной степени один из корней всегда равен –1

Очевидно 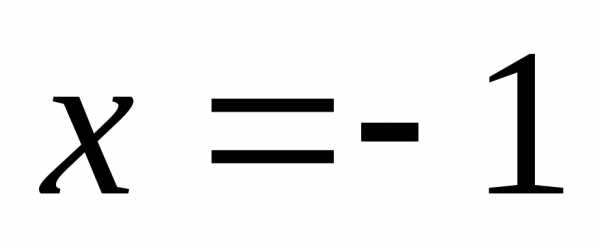— корень уравнения.

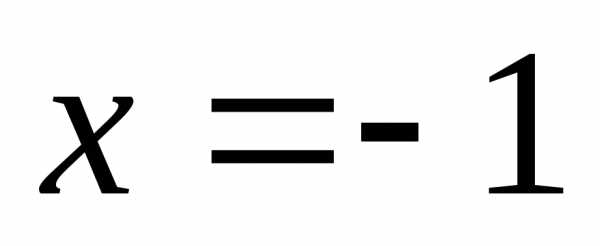или

т.к — не является корнем уравнения, то разделим обе части

уравнения на

Введем замену.

Пусть 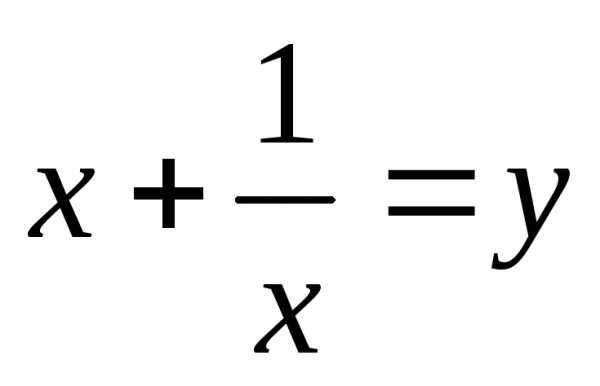,,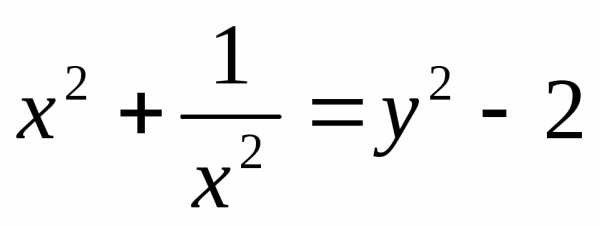, 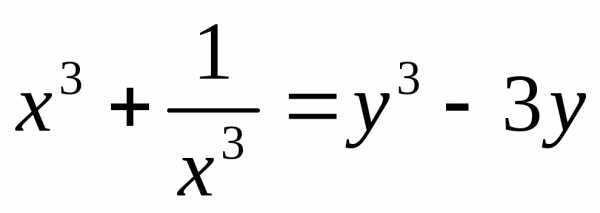получим

илиили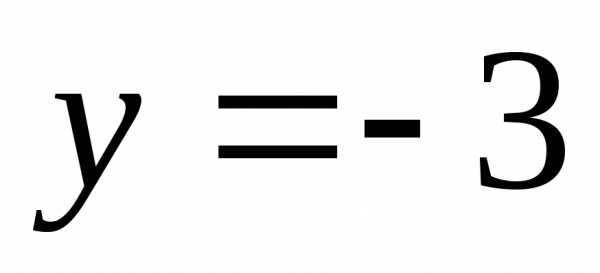

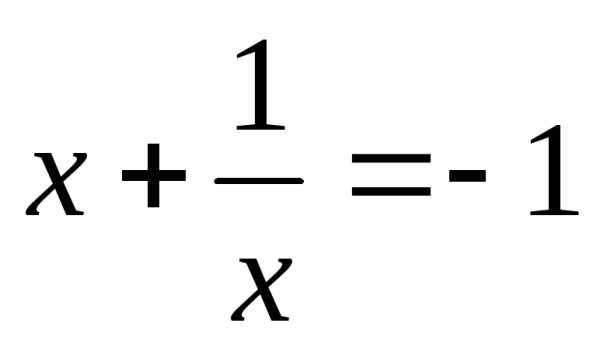
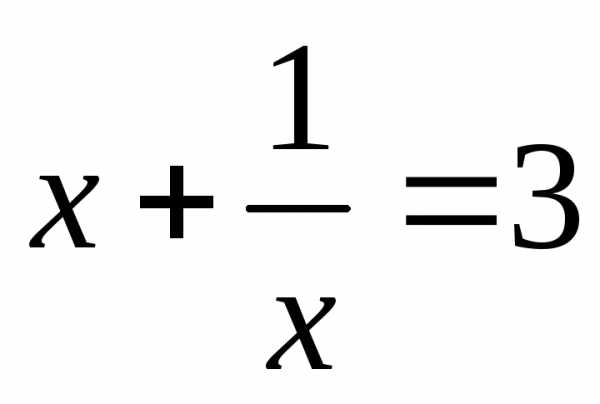
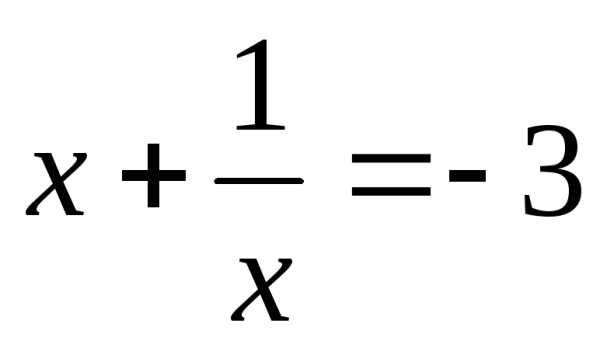
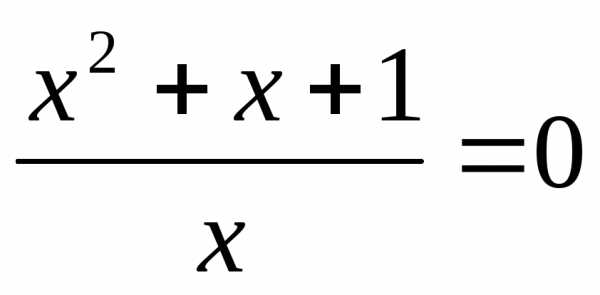
корней нет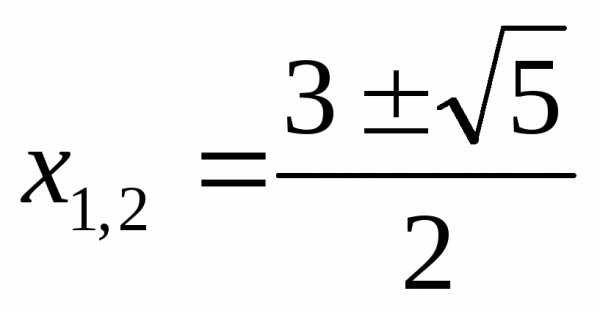

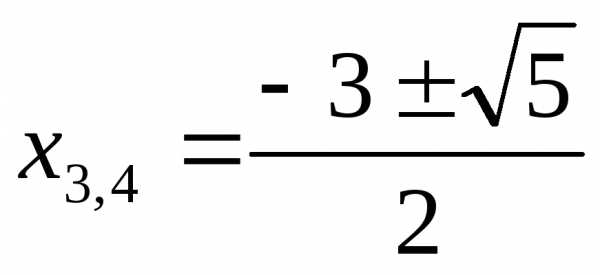
Ответ: ,,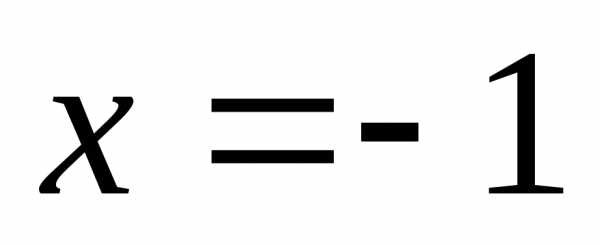

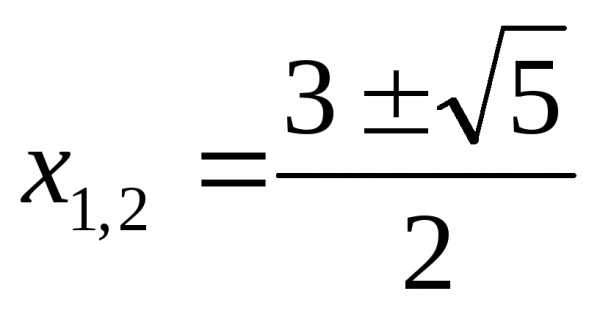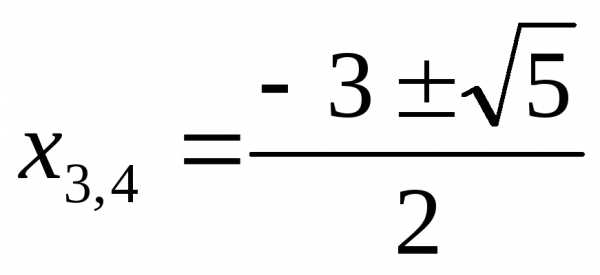
III) Уравнения вида, где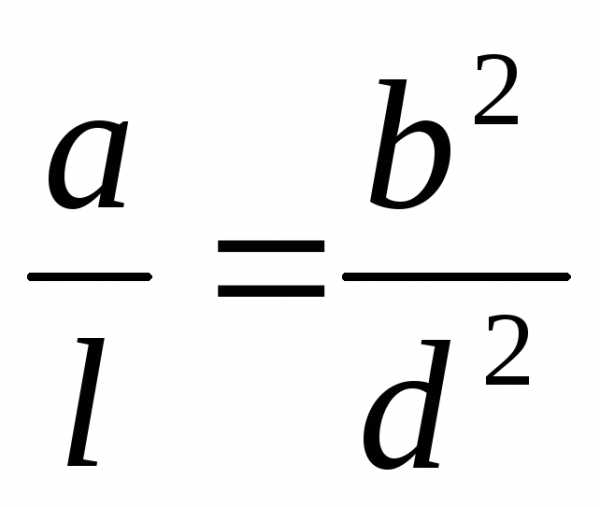решаются как возвратные.

IV) Замена переменных по явным признакам.

V) В следующих уравнениях используется “идея однородности”.

Пример №1

Введем замену.

Пусть 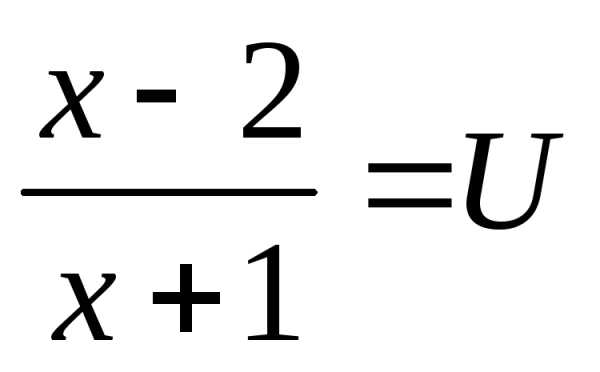,, тогда

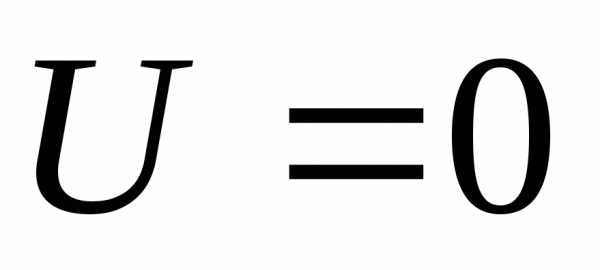1) если , тогда, тогда

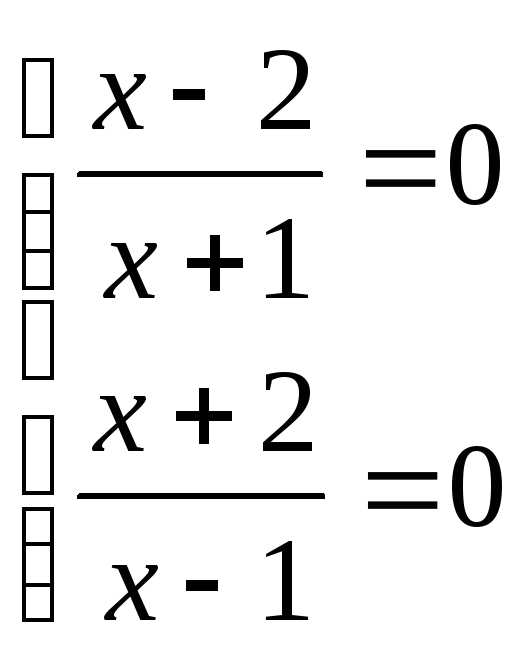
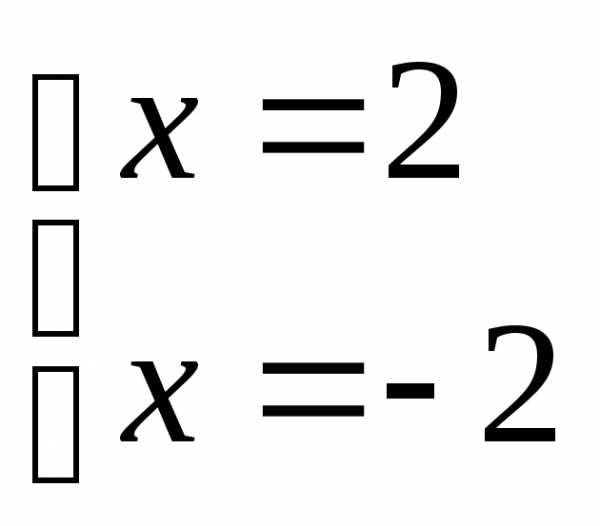решений нет

2) Разделим обе части уравнения на 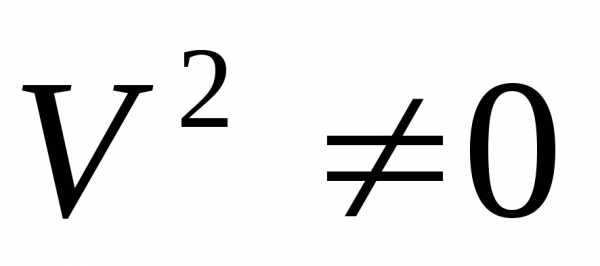, получим

Решим последнее уравнение, как квадратное относительно , получим

;

;

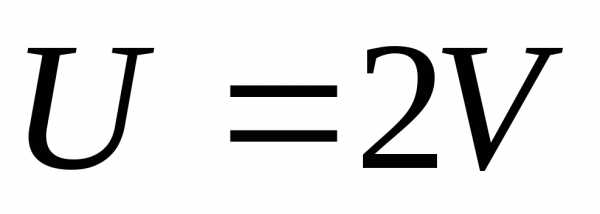Вернемся к замене.

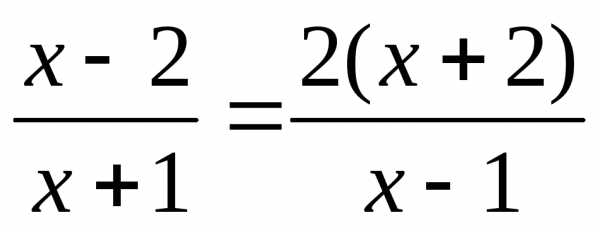или

корней нет

Ответ: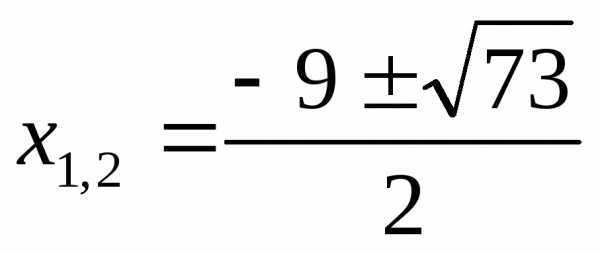

Пример №2.

Пусть ,, тогда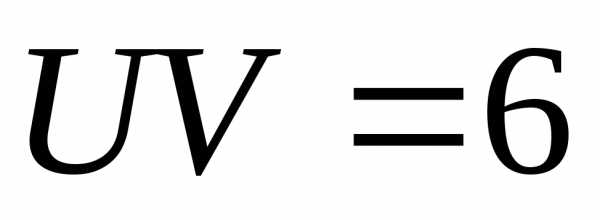

Найдем

Составим систему:

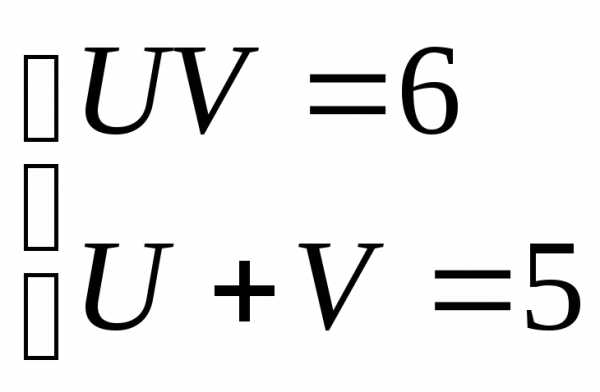
Решая систему подстановкой, получим

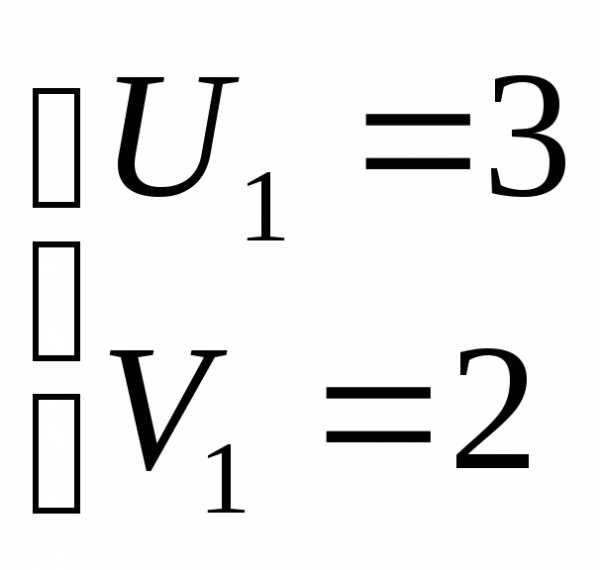или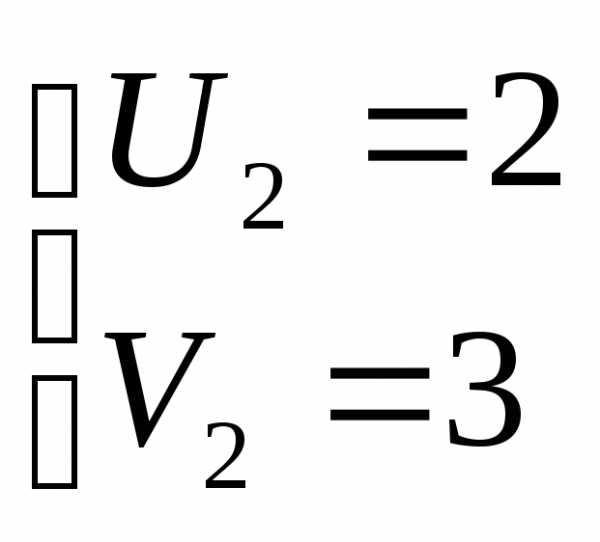

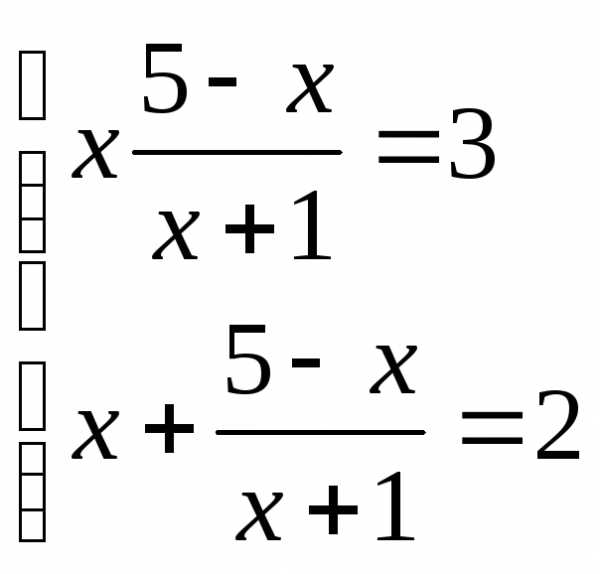
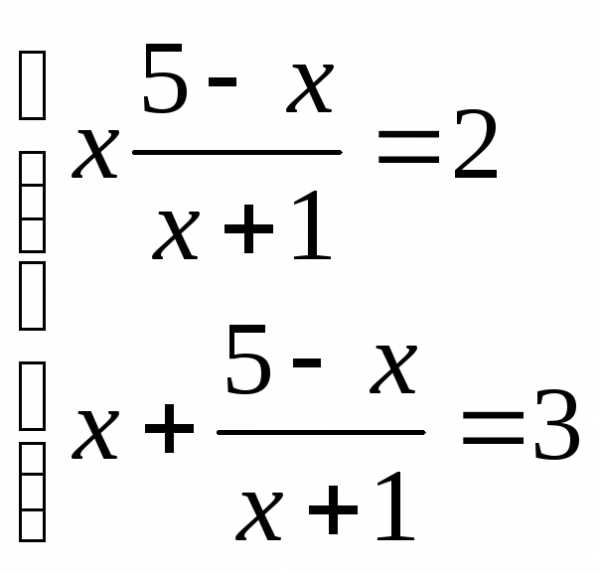
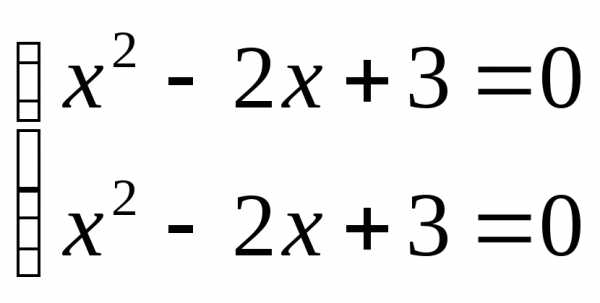
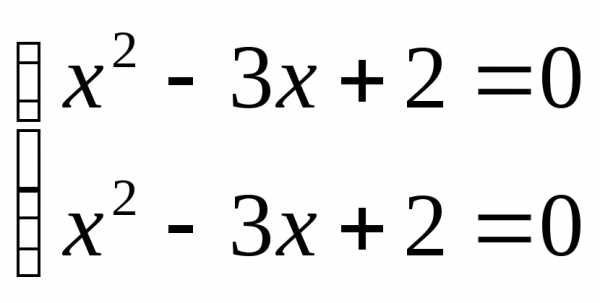
корней нет ;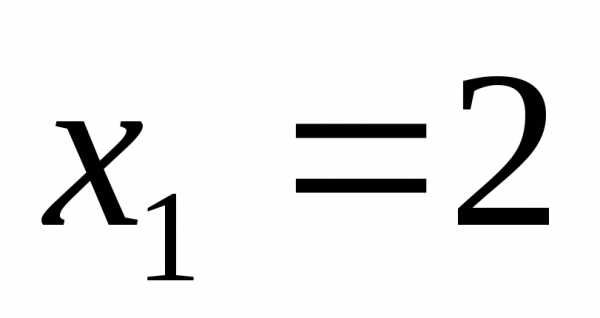

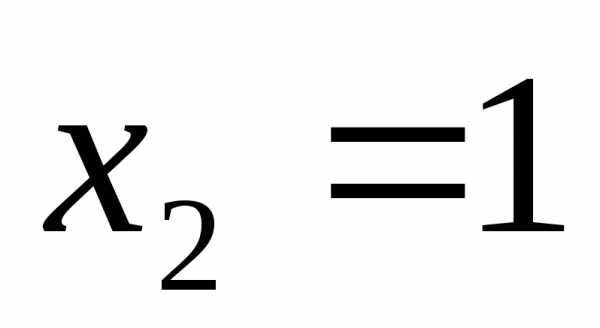
Ответ: ;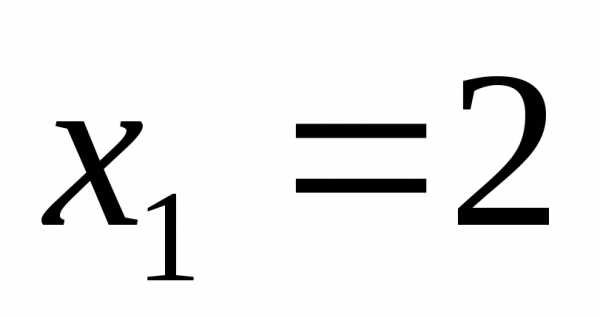

Пример №3.

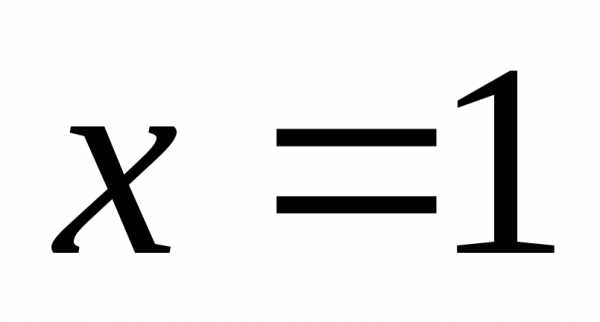— не является корнем уравнения

Разделим обе части уравнения на , получим

Введем замену.

Пусть 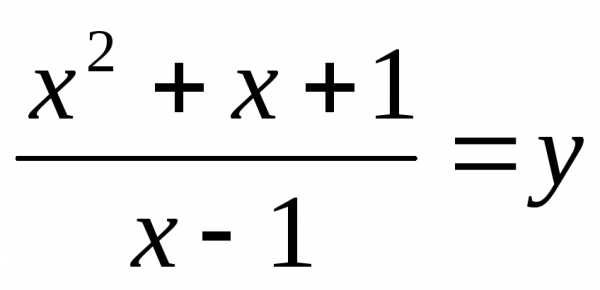, тогда

;

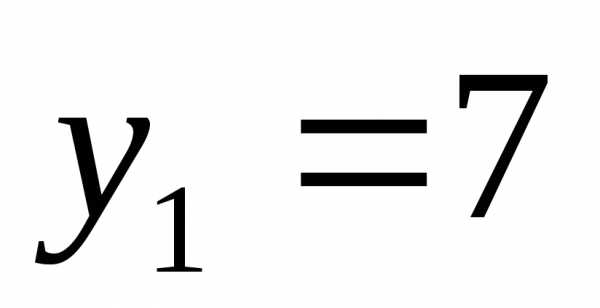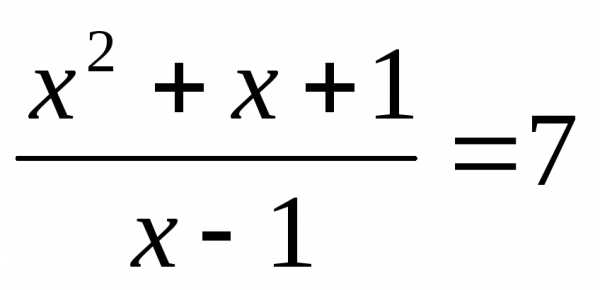или

;;

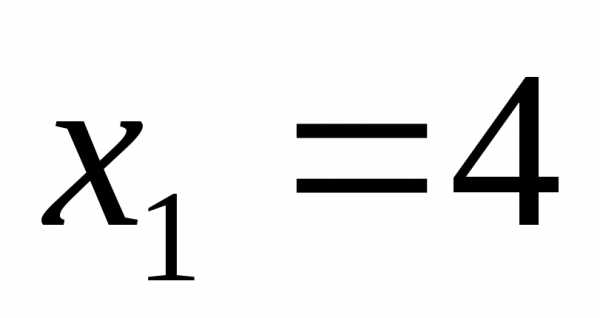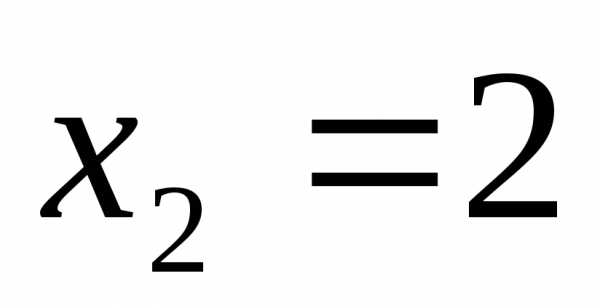
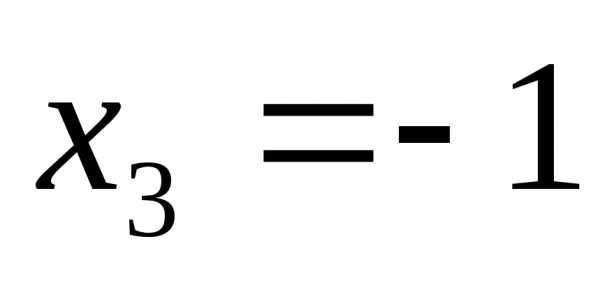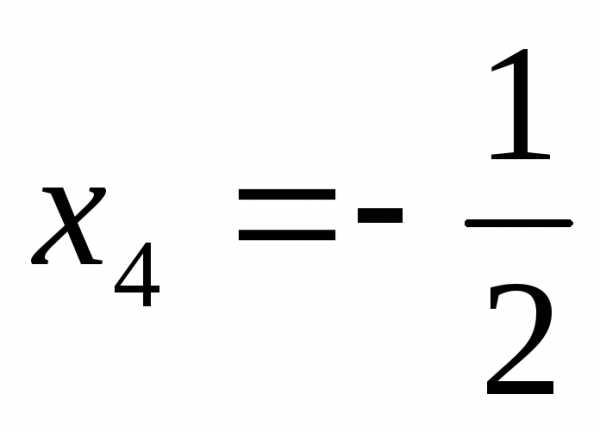
Ответ: ;;;

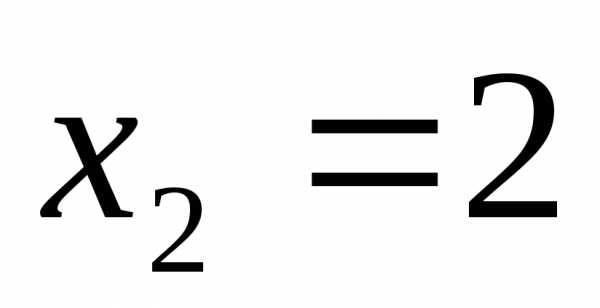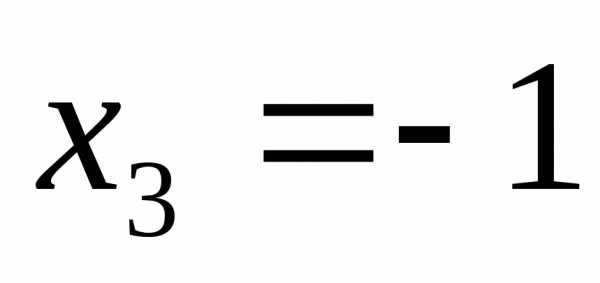VI) Уравнения вида, гдеэффективно решать перемножениеми, а затем делать замену.

VII) В уравнениях вида и в уравнениях к ним сводящимся, в знаменателях обоих дробей необходимо вынести х за скобки и сделать замену.

(1)

(2)

При переходе область определения уравнения сузилась на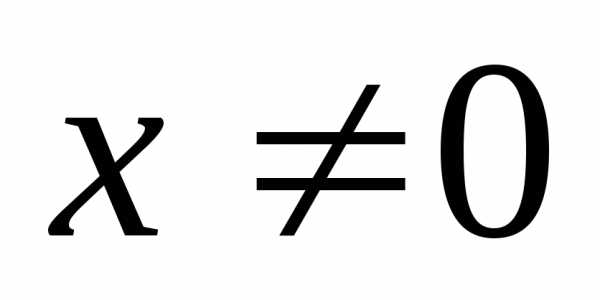. Проверим, является ли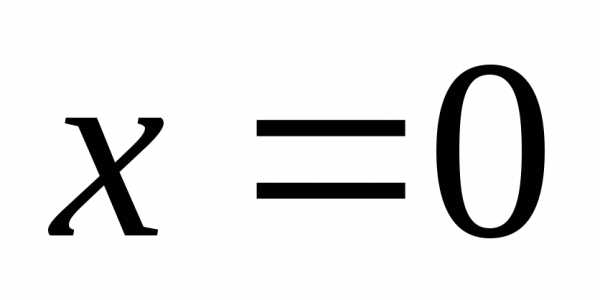корнем уравнения. Не является.

Введем замену.

Пусть 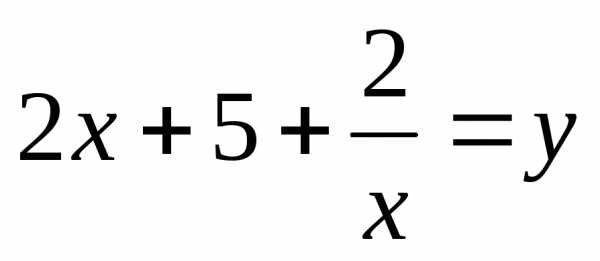,,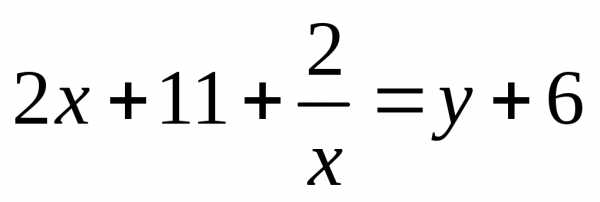 тогда

;

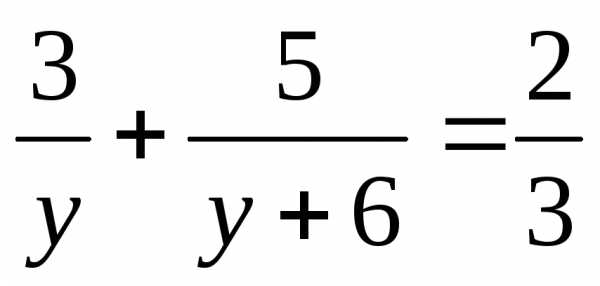
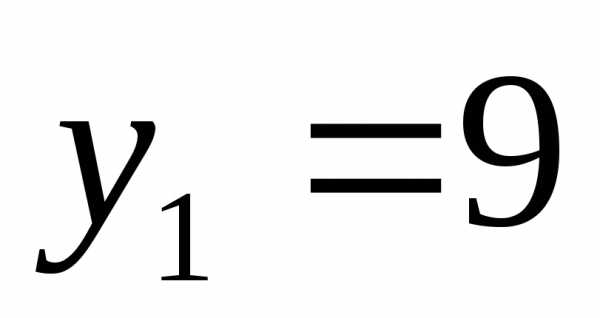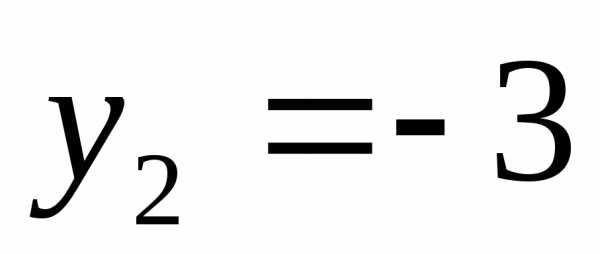
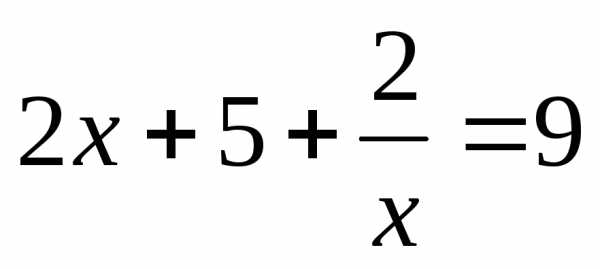или

Ответ: ;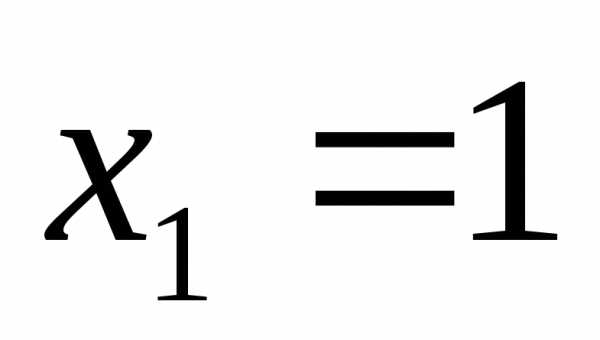

VIII) В уравнениях вида обе части уравнения делятся на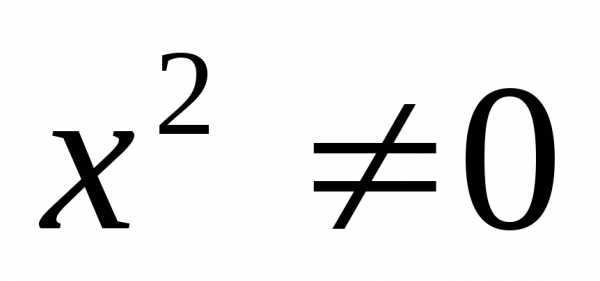

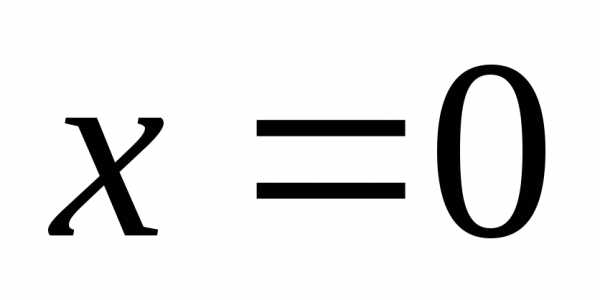— не является корнем уравнения. Разделим на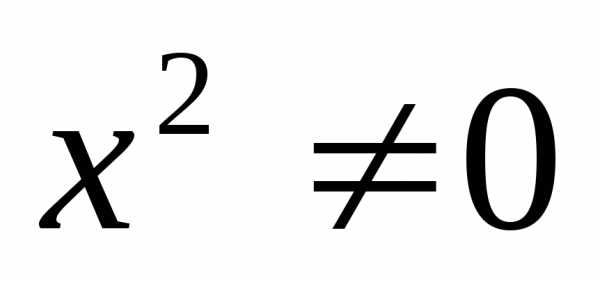, получим

Введем замену.

Пусть 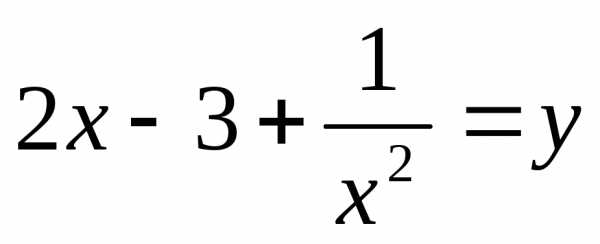;, тогда

;

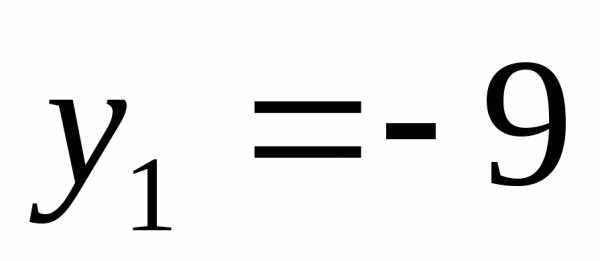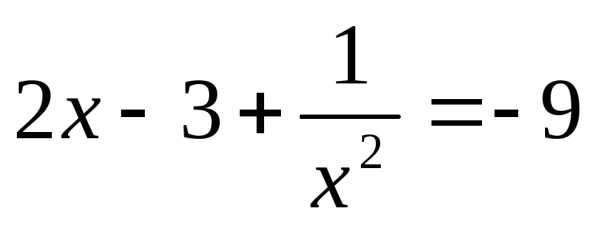или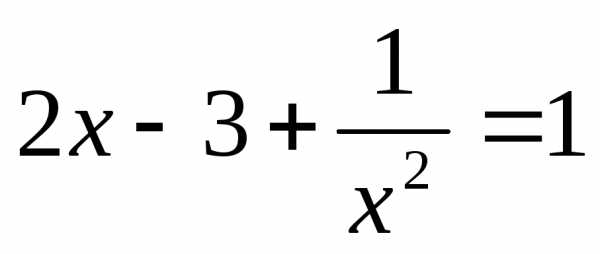

Ответ: ;

IX) Выделение полного квадрата.

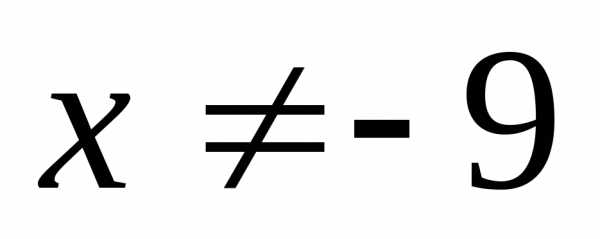
Введем замену.

Пусть 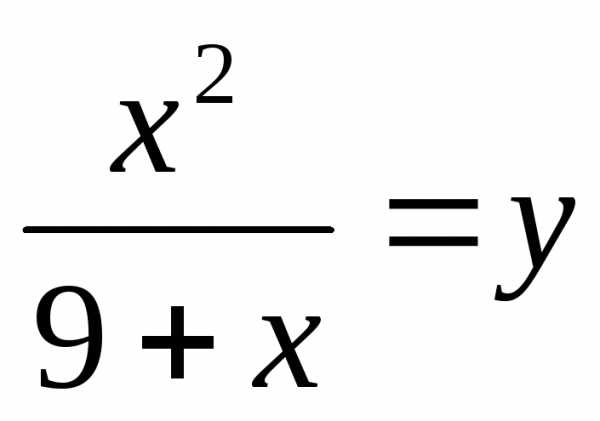, тогда

;

Вернемся к замене.

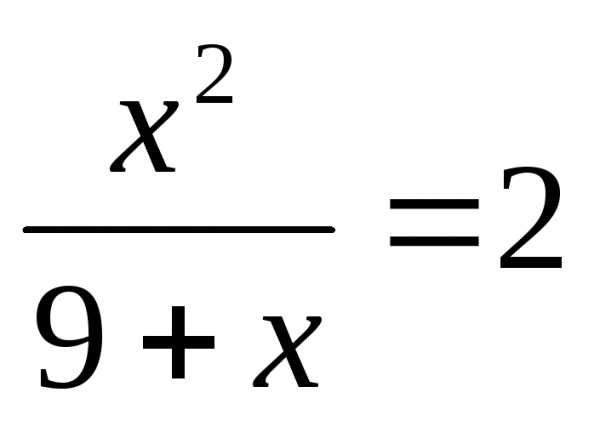или

корней нет

Ответ:

X) Решение уравнений с помощью формулы

или

корней нет

XI) Уравнения вида и к ним сводящиеся решаются при помощи замены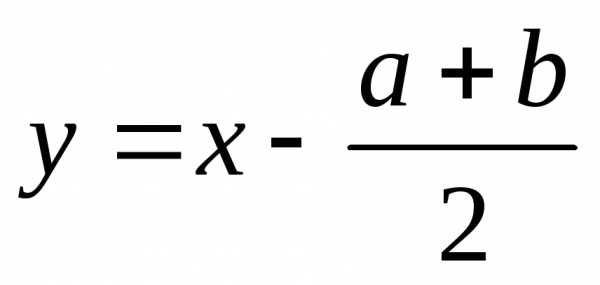

Введем замену.

Пусть 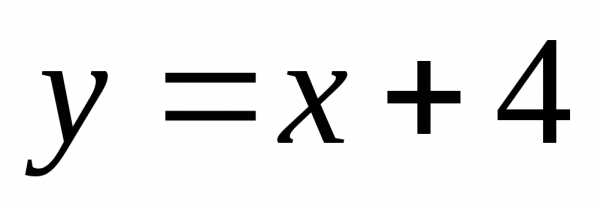, тогда

иликорней нет

;

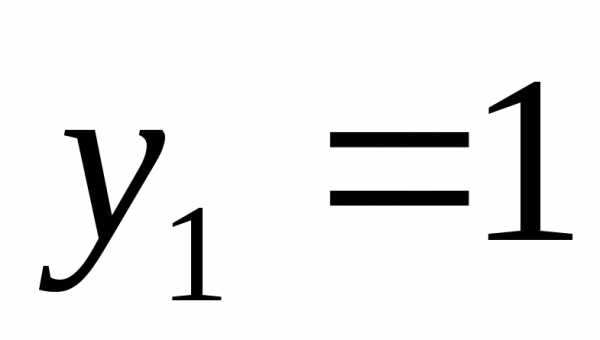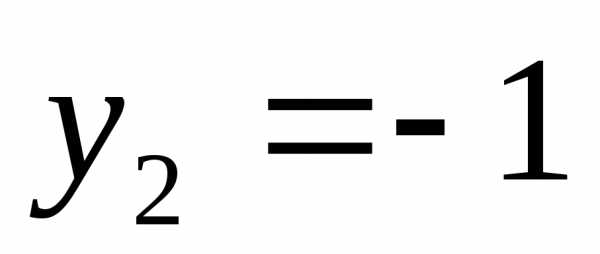
Вернемся к замене.

или

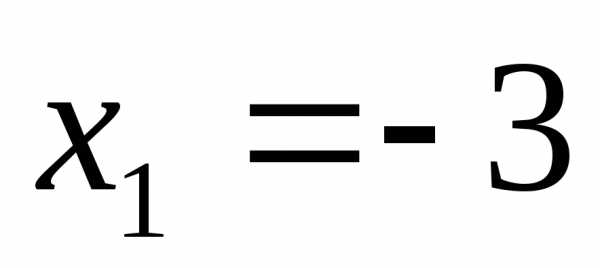
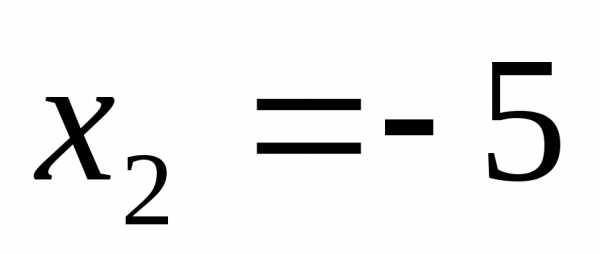
Ответ: ;

XII) Решение уравнений относительно коэффициентов.

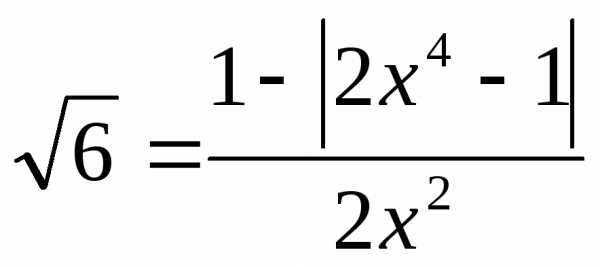или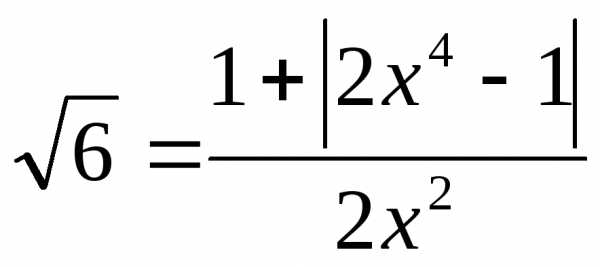

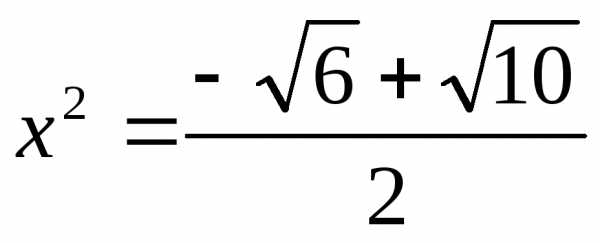
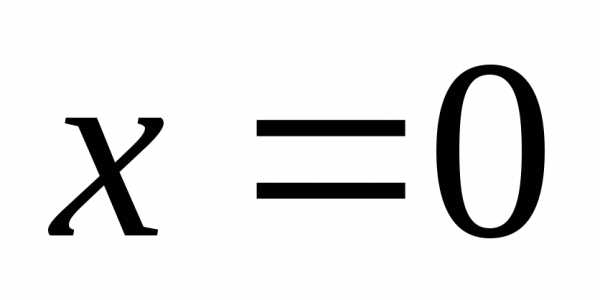;— посторонний корень

корней нет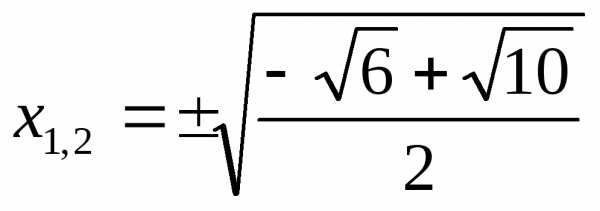

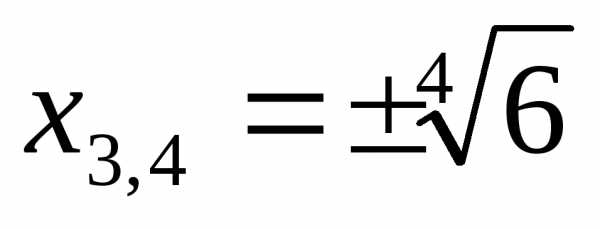
Ответ: ;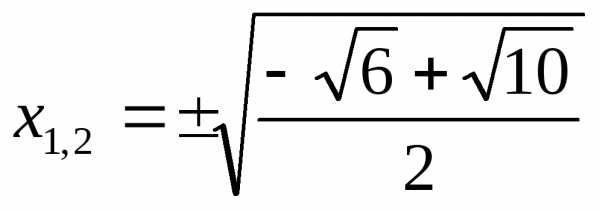

XIII) Метод разложения на простейшие дроби.

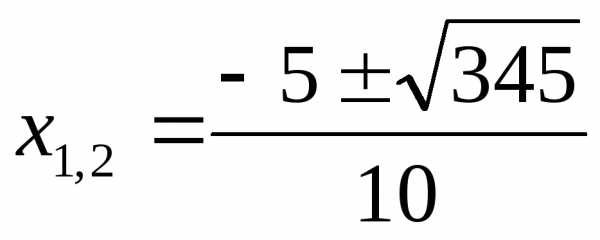
Ответ: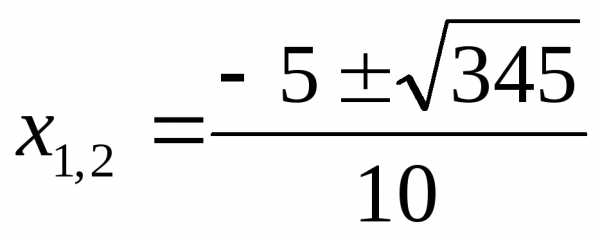

studfiles.net

Показательно-степенные уравнения и неравенства

белгородский государственный университет

КАФЕДРА алгебры, теории чисел и геометрии

Тема работы: Показательно-степенные уравнения и неравенства.

Дипломная работа студента физико-математического факультета

Научный руководитель:

______________________________

Рецензент : _______________________________

________________________

Белгород. 2006 г.

Содержание.

Введение.

«…радость видеть и понимать…»

А.Эйнштейн.

В этой работе я попыталась передать свой опыт работы учителем математики, передать хоть в какой-то степени свое отношение к ее преподаванию — человеческому делу, в котором удивительным образом переплетаются и математическая наука, и педагогика, и дидактика, и психология, и даже философия.

Мне довелось работать с малышами и выпускниками, с детьми, стоящими на полюсах интеллектуального развития: теми, кто со­стоял на учете у психиатра и кто действительно интересовался математикой

Мне довелось решать множество методических задач. Я попы­таюсь рассказать о тех из них, которые мне удалось решить. Но еще больше — не удалось, да и в тех, что вроде бы решены, появ­ляются новые вопросы.

Но еще важнее самого опыта — учительские размышления и сомнения: а почему он именно такой, этот опыт?

И лето нынче на дворе иное, и разворот образования стал поинтереснее. «Под юпи­терами» нынче не поиски мифической оптимальной системы обучения «всех и всему», а сам ребенок. Но тогда — с необходи­мостью — и учитель.

В школьном курсе алгебры и начал анализа, 10 – 11 класс, при сдаче ЕГЭ за курс средней школы и на вступительных экзаменах в ВУЗы встречаются уравнения и неравенства, содержащее неизвестное в основании и показатели степени – это показательно-степенные уравнения и неравенства.

В школе им мало уделяется внимания, в учебниках практически нет заданий на эту тему. Однако, овладение методикой их решения, мне кажется, очень полезным: оно повышает умственные и творческие способности учащихся, перед нами открываются совершенно новые горизонты. При решении задач ученики приобретают первые навыки исследовательской работы, обогащается их математическая культура, развиваются способности к логическому мышлению. У школьников формируются такие качества личности как целеустремленность, целеполагание, самостоятельность, которые будут полезны им в дальнейшей жизни. А также происходит повторение, расширение и глубокое усвоение учебного материала.

Работать над данной темой дипломного исследования я начала еще с написания курсовой. В ходе, которой я глубже изучила и проанализировала математическую литературу по этой теме, выявила наиболее подходящий метод решения показательно-степенных уравнений и неравенств.

Он заключается в том, что помимо общепринятого подхода при решении показательно-степенных уравнений (основание берется больше 0) и при решении тех же неравенств (основание берется больше 1 или больше 0, но меньше 1), рассматриваются еще и случаи, когда основания отрицательны, равны 0 и 1.

Анализ письменных экзаменационных работ учащихся показывает, что неосвещенность вопроса об отрицательном значении аргумента показательно-степенной функции в школьных учебниках, вызывает у них ряд трудностей и ведет к появлению ошибок. А также у них возникают проблемы на этапе систематизации полученных результатов, где могут в силу перехода к уравнению – следствию или неравенству – следствию, появиться посторонние корни. С целью устранения ошибок мы используем проверку по исходному уравнению или неравенству и алгоритм решения показательно-степенных уравнений, либо план решения показательно-степенных неравенств.

Чтобы учащиеся смогли успешно сдать выпускные и вступительные экзамены, я считаю, необходимо уделять больше внимания решению показательно-степенных уравнений и неравенств на учебных занятиях, либо дополнительно на факультативах и кружках.

Таким образом тема , моей дипломной работы определена следующим образом: «Показательно-степенные уравнения и неравенства».

Целями настоящей работы являются:

1. Проанализировать литературу по данной теме.

2. Дать полный анализ решения показательно-степенных уравнений и неравенств.

3. Привести достаточное число примеров по данной теме разнообразных типов.

4. Проверить на урочных, факультативных и кружковых занятиях как будет восприниматься предлагаемые приемы решения показательно-степенных уравнений и неравенств. Дать соответствующие рекомендации к изучению этой темы.

Предметом нашего исследования является разработка методики решения показательно-степенных уравнений и неравенств.

Цель и предмет исследования потребовали решения следующих задач:

1. Изучить литературу по теме: «Показательно-степенные уравнения и неравенства».

2. Овладеть методиками решения показательно-степенных уравнений и неравенств.

3. Подобрать обучающий материал и разработать систему упражнений разных уровней по теме: «Решение показательно-степенных уравнений и неравенств».

В ходе дипломного исследования было проанализировано более 20 работ, посвященных применению различных методов решения показательно-степенных уравнений и неравенств. Отсюда получаем.

План дипломной работы:

Введение.

Глава I. Анализ литературы по теме исследования.

Глава II. Функции и их свойства, используемые при решении показательно-степенных уравнений и неравенств.

II.1. Степенная функция и ее свойства.

II.2. Показательная функция и ее свойства.

Глава III. Решение показательно-степенных уравнений, алгоритм и примеры.

Глава IV. Решение показательно-степенных неравенств, план решения и примеры.

Глава V. Опыт проведения занятий со школьниками по данной теме.

1.Обучающий материал.

2.Задачи для самостоятельного решения.

Заключение. Выводы и предложения.

Список использованной литературы.

В I главе проанализирована литература по теме: «Решения показательно-степенных уравнений и неравенств».

В II главе теоретические сведения о степенной и показательной функциях и применение их свойств при решении показательно-степенных уравнений и неравенств, выявляются недостатки в понимании учащимися отрицательного аргумента показательно-степенной функции.

В III главе «Решение показательно-степенных уравнений, алгоритм и примеры» приведен полный анализ решения показательно-степенных уравнений, рассмотрен алгоритм решения показательно-степенных уравнений и примеры, и примеры в которых он применяется.

В IV главе «Решение показательно-степенных неравенств, план решения и примеры» приведен полный анализ решения показательно-степенных неравенств и рассмотрен план решения показательно-степенных неравенств и примеры, в которых он применяется.

В V главе рассматривается методика обучения учащихся решению показательно-степенных уравнений и неравенств, приведен обучающий материал, разработана система заданий с учетом разного уровня сложности, которая содержит в себе задания используемые на уроке, задания для самостоятельного решения.

Глава II . Функции и их свойства, используемые при решении показательно-степенных уравнений и неравенств.

Для решения показательно-степенных уравнений и неравенств необходимо знать свойства показательной и степенной функции и уметь ими пользоваться. В этой главе мы рассмотрим данный вопрос.

II .1. Степенная функция и ее свойства.

Прямая пропорциональность . Прямой пропорциональ­ностью называется функция, заданная формулой у = kxⁿ , где число k называется коэффициентом пропорциональ­ности.

Перечислим свойства функции у = kx .

1) Область определения функции — множество всех действительных чисел.

2) y = kx — нечетная функция ( f ( — х) = k ( — х)= — kx = — k (х)).

Гра­фик (прямая) изображен на рисунке II.1.

Рис. II.1.

При n =2 получаем функцию y = х² , ее свойства:

Функция у —х² . Перечислим свойства функции у = х² .

mirznanii.com

показательные уравнения | математика-повторение

Многие показательные уравнения заменой переменной сводятся к квадратному уравнению вида: ax²+bx+c=0.

Примеры.

Решить уравнение:

1) 4^x+2^x+1-3=0. Представим 4^x в виде степени с основанием 2.

(2²)^x+2^x∙2¹-3=0; при возведении степени в степень основание оставляют, а показатели перемножают: 2·х=х·2, поэтому:

(2^x)²+2∙2^x-3=0;

вводим новую переменную: пусть 2^x=y;

y²+2y-3=0.

Дискриминант для четного второго коэффициента: D₁=1²-1∙(-3)=1+3=4=2² – полный квадрат, поэтому применим теорему Виета: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

y₁+y₂=-2, y₁∙y₂=-3. Подбираем корни: y₁=-3, y₂=1.

Возвращаемся к переменной х:

1) 2^x=-3, нет решений, так как значения показательной функции: Е(у)=(0; +∞). (только положительные числа).

2) 2^x=1. Число 1 можно представлять в виде нулевой степени по любому основанию.

2^x=2⁰;

x=0.

Ответ: 0.

2) 0,25^2x-5∙0,5^2x+4=0.  Решаем аналогично. Представляем 0,25^2x— в виде степени с основанием 0,5.

(0,5²)^2x-5∙0,5^2x+4=0;

(0,5^2x)²-5∙0,5^2x+4=0.

0,5^2x=y; ввели новую переменную у и получили приведенное квадратное уравнение:

y²—5y+4=0;

Дискриминант D=b²-4ac=5²-4∙1∙4=25-16=9=3² — полный квадрат, применяем теорему Виета: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

y₁+y₂=5, y₁+y₂=4. Корни приведенного квадратного уравнения находим подбором: y₁=1, y₂=4 и возвращаемся к переменной х:

1) 0,5^2x=1; число 1 можно представлять в виде нулевой степени по любому основанию.

0,5^2x=0,5⁰;

2x=0;

x=0.

2) 0,5^2x=4; приведем степень  0,5^2x  к основанию 2, применив формулу:   (1/a)^x =а^-х 

(¹/₂)^2x=2²;

2^-2x=2²; приравниваем показатели:

— 2x=2 |:(-2)

x=-1.

Ответ: -1; 0.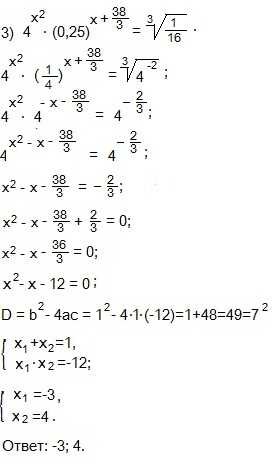

Представим левую и правую части в виде степеней с основанием 4, используя формулы: а^-х=1/a^x  и  a^x∙a^y=a^x+y .

Если равны две степени с одинаковыми основаниями, то основания можно опустить и приравнять показатели степеней. Переносим дробь из правой части равенства в левую и упрощаем левую часть.

Находим дискриминант приведенного квадратного уравнения. Дискриминант является квадратом целого числа, поэтому, подбираем корни, пользуясь теоремой Виета:  сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.

Уравнения, содержащие переменную в показателе степени, называются показательными уравнениями.

Простейшие показательные уравнения — это уравнения вида: a^x=a^y. Отсюда следует равенство: х=у. В самом деле, степени с одинаковыми основаниями могут быть равными только в том случае, если равны показатели этих степеней.

Примеры.

Решить уравнение:

1) 5^x=125.  Представим число 125 в виде степени числа 5:

5^x=5³; Степени равны, их основания равны, значит, и показатели степеней будут равны:

x=3.

2) 4^x=32. Представим левую и правую части в виде степеней с основанием 2:

(2²)^x=2⁵; используем формулу возведения степени в степень: (a^x)^y=a^xy  

2^2x=2⁵;

2x=5  |:2

x=2,5.

 3) 3^2x-1=81. Число 81 представим в виде степени числа 3:

3^2x-1=3⁴;  приравняем показатели степеней с одинаковыми основаниями:

2x-1=4;  решаем простейшее линейное уравнение:

2x=4+1;

2x=5  |:2;

x=2,5.

К правой части применяем формулу: (a/b)^-x=(b/a)^x. Получим равенство степеней с одинаковыми основаниями.

Приравниваем показатели степеней и находим х из полученного линейного уравнения.

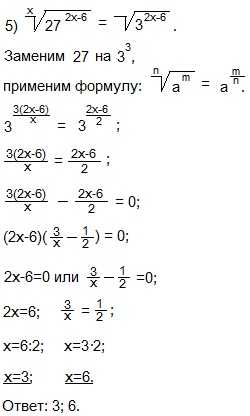
Приравняем показатели степеней с одинаковыми основаниями.

Переносим степень из правой части уравнения в левую.

Вынесли общий множитель (2х-6) за скобки. Произведение двух или нескольких множителей равно нулю, если один из множителей равен нулю, а другие при этом значении не теряют смысла. Содержимое каждой из скобок приравниваем к нулю и решаем простейшие уравнения.

6) 7∙5^x-5^x+1=2∙5³.

Показатели степеней складываются, если степени перемножаются ( a^x∙a^y=a^x+y ), поэтому:

7∙5^x-5^x∙5¹=2∙5³;

5^x(7-5)=2∙5³;  вынесли общий множитель за скобки.

5^x∙2=2∙5³     |:2

5^x=5³;  отсюда следует:

x=3.

7) 3^x+2+4∙3^x+1=21.  Применим формулу: a^x+y=a^x∙a^y  (При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают):

3^x∙3²+4∙3^x∙3¹=21; вынесем общий множитель за скобки:

3^x(9+12)=21;

3^x∙21=21  |:21

3^x=1; число 1 можно представлять в виде нулевой степени с любым основанием.

3^x=3⁰;

x=0.

5^1+2x+5^2x+3=650.  Решаем аналогично.

5¹∙5^2x+5^2x∙5³=650;

5^2x(5+125)=650;

5^2x∙130=650   |:130

5^2x=5; приравняем показатели равных степеней с основаниями 5.

2x=1  |:2

x=0,5.

www.mathematics-repetition.com

11. Методы решения показательных уравнений

12. Логарифмы

13. Логарифмическая функция

Р

ности логарифмической функции (а>0, а≠1).

.

x>0

при любом

у

1 0<а<1

0 1 а х 0 1 х

возрастающая функция убывающая функция

14. Методы решения логарифмических уравнений

15. Тригонометрические функции

studfiles.net