Графический (геометрический) метод решения задач ЛП
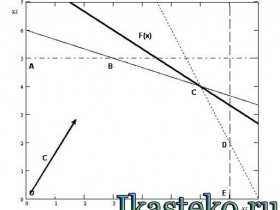
Пример 6.1. Решить следующую задачу ли-нейного программирования геометрическим методом:
.
Решение:
Задача линейного программирования задана в стандартной форме и имеет два проектных параметра, следовательно
, воз-можно ее решение геометрическим методом.
1 этап: построение прямых, ограничивающих область допустимых решений ( ОДР).
Рассмотрим систему ограничений задачи линейного програм-мирования (для удобства пронумеруем неравенства):
Рассмотрим первое ограничение, заменим знак неравенства знаком равенства и выразим переменную х2 через х1:
.
Для построения прямой по данному уравнению зададим две произвольные точки, к примеру:
2 этап: определение решения каждого из нера-венств системы ограничений.
Определим полуплоскости – решения каждого из неравенств.
Рассмотрим первое неравенство системы ограничений задачи. Возьмем какую-либо точку (контрольную точку), не принадлежащую соответствующей данному неравенству прямой, например, точку (0; 0). Подставим ее в рассматриваемое неравенство:
.
При подстановке координат контрольной точки неравенство остается справедливым. Следовательно, множество точек, принадлежащих данной прямой (т.к. неравенство не строгое), а также расположенных ниже ее, будут являться решениями рассматриваемого неравенства (пометим на графике (рис. 1) найденную полуплоскость двумя стрелками направленными вниз рядом с прямой I) .
Аналогично определяем решения других неравенств и соответственно помечаем их графике. В результате график примет следующий вид:
3 этап: определение ОДР задачи линейного про- граммирования.
Найденные полуплоскости (решения каждого из неравенств системы ограничений) при пересечении образуют многоугольник ABCDEO, который и является ОДР рассматриваемой задачи.
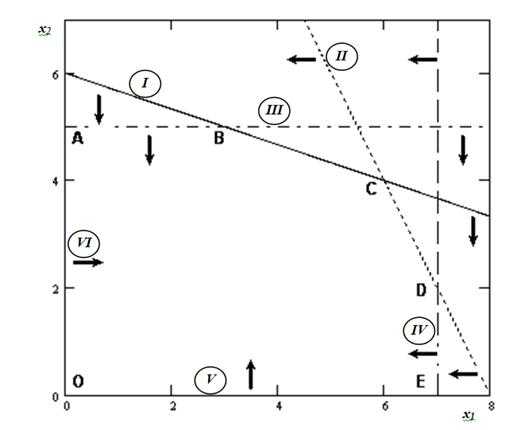
Рис. 1. Область допустимых решений задачи
4 этап: построение вектора-градиента.
Вектор-градиент показывает направление максимизации целевой функции . Определим его координаты: координаты начальной его точки (точки приложения) – (0; 0), координаты второй точки:
Построим данный вектор на графике (рис. 2).
5 этап: построение прямой целевой функ-ции
Рассмотрим целевую функцию данной задачи:
.
Зададим ей какое-либо значение, к примеру, . Выразим переменную х2 через х1:
.
Для построения прямой по данному уравнению зададим две произвольные точки, к примеру:
Построим прямую соответствующую целевой функции (рис. 2).
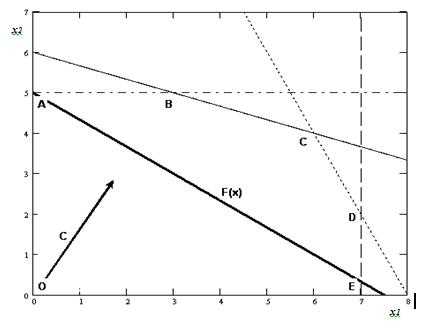
Рис. 2. Построение целевой функции F(X) и вектора-градиента С
6 этап: определение максимума целевой функ-ции.
Перемещая прямую F(X) параллельно са-мой себе по направлению вектора-градиента, определяем крайнюю точку (точки) ОДР. Согласно графику (рис. 3), такой точкой является точка С – точка пересечения прямых I и II.
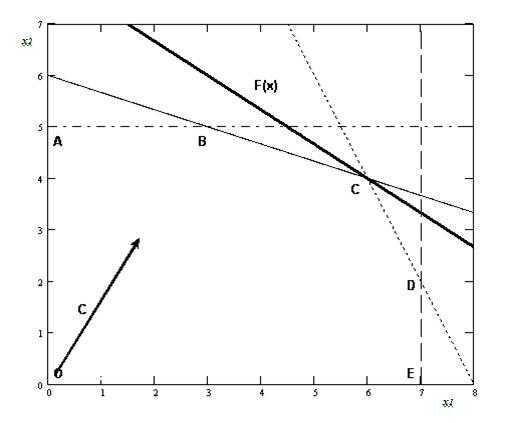
Рис. 3. Определение точки максимума целевой функции F(X)
Определим координаты точки С, с этой целью, решим сле-дующую систему линейных уравнений:
Подставим найденные координаты в целевую функцию и найдем ее оптимальное (максимальное) значение:
Ответ: при заданных ограничениях макси-мальное значение целевой функции F(Х)=24, которое достигается в точке С, координаты которой х1=6, х2=4.
Пример 6.2. Решить задачу линейного про- граммирования геометрическим методом:
Решение:
Этапы 1-3 аналогичны соответствующим этапам предыдущей задачи.
4 этап: построение вектора-градиента.
Построение вектора-градиента осуществляется аналогично, как и в предыдущей задаче. Построим данный вектор на графике (рис. 4). Отметим также на данном графике стрелкой направление, обратное вектору-градиенту, – направление минимизации целевой функции
5 этап: построение прямой целевой функ-ции.
Построение прямой целевой функции F(X) осуществляется аналогично, как и в предыдущей задаче (результат построения приведен на рис. 4).
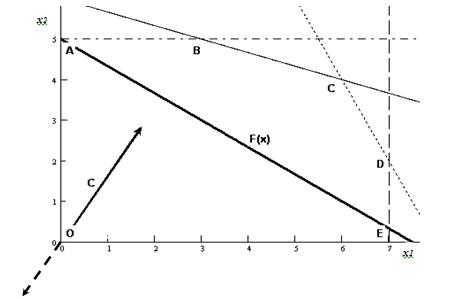
Рис. 4. Построение целевой функции F(x) и вектора-градиента С
6 этап: определение оптимума целевой функ-ции.
Перемещая прямую F(x) параллельно са-мой себе в направлении, обратном вектору-градиенту, опреде-ляем крайнюю точку (точки) ОДР. Согласно графику (рис. 5), та- кой точкой является точка О с координатами (0; 0).
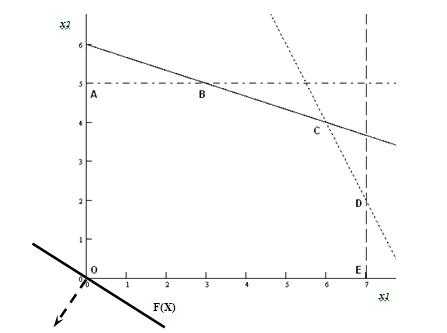
Рис. 5. Определение точки минимума целевой функции
Подставляя координаты точки минимума в целевую функ-цию, определяем ее оптимальное (минимальное) значение, которое равно 0.
Ответ: при заданных ограничениях минимальное значение целевой функции F(Х)=0, которое достигается в точке О (0; 0).
Пример 6.3. Решить следующую задачу ли-нейного программирования геометрическим методом:
Решение:
Рассматриваемая задача линейного программирования задана в канонической форме, выделим в качестве базисных переменные x 1 и x2.
Составим расширенную матрицу и выделим с помощью метода Жордана- Гаусса базисные переменныеx1 и x 2.
Умножим (поэлементно) первую строку на –3 и сложим со вто-рой:
Умножим вторую строку на :
.
Сложим вторую с первой строкой:
.
В результате система ограничений примет следующий вид:
Выразим базисные переменные через свободные:
Выразим целевую функцию также через свободные перемен-ные, для этого подставим полученные значения базисных переменных в целевую функцию:
.
Запишем полученную задачу линейного программирования:
Так как переменные x1 и x2 неотрицательные, то полученную систему ограничений можно записать в следующем виде:
Тогда исходную задачу можно записать в виде следующей эк- вивалентной ей стандартной задаче линейного программирования:
Данная задача имеет два проектных параметра, следовательно, возможно ее решение геометрическим мето-дом.
1 этап: построение прямых, ограничивающих область допустимых решений ( ОДР).
Рассмотрим систему ограничений задачи линейного програм-мирования (для удобства пронумеруем неравенства):
Построим прямые, соответствующие каждому неравенству (рис. 6). Прямые пронумеруем согласно принятой ранее схе-ме.
2 этап: определение решения каждого из нера-венств системы ограничений.
С помощью контрольных точек определим полуплоскости – решения каждого из неравенств, и пометим их на графике (рис. 6) с помощью стрелок.
3 этап: определение ОДР задачи линейного про- граммирования.
Найденные полуплоскости (т.е. решения каждого из неравенств системы ограничений) не имеют общего пересечения (так решения неравенства I противоречат в целом остальным неравенствам системы ограничений), следовательно, система ограничений не совместна и задача линейного программирования в силу этого не имеет решения.
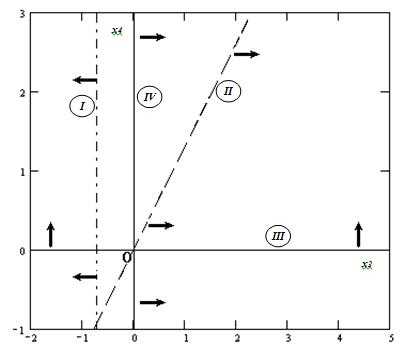
Рис. 6. Фрагмент MathCAD-документа:
построение области допустимых решений задачи
Ответ: рассматриваемая задача линейного программирования не имеет решения в силу несовместности системы ограничений.
Если после подстановки координат контрольной точки в неравенство его смысл нарушается, то решением данного неравенства является полуплоскость не содержащая данную точку (т.е. расположенная по другую сторону прямой).
Направление, обратное вектору-градиенту, соответствует направлению минимизации целевой функции.
Еще записи по теме
www.ikasteko.ru
Графическое решение задачи линейного программирования
Пример.
Решить графически данную задачу линейного программирования.
Решение. Найдем вначале область допустимых решений (ОДР). Решим графически первое неравенство:
(1)
Для этого построим вначале прямую линию, соответствующую уравнению:
. (11)
Поскольку, если то то прямая (11) проходит через точку М1(0;8). Аналогично, если то и прямая (11) проходит также через точку М2 (8;0). Проведем через эти две точки прямую линию и отметим ее с помощью 1 (см. рис. 1). Эта линия делит плоскость на две полуплоскости, которые мы условно назовем верхней и нижней полуплоскостями. Так как координаты точки (0;0) удовлетворяют неравенству (1), то этому неравенству соответствует нижняя полуплоскость, которая содержит эту точку. Этот факт мы изобразим на рис. 1 штрихами, направленными вниз от линии 1 .
Теперь решим графически второе неравенство:
(2)
Ему соответствует прямая, заданная уравнением:
(21)
Ее мы построим несколько иначе. Перепишем уравнение (21) в виде:
Тогда при оказывается , что дает точку М3 (0;3) искомой прямой. Угловой коэффициент этой прямой Но угловой коэффициент любой прямой равен где — угол наклона прямой к оси 0х: . Если теперь мы отложим три единицы вправо от точки М3 (0;3) и затем две единицы вверх, то получим другую точку М4 (3;5) которая также лежит на прямой (21). Через точки М3 и М4 мы проводим прямую 2 (рис.1). Начало координат (0;0) удовлетворяет (2) и лежит ниже графика линии 2 , поэтому соответствующая полуплоскость является «нижней», что мы и отмечаем штрихами, направленными вниз от прямой 2 (рис.1). Аналогично строим прямую 3.
Уравнение
(31)
Заменяем на уравнение .
Ясно, что прямая проходит через т. М5 (5;0), и имеет угловой коэффициент к = 2. При этом самому неравенству
Соответствует верхняя полуплоскость, отмеченная штрихами вверх от прямой 3.
Тривиальному неравенству соответствует правая полуплоскость координатной плоскости, то есть полуплоскость, лежащая справа от вертикальной оси Ее отмечаем штрихами, направленными вправо от оси 0 Наконец неравенству соответствует верхняя полуплоскость координатной плоскости, отмеченная штрихами, направленными вверх от оси 0. Пересечение всех указанных полуплоскостей определяет ОДР данной задачи. На рисунке 1 это область, ограниченная выпуклым пятиугольником ОАВСD.
Изобразим на рисунке 1 вектор роста целевой функции . Это вектор началом в т. (0;0) и концом в точке М (4;3), поскольку .
Построим теперь линию уровня . Она определяется уравнением:
(4)
Мы взяли здесь константу С =11, для того чтобы точки пересечения прямой (4) с осями имели целые координаты. Действительно, если то и, если То Что дает две точки М1 (0;4) и М2 (3;0) линии уровня (4). Через них проводим пунктиром соответствующую линию уровня (рис. 1). Она оказывается перпендикулярна вектору роста . Отрезок пересекается с ОДР и в каждой его точке х значение целевой функции равно 11:
.
Мы знаем, что значение функции F увеличивается в направлении вектора роста . Чтобы найти максимальное значение на ОДР будем параллельно перемещать линию уровня в направлении вектора роста До тех пор, пока, она будет иметь хотя бы одну точку пересечения с ОДР задачи. Из рисунка 1 ясно, что последнее пересечение смещенной линии уровня (4) будет точка
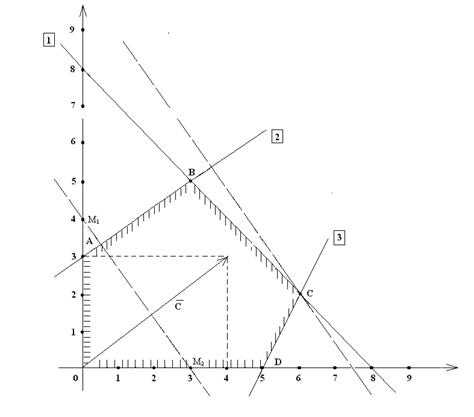Рисунок 1. Графическое решение задачи ЛП.
На этой линии очевидно и будет достигаться максимальное значение целевой функции F в ОДР, поскольку при дальнейшем движении линии уровня в направлении вектора роста, она перестает пересекаться с ОДР. Итак, максимальное значение функция F(х) имеет в точке . Так как точка является пересечением прямых 1 и 3, то ее координаты находятся из системы:
(5)
Чтобы решить эту систему, сложим оба уравнения. Тогда получим, что или .
Из первого уравнения находим, что
Итак, координаты точки С найдены : С (6;2). Найдем максимальное значение функции:
.
Задача решена.
Ответ: максимальное значение целевой функции F достигается в точке С (6;2) и равно 29:
.
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Решение задачи линейного программирования графическим методом
Министерство образования Российской Федерации
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Пояснительная записка к курсовому проекту по дисциплине
Вариант №3
28 марта 2008 г.
ТОМСК 2008
Содержание.
ВВЕДЕНИЕ
Исследование операций – это математическая дисциплина, занимающаяся разработкой и применением методов нахождения наилучших решений в различных областях человеческой деятельности.
Термин «Исследование операций» («Operation Research») заимствован из западной литературы. Сейчас, пожалуй, нельзя точно назвать, ни дату его возникновения, ни автора, да и вряд ли найдется исчерпывающее определение этого понятия.
Под операциями обычно понимают целенаправленные управляемые процессы. Природа их может быть различной — это могут быть военные действия, производственные процессы, коммерческие мероприятия, административные решения, и т.д. Что интересно — операции эти (совершенно несхожие по своей природе) могут быть описаны одними и теми же математическими моделями, более того, анализ этих моделей позволяет лучше понять суть того или иного явления и даже предсказать его дальнейшее развитие. Мир, как оказалось, устроен необычайно компактно (в информационном смысле), поскольку одна и та же информационная схема реализуется в самых разных физических (и не только физических) проявлениях. В кибернетике это называется термином «изоморфизм моделей».
Если бы не изоморфизм моделей, для каждой конкретной ситуации пришлось бы отыскивать собственный, уникальный метод решения, и исследование операций как научное направление не сформировалось бы. К счастью, дело обстоит иначе. Благодаря наличию общих закономерностей в развитии самых разных систем возможно исследование их математическими методами. Исследование операций как математический инструментарий, поддерживающий процесс принятия решений в самых разных областях человеческой деятельности, как совокупность средств, позволяющих обеспечить лицо, принимающее решение, необходимой количественной информацией, полученной научными методами, сформировалось на стыке математики и разнообразных социально-экономических дисциплин. Свой вклад в его становление внесли представители самых различных областей науки.
История возникновения исследования операций уходит корнями в далекое прошлое. Так, еще в 1885 году Фредерик Тейлор пришел к выводу о возможности применения научного анализа в сфере производства. Проблема, рассмотренная им, на первый взгляд, кажется тривиальной: «как оптимальным образом организовать работу землекопов?» Казалось бы, ответ давно известен — «Бери больше, кидай дальше, отдыхай, пока летит». Однако применение математического аппарата показало несостоятельность этого принципа. Оказалось, что оптимальный вес груза, позволяющий максимизировать количество перебрасываемого материала (при разумной экономии рабочей силы) значительно меньше того, что может поднять человек при максимальной нагрузке.
Пионером в области перевода сложных военно-стратегических задач на язык математики стал Фредерик Ланчестер. Одним из наиболее значительных результатов, полученных ученым, стало открытие в 1916 г. так называемого квадратичного закона, количественно связывающего достижение победы с двумя основными факторами: численным превосходством живой силы и эффективностью оружия. Было показано, что при одновременном вступлении в бой численное превосходство в живой силе более важно, чем применение более совершенного вооружения, поскольку главную роль играет сосредоточение собственных войск и расчленение сил противника. Классическим примером использования квадратичного закона Ланчестера является тактика Нельсона в сражении при Трафальгаре.
В 1917 году датский математик А.К.Эрланг, работавший в телефонной компании, поставил задачу минимизации потерь времени на установление телефонной связи. Полученные им результаты стали основополагающими принципами в теории телефонной связи. Формулы Эрланга (среднее время ожидания вызова и др.) были приняты министерством связи Англии в качестве стандартов для расчета эффективности телефонных линий. Идеи Эрланга почти на полвека предвосхитили современные теории расчета телефонных узлов.
В 1930 г. Г.Левинсон начал применять научный анализ к решению задач, возникающих в торговле. Методика исследования операций была использована для исследования эффективности рекламы, размещения товаров, влияния конъюнктуры на номенклатуру и количество проданных товаров.
В годы второй мировой войны исследование операций широко применялось для планирования боевых действий. Так, специалисты по исследованию операций работали в командовании бомбардировочной авиации США, дислоцированном в Англии. Ими исследовались многочисленные факторы, влияющие на эффективность бомбометания. Были выработаны рекомендации, приведшие к 4-х-кратному повышению эффективности бомбометания.
В начале войны боевое патрулирование самолетов союзников для обнаружения кораблей и подводных лодок противника носило неорганизованный характер. Привлечение к командованию специалистов по исследованию операций позволило установить такие маршруты патрулирования и такое расписание полетов, при которых вероятность оставить объект незамеченным была сведена до минимума. Полученные рекомендации были применены для организации патрулирования над Южной частью Атлантического океана с целью перехвата немецких кораблей с военными материалами. Из пяти вражеских кораблей, прорвавших блокаду, три были перехвачены на пути из Японии в Германию, один был обнаружен и уничтожен в Бискайском заливе и лишь одному удалось скрыться благодаря тщательной маскировке.
Мы привели лишь два примера использования методов исследования операций в военной практике. Число их очень велико. В годы войны все эти работы по применению были совершенно секретны, в последствии многие из них нашли свое отражение в специальной литературе.
По окончании второй мировой войны группы специалистов по исследованию операций продолжили свою работу в вооруженных силах США и Великобритании. Публикация ряда результатов в открытой печати вызвала всплеск общественного интереса к этому направлению. Возникает тенденция к применению методов исследования операций в коммерческой деятельности, в целях реорганизации производства, перевода промышленности на мирные рельсы. На развитие математических методов исследования операций в экономике ассигнуются миллионы долларов.
В Великобритании национализация некоторых видов промышленности создала возможность для проведения исследований экономических на базе математических моделей в общегосударственном масштабе. Исследование операций стало применяться при планировании и проведении некоторых государственных, социальных и экономических мероприятий. Так, например, исследования, проведенные для министерства продовольствия, позволили предсказать влияние политики правительственных цен на семейный бюджет.
В США внедрение методов исследования операций в практику управления экономикой происходило несколько медленнее — но и там многие концерны вскоре стали привлекать специалистов такого рода для решения проблем, связанных с регулированием цен, повышением производительности труда, ускорением доставки товаров потребителям и пр. Лидерство в области применения научных методов управления принадлежало авиационной промышленности, которая не могла не идти в ногу с растущими требованиями к ВВС. В 50-е-60-е годы на Западе создаются общества и центры исследования операций, выпускающие собственные научные журналы, ряд американских университетов включает эту дисциплину в свои учебные планы.
В настоящее время в рамках исследования операций сформированы отдельные самостоятельные направления — линейное программирование, выпуклое программирование, теория игр, теория массового обслуживания, и др.
mirznanii.com