Решить уравнение с дробью онлайн: FindHow.org — Найди как — инфопортал

alexxlab / / Разное

Содержание

Решать уравнения с дробями онлайн решателем

Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте. Уравнения человек использовал еще в древности и с тех пор их применение только возрастает. Уравнения с десятичными дробями изучают в 5 классе, и они не являются сложными математически уравнениями. Однако, не зная алгоритма их решения, они могут стать проблемой. Данного рода уравнения решаются такими же методами, как и обычные линейные уравнения, но для облегчения процесса решения лучше сначала уравнения упростить с целью избавления от десятичных дробей.

Так же читайте нашу статью «Решить уравнения с дробями онлайн решателем»

Допустим, необходимо решить такого вида уравнение:

\[2,4(6 — 3x) + 4,3 = 1,7 — 5,2x\]

Его можно решить двумя стандартными способами:

Первый способ заключается в группировке членов уравнения и распределение их по сторонам от знака \[=:\]

Раскрыв скобки с учетом правил, получим уравнение такого вида:

\[14,4 — 7,2x + 4,3 = 1,7 — 5,2x\]

Выполняем группировку и перенос членов:

\[-7,2x — 5,2x = 1,7 — 14. 4 — 4,3\]

Производим деление на -2 (число перед x):

\[-2x = -17\]

\[x = 8,5\]

Второй способ заключается в переводе десятичных чисел в целые с помощью умножения левой и правой части на 10:

\[2,4 (6 — 3x) + 4,3 = 1,7 — 5,2x\]

Получим:

\[24(6 — 3x) + 43 = 17 — 52x\]

Решаем обычное линейное уравнение стандартным методом, описанным в 1 способе:

\[144 — 72x + 43 = 17 — 52x\]

\[-72x = 52x = 17 — 144 — 43 \]

\[-20x = -170\]

Делим на -20:

\[x = 8,5\]

Где можно решить уравнение онлайн с десятичными дробями?

Решить уравнение вы можете на нашем сайте pocketteacher.ru. Бесплатный онлайн решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте: pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

Уравнения со смешанными дробями | Математика

Уравнения со смешанными дробями можно решать двумя способами. Рассмотрим каждый из них на примере.

Решить уравнение со смешанными дробями:

   

1 способ: Это — линейное уравнение. Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:

   

Складываем и вычитаем смешанные числа:

   

 

   

   

Обе части уравнения делим  на число, стоящее перед иксом:

   

   

   

2способ:

Смешанные числа переведем в неправильные дроби:

   

   

Теперь обе части уравнения умножаем на наименьший общий знаменатель всех входящих в него дробей:

   

Таким образом, уравнение со смешанными дробями заменили на уравнение с целыми числами:

   

Это — линейные уравнения. Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:

   

   

Обе части уравнения делим на число, стоящее перед иксом:

   

Ответ записываем в виде обыкновенной дроби:

   

Ответ: 14/27.

Решать уравнения со смешанными числами можно обоими способами. На мой взгляд, второй способ удобнее. Еще два уравнения со смешанными дробями, решенные с помощью умножения на наименьший общий знаменатель.

   

Переводим смешанные числа в неправильные дроби:

   

Обе части уравнения умножаем на наименьший общий знаменатель всех дробей:

   

От уравнения со смешанными числами переходим к уравнению с целыми числами:

   

неизвестные слагаемые переносим в одну сторону, известные — в другую, изменяя при переносе знаки:

   

   

Обе части уравнения делим на число, стоящее перед иксом:

   

   

Сокращаем дробь на 2:

   

Ответ: -11/15.

   

   

   

   

   

   

Ответ: -1.

Решение уравнений с переменной в знаменателе дроби

$\frac{2x+3}{2x-1}=\frac{x-5}{x+3}$

Решение:

1.Перенесем дробь из правой части уравнения в левую

\[\frac{2x+3}{2x-1}-\frac{x-5}{x+3}=0\]

Для того чтобы правильно это сделать, вспомним, что при перенесении элементов в другую часть уравнения меняется знак перед выражениями на противоположный. Значит, если в правой части перед дробью был знак «+», то в левой перед ней будет знак «-».Тогда в левой части получим разность дробей.

2.Теперь отметим что у дробей разные знаменатели, значит для того, чтобы составить разность необходимо привести дроби к общему знаменателю. Общим знаменателем будет произведение многочленов, стоящих в знаменателях исходных дробей: $(2x-1)(x+3)$

Для того чтобы получить тождественное выражение, числитель и знаменатель первой дроби необходимо умножить на многочлен $(x+3)$, а второй на многочлен $(2x-1)$. 2+11х-5=20х+4$

Тогда дробь примет вид

\[\frac{{\rm 20х+4}}{(2x-1)(х+3)}=0\]

3.Дробь равна $0$, если ее числитель равен 0. Поэтому мы приравниваем числитель дроби к $0$.

\[{\rm 20х+4=0}\]

Решим линейное уравнение:

$20x=-4$

$X=-0,2$

4.Проведем выборку корней. Это значит, что необходимо проверить, не обращаются ли знаменатели исходных дробей в $0$ при найденных корнях.

Поставим условие, что знаменатели не равны $0$

\[2x-1\ne 0 x+3\ne 0\]

х$\ne 0,5$ х$\ne -3$

Значит допустимы все значения переменных, кроме $-3$ и $0,5$.

Найденный нами корень является допустимым значением, значит его смело можно считать корнем уравнения. Если бы найденный корень был бы не допустимым значением, то такой корень был бы посторонним и ,конечно, не был бы включен в ответ.

Ответ:$-0,2.$

Решение уравнений — калькулятор от Intemodino

Могу ли я решить неполные квадратные уравнения, например без линейного или свободного члена?
Да, калькулятор позволяет решать полные и неполные квадратные уравнения.
В зависимости от того, в каком виде записано уравнение, Вы можете выбрать Advanced формат или использовать встроенные форматы, которые позволяют вводить только коэффициенты уравнения.
Как вводить уравнения со скобками?
Для того чтобы ввести уравнение, содержащее скобки, надо выбрать Advanced формат.
Как вводить уравнения с дробями?
В зависимости от того какой ввод уравнения Вы выбрали, существует два способа ввода дробных коэффициентов:
— если Вы собираетесь вводить уравнение, используя встроенные форматы, то Вам надо переключится в режим ввода дробей, выбрав «Дроби» в верхнем меню калькулятора.
— если Вы выбрали ввод уравнения в формате Advanced, для того чтобы отделить целую часть от дробной при вводе смешанных чисел, используйте знак подчеркивания. Между числителем и знаменателем дроби ставится наклонная черта. Пример: 3_1/2, 5/8 и т.д.
Где я могу посмотреть подробное решение уравнения?
При решении линейних и квадратных уравнений наш математический калькулятор показывает пошаговое решение с пояснениями, что может быть полезно не только школьникам, но и их родителям при проверке домашних заданий.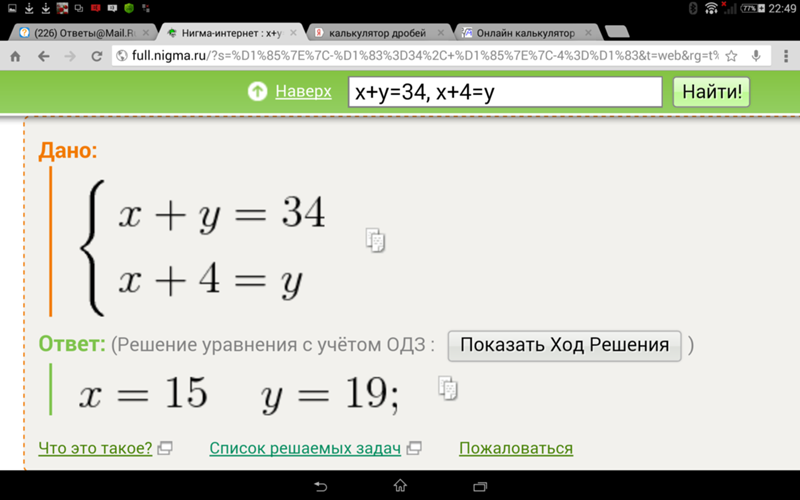
Как распечатать решение уравнения?
Вы можете отправить решение конкретного уравнения или историю всех проведенных вычислений по электронной почте и затем распечатать решение из почты.
Где найти ранее решённые уравнения?
Чтобы просмотреть или отредактировать ранее решённые уравнения, используйте стрелки «вперед» и «назад» в верхнем меню калькулятора.
Какой алгоритм используется для решения кубических уравнений?
Калькулятор решает кубические уравнения, используя формулу Кардано.
Каким способом решаются уравнения четвертой степени?
Для решения уравнений четвертой степени используется метод Феррари.

Решение уравнений с десятичными дробями

1. «Решение уравнений с десятичными дробями» 5 класс

2. Реши уравнение:

К. 4х = 0,22+0,26;
Т. 5х = 8,17+2,48;
З. 6х = 3,9*8;
Х. 7х-4х = 0,96;
А. х+2х = 21,42;
С. 2х+5х = 42,7;
Н. 12х-3х = 41,4.
0,12
7,14
5,2
7,14
0,32
6,1
2,13
7,14
4,6

3.

Прогулка в лес Вы бывали летом в лесу?
Прогулка по лесу – это так приятно,
а наблюдательному человеку ещё и
интересно!

4. «На опушке леса»

5. Сформулируйте правила нахождения неизвестных компонентов в уравнении.

Как найти неизвестное
слагаемое?
Как умножить десятичную
дробь на 0,1; 0,01; 0,001?

8. Сформулируйте правило умножения десятичных дробей.

Что надо сделать при
умножении на десятичную
дробь, если в произведении
меньше цифр, чем надо
отделить запятой?
«Собери грибы в лукошко»
Лес – это кладовая, щедро отдающая свои дары.

11. Поставьте запятые в произведении

2,31 ∙ 5,4 = 12474;
,
2,31 ∙ 0,54 = 12474;
,
23,1 ∙ 5,4 = 12474;
,
0,231 ∙ 54 = 12474;
,
0,231 ∙ 0,54 =0, 12474.
проверить

12. «Молчанка»

6,7 ∙ 8,4 + 6,7 ∙ 1,6
43,2
12,37 ∙ 4,185 – 12,37 ∙ 3,185
67
6,1 ∙ 3,4 + 6,1 ∙ 2,6
36,6
9,1 ∙ 0,387 – 9,1 ∙ 0,287
12,37
0,5 ∙ 43,2 ∙ 2
6,2711
1,25 ∙ 3,27 ∙ 8
4,516
62,711 : 10
0,91
451,6 ∙ 0,01
32,7

13.

«В гостях у Старичка – лесовичка» -А у меня для вас задание припасено.
Если выполните его, то смело заходите
в глубь леса!

14. «Привал»

0,3 · 2,25
3,03 ∙ 0,01
1,05 ∙ 5,27
2,8 ∙ 6,28
4,2 ∙ 6,3
7,3 ∙ 4
17,3 · 12,25
1,103 · 2,65
20,3 · 0,2
0,0003 ∙ 1,2
10,5 ∙ 4,2
3 · 2,2

15. «На лесной полянке» Лес – это источник радости и здоровья.

Хвоя сосны
Вы можете
158,6
Зверобой
16,362
Земляника
лесная
Медуница
лекарственная
2,08
Крапива
0,74
Подорожник
1,44
1,08
Узнай, какое растение леса — клад витаминов.
Для этого найди корень уравнения:
(х + 2,4) : 0,8 = 5,6
Узнай, какое растение леса — клад витаминов.
Для этого найди корень уравнения:
(х + 2,4) : 0,8 = 5,6
Плоды растения издревле употребляются человеком
в пищу. Водный настой листьев земляники лесной
применяются в качестве мочегонного средства при
мочекаменной и желчнокаменной болезнях. Их
употребление также назначается при диабете и
малокровии. Плоды применяют как витаминное
средство.
О каком растении говорится в загадке?
Это зелье ты не тронь:
Жжется больно, как огонь.
Ответь на вопрос, решив уравнение.
(3,5 — х) : 2,3 = 1,2

19. О каком растении говорится в загадке? Это зелье ты не тронь: Жжется больно, как огонь. Ответь на вопрос, решив уравнение.

(3,5 — х) : 2,3 = 1,2
Крапива используется в народной медицине для
лечения многих болезней, применяется при
различных кровотечениях, почечнокаменной,
желчекаменной болезни, удушье, болезнях печени и
желчных путей, отеках, заболеваниях сердца,
туберкулезе, бронхиальной астме,
бронхитах, аллергиях. Наружно крапиву
используют при открытых ранах,
кровотечениях, кожных заболеваниях, для
укрепления и роста волос.
Если ты порезал ногу, не рыдай и не реви.
Вот растенье на подмогу. Ты скорей его зови!
Что это за растение? Правильное решение уравнения
поможет ответить на этот вопрос.
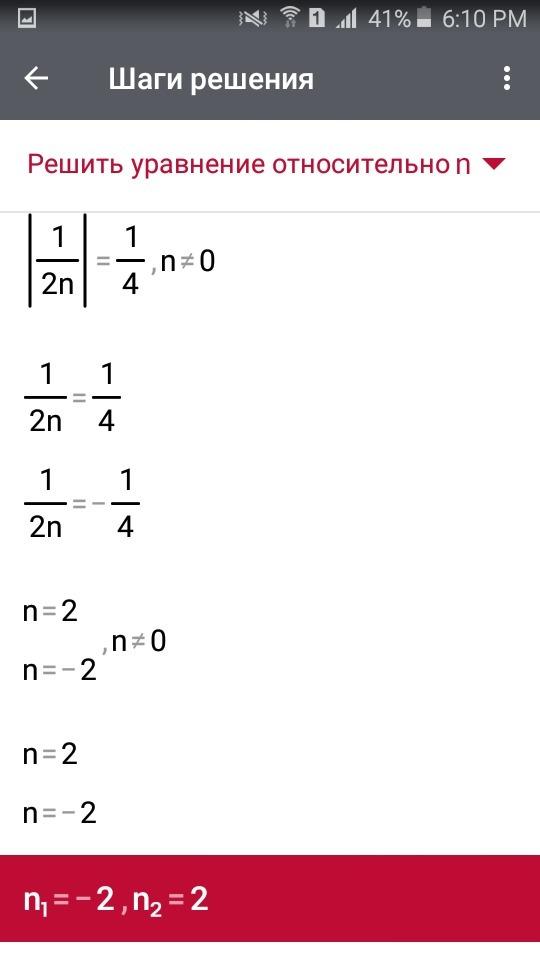
х : 4,8 + 3,6 = 3,9

21. Если ты порезал ногу, не рыдай и не реви. Вот растенье на подмогу. Ты скорей его зови! Что это за растение? Правильное решение

уравнения
поможет ответить на этот вопрос.
х : 4,8 + 3,6 = 3,9
Настой из листьев подорожника обладает
отхаркивающим свойством, благодаря чему и
используется при лечении бронхитов, бронхиальной
астмы, туберкулеза легких. Сок свежих листьев
подорожника эффективен в лечении язвенной
болезни желудка и двенадцатиперстной кишки,
хронических гастритов. А водный настой
свежих листьев способствует быстрому
очищению и лечению ран, порезов,
кожных язв, нарывов и фурункулов.
Назови растение, имеющее репутацию лекарства от
100 болезней.
Реши уравнение и узнай ответ.
х : 2,7 — 5,16 = 0,9
Назови растение, имеющее репутацию лекарства от
100 болезней.
Реши уравнение и узнай ответ.
х : 2,7 — 5,16 = 0,9
Зверобой применяют для лечения многих
недугов: в качестве антисептического средства,
для смазывания десен и полосканий, при
заболеваниях дыхательных путей, гипертонии,
анемии, при лечении пролежней, аллергии, ран,
язв, сыпи, при болезнях мочевого пузыря,
желудочно-кишечного тракта, болезнях почек,
гриппе, слабости сердца, простудных
заболеваниях, туберкулезе, для лечения мастита,
желтухи, кашля, желудочных и легочных
заболеваний, мигрени, при язве желудка,
головной боли, нервных болезнях, повышенной
кислотности желудочного сока.

24. «Заветная тропинка»

Чтобы выйти из леса и вернуться
домой, вы должны проявить
самостоятельность, показать волю и
упорство.

25. Итог урока

Домашнее задание:
1 уровень: № 1476, № 1482,
2 уровень: № 1475, № 1513;

Тренажёры по математике. 5 класс.VI. Десятичные дроби и действия с ними.

Строева И.И.

Инструкция по применению тренажёров на уроках математики.

Тренажёры по математике, составленные учителем с категорией «Педагог –мастер» И.И.Строевой. Сборник содержит тренажёры по программе изучения математике в 5 классе, где закладываются навыки вычислений с рациональными числами, решения уравнений, неравенств и их систем. С помощью тренажёров можно повторять материал в старших классах при подготовке к промежуточному государственному контролю в 9 классе и тестированию в 11 классе. Тренажёры тренируют навыки быстрого выполнения задания. Что важно при решении тестовых заданий.

Тренажёры — один из видов самостоятельной работы ученика на уроке. Можно использовать как формативное оценивание с самопроверкой или взаимной проверкой. Они являются отработкой навыков решения примеров, применения правил и формул. Могут проводиться в любой части урока по усмотрению учителя.

Основной принцип проведения – 10 заданий за 5 минут. Учитель жёстко следит за временем и сообщает ученикам истечение каждой минуты. По истечении отведённых на решение примеров 5 минут, ученики за партой обмениваются выполненными заданиями тренажёра для проверки. Учитель диктует правильные ответы. Ученики сверяют их с написанными, и правильные ответы отмечают значком «+». Каждый «+» — 1балл. Затем, считают, сколько баллов «сосед» получил за решённый тренажер. Записывают количество баллов и делают запись «зачёт» или «не зачет». Ученик получает «зачет» за выполнение тренажёра, если имеет 8 – 10 правильных ответов(баллов). Если правильных ответов 0 – 7, то он получает «не зачёт». Ученики возвращают себе свои тренажёры. По просьбе учителя поднимают руки те, кто получил «зачёт». Учителю становится ясно, как усвоена тема, кто из детей имеет проблемы и стоит ли этой теме ещё уделить время.

Можно предложить ребятам, для того чтобы уложиться во время, экономить секунды на переписывании примера и часть примеров выполнять устно, действия записывать сразу в столбик.

  1. Десятичные дроби и действия с ними.

Тренажёр № 99. Записать десятичной дробью.

1) 2) 3) 4) 5)

6) 7) 8) 9) 10)

Тренажёр № 100. Записать десятичной дробью.

1) 2) 3) 4) 5)

6) 7) 8) 9) 8 10)

Тренажёр № 101. Записать десятичной дробью.

1) 2) 3) 4) 5)

6) 7) 8) 9) 10)

Тренажёр №102 Записать в виде обыкновенной дроби или смешанного числа.

1) 0, 7 2) 0,8 3) 0,034 4) 1,5 5) 1,06

6) 56,004 7) 6,25 8) 0,125 9) 0,016 10) 3,8

Тренажёр № 103. Записать частное десятичной дробью.

1) 37 : 100 2) 37 : 10 3) 37 : 1000 4) 29 : 1000 5) 29 : 1

6) 29 : 10 7) 158 : 1000 8) 158 : 10 9) 158 : 100 10) 27 :

Тренажёр № 104. Написать два числа равных данному.

1) 0,1 2) 1,9 3) 6,09 4) 11,004 5) 2,8

6) 15,7 7) 3,09 8) 0,005 9) 0,22 10) 1,7

Тренажёр № 105. Выписать большее число.

1) 0,25 и 0, 27 2) 3,981 и 39,81 3) 23,001 и 23, 01

4) 45, 992 и 45,009 5) 45, 992 и 45,999 6) 0,237 и 0,372

7) 1,5673 и 1,5672 8) 0,00967 и 0,00067 9) 1 и 0,9999

10) 3, 0001 и 3

Тренажёр № 106. Выписать меньшее число.

1) 1,4 и 2) и 3,9 3) и 1,06

4) и 1,7 5) и 60 6) и 56,5

7) и 11,3 8) и 1,19 9) 13,16 и

10) и 13,015

Тренажёр № 107. Вычислить.

1) 0,4 + 0,3 2) 1,5 + 2,2 3) 23,8 + 5,1

4) 3 + 5,6 + 1,2 5) 45,31 + 33,42 6) 0,456 + 0,201

7) 1,004 + 2,04 8) 1,003 + 2,004 9) 1,007 + 2,4

10) 2,3 + 23,04

Тренажёр № 108. Вычислить.

1) 12,345 + 2,485 6) 6,189 + 7,26

2) 11,67 + 18,113 7) 45,7 + 51,4

3) 23,7 + 6,831 8) 6,1 + 5,9

4) 0,86 + 0,909 9) 7,8 + 6,2

5) 3,47 + 5,8 10) 28,24 + 11,76

Тренажёр № 109. Привести подобные слагаемые.

1) 2,4х + 4,2х 6) 1,1c + 5c + 2,6c

2) 8,1с + 6,8с 7) 1,2k + k + 1,1k

3) 2,5х + 5х + х 8) 2,3x + 5y + 0, 7x

4) 3,6с + 1,4с + 50с 9) 1,6m + 2n + 4m

5) 12,3 + m + 2,4 10) 2,1 + 3x + 7,2 + 3x

Тренажёр № 110. Найти значение выражение при х = 2,4.

1) 10,3 + х 6) х + 2,4

2) 12,67 + х – 12,67 7) 13,5 + 10,5 + х

3) 4,8 + х + 1,2 8) 3х – 2х

4) 2,34 + х + 3,66 9) х + 7х – 7х

5) 24,67 + 0,13 + х 10) х + 23,674 – х

Тренажёр № 111. Перевести в заданную единицу измерения.

1) 234см в м 6) 1200м в км

2) 347г в кг 7) 67899см в м

3) 367дм в м 8) 2389м в км

4) 89см в мм 9) 41см в м

5) 600г в кг 10) 3см в дм

Тренажёр № 112. Вычислить.

1) + 2,3 6) 3,15 + 0,35

2) + 5,1 7) 13,8 + 0,6

3) 9,05 + 8) 80,01 + 0,16

4) 5,023 + 9) + 23,12

5) 2,4 + 0,049 10) 4,8 + 0,024

Тренажёр № 113. Решить уравнение.

1) х – 3,2 = 4,1 6) c – 4,67 = 0,032

2) С – 33,12 = 6,34 7) k – 45,998 = 0

3) х – 51,003 = 6 8) х – 11,09 = 12

4) с – 5,03 = 4,97 9) 2m + 3m – 4m = 1,1

5) m – 24,7 = 31,8 10) 8x – 7х = 2,675

Тренажёр № 114. Вычислить.

1) 0,34 – 0,27 2) 1,7 – 0,6 3) 34,9 – 4,7

4) 48,65 – 0,62 5) 456,1 – 56,1 6) 13,4 – 2,2

7) 26,967 – 5,2 8) 5,8 – 4,3

9) 4,7 – 3,1 10) 0,56 – 0,48

Тренажёр № 115. Вычислить.

1) 0,09 – 0,081 2) 8,45 – 7,67 3) 25,89 – 0,78

4) 3,6 – 2,56 5) 12,7 – 11,4 6) 56 – 55, 34

7) 5,1 – 3,1 8) 6,78 – 6,69

9) 28, 2 – 8,3 10) 7,7 – 6,9

Тренажёр № 116. Вычислить.

1) 6) – 0,05

2) 7) 2,36 –

3) 8) 35,78 –

4) – 0,6 9)

5) – 2,8 10)

Тренажёр № 117. Привести подобные слагаемые.

1) 2,7х + 2у – 0,4х 6) 23,7 + 5c + 2,6c – 4

2) 8,9 + с – 1,2 + 6с 7) 1,2k – 0,5k – 0,11k

3) 0,25х – 0,05х 8) 2,3x + 5y – 0,7x

4) 3,6с + 1,4с – 0,5с 9) 3,1n + 6m – 2,7n

5) 12,3 + m – 0,24 10) 21,6 + 3x – 2,1

Тренажёр № 118. Решить уравнение.

1) 2,3 – х = 1,2 6) 3,15 – n = 0

2) 1,2 – у = 0,3 7) 65,9 – m = 10

3) 4,8 – х = 1,2 8) 6,09 – k = 0,09

4) 2х – х = 9,5 9) 3,4m – 2,4m = 3

5) 2,4у – 1,4у = 8 10) 23,9 – p = 0,6

Тренажёр № 119. Найти значение выражения при у = 1,3.

1) 2,7у – 0,4 + 1,7у 6) у + 5,3у – 6,3у

2) 8,78 – у + 1,2 7) у – 1,2 + 1,1

3) у – у + у – 0,3 8) 2,13 + y – 3,43

4) 3,6у + 1,4у – 5у 9) 34,98 – у – 0,08

5) 12,3 + у – 2,4 10) у – 0,25

Тренажёр № 120. Выполнить действия удобным способом.

1) 2,3 + 4,5 – 1,6 6) 5,3 – 4,8 + 0,7

2) 8,34 – 2,04 + 2,5 7) 12,8 + 4,67 – 2,8

3) 45,98 – 0,78 – 0,2 8) 7,451 – 7,251 + 0,8

4) 6,5 + 1,5 – 2,9 9) 48,67 + 3,91 – 7,67

5) 3,4 + 6,6 – 6,9 10) 123,8 + 34,76 – 4,76

Тренажёр № 121. Выполнить умножение.

1) 2,5 · 3 2) 3,3 · 2 3) 1,2 · 4 4) 5 · 0,1

5) 6 · 5,1 6) 12,2 · 2 7) 14,3 · 2 8) 8,34 · 2

9) 23,23 · 3 10) 51,768 · 1

Тренажёр № 122. Выполнить умножение.

1) 2,6 · 3 2) 1,27 · 3 3) 4,82 · 5 4) 2,643 ·

5) 24,8653 · 0 6) 3 · 15,0056 7) 1,035 · 40

8) 800,008 · 55 9) 12,1 · 30 10) 67,81 · 20

Тренажёр № 123. Выполнить умножение.

1) 21,53 · 10 2) 13,354 · 10 3) 1,201 · 10

4) 100 · 0,145 5) 100 · 5,14 6) 11,2 · 100

7) 14,3 · 1000 8) 8,34 · 1000

9) 23,23 · 100 10) 51,768 · 10

Тренажёр № 124. Выполнить действия.

1) (1,4 + 2,6) · 3 6) 3 · (11,56 – 10,06)

2) (1,27 – 0,07) · 2 7) (1,05 + 2,95) · 40

3) (94,72 + 5,28) · 10,231 8) (8,008 + 1,992) · 0,34

4) (2,643 – 2,6) · 2 9) (5,9 + 12,1) · 20

5) (24,865 – 21,667) · 0 10) (67,81 + 32,19) · 2,41

Тренажёр № 125. Вычислить удобным способом.

1) 2,2 · 2 + 1,3 · 2 6) 12,2 · 2 – 11,8 · 2

2) 3,3 · 2,9 + 6,7 · 2,9 7) 14,3 · 2 + 0,2 · 2

3) 1,2 · 10 – 0,11 · 100 8) 5 · 8,34 · 2

4) 5 · 0,1 – 0,04 · 10 9) 2,5· 23,23 · 4

5) 6 · 5,1 + 2,9 · 6 10) 0,2 · 59,768 · 5

Тренажёр № 126. Найти значение выражения при с = 10.

1) 2,1с · 3 2) 1,2с · 2 3) 4,1 · 4с 4) 2,003 · 3с

5) 24,01с · 5 6) 3с · 1,001 7) 0,05 · (3с – 2с)

8) 8,02с · (5,5 – 4,5) 9) (12,1 + 0,9) · 0,3с 10) 6,81 · 2с

Тренажёр № 127. Решить уравнение.

1) Х : 2,5 = 3 2) Х : 3,3 = 3 3) Х : 1,2 = 10

4) Х : 5 = 0,6 5) Х : 6 = 5,2 6) Х : 12,29 = 10

7) Х : 1,3 = 6 8) Х : 8,254 = 10

9) Х : 23,23 = 2 10) Х : 59,761 = 1

Тренажёр № 128. Выполнить умножение.

1) 1,5 · 0,3 2) 0,12 · 0,3 3) 4,2 · 1,5

4) 2,6 · 0,02 5) 2,01 · 5,1 6) 3,2 · 15,005

7) 1,035 · 40 8) 8,08 · 5,5 9) 11,1 · 3,3

10) 6,01 · 0,02

Тренажёр № 129. Выполнить умножение.

1) 11,53 · 0,1 2) 93,35 · 0,01 3) 1,201 · 0,1 4) 0,001 · 1456,5 5) 0,01 · 5,1 6) 1,2 · 0,001

7) 14,3 · 0,001 8) 18,3 · 0,01 9) 23,23 · 0,1

10) 51,368 · 0,1

Тренажёр № 130. Выполнить действия.

1) (1,5 + 2,6) · 0,2 6) 1,01 · (11,5 – 10,3)

2) (4,37 – 3,07) · 0,05 7) (1,05 + 2,9) · 0,01

3) (4,7 + 5,2) · 0,1 8) (8,08 + 1,92) · 0,1

4) (5,6 – 2,1) · 4,6 9) (7,9 + 12,1) · 0,1

5) (21,67 – 21,67) · 10,59 10) (61,81 + 38,19) · 0,01

Тренажёр № 131. Вычислить удобным способом.

1) 2,8 · 0,2 – 1,3 · 0,2 6) 12,2 · 0,4 – 11,8 · 0,4

2) 3,2 · 0,1 + 6,7 · 0,1 7) 14,3 · 0,2 + 11,2 · 0,2

3) 1,2 · 0,1 – 11 · 0,01 8) 0,5 · 8,34 · 2

4) 5,3 · 0,1 – 4,9 · 0,1 9) 2,5· 23,23 · 0,4

5) 6,1 · 0,95 + 0,05 · 6,1 10) 0,2 · 59,8 · 0,5

Тренажёр № 132. Найти значение выражения при с = 0,1.

1) 3,1с · 3 6) 100с · 1,001

2) 5,2с · 5 7) 0,09 · (3,1с – 2,1с)

3) 4,1 · 0,2с 8) 8,02с · (5,6 – 4,6)

4) 2,3 · 10с 9) (12,1 + 0,9) · 0,2с

5) 2,01с · 5 10) 2,8 · 2с

Тренажёр № 133. Решить уравнение.

1) x : 0,2 = 3,1 6) х : 12,29 = 0,1

2) х : 3,5 = 0,02 7) х : 181,3 = 0,01

3) х : 0,35 = 0,2 8) х : 0,8 = 0,8

4) х : 5,18 = 0 9) х : 2,2 = 1,01

5) х : 0,896 = 1 10) х : 0,01 = 45,54

Тренажёр № 134. Выполнить умножение.

1) 1,5 · 0,1 6) 3,2

2) 0,1 · 0,4 7) 0,35

3) 4,2 8) 1,01

4) 2,1 9) 11,1

5) 2,01 10) 6,1 · 0,2

Тренажёр № 135. Вычислить площадь прямоугольника или квадрата, если

заданы стороны фигур.

1) Sпр, 1,3см и 1,1см 6) Sкв, 0,1км

2) Sпр, 1,03м и 10м 7) Sкв, 1,2см

3) Sпр, 0,3см и 10см 8) Sкв, 0,03м

4) Sпр, 0,5м и 20м 9) Sкв, 0,5м

5) Sпр, 0,7м и 0,8м 10) Sкв, 1,1дм

Тренажёр № 136. По данным скорости тела и времени вычислить путь.

1) v = 5,1км/ч, t = 3ч 6) v = 5км/ч, t = 0,3ч

2) v = 4км/ч, t = 2,1ч, 7) v = 5,4км/ч, t = 5ч

3) v = 60,5км/ч, t = 2ч 8) v = 500,2км/ч, t = 1,1ч

4) v = 55,2км/ч, t = 4ч 9) v = 4,5км/ч, t = 6ч

5) v = 15,1км/ч, t = 10ч 10) v = 150,2км/ч, t = 3ч

Тренажёр № 137. Выполнить деление.

1) 2,5 : 5 2) 3,3 : 3 3) 1,2 : 4 4) 1,5 : 3

5) 16,8 : 2 6) 12,2 : 2 7) 14,28 : 7 8) 8,32 : 8

9) 23,23 : 23 10) 151,768 : 1

Тренажёр № 138. Выполнить деление.

1) 2,6 : 5 6) 0,175 : 7

2) 1,275 : 3 7) 10,35 : 50

3) 44,82 : 9 8) 800,008 : 8

4) 2,3 : 2 9) 120,18 : 30

5) 21,42 : 6 10) 67,8 : 4

Тренажёр № 139. Выполнить деление.

1) 81,53 : 10 2) 13,500 : 10 3) 1,201 : 10

4) 0,14 : 10 5) 51,40 : 100 6) 115,2 : 100

7) 147,3 : 1000 8) 85,34 : 1000 9) 13,23 : 100

10) 510,7 : 10

Тренажёр № 140. Выполнить действия.

1) (1,4 + 2,7) : 4,1 6) 3,5 : (11,56 – 4,56)

2) (1,87 – 0,07) : 2 7) 16,28 : (1,05 + 2,95)

3) (94,71 + 5,29) : 10 8) 34,9 : (8,008 + 1,992)

4) (2,64 – 2,6) : 2 9) 36,18 : (5,9 + 12,1)

5) (24,653 – 24,653) : 2 10) 145 : (67,81 + 32,19)

Тренажёр № 141. Решить уравнение.

1) x · 2 = 3,8 2) 3x = 0,021 3) 4x = 0,24

4) 5x = 10,025 5) 6x = 12,06 6) 7x = 0,7

7) 8x = 0,32 – 0,08 8) 9x = 1,8 + 7,2

9) 10x = 1,01 10) х : 0,011 = 0

Тренажёр № 142. Вычислить удобным способом.

1) 1,5 · 0,1 : 0,1 2) 2,5 · 100 · 0,01 3) 4,2 : 3,5 · 2

4) 2,1 · 0,02 : 7 5) 2,02 · 0,1 : 2 6) 3,2 · 10 : 5

7) 0,35 · 100 : 20 8) 1,01 · 10 : 100

9) 11,1 : 0,8 · 4 10) 6,1 · 0,2 : 6,1

Тренажёр № 143. Выполнить деление.

1) 3,5 : 0,5 2) 8,8 : 0,8 3) 1,6 : 0,4 4) 21,6 : 0,3

5) 16,83 : 0,3 6) 121,22 : 1,1 7) 14,28 : 1,4

8) 10,413 : 8,01 9) 23,23 : 2,3 10) 151,78 : 151,78

Тренажёр № 144. Выполнить деление.

1) 2,16 : 0,1 6) 17,5 : 0,01

2) 1,275 : 0,1 7) 10,35 : 0,001

3) 44,82 : 0,1 8) 80,8 : 0,001

4) 2,3 : 0,1 9) 12,18 : 0,001

5) 21,42 : 0,01 10) 6,8001 : 0,001

Тренажёр № 145. Решить уравнение.

1) x · 0,2 = 3,8 6) 7,1x = 142

2) 0,7x = 0,021 7) 2,4x = 0,32 – 0,08

3) 0,06x = 0,24 8) 0,09x = 1,8 + 7,2

4) 0,005x = 10,5 9) 1,1x = 1,01 + 0,2

5) 1,6x = 8 10) 5,67x = 0

Тренажёр № 146. Вычислить удобным способом.

1) 1,5 · 2 : 0,1 6) 3,2 · 1,5 : 0,8

2) 2,51 · 100 : 0,1 7) 0,35 · 100 : 0,5

3) 4,2 : 21 · 5 8) 1,01 : 10 : 0,01

4) 2,1 · 1,5 : 0,7 9) 0,8 : 0,8 · 4,312

5) 2,02 · 1,1 : 0,202 10) 6,178 · 0,2 : 0,2

Тренажёр № 147. Вычислить сторону прямоугольника или квадрата, если

заданы вторая сторона и площадь фигуры.

1) Sпр = 1,82 см2, а = 1,3см 6) Sкв = 100см2

2) Sпр = 1,8см2, а = 1,5см 7) Sкв = 0,64м2

3) Sпр = 0,23см2, а = 0,1см 8) Sкв = 0,25м2

4) Sпр = 5,8м2, а = 10м 9) Sкв = 0,81см2

5) Sпр = 10,5см2, а = 2,1см 10) Sкв = 0,49км2

Тренажёр № 148. По данным расстоянию и времени вычислить скорость

тела.

1) S = 18,6км, t = 3ч 6) S = 15км, t = 0,3ч

2) S = 126км, t = 2,1ч, 7) S = 2,3км, t = 0,1ч

3) S = 113км, t = 2ч 8) S = 25км, t = 0,25ч

4) S = 246км, t = 4ч 9) S = 1986км, t = 10ч

5) S = 165км, t = 10ч 10) S = 227,5км, t = 3,25ч

Тренажёр № 149. Вычислить цену товара, если заданы количество товара М

и общая стоимость С.

1) С = 1092тг, М = 2,6кг 6) С = 96тг, М = 300г

2) С = 1400тг, М = 3,5кг 7) С = 100тг, М = 0,2кг

3) С = 120тг, М = 1кг 200г 8) С = 228тг, М = 800г

4) С = 1495тг, М = 2кг 300г 9) С = 450тг, М = 10кг

5) С = 513тг, М = 5кг 400г 10) С = 136000тг, М = 1т 600кг

Тренажёр № 150. Найти время движения катера, если даны направление

движения, скорость течения vр, собственная скорость

катера vк и пройденное расстояние S.

1) Sпо теч. = 51км, vр = 2км/ч, vк = 15км/ч

2) Sпо теч.= 50км, vр = 1,2км/ч, vк = 11,3км/ч

3) Sпр. теч.= 39км, vр = 2км/ч, vк = 15км/ч

4) Sпр. теч.= 45км, vр = 1,2км/ч, vк = 11,2км/ч

5) Sпо теч.= 55,5км, vр = 1,8км/ч, vк = 16,7км/ч

6) Sпо теч.= 41км, vр = 2,1км/ч, vк = 18,4км/ч

7) Sпр. теч.= 11,5км, vр = 2,2км/ч, vк = 13,7км/ч

8) Sпр. теч.= 96км, vр = 1км/ч, vк = 20,2км/ч

9) Sпр. теч = 2,25км, vр = 1,2км/ч, vк = 10,2км/ч

10) Sпо теч = 9,75км, vр = 1,5км/ч, vк = 11,5км/ч

Тренажёр № 151. Вычислить, ответ записать в виде десятичной дроби.

1) 6)

2) 7)

3) 8)

4) 9)

5) 10)

Тренажёр № 152. Вычислить, ответ записать в виде десятичной дроби.

1) 6)

2) 7)

3) 8)

4) 9)

5) 10)

Тренажёр № 153. Записать деление в виде обыкновенной дроби и вычислить.

1) 13,5 : 0,1 6) 0,32 : 0,8

2) 2,51 : 0,251 7) 0,35 : 0,5

3) 4,2 : 2,1 8) 1,01 : 0,01

4) 2,1 : 0,07 9) 0,008 : 0,8

5) 2,02 : 0,202 10) 6,178 : 0,002

розв язати рівняння з дробами 6 клас

Как решать уравнения с дробями в 5, 6 и 7 классах. Поэтапное решение дробных уравнений с примерами. Просто и понятно! На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное. Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.

Помощь школьникам, студентам в решении: Решение уравнений с дробями онлайн, можно заказать дипломную работу. Вы можете решать уравнения с дробями с помощью онлайн калькулятора, только есть одна проблема, которая возникает у учеников 5, 6, 7, 8 классов школы, а именно, как же вводить собственно дробь в форму калькулятора. Приведём пример в виде анимированной картинки («Дано» изображено сверху, что ввести в форму снизу)

Примечание: π записывается как pi; корень квадратный как sqrt(). Шаг 1. Введите заданный пример, состоящий из дробей. Шаг 2. Нажмите кнопку “Решить”. Шаг 3. Получите подробный результат. Чтобы калькулятор посчитал дроби правильно, вводите дробь через знак: “/”. Например: . Калькулятор посчитает уравнение и даже покажет на графике, почему получился такой результат. Что такое уравнение с дробями. Уравнение с дробями – это уравнение, в котором коэффициенты являются дробными числами. Линейные уравнения с дробями решается по стандартной схеме: неизвестные переносятся в одну сторону, а известные – в

Уравнения с дробями 6 класса онлайн на сайте Pocketteacher.ru. Калькулятор решения уравнений с дробями 6 класса помогает делать это быстро и качественно. Заходите на наш сайт и убедитесь в том, как выглядит уравнения с дробями 6 класса. Уравнения с дробями 6 класс — решить онлайн. Главная. Уравнения с дробями 6 класс — решить онлайн. Уравнения с дробями 6 класса по математике. Применение уравнений широко распространено в нашей жизни. Они используются во многих расчетах, строительстве сооружений и даже спорте.

В нашем магазине pribory-spb.ru вы можете купить AT-6 — тахометр. Доставка. · Продавец: ООО НПФ «ПРИБОРЫ». Адрес: Россия, Санкт-Петербург, Дерптский переулок, 13. ОГРН: 1157847172504

Линейные уравнения с дробями в 6 классе можно решать по обычной схеме: неизвестные — в одну сторону, известные — в другую, изменив при этом их знак. Другой путь — предварительно упростить уравнение, превратив его из линейного уравнения с дробями в линейное уравнение с целыми числами. Сначала на примере одного линейного уравнения с дробями рассмотрим оба способа решения.

Решение простых уравнений 5, 6, 7 класс. Родители могут проверять. Решение можно распечатать. Решение простых уравнений 5, 6, 7 класса. Квадратные и линейные уравнения с дробями. Расчет пропорций. Решение — с объяснением. Ответ выдается в форме простой и десятичной дроби, решение можно распечатать. Незаменим для учебы Корень уравнения — это значение буквы, при котором из уравнения получается верное числовое равенство.

Реши уравнение 5 класс дроби. с 60 №291 (6 уравнение) Математика 6 класс Мерзляк Решить уравнение со смешанными дробями. Антонина Аркадьевна Тофелева. Aufrufe 1,6 Tsd.Vor 2 years.

Калькулятор выполняет деление, умножение, вычитание и сложение дробей, а также нахождение квадратного корня из дроби. Также, калькулятор дробей умеет работать со степенями, с квадратным корнем . Калькулятор со скобками может использоваться для сокращения дробей. Калькулятор поддерживает работу со скобками, что позволяет решать дроби даже в сложных математических примерах. В частности, действия со скобками часто требуются при вычислении алгебраических дробей или отрицательных дробей, над которыми постоянно приходится корпеть всем школьникам средних классов. Дополнительно, вы можете использовать этот калькулятор для сокращения дробей или решения дробей с разными знаменателями.

С дробями ученики знакомятся еще в 5 классе. Раньше людей, которые умели производить действия с дробями, считали очень умными. Первой дробью была 1/2, то есть половина, дальше появились 1/3 и т.д. Несколько веков примеры считались слишком сложными. Сейчас же разработаны подробные правила по преобразованию дробей, сложению, умножению и другим действиям. Достаточно немного разобраться в материале, и решение будет даваться легко. Содержание статьи. Повторение обычные дроби 6 класс. Действия с обыкновенными дробями 6 класс. Сокращенные дроби 6 класс. Смешанные дроби 6 класс. Вычисления с дробями 6

Дробові рівняння. Схема розвязування дробових рівнянь. Рівносильні перетворення найпростіших дробових рівнянь. Як розвязати дробове рівняння. Розвязування дробого рівняння. Приклад розвязування дробових рівнянь.

Переводите обыкновенные и смешанные дроби (дроби с целой частью). Чтобы рассчитать сумму, разность, произведение, частное двух дробей и получить решение, введите числитель, знаменатель, целую часть дроби и выберите операцию из списка. Чтобы ввести отрицательную дробь, поставьте знак минус в целой части дроби.

Расчет неизвестной дроби

Найдите неизвестный числитель или знаменатель дроби с помощью нашего простого калькулятора. Оставьте одно поле пустым, и калькулятор решит это поле.

Решение:

x = 4,5

Начните с перекрестного умножения дробей

3x = 23 = (3 × 3) = (x × 2)

Упростите выражение

3 × 3 = 2x

Умножьте известные значения

9 = 2x

Разделите обе стороны на 2, чтобы получить x

92 = 2×2

92 = x

4.5 = х

Решение дробей в алгебраических уравнениях

Вы можете найти неизвестное значение x в алгебраических уравнениях, содержащих дроби, с помощью нескольких простых шагов.

Шаг первый: умножьте дробь крестиком

Первый шаг к поиску неизвестного числителя или знаменателя дроби — это перемножение числителей и знаменателей.Для перекрестного умножения умножьте каждый числитель на знаменатель в противоположной дроби. Это создаст новое уравнение, которое не является дробью и которое легче решить.

Например, произведите перекрестное умножение следующего уравнения, чтобы создать новое уравнение без дроби:
x3 = 34

x3 = 34
(4 × x) = (3 × 3)
4x = 9

Шаг второй: решите уравнение

Следующим шагом будет решение полученного уравнения. Для начала получите x отдельно, разделив обе части уравнения на число перед x.

Например, решим уравнение 4x = 9.

4x = 9
4×4 = 94
x = 94

Шаг третий: Уменьшите дробь

Последний шаг — уменьшить дробь. Начните с поиска наибольшего общего делителя числителя и знаменателя. Затем разделите числитель и знаменатель на общий множитель. Если вы все еще не уверены, воспользуйтесь нашим упрощением дробей, чтобы уменьшить дробь.

Если числитель дроби больше 1, вы можете преобразовать дробь в смешанное число.Для этого разделите числитель на знаменатель. Частное будет целым числом, остаток — числителем, а исходный знаменатель — знаменателем.

Например, дробь из приведенных выше примеров не может быть упрощена, но ее можно превратить в смешанное число.

94 = 9 ÷ 4
9 ÷ 4 = 2 R1
2 14

Калькулятор алгебраических дробей

Наших пользователей:

Я действительно боролся с уравнениями алгебры.Мне стыдно сказать, но факт в том, что я плохо разбираюсь в математике. Поэтому мне постоянно нужна помощь. Потом я наткнулся на программу «Алгебратор». И, клянусь !! Это изменило мою жизнь. Я больше ни от кого не зависим, кроме этого маленького программного обеспечения.
Мерв Хасс, Пенсильвания

Я никогда не жалею о том дне, когда купил Algebrator и был потрясен. Пошаговый метод решения задач не похож ни на одну другую программу алгебры, которую я видел.
Барбара Фергюсон, Лос-Анджелес

Эта версия в 1000 раз лучше предыдущей.Это проще использовать и понять. Я люблю это! Прекрасная работа!
Боб Альберт, Калифорния

Алгебратор мне очень помог, он помог мне вернуться на правильный путь и вернуть свои навыки к следующему школьному сезону. Программа показывает пошаговые решения, которые упростили обучение. Я думаю, что это будет очень полезно для всех, кто только начинает изучать алгебру, или даже если они уже знают ее, это отточит их навыки.
Оуэн Паттон, Юта.

Я использовал ваше программное обеспечение, чтобы подготовиться к экзамену по алгебре.Мне очень нравится пошаговый процесс решения и объяснения.
Алексис Страттон, Флорида

Студенты, решающие всевозможные алгебры, узнают, что наше программное обеспечение спасает жизнь.

Вот поисковые фразы, которые использовали сегодняшние поисковики, чтобы найти наш сайт. Можете ли вы найти среди них свою?
Поисковые фразы, использованные в 2011-05-31:
  • Упрощающие выражения шестиклассные .edhelper
  • квадратичная формула дробей
  • радикальное выражение с уменьшением индекса
  • онлайн-калькулятор с круговой кнопкой
  • рабочие листы вычисления сложения алгебраических выражений и вычитания
  • Таблицы с коэффициентами и кратными
  • Заметки по алгебре для девятого класса
    • Аплет полиномиального разложения
  • онлайн-курс 8 тест по математике по алгебре
  • помощь с сложением и вычитанием десятичных рациональных целых чисел
  • Калькулятор умножения и деления квадратного корня
  • решать алгебраические уравнения с квадратным корнем
  • бесплатных домашних заданий с ответами на функциональные таблицы
  • одномерное волновое уравнение неоднородно
  • «Рабочий лист порядковых номеров»
  • приложений алгебры
  • записки по алгебре для печати
  • высшая школа алгебры
  • Алгебра Холта 1 ответы
  • freshers вербальные и невербальные знания английского языка вопросы и ответы
  • Интересные способы обучения факторингу, GCF и LCM
  • самый простой способ выучить алгебру
  • мат; лабораторная решающая нелинейная система
  • математические формулы бесплатные рабочие листы KS2
  • дробей от наименьшей к наибольшей рабочий лист
  • решение квадратного уравнения третьего порядка
  • факторинг на калькуляторе casio
  • лист сложения и вычитания одинаковых дробей для 2 степени
    • Рабочие листы
  • факторного дерева
  • 10 класс + вопросы по триггерной практике
  • Рационализируйте квадратный корень из 5, деленный на квадратный корень из 8.
  • делящиеся одночлены
  • бесплатные ответы на математические задачи
  • преобразование квадратного уравнения в десятичное (двоичное)
  • факторинг онлайн
  • домашнее задание по алгебре графиков
  • правил квадратов чисел
  • Формула Триг Лист средней школы
  • как преобразовать десятичную дробь в смешанное число
  • запись уравнения графа в вершинной форме
  • Калькулятор рациональных выражений
  • как делать дроби на ti-83 плюс
  • пример математической мелочи
  • решить задачи по алгебре показать работу
  • алгебра 1a бесплатные вопросы
  • aptitude русский вопрос и ответ
  • математические формулы процентов
  • Саксонская математическая онлайн-задача ответы
  • квадратичный метод из Индии
  • графики неравенств рабочих листов
  • вопрос о способностях и ответ
  • как вычислить квадратный корень из дроби на калькуляторе
  • вопросы о способностях и ответы с пояснениями
  • решений дугопольского, м. (2009) элементарная и промежуточная алгебра
  • решений нелинейных дифференциальных уравнений
  • триггерный онлайн-калькулятор
  • кубический корень прикорневой и 8-й степени
  • саксонская математика и алгебра II ответы
  • инструмент поиска наименьшего общего знаменателя
  • Рабочий лист решения уравнений типа 3
  • TI-83 Plus шпаргалка
  • как построить боковые параболы на графике calc
  • сумм по перестановкам
  • Уравнение прямых из упорядоченных пар
  • распечатанные промежуточные задачи по алгебре
  • калькулятор онлайн, чтобы решить уравнение
  • онлайн ответы кумон
  • рабочий лист по алгебре для 7 класса делать дома
  • «наибольшие общие факторы»
  • решить корневые многочлены с ti-83
  • решение уравнений в частных производных 1-го порядка примеры
  • Предварительный экзамен по алгебре
  • смешанное число целое число сложение
  • квадратный корень из 54 умноженных на p в третью
  • математическое уравнение женщины = зло
  • Калькулятор операций алгебры
  • разделение задач
  • решатели коников
  • nc edition algebra 1 ответы
  • квадратный корень из смешанных чисел

Перемножение крестиком для решения уравнений с дробями

Дроби не так сложно, как вы думаете. Если вы хотите научиться решать уравнения с дробями путем перекрестного умножения, например, решая «x / 7 = 2/3» и «7/3 = 2 / x» относительно x, вы находитесь в нужном месте.

Решение уравнений: Золотое правило

Цель решения уравнения относительно x состоит в том, чтобы закончить с утверждением, в котором x равно чему-то, что не включает x.

Золотое правило решения уравнений — применять одну и ту же операцию к обеим сторонам уравнения. Это может включать добавление, вычитание или умножение обеих сторон на одинаковую величину.

Например, если x / 37 = 5, вы можете умножить обе стороны на 37. Поскольку x, разделенное на 37, умноженное на 37, просто равно x, тогда x = 5 * 37, что = 185.

Решение уравнений с выборочными долями

Вот пример уравнения и пошаговый процесс его решения:

Пример уравнения: x / 7 = 2/3

Шаг первый: умножьте обе стороны на 7.

x / 7 * 7 = 2/3 * 7

Умножьте 2 и 7, чтобы получить 14.

x / 7 * 7 = 14/3

Отменить / 7 * 7, чтобы оставить x, и преобразовать в решение относительно x.

х = 14/3 = 4 2/3

Вы умножаете обе части на 7, чтобы исключить знаменатель в левой части уравнения. Семерки сокращаются слева. Затем вы решаете уравнение относительно x. В качестве последнего шага вы конвертируете неправильную дробь 14/3 в смешанную дробь 4 и 2/3.

Обратите внимание, что вы просто перемножили 7 в знаменателе. Если бы вы начали с 23 * x / 7 = 2/3, вы бы крестом умножили обе стороны на 7/23 вместо 7. Это оставило бы только x с левой стороны.

Смешанные фракции: еще один пример

Пример специального перекрестного умножения: Изображение Майка ДеХаана

Во втором примере «7/3 = 2 / x» смешанная дробь уже преобразована из 2 1/3 в 7/3. Намного проще решать уравнения с дробями, содержащие неправильные дроби, чем уравнения со смешанными дробями.

Обратите внимание, что в этом примере в знаменателе стоит x. Вы должны явно указать предположение, что x не равен нулю.

Пример уравнения: 7/3 = 2 / x

Умножьте обе стороны на x, чтобы x был в числителе.

7/3 * x = 2 / x * x

Сократить / x * x.

7 * x / 3 = 2

Умножьте обе стороны на 3/7, чтобы сократить 7/3.

x * (7/3) * (3/7) = 2 * (3/7)

Сократите 7/3 на 3/7 и умножьте, чтобы найти x.

х = 2 * 3/7 = 6/7

Если перемножить все за один шаг, получится:

7/3 = 2 / x
(7/3) * (3 * x / 7) = (2 / x) * (3 * x / 7)
x = 6/7

Перекрестное умножение легче распознать, когда числители и знаменатели проходят через знак равенства для умножения.

Пример специального перекрестного умножения: изображение Майка ДеХаана

Решение общих уравнений с дробями

Затем попробуйте решить дроби в общем случае, когда «a», «b», «c» и «d» ненулевые целые числа. Опять же, решите относительно X, начиная с числителя или знаменателя.

х / б = в / д

Умножить обе части на b

х / б * б = в / г * б

Вычеркните / b * b в левой части и объедините правую часть уравнения.

X = (b * c) / d

В аналогичном случае перекрестное умножение было бы более очевидным:

а * Х / б = в / д

Умножить обе стороны на b / a

a * X / b * b / a = c / d * b / a

Вычеркните «a / b * b / a» в левой части уравнения и свяжите числитель («c» и «b») и знаменатель («d» и «a») справа.

Х = с * б / д * а

Следующий пример начинается с X в знаменателе и решает самый сложный пример: c / d = a / (b * X).

c / d = a / (b * X)

Умножьте обе стороны на X * (d / c).

(c / d) * X * (d / c) = a / (b * X) * X * (d / c)

Отмените «c / d * d / c» слева и «/ X * X» справа.

Х = (а * г) / (б * в)

Пятишаговая сводка для решения уравнений с дробями

Простейшее перекрестное умножение дробей. Изображение Майка ДеХаана

Из приведенных выше примеров вы видели, как умножать дроби крестом: возьмите знаменатель одной дроби и умножьте обе части уравнения на это значение.

Одна часть уравнения упрощается, поскольку знаменатель сокращается, а другая часть увеличивается в том же соотношении, поэтому уравнение остается сбалансированным.

Пять основных шагов для решения уравнений с дробями:

  1. При необходимости замените любые смешанные фракции на неправильные. Например, измените 2 1/3 на 7/3.
  2. Определите простейший метод выделения неизвестного x только в одну сторону уравнения.
  3. Перекрестное умножение обеих сторон на одинаковые значения.Например, выберите знаменатель с одной стороны, который будет числителем нового множителя с обеих сторон.
  4. Если вам нужно упростить уравнение пошагово, сделайте это, повторяя шаг 3 по мере необходимости.
  5. При необходимости замените оставшиеся неправильные фракции на смешанные.

Не забудьте использовать пошаговый подход, когда вы узнаете, как решать уравнение; со временем вы сможете быстро решать уравнения дробей.

Дополнительная справка по перекрестному умножению уравнений на дроби

Возможно, вам потребуется дополнительная помощь или попрактиковаться в решении уравнений с дробями или с перекрестным умножением.Если вы изучаете математику в школе, первое предложение — попросить учителя помочь вам научиться решать задачи с дробями. Кроме того, вы можете найти репетитора по математике в Интернете или по объявлениям в местных газетах. Онлайн-репетиторство по математике или онлайн-упражнения с таблицами дробей могут быть рентабельными способами улучшить свои математические навыки.

Номер ссылки

Обучение математике онлайн. Перемножение крестиком . По состоянию на 7 февраля 2013 г.

Майк ДеХаан применяет свою степень бакалавра математики в области компьютерных наук, годы программирования на языке Cobol и контроля качества (включая тестирование расчетов процентов по кредитным картам) для исследования и представления математической теории для непрофессионала.

Здесь, в Decoded Science, Майк занимается математикой. Он изучает основы математической теории, раскрывает парадоксы, применяет вычисления к популярным фильмам и сообщает о математических новостях.
Майк начал профессионально писать в 2010 году как единственный владелец DeHaan Services.

Найди Майка в Google+

8.6: Решение уравнений с дробными или десятичными коэффициентами

Решение уравнений с дробными коэффициентами

Давайте воспользуемся общей стратегией решения линейных уравнений, представленной ранее, для решения уравнения \ (\ dfrac {1} {8} x + \ dfrac {1} {2} = \ dfrac {1} {4} \).

Чтобы изолировать член x, вычтите \ (\ dfrac {1} {2} \) с обеих сторон. $$ \ dfrac {1} {8} x + \ dfrac {1} {2} \ textcolor {red} {- \ dfrac {1} {2}} = \ dfrac {1} {4} \ textcolor {красный } {- \ dfrac {1} {2}} $$
Упростите левую часть. $$ \ dfrac {1} {8} x = \ dfrac {1} {4} — \ dfrac {1} {2} $$
Измените константы на эквивалентные дроби с помощью ЖК-дисплея. $$ \ dfrac {1} {8} x = \ dfrac {1} {4} — \ dfrac {2} {4} $$
Вычесть. $$ \ dfrac {1} {8} x = — \ dfrac {1} {4} $$
Умножьте обе части на обратную величину \ (\ dfrac {1} {8} \). $$ \ textcolor {red} {\ dfrac {8} {1}} \ cdot \ dfrac {1} {8} x = \ textcolor {red} {\ dfrac {8} {1}} \ left (- \ dfrac {1} {4} \ right) $$
Упростить. $$ x = -2 $$

Этот метод работал нормально, но многие студенты не чувствуют себя уверенно, когда видят все эти дроби.Итак, мы собираемся показать альтернативный метод решения уравнений с дробями. Этот альтернативный метод исключает дроби.

Мы применим свойство равенства умножения и умножим обе части уравнения на наименьший общий знаменатель всех дробей в уравнении. Результатом этой операции будет новое уравнение, эквивалентное первому, но без дробей. Этот процесс называется , очищая уравнение дробей . Давайте снова решим то же уравнение, но на этот раз воспользуемся методом очистки дробей.

Пример \ (\ PageIndex {1} \):

Решение: \ (\ dfrac {1} {8} x + \ dfrac {1} {2} = \ dfrac {1} {4} \).

Решение

Найдите наименьший общий знаменатель всех дробей в уравнении. $$ \ dfrac {1} {8} x + \ dfrac {1} {2} = \ dfrac {1} {4} \ quad LCD = 8 $$
Умножьте обе части уравнения на этот ЖК-дисплей, 8. Это очистит дроби. $$ \ textcolor {красный} {8} \ left (\ dfrac {1} {8} x + \ dfrac {1} {2} \ right) = \ textcolor {red} {8} \ left (\ dfrac { 1} {4} \ right) $$
Используйте свойство распределения. $$ 8 \ cdot \ dfrac {1} {8} x + 8 \ cdot \ dfrac {1} {2} = 8 \ cdot \ dfrac {1} {4} $$
Упростите — и заметьте, никаких дробей! $$ x + 4 = 2 $$
Решите, используя общую стратегию решения линейных уравнений. $$ x + 4 \ textcolor {красный} {- 4} = 2 \ textcolor {красный} {- 4} $$
Упростить. $$ x = -2 $$
Проверка: пусть x = −2. $$ \ begin {split} \ dfrac {1} {8} x + \ dfrac {1} {2} & = \ dfrac {1} {4} \\ \ dfrac {1} {8} (\ textcolor { красный} {- 2}) + \ dfrac {1} {2} & \ stackrel {?} {=} \ dfrac {1} {4} \\ — \ dfrac {2} {8} + \ dfrac {1} {2} & \ stackrel {?} {=} \ Dfrac {1} {4} \\ — \ dfrac {2} {8} + \ dfrac {4} {8} & \ stackrel {?} {=} \ dfrac {1} {4} \\ \ dfrac {2} {4} & \ stackrel {?} {=} \ dfrac {1} {4} \\ \ dfrac {1} {4} & = \ dfrac {1 } {4} \; \ checkmark \ end {split} $$

Упражнение \ (\ PageIndex {1} \):

Решение: \ (\ dfrac {1} {4} x + \ dfrac {1} {2} = \ dfrac {5} {8} \).

Ответ

\ (x = \ frac {1} {2} \)

Упражнение \ (\ PageIndex {2} \):

Решение: \ (\ dfrac {1} {6} y — \ dfrac {1} {3} = \ dfrac {1} {6} \).

Ответ

г = 3

Обратите внимание в Примере 8.37, что после того, как мы очистили уравнение дробей, оно было похоже на те, которые мы решили ранее в этой главе. Мы изменили проблему на ту, которую уже знали, как решить! Затем мы использовали общую стратегию решения линейных уравнений.

КАК: РЕШИТЬ УРАВНЕНИЯ С КОЭФФИЦИЕНТАМИ ДРОБ, ОЧИСТЯ ДРОБИ

Шаг 1. Найдите наименьший общий знаменатель всех дробей в уравнении.

Шаг 2. Умножьте обе части уравнения на этот ЖК-дисплей. Это очищает фракции.

Шаг 3. Решите, используя общую стратегию решения линейных уравнений.

Пример \ (\ PageIndex {2} \):

Решение: 7 = \ (\ dfrac {1} {2} x + \ dfrac {3} {4} x — \ dfrac {2} {3} x \).

Решение

Мы хотим очистить дроби, умножив обе части уравнения на ЖК-дисплей всех дробей в уравнении.

Найдите наименьший общий знаменатель всех дробей в уравнении. $$ 7 = \ dfrac {1} {2} x + \ dfrac {3} {4} x — \ dfrac {2} {3} x \ quad LCD = 12 $$
Умножьте обе части уравнения на 12. $$ \ textcolor {red} {12} (7) = \ textcolor {red} {12} \ cdot \ dfrac {1} {2} x + \ dfrac {3} {4} x — \ dfrac {2} {3} х $
Распространить. $$ 12 (7) = 12 \ cdot \ dfrac {1} {2} x + 12 \ cdot \ dfrac {3} {4} x — 12 \ cdot \ dfrac {2} {3} x $$
Упростите — и заметьте, никаких дробей! $$ 84 = 6x + 9x — 8x $$
Объедините похожие термины. $$ 84 = 7x $$
Разделить на 7. $$ \ dfrac {84} {\ textcolor {red} {7}} = \ dfrac {7x} {\ textcolor {red} {7}} $$
Упростить. $$ 12 = x $$
Проверка: пусть x = 12. $$ \ begin {split} 7 & = \ dfrac {1} {2} x + \ dfrac {3} {4} x — \ dfrac {2} {3} x \\ 7 & \ stackrel {?} { =} \ dfrac {1} {2} (\ textcolor {red} {12}) + \ dfrac {3} {4} (\ textcolor {red} {12}) — \ dfrac {2} {3} (\ textcolor {красный} {12}) \\ 7 & \ stackrel {?} {=} 6 + 9 — 8 \\ 7 & = 7 \; \ checkmark \ end {split} $$

Упражнение \ (\ PageIndex {3} \):

Решение: 6 = \ (\ dfrac {1} {2} v + \ dfrac {2} {5} v — \ dfrac {3} {4} v \).

Ответ

v = 40

Упражнение \ (\ PageIndex {4} \):

Решить: -1 = \ (\ dfrac {1} {2} u + \ dfrac {1} {4} u — \ dfrac {2} {3} u \).

Ответ

u = -12

В следующем примере у нас будут переменные и дроби с обеих сторон уравнения.

Пример \ (\ PageIndex {3} \):

Решение: \ (x + \ dfrac {1} {3} = \ dfrac {1} {6} x — \ dfrac {1} {2} \).

Решение

Найдите на ЖК-дисплее все дроби в уравнении. $$ x + \ dfrac {1} {3} = \ dfrac {1} {6} x — \ dfrac {1} {2} \ quad LCD = 6 $$
Умножьте обе стороны на ЖК-дисплей. $$ \ textcolor {красный} {6} \ left (x + \ dfrac {1} {3} \ right) = \ textcolor {red} {6} \ left (\ dfrac {1} {6} x — \ dfrac {1} {2} \ right) $$
Распространить. $$ 6 \ cdot x + 6 \ cdot \ dfrac {1} {3} = 6 \ cdot \ dfrac {1} {6} x — 6 \ cdot \ dfrac {1} {2} $$
Упростите — больше никаких дробей! $$ 6x + 2 = x — 3 $$
Вычтите x с обеих сторон. $$ 6x \ textcolor {красный} {- x} + 2 = x \ textcolor {красный} {- x} — 3 $$
Упростить. $$ 5x + 2 = -3 $$
Вычтем 2 с обеих сторон. $$ 5x + 2 \ textcolor {красный} {- 2} = -3 \ textcolor {красный} {- 2} $$
Упростить. $$ 5x = -5 $$
Разделить на 5. $$ \ dfrac {5x} {\ textcolor {red} {5}} = \ dfrac {-5} {\ textcolor {red} {5}} $$
Упростить. $$ x = -1 $$
Проверить: подставить x = −1. $$ \ begin {split} x + \ dfrac {1} {3} & = \ dfrac {1} {6} x — \ dfrac {1} {2} \\ (\ textcolor {red} {- 1} ) + \ dfrac {1} {3} & \ stackrel {?} {=} \ dfrac {1} {6} (\ textcolor {red} {- 1}) — \ dfrac {1} {2} \\ ( -1) + \ dfrac {1} {3} & \ stackrel {?} {=} — \ dfrac {1} {6} — \ dfrac {1} {2} \\ — \ dfrac {3} {3} + \ dfrac {1} {3} & \ stackrel {?} {=} — \ dfrac {1} {6} — \ dfrac {3} {6} \\ — \ dfrac {2} {3} & \ stackrel {?} {=} — \ dfrac {4} {6} \\ — \ dfrac {2} {3} & = — \ dfrac {2} {3} \; \ checkmark \ end {split} $$

Упражнение \ (\ PageIndex {5} \):

Решение: \ (a + \ dfrac {3} {4} = \ dfrac {3} {8} a — \ dfrac {1} {2} \).

Ответ

а = -2

Упражнение \ (\ PageIndex {6} \):

Решение: \ (c + \ dfrac {3} {4} = \ dfrac {1} {2} c — \ dfrac {1} {4} \).

Ответ

с = -2

В примере 8. 40 мы начнем с использования свойства распределения. Этот шаг сразу очистит дроби!

Пример \ (\ PageIndex {4} \):

Решить: 1 = \ (\ dfrac {1} {2} \) (4x + 2).

Решение

Распространить. $$ 1 = \ dfrac {1} {2} \ cdot 4x + \ dfrac {1} {2} \ cdot 2 $$
Упростить. Теперь дробей нет! $$ 1 = 2x + 1 $$
Вычтем 1 с обеих сторон. $$ 1 \ textcolor {красный} {- 1} = 2x + 1 \ textcolor {красный} {- 1} $$
Упростить. $$ 0 = 2x $$
Разделить на 2. $$ \ dfrac {0} {\ textcolor {red} {2}} = \ dfrac {2x} {\ textcolor {red} {2}} $$
Упростить. $$ 0 = x $$
Проверка: пусть x = 0. $$ \ begin {split} 1 & = \ dfrac {1} {2} (4x + 2) \\ 1 & \ stackrel {?} {=} \ Dfrac {1} {2} [4 (\ textcolor { красный} {0}) + 2] \\ 1 & \ stackrel {?} {=} \ dfrac {1} {2} (2) \\ 1 & \ stackrel {?} {=} \ dfrac {2} { 2} \\ 1 & = 1 \; \ checkmark \ end {split} $$

Упражнение \ (\ PageIndex {7} \):

Решить: −11 = \ (\ dfrac {1} {2} \) (6p + 2).

Ответ

п = -4

Упражнение \ (\ PageIndex {8} \):

Решение: 8 = \ (\ dfrac {1} {3} \) (9q + 6).

Ответ

q = 2

Часто дроби остаются даже после распределения.

Пример \ (\ PageIndex {5} \):

Решение: \ (\ dfrac {1} {2} \) (y — 5) = \ (\ dfrac {1} {4} \) (y — 1).

Решение

Распространить. $$ \ dfrac {1} {2} \ cdot y — \ dfrac {1} {2} \ cdot 5 = \ dfrac {1} {4} \ cdot y — \ dfrac {1} {4} \ cdot 1 $
Упростить. $$ \ dfrac {1} {2} y — \ dfrac {5} {2} = \ dfrac {1} {4} y — \ dfrac {1} {4} $$
Умножить на ЖК-дисплей, 4. $$ \ textcolor {красный} {4} \ left (\ dfrac {1} {2} y — \ dfrac {5} {2} \ right) = \ textcolor {red} {4} \ left (\ dfrac { 1} {4} y — \ dfrac {1} {4} \ right) $$
Распространить. $$ 4 \ cdot \ dfrac {1} {2} y — 4 \ cdot \ dfrac {5} {2} = 4 \ cdot \ dfrac {1} {4} y — 4 \ cdot \ dfrac {1} {4 } $$
Упростить. $$ 2y — 10 = y — 1 $$
Соберите элементы y слева. $$ 2y — 10 \ textcolor {красный} {- y} = y — 1 \ textcolor {красный} {- y} $$
Упростить. $$ y — 10 = -1 $$
Соберите константы справа. $$ y — 10 \ textcolor {красный} {+ 10} = -1 \ textcolor {красный} {+ 10} $$
Упростить. $$ y = 9 $$
Проверка: замените 9 на y. $$ \ begin {split} \ dfrac {1} {2} (y — 5) & = \ dfrac {1} {4} (y — 1) \\ \ dfrac {1} {2} (\ textcolor { красный} {9} — 5) & \ stackrel {?} {=} \ dfrac {1} {4} (\ textcolor {red} {9} — 1) \\ \ dfrac {1} {2} (4) & \ stackrel {?} {=} \ dfrac {1} {4} (8) \\ 2 & = 2 \; \ checkmark \ end {split} $$

Упражнение \ (\ PageIndex {9} \):

Решение: \ (\ dfrac {1} {5} \) (n + 3) = \ (\ dfrac {1} {4} \) (n + 2).

Ответ

п = 2

Упражнение \ (\ PageIndex {10} \):

Решение: \ (\ dfrac {1} {2} \) (m — 3) = \ (\ dfrac {1} {4} \) (m — 7).

Ответ

м = -1

Решите уравнения с десятичными коэффициентами

В некоторых уравнениях есть десятичные дроби. Такое уравнение возникает, когда мы решаем проблемы, связанные с деньгами и процентами. Но десятичные дроби — это еще один способ представления дробей.Например, 0,3 = \ (\ dfrac {3} {10} \) и 0,17 = \ (\ dfrac {17} {100} \). Итак, когда у нас есть уравнение с десятичными знаками, мы можем использовать тот же процесс, который мы использовали для очистки дробей, — умножить обе части уравнения на наименьший общий знаменатель.

Пример \ (\ PageIndex {6} \):

Решить: 0,8x — 5 = 7.

Решение

Единственная десятичная дробь в уравнении — 0,8. Так как 0. 8 = \ (\ dfrac {8} {10} \), на ЖК-дисплее будет 10. Мы можем умножить обе стороны на 10, чтобы очистить десятичную дробь.

Умножьте обе стороны на ЖК-дисплей. $$ \ textcolor {красный} {10} (0,8x — 5) = \ textcolor {красный} {10} (7) $$
Распространить. $$ 10 (0,8x) — 10 (5) = 10 (7) $$
Умножьте и заметьте, больше никаких десятичных знаков! $$ 8x — 50 = 70 $$
Добавьте 50, чтобы сдвинуть все константы вправо. $$ 8x — 50 \ textcolor {красный} {+ 50} = 70 \ textcolor {красный} {+ 50} $$
Упростить. $$ 8x = 120 $$
Разделите обе стороны на 8. $$ \ dfrac {8x} {\ textcolor {red} {8}} = \ dfrac {120} {\ textcolor {red} {8}} $$
Упростить. $$ x = 15 $$
Проверка: пусть x = 15. $$ \ begin {split} 0.8 (\ textcolor {red} {15}) — 5 & \ stackrel {?} {=} 7 \\ 12 — 5 & \ stackrel {?} {=} 7 \\ 7 & = 7 \; \ checkmark \ end {split} $$

Упражнение \ (\ PageIndex {11} \):

Решить: 0.6x — 1 = 11.

Ответ

х = 20

Упражнение \ (\ PageIndex {12} \):

Решить: 1,2x — 3 = 9.

Ответ

х = 10

Пример \ (\ PageIndex {7} \):

Решить: 0,06x + 0,02 = 0,25x — 1,5.

Решение

Посмотрите на десятичные дроби и подумайте об эквивалентных дробях.

\ [0.06 = \ dfrac {6} {100}, \ qquad 0.02 = \ dfrac {2} {100}, \ qquad 0.25 = \ dfrac {25} {100}, \ qquad 1.5 = 1 \ dfrac {5} {10} \]

Обратите внимание, на ЖК-дисплее 100. Умножая на ЖК-дисплей, мы очищаем десятичные дроби.

Умножьте обе стороны на 100.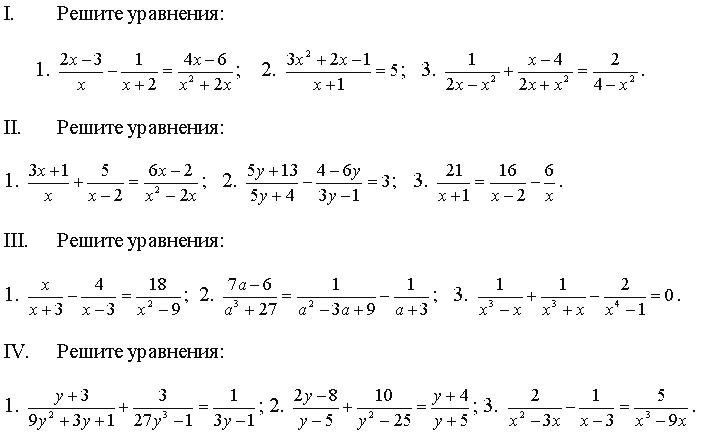 $$ \ textcolor {красный} {100} (0,06x + 0,02) = \ textcolor {красный} {100} (0,25x — 1,5) $$
Распространить. $$ 100 (0,06x) + 100 (0,02) = 100 (0,25x) — 100 (1,5) $$
Умножьте, и больше никаких десятичных знаков. $$ 6x + 2 = 25x — 150 $$
Соберите переменные справа. $$ 6x \ textcolor {красный} {- 6x} + 2 = 25x \ textcolor {красный} {- 6x} — 150 $$
Упростить. $$ 2 = 19x — 150 $$
Соберите константы слева. $$ 2 \ textcolor {красный} {+ 150} = 19x — 150 \ textcolor {красный} {+ 150} $$
Упростить. $$ 152 = 19x $$
Разделить на 19. $$ \ dfrac {152} {\ textcolor {red} {19}} = \ dfrac {19x} {\ textcolor {red} {19}} $$
Упростить. $$ 8 = x $$
Проверить: Пусть x = 8. $$ \ begin {split} 0,06 (\ textcolor {red} {8}) + 0,02 & = 0,25 (\ textcolor {red} {8}) — 1,5 \\ 0,48 + 0,02 & = 2,00 — 1,5 \\ 0,50 & = 0,50 \; \ checkmark \ end {split} $$

Упражнение \ (\ PageIndex {13} \):

Решить: 0.14ч + 0,12 = 0,35ч — 2,4.

Ответ

ч = 12

Упражнение \ (\ PageIndex {14} \):

Решить: 0,65k — 0,1 = 0,4k — 0,35.

Ответ

к = -1

В следующем примере используется уравнение, типичное для тех, которые мы увидим в денежных приложениях в следующей главе. Обратите внимание, что мы сначала распределим десятичные дроби, прежде чем очистим все десятичные дроби в уравнении.

Пример \ (\ PageIndex {8} \):

Решить: 0,25x + 0,05 (x + 3) = 2,85.

Решение

Распределить первым. $$ 0,25x + 0,05x + 0,15 = 2,85 $$
Объедините похожие термины. $$ 0,30x + 0,15 = 2,85 $$
Чтобы очистить десятичные дроби, умножьте на 100. $$ \ textcolor {красный} {100} (0,30x + 0,15) = \ textcolor {красный} {100} (2.85) $$
Распространить. $$ 30x + 15 = 285 $$
Вычтем 15 с обеих сторон. $$ 30x + 15 \ textcolor {красный} {- 15} = 285 \ textcolor {красный} {- 15} $$
Упростить. $$ 30x = 270 $$
Разделить на 30. $$ \ dfrac {30x} {\ textcolor {red} {30}} = \ dfrac {270} {\ textcolor {red} {30}} $$
Упростить. $$ x = 9 $$
Проверка: пусть x = 9. $$ \ begin {split} 0,25x + 0,05 (x + 3) & = 2,85 \\ 0,25 (\ textcolor {red} {9}) + 0,05 (\ textcolor {red} {9} + 3) & \ stackrel {?} {=} 2,85 \\ 2,25 + 0,05 (12) & \ stackrel {?} {=} 2,85 \\ 2,25 + 0,60 & \ stackrel {?} {=} 2,85 \\ 2,85 & = 2,85 \; \ checkmark \ end {split} $$

Упражнение \ (\ PageIndex {15} \):

Решить: 0,25n + 0,05 (n + 5) = 2. 95.

Ответ

п = 9

Упражнение \ (\ PageIndex {16} \):

Решить: 0,10d + 0,05 (d — 5) = 2,15.

Ответ

г = 16

8. Уравнения с дробями

В этом разделе мы можем легко найти решение, умножив его на наименьший общий знаменатель (LCD) . Это упростит наше уравнение и облегчит его решение.

Нам нужно помнить, что нужно умножить все члены в уравнении (обе стороны от знака равенства) на ЖК-дисплей, иначе окончательный ответ будет неправильным.

Мы начнем с некоторых алгебраических примеров, а затем перейдем к некоторым задачам со словами, связанным с дробями.

а. Алгебраические типы

Пример 1

Решить относительно x :

`x / 5 + 3/10 = 1/2`

Ответ

Сначала мы смотрим на знаменателей дробей и определяем наименьший общий знаменатель. В данном случае это будет «10.»

Мы умножаем все на `10` и получаем:

`10xx (x / 5 + 3/10) = 10xx (1/2)`

`2x + 3 = 5`

Затем мы просто решаем более простое уравнение, которое мы нашли.

Вычтем `3` с обеих сторон:

`2x = 2`

Разделите обе стороны на `2`, и мы получим окончательный ответ:

`x = 1`

Пример 2

Решить относительно x :

`(2x) / 3 + 2/5 = 8 + x / 2`

Ответ

Еще раз смотрим на знаменателей и дробей и определяем наименьший общий знаменатель.В данном случае это будет «30».

Мы умножаем все на `30` и получаем:

`30xx ((2x) / 3 + 2/5) = 30xx (8 + x / 2)`

`20x + 12 = 240 + 15x`

Вычитая `12` с обеих сторон:

`20x = 228 + 15x`

Вычтите `15x` с обеих сторон:

`5x = 228`

Разделите обе стороны на «5», и мы получим окончательный ответ:

x = 228/5 = 45,6

Пример 3

Следующий имеет переменную в знаменателе . Нам по-прежнему нужно будет найти ЖК-дисплей.

Решить относительно x :

`4 / x + 1/3 = 7 / (5x)`

Ответ

В данном случае наименьший общий знаменатель — «15x».

Мы умножаем все на `15x` и получаем:

`15x xx (4 / x + 1/3) = 15x xx (7 / (5x))`

`60 + 5x = 21`

Вычитая `60` с обеих сторон:

`5x = -39`

Разделите обе стороны на «5», и мы получим окончательный ответ:

`х = -39 / 5 = -7.8`

г. Проблемы со словами

Пример 4

Аквариум можно наполнить одним шлангом за 7 минут и вторым более тонким шлангом за 10 минут.

Сколько времени потребуется для заполнения бака, если оба шланга работают вместе?

Ответ

Поскольку каждый шланг сокращает время наполнения на до , мы имеем чтобы сложить обратные величины и получить обратную величину от результата.

Нам нужно использовать:

`1 / T = 1 / T_1 + 1 / T_2`

Итак имеем:

`1 / T = 1/7 + 1 / 10`

`1 / T = (10 + 7) / 70 = 17 / 70`

Так

`Т = 70/17 = 4.1176`

Таким образом, заполнение бака при одновременном соединении обоих шлангов займет 4,1 минуты.

Пример 5

Связанные страницы

Вам могут пригодиться:

Для 2 резисторов с сопротивлениями R 1 и R 2 параллельно, комбинированное сопротивление R определяется по формуле:

`1 / R = 1 / R_1 + 1 / R_2`

Для конкретной цепи суммарное сопротивление R оказалось равным 4 Ом (Ом), а R 1 = 10 Ом.Найдите R 2 .

Ответ

У нас:

`1/4 = 1/10 + 1 / R_2`

Нам нужно всюду умножить на наименьший общий знаменатель : 20 R 2

`1/4 = 1/10 + 1 / R_2`

`(20R_2) / 4 = (20R_2) / 10 + (20R_2) / (R_2)`

`5R_2 = 2R_2 + 20`

`3R_2 = 20`

`R_2 = 20/3 = 6 2 / 3Omega`

«Омега» — обозначение единицы измерения сопротивления «Ом».

Пример 6

Средняя скорость автомобиля 30 км / ч от дома до работы и 40 км / ч на обратном пути. Если общее время для двух поездок составляет 50 минут, как далеко от дома до работы?

Ответ

Пусть длина пути от дома до работы составит x км.

Напомним, что

`текст (скорость) = текст (расстояние) / текст (время)`

Так

`текст (время) = текст (расстояние) / текст (скорость)`

Мы должны использовать одни и те же единицы времени повсюду.Будем использовать часы.

Сейчас

`50 \ text (минуты) = 50/60 = 5 / 6text (часы)`

Время в пути вперед составило «x / 30» часов.

Для обратного пути время составляло «x / 40» часов.

Общее время было `x / 30 + x / 40 = 5/6 \ text (часы)`

Итак, `(4x + 3x) / 120 = (7x) / 120 = 5/6`

Это дает нам `7x = (5xx120) / 6 = 100`

То есть x = 100/7 = 14. 286

Таким образом, расстояние от дома до работы составляет 14,3 км.

Калькулятор очищающих дробей

Наших пользователей:

Спасибо, что очень быстро ответили на мой вопрос, буду рекомендовать вас по всему миру.
Джули Саймонс, Джорджия

Если у вас возникли проблемы со сложными алгебраическими уравнениями, у меня есть два слова для вас: Алгебратор! Попробуйте, я гарантирую, вы увидите результаты в своей математической работе. Это помогло мне и моим друзьям пройти сложный урок математики для первокурсников.
Victoria Hill, CO

Мой четырнадцатилетний сын Брэдли считался в школе подверженным риску. Но я не мог заставить его слушать меня.Затем, когда учитель в его школе, мистер Киндлер, благословил его сердце, заставил его попробовать внешкольную программу, это было похоже на чудо! Я бы не сказал, что Брэдли стал образцовым учеником, но он больше не пропускал уроки математики. Поэтому, когда я узнал, что мистер Киндлер основал всю свою программу на использовании Алгебратора, мне просто пришлось написать это письмо, чтобы поблагодарить вас! Представь это!
Монтгомери Гросс, Вирджиния

Мне очень понравилась возможность выбрать конкретное преобразование для выполнения, а не слепое копирование процесса решения. .
J.F., Аляска

Я считаю, что эта программа очень полезна! Спасибо!
C.B., Оклахома

Студенты, решающие всевозможные алгебры, узнают, что наше программное обеспечение спасает жизнь. Вот поисковые фразы, которые использовали сегодняшние поисковики, чтобы найти наш сайт. Можете ли вы найти среди них свою?


Поисковые фразы, использованные на 2014-09-08:
  • вопросник модели aptitude
  • рабочие листы с уравнениями
  • Рабочие листы с дробями, добавление терминов
  • год 8 тест по математике
  • математические формулы для парабол
  • онлайн-калькулятор экспонент и дробей
  • алгебратора.com
  • английский 4 единицы рабочий лист 5 возраст бесплатно
  • домашнее задание и решение упражнения на перестановку
  • бесплатные онлайн-уроки математики для 9-го класса
  • Бесплатная справка по линейным задачам со словами
  • образцов тестов коэффициентов и соотношений
  • решить алгебру колледжа
  • Калькулятор общего знаменателя
  • www. math fration chart
  • как рассчитать комбинацию по TI-83
  • мелочи по elipse
  • решатель комплексных корней
  • бесплатный эмулятор TI 30X IIS
  • Калькулятор дифференциальных уравнений
  • комбинаций и перестановок математика средней школы
  • рабочих листов + третий класс
  • aptitude test загрузить
  • балансировочные уравнения онлайн
  • скачать образ ROM калькулятора
  • метод подстановки с тремя переменными
  • примеров решения полиномиальных неравенств в кубе
  • фиолетовый задания и тесты по математике для 5 класса
  • mathematica скачать бесплатно
  • дробей каково расположение каждой точки в виде десятичной дроби и дроби
  • gmat практика
  • онлайн калькулятор второй производной
  • мелочи по экспоненциальной функции
  • сложение непохожих целых чисел
  • словесных задач по алгебре 2 листа максимум минимум
  • принцип математического анализа вальтер рудин «руководство по решению
  • решатель задач алгебры 2
  • Квадратный корень 7-й класс рабочих листов
  • бесплатная онлайн-распечатка вопросов по математике KS2
  • Виртуальные манипуляторы + объединение одинаковых терминов
  • Рабочий лист задач по преалгебре
  • листов с упражнениями для решения заменой
    • История символа квадратного корня
  • Тригонометрическая поэма
  • СБ-9 вопросов на бесплатную практику
  • листы по алгебре полиномов
  • поиск журнала с помощью калькулятора ti
  • Мир химии Книга Макдугала Литтелла ответы
  • Проблемы в реальном анализе: рабочая тетрадь с решениями скачать
  • Ti-84 баланс химического уравнения
  • листы сложения положительных и отрицательных чисел
    • Раздел обзора концепции рабочего листа
  • навыков: использование ответов на вопросы
  • уравнения умножения и деления
  • МАТЕМАТИЧЕСКИЕ ТРИВИАС
  • Калькулятор для поиска ответов на дроби с разными знаменателями
  • онлайн-упражнения по неравенству по математике
  • Matlab решение системных уравнений
  • балдор математика
  • как решить для y с помощью решения в калькуляторе TI-89 Titanium
  • Преобразование дробей в десятичные. Планы уроков 9 класс
  • Упрощение уравнений
  • рабочий лист для 6-го класса для печати бесплатно
  • деление многочленов активность онлайн
  • Математика до алгебры саксонская онлайн
  • успеваемость по математике за 10 класс
  • счетчики геометрии
  • триггер по алгебре 2 минуты на ti 84
  • АЛГЕБРА С ПИЦЦАЦ
  • скачать бесплатно программу решения уравнений
  • Рабочие листы шестого класса с целыми числами
  • логарифмирование слов задачи по алгебре II
  • построение квадратичных уравнений на TI-84 плюс
  • Таблицы алгебры
  • 2.125 дюймов преобразовать в дробь
  • «комбинаций» + «рабочий лист» + «бесплатно»
  • Вопросы по математике для 4 класса экзамен по индии
  • Алгебра 1 Учебное пособие для печати
  • урок 92 алгебра 1/2 постепенное развитие ответы
  • квадратный корень для чайников
  • коэффициент умножения и деления общий знаменатель
  • решение квадратного корня из отрицательного 1

Калькулятор дробей — онлайн-инструмент для упрощения дробей

Поиск инструмента

Калькулятор с дробями

Инструмент / Калькулятор с дробями и упрощением. Вычисление с использованием дробей включает определенные шаги вычисления числителя и знаменателя, прежде чем упрощать.

Результаты

Калькулятор с дробями — dCode

Тег (и): символическое вычисление

Поделиться

dCode и другие

dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !

Рекламные объявления

Ответы на вопросы (FAQ)

Как упростить дроби до неразложимой формы?

dCode сначала выполняет вычисления (сложение, вычитание, умножение или любое другое вычисление исходного математического выражения) и превращает их в несводимые дроби, сводя их к одному знаменателю.В результате дано упрощение в виде дроби в несократимой форме.

Пример: $$ \ frac12 + \ frac14 = \ frac34 $$

dCode позволяет проверять результаты школьных упражнений и скоро покажет пошаговые вычисления, а пока используйте инструменты LCM и GCD.

Как привести к тому же знаменателю?

dCode может вычислять наименьшее общее кратное знаменателей для реализации сложения и вычитания.

Пример: Если знаменатели добавляемых дробей равны 8 и 3, то НОК (8,3) = 24 и дробь должна иметь знаменатель 24: 15 / 8-2 / 3 = 29/24.

Умножение числителя подразумевает умножение знаменателя, чтобы сохранить равенство дроби.

Как складывать дроби?

Сложение дроби требует уменьшения дробей до одного знаменателя (попытка упростить дроби заранее, если возможно), а затем добавления числителей (попытка упростить полученную дробь, если возможно).

Пример: $$ \ frac {1} {2} + \ frac {1} {3} = \ frac {1 \ times 3} {2 \ times 3} + \ frac {1 \ times 2} { 3 \ times 2} = \ frac {3} {6} + \ frac {2} {6} = \ frac {3 + 2} {6} = \ frac {5} {6} $$

Как вычесть дроби?

Вычитание дробей такое же, как и сложение, за исключением того, что вам нужно вычитать числители, а не складывать их.

Пример: $$ \ frac {1} {2} — \ frac {1} {3} = \ frac {1 \ times 3} {2 \ times 3} — \ frac {1 \ times 2} { 3 \ times 2} = \ frac {3} {6} — \ frac {2} {6} = \ frac {3-2} {6} = \ frac {1} {6} $$

Как умножать дроби?

Умножение дробей на состоит в умножении числителя между ними, а затем знаменателей между ними (постарайтесь упростить дроби до и / или после, если это возможно).

Пример: $$ \ frac {1} {2} \ times \ frac {2} {3} = \ frac {1 \ times 2} {2 \ times 3} = \ frac {2} {6} = \ frac {1} {3} $$

Как разделить дроби?

Деление дробей можно записать как умножение первой дроби на обратную для второй дроби (обращение числителя и знаменателя).Затем примените технику умножения.

Задайте новый вопрос

Исходный код

dCode сохраняет за собой право собственности на исходный код онлайн-инструмента «Калькулятор с дробями». За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / free), любой алгоритм, апплет или фрагмент «Калькулятор с дробями» (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любой «Калькулятор» с функцией Fractions (вычислить, преобразовать, решить, расшифровать / зашифровать, расшифровать / зашифровать, декодировать / закодировать, перевести), написанную на любом информатическом языке (Python, Java, PHP, C #, Javascript, Matlab и т. д.)) и никакая загрузка данных, скрипт, копипаст или доступ к API для «Калькулятора с дробями» не будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.

Нужна помощь?

Пожалуйста, посетите наше сообщество dCode Discord для получения помощи!
NB: для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!

Вопросы / Комментарии

Сводка

Похожие страницы

Поддержка

Форум / Справка

Ключевые слова

дробь, числитель, знаменатель, частное, то же самое, сложение, вычитание, умножение, деление, упрощение, упрощение, шаг, выражение, математика, переменная, уменьшение, калькулятор

Ссылки


Источник: https: // www.dcode.fr/fractions-calculator

© 2021 dCode — Идеальный «инструментарий» для решения любых игр / загадок / геокэшинга / CTF.

No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *