Как решать неполные квадратные уравнения
Как решать неполные квадратные уравнения
Квадратное уравнение имеет вид , где . Если или , то уравнение называется неполным и допускает решение без использования дискриминанта (подробнее о дискриминанте в статье Как решать квадратные уравнения). Рассмотрим каждый случай на примерах.
а) случай
Неполное квадратное уравнение имеет вид , где .
Пример 1. .
В этом уравнении корней нет, так как левая часть при любых значениях положительна, в то время как правая часть равна нулю. Следовательно, равенство невозможно. Ответ: нет корней.
Пример 2. .
Правая часть уравнения отрицательна (-4<0), а левая часть при любых таковой не является, ведь любое число в квадрате неотрицательно. Ответ: нет корней.
Пример 3. .
Уравнение имеет единственный корень, равный нулю. Ответ: 0.
Пример 4. .
Типичной ошибкой является ответ . На самом деле . То есть уравнение имеет два корня.
Пример 5. .
Перенесем число в правую часть. При этом слагаемое поменяет знак. Тогда . Откуда . Остается немного упростить полученное выражение. Ответ: .
Пример 6. .
Важно не забыть проанализировать знак правой части. Число , так как , поэтому уравнение не имеет корней. Ошибкой было бы считать, что , ведь квадратный корень из отрицательного числа не существует.
Таким образом, в случае сначала упрощаем уравнение к виду , затем определяем знак числа . Если , то корней нет. Если , то . И если , то уравнение имеет два корня .
б) случай
Уравнение имеет вид , где .
Пример 7. .
Наша цель применить метод разложения на множители. Для этого в правой части должен быть 0, а в левой части — произведение. Вынесем за скобки, тогда . Произведение равно нулю, значит, хотя бы один из множителей равен нулю. Поэтому или , откуда или . То есть уравнение распалось на два более простых (линейных) уравнения. Ответ: .
Пример 8.
Раскроем скобки и приведем подобные слагаемые:
Далее разложим левую часть на множители.
Получим два линейных уравнения.
или , откуда или .
Ответ:
Таким образом, в случае неполное квадратное уравнение решается методом разложения на множители.
Если у вас трудности с арифметическими вычислениями, потренироваться можно здесь.
Задачи для самостоятельного решения
Ответы
- 0; -3/7
- 0; 5/4
- -2; 2
- -4; 4
еще задачи здесь (номера 1-4, 29-34, ответы в комментариях)
еще статья Как решать квадратные уравнения
все статьи по школьной математике
Виды неполных квадратных уравнений
☰
Квадратное уравнение имеет вид ax
Неполными квадратными уравнениями являются уравнения трех видов:
- ax2 + bx = 0, когда коэффициент c = 0.
- ax2 + c = 0, когда коэффициент b = 0.

- ax2 = 0, когда и b и с равны 0.
Коэффициент же a по определению квадратного уравнения не может быть равен нулю.
Неполные квадратные уравнения решаются проще, чем полные квадратные. Способы решения различаются в зависимости от вида неполного квадратного уравнения.
Проще всего решаются уравнения вида ax2 = 0. Если a по определению квадратного уравнения не может быть равно нулю, то очевидно, что нулю может быть равен только x2, а значит, и сам x. У уравнений такого вида всегда есть один корень, он равен 0. Например:
–3x2 = 0
x2 = 0
x = √0
x = 0
Уравнения вида ax2 + c = 0 преобразуются к виду ax2 = –c и решаются аналогично предыдущему. Однако корней здесь либо два, либо не одного.
ax2 + c = 0
ax2 = –c
x2 = –c/a
x = √(–c/a)
Здесь если подкоренное выражение отрицательно, то корней у уравнения нет. Если положительно, то корней будет два: √(–c/a) и –√(–c/a). Пример решения подобного уравнения:
Если положительно, то корней будет два: √(–c/a) и –√(–c/a). Пример решения подобного уравнения:
4x2 – 16 = 0
4x2 = 16
x2 = 16 / 4
x2 = 4
x = √4
x1 = 2; x2 = –2
Неполные квадратные уравнения вида ax2 + bx = 0 решается вынесением общего множителя за скобку. В данном случае им является x. Получается уравнение x(ax + b) = 0. Это уравнение имеет два корня: либо x = 0, либо ax + b = 0. Решая второе уравнение получаем x = –b/a. Таким образом, уравнения вида ax
3x2 – 10x = 0
x(3x – 10) = 0
x1 = 0; x2 = 10/3 = 3,(33)
Неполные квадратные уравнения с дробями. Как решать неполное квадратное уравнение пример
В данной статье мы рассмотрим решение неполных квадратных уравнений.
Но сначала повторим какие уравнения называются квадратными. Уравнение вида ах 2 + bх + с = 0, где х – переменная, а коэффициенты а, b и с некоторые числа, причем а ≠ 0, называется квадратным . Как мы видим коэффициент при х 2 не равен нулю, а следовательно коэффициенты при х или свободный член могут равняться нулю, в этом случае мы и получаем неполное квадратное уравнение.
Неполные квадратные уравнения бывают трех видов
:1) Если b = 0, с ≠ 0, то ах 2 + с = 0;
2) Если b ≠ 0, с = 0, то ах 2 + bх = 0;
3) Если b= 0, с = 0, то ах 2 = 0.
- Давайте разберемся как решаются уравнения вида ах 2 + с = 0.
Чтобы решить уравнение перенесем свободный член с в правую часть уравнения, получим
ах 2 = ‒с. Так как а ≠ 0, то разделим обе части уравнения на а, тогда х 2 = ‒с/а.
Если ‒с/а > 0 , то уравнение имеет два корня
x = ±√(–c/a) .
Если же ‒c/a
Давайте попробуем разобраться на примерах, как решать такие уравнения.
Пример 1 . Решите уравнение 2х 2 ‒ 32 = 0.
Ответ: х 1 = ‒ 4, х 2 = 4.
Пример 2 . Решите уравнение 2х 2 + 8 = 0.
Ответ: уравнение решений не имеет.
- Разберемся как же решаются уравнения вида ах 2 + bх = 0.
Чтобы решить уравнение ах 2 + bх = 0, разложим его на множители, то есть вынесем за скобки х, получим х(ах + b) = 0. Произведение равно нулю, если хотя бы один из множителей равен нулю. Тогда или х = 0, или ах + b = 0. Решая уравнение ах + b = 0, получим ах = ‒ b, откуда х = ‒ b/a. Уравнение вида ах 2 + bх = 0, всегда имеет два корня х 1 = 0 и х 2 = ‒ b/a. Посмотрите как выглядит на схеме решение уравнений этого вида.
Закрепим наши знания на конкретном примере.
Пример 3 . Решить уравнение 3х 2 ‒ 12х = 0.
х(3х ‒ 12) = 0
х= 0 или 3х – 12 = 0
Ответ: х 1 = 0, х 2 = 4.
- Уравнения третьего вида ах 2 = 0 решаются очень просто.
Если ах 2 = 0, то х 2 = 0. Уравнение имеет два равных корня х 1 = 0, х 2 = 0.
Уравнение имеет два равных корня х 1 = 0, х 2 = 0.
Для наглядности рассмотрим схему.
Убедимся при решении примера 4, что уравнения этого вида решаются очень просто.
Пример 4. Решить уравнение 7х 2 = 0.
Ответ: х 1, 2 = 0.
Не всегда сразу понятно какой вид неполного квадратного уравнения нам предстоит решить. Рассмотрим следующий пример.
Пример 5. Решить уравнение
Умножим обе части уравнения на общий знаменатель, то есть на 30
Сократим
5(5х 2 + 9) – 6(4х 2 – 9) = 90.
Раскроем скобки
25х 2 + 45 – 24х 2 + 54 = 90.
Приведем подобные
Перенесем 99 из левой части уравнения в правую, изменив знак на противоположный
Ответ: корней нет.
Мы разобрали как решаются неполные квадратные уравнения. Надеюсь, теперь у вас не будет сложностей с подобными заданиями. Будьте внимательны при определении вида неполного квадратного уравнения, тогда у вас все получится.
Если у вас появились вопросы по данной теме, мы вместе решим возникшие проблемы.
Квадратные уравнения изучают в 8 классе, поэтому ничего сложного здесь нет. Умение решать их совершенно необходимо.
— это уравнение вида ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, причем a ≠ 0.
Прежде, чем изучать конкретные методы решения, заметим, что все квадратные уравнения можно условно разделить на три класса:
- Не имеют корней;
- Имеют ровно один корень;
- Имеют два различных корня.
В этом состоит важное отличие квадратных уравнений от линейных, где корень всегда существует и единственен. Как определить, сколько корней имеет уравнение? Для этого существует замечательная вещь — дискриминант .
Дискриминант
Пусть дано квадратное уравнение ax 2 + bx + c = 0.
Тогда — это просто число D = b 2 − 4ac.
Эту формулу надо знать наизусть. Откуда она берется — сейчас неважно. Важно другое: по знаку дискриминанта можно определить, сколько корней имеет квадратное уравнение. А именно:
- Если D
- Если D = 0, есть ровно один корень;
- Если D > 0, корней будет два.
Обратите внимание: дискриминант указывает на количество корней, а вовсе не на их знаки, как почему-то многие считают. Взгляните на примеры — и сами все поймете:
Задача. Сколько корней имеют квадратные уравнения:
- x 2 − 8x + 12 = 0;
- 5x 2 + 3x + 7 = 0;
- x 2 − 6x + 9 = 0.
Выпишем коэффициенты для первого уравнения и найдем дискриминант:
a = 1, b = −8, c = 12;
D = (−8) 2 − 4 · 1 · 12 = 64 − 48 = 16
Итак, дискриминант положительный, поэтому уравнение имеет два различных корня. Аналогично разбираем второе уравнение:
a = 5; b = 3; c = 7;
D = 3 2 − 4 · 5 · 7 = 9 − 140 = −131.
Дискриминант отрицательный, корней нет. Осталось последнее уравнение:
a = 1; b = −6; c = 9;
D = (−6) 2 − 4 · 1 · 9 = 36 − 36 = 0.
Дискриминант равен нулю — корень будет один.
Обратите внимание, что для каждого уравнения были выписаны коэффициенты. Да, это долго, да, это нудно — зато вы не перепутаете коэффициенты и не допустите глупых ошибок. Выбирайте сами: скорость или качество.
Кстати, если «набить руку», через некоторое время уже не потребуется выписывать все коэффициенты. Такие операции вы будете выполнять в голове. Большинство людей начинают делать так где-то после 50-70 решенных уравнений — в общем, не так и много.
Корни квадратного уравнения
Теперь перейдем, собственно, к решению. Если дискриминант D > 0, корни можно найти по формулам:
Когда D = 0, можно использовать любую из этих формул — получится одно и то же число, которое и будет ответом. Наконец, если D
Решить квадратные уравнения:
- x 2 − 2x − 3 = 0;
- 15 − 2x − x 2 = 0;
- x 2 + 12x + 36 = 0.
Первое уравнение:
x 2 − 2x − 3 = 0 ⇒ a = 1; b = −2; c = −3;
D = (−2) 2 − 4 · 1 · (−3) = 16.
D > 0 ⇒ уравнение имеет два корня. Найдем их:
Второе уравнение:
15 − 2x − x 2 = 0 ⇒ a = −1; b = −2; c = 15;
D = (−2) 2 − 4 · (−1) · 15 = 64.
D > 0 ⇒ уравнение снова имеет два корня. Найдем их
\[\begin{align} & {{x}_{1}}=\frac{2+\sqrt{64}}{2\cdot \left(-1 \right)}=-5; \\ & {{x}_{2}}=\frac{2-\sqrt{64}}{2\cdot \left(-1 \right)}=3. \\ \end{align}\]
Наконец, третье уравнение:
x 2 + 12x + 36 = 0 ⇒ a = 1; b = 12; c = 36;
D = 12 2 − 4 · 1 · 36 = 0.
D = 0 ⇒ уравнение имеет один корень. Можно использовать любую формулу. Например, первую:
Как видно из примеров, все очень просто. Если знать формулы и уметь считать, проблем не будет. Чаще всего ошибки возникают при подстановке в формулу отрицательных коэффициентов. Здесь опять же поможет прием, описанный выше: смотрите на формулу буквально, расписывайте каждый шаг — и очень скоро избавитесь от ошибок.
Неполные квадратные уравнения
Бывает, что квадратное уравнение несколько отличается от того, что дано в определении. Например:
- x 2 + 9x = 0;
- x 2 − 16 = 0.
Несложно заметить, что в этих уравнениях отсутствует одно из слагаемых. Такие квадратные уравнения решаются даже легче, чем стандартные: в них даже не потребуется считать дискриминант. Итак, введем новое понятие:
Уравнение ax 2 + bx + c = 0 называется, если b = 0 или c = 0, т.е. коэффициент при переменной x или свободный элемент равен нулю.
Разумеется, возможен совсем тяжелый случай, когда оба этих коэффициента равны нулю: b = c = 0. В этом случае уравнение принимает вид ax 2 = 0. Очевидно, такое уравнение имеет единственный корень: x = 0.
Рассмотрим остальные случаи. Пусть b = 0, тогда получим неполное квадратное уравнение вида ax 2 + c = 0. Немного преобразуем его:
Поскольку арифметический квадратный корень существует только из неотрицательного числа, последнее равенство имеет смысл исключительно при (−c/a) ≥ 0. Вывод:
Вывод:
- Если в неполном квадратном уравнении вида ax 2 + c = 0 выполнено неравенство (−c/a) ≥ 0, корней будет два. Формула дана выше;
- Если же (−c/a)
Как видите, дискриминант не потребовался — в неполных квадратных уравнениях вообще нет сложных вычислений. На самом деле даже необязательно помнить неравенство (−c/a) ≥ 0.
Решение неполных квадратных уравнений.
Достаточно выразить величину x 2 и посмотреть, что стоит с другой стороны от знака равенства. Если там положительное число — корней будет два. Если отрицательное — корней не будет вообще.
Теперь разберемся с уравнениями вида ax 2 + bx = 0, в которых свободный элемент равен нулю. Тут все просто: корней всегда будет два. Достаточно разложить многочлен на множители:
Произведение равно нулю, когда хотя бы один из множителей равен нулю. Отсюда находятся корни. В заключение разберем несколько таких уравнений:
Задача. Решить квадратные уравнения:
- x 2 − 7x = 0;
- 5x 2 + 30 = 0;
- 4x 2 − 9 = 0.
x 2 − 7x = 0 ⇒ x · (x − 7) = 0 ⇒ x 1 = 0; x 2 = −(−7)/1 = 7.
5x 2 + 30 = 0 ⇒ 5x 2 = −30 ⇒ x 2 = −6. Корней нет, т.к. квадрат не может быть равен отрицательному числу.
4x 2 − 9 = 0 ⇒ 4x 2 = 9 ⇒ x 2 = 9/4 ⇒ x 1 = 3/2 = 1,5; x 2 = −1,5.
Смотрите также:
Квадратное уравнение имеет вид ax 2 + bx + c = 0.
Неполными квадратными уравнениями являются уравнения трех видов:
- ax 2 + bx = 0, когда коэффициент c = 0.
- ax 2 + c = 0, когда коэффициент b = 0.
- ax 2 = 0, когда и b и с равны 0.
Коэффициент же a по определению квадратного уравнения не может быть равен нулю.
Неполные квадратные уравнения решаются проще, чем полные квадратные. Способы решения различаются в зависимости от вида неполного квадратного уравнения.
Проще всего решаются уравнения вида ax 2 = 0. Если a по определению квадратного уравнения не может быть равно нулю, то очевидно, что нулю может быть равен только x 2 , а значит, и сам x. У уравнений такого вида всегда есть один корень, он равен 0.
У уравнений такого вида всегда есть один корень, он равен 0.
Неполные квадратные уравнения. Решение неполных квадратных уравнений
Например:
–3x 2 = 0
x 2 = 0/–3
x 2 = 0
x = √0
x = 0
Уравнения вида ax 2 + c = 0 преобразуются к виду ax 2 = –c и решаются аналогично предыдущему. Однако корней здесь либо два, либо не одного.
ax 2 + c = 0
ax 2 = –c
x 2 = –c/a
x = √(–c/a)
Здесь если подкоренное выражение отрицательно, то корней у уравнения нет. Если положительно, то корней будет два: √(–c/a) и –√(–c/a). Пример решения подобного уравнения:
4x 2 – 16 = 0
4x 2 = 16
x 2 = 16 / 4
x 2 = 4
x = √4
x 1 = 2; x 2 = –2
Неполные квадратные уравнения вида ax 2 + bx = 0 решается вынесением общего множителя за скобку. В данном случае им является x. Получается уравнение x(ax + b) = 0. Это уравнение имеет два корня: либо x = 0, либо ax + b = 0. Решая второе уравнение получаем x = –b/a. Таким образом, уравнения вида ax 2 + bx = 0 имеют два корня: x 1 = 0, x 2 = –b/a. Пример решения такого уравнения:
Пример решения такого уравнения:
3x 2 – 10x = 0
x(3x – 10) = 0
x 1 = 0; x 2 = 10/3 = 3,(33)
Нахождение корней квадратного уравнения 8 класс
Формула
Корни квадратного уравнения ax 2 + bx + c = 0 можно найти по
формуле: , где — дискриминант
квадратного уравнения.
Возможны три правила:
Правило 1
1. D > 0.
8.2.1. Решение неполных квадратных уравнений
Тогда уравнение имеет 2 различных корня:
Пример
2x 2 + 7x — 4 = 0;
a = 2, b = 7, c = -4.
D = 7 2 — 4 2 (- 4) = 81 > 0,
x 1 = -7 — ? 81 2 2 = — 4;
x 2 = -7 + ? 81 2 2 = 1 2 .
Правило 2
2. D = 0. Тогда уравнение имеет единственный корень.
Пример
x 2 — 4x + 4 = 0.
D = (-4) 2 — 4 1 4 = 0, x = — -4 2 1 = 2.
Заметим, что x 2 — 4x + 4 = 0 x = 2.
Правило 3
3. D
Пример
3x 2 — x + 7 = 0.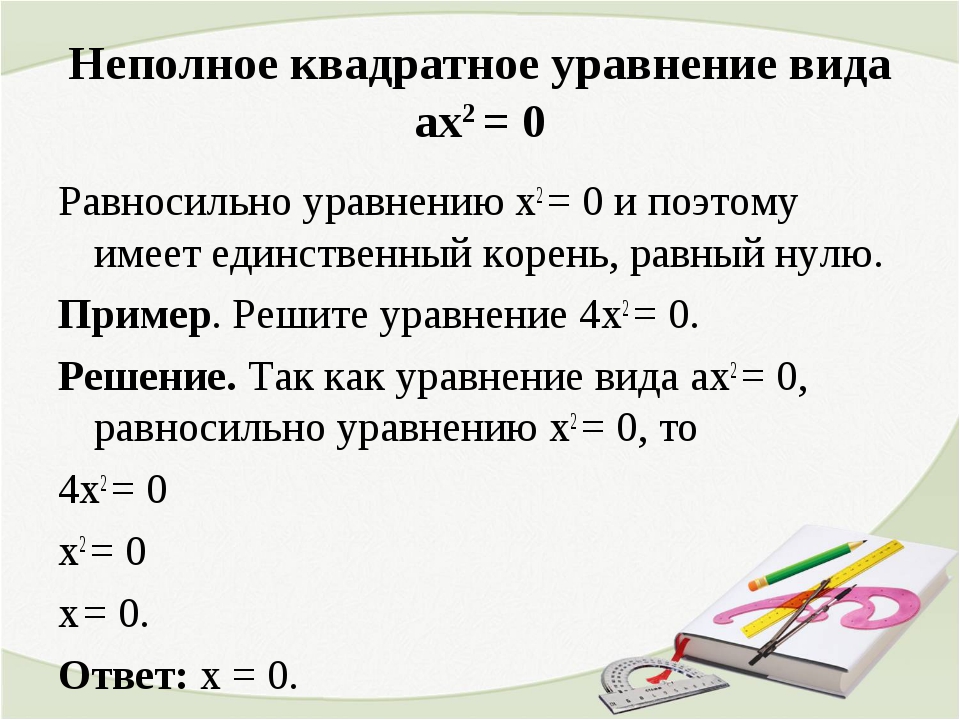
D = (-1) 2 — 4 3 7 = -83
С четным вторым коэффициентом
Правило, формулы
Если b = 2k, то корни уравнения ax + 2kx + c = 0 находятся по формуле:
Пример 1
1. x + 18x + 32 = 0.
a = 1; b = 18 => k = b 2 = 9; c = 32.
D 1 = D 4 = (18 2 ) 2 — 1 32 = 49 > 0, значит уравнение имеет 2 корня:
x 1 = -9 -? 49 1 = -16, x 2 = -9 + 7 = -2.
Пример 2
2. 3x 2 + 2x + 1 = 0.
a = 3; b 2 = 1; c = 1.
D 1 = D 4 = 1 2 — 1 3 = -2
Пример 3
3. 196x 2 + 28x + 1 = 0.
a = 196; b 2 = -14; c = 1.
D 1 = D 4 = (- 14) 2 — 196 = 0, значит уравнение имеет один корень.
x = 14 196 = 1 14 .
Формулы сокращенного умножения
Формулы сокращенного умножения.
— Изучение формул сокращенного умножения: квадрата суммы и квадрата разности двух выражений; разности квадратов двух выражений; куба суммы и куба разности двух выражений; суммы и разности кубов двух выражений.
— Применение формул сокращенного умножения при решении примеров.
Для упрощения выражений, разложения многочленов на множители, приведения многочленов к стандартному виду используются формулы сокращенного умножения.
Решение квадратных уравнений
Формулы сокращенного умножения нужно знать наизусть .
Пусть а, b R. Тогда:
1. Квадрат суммы двух выражений равен квадрату первого выражения плюс удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a + b) 2 = a 2 + 2ab + b 2
2. Квадрат разности двух выражений равен квадрату первого выражения минус удвоенное произведение первого выражения на второе плюс квадрат второго выражения.
(a — b) 2 = a 2 — 2ab + b 2
3. Разность квадратов двух выражений равна произведению разности этих выражений и их суммы.
a 2 — b 2 = (a -b) (a+b)
4. Куб суммы двух выражений равен кубу первого выражения плюс утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго плюс куб второго выражения.
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
5. Куб разности двух выражений равен кубу первого выражения минус утроенное произведение квадрата первого выражения на второе плюс утроенное произведение первого выражения на квадрат второго минус куб второго выражения.
(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3
6. Сумма кубов двух выражений равна произведению суммы первого и второго выражения на неполный квадрат разности этих выражений.
a 3 + b 3 = (a + b) (a 2 — ab + b 2)
7. Разность кубов двух выражений равна произведению разности первого и второго выражения на неполный квадрат суммы этих выражений.
Применение формул сокращенного умножения при решении примеров.
Пример 1.
Вычислить
а) Используя формулу квадрата суммы двух выражений, имеем
(40+1) 2 = 40 2 + 2 · 40 · 1 + 1 2 = 1600 + 80 + 1 = 1681
б) Используя формулу квадрата разности двух выражений, получим
98 2 = (100 – 2) 2 = 100 2 — 2 · 100 · 2 + 2 2 = 10000 – 400 + 4 = 9604
Пример 2.
Вычислить
Используя формулу разности квадратов двух выражений, получим
Пример 3.
Упростить выражение
(х — у) 2 + (х + у) 2
Воспользуемся формулами квадрата суммы и квадрата разности двух выражений
(х — у) 2 + (х + у) 2 = х 2 — 2ху + у 2 + х 2 + 2ху + у 2 = 2х 2 + 2у 2
Формулы сокращенного умножения в одной таблице:
(a + b) 2 = a 2 + 2ab + b 2
(a — b) 2 = a 2 — 2ab + b 2
a 2 — b 2 = (a — b) (a+b)
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
(a — b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3
a 3 + b 3 = (a + b) (a 2 — ab + b 2)
a 3 — b 3 = (a — b) (a 2 + ab + b 2)
1.Выделение полного квадрата. Формулы корней квадратного уравнения.
2.Примеры решения квадратных уравнений.
3.Решение неполных квадратных уравнений.
4.Разложение квадратного трехчлена на сомножители.
Квадратные уравнения. Общая информация.
В квадратном уравнении обязательно должен присутствовать икс в квадрате (поэтому оно и называется
«квадратным»). Кроме него, в уравнении могут быть (а могут и не быть!) просто икс (в первой степени) и
Кроме него, в уравнении могут быть (а могут и не быть!) просто икс (в первой степени) и
просто число (свободный член ). И не должно быть иксов в степени, больше двойки.
Алгебраическое уравнение общего вида.
где x — свободная переменная, a , b , c — коэффициенты, причём a ≠0 .
Например :
Выражение называют квадратным трёхчленом .
Элементы квадратного уравнения имеют собственные названия:
· называют первым или старшим коэффициентом,
· называют вторым или коэффициентом при ,
· называют свободным членом.
Полное квадратное уравнение.
В этих квадратных уравнениях слева присутствует полный набор членов. Икс в квадрате с
коэффициентом а, икс в первой степени с коэффициентом b и свободный член с. В се коэффициенты
должны быть отличны от нуля.
Неполным называется такое квадратное уравнение, в котором хотя бы один из коэффициентов, кроме
старшего (либо второй коэффициент, либо свободный член), равен нулю.
Предположим, что b = 0, — пропадёт икс в первой степени. Получается, например:
2х 2 -6х=0,
И т.п. А если оба коэффициента, b и c равны нулю, то всё ещё проще, например:
2х 2 =0,
Обратите внимание, что икс в квадрате присутствует во всех уравнениях.
Почему а не может быть равно нулю? Тогда исчезнет икс в квадрате и уравнение станет линейным .
И решается уже совсем иначе…
Известно, что оно является частным вариантом равенства ах 2 +вх+с = о, где а, в и с — вещественные коэффициенты при неизвестном х, и где а ≠ о, а в и с будут нулями — одновременно или порознь. Например, с = о, в ≠ о или наоборот. Мы почти вспомнили определение квадратного уравнения.
Трехчлен второй степени равен нулю. Первый его коэффициент а ≠ о, в и с могут принимать любые значения. Значение переменной х тогда будет когда при подстановке обратит его в верное числовое равенство. Остановимся на вещественных корнях, хотя решениями уравнения могут быть и Полным принято называть уравнение, в котором ни один из коэффициентов не равен о, а ≠ о, в ≠ о, с ≠ о.
Первый его коэффициент а ≠ о, в и с могут принимать любые значения. Значение переменной х тогда будет когда при подстановке обратит его в верное числовое равенство. Остановимся на вещественных корнях, хотя решениями уравнения могут быть и Полным принято называть уравнение, в котором ни один из коэффициентов не равен о, а ≠ о, в ≠ о, с ≠ о.
Решим пример. 2х 2 -9х-5 = о, находим
D = 81+40 = 121,
D положительный, значит корни имеются, х 1 = (9+√121):4 = 5, а второй х 2 = (9-√121):4 = -о,5. Проверка поможет убедиться, что они верные.
Вот поэтапное решение квадратного уравнения
Через дискриминант можно решить любое уравнение, в левой части которого известный квадратный трехчлен при а ≠ о. В нашем примере. 2х 2 -9х-5 = 0 (ах 2 +вх+с = о)
Рассмотрим, какие бывают неполные уравнения второй степени
- ах 2 +вх = o. Свободный член, коэффициент с при х 0 , здесь равен нулю, в ≠ o.
Как решать неполное квадратное уравнение такого вида? Выносим х за скобки. Вспоминаем, когда произведение двух множителей равно нулю.
Вспоминаем, когда произведение двух множителей равно нулю.
x(ax+b) = o, это может быть, когда х = о или когда ax+b = o.
Решив 2-е имеем x = -в/а.
В результате имеем корни х 1 = 0, по вычислениям x 2 = -b/a . - Теперь коэффициент при х равен о, а с не равен (≠) о.
x 2 +с = о. Перенесем с в правую часть равенства, получим x 2 = -с. Это уравнение только тогда имеет вещественные корни, когда -с положительное число (с ‹ о),
х 1 тогда равен √(-с), соответственно х 2 ― -√(-с). В противном случае уравнение совсем не имеет корней. - Последний вариант: b = c= o, то есть ах 2 = о. Естественно, такое простенькое уравнение имеет один корень, x = о.
Частные случаи
Как решать неполное квадратное уравнение рассмотрели, а теперь возмем любые виды.
- В полном квадратном уравнении второй коэффициент при х ― четное число.
Пусть k = o,5b. Имеем формулы для вычисления дискриминанта и корней.
D/4 = k 2 — ас, корни вычисляются так х 1,2 = (-k±√(D/4))/а при D › o.
x = -k/a при D = o.
Нет корней при D ‹ o. - Бывают приведенные квадратные уравнения, когда коэффициент при х в квадрате равен 1, их принято записывать x 2 +рх+ q = o. На них распространяются все вышеприведенные формулы, вычисления же несколько проще.
Пример, х 2 -4х-9 = 0. Вычисляем D: 2 2 +9, D = 13.
х 1 = 2+√13, х 2 = 2-√13. - Кроме того, к приведенным легко применяется В ней говорится, что сумма корней уравнения равна -p, второму коэффициенту с минусом (имеется ввиду противоположный знак), а произведение этих же корней будет равно q, свободному члену. Проверьте, как легко можно было бы устно определить корни этого уравнения. Для неприведенных (при всех коэффициентах, не равных нулю) эта теорема применима так: сумма x 1 +x 2 равна -в/а, произведение х 1 ·х 2 равно с/a.
Сумма свободного члена с и первого коэффициента а равна коэффициенту b. В этой ситуации уравнение имеет не менее чем один корень (легко доказывается), первый обязательно равен -1, а второй -с/а, если он существует. Как решать неполное квадратное уравнение, можно проверить самостоятельно. Проще простого. Коэффициенты могут находиться в некоторых соотношениях между собой
Как решать неполное квадратное уравнение, можно проверить самостоятельно. Проще простого. Коэффициенты могут находиться в некоторых соотношениях между собой
- x 2 +x = o, 7х 2 -7 = o.
- Сумма всех коэффициентов равна о.
Корни у такого уравнения — 1 и с/а. Пример, 2х 2 -15х+13 = o.
x 1 = 1, х 2 = 13/2.
Существует ряд других способов решения разных уравнениий второй степени. Вот, например, метод выделения из данного полинома полного квадрата. Графических способов несколько. Когда часто имеешь дело с такими примерами, научишься «щелкать» их, как семечки, ведь все способы приходят на ум автоматически.
Квадратное уравнение – решается просто! *Далее в тексте «КУ». Друзья, казалось бы, что может быть в математике проще, чем решение такого уравнения. Но что-то мне подсказывало, что с ним у многих есть проблемы. Решил посмотреть сколько показов по запросу в месяц выдаёт Яндекс. Вот что получилось, посмотрите:
Что это значит? Это значит то, что около 70000 человек в месяц ищут данную информацию, при чём это лето, а что будет среди учебного года — запросов будет в два раза больше. Это и неудивительно, ведь те ребята и девчата, которые давно окончили школу и готовятся к ЕГЭ, ищут эту информацию, также и школьники стремятся освежить её в памяти.
Это и неудивительно, ведь те ребята и девчата, которые давно окончили школу и готовятся к ЕГЭ, ищут эту информацию, также и школьники стремятся освежить её в памяти.
Несмотря на то, что есть масса сайтов, где рассказывается как решать это уравнение, я решил тоже внести свою лепту и опубликовать материал. Во-первых, хочется чтобы по данному запросу и на мой сайт приходили посетители; во-вторых, в других статьях, когда зайдёт речь «КУ» буду давать ссылку на эту статью; в-третьих, расскажу вам о его решении немного больше, чем обычно излагается на других сайтах. Приступим! Содержание статьи:
Квадратное уравнение – это уравнение вида:
где коэффициенты a, b и с произвольные числа, при чём a≠0.
В школьном курсе материал дают в следующем виде – условно делается разделение уравнений на три класса:
1. Имеют два корня.
2. *Имеют только один корень.
3. Не имеют корней. Здесь стоит особо отметить, что не имеют действительных корней
Как вычисляются корни? Просто!
Вычисляем дискриминант.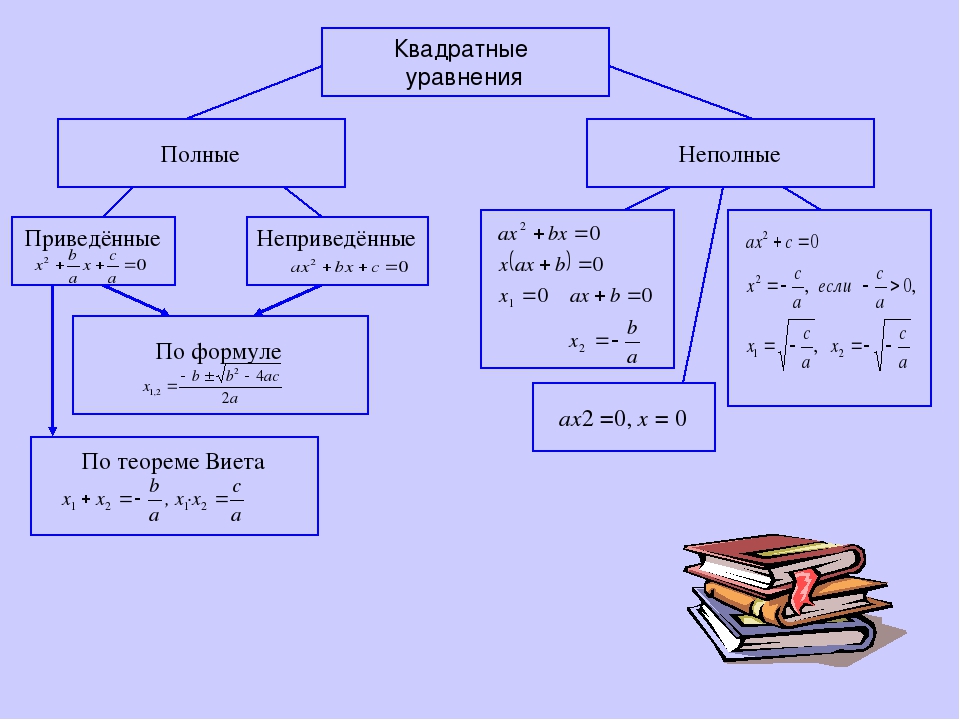 Под этим «страшным» словом лежит вполне простая формула:
Под этим «страшным» словом лежит вполне простая формула:
Формулы корней имеют следующий вид:
*Эти формулы нужно знать наизусть.
Можно сразу записывать и решать:
Пример:
1. Если D > 0, то уравнение имеет два корня.
2. Если D = 0, то уравнение имеет один корень.
3. Если D
Давайте рассмотрим уравнение:
По данному поводу, когда дискриминант равен нулю, в школьном курсе говорится о том, что получается один корень, здесь он равен девяти. Всё правильно, так и есть, но…
Данное представление несколько несколько некорректно. На самом деле получается два корня. Да-да, не удивляйтесь, получается два равных корня, и если быть математически точным, то в ответе следует записывать два корня:
х 1 = 3 х 2 = 3
Но это так – небольшое отступление. В школе можете записывать и говорить, что корень один.
Теперь следующий пример:
Как нам известно – корень из отрицательного числа не извлекается, поэтому решения в данном случае нет.
Вот и весь процесс решения.
Квадратичная функция.
Здесь показано, как решение выглядит геометрически. Это крайне важно понимать (в дальнейшем в одной из статей мы подробно будем разбирать решение квадратного неравенства).
Это функция вида:
где х и у — переменные
a, b, с – заданные числа, при чём a ≠ 0
Графиком является парабола:
То есть, получается, что решая квадратное уравнение при «у» равном нулю мы находим точки пересечения параболы с осью ох. Этих точек может быть две (дискриминант положительный), одна (дискриминант равен нулю) и ни одной (дискриминант отрицательный). Подробно о квадратичной функции можете посмотреть статью у Инны Фельдман.
Рассмотрим примеры:
Пример 1: Решить 2x 2 +8 x –192=0
а=2 b=8 c= –192
D = b 2 –4ac = 8 2 –4∙2∙(–192) = 64+1536 = 1600
Ответ: х 1 = 8 х 2 = –12
*Можно было сразу же левую и правую часть уравнения разделить на 2, то есть упростить его. Вычисления будут проще.
Вычисления будут проще.
Пример 2: Решить x 2 –22 x+121 = 0
а=1 b=–22 c=121
D = b 2 –4ac =(–22) 2 –4∙1∙121 = 484–484 = 0
Получили, что х 1 = 11 и х 2 = 11
В ответе допустимо записать х = 11.
Ответ: х = 11
Пример 3: Решить x 2 –8x+72 = 0
а=1 b= –8 c=72
D = b 2 –4ac =(–8) 2 –4∙1∙72 = 64–288 = –224
Дискриминант отрицательный, решения в действительных числах нет.
Ответ: решения нет
Дискриминант отрицательный. Решение есть!
Здесь речь пойдёт о решении уравнения в случае когда получается отрицательный дискриминант. Вы что-нибудь знаете о комплексных числах? Не буду здесь подробно рассказывать о том, почему и откуда они возникли и в чём их конкретная роль и необходимость в математике, это тема для большой отдельной статьи.
Понятие комплексного числа.
Немного теории.
Комплексным числом z называется число вида
z = a + bi
где a и b – действительные числа, i – так называемая мнимая единица.
a+bi – это ЕДИНОЕ ЧИСЛО, а не сложение.
Мнимая единица равна корню из минус единицы:
Теперь рассмотрим уравнение:
Получили два сопряжённых корня.
Неполное квадратное уравнение.
Рассмотрим частные случаи, это когда коэффициент «b» или «с» равен нулю (или оба равны нулю). Они решаются легко без всяких дискриминантов.
Случай 1. Коэффициент b = 0.
Уравнение приобретает вид:
Преобразуем:
Пример:
4x 2 –16 = 0 => 4x 2 =16 => x 2 = 4 => x 1 = 2 x 2 = –2
Случай 2. Коэффициент с = 0.
Уравнение приобретает вид:
Преобразуем, раскладываем на множители:
*Произведение равно нулю тогда, когда хотя бы один из множителей равен нулю.
Пример:
9x 2 –45x = 0 => 9x (x–5) =0 => x = 0 или x–5 =0
x 1 = 0 x 2 = 5
Случай 3. Коэффициенты b = 0 и c = 0.
Здесь понятно, что решением уравнения всегда будет х = 0.
Полезные свойства и закономерности коэффициентов.
Есть свойства, которые позволяют решить уравнения с большими коэффициентами.
а x 2 + bx + c =0 выполняется равенство
a + b + с = 0, то
— если для коэффициентов уравнения а x 2 + bx + c =0 выполняется равенство
a + с = b , то
Данные свойства помогают решить определённого вида уравнения.
Пример 1: 5001 x 2 –4995 x – 6=0
Сумма коэффициентов равна 5001+(– 4995)+(– 6) = 0, значит
Пример 2: 2501 x 2 +2507 x +6=0
Выполняется равенство a + с = b , значит
Закономерности коэффициентов.
1. Если в уравнении ax 2 + bx + c = 0 коэффициент «b» равен (а 2 +1), а коэффициент «с» численно равен коэффициенту «а», то его корни равны
аx 2 + (а 2 +1)∙х+ а= 0 = > х 1 = –а х 2 = –1/a.
Пример. Рассмотрим уравнение 6х 2 +37х+6 = 0.
х 1 = –6 х 2 = –1/6.
2. Если в уравнении ax 2 – bx + c = 0 коэффициент «b» равен (а 2 +1), а коэффициент «с» численно равен коэффициенту «а», то его корни равны
аx 2 – (а 2 +1)∙х+ а= 0 = > х 1 = а х 2 = 1/a.
Пример. Рассмотрим уравнение 15х 2 –226х +15 = 0.
х 1 = 15 х 2 = 1/15.
3. Если в уравнении ax 2 + bx – c = 0 коэффициент «b» равен (a 2 – 1), а коэффициент «c» численно равен коэффициенту «a» , то его корни равны
аx 2 + (а 2 –1)∙х – а= 0 = > х 1 = – а х 2 = 1/a.
Пример. Рассмотрим уравнение 17х 2 +288х – 17 = 0.
х 1 = – 17 х 2 = 1/17.
4. Если в уравнении ax 2 – bx – c = 0 коэффициент «b» равен (а 2 – 1), а коэффициент с численно равен коэффициенту «а», то его корни равны
аx 2 – (а 2 –1)∙х – а= 0 = > х 1 = а х 2 = – 1/a.
Пример. Рассмотрим уравнение 10х 2 – 99х –10 = 0.
х 1 = 10 х 2 = – 1/10
Теорема Виета.
Теорема Виета называется по имени знаменитого французского математика Франсуа Виета. Используя теорему Виета, можно выразить сумму и произведение корней произвольного КУ через его коэффициенты.
45 = 1∙45 45 = 3∙15 45 = 5∙9.
В сумме число 14 дают только 5 и 9. Это корни. При определённом навыке, используя представленную теорему, многие квадратные уравнения вы сможете решать сходу устно.
Теорема Виета, кроме того. удобна тем, что после решения квадратного уравнения обычным способом (через дискриминант) полученные корни можно проверять. Рекомендую это делать всегда.
СПОСОБ ПЕРЕБРОСКИ
При этом способе коэффициент «а» умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
Если а ± b+c ≠ 0, то используется прием переброски, например:
2х 2 – 11х+ 5 = 0 (1) => х 2 – 11х+ 10 = 0 (2)
По теореме Виета в уравнении (2) легко определить, что х 1 = 10 х 2 = 1
Полученные корни уравнения необходимо разделить на 2 (так как от х 2 «перебрасывали» двойку), получим
х 1
= 5 х 2
=
0,5.
Каково обоснование? Посмотрите что происходит.
Дискриминанты уравнений (1) и (2) равны:
Если посмотреть на корни уравнений, то получаются только различные знаменатели, и результат зависит именно от коэффициента при х 2:
У второго (изменённого) корни получаются в 2 раза больше.
Потому результат и делим на 2.
*Если будем перебрасывать тройку, то результат разделим на 3 и т.д.
Ответ: х 1 = 5 х 2 = 0,5
Кв. ур-ие и ЕГЭ.
О его важности скажу кратко – ВЫ ДОЛЖНЫ УМЕТЬ РЕШАТЬ быстро и не задумываясь, формулы корней и дискриминанта необходимо знать наизусть. Очень многие задачи, входящие в состав заданий ЕГЭ, сводятся к решению квадратного уравнения (геометрические в том числе).
Что стоит отметить!
1. Форма записи уравнения может быть «неявной». Например, возможна такая запись:
15+ 9x 2 — 45x = 0 или 15х+42+9x 2 — 45x=0 или 15 -5x+10x 2 = 0.
Вам необходимо привести его к стандартному виду (чтобы не запутаться при решении).
2. Помните, что х это неизвестная величина и она может быть обозначена любой другой буквой – t, q, p, h и прочими.
Урок 21. Неполные квадратные уравнения
Упражнение 512
Условие:
Является ли квадратным уравнение:
Решение:
а) Является
б) Не является
в) Является
г) Является
д) Является
е) Является
Советы:
В квадратном уравнении наибольшая степень х — квадрат
Упражнение 513
Условие:
Назовите в квадратном уравнении его коэффициенты.
Решение:
Советы:
а-первый коэффициент ,b- второй коэффициент , с-свободный член
Упражнение 514
Условие:
Приведите примеры неполных квадратных уравнений различных видов.
Решение:
Советы:
Рассмотреть случаи когда коэффициент b=0, c=0 или одновременно b=0 и c=0
Упражнение 515
Условие:
Найдите корни уравнения:
Решение:
Советы:
Для начала перенесите свободный член в правую часть уравнения
Упражнение 516
Условие:
Решите уравнение и укажите приближенные значения корней с точностью до 0,1
Решение:
Советы:
Воспользуйтесь калькулятором, воспользуйтесь правилом округления чисел
Упражнение 517
Условие:
Решите уравнение
Решение:
Советы:
Разложите левую часть уравнения на множители
Упражнение 518
Условие:
Решите уравнение:
Решение:
Советы:
Если с=0 , разложите на множители левую часть; если b=0 — перенесите свободный член в правую часть.
Упражнение 519
Условие:
Какое из данных неполных квадратных уравнений не имеет корней?
Решение:
Советы:
Число в квадрате не может быть отрицательным — в таком случае нет корней
Упражнение 520
Условие:
При каких значениях а уравнение является неполным квадратным уравнением? Выберите верный ответ.
Решение:
Советы:
Первый коэффициент не должен быть равен нулю, свободный член должен быть равен нулю
Упражнение 521
Условие:
Решите уравнение:
Решение:
Советы:
Для начала приведите подобные слагаемые
Упражнение 522
Условие:
Найдите корни уравнения
Решение:
Советы:
Раскройте скобки и приведите подобные слагаемые
Упражнение 523
Условие:
Решите уравнения:
Решение:
Советы:
Для раскрытия скобок воспользуйтесь формулой сокращенного умножения
Упражнение 524
Условие:
Произведение двух последовательных целых чисел в 1,5 раза больше квадрата меньшего из них. Найдите эти числа.
Найдите эти числа.
Решение:
Советы:
Взять одно число за х и составить уравнение
Упражнение 525
Условие:
Теннисный корт представляет собой прямоугольную площадку, длина которой вдвое больше ширины, а площадь равна 800 м2. Найдите длину и ширину корта.
Решение:
Советы:
Составьте уравнение к задаче
Упражнение 526
Условие:
Если от квадрата отрезать треугольник площадью 59 см2 , то площадь оставшейся части будет равна 85 см2. Найдите сторону квадрата.
Решение:
Советы:
Обозначить сторону квадрата за х и решить уравнение
Упражнение 527
Условие:
Две группы туристов отправились одновременно из одного пункта — одна на север со скоростью 4 км/ч, а другая на запад со скоростью 5 км/ч. Через какое время расстояние между туристами окажется равным 16 км?
Решение:
Советы:
Составьте уравнение с неизвестным t
Упражнение 528
Условие:
Путь свободно падающего тела вычисляется по формуле s=gt²/2 где t(c) — время, g ≈ 10 м/с², s(м) — пройденный путь. через сколько сек от начала падения камень достигнет дна шахты глубиной 80 м?
через сколько сек от начала падения камень достигнет дна шахты глубиной 80 м?
Решение:
Советы:
С помощью формулы составь уравнение
Упражнение 529
Условие:
Ширина земельного участка имеющего форму прямоугольника составляет 75% его длины а его площадь равна 4800м2 Найдите длину изгороди ограждающей этот участок.
Решение:
Советы:
Возьмите неизвестное за х и решите уравнение
Упражнение 531
Условие:
В каких координатных четвертях расположен график функции?
Решение:
Советы:
Вспомни как зависит расположение графика от знака коэффициента k
Упражнение 532
Условие:
Найдите значение выражения
Решение:
Советы:
Используй формулу сокращенного умножения
Решение неполных квадратных уравнений — презентация онлайн
1. Решение неполных квадратных уравнений
8 классРазработано: учителем математики
МОУ «СОШ» п. Аджером
Корткеросского района
Республики Коми
Мишариной Альбиной
Геннадьевной
4.
 Методы решения неполных квадратных уравнений 1 случай: если с=0, то получим неполное
Методы решения неполных квадратных уравнений 1 случай: если с=0, то получим неполноеквадратное уравнение ax² + bx = 0
Решение: ax² + bx = 0
х(ах + b) = 0
х = 0 или ах + b = 0
ах = — b
х = — b/а
Ответ: 0; — b/а
5. Например
Решить уравнение: 2х²- 9х = 0Решение: х(2х — 9) = 0
х = 0 или 2х – 9 = 0
2х = 9
х = 4,5
Ответ: 0; 4,5
6. Решить в парах
1) х² + 5х = 02) – 2х² + 8х = 0
3) 19х — х² = 0
4) 3х — х² = 0
Проверим ответы:
1) 0; -5
2) 0; 4
3) 0; 19
4) 0; 3
7. Методы решения неполных квадратных уравнений
2 случай: если b = 0, то получимнеполное квадратное уравнение ax² + с = 0
Решение: ax² + с = 0
ax² = — с
x² = — с/а. Возможны 2 случая:
1) если -с/а
2) если -с/а>0, то х = ±√-с/а
8. Например:
Решить уравнения:5х² — 45 = 0 и 3х² +7 = 0
Решение: 5х² = 45
3х² = — 7
х² = 9
х² = — 7/3
х=±3
нет решения
Ответ: ± 3
Ответ: нет решения
9.
 Решить в парах: 1) -2х² + 50 = 0
Решить в парах: 1) -2х² + 50 = 02) 5х² + 17 = 0
3) 13 — 9х² = 0
4) 8х² — 64 = 0
Проверим ответы:
1) ± 5
2) нет решения
3) ±
=
4) ± = 2
13
9
13
3
8
2
10. Методы решения неполных квадратных уравнений.
3 случай: если b = 0 и с = 0, то получимнеполное квадратное уравнение ax² = 0
Решение: ax² = 0
а ≠ 0 значит x² = 0
х=0
Ответ: 0
11. Например:
Решить уравнение: 13х² = 0Решение: т.к. 13 ≠ 0, то х² = 0
х=0
Ответ: 0
12. Решить в парах:
1) 6х² = 02) -103х² = 0
3) 1256х² = 0
4) — 80х² = 0
Проверим ответы:
1) 0
2) 0
3) 0
4) 0
13. Решить самостоятельно
1) х² — 25 = 02) 16а² = 0
3) х² — 100х = 0
4) х² + 64 = 0
5) 3х² — 12 = 0
6) х² +10х = 0
7) х² — 7 = 0
8) 4х² — 9 = 0
9) -7х² = 0
10) 3х² — 12х = 0
Проверим ответы:
1) ± 5
9) 0
2) 0
10) 0; 4
3) 0; 100
4) нет решения
5) ± 2
6) 0; -10
7) ± √7
8) ± 3/2
15.
 Интернет-ресурсы Циркуль: http://www.daviddarling.info/images/compasses.jpg
Интернет-ресурсы Циркуль: http://www.daviddarling.info/images/compasses.jpgКарандаш:
http://www.proshkolu.ru/content/media/pic/std/3000000/2240000/22390937acd9447b354cc7e.gif
Угольник-транспортир:
http://p.alejka.pl/i2/p_new/25/38/duza-ekierka-geometryczna-z-uchwytemrotring-14-cm_0_b.jpg
Фон «тетрадная клетка»:
http://radikal.ua/data/upload/49112/4efc3/3bd0a3d6bb.jpg
Неполные квадратные уравнения
Фарафонова Наталия Игоревна
Тема: Неполные квадратные уравнения.
Цели урока: — Ввести понятие неполного квадратного уравнения;
— научить решать неполные квадратные уравнения.
Задачи урока: — Уметь определять вид квадратного уравнения;
— решать неполные квадратные уравнения.
Уебник: Алгебра: Учеб. для 8 кл. общеобразоват. учреждений/ Ш. А. Алимов, Ю. М. Колягин, Ю. В. Сидоров и др. – М. : Просвещение, 2010.
для 8 кл. общеобразоват. учреждений/ Ш. А. Алимов, Ю. М. Колягин, Ю. В. Сидоров и др. – М. : Просвещение, 2010.
Ход урока.
1. Напомнить учащимся о том, что прежде, чем решать любое квадратное уравнение, необходимо привести его к стандартному виду. Вспомнить определение полного квадратного уравнения: ax2 + bx + c = 0, a ≠ 0.
В данных квадратных уравнениях назвать коэффициенты a, b, c:
а) 2x2 – x + 3 = 0; б) x2 + 4x – 1 = 0; в) x2 – 4 = 0; г) 5x2 + 3x = 0.
2. Дать определение неполного квадратного уравнения:
Квадратное уравнение ax2 + bx + c = 0 называют неполным, если хотя бы один из коэффициентов, bили c, равен 0. Обратить внимание, что коэффициент а ≠ 0. Из уравнений представленных выше, выбрать неполные квадратные уравнения.
Обратить внимание, что коэффициент а ≠ 0. Из уравнений представленных выше, выбрать неполные квадратные уравнения.
3. Виды неполных квадратных уравнений с примерами решений удобнее представить в виде таблице:
|
b =c = 0 ax2 =0 |
b ≠ 0, c = 0 ax2 + bx = 0 |
b = 0, c ≠ 0 |
|
|
ax2 + c = 0, c < 0 |
ax2 + c = 0, c > 0 |
||
|
4x2 = 0 x2 = 0 x = 0 |
7x2 + 14x =0 7x(x + 2) = 0 x1 = 0; x2 = -2
(разложением на множители лев. |
3x2 – 48 = 0 3x2 = 48 x2 = 16 x1 = 4; x2 = — 4 |
3x2 + 48 = 0 3x2 = — 48 x2 = — 16 решений нет |
|
1 корень x = 0 |
2 корня x1, x2 |
2 корня x1 , x2 |
решений нет |
- Не решая, определите количество корней для каждого неполного квадратного уравнения:
а) 2x2 – 3 = 0; б) 3x2 + 4 = 0; в) 5x2 – x = 0; г) 0,6x2 = 0; д) -8x2 – 4 = 0.
- Решить неполные квадратные уравнения (решение уравнений, с проверкой у доски, 2 варианта):
а) 0,5x2 = 0
б) x2 – 9 = 0
в) 2x2 + 15 = 0
г) 3x2 + 2x = 0
д) 2x2 – 16 = 0
е) 5(x2 + 2) = 2(x2 + 5)
ж) (x + 1)2 – 4 = 0
а) -1,5x2 = 0
б) x2 – 4 = 0
в) 2x2 + 7 = 0
г) x2 + 9x = 0
д) 81x2 – 64 = 0
е) 2(x2 + 4) = 4(x2 + 2)
ж) (x – 2)2 – 8 = 0.
6. Самостоятельная работа по вариантам:
1 вариант
а) 3x2 – 12 = 0
б) 2x2 + 6x = 0
в) 1,8x2 = 0
г) x2 + 9 = 0
д) 7x2 – 14 = 0
е) x2 – 3x =0
2 вариант
а) -x2 = 0
б) 6x2 + 24 = 0
в) 9y2 – 4 = 0
г) -y2 + 5 = 0
д) 1 – 4y2 = 0
е) 8y2 + y = 0
3 вариант
а) 6y – y2 = 0
б) 0,1y2 – 0,5y = 0
в) (x + 1)(x -2) = 0
г) x(x + 0,5) = 0
д) x2 – 2x = 0
е) x2 – 16 = 0
4 вариант
а) 9x2 – 1 = 0
б) 3x – 2x2 = 0
в) x2 = 3x
г) x2 + 2x – 3 = 2x + 6
д) 3x2 + 7 = 12x+ 7
е) 4 =
5 вариант
а) 2x2 – 18 = 0
б) 3x2 – 12x = 0
в) 2,7x2 = 0
г) x2 + 16 = 0
д) 6x2 – 18 = 0
е ) x2 – 5x = 0
6 вариант
а ) -x2 = 0
б ) 4x2 + 36 = 0
в) 25y2 – 1 = 0
г) -y2 + 2 = 0
д) 9 – 16y2 = 0
е) 7y2 + y = 0
7 вариант
а) 4y – y2 = 0
б) 0,2y2 – y = 0
в) (x + 2)(x – 1) = 0
г) (x — 0,3)x = 0
д) x2 + 4x = 0
е) x2 – 36 = 0
8 вариант
а ) 16x2 – 1 = 0
б) 4x – 5x2 = 0
в) x2 = 7x
г) x2 – 3x – 5 = 11 – 3x
д) 5x2 – 6 = 15x – 6
е) 3 =
7. Домашнее задание: №№ 421(2), 422(2), 423(2,4), 425.
Домашнее задание: №№ 421(2), 422(2), 423(2,4), 425.
Дополнительное задание:
При каких значениях a уравнение является неполным квадратным уравнением? Решите уравнение при полученных значениях a:
а) x2 + 3ax + a – 1 = 0
б) (a – 2)x2+ ax = 4 – a2= 0
Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра
Квадратным трёхчленом относительно переменной x называют многочлен
где a, b и c – произвольные вещественные числа, причем
Квадратным уравнением относительно переменной x называют уравнение
где a, b и c – произвольные вещественные числа, причем
Полным квадратным уравнением относительно переменной x называют уравнение
ax2 + bx + c = 0,
где a, b и c – произвольные вещественные числа, отличные от нуля.
Неполными квадратными уравнениями называют квадратные уравнения следующих типов:
Решение неполных квадратных уравнений
Покажем, как решаются неполные квадратные уравнения на примерах.
Пример 1. Решить уравнение
5x2 = 0 .
Решение.
Ответ: 0 .
Пример 2. Решить уравнение
Решение. Вынося в левой части уравнения (3) переменную x за скобки, перепишем уравнение в виде
Поскольку произведение двух сомножителей равно нулю тогда и только тогда, когда, или первый сомножитель равен нулю, или второй сомножитель равен нулю, то из уравнения (4) получаем:
Ответ: .
Пример 3. Решить уравнение
Решить уравнение
2x2 – 5 = 0 .
Решение.
Ответ: .
Пример 4. Решить уравнение
Решение. Поскольку левая часть уравнения (5) положительна при всех значениях переменной x, а правая часть равна 0, то уравнение решений не имеет.
Ответ: .
Выделение полного квадрата
Выделением полного квадрата называют представление квадратного трёхчлена (1) в виде:
| (6) |
Для того, чтобы получить формулу (6), совершим следующие преобразования:
Формула (6) получена.
Дискриминант
Дискриминантом квадратного трёхчлена (1) называют число, которое обозначается буквой D и вычисляется по формуле:
Дискриминант квадратного трёхчлена играет важную роль, и от того, какой знак он имеет, зависят различные свойства квадратного трёхчлена.
Используя дискриминант, формулу (6) можно переписать в виде
| (8) |
Разложение квадратного трёхчлена на множители
Утверждение. В случае, когда , квадратный трёхчлен (1) разлагается на линейные множители. В случае, когда D < 0, квадратный трехчлен нельзя разложить на линейные множители.
Доказательство. В случае, когда D = 0, формула (8) и является разложением квадратного трехчлена на линейные множители:
| (9) |
В случае, когда D > 0, выражение, стоящее в квадратных скобках в формуле (8), можно разложить на множители, воспользовавшись формулой сокращенного умножения «Разность квадратов»:
Таким образом, в случае, когда D > 0, разложение квадратного трехчлена (1) на линейные множители имеет вид
| (10) |
В случае, когда D < 0, выражение, стоящее в квадратных скобках в формуле (8), является суммой квадратов и квадратный трёхчлен на множители не раскладывается.
Замечание. В случае, когда D < 0, квадратный трехчлен всё-таки можно разложить на линейные множители, но только в области комплексных чисел, однако этот материал выходит за рамки школьного курса.
Формула для корней квадратного уравнения
Из формул (9) и (10) вытекает формула для корней квадратного уравнения .
Действительно, в случае, когда D = 0, из формулы (9) получаем:
Следовательно, в случае, когда D = 0, уравнение (1) обладает единственным корнем, который вычисляется по формуле
| (11) |
В случае, когда D > 0, из формулы (10) получаем:
Таким образом, в случае, когда D > 0, уравнение (1) имеет два различных корня, которые вычисляются по формулам
| (12) | |
| (13) |
Замечание 1. Формулы (12) и (13) часто объединяют в одну формулу и записывают так:
Формулы (12) и (13) часто объединяют в одну формулу и записывают так:
| (14) |
Замечание 2. В случае, когда D = 0, обе формулы (12) и (13) превращаются в формулу (11). Поэтому часто говорят, что в случае, когда D = 0, квадратное уравнение (1) имеет два совпавших корня, вычисляемых по формуле (11), а саму формулу (11) переписывают в виде:
| (15) |
Замечание 3. В соответствии с материалом, изложенным в разделе «Кратные корни многочленов», корень (11) является корнем уравнения (1) кратности 2.
В случае, когда D = 0, разложение квадратного трехчлена на линейные множители (9) можно переписать по-другому, воспользовавшись формулой (15):
| ax2 + bx + c = = a (x – x1)2. | (16) |
В случае, когда D > 0, разложение квадратного трехчлена на линейные множители (10) с помощью формул (12) и (13) переписывается так:
| ax2 + bx + c = = a (x – x1) (x – x2) .  | (17) |
Замечание 4. В случае, когда D = 0, корни x1 и x2 совпадают, и формула (17) принимает вид (16).
Прямая и обратная теоремы Виета
Раскрывая скобки и приводя подобные члены в правой части формулы (17), получаем равенство
ax2 + bx + c =
= a (x – x1) (x – x2) =
= a [x2 – (x1 + x2) x + x1x2] =
= ax2 – a(x1 + x2) x + ax1x2 .
Отсюда, поскольку формула (17) является тождеством, вытекает, что коэффициенты многочлена
ax2 + bx + c
равны соответствующим коэффициентам многочлена
ax2 – a (x1 + x2) x + a x1x2 .
Таким образом, справедливы равенства
следствием которых являются формулы
| (18) |
Формулы (18) и составляют содержание теоремы Виета (прямой теоремы Виета).
Словами прямая теорема Виета формулируется так: — «Если числа x1 и x2 являются корнями квадратного уравнения (1), то они удовлетворяют равенствам (18)».
Обратная теорема Виета формулируется так: — «Если числа x1 и x2 являются решениями системы уравнений (18), то они являются корнями квадратного уравнения (1)».
Для желающих ознакомиться с примерами решений различных задач по теме «Квадратные уравнения» мы рекомендуем наше учебное пособие «Квадратный трехчлен».
Графики парабол и решение с их помощью квадратных неравенств представлены в разделе «Парабола на координатной плоскости. Решение квадратных неравенств» нашего справочника.
Решение квадратных неравенств» нашего справочника.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
{{2}} — {7} {x} = {0} $$$.Перепишем уравнение в следующем виде: $$$ {3} {x} \ cdot {x} — {7} {x} = {0} $$$.
Теперь перепишем уравнение, используя распределительное свойство умножения: $$$ {x} {\ left ({3} {x} — {7} \ right)} = {0} $$$.
Когда произведение чисел равно 0?
Когда хотя бы один множитель равен 0.
Итак, либо $$$ {x} = {0} $$$, либо $$$ {3} {x} — {7} = {0} $$$.
Второе уравнение является линейным, его корень равен $$$ {x} = \ frac {{7}} {{3}} $$$.
Ответ : $$$ {x} = {0} $$$ и $$$ {x} = \ frac {{7}} {{3}} $$$.{{2}} — {9} = {0} $$$.
Ответ : $$$ {0} $$$ и $$$ — \ frac {{9}} {{4}} $$$.
Завершение площади
Заполнение Квадрата — это метод, используемый для решения
квадратное уровненеие
изменив форму уравнения так, чтобы левая часть
идеальный квадрат
трехчлен
.
Решать а Икс 2 + б Икс + c знак равно 0 завершив квадрат:
1.Преобразуйте уравнение так, чтобы постоянный член,
c
, один на правой стороне.
2. Если
а
, старший коэффициент (коэффициент
Икс
2
срок), не равно
1
, разделите обе стороны на
а
.
3. Добавьте квадрат половины коэффициента Икс -срок, ( б 2 а ) 2 к обеим сторонам уравнения.
4. Разложите левую часть на множители квадрата двучлена.
5. Возьмите
квадратный корень
с обеих сторон. (Помнить:
(
Икс
+
q
)
2
знак равно
р
эквивалентно
Икс
+
q
знак равно
±
р
. )
)
6. Решите для Икс .
Пример 1:
Решать Икс 2 — 6 Икс — 3 знак равно 0 заполнив квадратик.
Икс 2 — 6 Икс знак равно 3 Икс 2 — 6 Икс + ( — 3 ) 2 знак равно 3 + 9 ( Икс — 3 ) 2 знак равно 12 Икс — 3 знак равно ± 12 знак равно ± 2 3 Икс знак равно 3 ± 2 3
Пример 2:
Решать: 7 Икс 2 — 8 Икс + 3 знак равно 0
7 Икс 2 — 8 Икс знак равно — 3 Икс 2 — 8 7 Икс знак равно — 3 7 Икс 2 — 8 7 Икс + ( — 4 7 ) 2 знак равно — 3 7 + 16 49 ( Икс — 4 7 ) 2 знак равно — 5 49 Икс — 4 7 знак равно ± 5 7 я Икс знак равно 4 7 ± 5 7 я ( Икс — 3 ) 2 знак равно 12 Икс — 3 знак равно ± 12 знак равно ± 2 3 Икс знак равно 3 ± 2 3
Квадратное уравнение
Квадратное уравнение
Введение
Квадратное уравнение — это уравнение вида ax 2 + bx + c = 0, где a, b и c — константы, а a 0.
Слово «квадратичный» происходит от латинского. В латинском языке «квадратичный» используется вместо «квадрат» . Поскольку наибольшая степень неизвестной переменной, которая появляется в уравнении, равна квадрату, поэтому подобные уравнения стали известны как квадратные уравнения.
Стандартная форма квадратного уравнения
Стандартная форма квадратного уравнения — ax 2 + bx + c = 0, где
◾ a, b и c — постоянные, а
◾ a не равно 0 (нулю).
Вот несколько примеров стандартной формы квадратного уравнения:
| Уравнение | Коэффициент |
|---|---|
| x 2 + 2x + 1 = 0 | , где a = 1, b = 2 и c = 1 |
| x 2 + 5x + 11 = 0 | , где a = 1, b = 5 и c = 11 |
Полное квадратное уравнение
◾ Когда b не равно нулю
| Некоторые примеры полной формы квадратного уравнения |
|---|
| ◾ x 2 + 2x + 1 = 0, где a = 1, b = 2 и c = 1 |
| ◾ x 2 + 5x + 11 = 0, где a = 1, b = 5 и c = 11 |
Чистое или неполное квадратное уравнение
◾ Когда b равно нулю, уравнение известно как чистое или неполное квадратное уравнение относительно x.
| Некоторые примеры чистой или неполной формы квадратного уравнения |
|---|
| ◾ 6x 2 -24 = 0, где b = 0 |
| ◾ 6x 2 -11 = 0, где b = 0 |
Корни квадратного уравнения
Корни или решение квадратного уравнения ax 2 + bx + c = 0 — это значения переменной ‘x’, которые удовлетворяют квадратному уравнению i.е. сделать топор 2 + bx + c равным нулю.
Например:
х 2 + 5х — 50 = 0
x 2 — 5x + 10x -50 = 0
х (х — 5) + 10 (х — 5) = 0
(х — 5) (х + 10) = 0
x = 5 и x = -10
Как видите, если поставить 5 или -10 вместо x, квадратное уравнение x 2 + 5x — 10 будет равно нулю. Следовательно, 5 и -10 являются корнями квадратного уравнения x 2 + 5x — 50 = 0.
Решение квадратного уравнения
Есть три метода решения квадратного уравнения:
◾ Факторизация
◾ Заполнив квадрат
◾ Используя формулу корней квадратного уравнения
Решение по факторизации
Пошаговый процесс решения квадратного уравнения методом факторизации:
Шаг 1: Преобразуйте уравнение в стандартную форму: ax 2 + bx + c = 0. Если правая часть не равна нулю, перенесите ее в левую и сделайте правую часть равной нулю.
Если правая часть не равна нулю, перенесите ее в левую и сделайте правую часть равной нулю.
Шаг 2: Полностью разложите левую часть на множители.
Шаг 3: Используйте закон нулевого фактора: если ab = 0, то a = 0 или b = 0.
Шаг 4: Решите полученные линейные уравнения, приравняв каждый линейный коэффициент к нулю. Эти значения x будут решением квадратного уравнения.
Пример: Решить 3x 2 + 5x — 5 = -3
Шаг 1: Преобразование в стандартную форму
3x 2 + 5x -5 + 3 = 0
3x 2 + 5x — 2 = 0
Шаг 2: Разложите левую часть на множители
3x 2 + 6x — x — 2 = 0
3x (x + 2) -1 (x + 2) = 0
(3x — 1) (x + 2) = 0
Шаг 3: Приравняйте каждый линейный коэффициент к нулю.
3x — 1 = 0 или x + 2 = 0
3x = 1 или x = -2
x = 1/3, x = — 2 являются корнями уравнения.
Ловушка:
У вас может возникнуть соблазн разделить обе части выражением, содержащим x. Если вы сделаете это, вы получите только одно решение уравнения (одно значение или один корень от x) и можете потерять другое решение (значение x).
Например: рассмотрим x 2 = 7x
Правильное решение:
x 2 = 7x
x 2 -7x = 0
х (х-7) = 0
x = 0 и X = 7
Неправильное решение:
x 2 = 7x
Разделив обе стороны на x, получим
Х = 7
выше — неправильный способ решения уравнения, поскольку мы не смогли найти другое значение x, равное нулю.
Решение Завершив квадрат
Как вы уже знаете, все квадраты не могут быть легко разложены на множители. Например, x 2 + 4x + 1 не может быть разложено на множители простой факторизацией. Это означает, что мы не можем записать x 2 + 4x + 1 в форме (x — a) (x — b), где a, b — рациональные числа.
Существует альтернативный способ решения уравнений, например x 2 + 4x + 1 = 0, то есть завершением квадрата .
Уравнения вида ax 2 + bx + c = 0 можно преобразовать в форму (x + p) 2 = q. Так легко найти решения.
Пошаговый процесс решения квадратного уравнения путем заполнения квадрата:
Шаг I: Составьте квадратное уравнение в стандартной форме ax 2 + bx + c = 0.
Шаг II: теперь разделите обе части уравнения на коэффициент x 2 , если он еще не равен 1.
Шаг III: Сдвиньте постоянный член вправо.
Шаг IV: Добавьте квадрат половины коэффициента x к L.H.S. и R.H.S.
Шаг V: Запишите L.H.S в виде полного квадрата и упростите R.H.S.
Шаг VI: Найдите x, извлекая квадратный корень из L. H.S. и R.H.S.
H.S. и R.H.S.
Решим квадратное уравнение -3x 2 + 12x + 5 = 0 по «завершая квадрат»
-3x 2 + 12x + 5 = 0
x 2 — 4x — (5/3) = 0
x 2 — 4x = (5/3)
x 2 — 4x + 2 2 = (5/3) + 2 2
(х — 2) 2 = (17/3)
x — 2 = & pm; & Sqrt; (17/3)
x = 2 & pm; & Sqrt; (17/3)
x 1 = 2 + & Sqrt; (17/3)
x 2 = 2 — & Sqrt; (17/3)
Итак, Здесь x 1 и x 2 — корни уравнения.Используя формулу корней квадратного уравнения
Квадратичная формула, которая также может использоваться для решения любого квадратного уравнения, получается в результате решения квадратного уравнения ax 2 + bx + c = 0, a ≠ 0 для x путем заполнения квадрата.
Есть определенные случаи, когда решение квадратного уравнения факторизацией или завершение квадрата занимает много времени, долго или сложно. В таких случаях мы используем квадратную формулу для решения квадратного уравнения.
В таких случаях мы используем квадратную формулу для решения квадратного уравнения.
Пошаговый процесс решения квадратного уравнения по формуле корней квадратного уравнения:
Шаг I: Составьте квадратное уравнение в стандартной форме ax 2 + b x + c = 0.
Шаг II: Сравните решаемое квадратное уравнение со стандартным квадратным уравнением и найдите значения коэффициентов a, b, c.
Шаг III: Поместите эти значения a, b, c в формулу квадратного уравнения.
| Корни (x 1 , x 2 ) = | −b ± & Sqrt; b2 — 4ac |
| 2a |
Как вы можете заметить в формуле. Квадратичная формула вычисляет два значения x: x 1 и x 2 , где
| x 1 = | −b + & Sqrt; b2 — 4ac |
| 2a |
| x 2 = | −b — & Sqrt; b2 — 4ac |
| 2a |
Эти два значения x, для которых выполняется ax 2 + bx + c = 0, называются решениями квадратного уравнения, также называемыми корнями квадратного уравнения.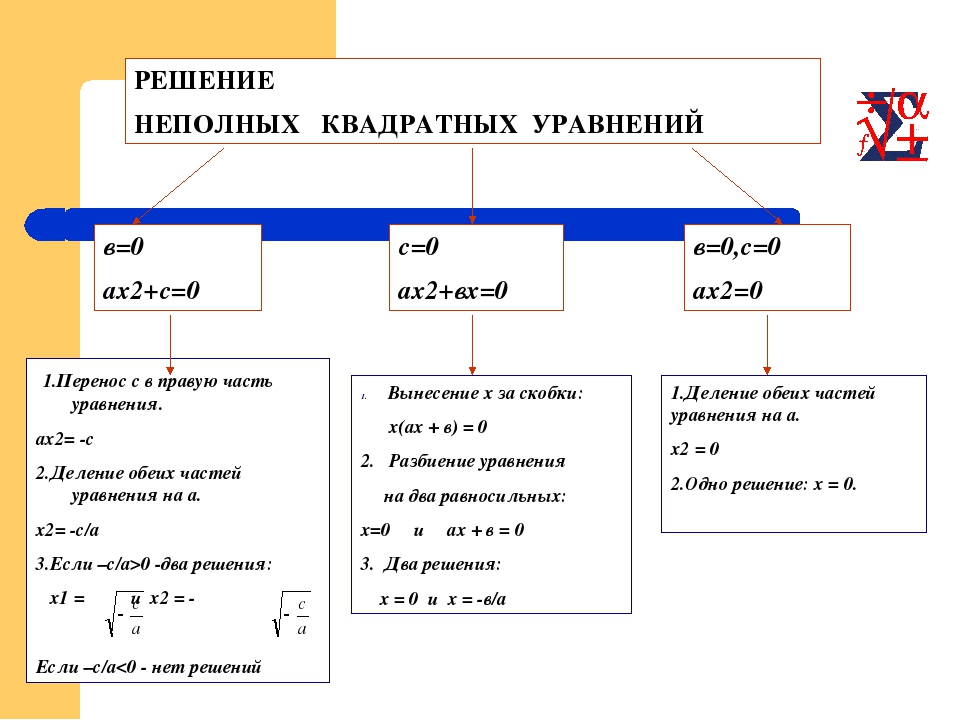
Шаг I: — Преобразуйте квадратное уравнение, которое вы хотите решить, в стандартную форму квадратного уравнения, ax 2 + bx + c = 0
Например, если у вас есть квадратное уравнение в форме x 2 — 10x = -24, преобразуйте его в стандартную форму квадратного уравнения.
x 2 -10x = -24 преобразуется в x 2 — 10x + 24 = 0
Шаг II: — Найдите значение коэффициентов a, b и c, сравнив его со стандартной формой квадратного уравнения ax 2 + bx + c = 0
Например, сравнивая x 2 — 10x + 24 = 0 с ax 2 + bx + c = 0, получаем
a = 1,
b = -10,
c = 24
Шаг III:
| Корни (x 1 , x 2 ) = | −b ± & Sqrt; b2 — 4ac |
| 2a |
| x 1 = | −b + & Sqrt; b2 — 4ac |
| 2a |
| = | — (- 10) + & Sqrt; (-10) 2-4 (1) (24) | = 6 |
| 2 (1) |
| x 2 = | −b — & Sqrt; b2 — 4ac |
| 2a |
| = | — (- 10) — & Sqrt; (-10) 2-4 (1) (24) | = 4 |
| 2 (1) |
Дискриминант
Мы узнали, что квадратная формула
| Корни (x 1 , x 2 ) = | −b ± & Sqrt; b2 — 4ac |
| 2a |
В приведенной выше квадратной формуле величина «b 2 — 4ac» , которая находится под знаком квадратного корня, называется дискриминантом квадратного уравнения.
Дискриминант = b 2 — 4ac
Выражение «b 2 — 4ac» говорит о природе корней квадратного уравнения. Корни могут быть реальными, равными или мнимыми.
Возможны три случая:
◾ Если b 2 — 4ac мнимый и неравный.
◾ Если b 2 — 4ac = 0, то корни будут действительными, равными и рациональными .(Это означает, что левая часть уравнения представляет собой полный квадрат).
◾ Если b 2 — 4ac> 0, то корни действительные и неравные.
Если b 2 — 4ac> 0, то корни действительные и неравные, и есть две возможности — здесь корни могут быть рациональными или иррациональными
◾ b 2 — 4ac — это полный квадрат, корни действительные, рациональные и неравные . (Это означает, что уравнение можно решить путем факторизации).
◾ b 2 — 4ac не является совершенным, тогда корни действительны, иррациональны и неравны.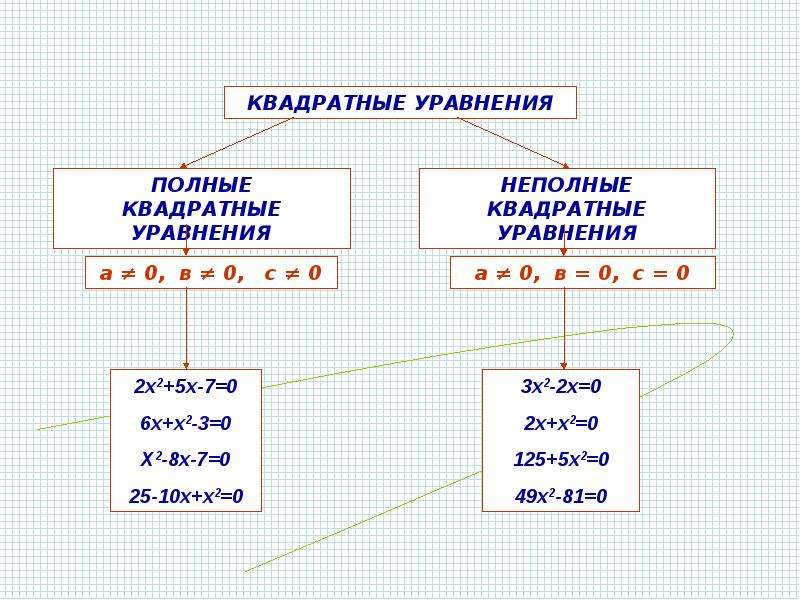
Сводка
| Дискриминантное значение Случаи | Корни квадратичной | Факторизация квадратичной |
|---|---|---|
| Дискриминантное значение> 0 | два настоящих разных корня | два различных линейных фактора |
| Дискриминантное значение = 0 | два одинаковых настоящих корня | два одинаковых линейных фактора |
| Дискриминантное значение | Настоящих корней нет | Невозможно разложить на множители |
Случай I — когда дискриминант> 0
Для квадратного уравнения x 2 + 7x + 4 = 0, определить природу корней по его определителю
Ответ
х 2 + 7х + 4 = 0
Дискриминант = b 2 — 4ac
Здесь a = 1, b = 7, c = 4
Дискриминант = 7 2 — 4 x 1 x 4 = 49 — 16 = 33
Дискриминант> 0, следовательно, есть два настоящих корня
Случай II — Когда Дискриминант = 0
Для квадратного уравнения x 2 + 6x + 9 = 0, определить природу корней по его определителю
Ответ
х 2 + 6х + 9 = 0
Дискриминант = b 2 — 4ac
Здесь a = 1, b = 6, c = 9
Дискриминант = 6 2 — 4 x 1 x 9 = 36 — 36 = 0
Дискриминант = 0, следовательно, есть два одинаковых реальных корня
Случай III- Когда Дискриминант
Для квадратного уравнения x 2 + 4x + 4 = 0, определить природу корней по его определителю
Ответ
х 2 + 4х + 5 = 0
Дискриминант = b 2 — 4ac
Здесь a = 1, b = 4, c = 5
Дискриминант = 4 2 — 4 x 1 x 5 = 16-20 = -4
Дискриминант
Обзор различных методов решения квадратного уравнения — Концепция
Решение квадратных уравнений может быть трудным, но, к счастью, есть несколько различных методов, которые мы можем использовать в зависимости от того, какой тип квадратичного уравнения мы пытаемся решить. Четыре метода решения квадратного уравнения — это факторизация с использованием квадратных корней, завершение квадрата и квадратичной формулы.
Четыре метода решения квадратного уравнения — это факторизация с использованием квадратных корней, завершение квадрата и квадратичной формулы.
Итак, сейчас я хочу поговорить об обзоре всех различных способов решения квадратного уравнения. Под этим я подразумеваю что-нибудь в форме: ax² плюс bx плюс c. Итак, у нас есть четыре различных способа, которые нам удобны.У нас есть факторизация, свойство извлечения квадратного корня, завершение квадрата и квадратная формула. Мы можем использовать эти методы в разное время, и я просто хочу поговорить о том, когда мы можем их использовать, почему они хороши и почему плохи. Так что я просто спущусь вниз по ряду и расскажу о каждом из них. «Чек» означает «за», а «минус» — «против». Факторинг обычно является самым быстрым и простым способом решения чего-либо, когда это возможно. Часто мы имеем дело с квадратичным коэффициентом, который невозможно факторизовать, поэтому факторинг нам не поможет. Таким образом, это быстро и просто, когда его можно использовать, но не всегда можно использовать. Так быстро и просто, но не всегда применимо.
Таким образом, это быстро и просто, когда его можно использовать, но не всегда можно использовать. Так быстро и просто, но не всегда применимо.
Следующее, о чем мы поговорим, — это свойство квадратного корня. Это когда у нас есть что-то квадратное. Итак, профи: это здорово, когда вы решаете что-то квадратное. Единственная проблема в том, что мы не всегда имеем дело с ситуацией. Каждый раз, когда у вас есть X-термин или что-то в этом роде, мы не сможем его использовать. Так что это не всегда квадратный термин.Когда это применимо, это здорово, но не всегда. На самом деле это не так часто.
Завершение кв. Самое замечательное в завершении квадрата — это то, что мы всегда можем это сделать. Никогда не будет времени, когда вы не сможете завершить квадрат. Но недостаток в том, что это может стать некрасивым. Если вы имеете дело с коэффициентом или нечетным средним членом или чем-то в этом роде, вы собираетесь ввести дроби. Это не всегда лучшая ситуация.
И, наконец, формула корней квадратного уравнения. Опять же, это здорово, потому что им всегда можно воспользоваться. И минусы, это зависит от человека. Если вы используете квадратные корни, что не всегда нравится некоторым людям, вам всегда нужно использовать квадратные корни. Обычно это не так просто, как некоторые из этих других методов, я бы сказал, что завершение квадрата немного проще, но это то, что вы должны запомнить. Поэтому вам нужно запомнить формулу, и она может стать некрасивой.
Опять же, это здорово, потому что им всегда можно воспользоваться. И минусы, это зависит от человека. Если вы используете квадратные корни, что не всегда нравится некоторым людям, вам всегда нужно использовать квадратные корни. Обычно это не так просто, как некоторые из этих других методов, я бы сказал, что завершение квадрата немного проще, но это то, что вы должны запомнить. Поэтому вам нужно запомнить формулу, и она может стать некрасивой.
Итак, это четыре разных способа, плюсы и минусы, а также некоторые вещи, о которых следует подумать, когда вы решаете проблему.На самом деле я не собираюсь ничего решать за вас. Я только что сделал небольшую диаграмму, чтобы вы знали, какие ресурсы у вас есть, а также плюсы и минусы каждого из них.
1. Решение квадратных уравнений с помощью факторинга
Общая форма квадратного уравнения —
топор 2 + bx + c = 0
, где x — переменная, а a , b и c — константы
Примеры квадратных уравнений
(а) 5 x 2 — 3 x — 1 = 0 является квадратное уравнение в квадратичной форме где
`a = 5`,` b = -3`, `c = -1`
(б) 5 + 3 т — 4. 9 t 2 = 0 — это
квадратное уравнение в квадратичной форме.
9 t 2 = 0 — это
квадратное уравнение в квадратичной форме.
Здесь a = -4.9, b = 3, c = 5
[Это уравнение возникло из определения времени, когда снаряд под действием силы тяжести попадает в земля.]
(c) ( x + 1) 2 = 4 является квадратичным уравнение, но , а не в квадратичной форме.
Его необходимо расширить и упростить до:
x 2 + 2 x — 3 = 0
Сводка
В общем, квадратное уравнение:
- должен содержать термин x 2
- НЕ должен содержать термины со степенью выше x 2 например. x 3 , x 4 и т. Д.
Примеры неквадратичных уравнений
- bx — 6 = 0 НЕ является квадратным уравнением, потому что нет члена x 2 .

- x 3 — x 2 -5 = 0 НЕ является квадратным уравнением, потому что существует член x 3 (не допускается в квадратных уравнениях).
Решения квадратичной Уравнение
Решение уравнения состоит из всех чисел (корней), которые делают уравнение истинным .
Все квадратные уравнения имеют 2 решения (т. Е. 2 корня). Их может быть:
- настоящие и отличные
- настоящие и равные
- мнимая (сложная)
Пример 1
Квадратное уравнение x 2 -7 x + 10 = 0 имеет корни из
`x = 2` и` x = 5`. (Ниже мы покажем, как найти эти корни.)
Это можно увидеть, подставив в уравнение:
Когда x = 2,
x 2 -7 x + 10
= (2) 2 — 7 (2) + 10
= 4–14 + 10
= 0
(аналогично можно отобразить для x = 5).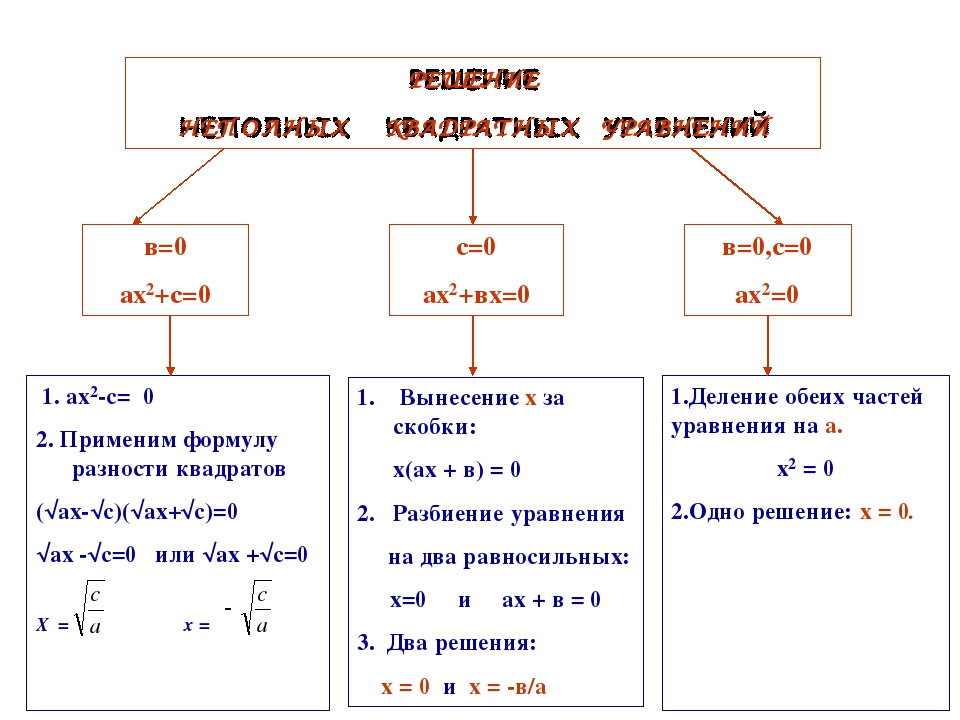 В этом примере корнями являются действительных и различных .
В этом примере корнями являются действительных и различных .
Пример 2
Квадратное уравнение x 2 -6 x + 9 = 0 имеет двойных корней из x = 3 (оба корня одинаковые)
Это можно увидеть, подставив x = 3 в уравнение:
x 2 — 6 x + 9
= (3) 2 — 6 (3) + 9
= 9–18 + 9
= 0
Пример 3
Квадратное уравнение
x 2 + 9 = 0
имеет мнимых корней из
`x = sqrt (-9)` или `-sqrt (-9)`
Узнайте больше о мнимых числах.
Решение квадратного уравнения с помощью факторинга
Пока мы будем иметь дело только с квадратными уравнениями, которые можно факторизовать (факторизовать).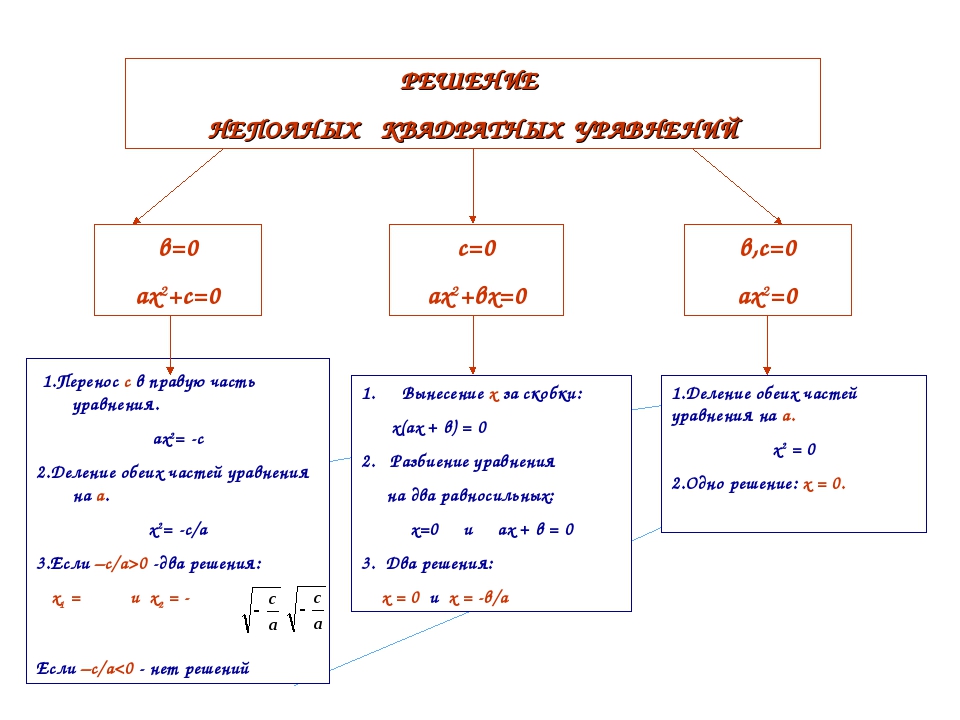
Если вам нужно напоминание о том, как учитывать фактор, вернитесь в раздел:
Факторинг триномов.
Используя тот факт, что продукт равен нулю, если какой-либо из его факторов равен нулю, мы выполняем следующие шаги:
(i) Переместите все термины влево и упростите, оставив ноль на правая сторона.
(ii) Факторизуйте квадратичное выражение
(iii) Установить каждый коэффициент равным нулю
(iv) Решите полученные линейные уравнения
(v) Проверьте решения в исходном уравнении
Пример 4
Решить x 2 — 2 x — 15 = 0
Ответ
x 2 — 2 x -15 = 0
Факторинг дает:
( x -5) ( x + 3) = 0
Теперь, если любое из членов ( x — 5) или ( x + 3) равно 0, произведение равно нулю.Итак, делаем вывод:
( x -5) = 0, следовательно,
x = 5
или
( x + 3) = 0, следовательно,
x = — 3
Следовательно, корни равны x = 5 и x = — 3.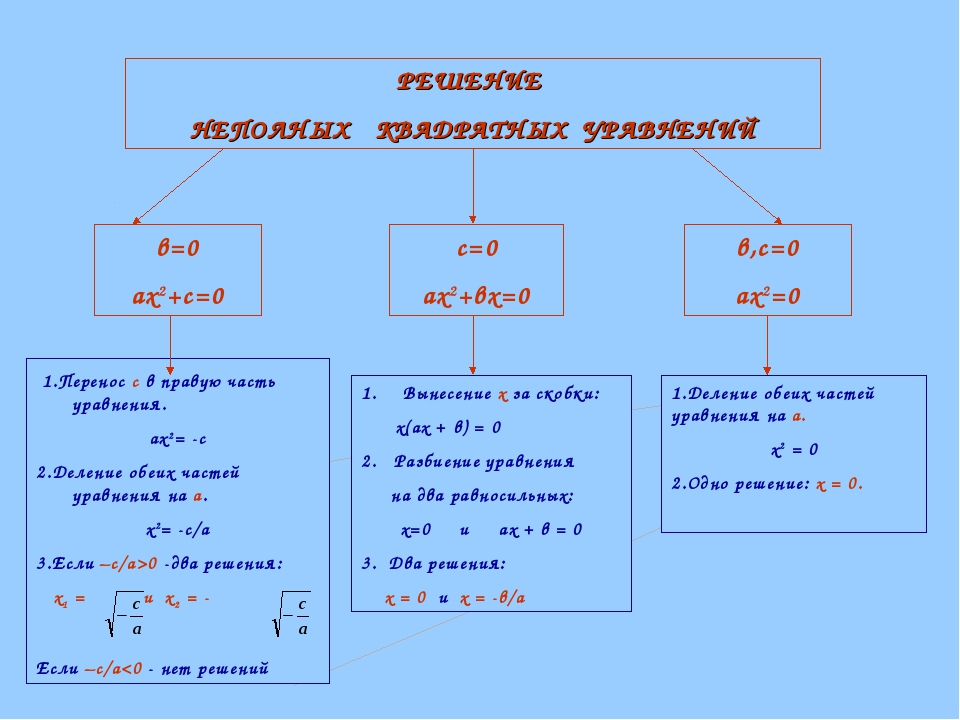 2 + 6x + 1 = 0`
2 + 6x + 1 = 0`
Ответ
9 x 2 + 6 x + 1 = 0
Факторинг дает:
(3 x + 1) (3 x + 1) = 0
Итак, делаем вывод:
(3 x + 1) = 0,
следовательно
`x = -1 / 3`
Мы говорим, что есть двойной корень из `x = -1 / 3`.2 = 0`
`u = 0`
Шаг 5: Подставьте `u = 0` в выражения скобок` u`, получив тот же (повторяющийся) корень квадратного уравнения, который мы нашли выше:
`x = -1 / 3-0 = -1 / 3,` или `x = -1 / 3 + 0 = -1 / 3`
Пример 6 (с дробями)
Решить
`2-1 / x = 3 / (x + 2)`
Ответ
`2-1 / x = 3 / (x + 2)`
Умножаем всю длину на `x (x + 2)`, чтобы удалить знаменатели (нижние части) дробей:
`2x (x + 2) — (x (x + 2)) / x = (3 (x) (x + 2)) / (x + 2)`
Отмена дает:
`2x (x + 2) — (x + 2) = 3x`
Раскрываем скобки:
`2x ^ 2 + 4x-x-2 = 3x`
`2x ^ 2-2 = 0`
`x ^ 2-1 = 0`
Факторинг дает:
`(x + 1) (x-1) = 0`
Итак, `x = -1` или` x = 1`.
ПРОВЕРКА: Подстановка `x = -1` как в левую, так и в правую части вопроса дает:
«» LHS «= 2-1 / x = 2-1 / -1 = 3`
`« ПРАВЫЙ »= 3 / (x + 2) = 3 / (- 1 + 2) = 3 =« ЛЕВЫЙ »`
Аналогично, для `x = + 1`
LHS `= 2 — 1 = 1`
RHS `= 3/3 = 1 =` LHS
Упражнения
- Определите, являются ли следующие уравнения квадратными. Если так, определить a , b и г.
а.2− 12x + 2 = 0`
Итак, да, это квадратное уравнение с
`a = 9`,` b = -12`, `c = 2`
- Решить для x :
2 x 2 -7 x + 6 = 3
Ответ
2 x 2 -7 x + 6 = 3
2 x 2 -7 x + 3 = 0
(2 x — 1) ( x — 3) = 0
Так
`x = 1 / 2` или` x = 3`.
2 = 49/16 — 24/16 = 25/16`
`u = + -5 / 4`
Шаг 5: Подставьте любое значение (мы будем использовать `+ 5 / 4`) в выражения скобок` u`, получив те же корни квадратного уравнения, которые мы нашли выше:
`x = 7 / 4-5 / 4 = 1/2,` или `x = 7/4 + 5/4 = 3`
Урок изложение неполных квадратных уравнений. Квадратное уравнение называется
. Slide 2
«Мне приходится делить свое время между политикой и уравнениями.Однако уравнения, на мой взгляд, гораздо важнее, потому что политика существует только в данный момент, а уравнения будут существовать вечно ». А. Эйнштейн.
Slide 3
Привет, ребята!
Повторяю: я ваш помощник, я проведу вас через всю большую тему «Квадратные уравнения». В 7-8 классе вы уже рассматривали и даже решали квадратные уравнения.
Slide 4
Сегодня вы узнаете: 1. Какие уравнения называются квадратными? 2. Что главное в определении квадратного уравнения, которое следует запомнить и учесть? 3. Какие бывают частные случаи квадратных уравнений? 4. Как можно решать квадратные уравнения в каждом конкретном случае? Теперь давайте вместе поищем ответы на эти вопросы. Удачи!
Что главное в определении квадратного уравнения, которое следует запомнить и учесть? 3. Какие бывают частные случаи квадратных уравнений? 4. Как можно решать квадратные уравнения в каждом конкретном случае? Теперь давайте вместе поищем ответы на эти вопросы. Удачи!
Slide 5
Что общего у этих уравнений?
Slide 6
Квадратное уравнение — это уравнение вида… ax² + bx + c = 0, где a ≠ 0, x — переменная, a, b, c — некоторые числа.а — старший (первый) коэффициент, б — второй коэффициент, в — свободный срок. а — старший (первый) коэффициент, б — второй коэффициент, в — свободный срок. а — старший (первый) коэффициент, б — второй коэффициент, в — свободный срок.
Slide 7
Если a = 1, то квадратное уравнение x² + bx + c = 0 называется приведенным. Решим № 513 (устно).
Slide 8
Попробуем решить:
5 5 -3 3 2 -4 1 4 3 -2 1 -1 4 -4 1
Slide 9
Интересно, что будет, если коэффициенты квадратного уравнения по очереди или все сразу (кроме а) превратятся в нули. Давайте проведем небольшое исследование.
Давайте проведем небольшое исследование.
Слайд 10
Неполные квадратные уравнения
10.01.2017 10 Если c = 0, ax2 + bх = 0 ax2 ax2 Если b, c = 0, ax2 = 0 Если b = 0, ax2 + c = 0
Слайд 11
Рассмотрим все возможные случаи
Слайд 12
Slide 13
Неполные квадратные уравнения вида: без корней.
Слайд 14
Неполные квадратные уравнения вида:
Слайд 15
Ответ: x = 0.без корней. Выпишите неполные квадратные уравнения:
Slide 16
Запишите квадратные уравнения с указанными коэффициентами: a = 1, b = 0, c = 16; а = -1, б = 5, с = 0; б = 0, а = -3, с = 0; c = -8, a = 1, b = 0; а = 1,5, с = 0, b = -3; b =, a =, c Установите соответствие между уравнениями и следующими: а) уравнение имеет два корня, б) уравнение имеет один корень, в) уравнение не имеет корней.(c) (a) (b) (a) (a) (a) Установите соответствие между уравнениями и следующими утверждениями:
Слайд 17
17 Проверьте раствор № 515 (a, c, d). а) .4х2-9 = 0 в). -0,1х2 + 10 = 0 г). 6v2 + 24 = 0 4×2 = 9 -0,1×2 = -10 6v2 = -24 x2 = 9 / 4×2 = -10 / (- 0,1) v2 = -24 / 6 x1 = -3 / 2 = -1, пять; х2 = 100 v2 = -4 х2 = 3/2 = 1,5; х1 = -10 Ответ: решения нет. Ответ: -1,5; 1.5; Ответ: -10; 10;
а) .4х2-9 = 0 в). -0,1х2 + 10 = 0 г). 6v2 + 24 = 0 4×2 = 9 -0,1×2 = -10 6v2 = -24 x2 = 9 / 4×2 = -10 / (- 0,1) v2 = -24 / 6 x1 = -3 / 2 = -1, пять; х2 = 100 v2 = -4 х2 = 3/2 = 1,5; х1 = -10 Ответ: решения нет. Ответ: -1,5; 1.5; Ответ: -10; 10;
Slide 18
10.01.2017 18 Рассмотрим решение неполных квадратных уравнений № 517 (b, d, e) b). -5х2 + 6х = 0 г). 4a2 — 3a = 0e). 6z2– z = 0 x (-5x + 6) = 0 a (4a-3) = 0 z (6z –1) = 0 x = 0 или -5x + 6 = 0 a = 0 или 4a-3 = 0 z = 0 или 6z –1 = 0 -5x = -6 4a = 36z = 1 x = -6 / (- 5) = 1,2 a = 3/4 = 0,75 z = 1/6 Ответ: 0; 1.2. Ответ: 0; 0,75.Ответ: 0; 1/6 …
Проведение урока алгебры в 8 классе по теме «Квадратные уравнения. Решение неполных квадратных уравнений». Введение понятия полных и неполных квадратных уравнений. Первичная консолидация методов решения неполных квадратных уравнений.
Загрузить:
Предварительный просмотр:
Чтобы использовать предварительный просмотр презентаций, создайте себе учетную запись (учетную запись) Google и войдите в нее: https://accounts. google.com
google.com
Подписи к слайдам:
Презентация урока алгебры в 8 классе «Квадратные уравнения.Решение неполных квадратных уравнений »
Загадочно, но знакомо нам. В нем есть что-то неизвестное. Его корень — это то, что мы ищем. Найти — интересно каждому. Все скажут без сомнения. Перед вами (уравнение)
Решите уравнения а) у — 7 = 0; б) х + 0,5 = 0; в) ах = 0; г) 2 х — 1/3 = 0; д) а (а — 1) = 0; f ) x 2 + 4 = 0.
Задача В кинотеатре количество мест в каждом ряду больше количества рядов 8. Всего на сеанс пришло 884 зрителя и все места были заняты.Сколько рядов в кинотеатре?
х — ряды; x +8 — места в каждой строке C оставим уравнение: x (x + 8) = 884; x 2 + 8x-884 = 0.
«Квадратные уравнения. Решение неполных квадратных уравнений» Тема урока a: эпиграф: уравнение — это ключ, который может открыть тысячу дверей в неизвестное.
цель: познакомить с концепцией квадратного уравнения; Научитесь решать неполные квадратные уравнения.
Определение квадратного уравнения Квадратное уравнение называется уравнением вида a ax² + bx + c = 0, de x — переменная, a, b, c — параметры, а ≠ 0.Число a называется первым коэффициентом, число b — вторым коэффициентом, а c — свободным членом. Квадратное уравнение также называют уравнением второй степени и, поскольку его головная часть является многочленом второй степени и.
Примеры уравнивания квадрата xy: abc -2x² + x-1,4 = 0-2 1 -1,4 5x²-4x = 0 5-4 0 3X² + 10,3 = 0 3 0 10,3
Задача 1 Являются ли эти уравнения квадратичными ? 4x²-5x + 2 = 0 -5,6x²-2x- 0,5 = 0 13-7x² = 0 16x²-x³-5 = 0 1-16x = 0 -x² = 0
Задача 2 Назовите коэффициент в квадратном уравнении.3x²-6x + 2 = 0 -x² + 5x + 10 = 0 x²-8x + 1,5 = 0 -4x² + 5 = 0 -36x²-3x = 0 12x² = 0
Неполные квадратные уравнения м на квадратный метр. abc -3x² + 5 = 0-3 0 5 2x²-10x = 0 2-10 0 16x² = 0 16 0 0
Классификация квадратных уравнений полная неполная Аль-Хорезми, где a ≠ 0 b = 0 b = 0, c = 0 c = 0 или или или
Решите уравнение, если b = 0. -4x² + 25 = 0 — 4x² = — 25 4x² = 25 или I
Решите уравнение если b = 0, c = 0.III
Решите уравнение, если C = 0. (35 + y) y = 0 35 + y = 0 или II y = 0 y = -35
Testing
1. 2. 3. 4. 5 0; -5-5; 5 0 Задача № 1. Указание корней уравнения Справка
Задача № 2. Укажите корни уравнения 1. 2. 3. 4. -4; 4-4; 0 16 0; 4
Задача № 3. Определить корни уравнения 1. 2. 3. 4. 3 -3; 0 -3 0; 3
Задача № 4. Укажите корни уравнения 1. 2. 3. 4. 0; 4 16-4; 4-4; 0
01.05.17 Задача № 5.Укажите корни уравнения 1. 2. 3. 4. -2; 2 4 2 2; 0
Краткое содержание урока: Сегодня на уроке я выучил … понял … выучил … мои успехи … Я почувствовал трудности … не мог, но теперь могу … в следующем уроке Хочу …
Неполные квадратные уравнения
Учитель математики и физики: Балакина Е.Н.
ЦЕЛИ ЗАНЯТИЯ:
- Познакомьтесь с понятием квадратного уравнения;
- Научитесь определять, является ли уравнение квадратичным; Научитесь определять коэффициенты квадратного уравнения; Составьте квадратное уравнение в соответствии с заданными коэффициентами; Научитесь определять тип квадратного уравнения: полное или неполное; Научитесь выбирать алгоритм решения неполного квадратного уравнения.
- Научитесь определять, является ли уравнение квадратичным;
- Научитесь определять коэффициенты квадратного уравнения;
- Составьте квадратное уравнение в соответствии с заданными коэффициентами;
- Научитесь определять тип квадратного уравнения: полное или неполное;
- Научитесь выбирать алгоритм решения неполного квадратного уравнения.
ВОПРОСЫ:
- Что такое уравнение?
- Что значит решить уравнение?
- Что называется корнем уравнения?
- Какие уравнения мы знаем?
Выберите квадратные уравнения:
5x + 26 = 8x — 3,
— 13x = 0,
9x + 2-17 = 0, 9
5 — 22x = 119x + 7-13 = 0,
— 42x — 29 = 0,
-3 — 35x + 14 = 0,
+22 — 5x = 0,
-7 — 46x + 17 = 0,
8x — 6 = 0,
25 — 4x — 9 = 0.
НАЗЫВАЕТСЯ КВАДРАТНОЕ УРАВНЕНИЕ
УРАВНЕНИЕ ВИДА
a + bx + c = 0,
где x — переменная,
a, b, c — некоторые номера,
кроме того a = 0.
a — первый коэффициент,
b — второй коэффициент,
в — свободный срок.
Составьте квадратное уравнение
-9 + 23x — 11 = 0
-4 + x + 5 = 0
4 + 9x = 0
07 + 7000×2
07 + 7000×2 90 1 = 0
-3 + 15 = 0
-3 — х + 7 = 0
4 + 3 = 0
a = 3, b = -7, c = 12
a = -9, b = 23, c = -11
a = 8, b \ u003d 0, c = 0
a = 5, b = -22, c = -3
a = -4, b = 1, c = 5
07
07
07
a = 4, b = 9, c = 0
a = 1, b = 7, c = 1
a = -3, b = 0, c = 15
a = -3, b = -1, c = 7
a = 4, b = 0, c = 3
Если в квадратном уравнении a + bx + c = 0 хотя бы один из коэффициентов b или из равно нулю, тогда такое уравнение называется неполным квадратным уравнением .
Неполные квадратные уравнения бывают трех типов:
- a = 0
- a + б x = 0
- a + c = 0
Вариант 1
-; Имеют 0; 3 И 0; -2 P н.р. AT -3; 3 R 0; 2 E 0 H 0; 4 А -2,5; 2,5 О -; D
Вариант 2
- + 2x = 0
- 2-18 = 0
- 4-11 = — 11+ 9x
- 9 + 1 = 0
- 2 = 4х
- 7-14 = 0
- 9-2 + 16x = 6 + 9
- -4 = 0
- 9 + 1 = 1
- 4-25 = 0
- -2 + 4x = 0
- — 3x = 0
- 7 = 0
- 12x = 6
- 2 = 7 + 2
- 6 + 24 = 0
- 3 + 7 = 12x + 7
- + 2x — 3 = 2x + 6
- 9-4 = 0
- 7x = 2 + 3x
На доске написаны числа 1 2 3 4 5 6 7 8 9 10 10 9 8 7 6 5 4 3 2 1
Учащиеся пишут буквы, соответствующие корням этих уравнений; варианты работают навстречу друг другу.
REDUCED КВАДРАТНОЕ УРАВНЕНИЕ
Вызываемое квадратное уравнение
, в котором коэффициент
при равен 1:
+ bx + c = 0
ДОМАШНИЕ
№ 24.11 (УСТНАЯ),
№ 24,16 (б, в, г),
№ 24,18 (б, в, г).
Историческая справка
Квадратные уравнения были решены в Вавилоне примерно в 2000 году до нашей эры.
В 2002 году в Европе отмечалось 800-летие квадратных уравнений. это было в 1202 году, когда итальянский ученый Леонард Фибоначчи изложил формулы для квадратного уравнения.
Только в 17 веке, благодаря Ньютону, Декарту и другим ученым, эти формулы приняли современный вид.
AT Древняя Индия Уже в 499 год были распространены публичные конкурсы на решение задач по составлению квадратных уравнений. Одна из таких задач — задача известного индийского математика Бхаскарас :
Резвая стая обезьян Наевшись досыта, развлекаясь, Часть восьмая в квадрате Меня на поляне позабавили. И двенадцать по виноградной лозе Начали прыгать на висе. Сколько было обезьян Ты мне в паке подскажи?
решить неполное квадратное уравнение методом квадратного корня 1) x / 4 = 9 / x
ОРАДИКАЛЫ И КВАДРАТИЧЕСКИЕ УРАВНЕНИЯ Решение квадратного уравнения с использованием квадратного корня pra Solve (y-3) ‘…
О РАДИКАЛЫ И КВАДРАТИЧЕСКИЕ УРАВНЕНИЯ Решение квадратного уравнения с использованием квадратного корня pra Solve (y-3) ‘- 49 = 0, где y — действительное число.Максимально упростите свой ответ. Если существует несколько решений, разделите их запятыми. Если решения нет, нажмите «Нет решения».
Решите квадратное уравнение с помощью свойства квадратного корня 2x² = 8 Набор решений: (Упростите свой …
Решите квадратное уравнение, используя свойство квадратного корня 2x² = 8. Набор решений: (Упростите ваши ответы. Введите точные ответы, используя радикалы по мере необходимости. Используйте запятую для разделения ответов по мере необходимости.)
40 Воспользуйтесь методом заполнения квадрата, чтобы преобразовать квадратное уравнение в уравнение.2 + 4 = 730
Решите квадратное уравнение, заполнив квадрат. Икс? + 18x + 66 = 0 Сначала выберите подходящую форму и …
Решите квадратное уравнение, заполнив квадрат. Икс? + 18x + 66 = 0 Сначала выберите соответствующую форму и заполните поля правильными числами. Затем решите уравнение. Если существует несколько решений, разделите их запятыми. Форма: . 0/0 00 … o (v + D² = 0 o (v — D ’= 0 X 5? Решение: x = -9 + √15, -9 — Vis
3 Метод Ньютона и Секанта [30 баллов].Мы хотим решить уравнение f (x) 0, где f (x) = (x-1) 4. …
Не могли бы вы помочь мне с частями от A до D? Спасибо 3 Метод Ньютона и Секанта [30 баллов]. Мы хотим решить уравнение f (x) 0, где f (x) = (x-1) 4. a) Запишите итерацию Ньютона для решения f (x) 0. b) Для начального значения xo 2 вычислите x c) Каков корень ξ функции f, т.е. f (5) = 0? Ожидаете ли вы линейного или квадратичного порядка сходимости к 5 и почему? г) Назовите одно преимущество Ньютона …
Решите следующие квадратные уравнения
А.Решите следующие квадратные уравнения. Обязательно покажите всю свою работу. Не используйте какой-либо метод (например, факторизацию, заполнение квадрата, квадратную формулу, построение графиков) более двух раз. Используйте метод построения графиков хотя бы один раз. 1. 3×2 + 11x — 20 = 0 2. x2 + 3x — 4 = 0 3. 3×2 — x — 1 = 0 B. Назовите различные методы, которые вы использовали для решения каждого уравнения. Убедитесь, что ваша работа демонстрирует как алгебраические, так и …





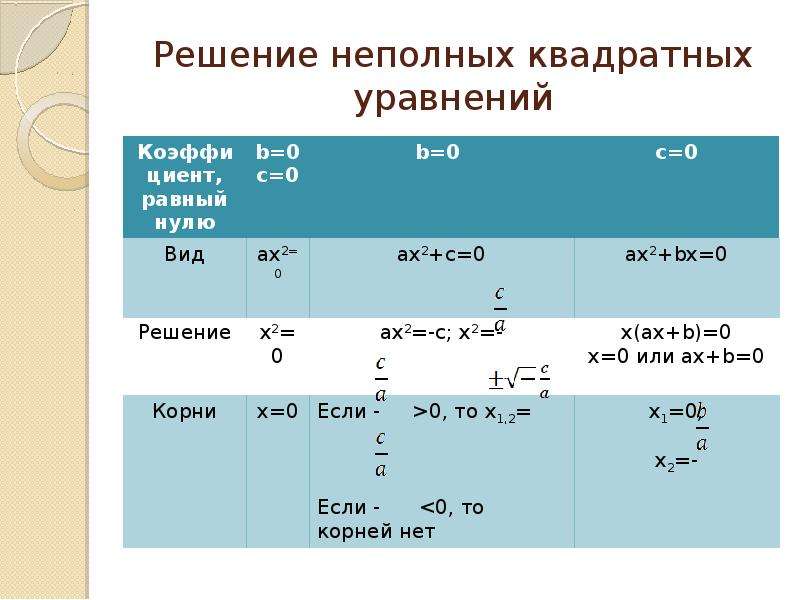 Вспоминаем, когда произведение двух множителей равно нулю.
Вспоминаем, когда произведение двух множителей равно нулю.
 части уравн.)
части уравн.)
 2 = 49/16 — 24/16 = 25/16`
2 = 49/16 — 24/16 = 25/16`