Решение задач по теории вероятностей
Теория вероятностей, в отличие от классического математического анализа, часто оперирует примерами и задачами из повседневной жизни. Применение ее в таких играх, как покер и рулетка, может существенно увеличить выигрыш, особенно если интуиция – не самая сильная ваша сторона. С другой стороны, законы теории вероятностей базируются на простой логике и могут быть поняты и освоены каждым. Поэтому читателю будет полезно ознакомиться с основными понятиями и принципами решения задач по данной теме.
Исходя из определения, вероятность наступления события (будем называть это событие А) есть отношения количества вариантов развития, где А происходит (m), к общему количеству вариантов развития (m).
Очевидно, что m всегда меньше или равно n, поэтому величина P никогда не превышает единицы. С другой стороны, m и n неотрицательны, поэтому вероятность не может быть меньше нуля. Часто величину вероятности выражают в процентах, умножая исходное выражение на 100%.
Попробуйте ответить на вопрос:
Какое количество автомобилей с одинаковыми цифрами на номере вы скорее всего встретите среди 300 проехавших мимо?
Теория вероятностей тесно связана с комбинаторикой – разделом математики, изучающем в том числе размещения, перестановки, сочетания элементов из множеств. Читателю стоит освоить следующие понятия: размещение, сочетание, размещение и сочетание с повторением из n различных элементов по m в каждом, перестановка из n элементов.
Например:
Сколькими способами можно взять три разных карточных короля – сочетание из 4 элементов по 3 в каждом?
Если комбинации из трех карт могут еще отличаться порядком – например, пики–крести–черви и черви-пики-крести, – размещение из 4 элементов по 3 в каждом. Если масти могут совпадать, но порядок не важен – сочетание с повторением, а если все-таки важен – то размещение с повторением. А вот сколькими способами можно упорядочить три карты – перестановка из 3 элементов. С формулами для расчета данных величин читатель может ознакомиться в любом учебном пособии по дисциплине «Теория вероятностей и математическая статистика».
Определите, сколькими способами можно наугад достать три белых шара из урны, где 5 белых шаров и 2 черных? Какова при этом вероятность такого исхода?
В качестве следующего этапа в освоении теории вероятностей следует изучить связи между вероятностями различных событий. Читателю стоит ознакомиться с такими понятиями, как совместные и несовместные события, благоприятствующие и противоположные события, сумма(объединение) событий, произведение(совмещение) событий, полная группа событий.
В качестве примера рассмотрим следующую ситуацию.
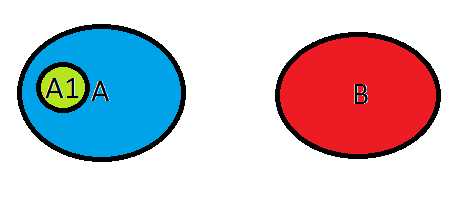
Лучник стреляет в мишень, при этом событие А состоит в том, что он поражает ее, событие А1 – стрела попадает в «десятку», а событие В – стрела летит в «молоко».
События А и B являются несовместными, так же как события А1 и В. События А и А1 являются совместными. Событие А1 благоприятствует событию А, но обратное утверждение неверно. Событие B является противоположным по отношению к А и А1. События А и В образуют полную группу событий, а А1 и В или А и А1 – нет.
Совмещение и произведение событий очень наглядно иллюстрируется графически. Рассмотрим события в качестве контуров, заключающих в себе все исходы, при которых эти события происходят. При этом площадь под контуром А1 также принадлежит к контуру А. Белым цветом будем обозначать пустое множество, а желтым — результаты суммы (объединения) или умножения (совмещения) различных комбинаций из А, А1 и В. Почему контур А1 внутри А?
Суммой (объединением) А и B будет событие А+В: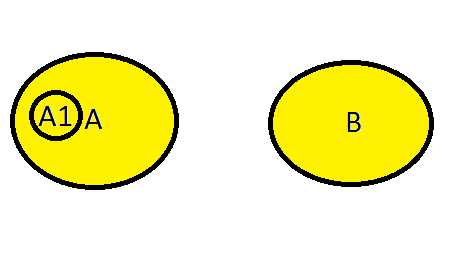
Произведением (совмещением) А и B будет событие AB, которое невозможно, так как контуры А и B не пересекаются: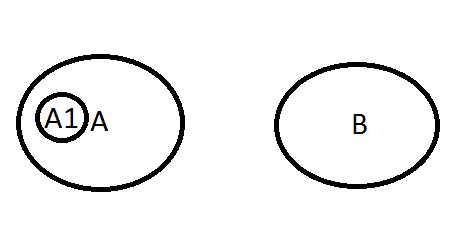
Сумма А + А1: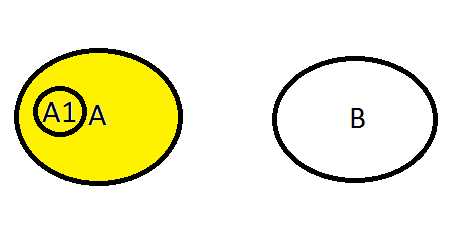
Произведение АА1: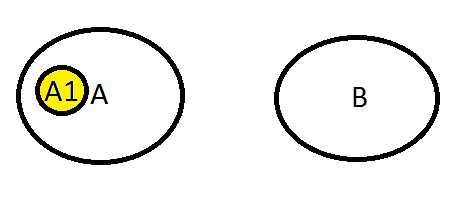
Сумма А1+В
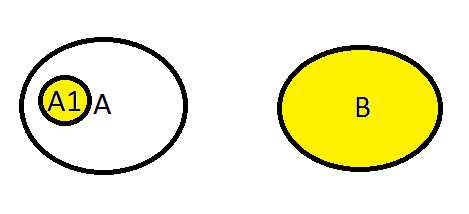
Произведение А1В: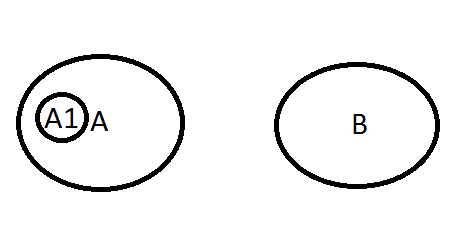
Cо всеми вышеизложенными понятиями и с формулами для сложения и умножения вероятностей читатель аналогичным образом может ознакомиться в любом учебном пособии по данному предмету. Изображение вероятностей в качестве геометрических контуров часто помогает при решении задач с множеством заданных условий и сложными связями между ними.
Попробуйте самостоятельно изобразить события А+А1В, А(А1+В), АВ +А1.
Если рассматривать цепочку событий, происходящих последовательно, необходимо ввести понятие условной вероятности PA(B) – вероятности события B, при условии, что А наступило. Читателю следует ознакомиться с формулой полной вероятности и с формулой Бейеса.
Представьте, что вы – участник шоу, в котором вам предстоит выбирать из трех закрытых дверей одну, за которой находится приз. За двумя другими дверями ничего нет. Ведущий знает, где находится приз, и предлагает вам выбрать дверь. После вашего предположения ведущий не открывает выбранную вами дверь, но из двух оставшихся открывает ту, за которой ничего нет. После этого он предлагает вам либо оставить свой выбор прежним, либо выбрать другую дверь. Станете ли вы менять свой выбор и почему?
Для решения задач с большим количеством испытаний классические формулы с использованием сочетаний и размещений неудобны, так как вычисляются с большим трудом (чему равен факториал 10000?). Как правило, подобные задачи легко узнаваемы, и их решение заключается в применении одной формулы, в выборе оной и состоит сложность задания. Читателю стоит освоить понятия и области применения для формул
При написании статьи автор использовал учебное пособие «Элементы теории вероятностей и математической статистики», авт. М.Ф.Рушайло, изд. РХТУ им. Д.И.Менделеева, 2005.
Решение теории вероятностей на заказ
Мы беремся решать задачи по теории вероятностей. Чтобы заказать у нас работу, вам нужно только прикрепить файл и указать срок.
Узнать цену работы можно абсолютно бесплатно.
reshatel.org
Решим задачи, контрольные, курсовые… — Решение задач по теории вероятности
Задача 106.( Гмурман, формула Байеса ) Батарея из трех орудий произвела залп, причем два снаряда попали в цель. Найти вероятность того, что первое орудие дало попадание, если вероятности попадания в цель первым, вторым и третьим орудиями соответственно равны P1= 0,4, р2 = 0,3, ;рз = 0,5.Решение. Обозначим через А событие—два орудия попали
в цель.
Сделаем два предположения (гипотезы):
B1—первое орудие
попало в цель;
В2—первое орудие не попало в цель.
По условию, P(В1) = 0,4; следовательно (событие В2 противоположно
событию B1),
Р(В2)= 1—0,4 = 0,6.
.
Найдем условную вероятность PB2(A), т. е. вероятность того,
что в цель попало два снаряда, причем первое орудие дало промах.
Другими словами, найдем вероятность того, что второе и третье орудия
попали в цель. Эти два события независимы, поэтому применима
теорема умножения:
.
Искомая вероятность того, что первое орудие дало попадание,
по формуле Бейеса равна
www.reshim.su
Случайные события. Вероятность события. Примеры решения задач
Случайные события. Вероятность события
Классическое определение вероятности
Вероятностью события А Р(A) называется отношение числа благоприятствующих этому событию исходов m к общему числу всех единственно возможных и равновозможных элементарных исходов n, Р(A)=.
Задача1
Из 20 экзаменационных билетов 3 содержат простые вопросы. Пять студентов по очереди берут билеты. Найти вероятность того, что хотя бы одному из них достанется билет с простыми вопросами.Решение:
Для начала найдем вероятность того, что ни одному из студентов не достанется билет с простыми вопросами.
Первая дробь показывает вероятность того, что первому студенту достался билет со сложными вопросами (их 17 из 20)
Вторая дробь показывает вероятность того, что второму студенту достался билет со сложными вопросами (их осталось 16 из 19)
Третья дробь показывает вероятность того, что третьему студенту достался билет со сложными вопросами (их осталось 15 из 18)
И так далее до пятого студента. Вероятности перемножаются т.к. по условию требуется одновременное выполнение этих условий.
Чтобы получить вероятность того, что хотя бы одному из студентов достанется билет с простыми вопросами надо вычесть полученную выше вероятность из единицы.
Ответ: 0,6009.
Задача2
Из множества всех последовательностей длины 10, состоящих из цифр 0; 1; 2; 3, наудачу выбирается одна. Какова вероятность того, что выбранная последовательность содержит ровно 5 нулей, причем два из них находятся на концах последовательности.
Вероятность события A – «Выбранная последовательность содержит ровно 5 нулей, причем два из них находятся на концах последовательности», согласно классическому определению, равна P(A) = , где n – полное число равновероятных исходов; m – число исходов, благоприятствующих событию A.
Число способов заполнить 10 позиций в последовательности цифрами 0; 1; 2; 3 составляет, с учетом возможности повторения цифр, n = 410 = 220 = 1048576.
Число способов разместить 5 нулей на 10 позициях в последовательности при условии, что нули обязательно находятся на первом и десятом месте в последовательности, равно числу способов разместить три нуля на восьми свободных позициях в последовательности и равно числу сочетаний из 8 элементов по 3: = = 56.
Оставшиеся 8 – 3 = 5 позиций в последовательности будут заполнены цифрами 1; 2; 3. Число способов осуществить это, с учетом возможности повторения, равно 35 = 243.
Т.о., число исходов, благоприятствующих событию A, равно m = ×35 = 56×243 = 13608.
Искомая вероятность события A равна:
P(A) = = 0,013.
Ответ: P(A) = = 0,013.
Задача 3.
Имеется 100 одинаковых деталей, среди которых 3 бракованных. Найти вероятность того, что взятая наудачу деталь без брака.Решение. В этой задаче производится испытание – извлекается одна деталь. Число всех исходов испытания равно 100, т. к. может быть взята любая деталь из 100. Эти исходы несовместны, равновозможны, единственно возможны. Таким образом, Событие — появилась деталь без брака. Всего в партии 97 деталей без брака, следовательно, число исходов, благоприятных появлению события А равно 97 . Итак, Тогда Задача 4.Решение. Так как на каждом из шести мест в шестизначном шифре может стоять любая из десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, то всех различных шестизначных номеров по правилу произведения будет . Номера, в которых все цифры различны, — это размещения из 10 элементов (10 цифр) по 6. Поэтому число благоприятствующих исходов . Искомая вероятность равна
Код банковского сейфа состоит из 6 цифр. Найти вероятность того, что наудачу выбранный код содержит различные цифры? Задача 5. Решение. Исход испытания — случайное расположение фирм в очереди. Число всех возможных исходов равно числу всех перестановок из шести элементов (фирм), т.е.Число исходов, благоприятствующих событию : m=1, если очередь выстроена по порядку. Тогда
Между шестью фирмами (А, Б, В, Г, Д, Е), занимающимися продажей компьютерной техники, проводится жеребьевка на предмет очередности предъявления своей продукции на выставке потенциальным потребителям. Какова вероятность того, что очередь будет выстроена по порядку, т. е. А, Б, В, Г, Д, Е?Задача 6. Решение
В компании 10 акционеров, из них трое имеют привилегированные акции. На собрание акционеров явилось 6 человек. Найти вероятность того, что среди явившихся акционеров:
а) все трое акционеров с привилегированными акциями отсутствуют;
б) двое присутствуют и один не явился.
а) испытанием является отбор 6 человек из 10 акционеров. Число всех исходов испытания равно числу сочетаний из 10 по 6, т. е.
Пусть событие — среди шести человек нет ни одного с привилегированными акциями. Исход, благоприятствующий событию ,- отбор шести человек среди семи акционеров, не имеющих привилегированных акций. Число всех исходов, благоприятствующих событию А, будет
Искомая вероятность
б) пусть событие — среди шести явившихся акционеров двое с привилегированными акциями, а остальные четыре – с общими акциями. Число всех исходов, Число способов выбора двух человек из необходимых трех Число способов выбора оставшихся четырех акционеров среди семи с общими акциями Тогда число всех способов отбора по правилу произведения
Искомая вероятность равна
www.matem96.ru