Заказ решений задач по линейной алгебре
Линейная алгебра – сложная математическая наука, при изучении которой студенту следует проявить максимум смекалки и способности к логическому мышлению. Прослушав дисциплину, студент должен овладеть инструментами, которые помогут решать любые задачи и системы уравнений.
Вариантов заданий, как и их решений, великое множество. Просто запоминая алгоритмы решений, выполнить все примеры подчас невозможно. Преподаватели специально строят задание так, чтобы проверить насколько студент глубоко понял предмет, а не просто запомнил ход решений.
Где найти помощь в решении задач по линейной алгебре
Если вы планируете заниматься линейным программированием или квантовой механикой, то мы советуем сосредоточиться на линейной алгебре, уделить ей достаточно много времени и внимания, а также постараться выполнить максимально количество заданий самостоятельно.
В любом другом случае, вы всегда можете найти помощь, если возникли проблемы с написанием решений. Осталось разобраться, к кому идти за помощью, если это нужно.
Во-первых, наверняка в вашей группе есть учащиеся, которые за невысокую плату помогут, и решат ваши задания. Кроме того, процесс заказа займет у вас немного времени, ведь вы вместе учитесь и находитесь в одних и тех же аудиториях.
Но тут есть и свои минусы. Первая опасность, преподаватель может узнать стиль решения вашего одногруппника, и заподозрить, что вы несамостоятельно выполняли задание. Вторая опасность кроется в том, что ваш одногруппник и сам может не справиться с заданием. Хорошо, если это выяснится заранее, и вы успеете найти другого помощника, но так бывает не всегда.
Во-вторых, помощь можно найти в Интернете. Тысячи объявлений на различных сайтах, предлагают недорогие услуги по подготовке работ школьникам и студентам. Увы, сегодня вы нашли объявление, сделали заказ и заплатили деньги, а завтра «помощник» не выходит на связь и его телефон отключен.
Если вы считаете, что нет оптимального варианта, и любая помощь с учебой – это риск, то вы, все же, ошибаетесь. Есть еще третий вариант помощников.
В-третьих, вы можете обратиться к специалистам. Наша компания собрала штат настоящих профессионалов. Мы 8 лет отбирали лучших сотрудников, которые могут выполнить качественно даже самые срочные заказы. Мы годами нарабатывали репутацию, ответственно относясь к своему делу.
Чтобы заказать работу у нас, ознакомьтесь с прайс-листом и оформите заказ.
Сколько стоят услуги по написанию работ по линейной алгебре
Цена услуги зависит от вида работы, объема, и сложности выполнения, а также от отведенного на работу срока. Учитывая, что клиенты компании – простые студенты, стоимость работ доступная для всех, чтобы каждый смог позволить себе оплатить услуги.
Чтобы точно узнать стоимость на конкретный вид работы, особенно если у вас нестандартный заказ, то вы можете связаться по указанному телефону с нами, и менеджер сориентирует вас по цене.
Заказ решения задач по алгебре: как правильно оформить
Заказать работу можно как онлайн, так и в офисе компании. Если вы решили не тратить время на дорогу и заказать услуги через Интернет, то при оформлении заявки внимательно укажите условия задач.
Напишите свои контактные данные, такие, как номера телефонов, адрес электронной почты. Все это необходимо, чтобы наш менеджер связался с вами, уточнил детали и принял заказ.
Как только мы принимаем заявку, наши сотрудники приступают к выполнению задания, подходя к нему со всей ответственностью. Уже скоро у вас будут готовые решения, за которые вы получите отличную оценку. Всегда рады вам помочь.
matematiku5.ru
3.2. Решение типовых задач по линейной алгебре
вводим матрицу второго порядка, используя кнопку , после чего нажимаем клавишу =.
Вычислим теперь алгебраическое дополнение A31. Для этого используем функцию submatrix.
A31:= (−1)1+3 |submatrix(A,1,2,2,3) |.
При помощи функции submatrix, из матрицы A порядка 3, извлекаем матрицу второго порядка, получающуюся вычеркиванием первого столбца и третьей строки. Вычисляем определитель из этой матрицы и умножаем его на знак алгебраического дополнения. Для вывода результата вычисления вводим имя переменнойA31, в которой хранится результат, и нажимаем клавишу =. Получаем,A31=–3.b) Теперь найдем те же величины для матрицы B.
Вводим переменную B1 и присваиваем ей значение, соответствующее квадратной матрицеB, состоящей из четырех строк
| 1 | −2 | 3 | 4 |
|
| 2 | 1 | −4 | 3 |
|
(Rows) и четырех столбцов (Columns). B := | . | ||||
| 3 | −4 | −1 | −2 |
|
|
| ||||
| 4 | 3 | 2 | −1 |
|
Вычисляем определитель |B|=900.
Теперь вычислим минор элемента B22. Для этого получим матрицуB22, исключив из матрицыB вторую строку и второй столбец. Проще набрать вручную эту матрицу. С целью демонстрации использования матричных функций получим матрицу
B22 при помощи функцийaugment, stack иsubmatrix. Чтобы фор-
мула была понятнее, используем две вспомогательные матрицы B1 иB2.B1 – это первая строка без второго столбца.B2 – третья и четвертая строки без второго столбца.
B1:= augment(submatrix(B,1,1,1,1), submatrix(B,1,1,3,4)). B2 := augment(submatrix(B,3,4,1,1), submatrix(B,3,4,3,4)).
Затем, используя функцию stack, соединяем эти две матрицы в одну матрицу B22.B22 := stack(B1,B2).
| 1 | 3 | 4 |
|
| 3 | −1 | −2 |
|
Получили матрицу B22 = | . | |||
| 4 | 2 | −1 |
|
|
|
studfiles.net
Решение задач по линейной алгебре
Задача 1.Решить матричное уравнение с помощью обратной матрицы. Сделать проверки обратной матрицы и матрицы-решения.
Решение.
Вычислим определитель матрицы А:
detA = =2*(2*2 — 1*1) — 1*(1*2 — 1*1) + 1*(1*1 — 2*1) = 4
Так как A невырожденная матрица, то существует обратная матрица A-1. Умножим слева обе части уравнения на A
Найдем обратную матрицу A-1.
Транспонированная матрица AT.
Алгебраические дополнения A11=
A12=, A13=
A21= A22=
A31= A33=
A32= A23=
Обратная матрица A-1.
Матрицу Х ищем по формуле: X = A-1·B
Ответ:
Проверка :
2. Методом Гаусса исследовать системы линейных алгебраических уравнений на совмесность, найти их общее и часное решение, определить фундаментальную систему решений соответствующих однородных систем, сделать проверки.
Составим расширенную матрицу системы.
Теперь исходную систему можно записать как:
x2 = [4 — (2x 3 + 5x4)]/3
x1 = [1 — ( — x2 + x3 — x4)]/1
x3,x4 будут свободные переменные, так как через них выразить можно выразить все остальные переменные.
Приравняем переменные x3,x4 к 0
3 . Методом Гаусса исследовать системы линейных алгебраических уравнений на совмесность, найти их общее и часное решение, определить фундаментальную систему решений соответствующих однородных систем, сделать проверки.
Составим расширенную матрицу системы.
Теперь исходную систему можно записать как:
x3 = [32 — (120x4)]/(-96)
x2 = [4 — ( — 63x3 + 66x4)]/34
x1 = [1 — (11x2 + 23x3 — 16x4)]/10
Свободная переменная x4 и через нее можно выразить остальные переменные.
4. . Для матрицы А найти: собственные значения
(1 — l)((2 — l)(3 — l)+4) — 2(-6 + 4l) = 0
(1 — l)((6-3l-2l + l2)+4) — 2(-6 + 4l) = 0
(1 — l)((6- 5l + l2)+4) +12 — 8l = 0
-l3 +6l2— 3 l-10 = 0
l1 = -1; l2 = 2; l3 = 5;
5. Для матрицы А найти собственные векторы.
Для l1 = -1:
Если принять х3 = 1, получаем х1 = 2, х2 = 2
Собственные векторы ×t, где t – параметр.
Для l2 = 2:
Если принять х3 = 1, получаем х1 = -1, х2 =
Собственные векторы ×t, где t – параметр.
Для l3 = 5:
Если принять х3 = 1, получаем х1 = , х2 =
Собственные векторы ×t, где t – параметр.
6. На векторах = (1,1, 3), = (1, 2, 2), = (0, 2, 1) построен параллелепипед. Используя произведение векторов: а) скалярное, б) векторное и в) смешанное вычислить
- пеоекцию вектора на направление вектора
- площадь грани, образованную векторами и
- высоту параллелепипеда, опущенную на грань, образованную векторами и
= (1,1, 3), = (1, 2, 2), = (0, 2, 1)
= (1-2*0, 2-2*2, 2-2*1) = (1,-2, 0)
Найдем скалярное произведение этих векторов
a · = 1 * 1 + 1 * -2 + 3 *0 = -1
Найдем модуль вектора =
Проекция вектора на направление вектора
Площадь грани, образованную векторами и
= (1,1, 3), = (1, 2, 2), = (0, 2, 1)
S =3
Высоту параллелепипеда, опущенную на грань, образованную векторами и
1*2*1+1*2*0+3*1*2-3*2*0- 1*1*1-1*2*2 =
Площадь грани из предыдущей задачи равна S = 3
7. В треугольнике с вершинами А(2;-3), В(6;5), С(-3;1), найти координаты проекции точки А на медиану, проведённую из точки В, а также расстояние от точки А до прямой ВС. Аналитическое решение проверить графически.
Решение.
Обозначим середину стороны AC буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам.
M(-1/2;-1)
Медиана BМ проходит через точки B(6;5) и М(-1/2;-1), поэтому:
Каноническое уравнение прямой:
или
13y -12x +7 = 0
Нормальный вектор медианы ВМ (-12,13), таким же будет и нормальный вектор прямой АN.
Мы знаем направляющий ветор прямой и координаты точки А(2,-3) следовательно сможем написать уравнение прямой или 13x-26=-12y-36
13x-26+12y+36 =0
13x+12y+10 =0
Решая систему, получим координаты проекции точки А на медиану
Далее находим расстояние от точки А до прямой ВС
Расстояние от точки до прямой — равно длине перпендикуляра, опущенного из точки на прямую.
Уравнение прямой BC —
или 9y -4x — 21 = 0 и точка А(2;-3),
Ответ: расстояние от точки А до прямой ВС — , проекции точки А на медиану
8. Составить общее уравнение плоскости, проходящей через прямые:
Найти угол между этой плоскостью и плоскостью x+y-2=0
Решение..
Прямые и параллельны, так как их направляющие векторы пропорциональны.
Координаты точки принадлежащей прямой
(0, -1 ,2) а для второго уравнения (1,1,5)
Чтобы написать уравнение плоскости нужны три точки, третью точку найдём, записав любое из уравнений параметрическом виде, тогда точка принадлежащая уравнению будет иметь координаты (1,0,3)
Теперь мы можем получить уравнение плоскости, проходящей через три точки , которое является искомым уравнением плоскости, проходящей через две заданные прямые:
Для вычисления угла φ между плоскостями воспользуемся формулой:
Уравнение первой плоскости x+y-2=0 и второй -x+2y-z=0
Ответ: Уравнение плоскости — -x+2y-z=0, угол между плоскостями arcos
9. Привести уравнение кривой к каноническому виду, определить её тип, расположение на плоскости (параметры, смещение), построить кривую и проверить координаты точек её пересечения с осями координат:
Дано уравнение кривой:
4x2 + y2 — 2y — 3 = 0
Решение.
4x2 + y2 — 2y — 3 = 0
4x2 + (y2-2*1y + 1) -1•1 =4x2 +(y-1)2-1=0
Можно записать
4x2 +(y-1)2-1=0
Разделим все выражение на 4
. Полуоси эллипса: a = 2;b = 1
Данное уравнение определяет эллипс с центром в точке:
C(0; 1) .. Фокусы эллипса:
С учетом центра, координаты фокусов равны:
Тогда эксцентриситет будет равен:
Вследствие неравенства c < a эксцентриситет эллипса меньше 1.
10. Привести уравнение поверхности к каноническому виду, определить её тип в пространстве (ориентация, смещение). Изобразить эскиз этой поверхности.
Составляем матрицу квадратичной формы и столбец коэффициентов линейной формы
Столбец коэффициентов линейной формы -16, -6 ,24
В результате получили, что матрица квадратичной формы диагональная,
В заданном уравнении имеются линейные члены всех неизвестных, а также квадраты неизвестных . Дополняем члены с этими неизвестными до полных квадратов
Коефициенты A11 =4, A22 =-3, A33 =12, a1 =-8, a2 =-3, a3 =12, a0 =24
Вычислим ортогональные инварианты
Так как уравнение задаёт одноплосный гиперболоид.
kursar.ru
3. Задачи линейной алгебры
3.Задачи линейной алгебры
3.1.Основные сведения о матричных операциях
Для решения инженерных задач часто приходится выполнять различные матричные операции: решать систему линейных алгебраических уравнений, вычислять нормы матриц, вычислять определитель, находить обратную матрицу, умножать матрицы, вычислять ранг матрицы, определять собственные числа и вектора и т.д. Задачи, использующие матричные операция, являются достаточно трудоемкими. Например, Для того чтобы выполнить простейшую матричную операцию, умножить две квадратные матрицы порядка N, необходимо выполнить2N3 арифметических операций. Поэтому, в пакете Mathcad, большое внимание уделено всевозможным матричным операциям.
Номера столбцов и строк матриц, по умолчанию, начинается с нуля. Так, квадратная матрица A второго порядка, по умолчанию, имеет следующие четыре элемента:A0,0, A0,1, A1,0, A1,1. В математике чаще принято нумеровать элементы массивов при помощи натурального ряда чисел. Для того чтобы определить нумерацию элементов массивов с единицы, применяется команда
ORIGIN :=1.
Теория на данную тему приведена в работе [1] глава V, поэтому все определения, теоремы и теоретические алгоритмы решения задач линейной алгебры мы не приводим. В данной работе познакомимся с основными функциями, предназначенными для решения задач линейной алгебры. При решении задач линейной алгебры используется панель операций с матрицами и векторами.
Рассмотрим инструменты, находящиеся в этой панели.
, «Ctrl+m» – создание объекта матрица с определением количества строк и столбцов.
, [ – вывести один элемент матрицы.

Например A1,3 .
– вычисление обратной матрицы. НапримерB−1 .
, | – вычисление определителя матрицы|A| =det A; вычисление длины вектора|x| .
, «Ctrl+» – поэлементные операции с матрицами. Напри-
мер: A B ─ умножить все соответствующие элементы двух матриц.
, «Ctrl+6» – получить столбец матрицы. Например,C 0 – задает нулевой столбец матрицы.
, «Ctrl+1» | – получить транспонированную матрицу. |
, * – вычислить скалярное произведение двух векторов. | |
, «Ctrl+8» | – вычислить векторное произведение двух век- |
торов. |
|
, «Ctrl+4» | – вычислить сумму компонент вектора. |
Чтобы выполнить любую операцию над матрицами при помощи панели инструментов, необходимо нажать на соответствующую кнопку и ввести в помеченной позиции имя матрицы и, возможно, параметры команды. На этапе ввода матрицы для перехода к следующему элементу можно использовать клавишу Tab
или “Shift+Tab”.
Для выполнения различных матричных преобразований в Mathcad встроено более сорока матричных функций. Все эти функции можно разделить на три группы.
1. Функции определения матриц и операции с блоками матриц.
38
3. Задачи линейной алгебры | 39 |
2.Функции вычисления числовых характеристик матриц.
3.Функции, реализующие численные алгоритмы решения задач линейной алгебры.
Чтобы вызвать список всех матричных и векторных функций,
необходимо войти в пункт меню Insert/Function. В списке из тридцати типов функций выбрать предпоследний пунктVector and Matrix и перейти в правое поле, в котором расположен список матричных и векторных функций. Рассмотрим только наиболее часто используемые функции.
1. Функции определения матриц и операции с блоками матриц.
matrix(N, M, fun) ─ создает и заполняет матрицу, состоящую изN строк иM столбцов. Третий параметрfun определяет имя функции двух переменныхfun(i, j), задающую формулу для заполнения элемента, стоящего на пересеченииi-йстроки иj-го
столбца. Функция fun должна быть определена выше. |
|
| ||
Пример: |
|
|
| . |
f (i,j):=10 (i +1)+(j +1) |
| 11 | 12 | 13 |
matrix(2,3, f) = | 21 | 22 |
| |
|
| 23 | ||
diag(V) – на базе вектораV создает диагональную матрицу, диагональные элементы которой равны компонентам заранее определенного вектораV.
|
| 1 |
|
| 1 | 0 | 0 |
|
Пример. |
| 2 |
|
| 0 | 2 | 0 |
|
V := |
| diag(V) = |
| |||||
|
| 3 |
|
| 0 | 0 | 3 |
|
|
|
|
|
|
identity(N) ─ создает единичную матрицу порядкаN.
| 1 | 0 |
|
Пример. A:= identity(2) A= | 0 | 1 |
|
|
|
augment(A, B, C, …) – на базе нескольких, заранее определенных матрицA, B, C и т.д., имеющих одинаковое количество строк, формирует матрицу, в первых столбцах которой расположен массивA, а в последующих ─ массивыB, C и т.д.
| 1 |
| 2 |
| 3 |
|
| 4 | 5 | 6 |
|
| M := | N := |
| 30 |
| C := | 40 | 50 |
|
| |
Пример. | 10 |
| 20 |
|
| 60 |
| ||||
|
|
|
| 1 | 2 | 3 | 4 | 5 | 6 |
| |
| augment(M, N,C) = | ||||||||||
|
|
| 20 | 30 | 40 | 50 | 60 | . | |||
|
|
|
| 10 |
| ||||||
stack(A, B, C, …) – на базе нескольких, заранее определенных матрицA, B, C и т.д., имеющих одинаковое количество столбцов, формирует матрицу, в первых строках которой расположен массивA, а в последующих – массивыB, C и т.д.
Пример. Используем матрицы предыдущего примера.
D := stack(MT , NT ,CT ) |
| 1 | 2 | 3 | 4 | 5 | 6 |
|
DT= |
| 20 | 30 | 40 | 50 | 60 | . | |
| 10 |
| ||||||
submatrix( A, RowBeg, RowEnd, ColumnBeg, ColumnEnd) – вы-
водит блок матрицы A, расположенный в строках сRowBeg по
RowEnd и в столбцах с ColumnBegпо ColumnEnd.
Пример. Используем матрицы предыдущего примера.
40 submatrix(D,3,4,1,1)=50 .
2. Функции вычисления числовых характеристик матриц.
studfiles.net
Решение линейной алгебры, решение задач по линейной алгебре. Решение линейной алгебры онлайн
- Нужна помощь при решении контрольной работы по линейной алгебре?
- Скоро зачет или экзамен, но не получается разобраться с материалом?
- Требуется поддержка на самостоятельной работе?
Вы нашли решение проблем! Мы вам поможем!
О нас
Агентство Neudoff.net на протяжении многих лет работает на рынке образовательных услуг. Мы занимаемся решением задач и контрольных работ по линейной алгебре (и иным физмат дисциплинам) на заказ.
У нас работают только лучшие специалисты. У каждого сотрудника нашей компании есть высшее физико-математическое образование и большой опыт работы в данной сфере. Мы поможем вам справиться с любыми проблемами, касающимися вашей учебы.
Наши возможности
Линейная алгебра довольно популярный предмет. Его изучают во всех высших учебных заведениях, в независимости от специальности. Он может проходиться как отдельная дисциплина, а может входить неявно в состав высшей математики.
За время работы сервиса наши сотрудники успешно выполнили далеко не один десяток контрольных работ по линейной алгебре. Специалисты сервиса с радостью возьмут на себя часть вашей учебной нагрузки.
К тому же, мы предлагаем услуги по онлайн помощи при решении задач по линейной алгебре, например на зачете.
Как сделать заказ?
Воспользуйтесь специальной «Формой отправки заказа» — так сделать нам заказ проще всего. С ее помощью вы отправляете нам информацию о правилах оформления, методические указания, сроки выполнения и, конечно, сами задания.
Есть и другой способ. Просто свяжитесь с нами и перешлите нам задания любым удобным для вас способом. Таких способов достаточно много:
Присылайте свои заказы в любое время. Агентство Neudoff.net остается на связи круглые сутки!
Наши гарантии
Neudoff.net — серьезная организация, которая очень дорожит своей репутацией. Мы хотим, чтобы каждый клиент оставался доволен, чтобы каждый получал правильное решение точно в срок.
Если вы заказываете у нас решение задач по линейной алгебре первый раз, то вы можете нас для начала проверить. Закажите решение не целой контрольной, а только нескольких задач. Ну и после получения решения можете смело заказать остаток.
Мы практикуем индивидуальный подход. Уверены, что вы останетесь довольны нашей работой!
Наши бонусы
Друзья, наши клиенты, сделав у нас заказ всего один раз, потом неоднократно приходили к нам снова и снова. Они много раз заказывали у нас решение контрольных работ не только по линейной алгебре, но и по другим предметам. Так же многие из них советовали нас друзьям и это очень лестно для нас!
Для своих постоянных клиентов мы предусмотрели ряд бонусов — скидок на заказы.
Чем больше заказываете работ, тем больше скидка на следующий заказ. Вплоть до 100%!
Если вам вдруг что-то стало не понятно, то не стоит тянуть — сразу напишите нам, и мы ответим на все вопросы! Способов связи достаточно! Мы всегда онлайн!
neudoff.net
Примеры решения задач типового расчёта по линейной алгебре и аналитической геометрии
Примеры решения задач типового расчёта
по линейной алгебре и аналитической геометрии.
Задача 1.1. Вычислить, представить ответ в алгебраической, тригонометрической, показательной формах.
Решение. Представим комплексное число в тригонометрической форме. Для этого находится его модуль: , далее вычисляется аргумент комплексного числа: , либо , наконец,
, где , если комплексное число находится в первой или четвертой четверти, , если комплексное число находится во второй или третьей четверти. В данном случае аргумент комплексного числа равен: .
Поэтому тригонометрическая форма имеет вид: .
По формуле Муавра , где — аргумент комплексного числа , получаем:
,
окончательно: =.
В алгебраической форме: =,
в показательной форме: =.
Задача 1.2. Вычислить .
Решение. Представим комплексное число в тригонометрической форме:
=. Воспользуемся следующей формулой извлечения корня из комплексного числа : ), где=0,1,2,…,.
Т.е. корень -ой степени из комплексного числа принимает ровно значений. Точки комплексной плоскости, соответствующие значениям , являются вершинами правильного многоугольника, вписанного в окружность радиуса с центром в начале координат.
В данном примере получаем: =, где . Тогда корни принимают значения:
=(+), =(+),
=(+), =(+).
Для построения этих комплексных чисел на комплексной плоскости проведем окружность радиуса . На окружности отметим точку =(+), далее, разбивая окружность на четыре равные части , изобразим остальные точки ,, . Заметим, что радиан соответствуют примерно.
Задача 2. Найти произведение матриц , где и .
Решение. ===
Задача 3. Найти матрицу, обратную данной. Сделать проверку. .
Решение. Находим определитель матрицы .
=, т.е. данная матрица является неособенной, обратная матрица существует. Вычислим соответствующие алгебраические дополнения :
==; ==; ;
; ; ;
; ; .
Находим обратную матрицу :
=. Проверка заключается в перемножении матриц
(единичная матрица). Последнюю операцию выполнять аналогично примеру 2.
Задача 4. Решить систему линейных алгебраических уравнений (СЛАУ) с помощью обратной матрицы: .
Решение. Найдем обратную матрицу к матрице системы .
Аналогично примеру 3 получаем =
Вектор – столбец решений находится по формуле:
=, или Проверка осуществляется непосредственной подстановкой найденных значений неизвестных в исходную СЛАУ.
Задача 5. Найти ранг матрицы .
Решение. Последовательно осуществляем линейные преобразования строк данной матрицы для приведения ее к ступенчатому виду.
Шаг 1. Переставим в данной матрице первую и вторую строки.
Шаг 2. Умножим первый столбец на 1/2, четвертый столбец умножим на 1/5. В результате получим: .
Шаг 3. Умножим на 2 первую строку и прибавим её к третьей («заработаем» нуль на месте «3-1»,т.е. вместо (–2) получим (0)). В результате получим: .
Шаг 4. Умножим на –3 вторую строку и прибавим её к третьей («заработаем» нуль на месте «3-2»,т.е. вместо (–3) получим (0)). Получим:
Таким образом, получили ступенчатую матрицу эквивалентную данной, в которой две ненулевые строки, значит ее ранг равен 2: .
Задача 6. Решить систему методом Гаусса: .
Решение. Запишем расширенную матрицу СЛАУ:
.
С помощью эквивалентных преобразований приведём матрицу к верхнетреугольному виду (прямой ход метода Гаусса).
Шаг1. Вычтем из второй строки первую, результат умножим на (–1/2):
Шаг 2. Вычитаем из третьей строки первую, умноженную на 2:
Шаг 3. Вычитаем из четвёртой строки первую, умноженную на 3:
Шаг 4. Прибавляем к третьей строке вторую, умноженную на 5, результат делим на 2:
Шаг 5. Вычитаем из четвёртой строки вторую:
Шаг 6. Прибавляем к четвёртой строке третью, умноженную на 6, результат делим на 17:
Теперь с помощью эквивалентных преобразований приведём матрицу к диагональному виду (обратный ход метода Гаусса).
Шаги 7, 8, 9. От третьей строки отнимаем четвёртую, умноженную на 2; от второй строки отнимаем четвёртую; от первой строки отнимаем четвёртую.
Шаги 10, 11. От первой строки отнимаем третью; от первой строки отнимаем вторую.
Теперь в последнем столбце получились искомые значения переменных, т.е.
Задача 7. Найти размерность и базис подпространства решений однородной системы линейных алгебраических уравнений (ОСЛАУ). .
Решение. Применим прямой ход метода Гаусса (приведем систему уравнений к верхнетреугольному виду). Поступая аналогично примеру 6 вычтем из второй строки первую, умноженную на 3; вычтем из третьей строки первую, умноженную на 2; прибавим первую строку к четвёртой; получим:
,
последние три строки оказались одинаковыми, значит, матрицу можно привести к следующему виду:
.
В качестве базисных переменных можно взять , свободные – .
Ранг матрицы равен 2, т.е. , следовательно, размерность подпространства решений тоже равна 2.
Формируем фундаментальную систему решений (ФСР). Пусть переменные принимают значения 1, 0 соответственно. Тогда из второго уравнения находим значение из первого уравнения находим значение Тогда .
Пусть теперь переменные принимают значения 0, 1 соответственно. Тогда, поступая аналогично, получим Откуда . — образуют ФСР, общее решение данной однородной СЛАУ имеет вид .
Задача 8. Доказать, что векторы образуют базис и разложить вектор по этому базису.
Решение. Ненулевые векторы образуют базис тогда и только тогда, когда они некомпланарны (т.е. не лежат в одной плоскости), значит их смешанное произведение не должно быть равно 0:
, 121 + 333 + 221 – 223 – 231 – 131 = 12 ≠ 0. Векторы образуют базис.
vunivere.ru
Практикум по линейной алгебре
39
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
Хабаровская государственная академия экономики и права
Кафедра математики и математических методов в экономике
МАТЕМАТИКА
Линейная алгебра
Варианты контрольных заданий
для студентов 1-го курса дневного отделения
Хабаровск 2008
ББК
Х 12
Математика. Линейная алгебра : варианты контрольных заданий для студентов 1-го курса дневного отделения / сост. Е. О. Старкова, М. Ф. Тиунчик, С. В. Тонконог. – Хабаровск : РИЦ ХГАЭП, 2008. – 32 с.
Рецензент канд. физ.-мат. наук, доцент, начальник отделения подготовки научно-педагогических кадров ХПИ ФСБ России Ивлева А.И.
Утверждено издательско-библиотечным советом академии в качестве методических указаний
Тиунчик Михаил Филиппович
Старкова Елена Олеговна
Тонконог Светлана Владимировна
МАТЕМАТИКА
Линейная алгебра
Варианты контрольных заданий
для студентов 1-го курса дневного отделения
Редактор Г.С. Одинцова
Подписано в печать Формат 80×64/16. Бумага писчая. Печать офсетная. Усл.п.л. 1,9 Уч.-изд.л. 1,3 Тираж 175 экз. Заказ № |
680042, Хабаровск, ул.Тихоокеанская, 134, ХГАЭП, РИЦ
© Хабаровская государственная академия экономики и права, 2008
Предисловие
В методической разработке приведены 30 вариантов контрольных упражнений по линейной алгебре. Каждый вариант состоит из 15 типовых заданий.
В вариантах предусмотрены задания на темы: действия над матрицами, вычисление определителей, методы исследования и решения систем линейных алгебраических уравнений, приведение систем к системе с базисом и нахождение базисных решений, нахождение опорных решений канонических систем уравнений методом однократного замещения, нахождение собственных векторов и собственных значений линейных преобразований, исследование квадратичных форм.
Материал соответствует государственным образовательным стандартам по математическим дисциплинам для студентов экономических специальностей.
Для студентов специальностей «Экономическая теория» и «Математически методы в экономике», изучающих линейную алгебру отдельной дисциплиной, вариант выдаётся в полном объёме как индивидуальное задание на семестр. По темам аналитической геометрии, изучение которых отнесено к этой дисциплине, выполняется отдельное индивидуальное задание или аудиторная контрольная работа.
Для остальных специальностей вариант выдаётся не в полном объёме, а только по материалу, изучение которого предусмотрено соответствующим стандартом.
Линейная алгебра
Контрольное задание для студентов 1-го
курса
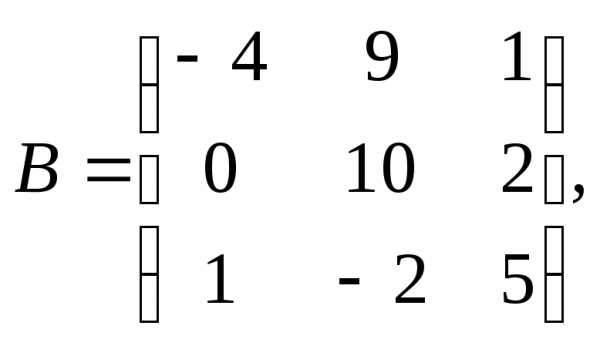
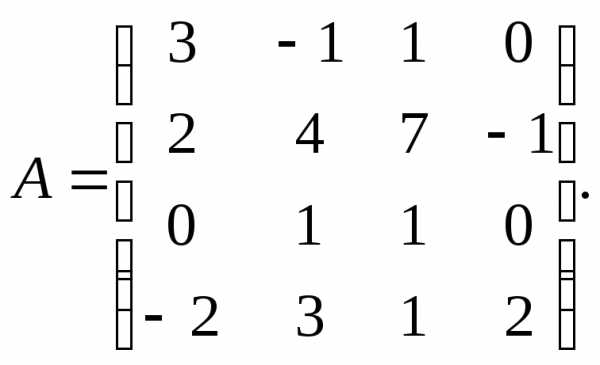
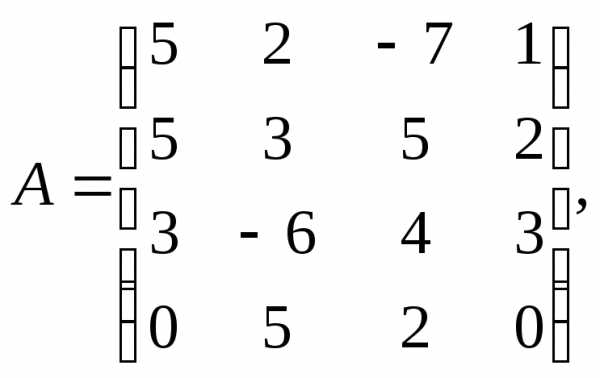
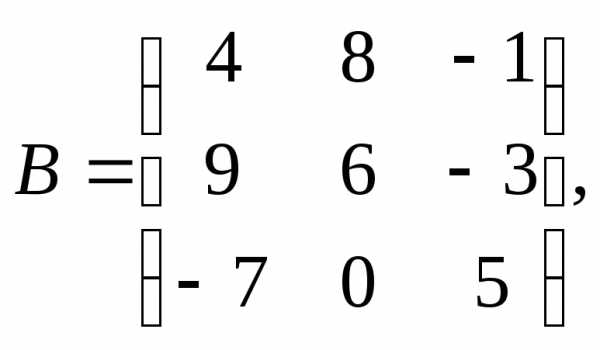
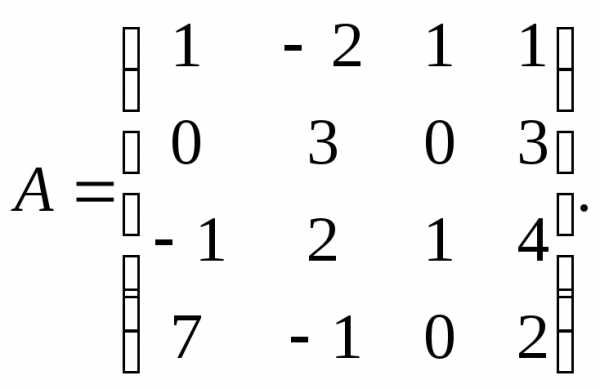
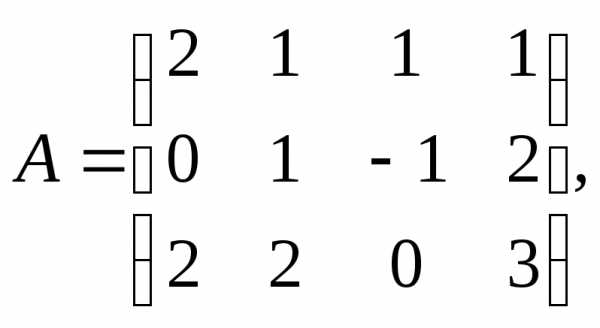
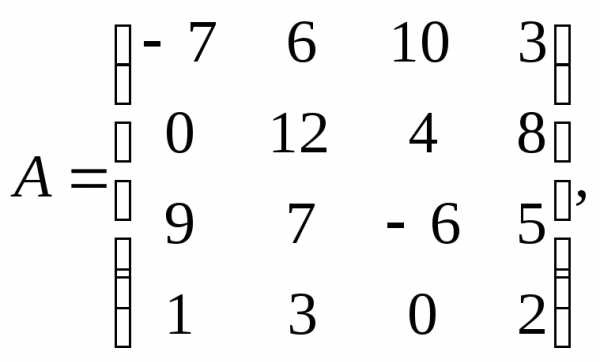
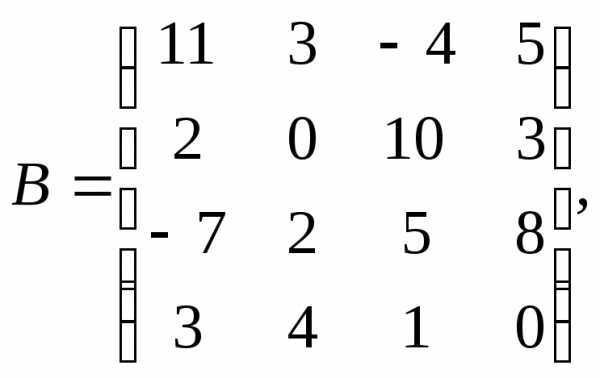
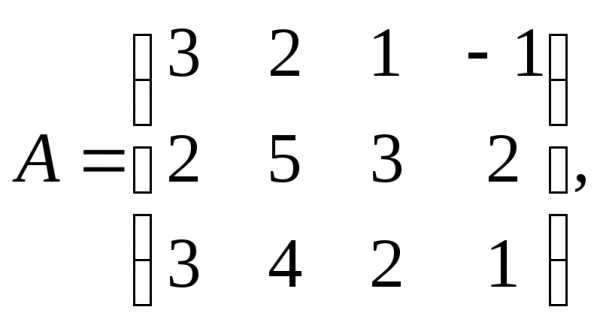
Для данных матриц А и В и заданных чисел α, β требуется найти:
1) АВ;
2) αА · В;
3) βА – Е, где Е – единичная матрица;
4) транспонированные матрицы АТ и ВТ.
По данной матрице вычислить её определитель следующими способами:
разложением по элементам какой-нибудь строки;
разложением по элементам какого-либо столбца;
методом Гаусса.
По заданной матрице А найти её обратную А-1 и проверить равенства
А · А-1 = А-1 · А = Е.
При заданных матрицах А и В найти неизвестную матрицу Х, удовлетворяющую матричному уравнению АХ = В.
Найти общее решение данной однородной системы линейных алгебраических уравнений с помощью её фундаментальной системы решений.
При заданных А и В найти общее решение неоднородной системы АХ = В, используя фундаментальную систему решений соответствующей приведённой однородной системы уравнений.
Найти общее решение данной системы линейных алгебраических уравнений методом Гаусса.
Вычислить ранг заданной матрицы.
Заданную систему линейных уравнений исследовать на совместность по критерию совместности (по теореме Кронекера – Капелли) и на определённость.
Решить систему линейных алгебраических уравнений следующими способами:
по формулам Крамера;
матричным методом;
методом Гаусса.
Данную систему линейных уравнений привести к системе с базисом методом Жордана – Гаусса и найти одно базисное решение.
Найти три опорных решения данной канонической системы линейных уравнений методом преобразования однократного замещения.
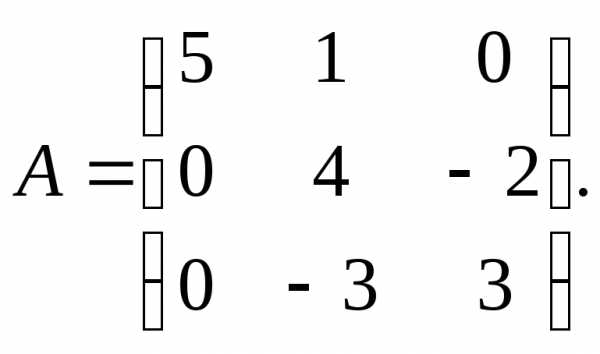
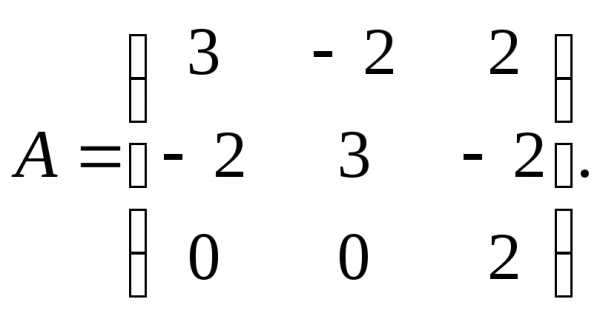
Найти собственные векторы и собственные значения линейного преобразования переменных, заданного матрицей А.
Привести данную квадратичную форму к каноническому виду методом ортогональных преобразований. Выяснить, является ли она положительно определённой.
Выяснить с помощью критерия Сильвестра, является ли квадратичная форма положительно определённой.
Вариант 1
1. 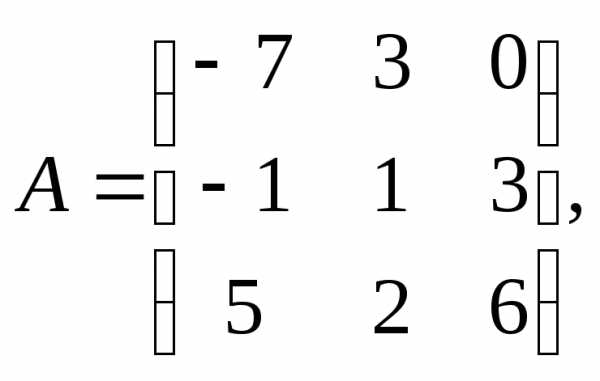
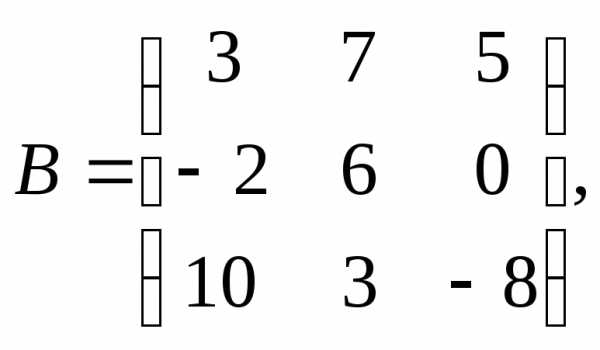 α = 6, β = 3.
α = 6, β = 3.
2. 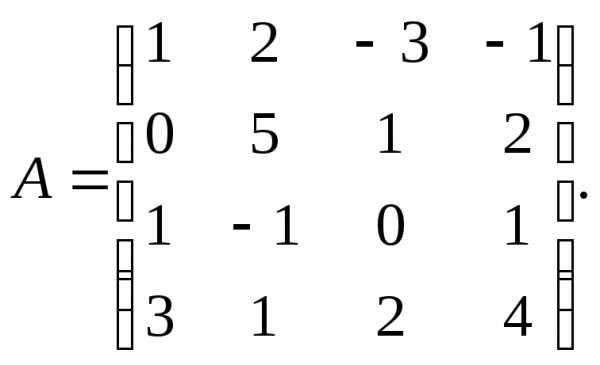 3.
3. 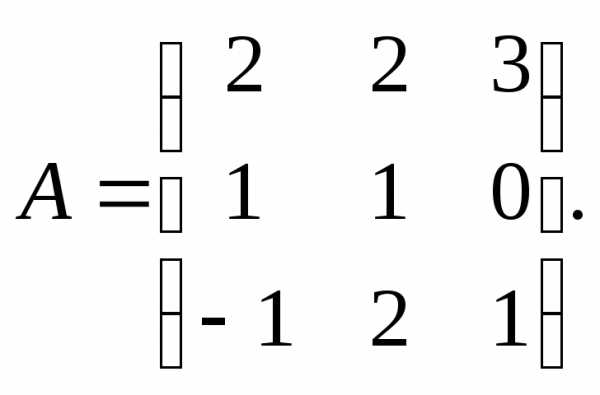
4. 5. 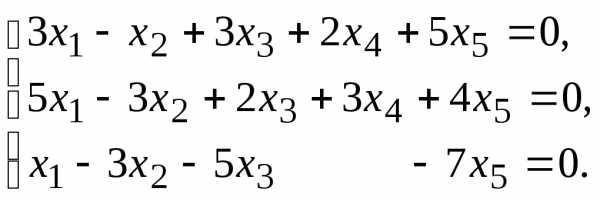

6.
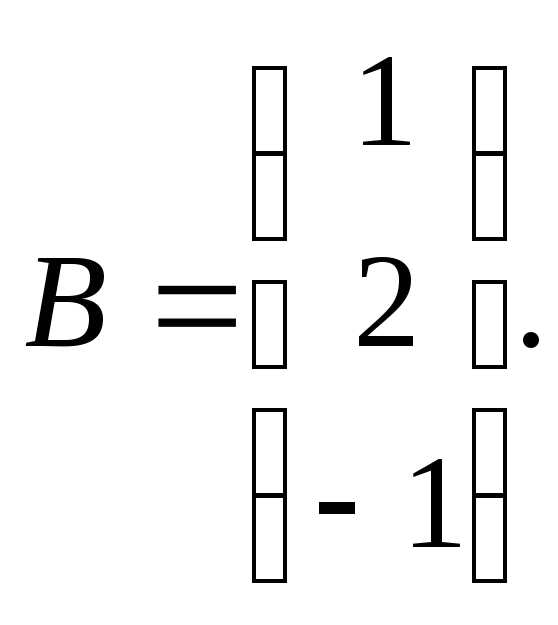 7.
7.
8. 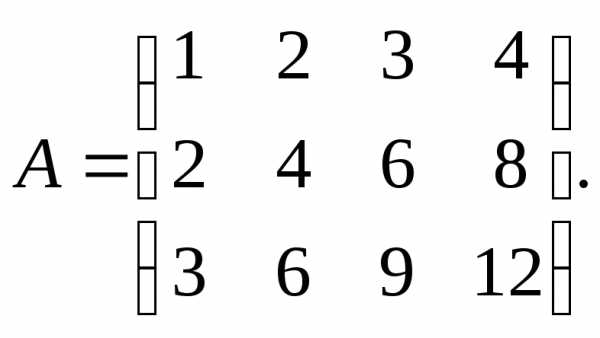 9.
9.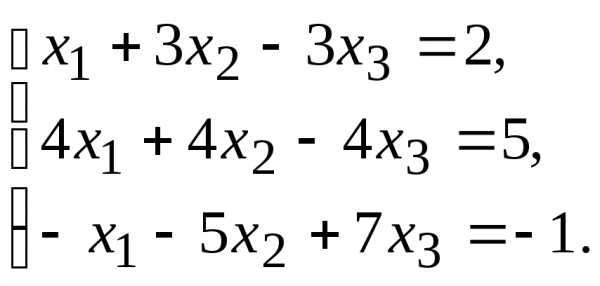
10.  11.
11.
12.  13.
13. 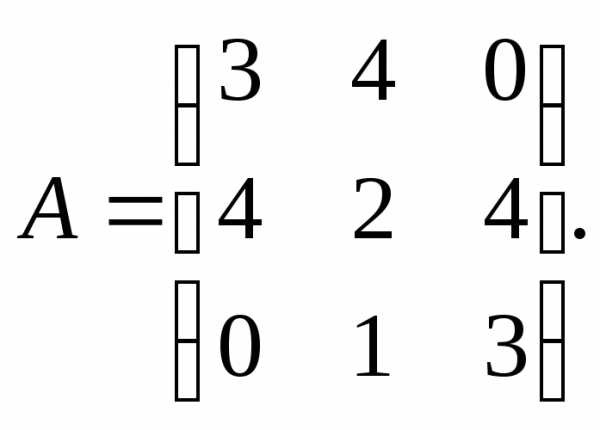
14. 15.
Вариант 2
1. 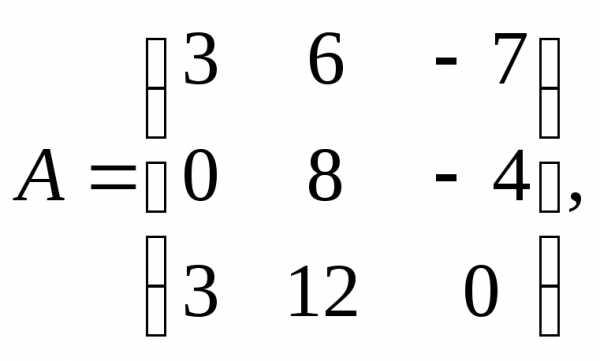
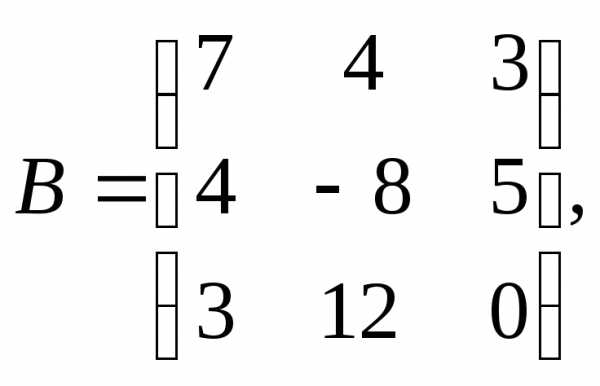 α = 2, β = 4.
α = 2, β = 4.
2. 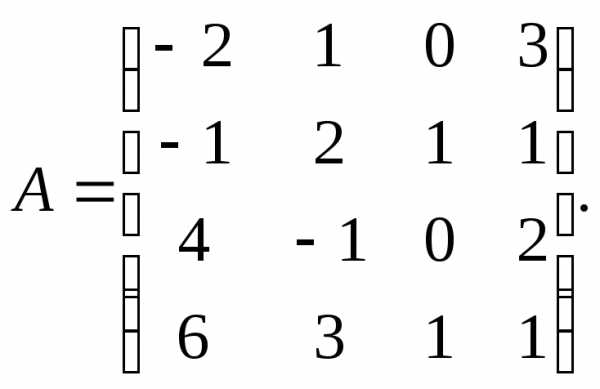 3.
3. 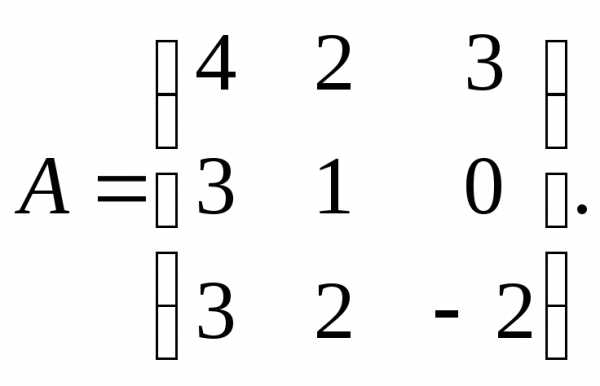
4. 5.
6. 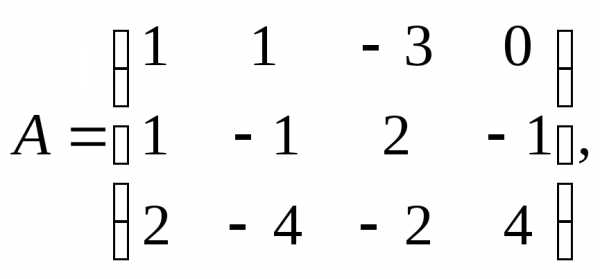
 7.
7.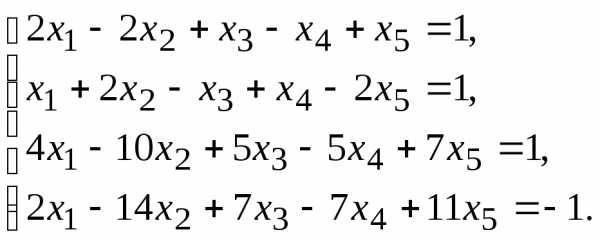
8.  9.
9.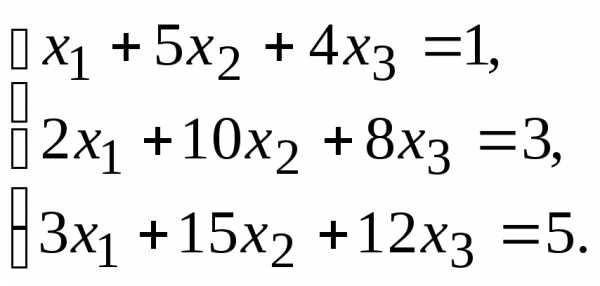
10. 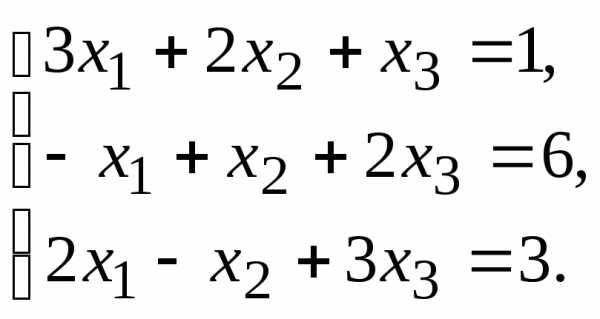 11.
11.
12. 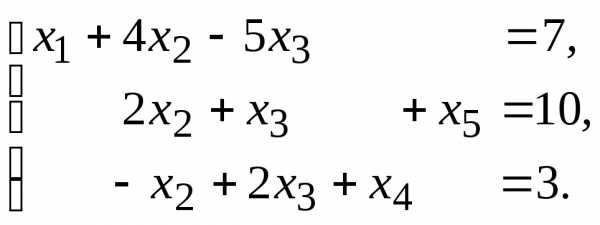 13.
13.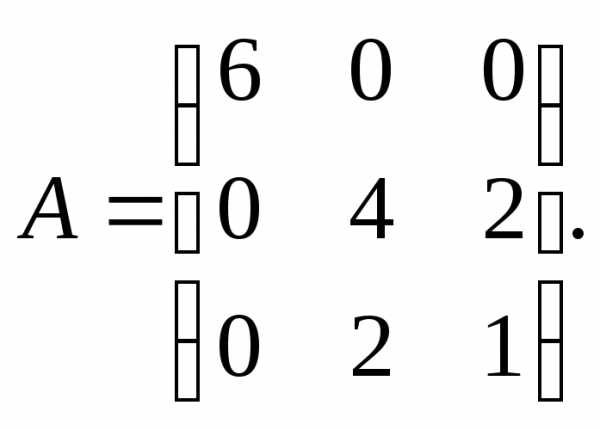
14. 15.
Вариант 3
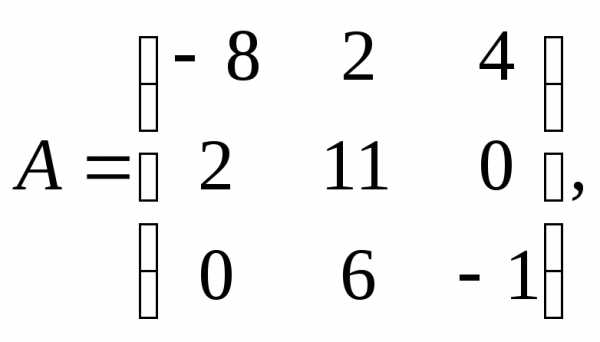
1. 
 α = – 2, β =
5.
α = – 2, β =
5.
2.  3.
3.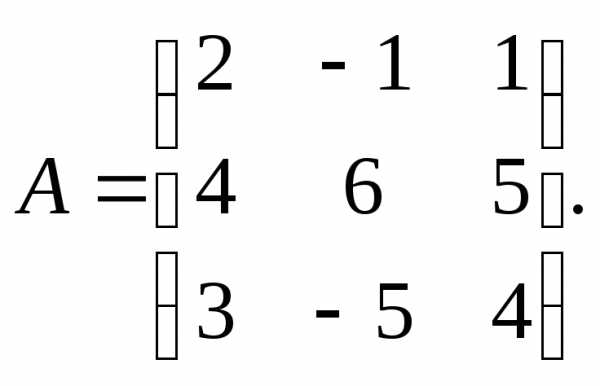
4. 5.
6. 
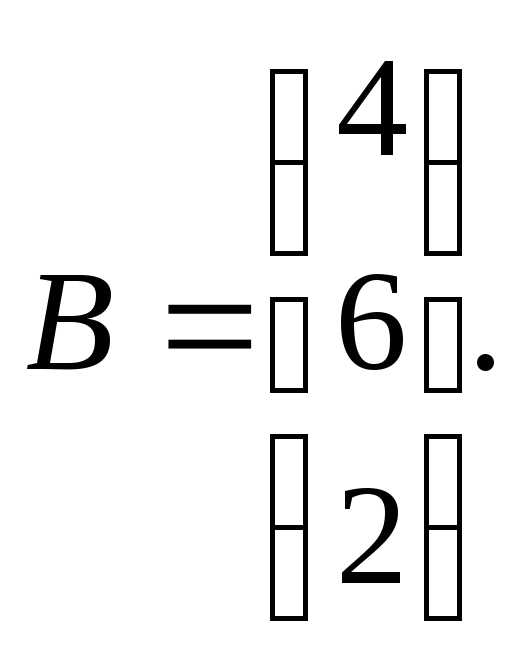 7.
7.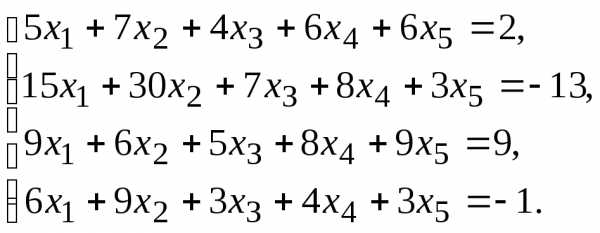
8. 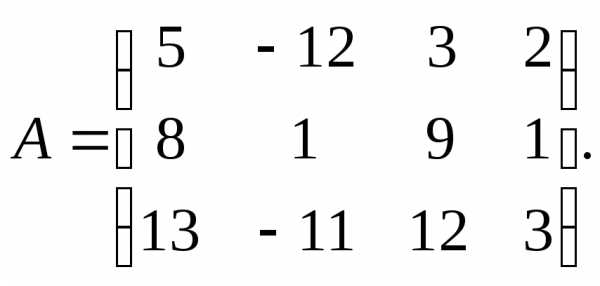 9.
9.
10. 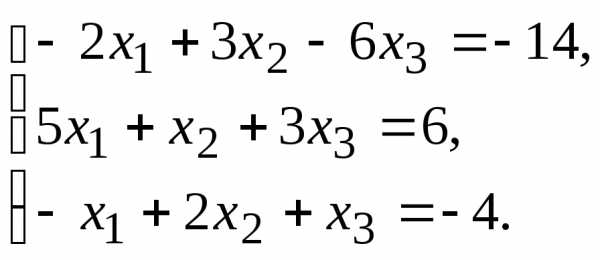 11.
11.
12.  13.
13. 
14. 15.
Вариант 4
1. 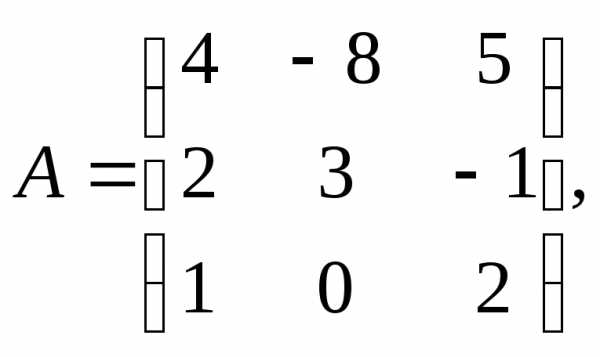
 α = 4, β =
α = 4, β = 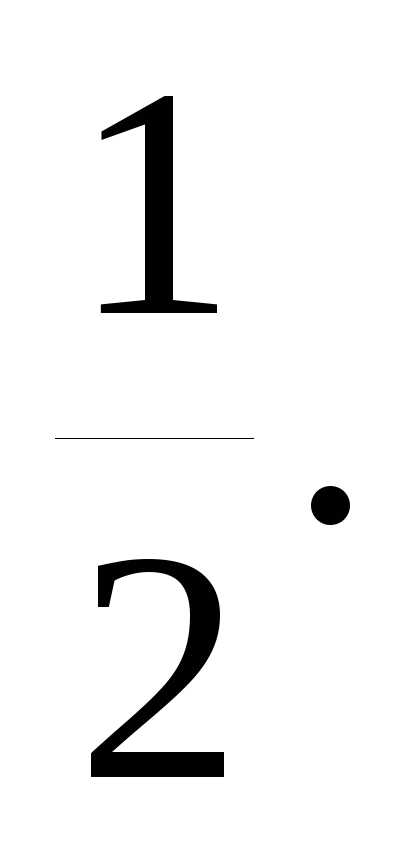
2. 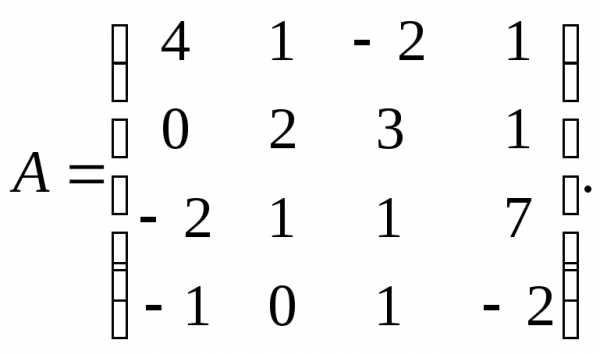 3.
3. 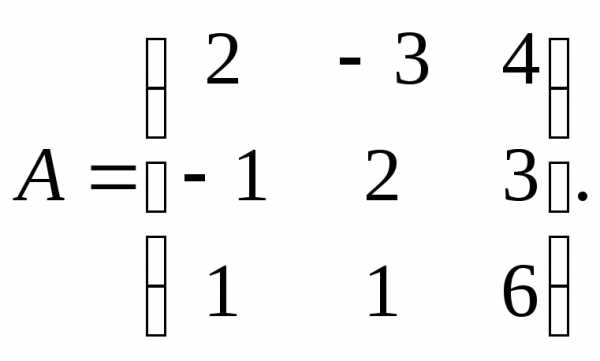
4.
5.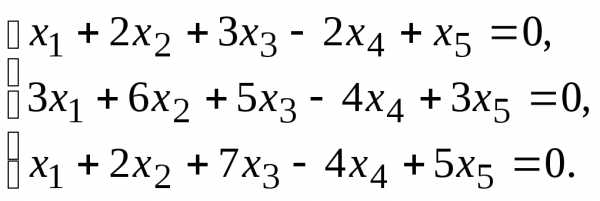
6. 
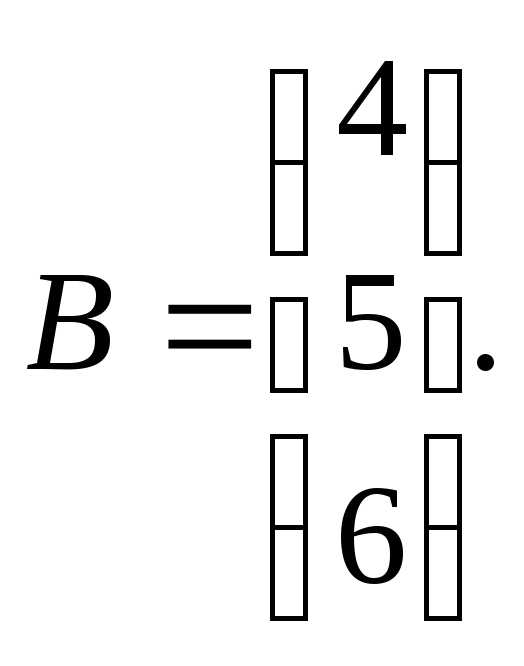 7.
7.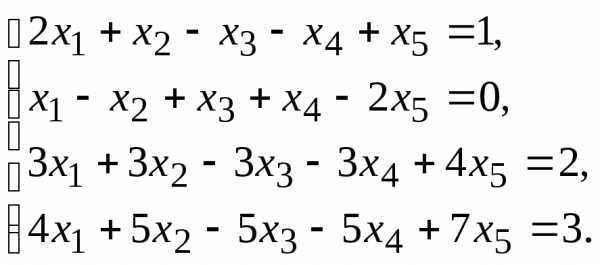
8.  9.
9.
10. 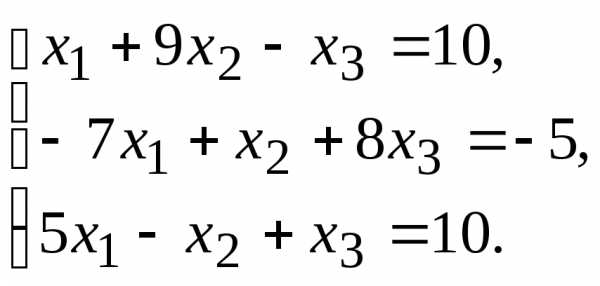 11.
11.
12. 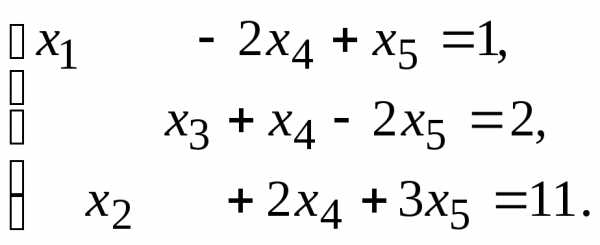 13.
13.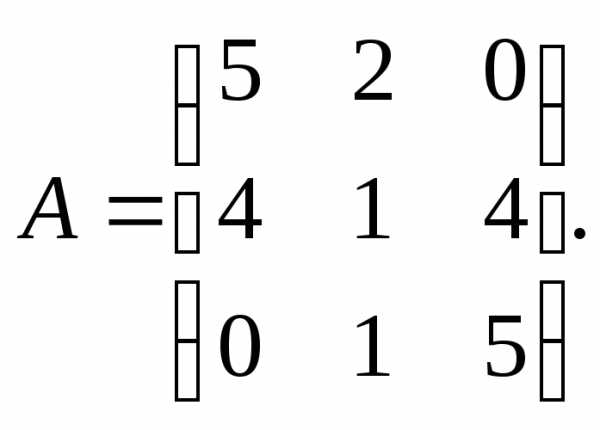
14. 15.
Вариант 5
1. 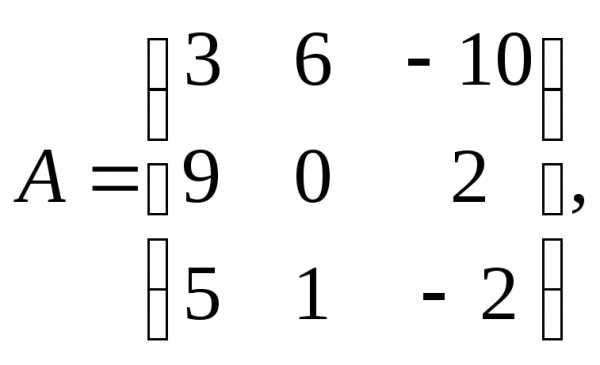
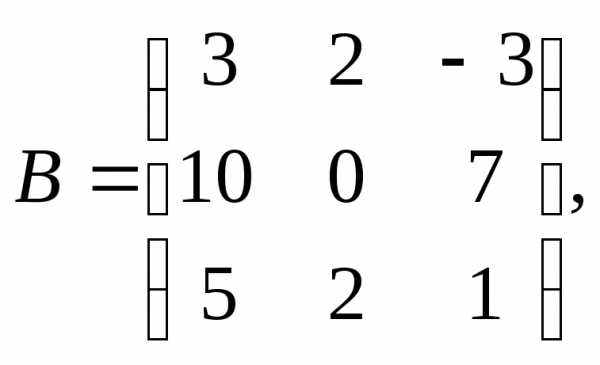 α = 3, β = 5.
α = 3, β = 5.
2. 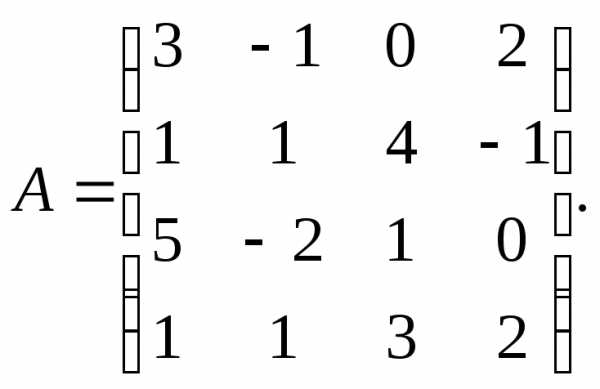 3.
3.
4. 5.
6.
7.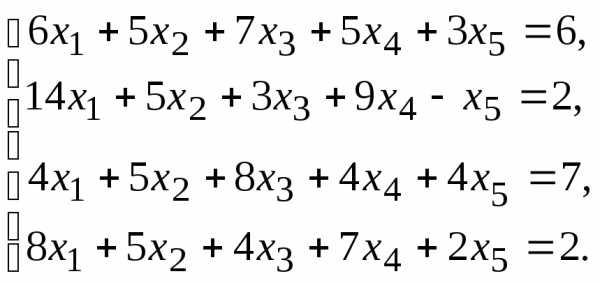
8. 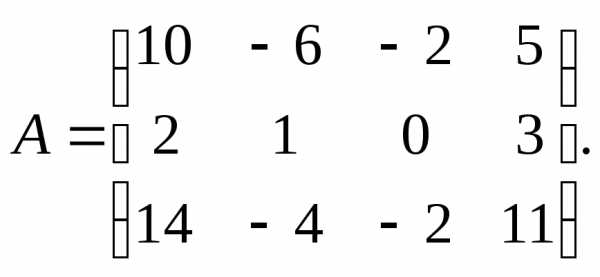 9.
9.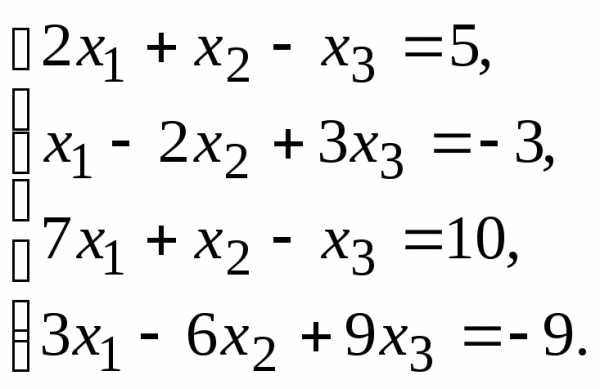
10. 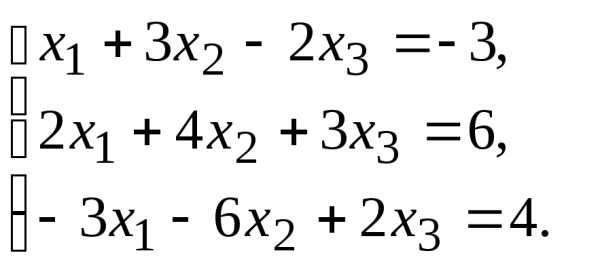 11.
11.
12. 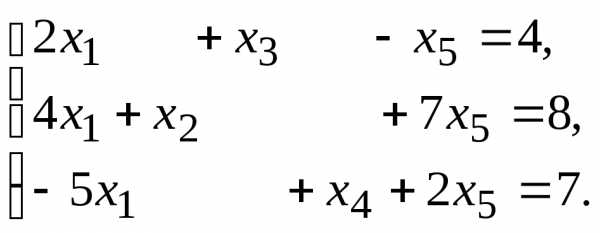 13.
13.
14. 15.
Вариант 6
1. 
 α = – 2, β =
3.
α = – 2, β =
3.
2.
3.
4. 5.
6. 
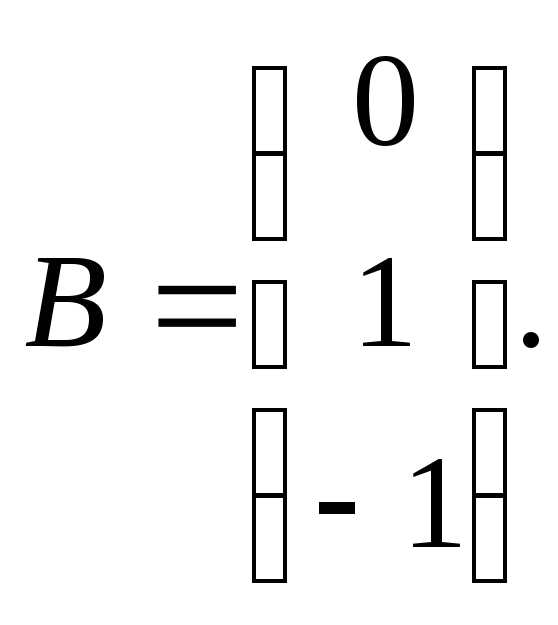 7.
7.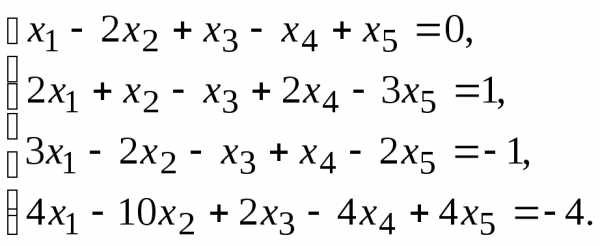
8.  9.
9.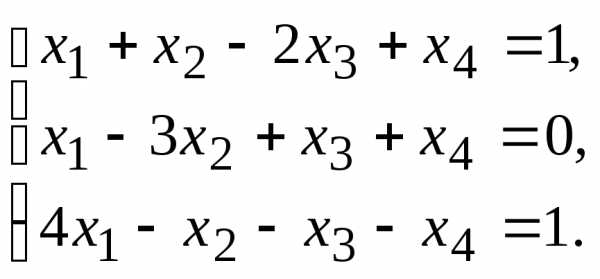
10. 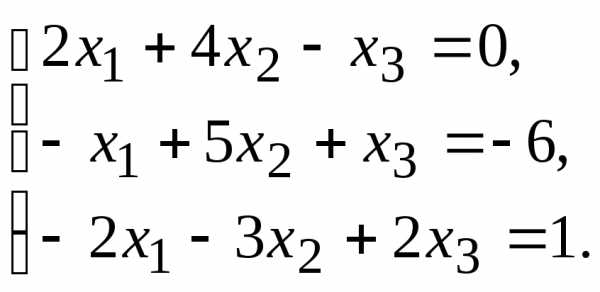 11.
11.
12. 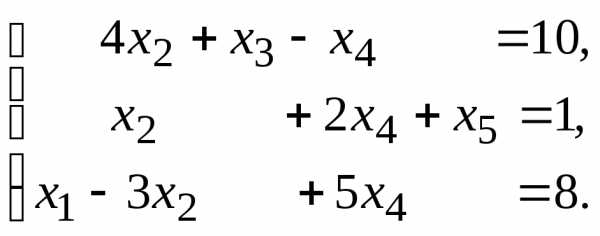 13.
13.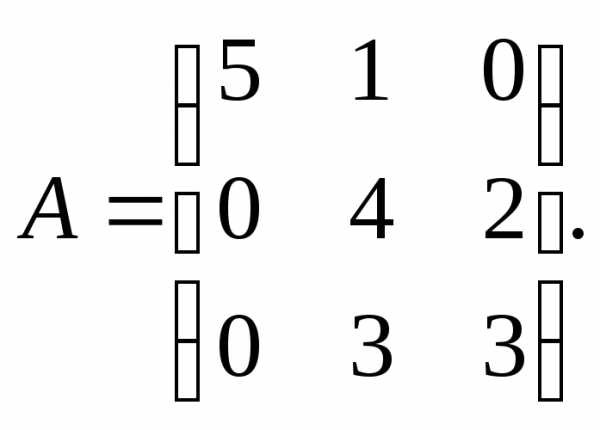
14. 15.
Вариант 7
1. 
 α= –
5,β = 3.
α= –
5,β = 3.
2.  3.
3.
4. 5.
6. 
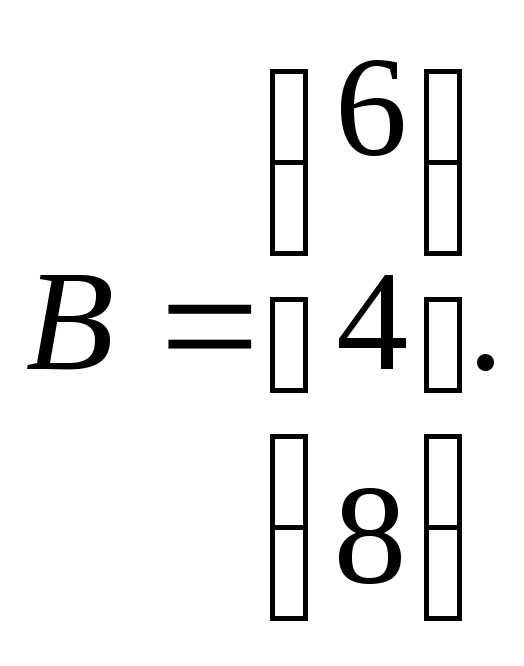 7.
7.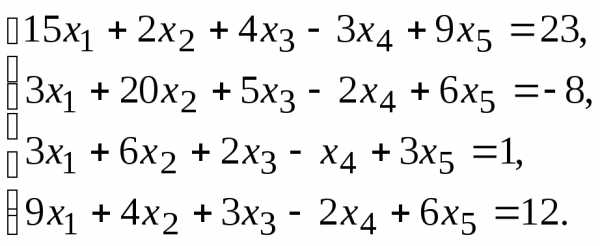
8.  9.
9.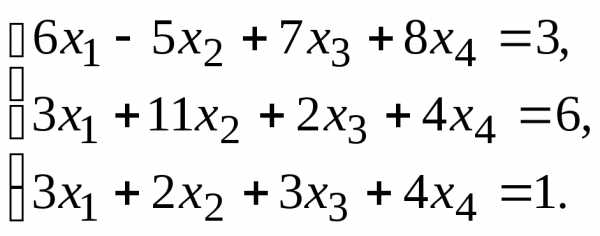
10. 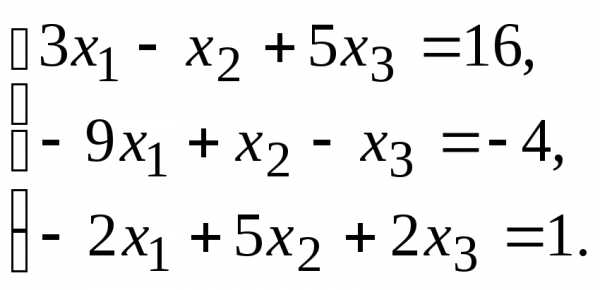 11.
11.
12. 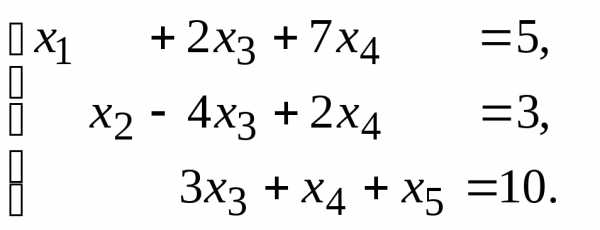 13.
13.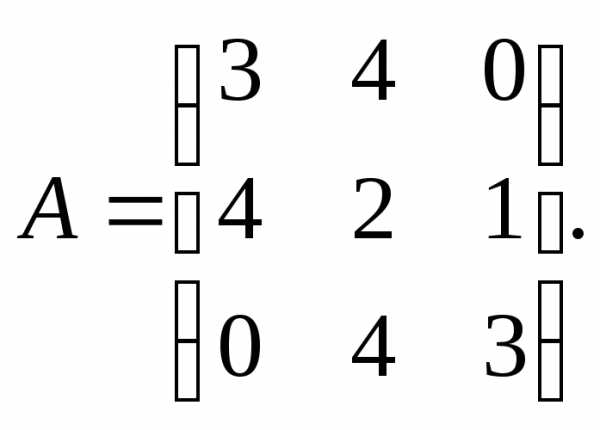
14. 15.
Вариант 8
1. 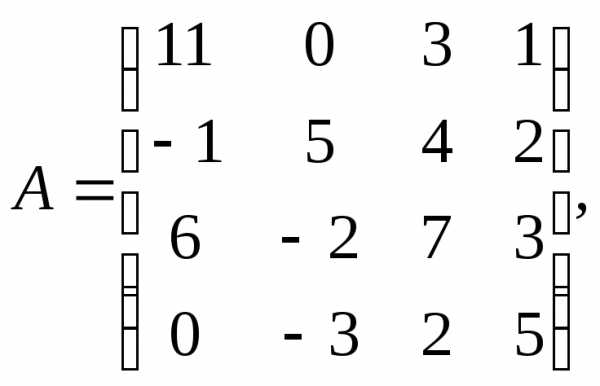
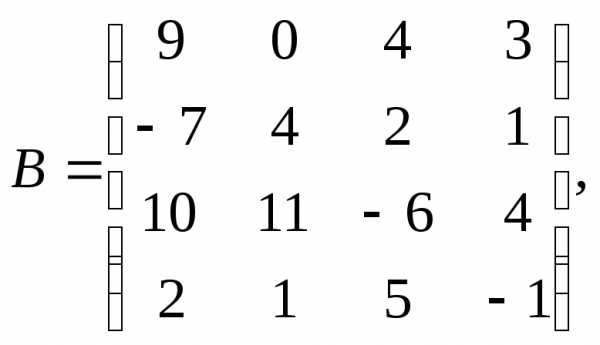 α= 10,β
= – 3.
α= 10,β
= – 3.
2.  3.
3.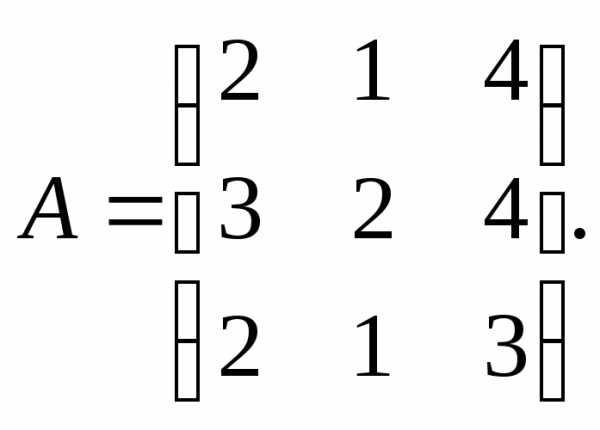
4.
5.
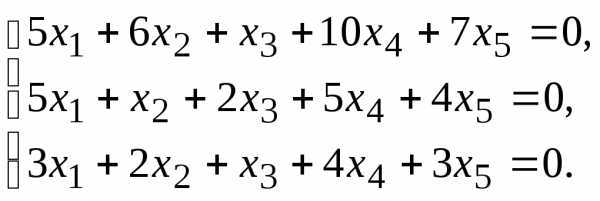
6. 
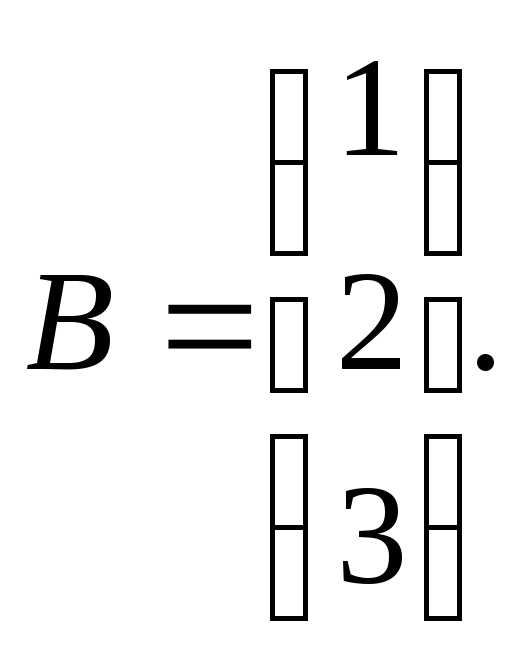 7.
7.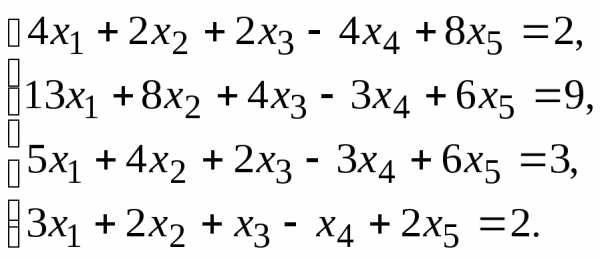
8.  9.
9.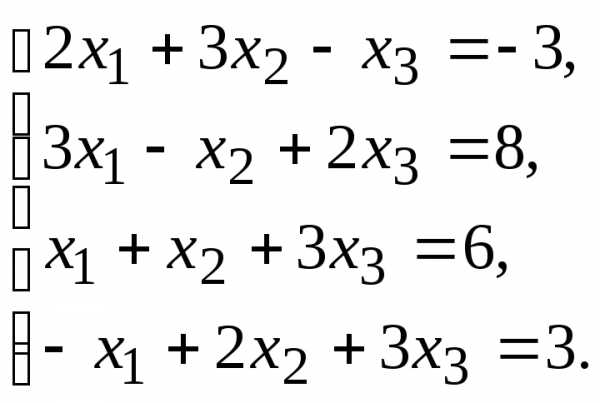
10. 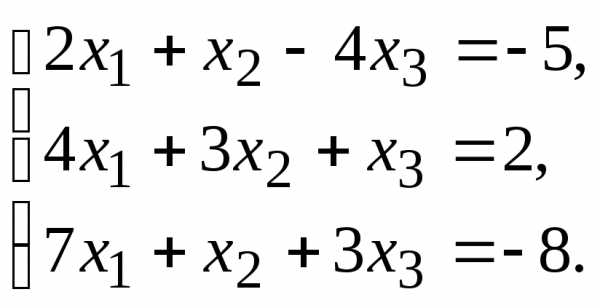 11.
11.
12. 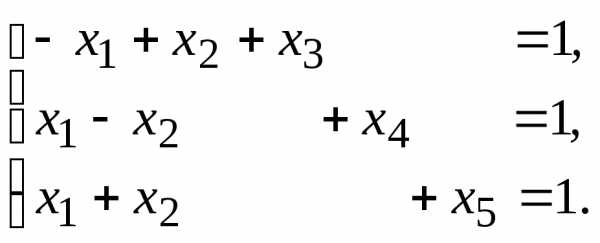 13.
13.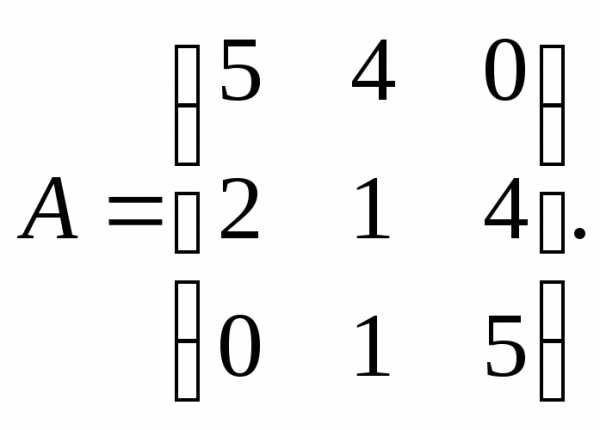
14. 15.
Вариант 9
1. 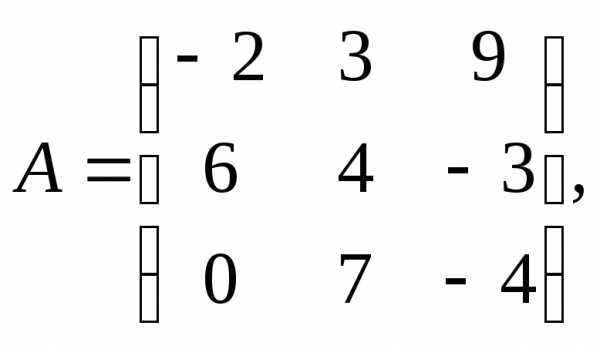
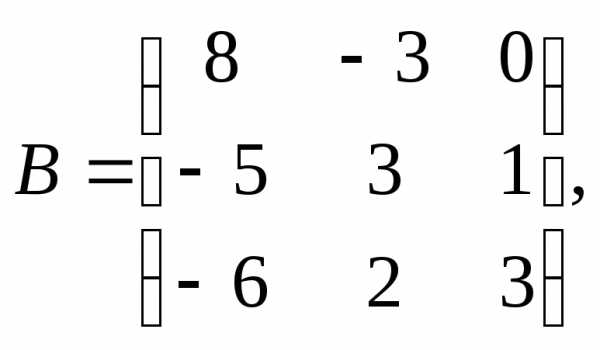 α= – 3,β = 10.
α= – 3,β = 10.
2.  3.
3. 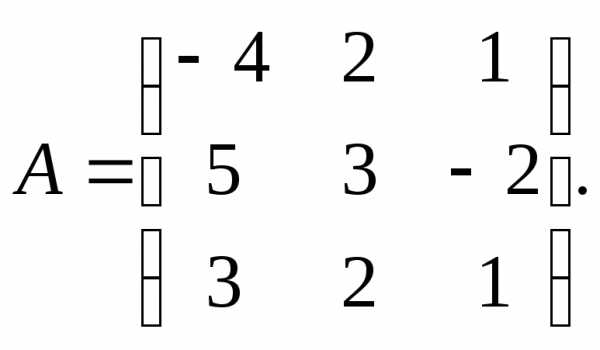
4. 5.
6. 
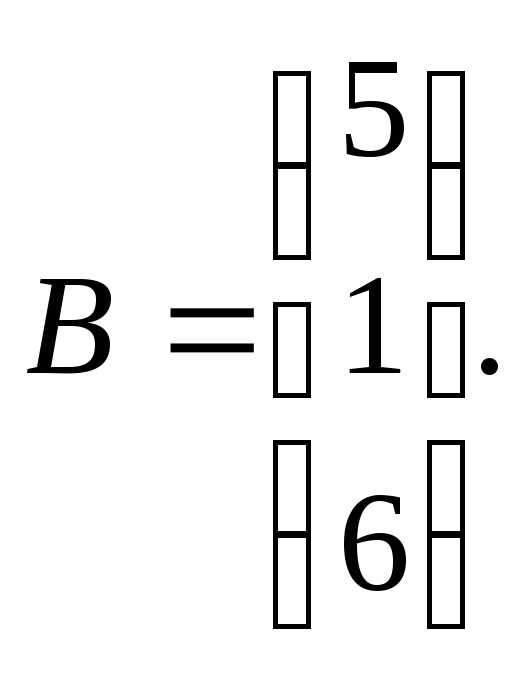 7.
7.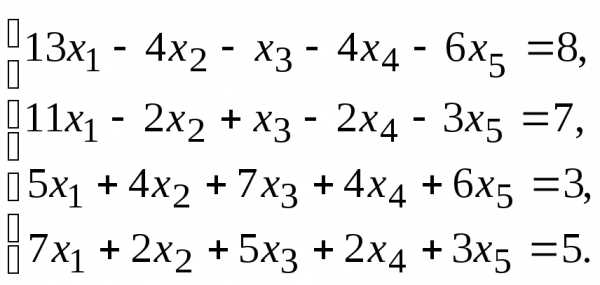
8. 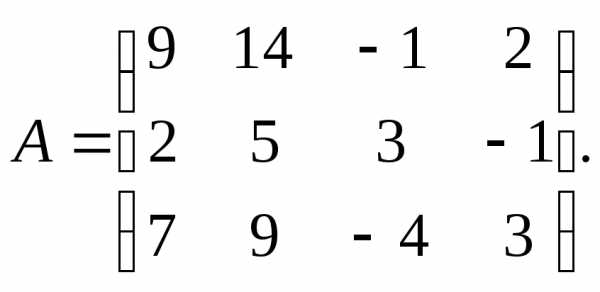 9.
9.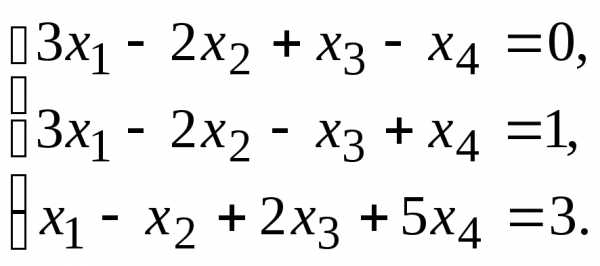
10. 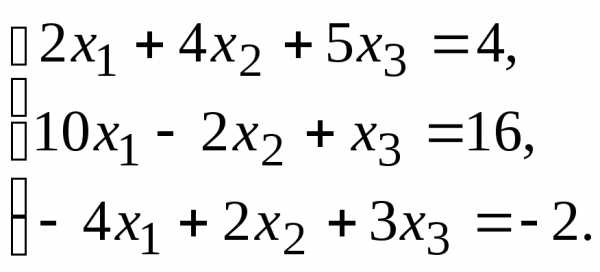 11.
11.
12. 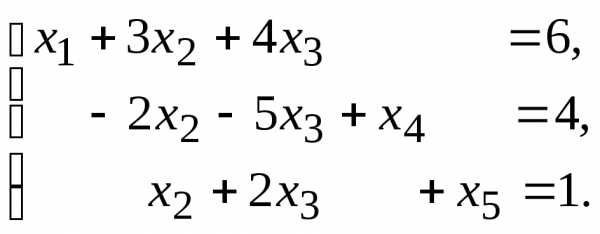 13.
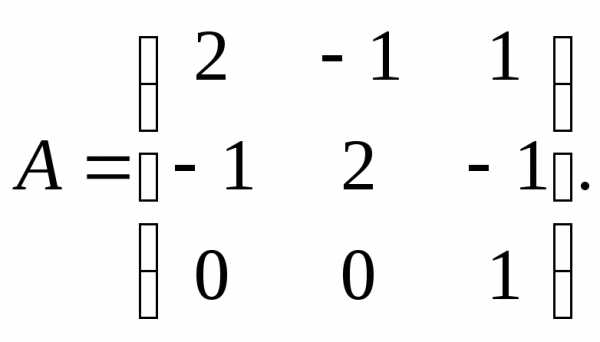
13.
14. 15.
Вариант 10
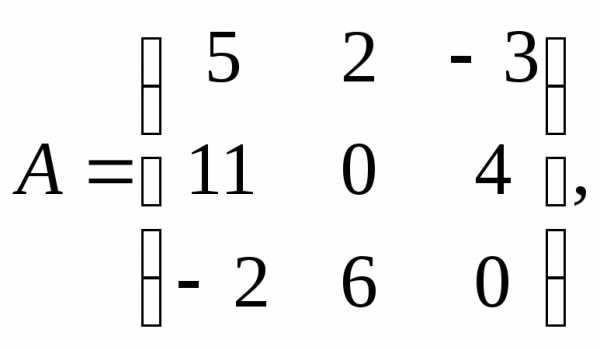
1. 
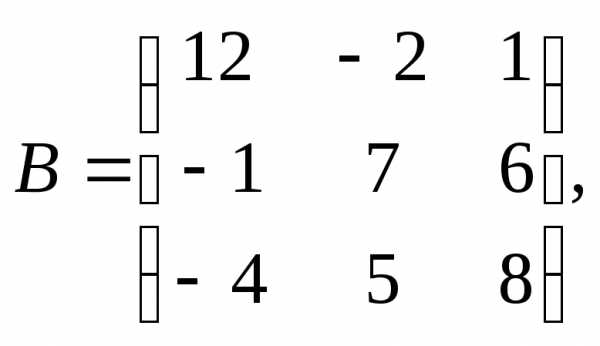 α= –
6,β = 4.
α= –
6,β = 4.
2. 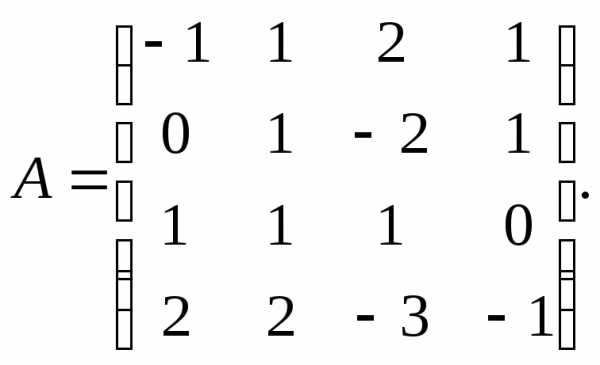 3.
3.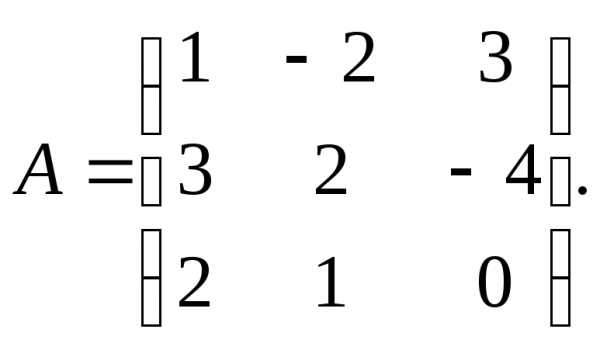
4. 5.
6. 
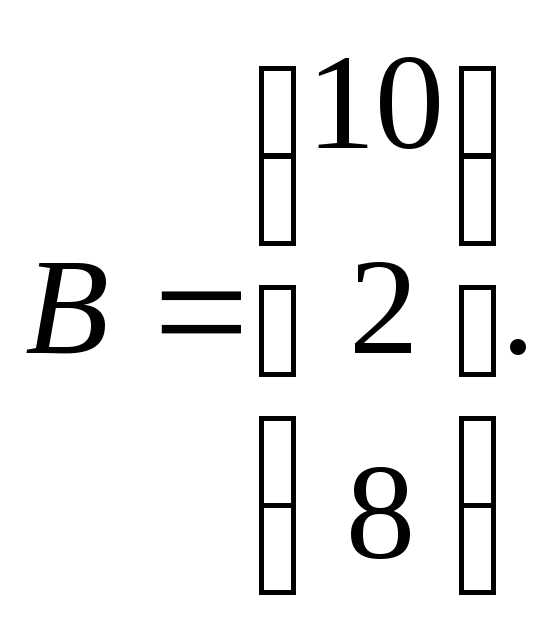 7.
7.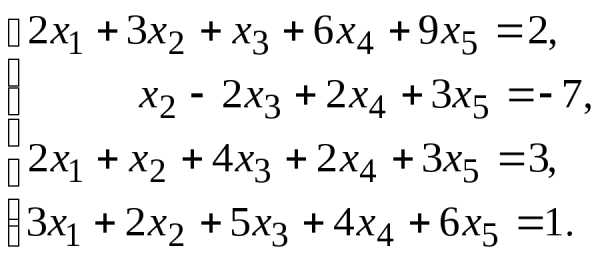
8.  9.
9.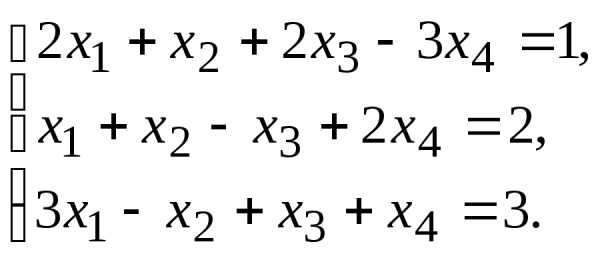
10. 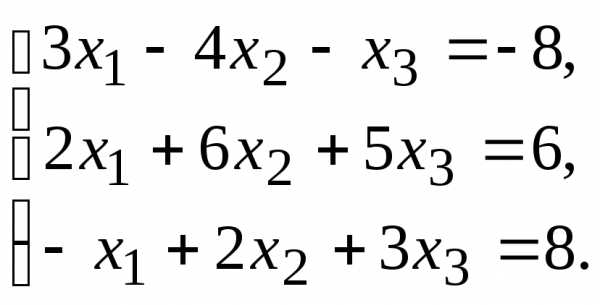 11.
11.
12. 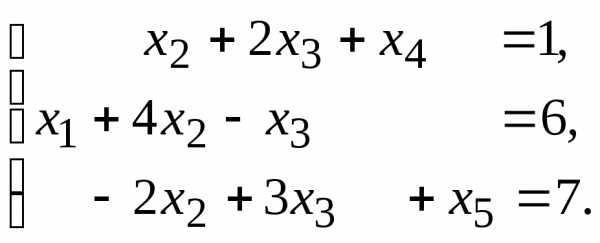 13.
13.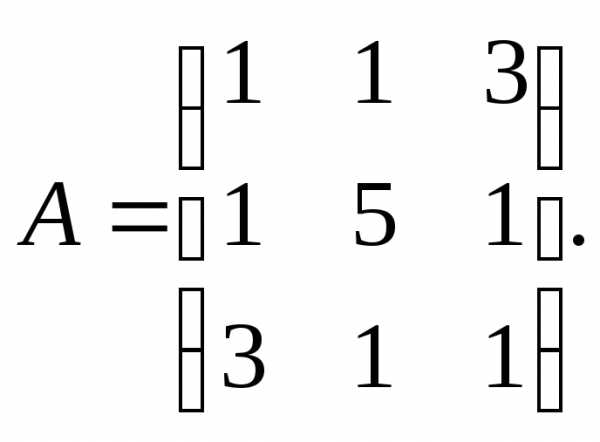
14. 15.
Вариант 11
1. 
 α= –
2,β = 3.
α= –
2,β = 3.
2.
3.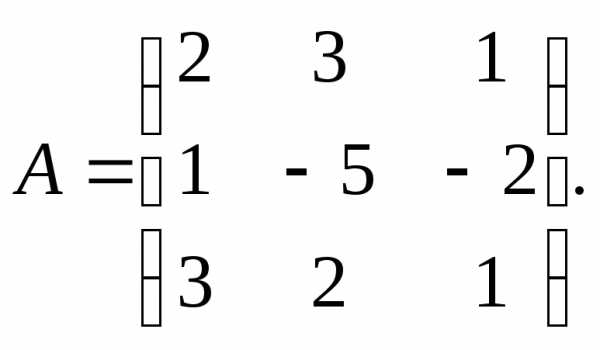
4.
5.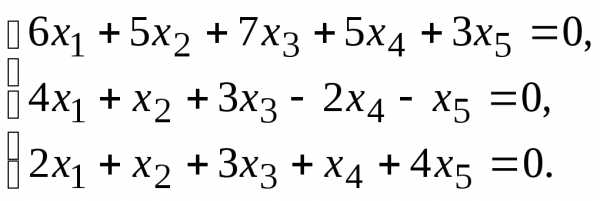
6. 
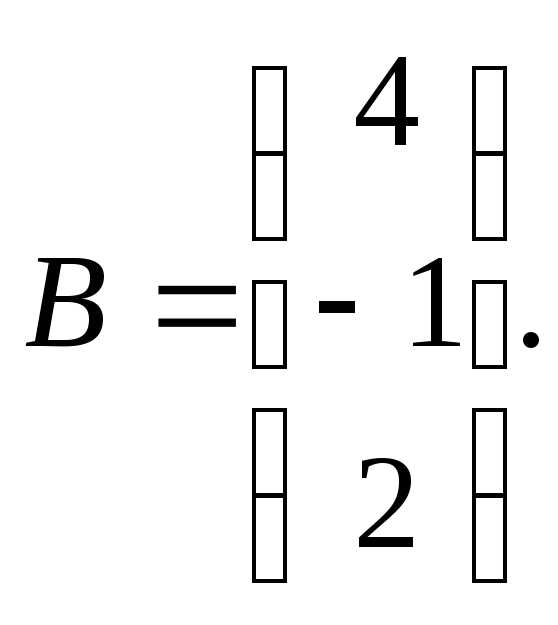 7.
7.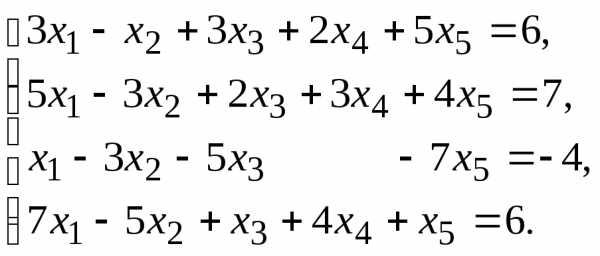
8.  9.
9.
10. 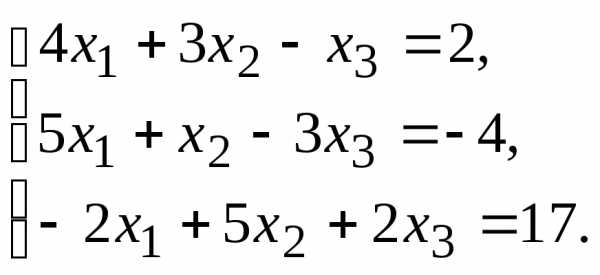 11.
11.
12.  13.
13.
14. 15.
Вариант 12
1. 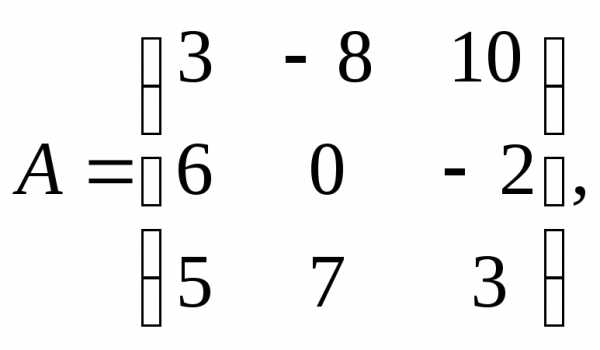
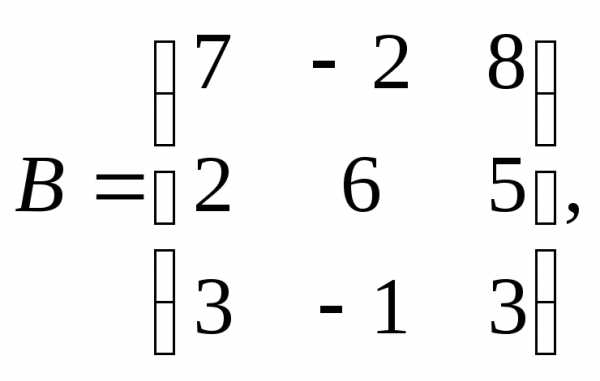 α= 9,β
= – 3.
α= 9,β
= – 3.
2. 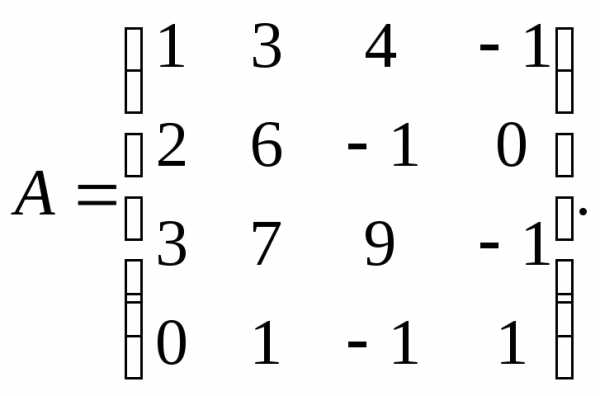 3.
3.
4. 5.
6. 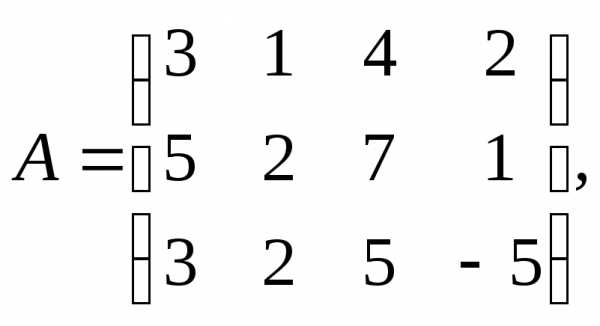
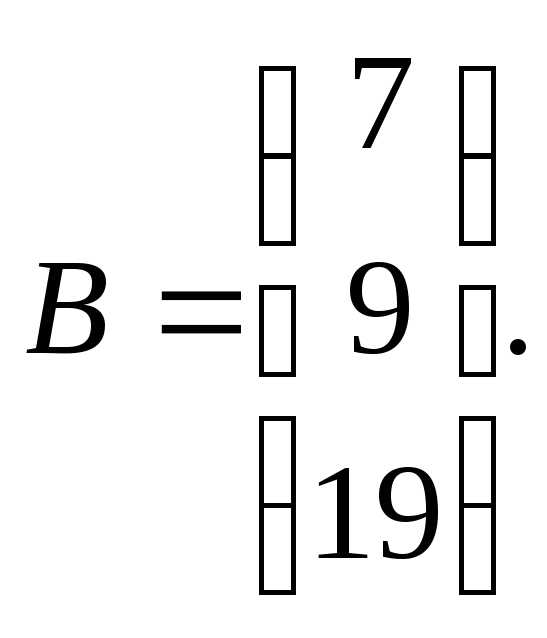 7.
7. 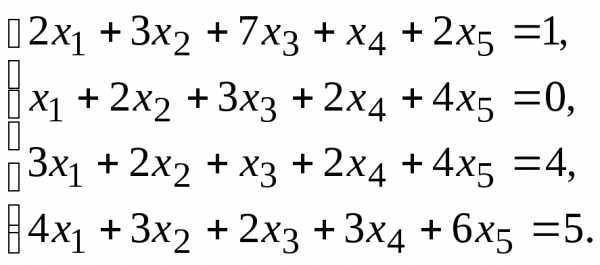
8. 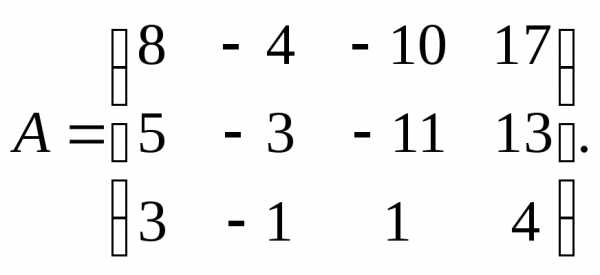 9.
9.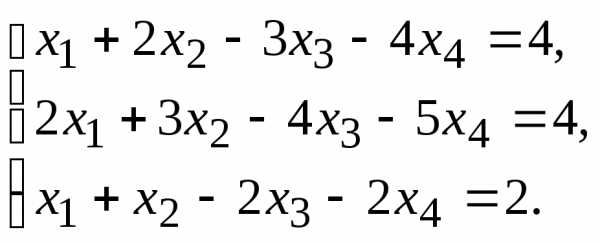
10. 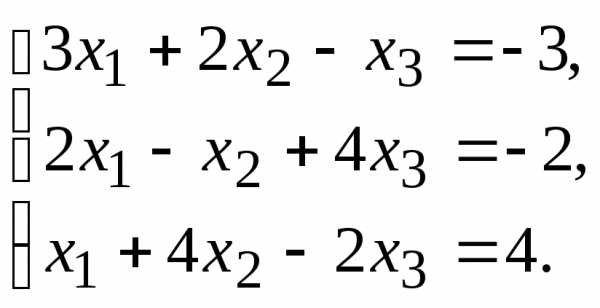 11.
11.
12. 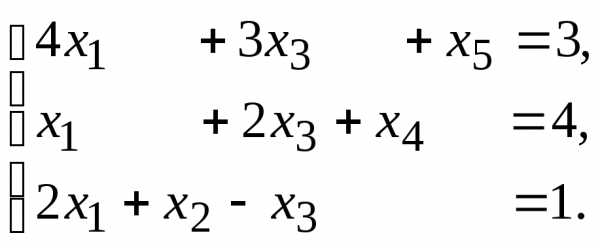 13.
13.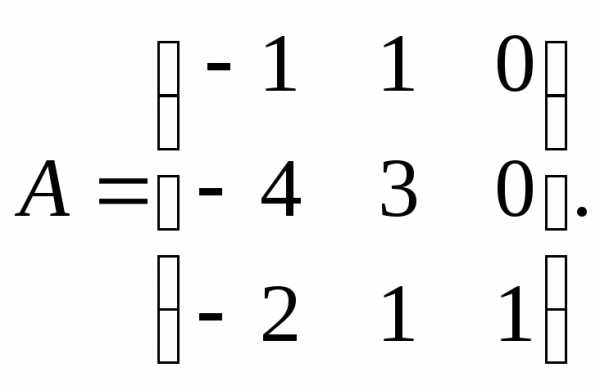
14. 15.
Вариант 13
1. 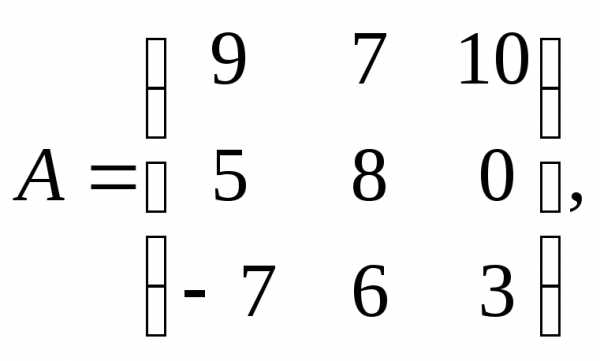
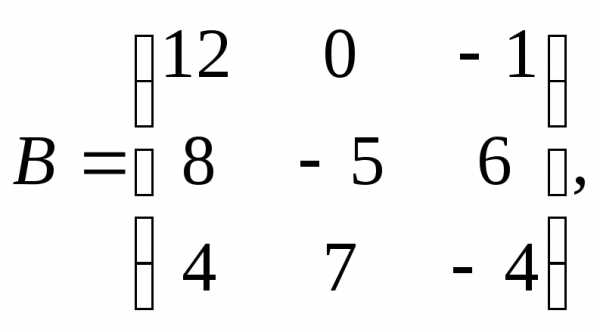 α = – 10, β = –
2.
α = – 10, β = –
2.
2. 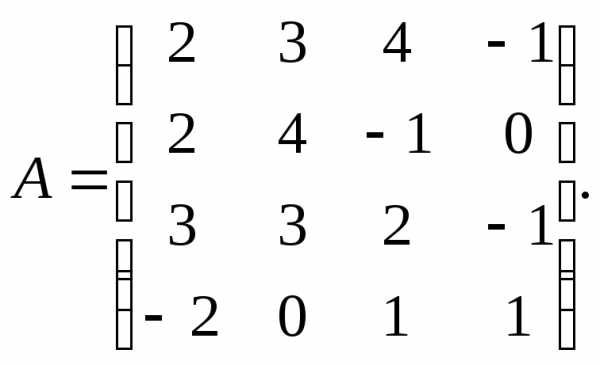 3.
3.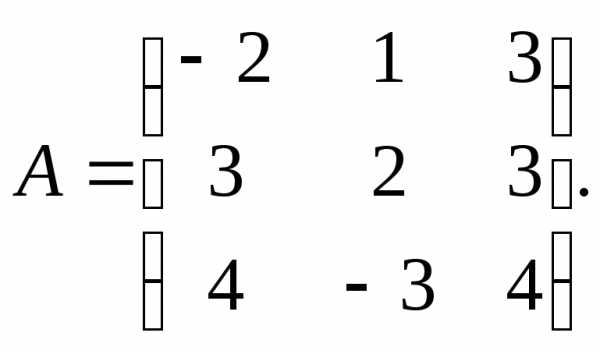
4.
5.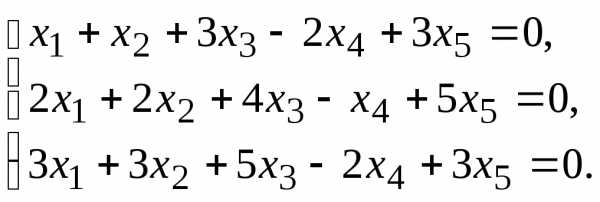
6. 
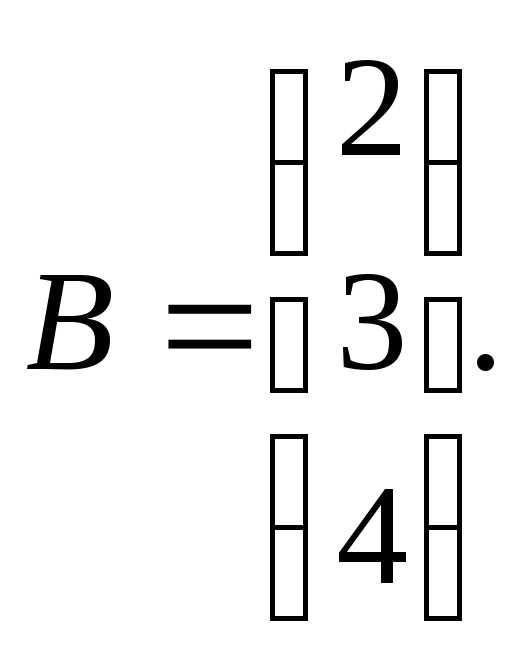 7.
7.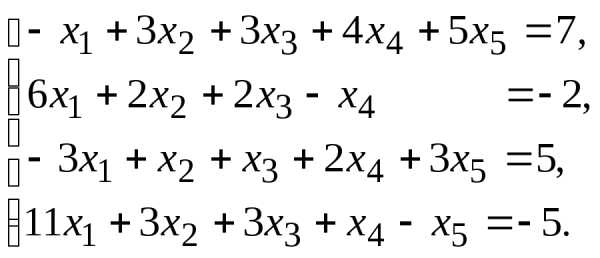
8.  9.
9.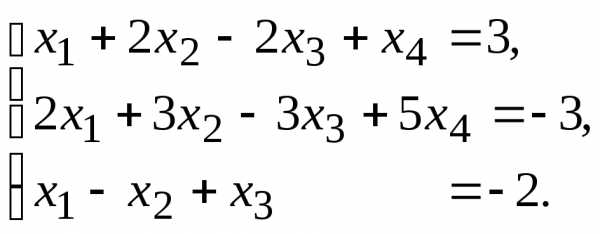
10.  11.
11.
12.  13.
13.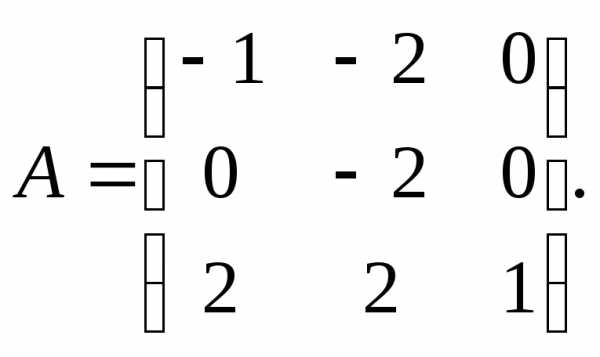
14. 15.
Вариант 14
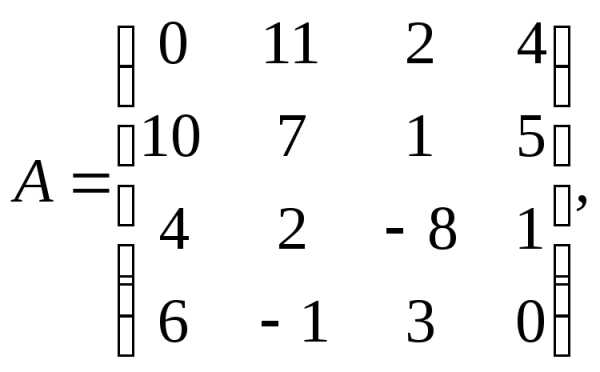
1. 
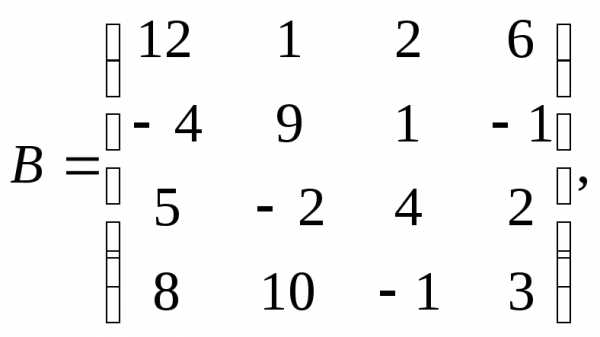 α = – 2, β =
4.
α = – 2, β =
4.
2. 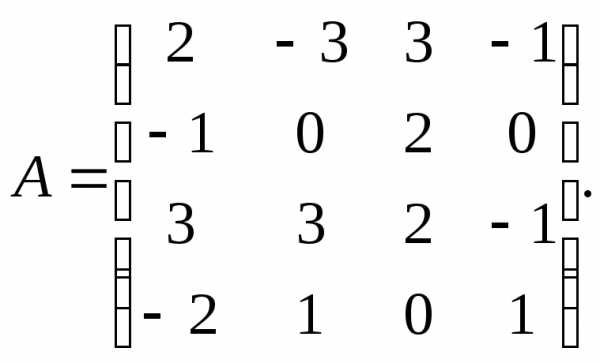 3.
3.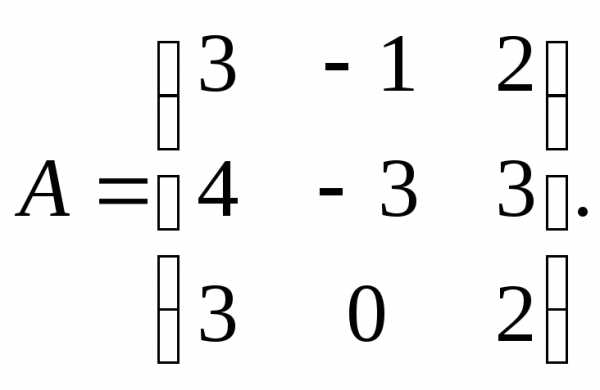
4. 5.
6. 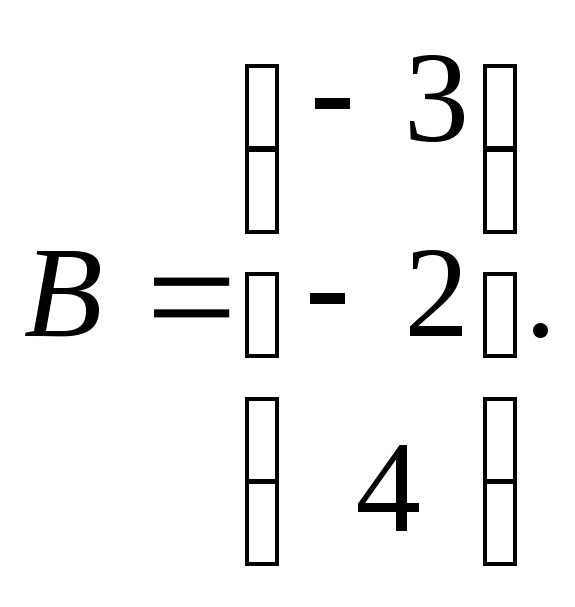 7.
7.
8.  9.
9.
10. 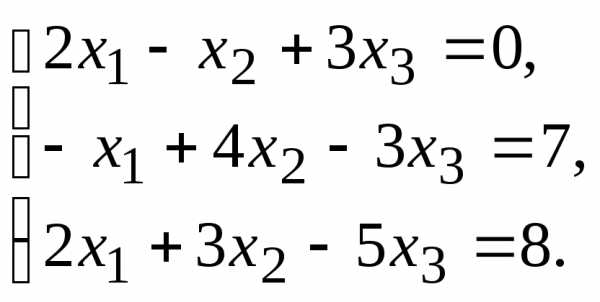 11.
11.
12.  13.
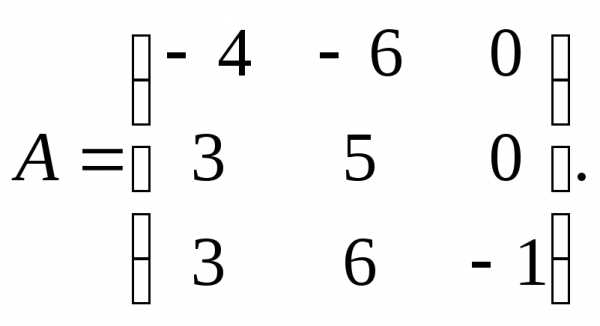
13.
14. 15.
Вариант 15
1. 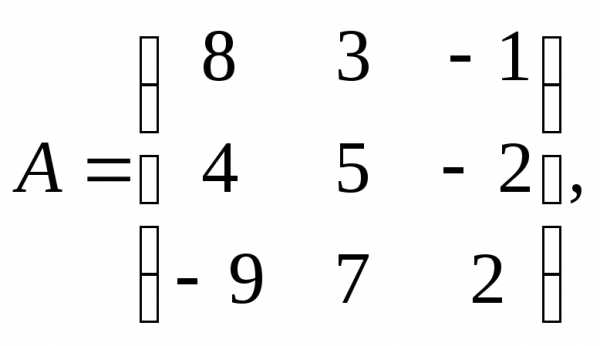
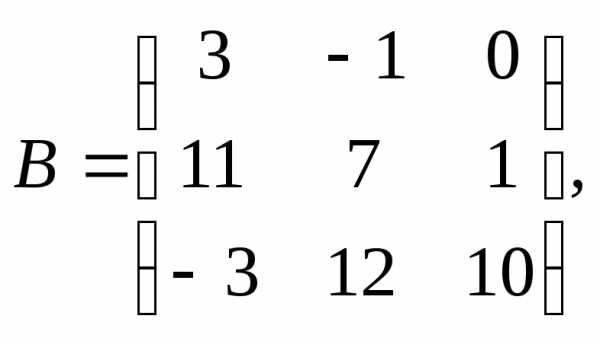 α = – 9, β =
5.
α = – 9, β =
5.
2. 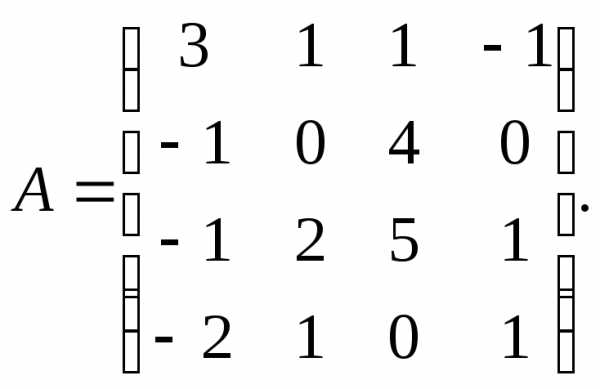 3.
3.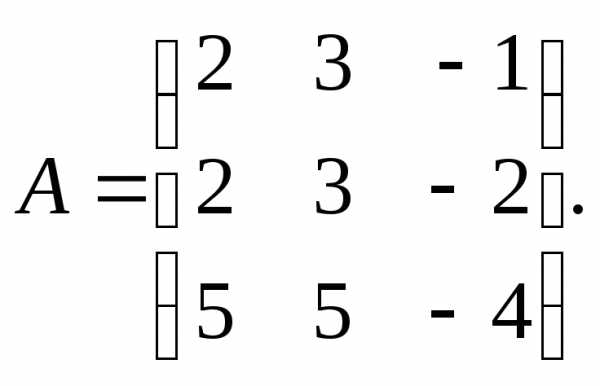
studfiles.net
