Вычисление двойных интегралов: теория и примеры
Записывается двойной интеграл так:
.
Здесь D – плоская фигура, ограниченная линиями, выражения которых (равенства) даны в задании вычисления двойного интеграла. Слева и справа – равенствами, в которых слева переменная x, а сверху и снизу – равенствами, в которых слева переменная y. Это место и далее – одно из важнейших для понимания техники вычисления двойного интеграла.
Вычислить двойной интеграл — значит найти число, равное площади упомянутой фигуры D.
Пока мы не касаемся определения двойного интеграла, а будем учиться его вычислять.
Понять, что такое двойной интеграл, проще, когда решены несколько задач на его вычисление, поэтому
определение двойного интеграла вы найдёте в конце этого урока. Чуть забегая вперёд, можно лишь
отметить, что определение двойного интеграла также связано с упоминавшейся фигурой
В случае если фигура D представляет собой прямоугольник, все линии, ограничивающие её – это прямые линии. Если фигура D — криволинейна, то слева и справа она ограничена прямыми, а сверху и снизу – кривыми линиями, заданными равенствами, которые даны в задании. Бывают и случаи, когда фигура D – треугольник, но о таких случаях чуть дальше.
Для вычисления двойного интеграла нужно, таким образом, рассортировать линии, огранивающие фигуру D, которая имеет строгое название – область интегрирования. Рассортировать на левые и правые и на верхние и нижние. Это потребуется при сведении двойного интеграла к повторному интегралу – методе вычисления двойного интеграла.
Случай прямоугольной области:
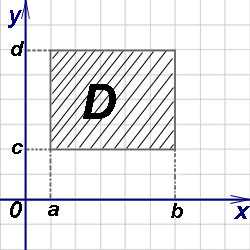
Случай криволинейной области:
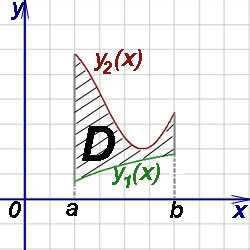
А это уже решение знакомых нам определённых интегралов, в которых заданы верхний и нижний пределы интегрирования. Выражения, задающие линии, которые ограничивают фигуру D, будут пределами интегрирования для обычных определённых интегралов, к которым мы уже подходим.
Случай прямоугольной области
Пусть дана функция двух переменных f(x, y)
и ограничения для D: D = {(x; y) | a ≤ x ≤ b; c ≤ y ≤ d},
означающие, что фигуру D слева и справа ограничивают
прямые x = a и x = b,
а снизу и сверху — прямые y = c и y = d.
Здесь
Пусть для такой функции существует двойной интеграл
.
Чтобы вычислить этот двойной интеграл, нужно свести его к повторному интегралу, который имеет вид
.
Здесь пределы интегрирования a, b, c, d — числа, о которых только что упоминалось.
Сначала нужно вычислять внутренний (правый) определённый интеграл, затем — внешний (левый) определённый интеграл.
Можно и поменять ролями x и y. Тогда повторный интеграл будет иметь вид
.
Такой повторный интеграл нужно решать точно так же: сначала — внутренний (правый) интеграл, затем — внешний (левый).
Пример 1. Вычислить двойной интеграл
,
где
.
Решение. Сводим данный двойной интеграл к повторному интегралу
.
На чертеже строим область интегрирования:
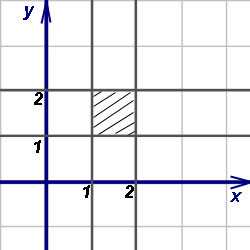
Вычисляем внутренний (правый) интеграл, считая игрек константой. Получаем.
.
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Результат и будет решением данного двойного интеграла.
Пример 2. Вычислить двойной интеграл
,
где
.
Решение. Сводим данный двойной интеграл к повторному интегралу
.
На чертеже строим область интегрирования:

Вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
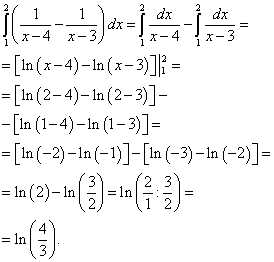
Результат и будет решением данного двойного интеграла.
Вычислить двойной интеграл самостоятельно, а затем посмотреть решение
Случай криволинейной или треугольной области
Пусть снова дана функция двух переменных f(x, y), а ограничения для D: уже несколько другого вида:
.
Эта запись означает, что фигуру D слева и справа ограничивают, как и в случае прямолинейной области — прямые x = a и x = b, но снизу и сверху — кривые, которые заданы уравнениями и . Иными словами, и — функции.
Пусть для такой функции также существует двойной интеграл
.
Чтобы вычислить этот двойной интеграл, нужно свести его к повторному интегралу, который имеет вид
.
Здесь пределы интегрирования a и b — числа, а и — функции. В случае треугольной области одна из функций или — это уравнение прямой линии. Такой случай будет разобран в примере 3.
Как и в случае прямолинейной области, сначала нужно вычислять правый определённый интеграл, затем — левый определённый интеграл.
Точно так же можно поменять ролями x и y. Тогда повторный интеграл будет иметь вид
.
Такой повторный интеграл нужно решать точно так же: сначала — внутренний (правый) интеграл, затем — внешний (левый).
Пример 5. Вычислить двойной интеграл
,
где
.
Решение. Сводим данный двойной интеграл к повторному интегралу
.
На чертеже строим область интегрирования и видим, что она треугольная:
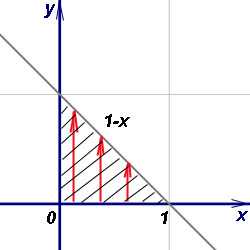
Вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого). Сначала представляем этот интеграл в виде суммы интегралов:
.
Вычисляем первое слагаемое:
Вычисляем второе слагаемое:
Вычисляем третье слагаемое:
Получаем сумму, которая и будет решением данного двойного интеграла:
.
Пример 6. Вычислить двойной интеграл
,
где
.
Решение. Сводим данный двойной интеграл к повторному интегралу
.
На чертеже строим область интегрирования:
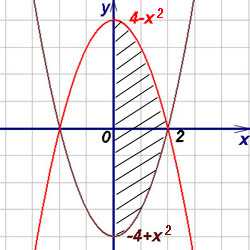
Вычисляем внутренний (правый) интеграл, считая икс константой. Получаем.
.
Теперь вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Результат и будет решением данного двойного интеграла.
Случается, область интегрирования двойного интеграла ограничена такими линиями, что возникает необходимость разбить область интегрирования на части и решать каждый соответствующий повторный интеграл отдельно. Это случаи, когда:
1) область интегрирования представляет собой фигуру, имеющую в виде нижней или верхней (левой или правой) границы две или более двух прямых или кривых линий;
2) область интегрирования представляет собой фигуру, границу которой прямые пересекают более чем в двух точках.
Если вышесказанное относится к левой или правой границе области интегрирования, то есть ограничениях, заданных линиями, выраженными через x, то область интегрирования называется x-неправильной. Если же прямая y = y0 пересекает соответствующую границу лишь в одной точке и если границей служит лишь одна прямая или кривая, то область интегрирования называется x-правильной
Аналогично, если границу, заданную линиями, выраженными через y, прямая x = x0 пересекает более чем в одной точке или если границей служат более одной прямой или кривой, то область интегрирования называется y-неправильной. Вывести теперь признаки y-правильной области, надо полагать, совсем просто.
До сих пор мы рассматривали примеры с x-неправильными и y-правильными областями интегрирования. Теперь рассмотрим случаи, когда условие правильности нарушается.
Как уже отмечалось выше, после приведения двойного интеграла к повторному интегралу, можно поменять переменные x и y ролями, или, говоря иначе, поменять порядок интегрирования.
Смена порядка интегрирования образно может быть описана следующими словами О’Генри:
«Так ведёт себя обитатель джунглей — зверь, попав в клетку, и так ведёт себя обитатель клетки —
человек, заблудившись в джунглях сомнений». Результат, так же по О’Генри один и тот же:
«Чалмерс разорвал письмо на тысячу мельчайших клочков и принялся терзать свой дорогой ковёр, расхаживая
по нему взад и вперёд». (
Тогда, если левый интеграл у нас по переменной x, а правый — по y, то после смены порядка интегрирования всё будет наоборот. Тогда пределы интегрирования для «нового» игрека нужно «позаимствовать» у «старого» икса, а пределы интегрирования для «нового» икса получить в виде обратной функции, разрешив относительно икса уравнение, задававшее предел для игрека.
Пример 8. Сменить порядок интегрирования для повторного интеграла
.
Решение. После смены порядка интегрирования интеграл по игреку станет левым, а интеграл по иксу — правым. Пределы интегрирования для «нового» игрека позаимствуем у «старого» икса, то есть нижний предел равен нулю, а верхний — единице. Пределы интегрирования для «старого» игрека заданы уравнениями и . Разрешив эти уравнения относительно икса, получим новые пределы интегрирования для икса:
(нижний) и (верхний).
Таким образом, после смены порядка интегрирования повторный интеграл запишется так:
.
После смены порядка интегрирования в двойном интеграле нередко область интегрирования превращается в y-неправильную или x-неправильную (см. предыдущий параграф). Тогда требуется разбить область интегрирования на части и решать каждый соответствующий повторный интеграл отдельно.
Поскольку разбиение области интегрирования на части представляет определённые трудности для многих студентов, то не ограничимся примером, приведённым в предыдущем параграфе, а разберём ещё пару примеров.
Пример 9. Сменить порядок интегрирования для повторного интеграла
.
Решение. Итак, область интегрирования данного повторного интеграла ограничена прямыми y = 1, y = 3, x = 0, x = 2y.
При интегрировании в другом порядке нижняя граница области состоит из двух прямых: AB и BC, которые заданы уравнениями y = 1 и y = x/2, что видно на рисунке ниже.
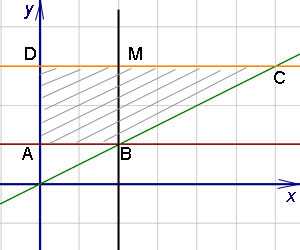
Выход из такой неопределённости состоит в разбиении области интегрирования на две части. Делить область интегрирования будет прямая BМ. Новые пределы интегрирования вычисляем, находя обратную функцию. Соответственно этому решению повторный интеграл после смены порядка интегрирования будет равным сумме двух интегралов:
Естественно, таким же будет решение двойного интеграла, который сводится к повторному интегралу, данному в условии этого примера.
Пример 10. Сменить порядок интегрирования для повторного интеграла
.
Решение. Итак, область интегрирования повторного интеграла ограничена прямыми x = 0, x = 2 и кривыми и .
Как видно на рисунке ниже, прямая, параллельная оси 0x, будет пересекать нижнюю границу области интегрирования более чем в двух точках.
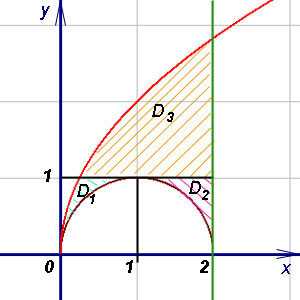
Поэтому разобьём область интегрирования на три части прямыми, которые на рисунке начерчены чёрным. Новые пределы интегрирования вычисляем, находя обратную функцию. Пределы для трёх новых областей интегрирования будут следующими.
Для :
Для :
Для :
Соответственно этому решению повторный интеграл после смены порядка интегрирования будет равным сумме трёх интегралов:
Той же сумме трёх интегралов будет равен и двойной интеграл, который сводится к повторному интегралу, данному в условии этого примера.
И всё же обстоятельства непреодолимой силы нередко мешают студентам уже на предыдущем шаге — расстановке пределов интегрирования. Тревога и смятение не лишены некоторого основания: если для разбиения области интегрирования на части обычно достаточно приглядеться к чертежу, а для решения повторного интеграла — таблицы интегралов, то в расстановке пределов интегрирования нужен некоторый опыт тренировок. Пробежим пример, в котором остановимся только на расстановке пределов интегрирования и — почти на автомате — на разбиении области и опустим само решение.
Пример 11. Найти пределы интегрирования двойного интеграла, если область интегрирования D задана следующим образом:
y — 2x ≤ 0;
2y — x ≥ 0;
xy ≤ 2.
Решение. В явном виде (через x и y «без примесей») линии, ограничивающие область интегрирования, не заданы. Так как для икса ими чаще всего оказываются прямые, касающиеся в одной точке верхней и нижней границ, выраженных через игрек, то пойдём именно по этому пути. Тем более, что при смене порядка интегирования мы получим область интегрирования с такой же площадью. Разрешим неравенства относительно игрека и получим:
y ≤ 2x;
y ≥ x/2;
y ≤ 2/x.
Строим полученные линии на чертёже. Пределами интегрирования по иксу действительно служат линии x = 0 и x = 2. Но область интегрирования оказалась y-неправильной, так как её верхнюю границу нельзя задать одной линией y = y(x).
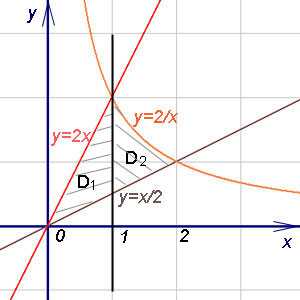
Поэтому разобьём область интегрирования на две части при помощи прямой x = 1 (на чертеже — чёрного цвета).
Теперь данный двойной интеграл можем записать как сумму двух повторных интегралов с правильно расставленными пределами интегрирования:
.
В этом параграфе даны примеры, в которых двойной интеграл равен отрицательному числу. Но, как отмечалось в теоретической справке в начале урока, площадь области интегрирования равна самому двойному интегралу. А если двойной интеграл — отрицательное число, то площадь равна его модулю.
Вычисление площади плоской фигуры с помощью двойного интеграла имеет более универсальный характер, чем вычисление площади криволинейной трапеции с помощью определённого интеграла. С помощью двойного интеграла можно вычислять площади не только криволинейной трапеции, но и фигур, расположенных произвольно по отношению к к координатным осям.
Пример 12. Вычислить площадь области, ограниченной линиями y² = x + 1 и x + y = 1.
Решение. Область интегрирования представляет собой фигуру, ограниченную слева параболой y² = x + 1, а справа прямой y = 1 — x. (рисунок ниже).
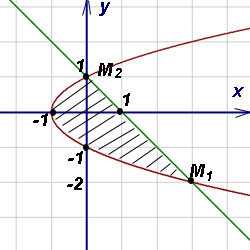
Решая как систему уравнения этих линий, получаем точки их пересечения: . Ординаты этих точек — — 2 и 1 будут соответственно нижним и верхним пределами интегрирования по игреку. Итак, площадь фигуры найдём как двойной интеграл, сведённый к повторному:
.
Вычисляем внутренний (правый) интеграл:
.
Вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Как видим, решение двойного интеграла — отрицательное число. За площадь данной плоской фигуры принимается модуль этого числа, то есть 4/9.
Объём криволинейного цилиндра, ограниченного сверху поверхностью , снизу плоскостью z = 0 и с боковых сторон цилиндрической поверхностью, у которой образующие параллельны оси 0z, а направляющей служит контур области, вычисляется также по формуле двойного интеграла. То есть, с помощью двойного интеграла можно вычислять объёмы тел.
Пример 13. Вычислить объём тела, ограниченного поверхностями x = 0, y = 0, z = 0 и x + y + z = 1 (рисунок ниже).
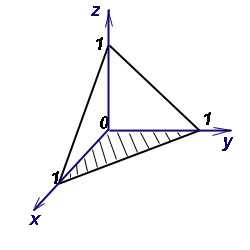
Расставляя пределы интегрирования, получаем следующий повторный интеграл:
.
Вычисляем внутренний (правый) интеграл:
.
Вычисляем внешний (левый) интеграл от вычисленного только что внутреннего (правого):
Вновь видим, что решение двойного интеграла — отрицательное число. За объём данного тела принимается модуль этого числа, то есть 1/6.
Мы уже знаем, что представляет собой область D. Пусть z = f(x, y) — некоторая функция двух переменных, определённая и ограниченная в этой области. Разобъём область D произвольно на n частей, не имеющих общих точек, с площадями . В каждой из этих частей выберем произвольную точку и составим сумму
,
которую назовём интегральной суммой. Диаметром области D условимся называть наибольшее расстояние между граничными точками этой области. Учитывается также наибольший из диаметров частичных областей.
Определение. Если интегральная сумма при неограниченном возрастании числа n разбиений области D и стремлении наибольшего из диаметров частичных областей к нулю имеет предел, то этот предел называется двойным интегралом от функции f(x, y) по области D.
Если областью интегрирования является окружность или часть окружности, то двойной интеграл проще вычислить в полярных координатах. Обобщением понятия двойного интеграла для функции трёх переменных является тройной интеграл.
Кратные и криволинейные интегралы
Поделиться с друзьями
function-x.ru
Двойные интегралы, примеры решений
Теория по двойным интегралам
Двойной интеграл от функции двух переменных по области G обозначается
Для вычисления двойного интеграла, его нужно свести к повторному интегралу. Возможны два случая. Пусть область интегрирования – элементарна относительно оси (рис. 1). Тогда двойной интеграл по области выражается через повторные по формуле:
Если же область интегрирования – элементарна относительно оси (рис. 2), то двойной интеграл по области выражается через повторные следующим образом:
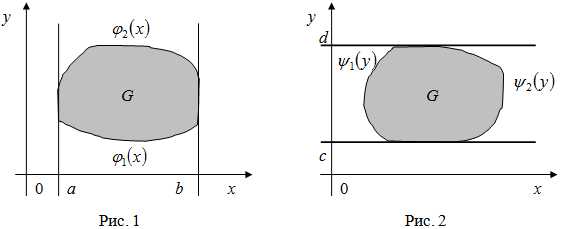
При решении задач иногда полезно разбить исходную область интегрирования на две или более областей и вычислять двойной интеграл в каждой области отдельно.
Примеры
ПРИМЕР 3| Задание | Вычислить двойной интеграл, если область – единичный круг с центром в начале координат. Интеграл:
|
| Решение | Если область, по которой вычисляется интеграл, является кругом или его частью, то интеграл проще вычислять в полярных координатах. Перейдем к полярным координатам:
В декартовых координатах уравнение единичной окружности с центром в начале координат имеет вид: ; запишем его в полярной системе координат:
Учитывая, что по определению , получим, что лежит в пределах . Так как интегрирование производится по всей окружности, то лежит в пределах . Подынтегральная функция в полярной системе координат примет вид:
Подставляя эту замену в исходный интеграл и переходя от двойного к повторному, получим:
Так как внутренний интеграл не зависит от , то его можно вычислить отдельно , осталось вычислить внутренний интеграл по :
|
| Ответ |
| Задание | С помощью двойного интеграла, вычислить площадь фигуры, ограниченной линиями: |
| Решение | Сделаем рисунок (рис. 4).
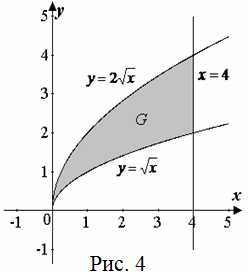
Площадь с помощью двойного интеграла вычисляется по формуле
Перейдем от двойного интеграла к повторному:
Вычислим этот интеграл, начиная с внутреннего:
(кв. ед.) |
| Ответ |
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Калькулятор двойных интегралов в Wolfram|Alpha
Для решения двойных интегралов Wolfram|Alpha используюет запросы специального вида, о которых уже шла речь в этом посте.Однако, все же самый простой способ найти двойной интеграл в Wolfram|Alpha — это калькулятор двойных интегралов, который выводится по запросу double integral. При этом, в качестве примера, в калькулятор интегралов автоматически подставляется функция x^2+y^2:
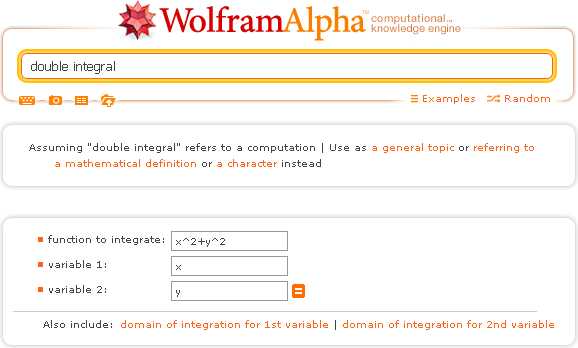
Решение неопределенных двойных интегралов в Wolfram|Alpha
Калькулятор двойных интегралов в Wolfram|Alpha позволяет получить решение любого другого неопределенного двойного интеграла. Для этого достаточно (1) — ввести новую подынтегральную функцию в поле с подписью function to integrate, (2), (3) — изменить наименования переменных интегрирования variable 1 и variable 2 (если они обозначены не x и y, как обычно, а какими-нибудь другими буквами), а затем (4) — нажать «=«:
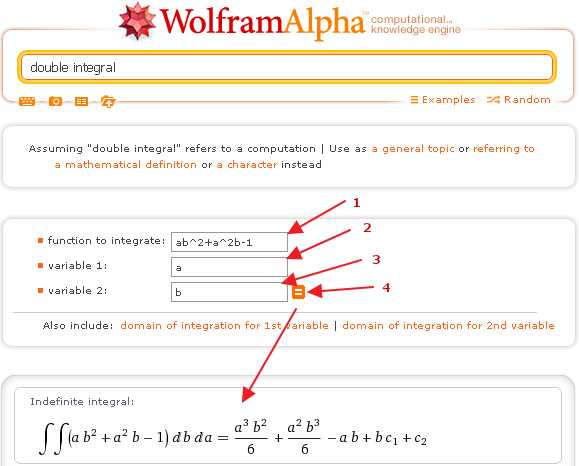
Вычисление двойных интегралов в Wolfram|Alpha
Чтобы вычислить определенный двойной интеграл при помощи калькулятора двойных интегралов Wolfram|Alpha, нужно явно указать пределы интегрирования.
Чтобы в калькуляторе двойных интегралов Wolfram|Alpha задать пределы интегрирования для определенного двойного интеграла, нужно последовательно клацнуть ссылки domain of integration for 1st variable (область интегрирования 1-й переменной) и domain of integration for 2nd variable ( область интегрирования 2-й переменной ) в нижней части калькулятора:
Сразу после этого Вы сможете явно указать пределы интегрирования для каждой переменной. При этом, для первой переменной интегрирования (variable 1) следует задавать постоянные пределы, а для второй (variable 2) можно задать как постоянные, так и переменные пределы, которые зависят от первой переменной:

Задавая пределы интегрирования учитывайте, что подынтегральная функция должна быть непрерывна в заданной области интегрирования. Если это условие будет нарушено, то Wolfram|Alpha, естественно, не сможет вычислить двойной интеграл.
В заключение хочу особо отметить, что с Wolfram|Alpha иногда бывает чрезвычайно интересно и поучительно наблюдать, как незначительное, на первый взгляд, изменение пределов интегрирования приводит к существенному изменению результата (сравните это с предыдущим примером):
P. S.
Нажмите слово «коммент.» внизу этого сообщения и оставьте свой комментарий!
www.wolframalpha-ru.com
Вычисление двойных интегралов.
Литература: Б.П. Демидович Сборник задач и упражнений по математическому анализу 624 стр. М.: «ЧеРо», 1997
Определение: Двойным интегралом от непрерывной функции $f(x, y)$ распространенным на ограниченную замкнутую квадрируемую область $\Omega$, называется число $$\iint\limits_{\Omega}f(x,y)dxdy=\lim\limits_{max|\Delta x_i|\rightarrow 0\quad max|\Delta y_i|\rightarrow 0}\sum\limits_i\sum\limits_j f(x_i, y_j)\Delta x_i\Delta y_j ,$$ где $\Delta x_i=x_{i+i}-x_i,$ $\Delta y_j=y_{j+1}-y_j$ и сумма распространяется на те значения $i$ и $j$ для которых $(x_i, y_j)\in\Omega.$
Непосредственное вычисление двойного интеграла.
Если область $\Omega$ задана неравенствами $$a\leq x\leq b,\qquad y_1(x)\leq y\leq y_2 (x),$$ где $y_1(x)$ и $y_2(x) -$ непрерывные функции на сегменте $[a, b],$ то соответствующий двойной интеграл может быть вычислен по формуле $$\iint\limits_{\Omega}f(x, y)dxdy=\int\limits_a^bdx\int\limits_{y_1(x)}^{y_2(x)}f(x, y)dy.$$
Замена переменных в двойном интеграле.
Если непрерывно дифференцируемые функции $$x=x(u, v),\quad y=y(u, v)$$ осуществляют взаимно однозначное отображение ограниченной и замкнутой области $\Omega$ в плоскости $Oxy$ на область $\Omega’$ в плоскости $Ouv$ и якобиан $$I=\frac{D(x, y)}{D(u, v)}$$ сохраняет постоянный знак в $\Omega$ за исключением, быть может, множества меры ноль, то справедлива формула $$\iint\limits_{\Omega}f(x, y)dxdy=\iint\limits_{\Omega’}f(x(u, v), y(u, v))|I|dudv.$$
В частности, для случая перехода к полярным $r$ и $\varphi$ координатам и по формулам имеем $$\iint\limits_{\Omega}f(x, y)dxdy=\iint\limits_{\Omega’}f(r\cos\varphi,\, r\sin\varphi)r drd\varphi.$$
Примеры:
Вычислить интегралы.
3906. $\int\limits_0^1dx\int\limits_0^1(x+y)dy.$
Решение.
$$\int\limits_0^1dx\int\limits_0^1(x+y)dy=\int\limits_0^1\left(\left.\left(xy+\frac{y^2}{2}\right)\right|_0^1\right)dx=\int\limits_0^1\left(x+\frac{1}{2}-0\right)dx=\left.\left(\frac{x^2}{2}+ \frac{1}{2}x\right)\right|_0^1= \frac{1}{2}+\frac{1}{2}-0=1.$$
Ответ: 1.
3908. $\int\limits_0^{2\pi}d\varphi\int\limits_0^ar^2\sin^2\varphi\,dr.$
Решение.
$$\int\limits_0^{2\pi}d\varphi\int\limits_0^ar^2\sin^2\varphi\,dr=\int\limits_0^{2\pi}\left(\int\limits_0^a r^2\sin^2\varphi\,dr\right)d\varphi=\int\limits_0^{2\pi}\left(\sin^2\varphi\left.\frac{r^3}{3}\right|_0^a\right)d\varphi=\int\limits_0^{2\pi}\sin^2\varphi\left(\frac{a^3}{3}-0\right)d\varphi=$$
$$=\frac{a^3}{3}\int\limits_0^{2\pi}\frac{1-cos2\varphi}{2}d\varphi=\frac{a^3}{3}\left.\left(\frac{1}{2}\varphi-\frac{1}{4}\sin2\varphi\right)\right|_0^{2\pi}=\frac{a^3}{3}\left(\frac{1}{2}2\pi-\frac{1}{4}\sin4\varphi-0\right)=\frac{a^3\pi}{3}.$$
Ответ: $\frac{a^3\pi}{3}.$
3912 а) Какой знак имеет интеграл $\iint\limits_{|x|+|y|\leq 1}\ln(x^2+y^2)\,dxdy;$
Изменить порядок интегрирования в следующих интегралах:
3924. $\int\limits_0^2dx\int\limits_x^{2x}f(x, y)dy.$
Решение.
Сделаем рисунок интегрируемой области:

Область интегрирования ограничена прямыми $y=x, y=2x$ и $x=2.$ Заметим, что в этой области если $y$ меняется от $0$ до $2,$ то координата $x$ меняется от прямой $y=2x$ (или $x=\frac{y}{2}$) до $y=x.$ Если же $y$ меняется от $2$ до $4,$ то координата $x$ меняется от прямой $y=2x$ ($x=\frac{y}{2}$) до $x=2.$ Таким образом,
$$\int\limits_0^2dx\int\limits_x^{2x}f(x, y)dy=\int\limits_0^2dy\int\limits_{\frac{y}{2}}^xdx+\int\limits_2^4dy\int\limits_{\frac{y}{2}}^{2}dx.$$
Ответ: $\int\limits_0^2dx\int\limits_x^{2x}f(x, y)dy=\int\limits_0^2dy\int\limits_{\frac{y}{2}}^xdx+\int\limits_2^4dy\int\limits_{\frac{y}{2}}^{2}dx.$
3928. $\int\limits_1^2dx\int\limits_{2-x}^{\sqrt{2x-x^2}}f(x, y)dy.$
3932. Вычислить интеграл $\iint\limits_{\Omega}xy^2dxdy,$ если область $\Omega$ ограничена параболой $y^2=2px$ и прямой $x=p/2\quad (p>0).$
3939. В двойном интеграле $\iint\limits_{\Omega}f(x,y)dxdy$ перейти к полярным координатам $r$ и $\varphi,$ полагая $x=r\cos\varphi$ и $y=r\sin\varphi,$ расставить пределы интегрирования, если $\Omega -$ кольцо $a^2\leq x^ 2+y^2\leq b^2.$
3944. Перейти к полярным координатам, $r$ и $\varphi,$ полагая $x=r\cos\varphi$ и $y=r\sin\varphi,$ и расставить пределы интегрирования в том и другом порядке в следующем интеграле: $\int\limits_0^1dx\int\limits_{1-x}^{\sqrt{1-x^2}}f(x, y)dy.$
3948. Предполагая, что $r$ и $\varphi,$ — полярные координаты, изменить порядок интегрирования в следующих интегралах: $\int\limits_{-\pi/2}^{\pi/2}d\varphi\int\limits_0^{a\cos\varphi}f(\varphi,r)dt\quad (a>0).$
3954. Переходя к полярным координатам, вычислить двойной интеграл $\iint\limits_{x^2+y^2\leq a^2}\sqrt{x^2+y^2}dxdy.$
3958. Вместо $x$ и $y$ ввести новые переменные $u$ и $v$ определить пределы интегрирования в следующих двойных интегралах $\int\limits_0^2dx\int\limits_{1-x}^{2-x}f(x, y)dy,$ если $u=x+y,\,\, v=x-y.$
3964. Произведя соответствующие замены переменных, свести двойные интегралы к однократным: $\iint\limits_{\Omega}f(xy)dxdy,$ где область $\Omega$ ограничена кривыми $xy=1,\,\, xy=2,\,\, y=x,\,\, y=4x\,\, (x>0, y>0).$
mathportal.net
WolframAlpha по-русски: Двойной интеграл в Wolfram|Alpha
Для нахождения неопределенных двойных интегралов Wolfram|Alpha использует следующий синтаксис: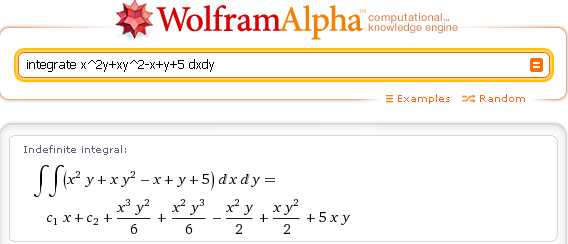
Важное замечание: обязательно нужно явно указывать переменные интегрирования, добавляя dxdy в конце подынтегрального выражения. Иначе Wolfram|Alpha неправильно интерпретирует запрос на нахождение двойного интеграла.
Для вычисления определенных двойных интегралов нужно просто указать пределы интегрирования. В простейшем случае, вычисление двойного интеграла в Wolfram|Alpha выполняется по запросу следующего вида:

Если двойной интеграл имеет переменные пределы, то форма запроса сохраняется. Однако, нужно быть внимательным и явно указывать порядок интегрирования. Так, если переменная x имеет постоянные пределы интегрирования, а переменная y — переменные пределы, то подынтегральное выражение должно заканчиваться символами dydx (сначала dy, а потом dx) (это поможет Wolfram|Alpha правильно определить последовательность повторного интегрирования при вычислении двойного интеграла). То есть корректный запрос на вычисление двойного интеграла в Wolfram|Alpha выглядит так:


Двойные интегралы с бесконечными пределами вычисляются в Wolfram|Alpha аналогично. Вот известный пример:

Однако, самый простой способ найти двойной интеграл в Wolfram|Alpha — это воспользоваться калькулятором двойных интегралов.
Калькулятор двойных интегралов в Wolfram|Alpha выводится по запросу
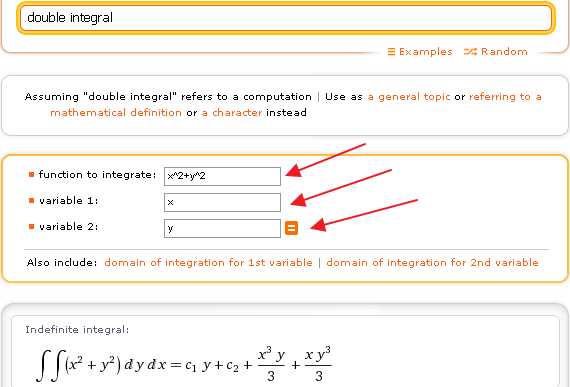
Для нахождения неопределенных двойных интегралов с помощью этого калькулятора здесь нужно сначала ввести свою подынтегральную функцию, затем указать первую и вторую переменную интегрирования, а после этого клацнуть знак «=».
Чтобы вычислить определенный двойной интеграл при помощи калькулятора, нужно указать пределы интегрирования для каждой переменной. Для этого следует последовательно клацнуть ссылки domain of integration for 1st variable и domain of integration for 2nd variable, которые подчеркнуты на этом рисунке:
После этого появится возможность ввести пределы интегрирования, и можно будет вычислить двойной интеграл, нажав кнопку «=»:

Нужно сказать, что Wolfram|Alpha вычисляет двойные интегралы не безупречно. Некоторые интегралы система не вычисляет, а лишь выводит условие примера. Возможно, это объясняется особенностями интернет-подключения, которое использую я.
www.wolframalpha-ru.com
Определенный интеграл онлайн. Несобственный интеграл онлайн.
Определенные интегралы онлайн на math34.su для закрепления студентами и школьниками пройденного материала. И тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса. Пошаговое вычисление определенных интегралов онлайн на сайте math34.su. Интегралы онлайн — определенный интеграл онлайн. Определенные интегралы онлайн на math34.su для полноценного закрепления студентами и школьниками пройденного материала и тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса. Пошаговое вычисление определенных интегралов онлайн на сайте math34.su. Интегралы онлайн — определенный интеграл онлайн. Для нас определенный интеграл онлайн взять не представляется чем-то сверх естественным, изучив данную тему по книге выдающихся авторов. Огромное им спасибо и выражаем респект этим личностям. Поможет определить определенный интеграл онлайн сервис по вычислению таких задач в два счета. Только укажите правильные данные и все будет Good! Всякий определенный интеграл как решение задачи повысит грамотность студентов. Об этом мечтает каждый ленивец, и мы не исключение, признаем это честно. Если все-таки получится вычислить определенный интеграл онлайн с решением бесплатно, то, пожалуйста, напишите адрес math34.su всем желающим им воспользоваться. Как говорится, поделишься полезной ссылкой — и тебя отблагодарят добрые люди за даром. Очень интересным будет вопрос разбора задачки, в которой определенный интеграл будет калькулятор решать самостоятельно, а не за счет траты вашего драгоценного времени. На то они и машины, чтобы пахать на людей. Однако решение определенных интегралов онлайн не всякому сайту по зубам, и это легко проверить, а именно, достаточно взять сложный пример и попытаться решить его с помощью каждого такого сервиса. Вы почувствуете разницу на собственной шкуре. Зачастую найти определенный интеграл онлайн без прилагаемых усилий станет достаточно сложно и нелепо будет выглядеть ваш ответ на фоне общей картины представления результата. Лучше бы сначала пройти курс молодого бойца. Всякое решение несобственных интегралов онлайн сводится сначала к вычислению неопределенного, а затем через теорию пределов вычислить как правило односторонние пределы от полученных выражений с подставленными границами A и B. Рассмотрев указанный вами определенный интеграл онлайн с подробным решением, мы сделали заключение, что вы ошиблись на пятом шаге, а именно при использовании формулы замены переменной Чебышева. Будьте очень внимательны в дальнейшем решении. Если ваш определенный интеграл онлайн калькулятор не смог взять с первого раза, то в первую очередь стоит перепроверить написанные данные в соответствующие формы на сайте. Убедитесь, что все в порядке и вперёд, Go-Go! Для каждого студента препятствием является вычисление несобственных интегралов онлайн при самом преподе, так как это либо экзамен, либо коллоквиум, или просто контрольная работа на паре. Непросто будет списать ответ вживую, но вы не унывайте, ведь с вами мы — math34.su. Как только заданный несобственный интеграл онлайн калькулятор будет в вашем распоряжении, то сразу вбивайте заданную функцию, подставляйте заданные пределы интегрирования и нажимайте на кнопку Решение, после этого вам будет доступен полноценный развернутый ответ. И все-таки хорошо, когда есть такой замечательный сайт как math34.su, потому что он и бесплатный, и простой в пользовании, также содержит очень много разделов. которыми студенты пользуются повседневно, один из них как раз есть определенный интеграл онлайн с решением в полном виде. В этом же разделе можно вычислить несобственный интеграл онлайн с подробным решением для дальнейших применений ответа как в институте, так и в инженерных работах. Казалось бы, всем определить определенный интеграл онлайн дело нехитрое, если заранее решить такой пример без верхней и нижней границы, то есть не интеграл Лейбница, а неопределенный интеграл. Но тут мы с вами не согласны категорически, так как на первый взгляд это может показаться именно так, однако есть существенная разница, давайте разберем все по полочкам. Такой определенный интеграл решение дает не в явном виде, а в следствие преобразования выражения в предельное значение. Другими словами, нужно сначала решить интеграл с подстановкой символьных значений границ, а затем вычислить предел либо на бесконечности, либо в определенной точке. Отсюда вычислить определенный интеграл онлайн с решением бесплатно означает ни что иное как представление точного решения по формуле Ньютона-Лейбница. Если же рассматривать наш определенный интеграл калькулятор поможет его подсчитать за несколько секунд прямо на ваших глазах. Такая спешка нужна всем желающим как можно быстрее справиться с заданием и освободиться для личных дел. Не стоит искать в интернете сайты, на которых попросят вас регистрироваться, затем пополнить деньги на баланс и все ради того, чтобы какой-нибудь умник подготавливал решение определенных интегралов якобы онлайн. Запомните адрес math34 — это бесплатный сервис для решения множества математических задач, в том же числе мы поможем найти определенный интеграл онлайн, и чтобы в этом убедиться, просим проверить наше утверждение на конкретных примерах. Введите подынтегральную функцию в соответствующее поле, затем укажите либо бесконечные предельные значения (в это случае будет вычислен и получено решение несобственных интегралов онлайн), либо задайте свои числовые или символьные границы и определенный интеграл онлайн с подробным решением выведется на странице после нажатия на кнопку «Решение». Неправда ли — это очень просто, не требует от вас лишних действий, бесплатно, что самое главное, и в то же время результативно. Вы можете самостоятельно воспользоваться сервисом, чтобы определенный интеграл онлайн калькулятор принес вам максимум пользы, и вы бы получили комфортное состояние, не напрягаясь на сложность всех вычислительных процессов, позвольте нам сделать все за вас и продемонстрировать всю мощь компьютерных технологий современного мира. Если погружаться в дебри сложнейших формул и вычисление несобственных интегралов онлайн изучить самостоятельно, то это похвально, и вы можете претендовать на возможность написания кандидатской работы, однако вернемся к реалиям студенческой жизни. А кто такой студент? В первую очередь — это молодой человек, энергичный и жизнерадостный, желающий успеть отдохнуть и сделать домашку! Поэтому мы позаботились об учениках, которые стараются отыскать на просторах глобальной сети несобственный интеграл онлайн калькулятор, и вот он к вашему вниманию — math34.su — самая полезная для молодежи решалка в режиме онлайн. Кстати наш сервис хоть и преподносится как помощник студентам и школьникам, но он в полной мере подойдет любому инженеру, потому что нам под силу любые типы задач и их решение представляется в профессиональном формате. Например, определенный интеграл онлайн с решением в полном виде мы предлагаем по этапам, то есть каждому логическому блоку (подзадачи) отводится отдельная запись со всеми выкладками по ходу процесса общего решения. Это конечно же упрощает восприятие многоэтапных последовательных раскладок, и тем самым является преимуществом проекта math34.su перед аналогичными сервисами по нахождению несобственный интеграл онлайн с подробным решением.
math24.su
Двойной интеграл по заданной области. Примеры решения задач
Решения типовых задач — Математический анализ
Двойной интеграл по заданной области
Задача
Вычислить двойной интеграл где область D задана неравенствами Решение
Уравнение определяет параболу, уравнение – верхнюю часть окружности
или . Область заключена между параболой и полуокружностью.
Изобразим область интегрирования на рисунке.
Очевидно, что область интегрирования является правильной областью в направлении обеих осей координат. Поэтому возможны два варианта выбора порядка интегрирования: вначале по , затем по или наоборот.
При первом варианте выбора порядка интегрирования область придется разбивать на две области и , так как в этом случае левая и правая границы области определяются двумя различными функциями.
При втором варианте выбора порядка интегрирования нет необходимости разбивать область на части, так как верхняя и нижняя границы области определяются одной функцией.
Выберем второй вариант.
Очевидно, что область определяется системой неравенств
Следовательно,
Задача 2. Вычислить Задача 3. Вычислить
www.matem96.ru
