Примеры решения задач по математической статистике и теории вероятности
1. Эксперт оценивает качественный уровень трех видов изделий по потребительским признакам. Вероятность ого, что изделию первого вида будет присвоен знак качества, равна 0,7; для изделия второго вида эта вероятность равна 0,9; а для изделия третьего вида 0,8. Найти вероятность того, что знак качества будет присвоен: а) всем изделиям; б) только одному изделию; в) хотя бы одному изделию
РЕШЕНИЕ
Испытание: знак качества будет присвоен всем изделиям.
Событие: А=07 – присвоен первому изделию, Р(В)=0,9 – присвоен второму изделию, Р(С)=0,8 – присвоен третьему изделию; тогда Р(А)=0,3; Р(В)=0,1; Р(С)=0,2.а) Рвсем изделиям = Р(А)*Р(В)*Р(С)
Рвсем изделиям =0,7*0,9*0,8=0,504.
в) Ртолько одному =Р(А,В,С или А,В,С или А,В,С)Ртолько .одному =0,7*0,1*0,2+0,3*0,9*0,2+
+0,3*0,1*0,8=0,014+0,054+0,024=0,092
с) Рхотя бы одному =1 — Рни одному =1-Р(А)*Р(В)*Р(С)Р
11. Оптовая база снабжает товаром 9 магазинов. Вероятность того, что в течение дня поступит заявка на товар, равна 0,5 для каждого магазина. Найти вероятность того, что в течение дня а) поступит 6 заявок, б) не менее 5 и не более 7 заявок, в) поступит хотя бы одна заявка. Каково наивероятнейшее число поступающих в течение дня заявок и чему равна соответствующая ему вероятность.
РЕШЕНИЕ
Обозначим событие А – поступила заявка
По условию р=Р(А)=0,5
q=P(A)=1-0,5=0,5
n= 9 к=6
а) Так как число повторных испытаний n= 9, применим формулу Бернулли.
Р9(6)=
*б) К1=5, К2=7
Р9(5≤m≤7)=P9 (5)+P9 (6)+P9 (7)
Р9(5)=
*Р9(7)=
*Р9(5≤m≤7)=0.246+0.0702+0.16=0.4762
в) Рn (событие наступит хотя бы 1 раз)=1-qn
Р9 =1-0,59 =1-0,001953=0,998
г) np-q≤K0 ≤np+p
9*0.5-0.5≤K0 ≤9*0.5+0.54≤K0 ≤5 K0 =5
K9 (5)=
*0.55 *0.59-5 =Ответ: а) 0,16 б) 0,4762 в) 0,998 г) K0 =5 Р(K0 )=0,246.
21. Найти: а) математическое ожидание, б) дисперсию, в) среднее квадратическое отклонение дискретной случайной величины Х по известному закону ее распределения, заданному таблично:
Решение
а) Найдем математическое ожидание Х:
М(Х)=8*0,2+4*0,5+6*0,2+5*0,1=5,3.
б) Для нахождения дисперсии запишем закон распределения Х2 :
Найдем математическое ожидание Х2 :
М(Х2 )=64*0,2+16*0,5+36*0,2+25*0,1=30,5
Найдем искомую дисперсию:
D(X)=M(X2 )-[M(X)]2
D(X)=30.5-(5.3)2 =2.41
в) найдем искомое среднее квадратическое отклонение:
Ответ: а) 5,3 б) 2,41 в) 1,55
31. Случайная величина Х интегральной функцией распределения F(Х).
Требуется: а) найти дифференциальную функцию распределения (плотность вероятности) б) найти математическое ожидание и дисперсию Х в) построить графики интегральной и дифференциальной функций распределения.
F(X
Решение:
а)
= F(Xб) М(х)=
.М(х2 )=
.D(x)=M(x2 )-[M(x)]2 =2-
в) построить графики функций F(x) и f(x):
41. Заданы математическое ожидание а=15 и среднее квадратичное отклонение б=2 нормально распределенной величины Х. Требуется найти: а) вероятность того, что Х примет значение, принадлежащие интервалу (9; 19). б) вероятность того, что абсолютная величина отклонения «Х-а» окажется меньше δ=3
Решение
а) воспользуемся формулой:
по условию задачи α=9 β=19 а=15 б=2 следовательно,
По таблице приложения 2:
0,4772;Искомая вероятность попадания нормально распределенной случайной величины в интервал (9; 19) равна:
0,4772+0,49865=0,976065б) вероятность того, что абсолютная величина отклонения «Х-а» окажется меньше δ=3, равна
Р(
Р(|х-а|<3)=2*Ф(3/2)=2*0,4332=0,8664.
Ответ: а)
0,976065; б) Р(|х-а|51. Даны выборочные варианты х1 и соответствующие им частоты ni количественного признака Х. а) найти выборочные среднюю дисперсию и среднеквадратическое отклонение. б) Считая, что количественный признак Х распределен по нормальному закону и что выборочная дисперсия равна генеральной дисперсии, найти доверительный интервал для оценки математического ожидания с надежностью γ=0,99
Решение
1. Объем выборки
n=
Средняя выборочная:
=Выборочная дисперсия:
Dв =
2 – 2 , где =23,76Средняя выборочная квадратов значений признака γ
=Тогда Dв =598,87-(23,76)2 =34,33
Среднее квадратичное отклонение:
σв =
σв =5,86пусть количественный признак Х генеральной совокупности распределен по нормальному закону, причем среднеквадратическое значение отклонение «σ» этого распределения известно. Тогда с вероятностью γ доверительный интервал заданный формулой
покрывает неизвестное математическое ожидание. Здесь число t находится из соотношения 2Ф(t)=γ с помощью таблицы интегральной функции Лапласса.
В данной задаче γ=0,99, поэтому 2Ф(t)=0,99, а Ф(t)=0,495, по таблице находим t=2,58.
По условию задачи дисперсия генеральной совокупности D=Dв и, следовательно, σ=σв =5,86. ранее найдены значения n=118, и Хв =23,76. Поэтому можно найти доверительный интервал:
(23,76-1,39; 23,76+1,39)
(22,37; 25,15).
Ответ: Хв =23,76; Dв =34,33; σв =5,86; а
(22,37; 25,15).61. По данным корреляционной таблицы найти условные средние Yx и Xy . Оценить тесноту линейной связи между признаками X и Y и составить уравнение линейной регрессии Y по X и X по Y. Сделать чертеж, нанеся на него условные средние и найденные прямые регрессии. Оценить силу связи между признаками с помощью корреляционного отношения.
mirznanii.com
145 решенных задач по теории вероятностей и математической статистике [DJVU]
Некоторые задачи взяты из книжкиБраилов А. В., Рябов П. Е. Теория вероятностей и математическая статистика: методические указания по выполнению самостоятельной работы. Часть 2.
- 702,87 КБ
- дата добавления неизвестна
- изменен
- 255,68 КБ
- дата добавления неизвестна
- изменен
40 решенных задач. Примеры решения задач по теории вероятностей и мат. статистике. В контрольной работе подробно разбираются задачи по теории вероятностей и математической статистике (Теория вероятности: классическая формула, теоремы сложения и умножения, формула полной вероятности, формула Байеса, формула Бернулли, теоремы Лапласа. Мат. статистика: математическое ожидание,…
- 259,37 КБ
- дата добавления неизвестна
- изменен
145 полностью решенных задач, охватывающих весь курс по теории вероятностей и математической статистике для нематематических специальностей вузов. Задачи взяты из контрольных работ ряда вузов, главным образом Уральского региона.
- 882,57 КБ
- дата добавления неизвестна
- изменен
Уфа, УГАТУ. — 19 с. Преподаватель: Савенко О.В. Тематика задач: Группировка и ее виды. Графическое построение рядов распределений Обобщающие статистические показатели Структурные средние величины Показатели вариации Выборочное наблюдение Корреляционно-регрессионный анализ Ряды динамики и их статистический анализ Экономические индексы Полностью решенный один вариант задач….
- 119,04 КБ
- дата добавления неизвестна
- изменен
40 решенных и подробно разобранных задач. Теория вероятности: классическая формула, теоремы сложения и умножения, формула полной вероятности, формула Байеса, формула Бернулли, теоремы Лапласа. Мат. статистика: математическое ожидание, дисперсия и среднее квадратическое отклонение, многоугольник распределения, полигон частот, корреляционная зависимость и т….
- 172,30 КБ
- дата добавления неизвестна
- изменен
www.twirpx.com
Задачи по теории вероятностей и математической статистике
84
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования
«Ковровская государственная технологическая академия имени
В.А. Дегтярева»
Учебно-методическое пособие
Составители:
И.Н. Марихов
С.Р. Марихова
Е.А. Миронова
Ковров 2009
УДК 519.2
Задачи по теории вероятностей и математической статистике. Учебно-методическое пособие/ Сост.: Марихов И.Н., Марихова С.Р., Миронова Е.А. – Ковров: КГТА им. В.А. Дегтярёва, 2009. – 83с.
В пособии даны основные понятия теории вероятностей и математической статистики, задания по выполнению самостоятельной работы студентов и примеры решения этих заданий.
Предназначено для студентов технических и экономических специальностей, изучающих теорию вероятностей и математическую статистику или их разделы.
Рецензент: д. ф.-м. н., проф. Ю.А. Алхутов (Владимирский государственный гуманитарный университет).
Содержание
Введение.……………………………………………………………………… | 4 |
Раздел 1. Теория вероятностей………………………………………………….. | 5 |
Раздел 2. Математическая статистика.…….……………………………… | 10 |
Задания для самостоятельной работы студентов.…………………………. | 15 |
Пример выполнения заданий самостоятельной работы студентов ….…… | 61 |
Литература………………….………………………………………………… | 83 |
Введение
Настоящее учебно-методическое пособие включает в себя краткие теоретические сведения из основных разделов теории вероятностей и математической статистики, задания для самостоятельной работы студентов и пример выполнения одного варианта заданий. В конце пособия приведён список литературы.
Содержание пособия подчинено требованиям современного государственного образовательного стандарта по математике для технических специальностей, изучающих теорию вероятностей и математическую статистику или их разделы. Краткие теоретические сведения разделов пособия даны в объёме достаточном для решения заданий самостоятельной работы студентов. Сами задания содержат условия 25 задач (по 30 вариантов каждой) для самостоятельных работ по темам: «Теория вероятностей», «Математическая статистика», «Методы математической статистики».
Материалы пособия предназначены для студентов, изучающих теорию вероятностей и математическую статистику или их разделы, будут полезны преподавателям для составления заданий самостоятельной работы студентов.
Раздел 1. Теория вероятностей Комбинаторные формулы
Декартовым
произведением множеств 
и 
называют множество 
,
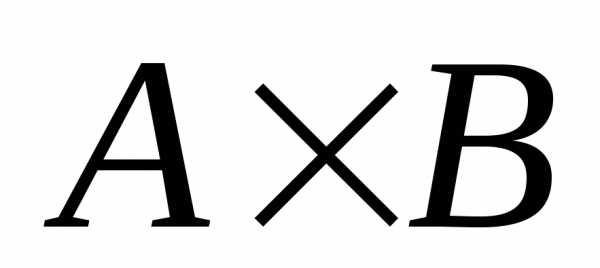состоящее из пар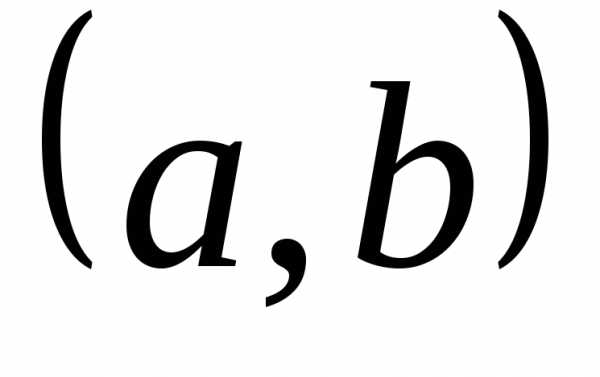 
элементов этих множеств.
Число элементов
множества
называют
его мощностью и обозначают
.
Число элементов
декартова произведения множеств 
и 
равно
произведению мощностей этих множеств
.
Множество называется упорядоченным, если все элементы этого множества пронумерованы.
Произвольное
упорядоченное подмножество, состоящее
из 
элементов множества 
,
содержащего 
различных элементов, называется размещением из 
элементов по 
.
Обозначим число
размещений из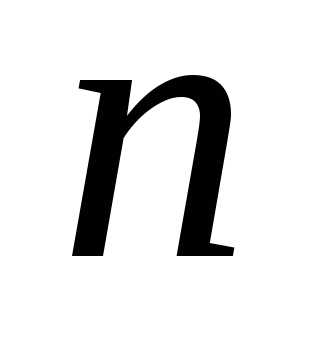 
элементов по 
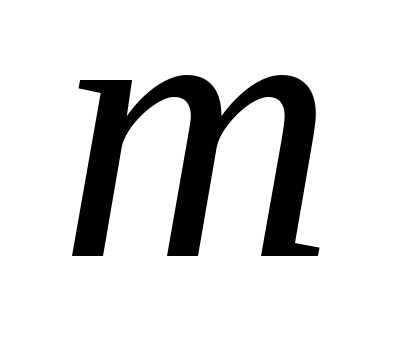символом. 
.
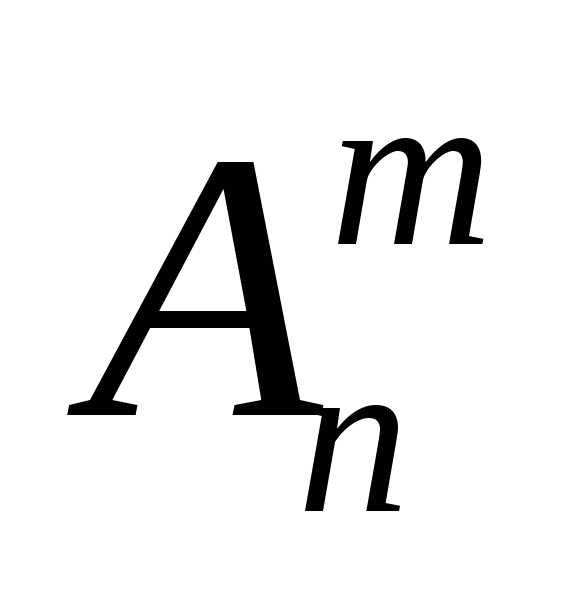Если
,
то
.
Упорядоченное
множество из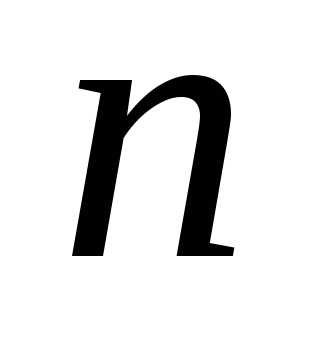 
элементов называется перестановкой этого множества и обозначается символом 
.
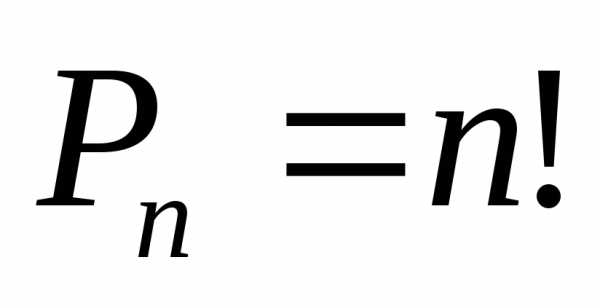Произвольное
(неупорядоченное) подмножество, состоящее
из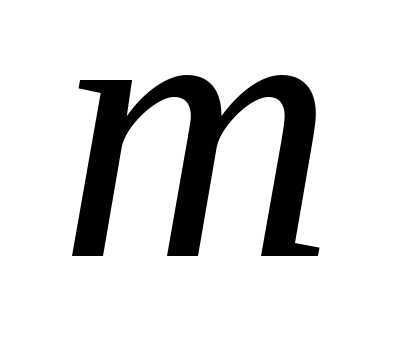 
элементов множества 
,
содержащего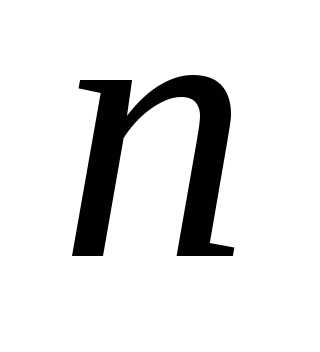 
различных элементов, называется сочетанием из 
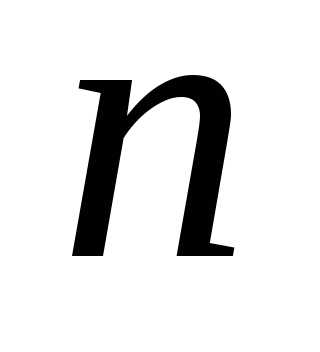элементов по и обозначается символом
.
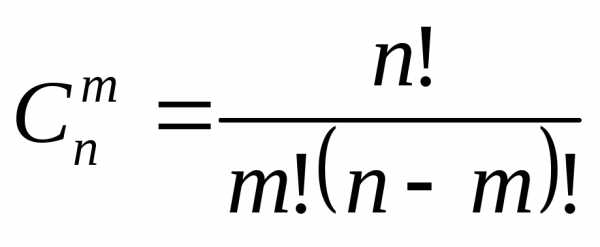studfiles.net
|
Вариант 7 1. В ходе аудиторской проверки строительной компании аудитор случайным образом отбирает 5 счетов. При условии, что 3% счетов содержат ошибки, найдите числовые характеристики этого распределения. Чему равна вероятность того, что хотя бы 1 счет будет с ошибкой. Решение Число правильных счетов есть случайная величина X, которая может принимать значения: 0, 1, 2, 3, 4. Вероятности этих значений определим по формуле Бернулли: pn(m) = , где q=0,03 — вероятность неправильного счета, а p=1-q=1-0,03 = 0,97 — вероятность правильного счета. Получим P (X=0) = p5(0) = 0,0000000243 P (X=1) = p5(1) = 0,000004 P (X=2) = p5(2) = 0,00025 P (X=3) = p5(3) = 0,0082 P (X=4) = p5(4) = 0,133 P (X=5) = p5(5) = 0,859 Сделаем проверку. Сумма вероятностей должна быть равна 1. Действительно, 0,0000000243+0,000004+ 0,00025+0,0082+0,133+0,859=1 Распределение случайной величины X
Определим числовые характеристики этого распределения. Математическое ожидание дискретной случайной величины X находим по формуле M (X) = , Где — возможные значения X, а — соответствующие вероятности. M(X) = 0*0,00000002 + 1*0,000004+2*0,00025+3*0,0082+4*0,133+5*0,859 = 4,85 Дисперсию случайной величины X находим по формуле . Так как M(X2) = 0*0,00000002 + 1*0,000004+4*0,00025+9*0,0082+16*0,133+25*0,859 = 23,68 То D(X) = 23,68 – (4,85)2 = 0,155 Среднее квадратическое отклонение случайной величины X равно Найдем функцию распределения вероятностей F(X). Если х ≤ 0, то F(x) = 0 Если 0 ≤ х ≤ 1, то F(x) = 0*0,00000002 Если 1 ≤ х ≤ 2, то F(x) = 0*0,00000002+0,000004 = 0,00000402 Если 2 ≤ х ≤ 3, то F(x) = 0*0,00000002+0,000004 +0,00025= 0,00025402 Если 3 ≤ х ≤ 4, то F(x) = 0*0,00000002+0,000004 +0,00025+0,0082= 0,00845402 Если 4 ≤ х ≤ 5, то F(x) = 0*0,00000002+0,000004 +0,00025+0,0082+0,133= 0,14145402 Если x > 5, то F(x) = 0*0,00000002+0,000004 +0,00025+0,0082+0,133+0,859 = 1 График функции
Событие A, состоящее в том, что хотя бы 1 счет будет с ошибкой, является противоположным к событию, что все счета будут правильными, следовательно, P(A) = 1 – P(X = 5) = 1-0,859 = 0,141 Вероятность того, что хотя бы 1 счет будет с ошибкой, равна 0,141. 2. Фирма, занимающаяся продажей товаров по каталогу, ежемесячно получает по почте заказы. Число этих заказов есть нормально распределенная случайная величина со средним квадратическим отклонением и неизвестным математическим ожиданием. В 90% случаев число ежемесячных заказов превышает 12439. Найдите ожидаемое среднее число заказов, получаемых фирмой за месяц. Решение Вероятность того, что число ежемесячных заказов превышает 12349: P(|X|>12349) = 1 — P(|X|<12349) = 0,9 По определению, для вероятности P(|X|<12349): P(|X|<12349) = Ф ( Где — математическое ожидание, то есть ожидаемое среднее число заказов, получаемых фирмой за месяц. По таблице функции Лапласа найдем Ф(х) = 0,1 , тогда х=0,25. Тогда: Ответ: 3. Длительность междугородних телефонных разговоров распределена примерно по показательному закону, разговор продолжается в среднем 3 мин. Найти вероятность того, что очередной разговор будет продолжаться более 3 мин. Найти вероятность того, что разговор, который длится уже 10 мин, закончится в течении ближайшей минуты, а также математическое ожидание и дисперсию длительности разговора. Решение Для показательного распределения математическое ожидание МХ = . Тогда Дисперсия длительности разговора равна: DX = Вероятность того, что разговор, будет продолжаться более 3 мин, является противоположным к событию, что разговор продолжается менее 3 мин: P(|X|>3) = 1 – P(|X|<3) = 1 — Вероятность того, что разговор, который длится уже 10 мин, закончится в течении ближайшей минуты: P{X<11|X>10} = Ответ: DX ; P(|X|>3) = 0; P{X<11|X>10} 2. Для заданного интервального ряда выборки проверить гипотезу: закон распределения генеральной совокупности является нормальным.
Решение Используя метод произведений, найдем выборочную среднюю и выборочное среднее квадратическое отклонение.
— выборочная средняя – выборочное среднее квадратическое отклонение Вычислим теоретические частоты:
Из расчетной таблицы получаем. Найдем по таблице критических точек распределения По уровню значимости α=0,05 и числу степеней свободы k=7-2=5 критическую точку правосторонней критической области (0,05; 5) = 11,1 Так как, то гипотеза о нормальном распределении отвергается. Ответ: гипотеза о нормальном распределении отвергается 3. В таблице случайных чисел цифры 0,1,2,3,4,5,6,7,8,9 встретились следующее число раз:
Здесь i – номер варианта. С помощью критерия Пирсона проверить гипотезу о том, что все цифры встречаются в таблице равновероятно. За уровень значимости принять Решение Найдем выборочную среднюю:
— выборочная средняя – выборочное среднее квадратическое отклонение Найдем параметры a и b: A*= = 0,5 B*= = 9,52 Найдем плотность предполагаемого равномерного распределения: F(x) = Найдем теоретические частоты: Длины третьего-девятого интервала равны длине второго интервала, поэтому теоретические частоты одинаковы и равны Сравним эмпирические и теоретические частоты, используя критерий Пирсона, приняв число степеней свободы k=s-3=10-3=7
Из расчетной таблицы получаем. Найдем по таблице критических точек распределения По уровню значимости α=0,05 и числу степеней свободы k=7 критическую точку правосторонней критической области (0,05; 7) = 14,1 Так как, то гипотеза о равномерном распределении отвергается. Ответ: гипотеза о равномерном распределении отвергается
|
matica.org.ua
2.3 Решение задач | Теория вероятностей и математическая статистика
На этой странице Вы найдете примеры решенных задач по теории вероятности и математической статистике по различным темам.
Презентации с задачами по темам:
1. Классическое определение вероятности.
2. Статистическое определение вероятности.
Электронные ресурсы с задачами:
1. Свойства вероятности, условная вероятность, независимость и зависимость, разные задачи (задача де Мере, задача о красных шарах, задача о размещении,задача о крэпсе, задача о красных, белых и розовых урнах)
2. Нахождение числа перестановок из n элементов, числа размещений из n по k, числа сочетаний из n по k, математического ожидания дискретного распределения, дисперсии дискретного распределения (online калькулятор)
3. 181 решенная задача по ТВ и МС
Видео уроки с задачами по темам:
1. Формула Бернулли.Вероятность всхожести.
2. Формула полной вероятности Байеса.
Литература с примерами решенных задач, доступная для скачивания :
1. Методическое пособие по выполнению практических работ по дисциплине «Теория вероятностей и математическая статистика»
2. Теория вероятностей в примерах и задачах. В.А. Колемаев, В.Н. Калинина, В.И. Соловьев, В.И. Малыхин, А.П. Курочкин. 2001 г.
3. Примеры решенных задач
4. Лабораторные работы по статистике
5. Задачи по ТВ и МС
Понравилось это:
Нравится Загрузка…
tvims.wordpress.com
Теория вероятности и математическая статистика1
Контрольные задания
І. Теория вероятностей.
1А. Определение сложных событий.
Задача 1.3. Техническое устройство состоит из трех последовательно и двух параллельно соединенных блоков. Определить сложное событие, характеризующее исправное состояние устройства.
Решение
Введем обозначения:
Событие A – блок 1 исправен (последовательно соединён)
Событие B – блок 2 исправен (последовательно соединён)
Событие C – блок 3 исправен (последовательно соединён)
Событие D – блок 4 исправен (параллельно соединён)
Событие E – блок 5 исправен (параллельно соединён)
Событие G — техническое устройство исправно.
Так как параллельному соединению соответствует сумма событий, а последовательному соединению — произведение событий.
Тогда Сложное событие G, характеризующее исправное состояние устройства, можно определить следующим образом:
G= A* B* C*( D+ E)
2А. Способы определения вероятностей.
Задача 2.3. В барабане револьвера семь гнезд, из них в шести заложены патроны, а один оставлен пустым. Барабан приводится во вращение, в результате чего против ствола случайным образом оказывается одно из гнезд. Нажимается спусковой крючок. Определить вероятность того, что выстрел произойдет.
Решение
В нашем случае элементарным исходом является появление одного из гнезд против ствола.
N=7 (количество гнёзд в барабане) — количество всех элементарных исходов.
Итак, все элементарные исходы равновозможны, следовательно, эксперимент, описанный в задаче, удовлетворяет классическому определению вероятности.
— против ствола случайным образом оказывается одно из шести гнезд, в которые заложены патроны.
— количество всех благоприятствующих исходов.
— искомая вероятность.
Ответ:
3А. Теоремы сложения и умножения вероятностей.
Задача 3.3. В урне 5 белых, 4 черных и 3 синих шара. Каждое испытание состоит в том, что наудачу извлекают один шар, не возвращая его обратно. Определить вероятность того, что при первом испытании появится белый шар (событие ), при втором – черный (событие ) и при третьем – синий (событие ).
Решение
Вероятность появления белого шара в первом испытании (всего в урне 5+4+3=12 шаров, из них белых 5 штук – по классическому определению вероятности).
Вероятность появления черного шара во втором испытании, вычисленная в предположении, что в первом испытании появился белый шар, т. е. условная вероятность .
Вероятность появления синего шара в третьем испытании, вычисленная в предположении, что в первом испытании появился белый шар, а во втором — черный, т. е. условная вероятность .
Искомая вероятность
Ответ:
5А. Закон распределения дискретной случайной величины и ее числовые характеристики.
Задача 5.3. По баскетбольному кольцу производится два независимых друг от друга броска. Вероятность попадания в кольцо при первом броске равна 0.4, втором – 0.6. Составить ряд распределения и найти дисперсию числа попаданий в кольцо при двух бросках.
Решение
Случайная величина Х – число попаданий мячом в кольцо при двух бросках. Она может принимать значения 0, 1, 2. Найдём соответствующие вероятности:
При х=0 – два промаха. Вероятность промаха при первом броске 1-0,4=0,6, при втором броске 1-0,6=0,4. По теореме умножения вероятностей независимых событий:
При х=2 – оба попадания. Вероятность попадания в кольцо при первом броске равна 0.4, втором – 0.6. По теореме умножения вероятностей независимых событий:
При х=1 – одно попадание и один промах. Так как события один промах одно попадание, оба промаха и оба попадания образуют полную группу событий то искомую вероятность найдём по формуле:
Получили ряд распределения
Xi | 0 | 1 | 2 |
Pi | 0,24 | 0,52 | 0,24 |
Дисперсию найдём по формуле , тогда
Получим
Ответ:
6А. Закон распределения непрерывной случайной величины и ее числовые характеристики.
Задача 6.3. Случайная величина имеет плотность распределения
.
Определить постоянное число «с», математическое ожидание и дисперсию случайной величины .
Решение
Для определения значения C воспользуемся условием . Вычислим интеграл ,
Плотность распределения случайной величины Х примет вид
Математическое ожидание находим по формуле :
Дисперсию найдем по формуле :
,
Тогда .
Контрольные задания
ІІ. Математическая статистика
13А. Выборочный метод математической статистики
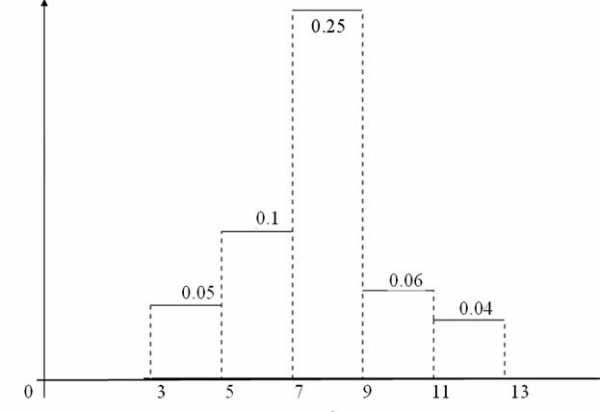
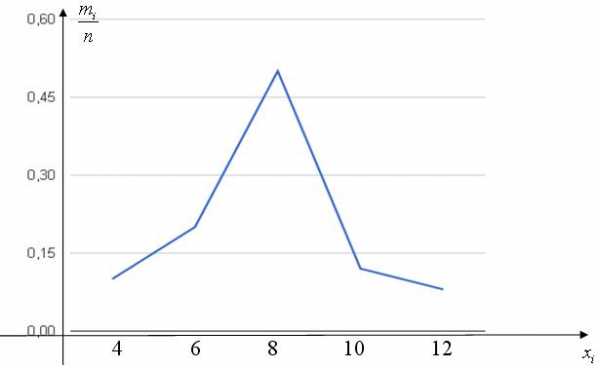
Пример 13.3. Построить полигон и гистограмму относительных частот по данному распределению
Ij | 3-5 | 5-7 | 7-9 | 9-11 | 11-13 |
Nj | 10 | 20 | 50 | 12 | 8 |
Решение
Объем выборки , длина интервала . Для построения гистограммы относительных частот дополним заданную таблицу следующими строками: строкой, в которой расположим средние точки каждого интервала, строкой относительных частот , строкой накопленных относительных частот и строкой, в которой вычислим высоты столбиков гистограммы относительных частот .
Группы | Xi | Кол-во, | |||
3-5 | 4 | 10 | 0.1 | 0.1 | 0.05 |
5-7 | 6 | 20 | 0.2 | 0.3 | 0.1 |
7-9 | 8 | 50 | 0.5 | 0.8 | 0.25 |
9-11 | 10 | 12 | 0.12 | 0.92 | 0.06 |
11-13 | 12 | 8 | 0.08 | 1 | 0.04 |
100 |
Построим гистограмму относительных частот, для этого на каждом интервале группированной выборки строим столбики, высоты которых вычислены в 6 столбце таблицы.
График гистограммы изображен на рис.
Строим полигон:
14А. Статистические оценки параметров распределения.
14.1.Точечные оценки параметров распределения
Примеры 1.– 10. Испытано 12 однотипных микросхем и с точностью до 1.0 часа зарегистрировано время безотказной работы каждой из них. Результаты испытаний сведены в таблицу:
№№ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
Ti[час] | 23 | 101 | 89 | 62 | 108 | 154 | 136 | 493 | 104 | 128 | 82 | 49 |
Найти оценку математического ожидания и дисперсии
Решение
1.Для оценки математического ожидания используем формулу
В нашем случае 2. Оценку для дисперсии проведём:
А) когда известно математическое ожидание = 130 [час].
Используем формулу
В нашем случае: б) когда неизвестно математическое ожидание .
В этом случае используем статистическое математическое ожидание и формулу
В нашем случае:
14.2. Интервальная оценка параметров распределения
Определить доверительный интервал.
Примеры 1.– 10. Построить 95-процентный (β=0.95) доверительный интервал для оценки неизвестного математического ожидания Случайной величины , если по результатам N =103 измерений получены оценки
Решение
Используем формулу для доверительного интервала
Значение табличной функции положим
В нашем случае
Тогда
Определить доверительный интервал .
Примеры 1.– 10. Построить 96-процентный (β=0.96) доверительный интервал для оценки неизвестной дисперсии случайной величины по результатам N =103 измерений.
Решение
Оценку для дисперсии проведём:
А) когда известно математическое ожидание и
Используем формулу Значение табличной функции положим
В нашем случае
Тогда
Б) когда неизвестно математическое ожидание и
Используем формулу
В нашем случае
Тогда
16А. Определение характеристик случайных величин и построение линий регрессии по данным выборки
Примеры 1.10. Дана выборка объёма , заданная в таблицах №№1–10. Номер таблицы определяется последней цифрой зачётной книжки.
Требуется: вычислить выборочные средние, выборочные дисперсии, средние квадратические отклонения, корреляционный момент и коэффициент корреляции. Составить уравнение линии регрессии . Построить график линии регрессии относительно точек таблицы. Найти остаточную дисперсию.
таблица №3
Х | -1.0 | -0.75 | -0.5 | -0.25 | 0 |
У | 2.08 | 1.83 | 1.57 | 1.13 | 0.89 |
Решение
Линейное уравнение регрессии имеет вид y = bx + a + ε
Здесь ε — случайная ошибка (отклонение, возмущение).
Так как отклонения εi для каждого конкретного наблюдения i – случайны и их значения в выборке неизвестны, то:
1) по наблюдениям xi и yi можно получить только оценки параметров α и β
2) Оценками параметров α и β регрессионной модели являются соответственно величины а и b, которые носят случайный характер, т. к. соответствуют случайной выборке;
Тогда оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где ei – наблюдаемые значения (оценки) ошибок εi, а и b соответственно оценки параметров α и β регрессионной модели, которые следует найти.
Для оценки параметров α и β — используют МНК (метод наименьших квадратов). Метод наименьших квадратов дает наилучшие (состоятельные, эффективные и несмещенные) оценки параметров уравнения регрессии.
Формально критерий МНК можно записать так:
S = ∑(yi — y*i)2 → min
Система нормальных уравнений.
A•n + b∑x = ∑y
A∑x + b∑x2 = ∑y•x
Для наших данных система уравнений имеет вид
5a + -2.5 b = 7.5
-2.5 a + 1.88 b = -4.52
Из первого уравнения выражаем А и подставим во второе уравнение:
Получаем эмпирические коэффициенты регрессии: b = -1.232, a = 0.884
Уравнение регрессии (эмпирическое уравнение регрессии):
Y = -1.232 x + 0.884
Эмпирические коэффициенты регрессии A и B являются лишь оценками теоретических коэффициентов βi, а само уравнение отражает лишь общую тенденцию в поведении рассматриваемых переменных.
Для расчета параметров регрессии построим расчетную таблицу
X | Y | X2 | Y2 | X • y |
-1 | 2.08 | 1 | 4.33 | -2.08 |
-0.75 | 1.83 | 0.56 | 3.35 | -1.37 |
-0.5 | 1.57 | 0.25 | 2.46 | -0.79 |
-0.25 | 1.13 | 0.0625 | 1.28 | -0.28 |
0 | 0.89 | 0 | 0.79 | 0 |
-2.5 | 7.5 | 1.88 | 12.21 | -4.52 |
1. Параметры уравнения регрессии.
Выборочные средние.
Выборочные дисперсии:
Среднеквадратическое отклонение
Коэффициент корреляции
Ковариация. (корреляционный момент)
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:
Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 < rxy < 0.3: слабая;
0.3 < rxy < 0.5: умеренная;
0.5 < rxy < 0.7: заметная;
0.7 < rxy < 0.9: высокая;
0.9 < rxy < 1: весьма высокая;
В нашем примере связь между признаком Y фактором X весьма высокая и обратная.
1.2. Уравнение регрессии (оценка уравнения регрессии).
Линейное уравнение регрессии имеет вид y = -1.23 x + 0.88
Для оценки качества параметров регрессии построим расчетную таблицу
x | Y | Y(x) | (y-y(x))2 |
-1 | 2.08 | 2.12 | 0.0013 |
-0.75 | 1.83 | 1.81 | 0.000484 |
-0.5 | 1.57 | 1.5 | 0.0049 |
-0.25 | 1.13 | 1.19 | 0.00384 |
0 | 0.89 | 0.88 | 0,000036 |
-2.5 | 7.5 | 7.5 | 0.0106 |
Остаточная дисперсия
В нашем случае
Построим график линии регрессии относительно точек таблицы.
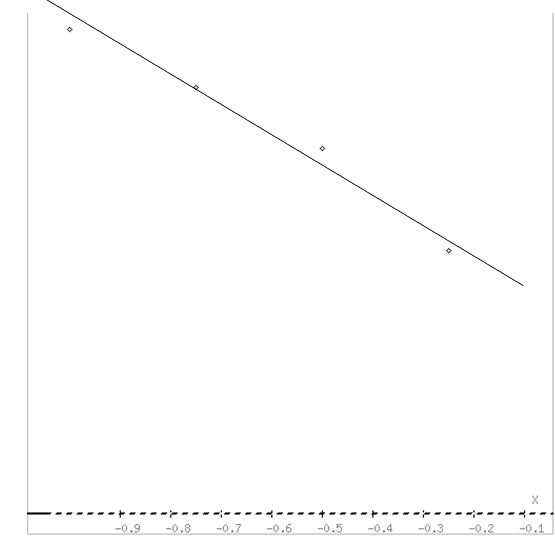
| < Предыдущая | Следующая > |
|---|
matica.org.ua
|
Элементы теории вероятности и математической статистики ЗАДАЧА Магазин получает электролампочки с двух заводов, причем доля первого завода составляет 25 %. Известно, что доля брака на этих заводах равна соответственно 5 % и 10 % от всей выпускаемой продукции. Продавец наугад берет одну лампочку. Какова вероятность того, что она окажется бракованной? Решение: Обозначим через А событие – «лампочка окажется бракованной». Возможны следующие гипотезы о происхождении этой лампочки: «лампочка поступила с первого завода», «лампочка поступила со второго завода». Так как доля первого завода составляет 25 %, то вероятности этих гипотез равны соответственно Условная вероятность того, что бракованная лампочка выпущена первым заводом – вторым заводом – искомую вероятность того, что продавец взял бракованную лампочку, находим по формуле полной вероятности . Ответ: Для решения задачи 5 см. глава 6 § 1–3, глава 7 § 1–2, глава 8 § 1–3. ЗАДАЧА 5 Задан закон распределения дискретной случайной величены Х:
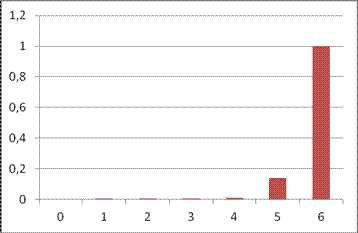
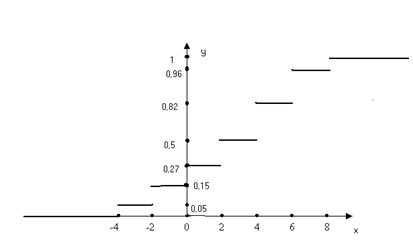
Найти: А) неизвестную вероятность Р, Б) математическое ожидание М, дисперсию D И среднее квадратическое отклонение данной случайной величены; В) функцию распределения F(x) и построить ее график; Г) закон распределения случайной величины Y, если ее значения заданы функциональной зависимостью Решение: А) так как сумма всех вероятностей должна равняться единице, то получим уравнение Отсюда Б) Математическое ожидание М это сумма всех произведений значений случайной величины на их вероятности: Дисперсия D=
Среднее квадратическое отклонение = В) Если < Если – 4< < Если – 2< < Если 0< 0,05 + 0,1 + 0,12 = 0,15 + 0,12 = 0,27 Если 2< 0,27 + 0,23 = 0,5; Если 4< 0,5 + 0,32 = 0,82; Если 6< 0,82 + 0,14=0,96; Если Х >8, То F(x)=Р( Х < Х )=0,96 + 0,04=1. Итак, функция распределения может быть записана так:
F (X) = График этой функции приведен на рисунке: Г) Сначала найдем значения случайной величены Y. По условиям задачи Поэтому Составим таблицу вида.
Чтобы получить закон распределения случайной величены Y необходимо: 1) рассмотреть ее значение в порядке возрастания; 2) сложить вероятности, соответствующие совпадающим значениям данной таблицы. Итак, закон распределения случайной величены Y:
Для решения задачи 6 см. глава 5, §2, §3.
|
matica.org.ua