Решение логарифмических уравнений и систем уравнений. Подготовка к ЕГЭ
Разделы: Математика
Ученик проходит в несколько лет дорогу, на которую человечество употребило тысячелетие.
Однако его следует вести к цели не с завязанными глазами, а зрячим:
он должен воспринимать истину, не как готовый результат, а должен её открывать.
Учитель должен руководить этой экспедицией открытий, следовательно, также присутствовать
не только в качестве простого зрителя. Но ученик должен напрягать свои силы;
ему ничто не должно доставаться даром.
Даётся только тому, кто стремится.
(А. Дистервег)
Форма урока: комбинированный урок
Тип урока:
Урок повторного контроля знаний.Обобщение и закрепление пройденного материала.
Цели урока:
- Образовательная — обобщение знаний учащихся по теме «Логарифмические уравнения и системы уравнений; закрепить основные приемы и методы решения логарифмических уравнений и систем уравнений; ознакомить учащихся с видами заданий повышенной сложности по данной теме в ЕГЭ.
- Развивающая — развитие логического мышления для сознательного восприятия учебного материала, внимание, зрительную память, активность учащихся на уроке. Предоставить каждому из учащихся проверить свой уровень подготовки по данной теме.
- Воспитывающая — воспитание познавательной активности, формирование личностных качеств: точность и ясность словесного выражения мысли; сосредоточенность и внимание; настойчивость и ответственность, положительной мотивации к изучению предмета, аккуратности, добросовестности и чувство ответственности. Осуществить индивидуальный подход и педагогическую поддержку каждого ученика через разноуровневые задания и благоприятную психологическую атмосферу.
Задачи урока:
- выработать у учащихся умение пользоваться алгоритмом решения логарифмических уравнений.
- осуществить формирование первоначальных знаний в виде отдельных навыков после определенной тренировки решения уравнений и систем уравнений.
- познакомить учащихся с частными случаями и отработать навыки по решению таких уравнений и систем уравнений.
Методы и педагогические приемы:
- Методы самообучения
- Приемы устного опроса.
- Приемы письменного контроля.
- Коллективная учебная деятельность.
- Организация работы в группах.
- Повышение интереса к учебному материалу.
Оборудование:
- компьютер, мультимедийный проектор и экран;
- тетради;
Раздаточный материал: задания для самостоятельной работы.
План урока:
- Организационный момент (1 мин)
- Проверка домашнего задания (3 мин)
- Входной контроль (повторение теоретического материала) (15 мин)
- Этап обобщения знаний учащихся. Решение уравнений и систем уравнений (45 мин)
- Разноуровневая самостоятельная работа (проверка знаний учащихся) (20 мин)
- Итоги урока (4 мин)
- Домашнее задание (2 мин)
Ход урока
1. Организационный момент
Взаимное приветствие; проверка готовности учащихся к уроку, организация внимания.
2. Проверка домашнего задания
Установить правильность и осознанность выполнения домашнего задания всеми учащимися; установить пробелы в знаниях.
3. Входной контроль (повторение теоретического материала)
Организация устной фронтальной работы с классом по повторению логарифмических формул и способов решения логарифмических уравнений.
Решение простейших уравнений:
Сравните числа:
а) и
б) и
2) Найдите Х, если х>0:
[1/5]
[4]
Перечислите: основные способы решения логарифмических уравнений.
Способы решения логарифмических уравнений
- По определению логарифма.
- Метод потенцирования.
- Метод введения новой переменной.
- Решение уравнений логарифмированием его обеих частей.
- Функционально-графический способ.
На экране уравнения:
- log2(3 — 6x) = 3
- lg(х2 — 2х) = lg (2х + 12)
- 5х + 1 — 5 х — 1 = 24
- хlg х = 10000
- 32х + 5 = 3х + 2 + 2
- log32x — log3 x = 3
- log2x — log4x = 3
- 2x = x2 — 2x
Среди данных уравнений выбрать логарифмические. Определить способ решения каждого уравнения. Решите уравнения.
По окончанию работы правильность решения уравнений осуществляется с помощью экрана.
Устно ответить на следующие вопросы (если имеется не один корень):
- Найти наименьший корень уравнения.
- Найти сумму корней уравнения.
- Найти разность корней уравнения.
- Найти произведение корней уравнения.
- Найти частное корней уравнения
Самооценка и взаимооценка деятельности учащихся (результаты заносятся в листы самоконтроля).
4. Этап обобщения знаний учащихся
Решение логарифмических уравнений из заданий ЕГЭ части В и С.
№ 1 (В) Найдите корень (или сумму корней, если их несколько) уравнения log6(3x + 88) — log6 11 = log6 x. [1]
№ 2 (B) Найдите произведение всех корней уравнения
№ 3 (B) Найдите сумму корней уравнения = log4 (x — 3) + 2. [2]
№ 4 (C) найти наибольший корень уравнения: log2(2+5)+ log0,5(-х-0,5) = 1 [-4]
№ 5 (C) Решите уравнение — log6x + 34 = ()2 + x. [2]
Уравнения №1-3 решает по два ученика на обратных крыльях доски с последующей проверкой решения всем классом.
Уравнение №4,5 решает ученик с подробным комментарием.
По окончании самооценка и взаимооценка учащихся (результаты заносятся в листы самоконтроля).
Простейшими логарифмическими уравнениями будем называть уравнения следующих видов:
log a x = b, a > 0, a 1.
log a f(x) = b, a > 0, a 1.
log f(x) b = c, b > 0.
Эти уравнения решаются на основании определения логарифма: если logb a = c, то a = b c.
Решить уравнение log2 x = 3.
Решение. Область определения уравнения x > 0. По определению логарифма x = 23, x = 8 принадлежит области определения уравнения.
Ответ: x = 8.
Уравнения вида loga f(x) = b, a > 0, a 1.
Уравнения данного вида решаются по определению логарифма с учётом области определения функции f(x).
Обычно область определения находится отдельно, и после решения уравнения f(x) = ab проверяется, принадлежат ли его корни области определения уравнения.
Пример. Решить уравнение log3(5х — 1) = 2.
Решение:
ОДЗ: 5х — 1 > 0; х > 1/5.
log3(5х- 1) = 2,
log3(5х — 1) = log332,
5х — 1 =9,
х = 2.
Ответ: 2.
Пример. Решить уравнение
Решение. Область определения уравнения находится из неравенства 2х2 — 2х — 1 > 0. Воспользуемся определением логарифма:
Применим правила действий со степенями, получим 2х2 — 2х — 1 = 3. Это уравнение имеет два корня х = -1; х = 2. Оба полученные значения неизвестной удовлетворяют неравенству 2х2 — 2х — 1 > 0, т.е. принадлежат области определения данного уравнения, и, значит, являются его корнями.
Ответ. х1 = -1, х2 = 2.
Уравнения вида logf(x) b = с, b > 0.
Уравнения этого вида решаются по определению логарифма с учётом области определения уравнения. Данное уравнение равносильно следующей системе
Чаще всего, область определения логарифмического уравнения находится отдельно, и после решения уравнения (f(x))c = b или равносильного уравнения проверяется, принадлежат ли его корни найденной области.
Пример. Решить уравнение
logx-19 = 2.
Решение. Данное уравнение равносильно системе
Ответ. x = 4.
2.. Потенцирование.
Суть метода заключается в переходе от уравнения
log a f(x) = log a g(x) к уравнению f(x) = g(x), которое обычно не равносильно исходному.
Уравнения вида
loga f(x) = loga g(x) , а > 0, а ?1.
На основании свойства монотонности логарифмической функции заключаем, что f(x) = g(x).
Переход от уравнения loga f(x) = loga g(x) к уравнению f(x) = g(x) называется потенцированием.
Нужно отметить, что при таком переходе может нарушиться равносильность уравнения. В данном уравнении f(x) > 0, g(x) > 0, а в полученном после потенцирования эти функции могут быть как положительными, так и отрицательными. Поэтому из найденных корней уравнения f(x) = g(x) нужно отобрать те, которые принадлежат области определения данного уравнения. Остальные корни будут посторонними.
Пример. Решить уравнение log3 (x2 — 3x — 5) = log3 (7 — 2x).
Решение. Область определения уравнения найдётся из системы неравенств:
x2 — 3x — 5>0, 7 — 2x>0
х> -1,5+ , х<3,5
х2 <-1,5-
Потенцируя данное уравнение, получаем х2 — 3х — 5 = 7 — 2х,
х2 — х — 12 = 0, откуда х1 = -3, х2 = 4. Число 4 не удовлетворяет системе неравенств.
Ответ. х = -3.
Cведение уравнений к виду log a f(x) = log a g(x) с помощью свойств логарифмов по одному основанию.
Если уравнение содержит логарифмы по одному основанию, то для приведения их к виду log a f(x) = log a g(x) используются следующие свойства логарифмов:
logb a + logb c = logb (a*c), где a > 0; c > 0; b > 0, b 1,
logb a — logb c = logb (a/c), где a > 0; c > 0; b > 0, b 1,
m logb a = logb a m, где a > 0; b > 0, b 1; m R.
Пример 1. Решить уравнение log6 (x — 1) = 2 — log6 (5x + 3).
Решение. Найдём область определения уравнения из системы неравенств
Применяя преобразования, приходим к уравнению
log6 (x — 1) + log6 (5x + 3) = 2,
log6 ((x — 1)(5x + 3)) = 2, далее, потенцированием, к уравнению
(х — 1)(5х + 3) = 36, имеющему два корня х = -2,6; х = 3. Учитывая область определения уравнения, х = 3.
Ответ. х = 3.
Пример 2. Решить уравнение
Решение. Найдём область определения уравнения, решив неравенство (3x — 1)(x + 3) > 0 методом интервалов.
Учитывая, что разность логарифмов равна логарифму частного, получим уравнение log5 (x + 3) 2 = 0. По определению логарифма (х + 3) 2 = 1, х = -4, х = -2. Число х = -2 посторонний корень.
Ответ. х = -4.
Пример 3. Решить уравнение log2 (6 — x) = 2 log6 x.
Решение. На области определения 0 < x < 6 исходное уравнение равносильно уравнению 6 — x = x2, откуда х = -3, х = 2. Число х = -3 посторонний корень.
Ответ. х = 2.
Уравнения вида Alog a f(x) + Blog b g(x) + C = 0.
Метод потенцирования применяется в том случае, если все логарифмы, входящие в уравнение, имеют одинаковое основание. Для приведения логарифмов к общему основанию используются формулы:
Пример 1. Решить уравнение
Решение. Область определения уравнения 1 < x < 2. Используя формулу (3), получим
Так как 3 = log28, то на области определения получим равносильное уравнение (2-x)/(x-1) = 8, откуда x = 10/9.
Ответ. x = 10/9.
Пример 2. Решить уравнение
Решение. Область определения уравнения x > 1. Приведём логарифмы к основанию 3, используя формулу (4).
Ответ. х = 6.
Пример 3. Решить уравнение
Решение. Область определения уравнения x > -1, x 0. Приведём логарифмы к основанию 3, используя формулу (2).
Умножим обе части уравнения на log 3(x + 1) ? 0 и перенесем все слагаемые в левую часть уравнения. Получим (log 3(x + 1)-1)2 = 0, откуда log 3(x + 1) = 1 и x = 2.
Ответ. x = 2.
3. Введение новой переменной
Рассмотрим два вида логарифмических уравнений, которые введением новой переменной приводятся к квадратным.
Уравнения вида
где a > 0, a 1, A, В, С — действительные числа.
Пусть t = loga f(x), t R. Уравнение примет вид t2 + Bt + C = 0.
Решив его, найдём х из подстановки t = loga f(x). Учитывая область определения, выберем только те значения x, которые удовлетворяют неравенству f(x) > 0.
Пример 1. Решить уравнение lg 2 x — lgx — 6 = 0.
Решение. Область определения уравнения - интервал (0; ).Введём новую переменную t = lg x, t R.
Уравнение примет вид t 2 — t — 6 = 0. Его корни t1 = -2, t2 = 3.
Вернёмся к первоначальной переменной lg x = -2 или lg x = 3, х = 10 -2 или х = 10 3.
Оба значения x удовлетворяют области определения данного уравнения (х > 0).
Ответ. х = 0,01; х = 1000.
Пример 2. Решить уравнение
Решение. Найдём область определения уравнения
Применив формулу логарифма степени, получим уравнение
Так как х < 0, то | x | = —x и следовательно
Введём новую переменную t = log3 (-x), t принадлежит R. Квадратное уравнение t 2 — 4t + 4 = 0
имеет два равных корня t1,2 = 2. Вернёмся к первоначальной переменной log3 (-x) = 2, отсюда —х = 9, х = -9. Значение неизвестной принадлежит области определения уравнения.
Ответ. х = -9.
Уравнения вида
где a > 0, a 1, A, В, С — действительные числа, A 0, В 0.
Уравнения данного вида приводятся к квадратным умножением обеих частей его на loga f(x) 0. Учитывая, что loga f(x) logf(x) a=1
(свойство logb a = 1/ loga b), получим уравнение
Замена loga f(x)=t, t R приводит его к квадратному At2 + Ct + B = 0.
Из уравнений loga f(x)= t1, logb f(x)= t2 найдем значения x и выберем среди них принадлежащие области определения уравнения:
f(x) > 0, f(x) 1.
Пример. Решить уравнение
Решение. Область определения уравнения находим из условий x+2>0, x+2 1, т.е. x >-2, x -1.
Умножим обе части уравнения на log5 (x+2) 0, получим
или, заменив log5(x+2) = t, придем к квадратному уравнению
t 2 — t — 2 = 0, t1 = -1, t2 =2.
Возвращаемся к первоначальной переменной:
log5 (x+2) = -1, x+2 = 1/5, x = -9/5,
log5 (x+2) = 2, x+2 = 25, x = 23.
Оба корня принадлежат области определения уравнения.
Ответ: x = -9/5, x = 23.
в) log2х — 2 logх2 = -1
Решение:
ОДЗ: x > 0, х 1
Используя формулу перехода к новому основанию, получим
urok.1sept.ru
Урок 4. Логарифмическая функция. Логарифмические уравнения. Системы логарифмических уравнений. Теория.
Подготовка к ЕГЭ по математике
Эксперимент
Урок 4. Логарифмическая функция. Логарифмические уравнения. Системы логарифмических уравнений.
Теория
Конспект урока
На предыдущем уроке мы определили понятие логарифма, обсудили его основные свойства.
Сегодня мы поговорим о решении простейших логарифмических уравнений и видах логарифмических уравнений.
По аналогии с решением показательных уравнений мы воспользуемся свойствами логарифмической функции для решения логарифмических уравнений.
Рассмотрим логарифмическую функцию:
Рассмотрим её свойства:
1) – это следует из определения логарифма (под логарифмом не может стоять отрицательное число или 0)
2) Стоит отметить, что показательная и логарифмическая функции являются взаимно обратными. Поэтому область определения показательной функции совпадает с областью значения логарифмической и наоборот (более подробно о свойствах прямой и обратной функции мы поговорим в теме «Функции»).
3) Точки пересечения с осями.
Ох (нули функции): так как логарифм от 1 по любому основанию равен 0 (любое положительное число в 0 степени равно 1). Значит, график логарифмической функции проходит через точку
Оу: – не существует, так как 0 не входит в область определения логарифмической функции.
4) Функция не является ни чётной, ни нечётной (функция общего вида), так как область определения не симметрична относительно 0 (то есть, функция не определена при отрицательных значениях переменной).
Также функция не является периодической.
5) При функция монотонно возрастает на всей области определения (обратите внимание на сходство с показательной функцией).
При функция монотонно убывает на всей области определения.
6) Графики логарифмической функции при и имеют вид:
Мы видим, что логарифмическая функция, как и показательная, является монотонной (монотонно возрастает при и монотонно убывает при ).
Это означает, что мы можем по аналогии с простейшими показательными уравнениями определить способ решения простейших логарифмических уравнений (): Однако при этом необходимо помнить, что под логарифмом должно стоять положительное число. Таким образом, при решении логарифмических уравнений необходимо учитывать ОДЗ, а именно: проверять, что все подлогарифмические выражения, а также основания логарифмов являются положительными и основания не равны 1.
Однако можно избежать определения ОДЗ исходного уравнения, выполнив в конце проверку полученных результатов (поскольку мы не сужаем область поиска корней, а расширяем её). В большинстве случаев такой подход облегчает решение логарифмических уравнений.
Таким образом, для
interneturok.ru
| 1. |
Система логарифмического и линейного уравнений (определение логарифма)
Сложность: лёгкое |
3 |
| 2. |
Система показательного и линейного уравнений (нулевая степень)
Сложность: лёгкое |
6 |
| 3. |
Система показательного и линейного уравнений
Сложность: лёгкое |
5 |
| 4. |
Система уравнений (показательное уравнение)
Сложность: среднее |
4 |
| 5. |
Система показательных уравнений
Сложность: среднее |
4 |
| 6. |
Система показательных уравнений
Сложность: среднее |
7 |
| 7. |
Система показательных уравнений (теорема Виета)
Сложность: среднее |
5 |
| 8. |
Система показательных уравнений (десятичные дроби)
Сложность: среднее |
7 |
| 9. |
Система показательных уравнений (обыкновенные дроби)
Сложность: среднее |
8 |
| 10. |
Система показательных уравнений (сумма)
Сложность: среднее |
5 |
| 11. |
Система логарифмических уравнений (сумма)
Сложность: среднее |
9 |
| 12. |
Система логарифмических уравнений (определение логарифма)
Сложность: среднее |
9 |
| 13. |
Система показательного и логарифмического уравнений (обыкновенные дроби)
Сложность: среднее |
10 |
| 14. |
Система показательного и логарифмического уравнений (целые числа)
Сложность: среднее |
8 |
| 15. |
Система логарифмического и линейного уравнений (разность)
Сложность: сложное |
16 |
www.yaklass.ru
Урок 4. Логарифмическая функция. Логарифмические уравнения. Системы логарифмических уравнений. Практика
В практической части урока мы рассмотрим основные методы решения логарифмических уравнений всех типов и систем логарифмических уравнений.
Подготовка к ЕГЭ по математике
Эксперимент
Урок 4. Логарифмическая функция. Логарифмические уравнения. Системы логарифмических уравнений.
Практика
Конспект урока
Пример №1. Решить уравнение .
Решим уравнение несколькими способами:
1 способ:
2 способ:
Проверка: ‑ верно.
Ответ: 9
Пример №2. Решить уравнение:
Проверка: — верно.
Ответ: .
Пример №3. Решить уравнение:
Проверка:
— не подходит.
— верно.
Ответ: 2.
Пример №4. Решить уравнение:
Проверка:
interneturok.ru
Конспект урока по математике по теме «Решение логарифмических уравнений. Решение систем уравнений, содержащих логарифмическую функцию»
Разделы: Математика
Цели урока:
- образовательная цель – рассмотреть решение систем логарифмических уравнений; рассмотреть логарифмические уравнения, включенные в «Открытый банк заданий по математике»;
- развивающая цель – способствовать формированию навыков решения логарифмических уравнений;
- воспитательная цель – способствовать воспитанию чувства ответственности, уверенности.
Тип урока: изучение новой темы.
Вид урока: традиционный с применением компьютера.
Форма проведения: групповая.
Оборудование: индивидуальные карточки, компьютер, мультимедийный проектор, презентация.
Ход урока
I. Организационный момент.
Сообщение темы, постановка цели, сообщение этапов урока.
II. Актуализация знаний учащихся.
1) Устная работа.
1. Дайте определение логарифмической функции. (Слайд 2 приложения 1)
Ответ: Функцию, заданную формулой , называют логарифмической функцией с основанием а.
2. Перечислите основные свойства логарифмической функции. (Слайд 3 приложения 1)
Ответ:
- Область определения логарифмической функции – множество всех положительных действительных чисел.
- Область значений логарифмической функции – множество всех действительных чисел.
- Логарифмическая функция на всей области определения возрастает (при а>1) или убывает (при 0<а<1).
3. Как расположены графики показательной и логарифмических функций, имеющих одинаковые основания? (Слайд 4 приложения 1)
Ответ: Графики показательной и логарифмических функций, имеющих одинаковые основания, симметричны относительно прямой у = х.
4. Какие уравнения называются логарифмическими? (Слайд 5 приложения 1)
Ответ: уравнение, содержащее переменную под знаком логарифма, называется логарифмическим.
5. Какими способами можно решить логарифмические уравнения? (Слайд 6 приложения 1)
Ответ: на основании определения логарифма, потенцированием, применением основного логарифмического тождества, логарифмированием.
2) Проверка домашнего задания.
1) Командиры групп докладывают о выполнении домашнего задания членами групп, отмечают трудности при выполнении №518 (б, г), 519 (в, г), 520 (г). (Ответы проверяют по слайду 7 приложения 1)
2) Выполняют тест по индивидуальным карточкам. (Приложение 2)
Те ученики, которые закончили работу раньше других, выполняют задания В7 по компьютеру «Открытый банк заданий по математике», потом присоединяются другие.
3) Проверка теста. Ответы проверяют по компьютеру. (Слайд 8 приложения 1).
Командиры групп оценивают ответы членов групп в баллах – за каждый пример 1 балл, помогают находить ошибки. Затем учащиеся докладывают результаты выполнения работ по компьютеру.
III. Объяснение новой темы.
Разобрать решение системы уравнений по учебнику. Пример 6, страница 243.
Показать решение системы уравнений
Решение: область определения системы .
Так как , то 1 уравнение системы примет вид .
Из 2 уравнения системы по определению логарифма получим или .
Имеем систему уравнений
Решая ее, получим решение исходной системы.
1 ученик показывает решение данной системы уравнений на доске.
Ответ: (3; 6), (6; 3).
IV. Работа по теме.
Решить № 521: 1 группа решает а и б, 2 группа — в и г. После выполнения работы объясняют решения.
№529(а) – сильный ученик показывает решение на доске.
V. Итоги урока.
1. Рассказать, как решаются системы, составленные из логарифмических уравнений?
2. Выставление оценок.
VI. Домашнее задание. (Слайд 9 приложения 1)
П. 39, № 522(а). Задание по карточкам: Решить систему уравнений
Индивидуальные задания для сильных учащихся: Из задания ЕГЭ – Часть 2, С1. Решить систему уравнений
9.05.2010
Поделиться страницей:urok.1sept.ru
Решение систем логарифмических уравнений — АЛГЕБРА — Уроки для 10 классов — конспекты уроков — План урока — Конспект урока — Планы уроков
УРОК 59
Тема. Решение систем логарифмических уравнений
Цель урока. Формирование умений учащихся решать системы логарифмических уравнений.
И. Проверка домашнего задания
Проводится коллективное обсуждение выполнения домашних упражнений по записям решения упражнений№ 52 (9; 11), 53 (12), 54 (2; 7), подготовленными к началу урока.
II. Самостоятельная работа
Вариант 1
Решите уравнение:
а) lg(x2 — 2х) = lg(2x + 12). (3 балла)
б) хlgх = 10. (3 балла)
в) log4 x + 3log4 x = 7. (3 балла)
г) log2 (x2 + 4x + 1) + 1 = log2(6x + 2). (3 балла)
Вариант 2
Решить уравнение:
а) lg(2×2 + 3x) = lg(6x + 2). (3 балла)
б) xlgx = 10 000. (3 балла)
в) log9 x + 2log9x = 5. (3 балла)
г) log2 (x2 — 3) + 1 = log2(6x — 10). (3 балла)
Ответы: В-1. а) 6; -2; б) 10; 0,1; в) 4; г) 0.
В-2. а) 2; б) 100; 0,01; в) 9; г) 2.
III. Решение систем логарифмических уравнений
При решении систем логарифмических уравнений используют те же способы, что и при решении алгебраических систем. Рассмотрим примеры.
Пример 1. Решите систему уравнений:
Решение
Добавим и вычтем почленно уравнения системы, тогда получим:
Ответ: (106; 10-1).
Пример 2. Решите систему уравнений
Решение
Тогда имеем или .
Проверкой убеждаемся, что(9; 7), (7; 9) — развязки системы.
Ответ: (9; 7), (7; 9).
IV. Формирование умений решать системы логарифмических уравнений
Решение упражнений№ 55 (3; 4), 56 (2; 4), 57 (2).
V. Подведение итогов урока
VI. Домашнее задание
Раздел V § 3. Вопросы и задания для повторения раздела V № 32. Упражнения№ 55 (1; 2), 56 (1, 3). Повторить свойства логарифмической функции.
na-uroke.in.ua
Решение систем логарифмических и показательных неравенств с репетитором

До сдачи ЕГЭ по математике остается все меньше времени. Обстановка накаляется, нервы у школьников, родителей, учителей и репетиторов натягиваются все сильнее. Снять нервное напряжение вам помогут ежедневные углубленные занятия по математике. Ведь ничто, как известно, так не заряжает позитивом и не помогает при сдаче экзаменов, как уверенность в своих силах и знаниях. Сегодня репетитор по математике расскажет вам о решении систем логарифмических и показательных неравенств, заданий, традиционно вызывающих трудности у многих современных старшеклассников.
Для того, чтобы научиться решать задачи C3 из ЕГЭ по математике как репетитор по математике рекомендую вам обратить внимание на следующие важные моменты.
1. Прежде чем приступить к решению систем логарифмических и показательных неравенств, необходимо научиться решать каждый из этих типов неравенств в отдельности. В частности, разобраться с тем, как находится область допустимых значений, проводятся равносильные преобразования логарифмических и показательных выражений. Некоторые связанные с этим тайны вы сможете постичь, изучив статьи «Решение задач C3 ЕГЭ по математике — логарифмические уравнения и неравенства» и «Решение задач C3 ЕГЭ по математике с репетитором — показательные уравнения и неравенства».
2. При этом необходимо осознавать, что решение системы неравенств не всегда сводится к решению отдельно каждого неравенства и пересечению полученных промежутков. Иногда, зная решение одного неравенства системы, решение второго значительно упрощается. Как репетитор по математике, занимающийся подготовкой школьников к сдаче выпускных экзаменов в формате ЕГЭ, раскрою в этой статье парочку связанных с этим секретов.
3. Необходимо четко уяснить для себя разницу между пересечением и объединением множеств. Это одно из важнейших математических знаний, которое опытный профессиональный репетитор старается дать своему ученику уже с первых занятий. Наглядное представление о пересечении и объединении множеств дают так называемые «круги Эйлера».
Пересечением множеств называется множество, которому принадлежат только те элементы, которые есть у каждого из этих множеств.Другими словами, если даны два множества и то их пересечением будет являться множество следующего вида:
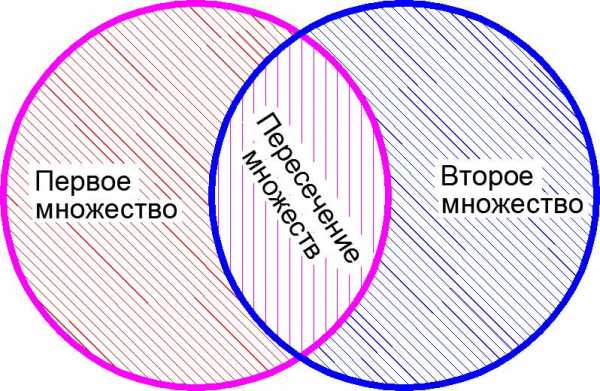
Изображение пересечения множеств с помощью «кругов Эйлера»
Объяснение на пальцах. У Дианы в сумочке находится «множество», состоящее из {ручки, карандаша, линейки, тетрадки, расчески}. У Алисы в сумочке находится «множество», состоящее из {записной книжки, карандаша, зеркальца, тетрадки, котлеты по-киевски}. Пересечением этих двух «множеств» будет «множество», состоящее из {карандаша, тетрадки}, поскольку оба этих «элемента» есть и у Дианы, и у Алисы.
Объединением множеств называется множество, которое состоит из всех элементов исходных множеств.Другими словами, если даны два множества и то их объединением будет являться множество следующего вида:

Изображение объединения множеств с помощью «кругов Эйлера»
Объяснение на пальцах. Объединением «множеств», взятых в предыдущем примере будет «множество», состоящее из {ручки, карандаша, линейки, тетрадки, расчески, записной книжки, зеркальца, котлеты по-киевски}, поскольку оно состоит из всех элементов исходных «множеств». Одно уточнение, которое может оказаться не лишним. Множество не может содержать в себе одинаковых элементов.
Перейдем непосредственно к примерам.
Пример 1. Решите систему неравенств:
Решение задачи C3.
1. Решаем сперва первое неравенств. Используя замену переходим к неравенству:
Переходим к обратной подстановке:
yourtutor.info
