Основание — высота — Большая Энциклопедия Нефти и Газа, статья, страница 1
Основание — высота
Cтраница 1
Основание высоты — точка 01 — есть центр основания пирамиды, следовательно, она является точкой пересечения его медиан. [1]
Основания высот некоторого остроугольного треугольника соединены прямыми. Доказать, что биссектрисы углов нового треугольника содержат высоты исходного. [2]
Основания высот ( остроугольного) треугольника соединены между собой. [3]
Основания высот некоторого остроугольного треугольника соединены прямыми. Доказать, что биссектрисами углов нового треугольника являются высоты исходного. [4]
Основание высоты, проведенной из вершины прямого угла, делит гипотенузу на два отрезка. На меньшем из отрезков как на диаметре построена полуокружность по одну сторону с данным треугольником. [5]
Основание D высоты CD лежит на стороне АВ, длина отрезка AD равна длине стороны ВС. [6]
Основание D высоты CD лежит на стороне АВ. Найти длину высоты АЕ, которая опущена из вершины А на сторону ВС. [7]
Основание D высоты CD лежит на стороне АВ, длина отрезка AD равна длине стороны ВС. [8]
Основание D высоты СЬ лежит на стороне АВ, длина отрезка AD равна длине стороны ВС. [9]
Основание D высоты CD лежит на стороне АВ. Найти длину высоты АЕ, которая опущена из вершины А на сторону ВС. [10]
Основание D высоты CD лежит на стороне АВ, длина отрезка AD равна длине стороны ВС. [11]
Основания высот остроугольного треугольника соединены между собой. [12]
Основание D высоты CD лежит на стороне АВ, длина отрезка AD равна длине стороны ВС. [13]
Основание высоты правильной четырехугольной пирамиды ( рис. 259 6) находим как точку пересечения диагоналей параллелограмма, изображающего основание этой пирамиды — квадрат ABCD. Аналогично находится на рисунке правильной шестиугольной пирамиды ( рис. 259, в) основание ее высоты. [14]
Основание высоты правильной четырехугольной пирамиды ( рис. 259, б) находим как точку пересечения диагоналей параллелограмма, изображающего основание этой пирамиды — квадрат ABCD. Аналогично находится на рисунке правильной шестиугольной пирамиды ( рис. 259, в) основание ее высоты. [15]
Страницы: 1 2 3 4
www.ngpedia.ru
Основание — высота — Большая Энциклопедия Нефти и Газа, статья, страница 3
Основание — высота
Cтраница 3
Искомый треугольник получим, соединяя основания высот. [31]
Докажите, что середины сторон и основания высот этого треугольника являются шестью вершинами правильного семиугольника. [32]
Доказать, что середины его сторон и основания высот являются шестью вершинами правильного семиугольника. [33]
Докажем сначала, что в тупоугольном треугольнике основание высоты, проведенной из вершины тупого угла, лежит на стороне треугольника. [34]
Докажем теперь, что в тупоугольном треугольнике основание высоты, проведенной из вершины острого угла, лежит на продолжении стороны треугольника. [35]
Докажите, что середины сторон треугольника, основания высот и середины отрезков, соединяющих точку пересечения высот с вершинами, лежат на одной окружности ( окружности девяти точек), причем центром этой окружности является середина отрезка ОН. [36]
Найти площадь треугольника, вершинами которого служат основания высот данного треугольника. [37]
Я должна совпадать с точкой Q — основанием высоты боковой грани ASB, опущенной из S на АВ. [38]
Найти величины углов треугольника с вершинами в основаниях высот
Найдите вектор ВМ, где точка М есть основание высоты, проведенной из вершины В. [40]
Найдите вектор ВМ, где точка М есть основание высоты, проведенной из вершины В. [41]
Через ортоцентр ( точку пересечения высот) и основания высот, опущенных на стороны АВ и ВС, проведена окружность. [42]
А А2, через Яь 2 Н3 — основания высот, проведенных из вершин Ль А2, А3, через Н — ортоцентр, через / Сь / С2 Кз — середины отрезков Л4Я, А2Н, Л3Я и через S — центр описанной окружности. [43]
Сами точки D, Е, F называются основаниями высот. [44]
Следовательно, придется построить сечение пирамиды, проходящее через основание высоты и перпендикулярное к боковому ребру пирамиды. [45]
Страницы: 1 2 3 4
www.ngpedia.ru
Высота основания правильной треугольной пирамиды равна 9
Задача.
Высота основания правильной треугольной пирамиды равна 9 см, а высота ее боковой грани, которая проведена к ребру основания, равна корню квадратному из 73 см. Найти боковое ребро пирамиды.
Решение.
Построим пирамиду МАВС, в основании которой лежит треугольник. Проведем в ее основании высоту СЕ, которая по условию равна 9 см.
Из вершины М пирамиды проведем к ребру основания высоту боковой грани МЕ, которая по условию равна корень из 73 см.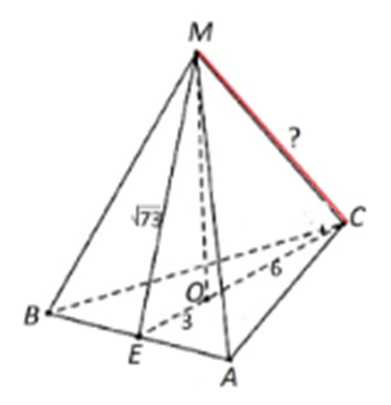
У правильной пирамиды основание высоты совпадает с центром О вписанной окруж-сти, то есть с точкой пересечения биссектрис, медиан и высот прав-ного треуг-ника.
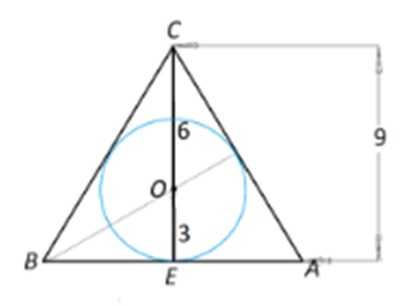
Согласно свойства медиан такая точка делит их в соотношении 2 к 1, начиная от вершины. Таким образом, отрезок ОЕ равен 1/3 СЕ:
ОЕ = 9 : 3 = 3 (см).
Найдем ОС:
ОС = СЕ — ОЕ = 9 — 3 = 6 (см).
Рассмотрим прямоугольный треугольник МЕО. Применим к нему теорему Пифагора и вычислим длину высоты МО пирамиды:
(см).
Рассмотрим прямоугольный треугольник МСО. Применим к нему теорему Пифагора и вычислим длину бокового ребра МС пирамиды:
(см).
Ответ. 10 см.
ru.solverbook.com
Основание — высота — Большая Энциклопедия Нефти и Газа, статья, страница 2
Основание — высота
Cтраница 2
Основание высоты правильной четырехугольной пирамиды ( рис. 242, б) находим как точку пересечения диагоналей параллелограмма, изображающего основание этой пирамиды-квадрат ABCD. Аналогично находится на рисунке правильной шестиугольной пирамиды ( рис. 242, в) основание ее высоты. [16]
Основание высоты правильной четырехугольной пирамиды ( рис. 242, б) находим как точку пересечения диагоналей параллелограмма, изображающего основание этой пирамиды — квадрат ABCD. Аналогично находится на рисунке правильной шестиугольной пирамиды ( рис. 242, в) основание ее высоты. [17]
Основание высоты правильной четырехугольной пирамиды ( рис. 259, б) находим как точку пересечения диагоналей параллелограмма, изображающего основание этой пирамиды — квадрат ABCD. Аналогично находится на рисунке правильной шестиугольной пирамиды ( рис., 259, в) основание ее высоты. [18]
Основанием высоты, опущенной из вершины S, является точка О, лежащая внутри треугольника ABC. Расстояния от точки О до сторон АВ, ВС и С А находятся в отношении 2: 1: 3 соответственно. [19]
Основанием высоты, опущенной из вершины S, является точка О, лежащая внутри треугольника ЛВС. [20]
Основанием высоты, опущенной из вершины S, является точка О, лежащая внутри треугольника ABC. Расстояния от точки О до сторон АВ, ВС и СА находятся в отношении 2: 1: 3 соответственно. [21]
Основанием высоты, опущенной из вершины 5, является точка О, лежащая внутри треугольника ABC. [22]
Основанием высоты, опущенной из вершины S, является точка О, лежащая внутри треугольника ABC. [23]
Основанием высоты правильной пирамиды согласно определению является центр основания этой пирамиды. Центр правильного треугольника ABC совпадает с точкой пересечения его медиан. В соответствии с этим на рис. 259, а построены медианы AM и BN. [24]
Основанием высоты правильной пирамиды согласно определению является центр основания этой пирамиды. [25]
Основанием высоты правильной пирамиды согласно определению является центр основания этой пирамиды. Центр правильного треугольника ЛВС совпадает с точкой пересечения его медиан. В соответствии с этим на рис. 259, а построены медианы AM и BN. [26]
Из основания высоты призмы О проводим перпендикуляр ОМ на AS и по условию СШ & ( черт. Из точки В проводим перпендикуляр BE и соединяем точки Е и С. [27]
Если основание высоты кругового конуса совпадает с центром круга, лежащего в основании конуса, то конус называется прямым круговым. [28]
Пусть Н — основание высоты, опущенной из вершины В, В % — середина стороны АС. [29]
Докажите, что отрезки, соединяющие основания высот остроугольного треугольника, образуют треугольник, в котором эти высоты являются биссектрисами. [30]
Страницы: 1 2 3 4
www.ngpedia.ru
Основание — высота — треугольник
Основание — высота — треугольник
Cтраница 1
Основание D высоты CD треугольника ABC лежит на стороне АВ, причем AD — ВС. [1]
Если основания высот треугольника соединим прямыми, то получим новый треугольник, для которого высоты первого треугольника служат биссектрисами. [2]
Множество оснований высот треугольников ABC есть дуга окружности, построенной на отрезке AM, как на диаметре. [3]
Обозначим через D основание высоты BD треугольника ЛВС, опущенной из вершины В на сторону ЛС. Треугольник ЛВС равнобедренный, поэтому BD есть биссектриса утла ЛВС. Так как окружность касается сторон ЛВ и ВС, то ее центр лежит на прямой ВО, и так как BD J ЛС, то окружность касается стороны ЛС в точке D. [4]
Доказать, что прямые, соединяющие основания высот треугольника, ограничивают новый треугольник, в котором эти высоты являются биссектрисами. [5]
Доказать, что прямые, соединяющие основания высот треугольника, ограничивают треугольник, для которого высоты данного треугольника оказываются биссектрисами. [6]
Рассматриваемые окружности проходят через основания высот треугольника, а значит, точки их пересечения лежат на сторонах треугольника. [7]
Доказать, что если основания высот треугольника соединить, то получим треугольник, для которого эти высоты будут биссектрисами. [8]
Докажите, что проекции основания высоты треугольника на стороны, ее заключающие, и на две другие высоты лежат на одной прямой. [9]
Пусть PQR — треугольник, образованный основаниями высот треугольника ABC, P Q R — любой другой треугольник, вписанный в треугольник ABC. [10]
Докажем, что h есть аффикс ортоцентра треугольника AhBhCh, образованного основаниями высот дандого треугольника. [11]
Если Я 1, то точки Р, Q, R совпадают соответственно с основаниями высот треугольника ЛВС. [12]
Доказать, что радиус описанной около треугольника окружности, проведенный в вершину треугольника, перпендикулярен прямой, соединяющей основания высот треугольника, проведенных из двух других его вершин. [13]
Покажите предварительно, что стороны любого треугольника ABC являются биссектрисами внешйих углов в треугольнике, вершинами которого служат основания высот треугольника ABC ( ср. Для возможности решения данные прямые должны образовывать остроугольный треугольник. [14]
Доказать, что радиус описанной около треугольника окружности, проведенный в вершину треугольника, перпендикулярен к прямой, соединяющей основания высот треугольника, проведенных из двух других его вершин. [15]
Страницы: 1 2
www.ngpedia.ru
Высота равнобедренного треугольника | Онлайн калькулятор
Равнобедренным треугольником называется такой треугольник, у которого две из трех сторон равны между собой. Равные стороны считаются боковыми сторонами а, а третья сторона в называется основанием равнобедренного треугольника.
Соответственно, в таком треугольнике можно провести три высоты, две из которых будут равны между собой, аналогично сторонам — это высоты, опущенные на боковую сторону треугольника а, а третья высота опускается на основание. Высота треугольника проводится из угла треугольника к противолежащей стороне под прямым углом. Большинство задач с высотой треугольника решаются через прямоугольные треугольники, которые она образует.
Рассмотрим каждый случай по отдельности.
Высота равнобедренного треугольника, опущенная на основание, обладает рядом индивидуальных свойств, присущих только ей и не распространяющихся на другие высоты в таком треугольнике. В частности, высота, проведенная к основанию равнобедренного треугольника, совпадает с медианой и биссектрисой, проведенным к основанию, следовательно, она не только образует прямой угол с основанием, но и делит его на две равные части, как медиана, и аналогично делит угол пополам, как биссектриса. В итоге, высота является своеобразной осью симметрии треугольника и разделяет его на два конгруэнтных прямоугольных треугольника. В таком треугольнике высота является катетом, и чтобы найти ее длину необходимо соотнести стороны равнобедренного треугольника со сторонами прямоугольного. Боковая сторона равнобедренного треугольника становится гипотенузой, а чтобы определить второй катет, основание равнобедренного треугольника нужно разделить пополам, по свойству медианы.
Длина высоты равнобедренного треугольника равна по теореме Пифагора квадратному корню из суммы квадрата боковой стороны равнобедренного треугольника и четверти квадрата основания равнобедренного треугольника:
Второй случай, когда условиями задачи нужно найти высоту, опущенную на боковую сторону равнобедренного треугольника, раскрывается проще всего через площадь треугольника.
Площадь любого треугольника можно найти несколькими способами — например, через три стороны треугольника по формуле Герона, или через высоту, умножив ее на половину стороны, на которую она опущена. И тем, и другим способом получаются одинаковые значения площади, следовательно обе эти формулы можно друг к другу приравнять и отсюда вывести окончательную формулу высоты, опущенную на боковую сторону равнобедренного треугольника.
Формула Герона для равнобедренного треугольника будет иметь несколько упрощенный вид за счет того, что значения боковых сторон повторяются:
Площадь равнобедренного треугольника через высоту, опущенную к боковой стороне
Эту же формулу можно применять для нахождения любой высоты в равнобедренном треугольнике, если поменять в формуле соответствующие стороны местами.
Формула высоты равнобедренного треугольника через боковую сторону и угол при основании α: h=a sinα
Формула через боковую сторону и угол напротив основания β:
Формула через основание и угол при нем α:
через основание и угол противолежащий ему β:
allcalc.ru
Основание — высота — пирамида
Основание — высота — пирамида
Cтраница 1
Основание высоты пирамиды совпадает с центром ромба. [1]
Основание высоты пирамиды совпадает с центром окружности, вписанной в основание пирамиды. [2]
Основание высоты пирамиды лежит вне пирамиды и от двух вершин основания удалено одинаково, а от третьей вершины находится на расстоянии, вдвое меньшем, чем от первых двух вершин. [3]
Основанием высоты пирамиды служит центр вписанной в основание пирамиды окружности, центр сферы лежит на продолжении высоты пирамиды. [4]
Соединим основание высоты пирамиды с точками А, В, С, D и спроектируем полученные отрезки на стороны основания. Пусть а, 6, с, d — длины этих проекций, h — высота пирамиды, х — искомое боковое ребро. [5]
Через основание высоты пирамиды проводим высоту ромба ME и соединяем точки М и Е с S ( черт. [6]
Точка О — основание высоты пирамиды, по доказанному есть цсьтр вписанной окружности. [7]
Точка О — основание высоты пирамиды, по доказанному есть центр вписанной окружности. [8]
Точка О — основание высоты пирамиды — по доказанному есть центр впнсапной окружности. [9]
Из условия задачи следует, что основание высоты пирамиды будет находиться на пересечении диагоналей прямоугольника, так как боковые ребра пирамиды наклонены под одинаковыми углами к основанию ( черт. [10]
Доказать, что если в основание пирамиды можно вписать окружность, а основание высоты пирамиды является центром этой окружности, то в пирамиду можно вписать сферу. [11]
Доказать, что если в основание пирамиды можно вписать окружность, а основание высоты пирамиды является центром этой окружности, то в пирамиду можно вливать сферу. [12]
Доказать, что если в основание пирамиды можно вписать окружность, а основание высоты пирамиды является центром этой окружности, то в пирамиду можно вписать сферу. [13]
Найти площадь грани BCD, если сечение DKM имеет площадь q, a основание высоты пирамиды попадает в точку пересечения медиан основания АСВ. [14]
Пирамидаможет не быть правильной, но если цилиндр в нее вписан, то основание высоты пирамиды должно лежать внутри многоугольника основания, а сам многоугольник основания должен быть таким, что в него можно вписать окружность. [15]
Страницы: 1 2 3
www.ngpedia.ru
