Мат статистика и теория вероятности – САФУ — Ошибка 404: такой страницы не существует

Содержание

ПРЕДМЕТ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ — Мегаобучалка

ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Необходимость освоения будущими бакалаврами менеджмента теории вероятностей и математической статистики продиктована широким использованием математических методов в современной экономической практике. Полученные математические знания делают возможным изучение прикладных и экономических наук, грамотное общение с компьютером.

Теоретический материал приведен только тот и в том объеме, который необходим для решения предлагаемых в контрольной работе задач. Каждая тема иллюстрирована большим количеством примеров, контрольная работа снабжена образцом ее выполнения.

Контрольная работа должна быть выполнена в срок (по графику учебного процесса до начала экзаменационной сессии) и оформлена в тетради в клетку. Титульный лист оформляется согласно приложению 4.

При выполнении контрольной работы студент должен придерживаться следующих требований:

— перед началом решения задачи необходимо написать полный текст условия задачи;

— решение задачи следует снабжать подробными пояснениями, расчёты по формулам должны быть приведены полностью, без сокращений;

— в задачах по математической статистике для получения правильного результата необходимо проводить промежуточные вычисления с достаточно высокой точностью (до 3 значащих цифр после запятой).

Перед решением заданий контрольной работы рекомендуется ознакомиться со всеми примерами, рассмотренными в данной работе. По каждому заданию контрольной работы в методических указаниях приводится основной теоретический материал и разбирается несколько типовых примеров.

Содержание

1 Предмет теории вероятностей и математической статистики. 4

2 Случайные события. 7

2.1. Испытания и события. 7

2.2. Виды событий. 7

2.3. Классическое определение вероятности. 9

2.4. Основные формулы комбинаторики. 10

2.5. Произведение и сумма событий. 12

2.6. Условная вероятность. вероятность произведения событий. 12

2.7. Вероятность суммы событий. 14

2.8. Формула полной вероятности. 17

2.9. Формула Байеса. 18

2.10. Последовательности испытаний. Формула Бернулли. 19

2.11. Предельные теоремы в схеме Бернулли. 21

3 Случайные величины.. 23

3.1. Понятие случайной величины.. 23

3.2. Закон распределения дискретной случайной величины.. 24

3.3. Функция распределения. 25

3.4. Вероятность попадания случайной величины на заданный интервал. 27

3.5. Плотность распределения. 28

3.6. Числовые характеристики случайной величины

.. 30

3.7. Примеры дискретных распределений. 34

3.8. Примеры непрерывных распределений. 35

4 Элементы математической статистики. 40

4.1. Выборочный метод. 41

4.1.1. Генеральная совокупность и выборочная. 41

4.1.2. Вариационный ряд. полигон частот и гистограмма эмпирическая функция распределения 42

4.2. Статистическое оценивание. 46

4.2.1. Оценка параметров генеральной совокупности. точечная оценка и ее свойства 46

4.2.2. Оценка с помощью интервалов. 50

4.3. Проверка статистических гипотез. 52

4.3.1 Проверка гипотез о виде распределения. критерий согласия Пирсона. 55

5 Контрольная работа. часть 1. 59

6 Контрольная работа. часть 2. 85

6.1. Пример выполнения контрольной работы.. 94

приложение 1. 102

приложение 2. 103

приложение 3. 105

приложение 4. 106

ПРЕДМЕТ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

Теория вероятностей – это математическая дисциплина, изучающая закономерности массовых случайных явлений.

Теория вероятностей не может предсказать результат отдельного опыта со случайными исходами, но она достаточно надежно предсказывает результат большого числа таких опытов.

Основными объектами изучения в теории вероятностей являются случайные события и случайные величины.

Случайное событие – это качественное понятие. Событие либо происходит, либо не происходит. Случайная величина – понятие количественное: в результате опыта случайная величина принимает одно из множества своих возможных значений.

Не все случайные явления (эксперименты) можно изучать методами теории вероятностей, а лишь те, которые могут быть воспроизведены в одних и тех же условиях. Случайность и хаос — не одно и то же. Оказывается, что и в случайных экспериментах наблюдаются некоторые закономерности, например, свойство статистической устойчивости: доля экспериментов, в которых рассматриваемое событие произошло, имеет тенденцию стабилизироваться с ростом общего числа экспериментов, приближаясь к некоторому числу. Это число служит объективной характеристикой степени возможности событию произойти.

Математической статистикой называется раздел прикладной математики, изучающий методы сбора, обработки и анализа статистических данных для научных и практических целей. Математическая статистика занимается изучением закономерностей, которым подчиняются массовые явления, на основе результатов наблюдений.

Предметом исследования в математической статистике

является совокупность объектов, однородных относительно некоторых признаков, например, мальчики 12 лет г.Томска; бегуны – мастера спорта России.

Приведем примеры применения теории вероятностей и математической статистики.

Пример 1.1. Из разговора заводских менеджеров: «мастерская дает двадцать три процента брака». Одна единица продукции не может быть дефектна на 23%. Она может быть либо годной, либо дефектной. Видимо, имеется в виду, что в партии большого объема содержится примерно 23% дефектных единиц продукции. Тогда возникает вопрос, а что значит «примерно»? Если из 100 проверенных единиц продукции 30 окажутся дефектными, или из 1000 – 300, или из 100000 – 30000 и т.д., то как оценить это «примерно»?

Пример 1.2. Контроль качества любой продукции. Чтобы решить, соответствует или не соответствует контролируемая партия продукции установленным требованиям, из нее отбирается выборка. По результатам контроля выборки делается заключение о всей партии. В этом случае очень важно избежать субъективизма при формировании выборки, т.е. необходимо, чтобы каждая единица продукции в контролируемой партии имела одинаковую вероятность быть отобранной в выборку. В производственных условиях отбор единиц продукции в выборку обычно осуществляют не с помощью жребия, а по специальным таблицам случайных чисел или с помощью компьютерных датчиков случайных чисел.

Похожие проблемы обеспечения объективности сравнения возникают при сопоставлении различных схем организации производства, оплаты труда, при проведении тендеров и конкурсов, подбора кандидатов на вакантные должности и т.п. Всюду нужна жеребьевка или подобные ей процедуры.

Пример 1.3. При любом измерении единиц продукции (с помощью штангенциркуля, микрометра, амперметра и т.п.) имеются погрешности. Чтобы выяснить, есть ли систематические погрешности, необходимо сделать многократные измерения единицы продукции, характеристики которой известны (например, стандартного образца). При этом следует помнить, что кроме систематической погрешности присутствует и случайная погрешность.

Поэтому встает вопрос, как по результатам измерений узнать, есть ли систематическая погрешность. Если отмечать только, является ли полученная при очередном измерении погрешность положительной или отрицательной, то, сопоставив измерение с бросанием монеты (положительную погрешность – с выпадением герба, отрицательную – решетки (нулевая погрешность при достаточном числе делений шкалы практически никогда не встречается)), сведем задачу проверки отсутствия систематической погрешности к проверке симметричности монеты.

Пример 1.4. При статистическом регулировании технологических процессов на основе методов математической статистики разрабатываются правила и планы статистического контроля процессов, направленные на своевременное обнаружение разладки технологических процессов и принятия мер к их наладке и предотвращению выпуска продукции, не соответствующей установленным требованиям. Эти меры нацелены на сокращение издержек производства и потерь от поставки некачественных единиц продукции. При статистическом приемочном контроле на основе методов математической статистики разрабатываются планы контроля качества путем анализа выборок из партий продукции. Сложность заключается в том, чтобы уметь правильно строить вероятностно-статистические модели принятия решений. В математической статистике для этого разработаны вероятностные модели и методы проверки гипотез, в частности, гипотез о том, что доля дефектных единиц продукции равна определенному числу

р₀, например, р₀ = 0.23 (см. пример 1.1).

СЛУЧАЙНЫЕ СОБЫТИЯ

Испытания и события

Случайным событием (или просто событием) называется любой факт, который может иметь место при наличии определенной совокупности условий.

Каждое осуществление требуемой совокупности условий называется испытанием или опытом.

События, которые могут произойти в результате испытания, называются исходами данного испытания. События принято обозначать заглавными (прописными) буквами начала латинского алфавита: А, В, С и т.д. Словесное описание события часто дается в такой форме:

А = {выпадение «орла» при бросании монеты}.

Виды событий

В теории вероятностей различают виды событий.

Достоверное событие. Так называют событие, которое обязательно происходит в результате испытания.

Невозможное событие – событие, которое не может произойти в данном испытании.

Совместные и несовместные события. Два события называются несовместными, если они не могут произойти вместе в одном испытании, в противном случае их называют совместными. События А₁, А₂

, …, А_n, называют попарно несовместными, если никакие два из них не могут произойти вместе в одном испытании.

Противоположным событию А называется событие `А, состоящее в непоявлении события А. Очевидно, что события А и `А являются несовместными.

Говорят, что события А₁, А₂ ,…,А_nв некотором испытании образуют полную группу, если в результате испытания обязательно должно произойти хотя бы одно из них.

Условимся полную группу несовместных исходов называть пространством элементарных событий.

Пример 2.1.Достоверным является событие А = {извлечение белого шара из урны, где все шары белые}.

Невозможным является событие B = {извлечение белого шара из урны, где все шары черные}.

Практически невозможное событие: C1={найти иголку в стоге сена}; C2=={вытащить белый шар из урны, где 1000 шаров черные, а 1 – белый}

Практически достоверное событие: D={вытащить белый шар из урны, где 999 шаров белые, а 1 – черный};

Пример 2.2.Испытание состоит в бросании игральной кости. Рассматриваем события:

А = {выпадение двух очков};

В = {выпадение трех очков};

С = {выпадение четного числа очков}.

События А и В, а также В и С являются несовместными. События А и С – совместные. Попарно несовместными события А, В, С не являются.

Пример 2.3.Производится бросание игральной кости.

А = {выпадение шести очков};

`А = {выпадение любого числа очков, кроме шести}.

Пример 2.4.Производится бросание монеты. Полную группу образуют события А = {выпадение «орла»}, В = {выпадение «решки»}.

megaobuchalka.ru

Теория вероятностей и математическая статистика. Обзорная лекция

для студентов 2 курса всех специальностей

Кафедра Высшей математики

Автор: к.э.н., проф. Н. Ш. Кремер

Вводная часть

Уважаемые студенты!

Вашему вниманию предлагается обзорная (установочная) лекция профессора Н.Ш.Кремера по дисциплине «Теория вероятностей и математическая статистика» для студентов второго курса ВЗФЭИ.

В лекции обсуждаются задачи изучения теории вероятностей и математической статистики в экономическом вузе и ее место в системе подготовки современного экономиста, рассматривается организация самостоятельной работы студентов с использованием компьютерной обучающей системы (КОПР) и традиционных учебников, даются обзор основных положений данного курса, а также методические рекомендации по ее изучению.

Среди математических дисциплин, изучаемых в экономическом вузе, теория вероятностей и математическая статистика занимает особое положение. Во-первых, она является теоретической базой статистических дисциплин. Во-вторых, методы теории вероятностей и математической статистики непосредственно используются при изучении массовых совокупностей наблюдаемых явлений, обработке результатов наблюдений и выявлении закономерностей случайных явлений. Наконец, теория вероятностей и математическая статистика имеет важное методологическое значение в познавательном процессе, при выявлении общей закономерности исследуемых процессов, служит логической основой индуктивно-дедуктивного умозаключения.

Каждый студент второго курса должен иметь следующий набор (кейс) по дисциплине «Теория вероятностей и математическая статистика»:

1. Обзорную установочную лекцию по данной дисциплине.

2. Учебник Н.Ш. Кремера «Теория вероятностей и математическая статистика» – М.: ЮНИТИ – ДАНА, 2007 (в дальнейшем будем называть просто «учебник»).

3. Учебно-методическое пособие «Теория вероятностей и математическая статистика»/ под ред. Н.Ш. Кремера. – М.: Вузовский учебник, 2005 (в дальнейшем «пособие»).

4. Компьютерную обучающую программу КОПР по дисциплине (в дальнейшем – «компьютерная программа»).

На сайте института на странице «Корпоративные ресурсы» размещены интернет-версии компьютерной программы КОПР2, обзорной установочной лекции и электронной версии пособия. Кроме того, компьютерная программа и пособие представлены на CD — ROM ах для студентов второго курса. Поэтому в «бумажном виде» студенту необходимо иметь лишь учебник.

Поясним назначение каждого из учебно-методических материалов, входящий в указанный набор (кейс).

В учебнике изложены основные положения учебного материала дисциплины, иллюстрируемые достаточно большим числом решенных задач.

В пособии даны методические рекомендации по самостоятельному изучению учебного материала, выделены наиболее важные понятия курса и типовые задачи, даны контрольные вопросы для самопроверки по данной дисциплине, приведены варианты домашних контрольных работ, которые должен выполнить студент, а также методические указания по их выполнению.

Компьютерная программа призвана оказать Вам максимальную помощь в усвоении курса в режиме диалога программы со студентом с тем, чтобы в наибольшей степени восполнить отсутствие у Вас аудиторных занятий, соответствующего контакта с преподавателем.

Для студента, обучающегося по системе дистанционного обучения, первостепенное, определяющее значение имеет организация самостоятельной работы.

Приступая к изучению данной дисциплины, прочтитедо конца настоящую обзорную (установочную) лекцию. Это позволит Вам получить в целом представление об основных понятиях и методах, используемых в курсе «Теория вероятностей и математическая статистика», и требованиях, предъявляемых к уровню подготовки студентов ВЗФЭИ.

Перед изучением каждой темы ознакомьтесь с методическими рекомендациями к изучению данной темы по пособию. Здесь Вы найдете перечень учебных вопросов данной темы, которые Вам предстоит изучить; выясните, какие понятия, определения, теоремы, задачи являются наиболее важными, которые надо изучить и освоить в первую очередь.

Затем перейдите к изучению основного учебного материала по учебнику в соответствии с полученными методическими рекомендациями. Советуем конспектировать в отдельной тетради основные определения, формулировки теорем, схемы их доказательств, формулы и решения типовых задач. Формулы целесообразно выписывать в специальные таблицы для каждой части курса: теория вероятностей и математическая статистика. Регулярное пользование конспектом, в частности, таблицами формул, способствует их запоминанию.

Лишь после проработки основного учебного материала каждой темы по учебнику можно перейти к изучению этой темы с помощью компьютерной обучающей программы (КОПР2).

Обратите внимание на структуру построения компьютерной программы по каждой теме. После названия темы приводится перечень основных учебных вопросов темы по учебнику с указанием номеров параграфов и страниц, которые необходимо изучить. (Напомним, что перечень этих вопросов по каждой теме приведен также и в пособии).

Затем в краткой форме дается справочный материал по данной теме (или по отдельным параграфам этой темы) – основные определения, теоремы, свойства и признаки, формулы и т.п. В процессе изучения темы Вы также можете вызвать на экран те фрагменты справочного материала (по данной или предыдущим темам), которые необходимы в данный момент.

Затем Вам предлагается учебный материал и обязательно типовые задачи ( примеры), решение которых рассматривается в режиме диалога программы со студентом. Функции ряда примеров ограничиваются выводом на экран по запросу обучаемого этапов правильного решения. Вместе с тем в процессе рассмотрения большинства примеров Вам будут задаваться вопросы того или иного характера. В качестве ответов на одни вопросы следует вводить с клавиатуры числовой ответ, на другие – выбирать правильный ответ (или ответы) из нескольких предложенных.

В зависимости от введенного Вами ответа программа подтверждает его правильность или предлагает, ознакомившись с подсказкой, содержащей необходимые теоретические положения, вновь попытаться дать правильные решение и ответ. Во многих заданиях установлено ограничение на количество попыток решения (при превышении этого ограничения на экран обязательно выводится правильный ход решения). Имеются и такие примеры, в которых количество информации, содержащееся в подсказке, возрастает по мере повторения неудачных попыток ответа.

После ознакомления с теоретическими положениями учебного материала и примерами, которые снабжены подробным разбором решения, Вы должны выполнить упражнения для самоконтроля, чтобы закрепить навыки решения типовых задач по каждой теме. Задания для самоконтроля также содержат элементы диалога со студентом. По завершению решения Вы можете ознакомиться с правильным ответом и сравнить его с тем, который Вы дали.

В завершение работы по каждой теме следует выполнить контрольные задания. Правильные ответы на них Вам не выводятся, а Ваши ответы записываются на жесткий диск компьютера для последующего ознакомления с ними преподавателя-консультанта (тьютора).

После изучения тем 1–7 Вы должны выполнить домашнюю контрольную работу № 3, а после изучения тем 8–11 – домашнюю контрольную работу № 4. Варианты указанных контрольных работ приведены в пособии (его электронной версии). Номер выполняемого варианта должен совпадать с последней цифрой номера Вашего личного дела (зачетной книжки, студенческого билета). По каждой контрольной работе Вы должны проходить собеседование, на котором необходимо показать умение решать задачи и знание основных понятий (определений, теорем (без доказательства), формул и т.п.) по теме контрольной работы. Завершается изучение дисциплины курсовым экзаменом.

Теория вероятностей – математическая наука, изучающая закономерности случайных явлений.

Предлагаемая для изучения дисциплина состоит из двух разделов «Теория вероятностей» и «Математическая статистика».

studfiles.net

Теория вероятностей и математическая статистика. Обзорная лекция

для студентов 2 курса всех специальностей

Кафедра Высшей математики

Автор: к.э.н., проф. Н. Ш. Кремер

Вводная часть

Уважаемые студенты!

В лекции обсуждаются задачи изучения теории вероятностей и математической статистики в экономическом вузе и ее место в системе подготовки современного экономиста, рассматривается организация самостоятельной работы студентов с использованием компьютерной обучающей системы (КОПР) и традиционных учебников, даются обзор основных положений данного курса, а также методические рекомендации по ее изучению.

Среди математических дисциплин, изучаемых в экономическом вузе, теория вероятностей и математическая статистика занимает особое положение. Во-первых, она является теоретической базой статистических дисциплин. Во-вторых, методы теории вероятностей и математической статистики непосредственно используются при изучении массовых совокупностей наблюдаемых явлений, обработке результатов наблюдений и выявлении закономерностей случайных явлений. Наконец, теория вероятностей и математическая статистика имеет важное методологическое значение в познавательном процессе, при выявлении общей закономерности исследуемых процессов, служит логической основой индуктивно-дедуктивного умозаключения.

Обзорную установочную лекцию по данной дисциплине.
Учебник Н.Ш. Кремера «Теория вероятностей и математическая статистика» – М.: ЮНИТИ – ДАНА, 2007 (в дальнейшем будем называть просто «учебник»).
Учебно-методическое пособие «Теория вероятностей и математическая статистика»/ под ред. Н.Ш. Кремера. – М.: Вузовский учебник, 2005 (в дальнейшем «пособие»).
Компьютерную обучающую программу КОПР по дисциплине (в дальнейшем – «компьютерная программа»).

На сайте института на странице «Корпоративные ресурсы» размещены интернет-версии компьютерной программы КОПР2, обзорной установочной лекции и электронной версии пособия. Кроме того, компьютерная программа и пособие представлены на CD — ROM ах для студентов второго курса. Поэтому в «бумажном виде» студенту необходимо иметь лишь учебник.

Поясним назначение каждого из учебно-методических материалов, входящий в указанный набор (кейс).

Компьютерная программа призвана оказать Вам максимальную помощь в усвоении курса в режиме диалога программы со студентом с тем, чтобы в наибольшей степени восполнить отсутствие у Вас аудиторных занятий, соответствующего контакта с преподавателем.

Приступая к изучению данной дисциплины, прочтите до конца настоящую обзорную (установочную) лекцию. Это позволит Вам получить в целом представление об основных понятиях и методах, используемых в курсе «Теория вероятностей и математическая статистика», и требованиях, предъявляемых к уровню подготовки студентов ВЗФЭИ.

Перед изучением каждой темы ознакомьтесь с методическими рекомендациями к изучению данной темы по пособию. Здесь Вы найдете перечень учебных вопросов данной темы, которые Вам предстоит изучить; выясните, какие понятия, определения, теоремы, задачи являются наиболее важными, которые надо изучить и освоить в первую очередь.

Затем перейдите к изучению основного учебного материала по учебнику в соответствии с полученными методическими рекомендациями. Советуем конспектировать в отдельной тетради основные определения, формулировки теорем, схемы их доказательств, формулы и решения типовых задач. Формулы целесообразно выписывать в специальные таблицы для каждой части курса: теория вероятностей и математическая статистика. Регулярное пользование конспектом, в частности, таблицами формул, способствует их запоминанию.

Затем Вам предлагается учебный материал и обязательно типовые задачи ( примеры), решение которых рассматривается в режиме диалога программы со студентом. Функции ряда примеров ограничиваются выводом на экран по запросу обучаемого этапов правильного решения. Вместе с тем в процессе рассмотрения большинства примеров Вам будут задаваться вопросы того или иного характера. В качестве ответов на одни вопросы следует вводить с клавиатуры числовой ответ, на другие – выбирать правильный ответ (или ответы) из нескольких предложенных.

Теория вероятностей – математическая наука, изучающая закономерности случайных явлений.

studfiles.net

Теория вероятности и математическая статистика

Федеральное агентство по образованию РФ

НОУ ВПО Международный университет бизнеса и новых технологий (академия)

Контрольная работа по теории организации и математической статистике

Вариант № 4

Выполнила: Спицина Н. Н.

Специальность: МН — 2

Задание 1

В коробке 12 зеленых, 5 красных, 6 синих карандашей. Из коробки наудачу берут три карандаша. Какова вероятность того, что все они будут синими? Рассмотреть случаи, когда карандаши: а) не возвращают в коробку; б) возвращают в коробку.

Решение:

а) Событие А – все три вынутые без возращения в коробку карандаши синие.

Согласно классическому определению вероятность события А равна:

В коробке 12+5+6=23 карандаша.

Общее число исходов равно:

Благоприятное число способов равно:

Ответ: вероятность того, что все три вынутые без возращения в коробку карандаши синие, равна 0,011.

б) Событие В – все три вынутые с возращением в коробку карандаши синие, то есть три раза будут выниматься 1 синий шар из 23.

Вероятность извлечения одного синего карандаша р = 6/23.

Воспользуемся схемой Бернулли:

q = 1-6/23=7/23

n = 3

m=3

Ответ: вероятность того, что все три вынутые с возращения в коробку карандаши синие, равна 0,018.

Задание 2

Из колоды в 32 карты наугад вынимают 5. Найти вероятность того, что среди них окажется ровно один туз.

Решение:

Событие А – из вынутых наугад 5 карт, ровно один туз.

Согласно классическому определению вероятность события А равна:

Пусть детали пронумерованы с 1 до 80, с 1 до 20 стандартные и с 21 по 80 не стандартные.

Общее число исходов равно:

Благоприятное исход состоит в том, что вынут 1 туз из 4-х возможных и 4 другие карты из оставшихся 28, таким образом, число благоприятных способов равно:

Ответ: вероятность того, что из вынутых наугад 5 карт, ровно один туз, равна 0,407.

Задание 3

Брак изделий цеха составляет 11%. Найти вероятность того, что из 250 изделий цеха окажется бракованными: а) ровно 45 изделий; б) от 145 до 155 изделий; в) не менее 101 изделий; г) не более 100 изделий.

Решение:

а) Вероятность того, что из 250 изделий цеха окажется бракованными ровно 45 изделий, найдем, используя локальную теорему Лапласа:

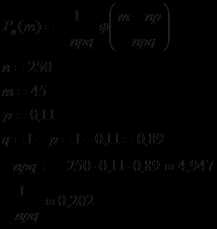
б) Вероятность того, что из 250 изделий цеха окажется бракованными от 145 до 155 изделий, найдем, используя интегральную теорему Лапласа:

где Ф – функция Лапласа (значения берутся из таблиц).

Подставляем:

в) Вероятность того, что из 250 изделий цеха окажется бракованными не менее 101 изделий, найдем, используя интегральную теорему Лапласа:

где Ф – функция Лапласа (значения берутся из таблиц).

Подставляем:

г) Вероятность того, что из 250 изделий цеха окажется бракованными не более 100 изделий, найдем, используя интегральную теорему Лапласа:

где Ф – функция Лапласа (значения берутся из таблиц).

Подставляем:

Задание 4

Радист трижды вызывает корреспондента. Вероятность того, что будет принят первый вызов, равна 0,2, второй вызов – 0,3, третий вызов 0,4. События, состоящие в том, что данный вызов будет услышан, независимы. Найти вероятность того, что корреспондент вообще услышит вызов.

Решение:

Событие А — корреспондент услышал вызов.

Событие Н1 — принят первый вызов.

Событие Н2 — принят второй вызов.

Событие Н3 — принят третий вызов.

Р( Н1 ) = 0,2, Р( Н2 ) = 0,3, Р( Н3 ) = 0,4.

Р (А / Н1) = 1/3; Р (А / Н2) = 1/3; Р( А/Н2 ) = 1/3.

Используя формулу полной вероятности, получим

Р( А ) = Р( А / Н1 ) · Р( Н1 ) + Р( А / Н2 ) · Р( Н2 ) + Р( А / Н3 ) · Р( Н3 ) =

Ответ: вероятность того, что корреспондент услышал вызов, равна 0,3.

Задание 5

Случайная величина ξ имеет распределение вероятностей, представленное таблицей:

Найти Р(3), функцию распределения F(Х). Построить многоугольник распределения.

Решение:

Найдем Р(3):

Найдем и построим функцию распределения F(Х):

Построим многоугольник распределения:

Задание 6

Найти М(ξ), D(ξ), σ(ξ) случайной величины ξ примера 5.

Решение:

Найдем М(ξ) случайной величины ξ из примера 5:

Найдем D(ξ) случайной величины ξ из примера 5:

Найдем

случайной величины ξ из примера 5:

Задание 7

ξ- непрерывная случайная величина с плотностью распределения φ(Х), заданной следующим образом:

φ(Х)=

Найти функцию распределения F(Х).

Решение:

Найдем функцию распределения F(Х):

При

Задание 8

ξ- непрерывная случайная величина из примера 7. Найти М(ξ), D(ξ).

Решение:

Найдем М(ξ):

Найдем D(ξ):

mirznanii.com

1. Основные понятия теории вероятностей и математической статистики

1.1. Случайные события. Испытания. Относительная частота и вероятность

Пусть требуется оценить качество изделий в некоторой партии объемом n. Для этого необходимо над каждым изделием провести наблюдение, т.е. осмотр, измерение, взвешивание и т.д. В теории вероятностей и математической статистике всем этим понятиям соответствует один термин – испытание.

В результате отдельного испытания изделие может быть признано либо годным, либо браком. Возможные исходы испытания в данном примере – это случайные события: А – годное изделие; В – брак. Эти события называются случайными, потому что заранее нельзя точно предсказать, какое из них наступит при следующем испытании.

Пусть после проверки всей партии изделий объемом n, т.е. после n испытаний, случайное событие А – число годных изделий – появилось n_А раз. Это значит, что относительная частота случайного события А равна

Если провести несколько серий испытаний (проверить несколько партий изделий), то относительные частоты в разных сериях будут группироваться около определенного числа, которое называется вероятностью случайного события А и обозначается Р(А). Как показала практика, с ростом объема партии изделий n относительные частоты теснее группируются около вероятности, т.е. обнаруживают устойчивость.

Устойчивость относительной частоты случайного события является определяющим его свойством, позволяющим использовать относительную частоту как оценку вероятности в различных практических расчетах.

1.2. Виды случайных событий

События, которые непременно происходят при каждом испытании, называются достоверными.

События, которые не могут произойти ни при каком испытании, называются невозможными.

Вероятность достоверного события равна единице, вероятность невозможного события равна нулю.

Если при осуществлении испытания может наступить хотя бы одно из двух событий А или В, то событие

С=А+В

называется суммой, или объединением событий А и В.

Два события А и В называются несовместными, если они не могут наступить вместе при одном испытании.

Случайные события образуют полную группу, если они попарно несовместны, и при любом отдельном испытании непременно должно наступить одно из них.

Сумма вероятностей событий, образующих полную группу, равна единице.

Два случайных события называются противоположными, если в одном испытании появление одного из них (А) исключает появление другого () – читается «неА».

Сумма вероятностей двух противоположных событий равна единице

Противоположные события образуют полную группу.

Если при осуществлении испытания может наступить и событие А, и событие В (совмещение событий А и В), то событие

называется произведением, или пересечением событий А и В.

Два случайных события называются независимыми, если при осуществлении испытаний появление одного из них не изменяет вероятности появления другого.

1.3. Определения вероятности

Классическое определение вероятности события А – отношение числа m элементарных событий (исходов испытаний), благоприятствующих событию А, к общему числу n равновозможных элементарных событий

Статистическое определение вероятности

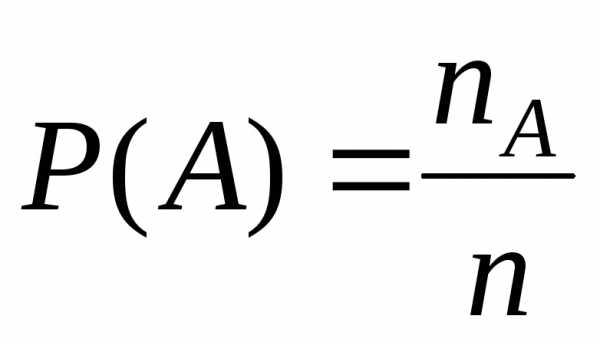где 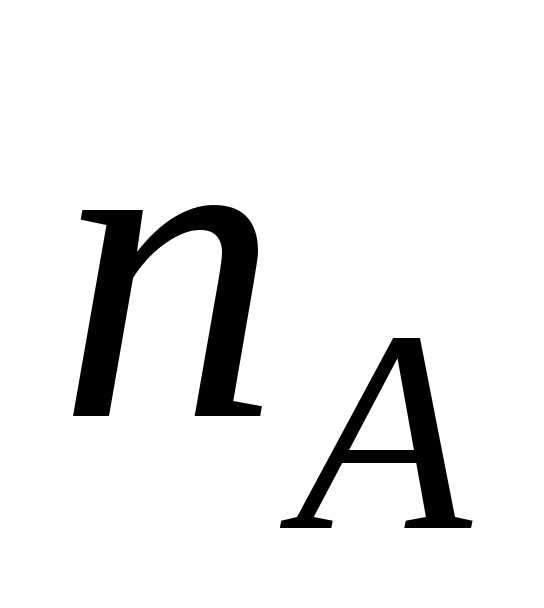– частота событияА при n испытаниях.

Геометрическая вероятность

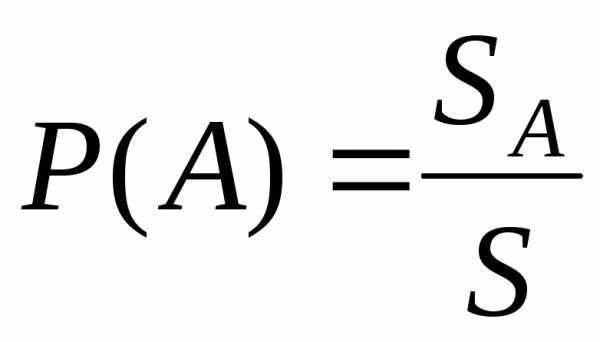где – площадь некоторого замкнутого контура, составляющая часть площадиS.

studfiles.net

Кафедра теории вероятностей и математической статистики

Шпоры для студентов специальности 220100 –Вычислительные машины, комплексы, системы и сети

Теория вероятностей

математическая статистика

Алексей Михайлович Протасов

Содержание

Кафедра теории вероятностей и математической статистики 5

Теория вероятностей 5

Введение в теорию вероятностей 5

Предмет теории вероятностей 5

Возникновение и развитие теории вероятностей 5

До появления аксиоматики Колмогорова 5

В наше время 5

Необходимость теории вероятностей как науки 6

Возможность анализа случайных явлений 6

Расчет шансов и прогнозирование последствий 6

Типичные ошибки при решении вероятностных задач без применения теории вероятностей 6

Ошибка шевалье де Мере (XVII век) 6

Ошибка Д’Аламбера 7

Задача о днях рождения 7

Понимание природы вещей и причин явлений 7

Парадокс движения автобусов 7

Игра с тремя разными костями 7

Новый язык для описания объектов 7

Распространение вероятностной и статистической терминологии 7

Примеры практических задач, при решении которых применяется теория вероятностей 8

Расчет размера буфера в устройствах передачи и обработки информации 8

Определение объема закупки товара или выпуска продукции на рынок 9

Управление продажей авиабилетов 9

Расчет надежности сложной системы 9

Оценка доли брака или стоимости коллекции 9

Принятие типового решения в условиях неопределенности 9

Задача о студенте на экзамене 9

Примеры практических задач, при решении которых не стоит применять теорию вероятностей 9

Принятие важного решения, от которого зависит успех всего проекта 9

Игра по крупному 9

Основные понятия и определения 10

Первичные понятия 10

Опыт (эксперимент) 10

Элементарный исход 10

Пространство элементарных исходов 11

Советы по построению пространства элементарных исходов. 11

Определения 11

Подмножества 11

Операции над подмножествами 12

Дополнение 12

Объединение 12

Пересечение 12

Разность 12

Симметричная разность 13

Количество элементов в подмножестве 13

Отношения между подмножествами 13

Вложение 13

Несовместность 13

Противоположность 13

Формулы 13

Полная группа подмножеств 14

Алгебра и сигма-алгебра 14

Случайные события 15

Полная группа событий 15

Конечно-аддитивная функция 15

Счетно-аддитивная функция 15

Мера 15

Конечная мера 15

Вероятность 15

Вероятностное пространство 16

Парадокс определения вероятностного пространства 16

Независимые события 16

Попарно 16

В совокупности 16

Условная вероятность 17

Свойства и теоремы 17

Простейшие свойства вероятности 17

Вероятность противоположного события 17

Вероятность невозможного события 17

Монотонность вероятности 17

Ограниченность вероятности 17

Вероятность объединения событий 17

Полуаддитивность вероятности 18

Вероятности полной группы событий 18

Формула полной вероятности 18

Формула Байеса 18

Дискретная вероятностная модель 18

Конечное пространство элементарных исходов 18

Классическая вероятностная модель 18

Связь классической вероятностной модели с комбинаторикой 19

Основная формула комбинаторики 20

Факториал 20

Формула Стирлинга 20

Биномиальный коэффициент 20

Бином Нютона 20

Полиномиальная формула 20

Схема выбора с возвращением 20

Схема выбора без возвращения 21

Урновая схема 22

Общее определение вероятности для экспериментов с конечным или счетным числом исходов 22

Дискретное распределение и вероятность 23

Равномерное распределение — классическая вероятностная модель 23

Биномиальное распределение – схема Бернулли 23

Мультиномиальное распределение – схема бросания частиц по ячейкам 24

Геометрическое распределение – испытания до первого успеха 25

Распределение Паскаля – испытания до m-того успеха 26

Пуассоновское распределение — теорема Пуассона 26

Теорема Пуассона. 27

Независимость событий и условная вероятность. Построение моделей. 27

Независимость 27

Различие между независимостью попарно и в совокупности. Пример Бернштейна 27

Использование понятия независимости для построения моделей. Произведение вероятностных пространств. 28

Примеры построения моделей. 29

Расчет надежности при параллельном соединении элементов. 29

Расчет надежности при последовательном соединении элементов 31

Расчет надежности сложной системы. 31

Замечания к примерам. 32

Условная вероятность 33

Урновая схема 33

Марковская зависимость 35

Формула полной вероятности и формула Байеса 36

Случайные величины 37

Отображения вероятностных пространств 37

Случайная величина 38

Борелевская сигма-алгебра 38

Определение случайной величины 38

Борелевская функция 39

Примеры борелевских функций 39

Примеры случайных величин 39

Индикатор события 39

Простая случайная величина 39

Дискретная случайная величина 40

Случайный вектор 40

Распределения случайных величин и векторов 40

Функция распределения 40

Дискретные распределения на прямой 41

Вырожденное распределение 41

Бернуллиевское распределение 41

Биномиальное распределение 42

Геометрическое распределение 43

Пуассоновское распределение 44

Произвольное дискретное распределение 44

Функция распределения случайной величины 45

Непрерывные распределения на прямой 45

Равномерное распределение на отрезке. 45

Мера Лебега на прямой. 46

Плотность распределения 46

Вероятностный смысл плотности распределения 48

Бета-распределение на отрезке [0,1] 48

Смеси распределений. 51

Нормальное (гауссовское) распределение. 52

Экспоненциальное (показательное) распределение. 54

Гамма-распределение. 55

Построение меры в конечномерном пространстве 56

Борелевская сигма-алгебра в конечномерном пространстве 56

Определение случайного вектора 57

Мера Лебега в конечномерном пространстве 57

Мера Лебега на квадрате — Задача о встрече 58

Независимые случайные величины 58

Многомерное нормальное распределение 59

Числовые характеристики случайных величин и векторов 60

Интеграл Лебега – математическое ожидание 60

Свойства интеграла Лебега (математического ожидания) 61

Неравенства 62

Неравенство Маркова 62

Неравенство Чебышева. Дисперсия 62

Неравенство Коши-Буняковского-Шварца. Ковариация 63

Неравенство Йенсена.Выпуклые функции 64

Моменты 64

Вычисление математического ожидания. 64

Теорема Лебега о замене переменных 65

Вычисление интеграла Лебега на прямой. 65

Вычисление маргинальных плотностей 66

Вычисление числовых характеристик важных распределений. 66

Суммирование независимых случайных величин 67

Распределение суммы независимых случайных величин 67

Распределение суммы двух независимых случайных величин. Формула свертки 67

Плотность распределения суммы двух независимых случайных величин 68

Кратные свертки 68

Примеры вычисления распределения сумм независимых случайных величин 68

Суммы независимых случайных величин. Нормальное распределение 68

Суммы независимых случайных величин.Биномиальное распределение 68

Суммы независимых случайных величин.Пуассоновское распределение 69

Суммы независимых случайных величин.Гамма распределение 69

Пуассоновский процесс 69

Сходимость последовательностей случайных величин и их распределений 70

Сходимость по вероятности 70

Сходимость в среднеквадратическом 70

Слабая сходимость распределений 71

Взаимосвязь различных видов сходимости 71

Закон больших чисел в форме Бернулли 72

Предельные теоремы теории вероятностей 72

Схема суммирования независимых слагаемых 72

Закон больших чисел в форме Чебышева 73

Закон больших чисел в форме Хинчина 73

Центральная предельная теорема в форме Леви 73

Теорема Леви 73

Теорема Муавра-Лапласа 74

Условное математическое ожидание, условная плотность и условное распределение 74

Определение условного распределения и условной плотности 75

Условное распределение 75

Кафедра находится на 4 этаже здания МГИЭМ на Б.Трехсвятительском пер. 3/12. Заведующий кафедрой – профессор, д.ф.-м.н ,академик Академии Криптографии, Ивченко Григорий Иванович

Теория вероятностей Введение в теорию вероятностей Предмет теории вероятностей

Математическая модель — это средство описания объектов и процессов реального мира в математических терминах, с помощью первичных, неопределяемых символических объектов (точка, множество …) и строго определяемых отношений между ними (функция, оператор…).

Теория вероятностей – это математическая дисциплина, изучающая математические модели случайных явлений. Предметом теории вероятностей является математический аппарат для построения и анализа математических моделей случайных явлений, возникающих в науке, технике, экономике, бизнесе и повседневной деятельности людей. Важным следствием построения такой модели является возможность находить вероятности случайных событий.

Возникновение и развитие теории вероятностей До появления аксиоматики Колмогорова

Развитие теории вероятностей как науки началось в середине XVII века в связи с расчетом шансов в азартных играх. Первые теоремы были доказаны Я.Бернулли и Муавром. В 1812 году появился первый большой трактат по теории вероятностей Лапласа. В это время теория вероятностей начинает применяться в естествознании, технике и военном деле (теория ошибок наблюдений, теория стрельбы). Во второй половине 19 века вероятностные методы уже используются в демографии, статистике и страховании. Первым российским математиком, внесшим значительный вклад в теорию вероятностей, был Чебышев, работы которого были продолжены Марковым и Ляпуновым.

В наше время

Современный период в развитии теории вероятностей начинается с работ Бернштейна, Бореля и Колмогорова. Теория вероятностей стала математической наукой в 1933 году после выхода книги Колмогорова «Основные понятия теории вероятностей», в которой предложена аксиоматика теории вероятностей. С помощью этой аксиоматики удалось объяснить многочисленные парадоксы теории вероятностей, в ее рамках теория вероятностей развивается до сих пор. Наиболее бурно развивающиеся сейчас разделы теории вероятностей это теория случайных процессов, стохастическая геометрия, статистические приложения теории вероятностей.

Необходимость теории вероятностей как науки

Теория вероятностей необходима тогда, когда требуется дать количественную оценку неопределенности, возникающей при анализе случайных явлений, предсказать наиболее вероятный исход опыта, оценить средние значения случайных факторов и отклонения от них, исследовать взаимосвязь явлений, между которыми нет жесткой зависимости. Теория вероятностей позволяет дать специальный язык для описания некоторых объектов реального мира. Методы теории вероятностей помогают анализировать большие объемы статистических данных и предлагать для них математические модели. Отказ от использования методов теории вероятностей при анализе даже простейших задач со случайными факторами или неправильное их применение может привести к значительным количественным ошибкам и ложным качественным заключениям.

studfiles.net

Теория вероятностей и математическая статистика

Sitemap || Главная страница / Учебная работа / Теория вероятностей и математическая статистика

Данный раздел находится в разработке. Если вы хотите следить за обновлениями сайта, пошлите мне электронное письмо по адресу

Теория вероятностей и математическая статистика — односеместровый общий курс для студентов физического факультета МГУ (6 семестр). На этой странице собраны материалы по варианту курса, читаемому с 2006 г. студентам, которые специализируются по кафедре квантовой статистики и теории поля.

Приводимые ниже даты соответствуют весеннему семестру 2007/8 ак. года.

Примерный план курса

Лекция 1 (08.02): Целочисленные случайные величины и метод производящих функций
Семинар 1 (13.02): Метод производящих функций
Лекция 2 (15.02): Непрерывные случайные величины и метод характеристических функций
Семинар 2 (20.02): Непрерывные распределения: первое знакомство
Лекция 3 (22.02): Случайные векторы и корреляции случайных величин
Семинар 3 (27.02): Формула замены переменных и статистическое моделирование
Лекция 4 (05.03): Закон больших чисел и сходимость по вероятности
Семинар 4 (07.03): Вокруг многомерного нормального распределения
Лекция 5 (12.03): Центральная предельная теорема, степенные законы, экстремальные значения
Семинар 5 (14.03): Вокруг многомерного нормального распределения (окончание)
Лекция 6 (19.03): Большие уклонения и энтропия
Семинар 6 (21.03): Энтропия и информация
Лекция 7 (26.03): Случайные события, алгебры событий, условные вероятности
Семинар 7 (28.03): Энтропия и информация (окончание)
Коллоквиум 1 (31.03)
Лекция 8 (02.04): Статистическое оценивание и метод наибольшего правдоподобия
Семинар 8 (04.04): Статистическое оценивание и метод наибольшего правдоподобия
Лекция 9 (09.04): Проверка статистических гипотез
Семинар 9 (11.04): Проверка статистических гипотез
Лекция 10 (16.04): Конечные однородные цепи Маркова, существование стационарного распределения
Семинар 10 (18.04): Симметричное случайное блуждание и электрические цепи
Лекция 11 (23.04): Цепи Маркова в непрерывном времени, уравнение марковской эволюции, процесс Пуассона
Семинар 11 (25.04): Случайное блуждание в непрерывном времени
Лекция 12 (30.04): Случайные блуждания и диффузионные процессы, уравнения Фоккера-Планка и Ито, процесс Винера (броуновское движение)
Семинар 12 (02.05): Диффузионные процессы с точки зрения уравнения Фоккера-Планка
Лекция 13 (07.05): резерв
Семинар 13 (14.05): Диффузионные процессы с точки зрения уравнения Ито
Коллоквиум 2

Отчетность по курсу теории вероятностей и математической статистики предусмотрена учебным планом в форме зачета и экзамена. Для получения зачета необходимо успешно сдать два коллоквиума (26.03 и 14.05).

Домашние задания

Зачет за специальный физический практикум в 6 семестре может быть проставлен за два выполненных домашних задания по теории вероятностей и математической статистике. Домашние задания включают в себя задачи для аналитического и численного решения. Форма сдачи — отчет, подготовленный в формате TeX, и собеседование.

Срок сдачи первого домашнего задания — понедельник 24.03, второго — понедельник 12.05.

Консультации по домашним заданиям проводятся по понедельникам 11.02 (организационная) (25.02) (10.03) (07.04) (21.04) (05.05) на 4 паре на кафедре (ауд. 4-67).

Инструкции по установке необходимого для выполнения домашних заданий программного обеспечения см. по следующим адресам:

система статистического анализа и моделирования R
система TeX

Задачи семинаров

Этот раздел будет пополняться.

Материалы к курсу

Конспект лекций

А.Н. Соболевский. Теория вероятностей и основы математической статистики для физиков. Учебное пособие по курсу лекций. — М.: Физический ф-т МГУ, 2007. PDF (632 KB).
Исправления замеченных опечаток: PDF (последнее обновление: 11 марта 2008)

Литература вне Сети

Книги, которые должен прочитать каждый:

В. Феллер. Введение в теорию вероятностей и ее приложения. В 2-х тт. — М.: Мир, 1984.
Г. Крамер. Математические методы статистики. — М.: Мир, 1976.

Учебники

Е.С. Вентцель. Теория вероятностей. — М.: Высшая школа, 2003 (и другие издания).
Б.В. Гнеденко. Курс теории вероятностей. — М.: Наука, 1969.
Ю.П. Пытьев, И.А. Шишмарев. Курс теории вероятностей и математической статистики для физиков. — М.: изд-во МГУ, 1983.
А.Н. Ширяев. Вероятность. В 2-х кн. — М.: МЦНМО, 2004.

Материалы по отдельным разделам курса

Д. Дюге. Теоретическая и прикладная статистика. — М.: Наука, 1972.
М. Кендалл, А. Стьюарт. Теория распределений. — М.: Наука, 1966.
М. Кендалл, А. Стьюарт. Статистические выводы и связи. — М.: Наука, 1973.
Дж. Кингман. Пуассоновские процессы. — М.: МЦНМО, 2007.
Худсон Д. Статистика для физиков. — М.: Мир, 1970.
А.М. Яглом, И.М. Яглом. Вероятность и информация. — М.: Наука, 1972; М.: УРСС, 2006.

Публикации основоположников

А.Н. Колмогоров. Основные понятия теории вероятностей. — М.: Наука, 1974; М.: Фазис, 1998.

Справочные издания

Вероятность и математическая статистика. Энциклопедия. Под ред. Ю.В. Прохорова. — М.: Большая Российская Энциклопедия, 1999.

Литература в Сети

Материалы по отдельным разделам курса

Публикации основоположников

R. Brown. A brief account of microscopical observations made in the months of June, July and August, 1827, on the particles contained in the pollen of plants; and on the general existence of active molecules in organic and inorganic bodies. Philosophical Magazine 4 (1828) 161-173. PDF (7.3 MB).
K. Itô. Markov katei wo sadameru bibunhouteishiki [Differential equations determining a Markov process]. Zenkoku shijo sugaku danwakai, 244 (1942) 1352–1400. PDF (1.3 MB; спасибо Такеши Мацумото за эту ссылку)
A. Rényi. On measures of information and entropy. In: Proceedings of the 4th Berkeley Symposium on Mathematics, Statistics and Probability 1960, 547-561. PDF (860 KB)

Справочные материалы

Исторические материалы

J. Aldrich. R.A. Fisher and the making of maximum likelihood 1912-1922. Statistical Science, 12:3 (1997) 162-176. PDF (260 KB)
K. Itô. Memoirs of my research on stochastic analysis. In: Stochastic Analysis and Applications, vol. 2 of Abel Symposia, Berlin etc: Springer, 2007, P. 1-6. 2007. PDF (104 KB)

Sitemap || Главная страница / Учебная работа / Теория вероятностей и математическая статистика

mccme.ru

ПРЕДМЕТ ТЕОРИИ ВЕРОЯТНОСТЕЙ И МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ — Мегаобучалка

Теория вероятностей и математическая статистика. Обзорная лекция

Вводная часть

Теория вероятностей и математическая статистика. Обзорная лекция

Теория вероятности и математическая статистика

1. Основные понятия теории вероятностей и математической статистики

1.1. Случайные события. Испытания. Относительная частота и вероятность

1.2. Виды случайных событий

1.3. Определения вероятности

Кафедра теории вероятностей и математической статистики

Теория вероятностей Введение в теорию вероятностей Предмет теории вероятностей

Возникновение и развитие теории вероятностей До появления аксиоматики Колмогорова

В наше время

Необходимость теории вероятностей как науки

Теория вероятностей и математическая статистика

Примерный план курса

Домашние задания

Задачи семинаров

Материалы к курсу

Конспект лекций

Литература вне Сети

Учебники

Материалы по отдельным разделам курса

Публикации основоположников

Справочные издания

Литература в Сети

Материалы по отдельным разделам курса

Публикации основоположников

Справочные материалы

Исторические материалы

Добавить комментарий Отменить ответ