Решение задач по теме первый признак равенства треугольников – Решение задач по теме «Первый признак равенства треугольников»

Решение задач по теме «Первый признак равенства треугольников»

Вспомним предварительно формулировку первого признака равенства треугольников.

                                    

Рис. 1. Первый признак равенства треугольников

Определение: Первый признак равенства треугольников – это равенство их по углу и прилежащим сторонам.

Из этих трех равенств и вытекает равенство самих треугольников.

Смысл равенства треугольников заключается в том, что при совмещении этих трех элементов гарантируется совмещение, то есть равенство всех остальных элементов двух треугольников.

Рассмотрим следующие задачи:

Пример 1: Измерить на местности расстояние между двумя точками A и B, между которыми нельзя пройти по прямой. Для этого выбирают такую точку С, из которой можно пройти и к точке А, и к точке В, и из которой видны обе эти точки. Провешивают расстояния АС и ВС, продолжают их за точку С и отмеряют СD = AC и ЕС = СВ. Тогда отрезок ED равен искомому расстоянию. Объясните, почему.

Решение:

Выполним пояснительный рисунок:

                

Рис. 2. Чертеж к примеру 1

Продлим отрезки АС и ВС. Отмеряем СЕ = СВ и CD = CA. ∆CDE = ∆CAB по первому признаку.

.

Из равенства треугольников следует, что ED = AB.

Ответ: Задача решена.

Пример 2: Через середину О отрезка АВ проведена прямая р, перпендикулярная прямой АВ. Докажите, что каждая точка Х этой прямой одинаково удалена от точек А и В (каждая точка серединного перпендикуляра к отрезку АВ равноудалена от его концов).

Решение:

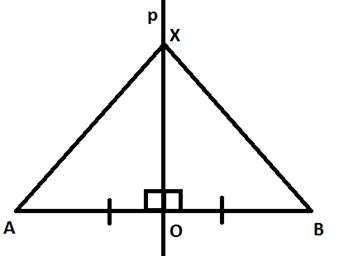
Рис. 3. Чертеж к примеру 2

Рассмотрим треугольники АОХ и ВОХ. ∆АОХ = ∆ВОХ – по первому признаку.

Из равенства треугольников следует, что АХ = ВХ для любой произвольной точки Х, которая принадлежит прямой р.

Ответ: Доказано.

Пример 3: На стороне АВ треугольника АВС взята точка D, а на стороне треугольника  взята точка . Известно, что треугольники ADC и  равны и отрезки DB и  равны. Докажите равенство треугольников АВС и .

Решение:

                                             

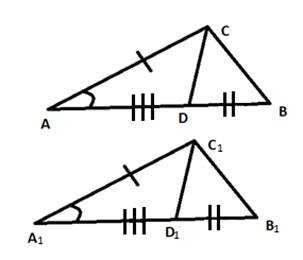
Рис. 4. Чертеж к примеру 3

Рассмотрим треугольники АВС и . В них . АС =  (поскольку треугольники ADC и  равны по условию). В нашем случае для доказательства необходимо лишь, чтобы АВ =  . Докажем, что это действительно так.

 

AD =  из равенства треугольников. DB =  по условию. Отсюда следует, что АВ = .  и прилежащие к ним стороны тоже равны у двух треугольников, значит, АВС = .

Ответ: Доказано.

Пример 4: На сторонах ВС и  равных треугольников АВС и  взяты соответственно точки М и , причем ВМ : BС = : = 1 : 3. Доказать, что АМ = .

Решение:

Рис. 5. Чертеж к примеру 4

Из равенства треугольников АВС и  следует, что , АВ = , ВС = . Для доказательства того, что ∆АВМ = ∆, у нас есть уже два необходимых элемента, это равенство углов  и равенство сторон АВ = , значит, нам необходимо доказать, что ВМ = .                                                          =

Треугольники ∆АВМ = ∆ по первому признаку. А значит, АМ = .

Ответ: Доказано.

Пример 5: На сторонах угла CAD отмечены точки В и Е так, что точка В лежит на отрезке АС, а точка Е – на отрезке AD, причем АС = AD и АВ = АЕ. Докажите, что .

Решение:

Рис. 6. Чертеж к примеру 5

Обозначим  как  и как . Доказать, что , – это то же самое, что доказать равенство смежных с ними углов и . ∆BAD = ∆EAC по первому признаку, поскольку у них общий, ВА = ЕА и AD = AC. , так как они лежат напротив равных сторон AD и AC соответственно. Мы доказали равенство смежных углов, а значит, и доказали равенство искомых. .

Ответ: Доказано.

На сегодняшнем уроке мы рассмотрели несколько примеров на первый признак равенства треугольника. На следующем уроке мы познакомимся с перпендикуляром, проведенным к прямой.

 

Список рекомендованной литературы

1. Александров А.Д., Вернер А.Л., Рыжик В.И. и др. Геометрия 7. – М.: Просвещение.
2. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 7. 5-е изд. – М.: Просвещение.
3. Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А. – М.: Просвещение, 2010.

 

Рекомендованные ссылки на интернет-ресурсы

1. Обобщающий урок по геометрии в 7-м классе (Источник).
2. Прямая линия, отрезок (Источник).

 

Рекомендованное домашнее задание

1. №35 (д). Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А. – М.: Просвещение, 2010.
2. Постройте треугольник по заданному углу и двум прилежащим к нему сторонам.
3. Докажите по первому признаку равенства треугольников, что диагональ квадрата делит его на 2 равных треугольника.

interneturok.ru

Задачи на первый признак равенства треугольников

Рассмотрим конкретные задачи на первый признак равенства треугольников.

1) Дано:

AB=AD,

∠BAC=∠DAC

Доказать: ∆ABC=∆ADC

Доказательство:

Выделим треугольники, равенство которых надо доказать, разными цветами.

Этот ход сразу позволяет увидеть, что данные треугольники имеют общую сторону AC.

Теперь запишем равные пары элементов.

 

1) AB=AD (по условию)

2) ∠BAC=∠DAC (по условию)

3) AC — общая сторона.

Следовательно, ∆ABC=∆ADC (по двум сторонам и углу между ними, то есть по первому признаку равенства треугольников).

Что и требовалось доказать.

2)

  Дано:

AO=BO,

CO=DO

Доказать: ∆AOC=∆BOD.

Доказательство:

Выделим треугольники, равенство которых доказываем, разными цветами.

Определяем те элементы, о равенстве которых известно по условию задачи:

1)  AO=BO (по условию)

2) CO=DO (по условию).

Для равенства треугольников осталось найти третью пару равных элементов. Это — углы AOC и BOD.

3) ∠AOC = ∠BOD (как вертикальные).

Все три пункта первого признака равенства треугольников есть. Следовательно, ∆AOC=∆BOD (по двум сторонам и углу между ними).

Что и требовалось доказать.

3)

  Дано:

AB=AC,

AF=AK

Доказать: ∆ABK=∆ACF

Доказательство:

Выделяем треугольники ABK  и ACF разными цветами.

Цветовая визуализация позволяет увидеть, что для данных треугольников угол A — общий .

Далее определяем, равенство каких элементов дано в условии. Записываем доказательство.

1) AB=AC (по условию)

2) AF=AK (по условию)

3) ∠A — общий.

Все три пункта первого признака равенства треугольников выполнены.

Следовательно, ∆ABK=∆ACF (по двум сторонам и углу между ними).

Что и следовало доказать.

 

В следующий раз рассмотрим задачи на второй признак равенства треугольников.

 

 

www.treugolniki.ru

Первый признак равенства треугольников. Решение задач

Разделы: Математика

---

Цели и задачи урока:

• повторение понятий треугольника и его элементов
• повторение понятия равных треугольников
• формирование у учащихся умения доказывать равенство треугольников
• умение выделять следствия, вытекающие из равенства треугольников.

Ход урока

Решение задач по готовым чертежам.

I. Проверка домашнего задания: № 90, № 94.

Перед уроком на доске выполнены чертежи и записано дано к каждой задаче:

№90.

Дано: треугол. АВС

АВ = 17 см, АС > AB в 2 раза, ВС < AC на 10 см.

Найти: P треугол. ABC = ?

№ 94.

Дано: АВ = АС, <1 = <2, АС= 15 см, DC= 5 см.  

а) Доказать: треугол. АВD = треугол. ACD

б) Найти: BD и АВ.

Далее с помощью фронтального опроса класса устно проверяем решение домашних задач.

№ 90. Решение:

1. Пусть АВ = 17 см (по условию), тогда AC = 2АВ = 17 * 2 = 34 см, а ВС = АС – 10 = 34 – 10 = 24 см
2. P АВС = АВ + ВС + АС = 17 + 34 + 24 = 75 см.

Ответ: Р треугольника. АВС = 75 см.

№ 94.

1) Рассмотрим треугольник АВС и треугольник АСD.

а) АВ = АС (по условию)

б) < 1 = < 2 (по условию)

в) AD – общая сторона

Из а, б, в следует => треугольник АВD = треугольнику АСD по двум сторонам и углу между ними (Первый признак равенства треугольников).

2) Треугольник АВD = треугольнику АСD, мы знаем, что в равных треугольниках против соответственно равных углов лежат равные стороны, т.е. т.к <1 = <2, то BD = DC = 5 см

3) АВ = АС = 15 см (по условию)

Ответ: АВ = 15 см, ВО = 5 см.

Попутно повторяем следующие понятия:

а) какая фигура называется треугольником;
б) элементы треугольника;
в) стороны и углы, противолежащие друг другу;

г) углы, прилежащие к сторонам треугольника;
д) что такое периметр треугольника

II. Опрос класса – доказательство I-ого признака равенства треугольников. Опрос называется – Каскад.

5 учеников из класса уже ответили учителю эту теорему и знают ее отлично. Знают все дополнительные вопросы (и ответы на них), которые надо задать по ходу доказательства этой теоремы. Причем это, как правило, слабые ученики класса, которые выучивают теорему, хорошо понимая ее, с помощью учителя. Они стремятся дотошно разобраться в доказательстве данной теоремы и всего теоретического материала, используемого в ней, так как знают, что на уроке они будут опрашивать и оценивать сильных учеников класса. Это стимулирует их на хорошую подготовку к уроку, детям всегда хочется побывать в роли учителя, тем более, что дети послабее опрашивают тех, кто лучше разбирается в данном предмете. Все ученики класса, кроме этих пятерых, достают листки и делают на них чертежи к теореме, и пишут дано. На первый взгляд дети работают сами, но на самом деле вся работа хорошо спланировано учителями. Весь класс у него на контроле. Как только работа с листочками закончена, учащиеся готовые отвечать поднимают руки и им учитель предлагает занять место рядом с одним из пятерых, уже ответивших теорему. Дети начинают тихим шепотом отвечать друг другу. Через 3-4 минуты в классе уже 10 человек, которые спрашивают, и так по нарастающей. Когда все ответили, учитель называет всех учеников по списку, и отметку говорит тот, кто его опрашивал. Отметки, как правило, бывают хорошими, двоек нет совсем, так как дети знают, что спросят всех. (Если оценки чуть завышены, это не страшно, важно, что они с желанием готовятся, следовательно учат теорию, владеют ей начинают лучше решать задачи, а это то, чего мы хотим добиться на уроках геометрии.

III. В это время I ученик за доской готовит материал для доказательства этой теоремы. Как только все ответили друг другу теорему и получили оценки, он отвечает устно эту же теорему. Ребята должны владеть собой при ответе для полной аудитории, тренировать хороший математический язык, логическую последовательность ответа. А аудитория уметь слушать, улавливать ошибки, если они есть, задавать вопросы отвечавшему и учиться правильно, оценивать ответы одноклассников.

IV. Решение задач. Устно по готовым чертежам.

Доказать равенство треугольников.

1.			2.
Доказать: треугол. АОВ = треугол. COD			Доказать: треугол. АВD = треугол. CDB

У доски ученик.

У доски ученик + фронтальная помощь класса. Решим письменно задачу с полным оформлением решения в тетради.

Дано:

< ABE = < DCE, BE = CE

BK = LC, < BKE = 110°

1) Доказать: треугол. BEK = треугол. CEL

2) Найти: < ELC

Решение:

1) < ABE + < 1 = 180° (смежные углы)

< DCE + < 2 = 180° (смежные углы)

< 1 = 180° — < ABE

< 2 = 180° — < DCE

и по условию < ABE = < DCE, следовательно < 1 = < 2/

2) Рассмотрим треугол. BEK и треугол. CEL:

а) BE = СE (по условию)

б) BK = LC (по условию)

в) <1 = < 2

из а, б, в следует => треугол. BEK = CEL по двум сторонам м углу между ними (I признак равенства треугольников) ч.т.д.

3) Треугол. BEK = треугол. CEL , а в равных треугольниках против соответственно равных сторон лежат равные углы, т.е. т.к BE=CE, то < ELC = < BKE = 110°.

Ответ: < BKE = 110°

2.

Дано:

треугол. BEC = DFA

Доказать: 1) треугол. ABC = треугол. CDA

2) треугол. ABE = треугол CDE

Доказательство:

1) Т.к. по условию треугол. BEC = треугол. DFA, то BC = DA, <BCE = < DAF.

2) Рассмотрим. треугол. ABC и треугол. CDA:

а) BC = DA

б) < BCA = <DAC

в) AC – общая сторона

Из а, б, в, следует => треугол. ABC = треугол. CDA по I признаку равенства треугольников (по двум сторонам и углу между ними).

3) Т.к треугол. BEC = треугол. DFA, то EC = FA.

Т.к треугол. АВС = треугол. CDA, то АС – общая сторона

Отсюда следует => AE = AC – EC

CF = AC – FA, т.е. AE = CF.

4) Т.к. треугол. BEC = треугол. DFA, то BE = Df и < BEC = < DFA, то они смежные соответственно с углами: < AEB и < CFD, т.е. < AEB = < СFD.

5) Рассмотрим треугол. ABE и треугол. СDF:

а) BE = DF

б) AE=СF

в) < AEB=< CFD

Из а,б,в следует => треугол. ABE = треугол. CDF по двум сторонам и углу между ними( I признак павенства треугольников) ч.т.д.

VI. Домашнее задание: параграф 14,15. № 95, 96, 92.

VII. Итог урока.

15.05.2010

xn--i1abbnckbmcl9fb.xn--p1ai

План-конспект урока «Решение задач по теме «Первый признак равенства треугольников»

План-конспект

урока геометрии в 7 классе

по теме «Решение задач на первый признак равенства треугольников»

Цели:

• Научить в равных треугольниках выделять пары равных элементов, распознавать на рисунке пары равных треугольников, применять признак равенства треугольников по двум сторонам и углу между ними при решении задач;

• развивать приемы логического мышления (сравнивать, обобщать), правильно формулировать и излагать мысли, умение анализировать факты и делать выводы; создать условия для развития познавательного интереса к математике;

• Воспитывать культуру умственного труда, ответственность при поверке решенных задач, дисциплинированность на уроке, взаимоуважение, трудолюбие.

Оборудование:

• учебник  «Геометрия 7-9 класс» автор Л.С. Атанасян,

• ТСО

• презентация

• карточка-подсказка

• набор задач по готовым чертежам

• карточки домашнее задание согласно уровню подготовки

План урока.

1. Орг. момент.(1 мин.)

2. Введение в тему урока.(2 мин.)

3. Сообщение темы урока и целеполагание (2 мин)

4. Актуализация опорных знаний.(3 мин.)

5. Опрос (доказательство первого признака равенства треугольников 3мин)

6. Решение задач по готовым чертежам (7 мин.)

7. Физкультминутка (2 мин)

8. Формирование навыка применения Признака (7 мин)

9. Самостоятельная работа.(6 мин.)

10. Итог урока (3 мин.)

11. Задание на дом. Рефлексия. (4 мин.)

Ход урока

Орг. момент

1мин

— Здравствуйте! Оглянитесь, сегодня у нас на уроке гости. Улыбнитесь гостям, улыбнитесь друг другу, пожелайте друг другу удачи.

Введение в тему урока

2мин

— Я сегодня предлагаю вам отправиться в путешествие, а что именно за путешествие, вы определите сами, прочитав эпиграф к уроку слайд2

— Как вы думаете, какова тема урока?

Читают эпиграф

Называют тему урока

Сообщение темы и целеполагание

2мин

— Да, ребята, вы правы, сегодня на уроке мы продолжим работать с одной из самых замечательных фигур в геометрии – треугольником. Итак, тема нашего урока «Решение задач на первый признак равенства треугольников» слайд 3

— Какие цели вы поставите для себя на этот урок?

-Научиться применять первый признак равенства треугольников при решении задач, -доказывать равенство треугольников

— Повторить изученные определения, вспомнить теорему.

— Научиться решать задачи, применяя первый признак равенства треугольников.

Актуализация знаний

(Остров определений)

3 мин

— Несмотря на то, что содержание геометрии расширилось далеко за пределы учения о земле, она по-прежнему продолжает называться «Геометрией». Мы с вами уже в течение 2 месяцев изучаем эту древнейшую науку, великую страну – Геометрия. Но в изучении этой страны мы еще новички, а все новички попадают на остров Определений

слайд 4

Фронтальный опрос

Опрос (Путешествие на пролив Признака)

3 мин

— А теперь паромщик перевезет нас через пролив Признака на материк. Плата – решение задач. Так как мы будем переплавляться через пролив Признака, каждый входящий на корабль вслух формулирует первый признак равенства треугольников.

— Кто желает доказать данный признак у доски?

Ребята в парах друг другу формулируют 1 признак равенства треугольников

1 ученик доказывает

признак у доски

Решение задач.

(Лес задач)

7 мин.

-И вот, мы на материке. Мне кажется, что вам хотелось бы посетить старинный город, но дорога к городу ведет через лес задач Задача 1 (1 мин)

— Для каждой задачи помимо элементов, отмеченных на чертеже, нужно использовать приём (приёмы), с помощью которых можно будет найти недостающие равные элементы для доказательства равенства треугольников.

Какой приём мы использовали в 1 задаче

Задача 2 (1 мин)

Задача 3 1(мин)

Задача 4 1 (мин)

Устное решение задач по готовым чертежам

Общая сторона

Вертикальные углы

Смежные углы

Биссектриса угла

Физкультминутка 2 мин

Путешествие по лесу задач оказалось сложным. Давайте чуть-чуть отдохнем и разомнёмся

Выполняют упражнения физкультминутки под музыку

Формирование навыков применения признака (Решение задач)

7 мин

— А сейчас вам предстоит письменно решить задачи по готовым чертежам

Пожалуйста, выполните предложенные вам задания

— Выполнили работу? Проверьте, пожалуйста,

Решают задачи

Проверяют работу, сверяя с правильными ответами на экране. (работа в парах, поменялись тетрадями)

Итог урока

3 мин.

6 мин

— Итак, ребята, мы в городе

А кто из вас догадался, как называется этот город?.

— Почему? Как вы думаете?

— Правильно. Молодцы. Значит, наше путешествие будет продолжаться и на следующих уроках, на которых мы с вами продолжим знакомиться с достопримечательностями города Треугольников, узнаем много нового и интересного.

— Ребята мы сегодня на уроке не просто решали задачи, мы анализировали и незаметно для себя составили карточку-подсказку в которой отразили Основные приёмы поиска недостающих равных элементов для доказательства равенства треугольников. Вы молодцы. Данная карточка будет помогать вам при решении задач уже сегодня на уроке (Раздать карточки)

У вас есть 6 минут для выполнения самостоятельной работы, результаты выполнения которой вы узнаете на следующем уроке

На «3» — № 1, 2, 7 — 1 уровень

На «;4» — №5, 13 — 2 уровень

На «5»- № 15, 17 — 3 уровень

— Это город треугольников Мы начали изучать признаки равенства треугольников, изучили только один, наверно еще есть, нам необходимо познакомиться и с другими признаками

Д/з: Саморефлексия

4 мин

— А сейчас, кому было комфортно на уроке, кто справился со всеми задачами без труда, для вас для решения дома карточки красного цвета.

-Те, кто еще затрудняется в решении задач, кому необходимо доучить формулировки теорем и определений – для вас, карточки зеленого цвета.

— А тем, кому сегодня было трудно и еще не все понятно, но есть желание узнать о стране геометрии много нового, научиться решать задачи – для вас, карточки желтого цвета.

— Большое спасибо за урок.

Выбирают домашнее задание, согласно уровню подготовки

infourok.ru

Решение задач по теме: «Первый признак равенства треугольников»

Слайды и текст этой презентации

Слайд 1

Решение задач по теме: «Первый признак равенства треугольников» 7 класс

Слайд 2

Цели и задачи: Повторить понятие треугольника, его элементов, понятие равных фигур, первый признак равенства треугольников. Учиться решать задачи на применение первого признака равенства треугольников.

Слайд 3

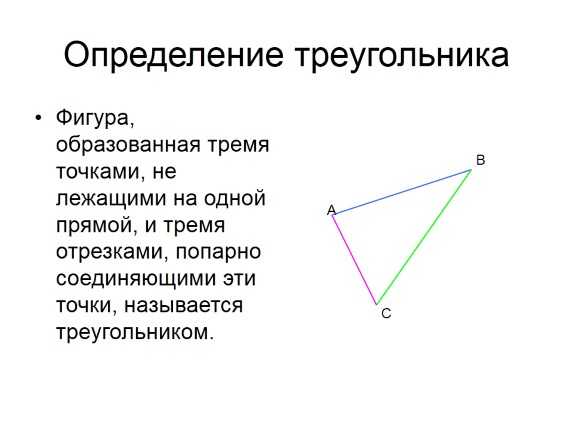
Определение треугольника
Фигура, образованная тремя точками, не лежащими на одной прямой, и тремя отрезками, попарно соединяющими эти точки, называется треугольником.
В
С
А

Слайд 4

Равенство геометрических фигур
Геометрические фигуры называют равными, если при наложении они совпадают.

Слайд 5

Равные фигуры

Слайд 6

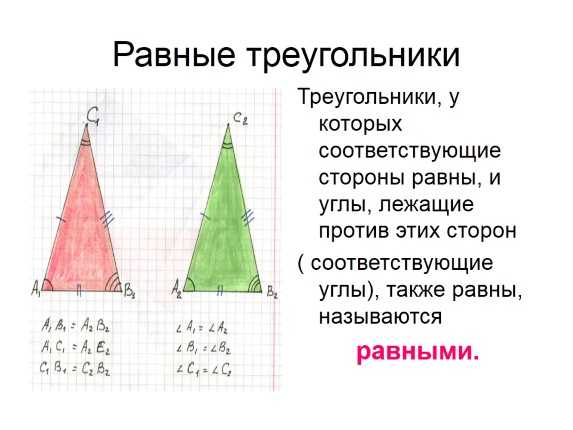
Равные треугольники
Треугольники, у которых соответствующие стороны равны, и углы, лежащие против этих сторон ( соответствующие углы), также равны, называются равными.

Слайд 7

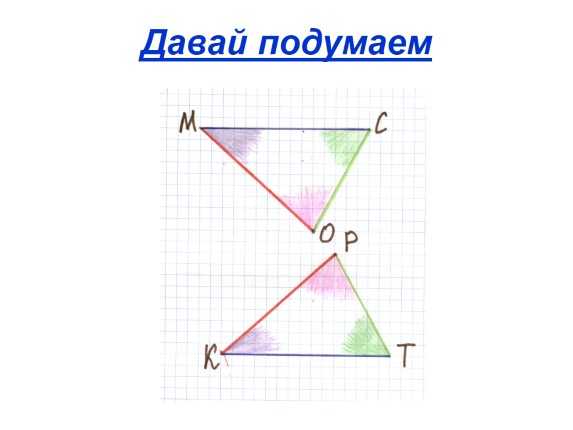
Давай подумаем

Слайд 8

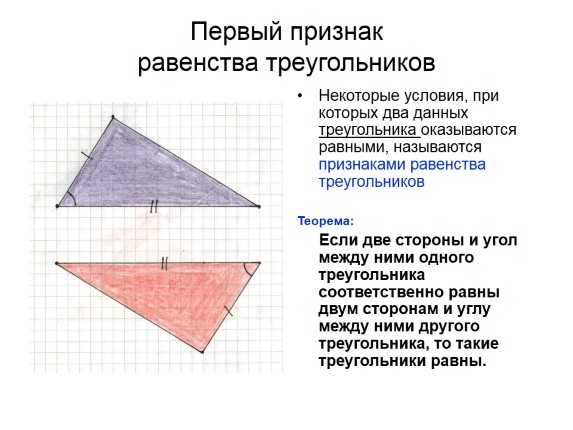
Первый признак равенства треугольников
Некоторые условия, при которых два данных треугольника оказываются равными, называются признаками равенства треугольников Теорема: Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Слайд 9

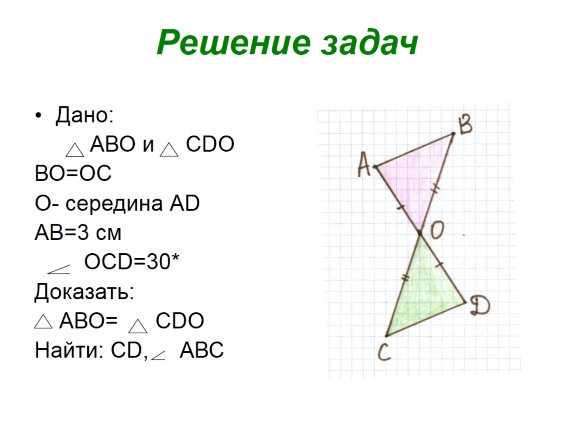
Решение задач
Дано: АВО и СDО ВО=ОС О- середина АD АВ=3 см ОСD=30* Доказать: АВО= СDО Найти: СD, АВС

Слайд 10

Доказательство:
АОВ= СОD (как вертикальные), АО=ОD( так как О — середина АD), ВО=ОС (по условию) АОВ= СОD (по I признаку равенства треугольников) Ч.Т.Д.

Слайд 11

Решение
Так как треугольники равны, равны их соответствующие элементы Т.о. СD=АВ=3 см АВС= ОСD=30* Ответ: 3 см, 30*

Слайд 12

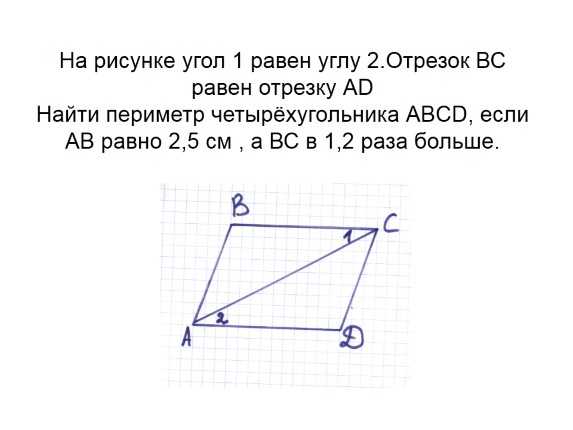
На рисунке угол 1 равен углу 2.Отрезок ВС равен отрезку АD Найти периметр четырёхугольника АBСD, если АВ равно 2,5 см , а ВС в 1,2 раза больше.

Слайд 13

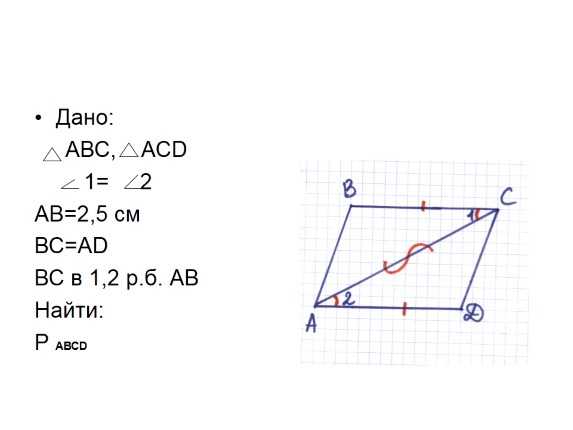
Дано: АВС, АСD 1= 2 АВ=2,5 см ВС=АD ВС в 1,2 р.б. АВ Найти: Р АВСD

Слайд 14

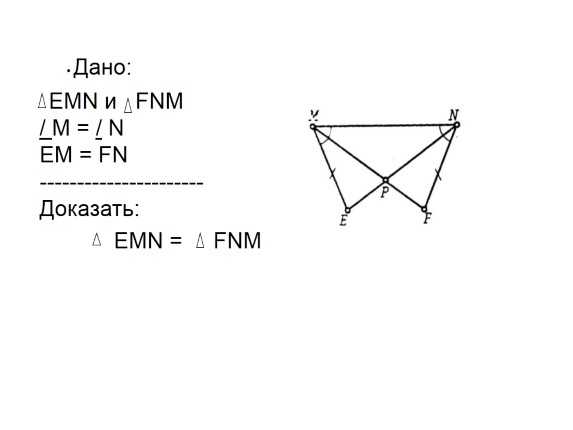
Дано:
EMN и FNM / М = / N EM = FN ———————- Доказать:
EMN = FNM

Слайд 15

Составьте задачу по рисунку и решите её.
ДОМАШНЕЕ ЗАДАНИЕ

lusana.ru

Открытый урок по геометрии в 7-м классе по теме «Решение задач. Первый признак равенства треугольников»

Разделы: Математика

---

Цель урока:

1. Систематизировать, обобщить основные понятия по теме “Треугольник”.
2. Закрепить основные шаги решения задач по темам “I признак равенства треугольников. Замечательные линии треугольника”.

Здравствуйте, ребята! Сегодня мы вместе вспомним основные понятия темы “Треугольник”, разберем три задачи с комментированием, напишем тест и закончим нашу встречу обсуждением творческого домашнего задания.

У каждого из вас на столе находится тетрадь – тетрадь одного урока.

Раскрываем тетрадь и смотрим на первую страницу.

Что мы знаем о треугольнике?

	Разно — сторонний	Равно — бедренный	Равно — сторонний
Тупо — угольный
Прямо — угольный
Остро — угольный

Вашему вниманию предлагается таблица классификации треугольников одновременно по сторонам и углам. Давайте заполним эту таблицу, нарисовав требуемый треугольник в каждой ячейки таблицы. Выполняя это задание, мы отвечаем на следующие вопросы.

1. Что такое треугольник?
2. Что называется высотой?
3. Что называется медианой?
4. Что называется биссектрисой?
5. На каком из предложенных рисунков изображены высота, медиана, биссектриса?

Назовите их. Объясните свой выбор.

6. Дайте двойные названия треугольникам, учитывая как величины углов, так и отношения длин сторон, например, в первой ячейке таблицы мы нарисуем ∆XYZ – это тупоугольный (угол Z – тупой) разносторонний (три стороны разной длины) треугольник.

Учащиеся могут сверить результаты своей работы с изображением готовой таблицы на интерактивной доске.

Смотрим на вторую страницу тетради!

Вам предлагается решить, аккуратно оформив на листке первую или вторую задачу, или обе вместе. На доске записываются решения сразу обеих задач учениками, пожелавшими объяснить ход рассуждений.

Решаем задачи! Удачи Вам!

Учащиеся могут проверить результаты своей работы с записями отвечающих у доски.

Задача 1.

Доказательство. Рассмотрим

1) сторона СО – общая;

2) АО = ВО, т.к. отрезок СО – медиана

3)

Вывод: по первому признаку равенства треугольников.

Задача 2.

Доказательство. По условию , а в равных треугольниках соответствующие элементы равны, т.е. АЕ = А₁Е₁; АС = А₁С₁; ЕС = Е₁С₁;

Рассмотрим

1) АС = А₁С₁ по доказанному;

2) по доказанному;

3) АР = А₁Р₁, т.к. АР = АЕ + ЕР и А₁Р₁ = А₁Е₁ + Е₁Р₁, и АЕ = А₁Е₁ по доказанному, ЕР = Е₁Р₁ по условию.

Вывод: по первому признаку равентства треугольников.

 Открываем третью страницу тетради!

Дан рисунок. Вам, ребята, необходимо записать дано, выбрать два треугольника, равенство которых вы сможете доказать. Задача имеет несколько решений – проведите исследование.

К доске приглашаются по желанию два ученика, которые записывают свои рассуждения.

Приведем один из возможных вариантов решения данной задачи.

Например, рассмотрим ∆BAP и ∆BCP

1) по условию;

2) ВА = ВС по условию;

3) АР = СР, т.к. АР = ЕР + АЕ = 2АЕ и СР = СМ + МР = 2АЕ, учитывая равенство отрезков АЕ, ЕР, РМ, МС.

Вывод: по первому признаку равентсва треугольников.

Можно доказать равентсво?

А теперь четвертая страница тетради!

Перед вами тест. Даны семь задач. Указаны три ответа на каждую задачу, из которых один верный. Вам необходимо записать соответствие номера задачи и буквы правильного ответа.

Попробуем выполнить тест! Смелее!

Тест рассчитан на 3 — 5 минут.

Вариант 1

1. а) ВО – медиана б) ВО – высота в) ВО – биссектриса	4. а) Р∆XYZ = 18cм б) Р∆XYZ = 36см в) Р∆XYZ= 9см
2. а) Р∆ОЕК  = 21см б) Р∆ОЕК  = 18см в) Р∆ОЕК  = 20см	5. а) СМ – медиана б) СМ – высота в) СМ – биссектриса
3. Дано: = 30° а) б) в)	6. Биссектриса треугольника – это… а) отрезок б) луч в) перпендикуляр. 7. Треугольник, имеющий прямой угол, называется: а) остроугольным; б) тупоугольным; в) прямоугольным.

Вариант 2

1. а) ВО – медиана б) ВО – биссектриса в) ВО – высота	4. а) Р∆XYZ =26cм б) Р∆XYZ = 13см в) Р∆XYZ = 52см
2. а) Р∆ОЕК = 11см б) Р∆ОЕК = 13см в) Р∆ОЕК = 12см	5. а) СМ – высота б) СМ – биссектриса в) СМ – медиана
3.  Дано: АО = 6см а) АВ = 6см б) АВ = 3см в) АВ = 12см	6. Высота треугольника – это… а) луч б) середина в) перпендикуляр. 7. Треугольник, имеющий тупой угол, называется: а) тупоугольным; б) прямоугольным; в) остроугольным.

 Проверить правильность выполнения теста можно на уроке во фронтальном опросе или после уроков, т.к. учащиеся сдают тетради по завершению занятия.

(Ключи к тесту: вариант 1 – 1а, 2б, 3б, 4а, 5б, 6а, 7в; вариант 2 – 1б, 2а, 3в, 4а, 5а, 6в, 7а)

Наша встреча завершается. Вам дома предлагалось выполнить творческое задание: посчитать треугольники на предложенных рисунках.

Давайте посмотрим на титульный лист тетради.

Но ведь мы определенно носим в себе ощущение
математической красоты, гармонии чисел и формы,
геометрического изящества.

Анри Пуанкаре

Обсуждение можно провести устно. Некоторые ученики демонстрируют свои решения в рисунках, которые отражают последовательность счета треугольников. Приветствуется использование интерактивной доски или мультимедийного проектора.

Спасибо за урок! До следующих встреч!

(Если учащиеся не смогли во время урока найти и доказать все пары равных треугольников в третьей задаче, то можно предложить продолжить решение этой задачи дома.)

8.04.2009

xn--i1abbnckbmcl9fb.xn--p1ai

7 класс. Геометрия. Треугольники, признаки равенства треугольников. — Решение задач по теме » Первый признак равенства треугольников».

Комментарии преподавателя

Вспом­ним пред­ва­ри­тель­но фор­му­ли­ров­ку пер­во­го при­зна­ка ра­вен­ства тре­уголь­ни­ков.

                                    

Рис. 1. Пер­вый при­знак ра­вен­ства тре­уголь­ни­ков

Опре­де­ле­ние: Пер­вый при­знак ра­вен­ства тре­уголь­ни­ков – это ра­вен­ство их по углу и при­ле­жа­щим сто­ро­нам.

Из этих трех ра­венств и вы­те­ка­ет ра­вен­ство самих тре­уголь­ни­ков.

Смысл ра­вен­ства тре­уголь­ни­ков за­клю­ча­ет­ся в том, что при сов­ме­ще­нии этих трех эле­мен­тов га­ран­ти­ру­ет­ся сов­ме­ще­ние, то есть ра­вен­ство всех осталь­ных эле­мен­тов двух тре­уголь­ни­ков.

Рас­смот­рим сле­ду­ю­щие за­да­чи:

При­мер 1: Из­ме­рить на мест­но­сти рас­сто­я­ние между двумя точ­ка­ми A и B, между ко­то­ры­ми нель­зя прой­ти по пря­мой. Для этого вы­би­ра­ют такую точку С, из ко­то­рой можно прой­ти и к точке А, и к точке В, и из ко­то­рой видны обе эти точки. Про­ве­ши­ва­ют рас­сто­я­ния АС и ВС, про­дол­жа­ют их за точку С и от­ме­ря­ют СD = AC и ЕС = СВ. Тогда от­ре­зок ED равен ис­ко­мо­му рас­сто­я­нию. Объ­яс­ни­те, по­че­му.

Ре­ше­ние:

Вы­пол­ним по­яс­ни­тель­ный ри­су­нок:

                

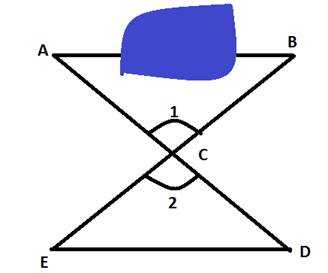
Рис. 2. Чер­теж к при­ме­ру 1

Про­длим от­рез­ки АС и ВС. От­ме­ря­ем СЕ = СВ и CD = CA. ∆CDE = ∆CAB по пер­во­му при­зна­ку.

.

Из ра­вен­ства тре­уголь­ни­ков сле­ду­ет, что ED = AB.

Ответ: За­да­ча ре­ше­на.

При­мер 2: Через се­ре­ди­ну О от­рез­ка АВ про­ве­де­на пря­мая р, пер­пен­ди­ку­ляр­ная пря­мой АВ. До­ка­жи­те, что каж­дая точка Х этой пря­мой оди­на­ко­во уда­ле­на от точек А и В (каж­дая точка се­ре­дин­но­го пер­пен­ди­ку­ля­ра к от­рез­ку АВ рав­но­уда­ле­на от его кон­цов).

Ре­ше­ние:

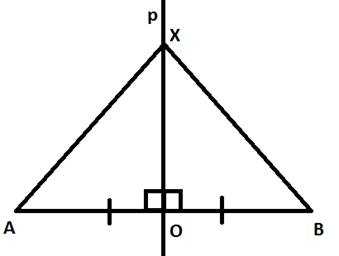
Рис. 3. Чер­теж к при­ме­ру 2

Рас­смот­рим тре­уголь­ни­ки АОХ и ВОХ. ∆АОХ = ∆ВОХ – по пер­во­му при­зна­ку.

Из ра­вен­ства тре­уголь­ни­ков сле­ду­ет, что АХ = ВХ для любой про­из­воль­ной точки Х, ко­то­рая при­над­ле­жит пря­мой р.

Ответ: До­ка­за­но.

При­мер 3: На сто­роне АВ тре­уголь­ни­ка АВС взята точка D, а на сто­роне тре­уголь­ни­ка  взята точка . Из­вест­но, что тре­уголь­ни­ки ADC и  равны и от­рез­ки DB и  равны. До­ка­жи­те ра­вен­ство тре­уголь­ни­ков АВС и .

Ре­ше­ние:

                                             

Рис. 4. Чер­теж к при­ме­ру 3

Рас­смот­рим тре­уголь­ни­ки АВС и . В них . АС = 

www.kursoteka.ru