Методы решения логических задач
Исходными данными в логических задачах являются высказывания. Эти высказывания и взаимосвязи между ними бывают так сложны, что разобраться в них без использования специальных методов достаточно трудно.
Многие логические задачи связаны с рассмотрением нескольких конечных множеств и связей между их элементами. Для решения таких задач зачастую прибегают к помощи таблиц или графов, при этом успешность решения во многом зависит от удачно выбранной структуры таблицы или графа. Аппарат же алгебры логики позволяет построить формальный универсальный способ решения логических задач.
Формальный способ решения логических задач
Выделить из условия задачи элементарные (простые) высказывания и обозначить их буквами.
Записать условие задачи на языке алгебры логики, соединив простые высказывания в сложные с помощью логических операций.
Составить единое логическое выражение для всех требований задачи.
Используя законы алгебры логики, попытаться либо упростить полученное выражение и вычислить все его значения, либо построить таблицу истинности для рассматриваемого выражения, либо доказать истинность (ложность) некоторых утверждений методом рассуждений.
Выбрать решение — набор значений простых высказываний, при котором построенное логическое выражение является истинным.
Проверить, удовлетворяет ли полученное решение условию задачи.
Рассмотрим, как можно использовать эти способы для решения задач.
Решение логических задач средствами алгебры логики
Задача «Уроки логики». На вопрос, кто из трех учащихся изучал логику, был получен ответ: «Если изучал первый, то изучал и второй, но неверно, что если изучал третий, то изучал и второй». Кто из учащихся изучал логику?
Решение. Введём обозначения:
Р1 – первый учащийся изучал логику;
Р2 – второй учащийся изучал логику;
Р3 – третий учащийся изучал логику.
Из условия задачи следует истинность высказывания . Воспользуемся соотношением (20) и упростим исходное высказывание:
.
Высказывание 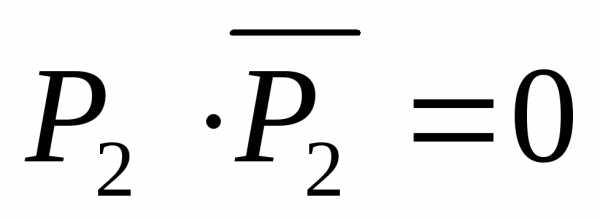 (согласно
(11)), а, следовательно, ложно и высказывание
(согласно
(11)), а, следовательно, ложно и высказывание  .
Поэтому должно быть истинным высказывание
.
Поэтому должно быть истинным высказывание 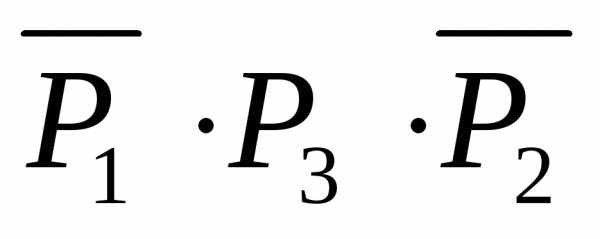 .
.
Ответ. Логику изучал третий учащийся, а первый и второй не изучали.
Задача «Прогноз». Трое друзей, болельщиков автогонок «Формула-1», спорили о результатах предстоящего этапа гонок.
— Вот увидишь, Шумахер не придет первым, — сказал Джон. Первым будет Хилл.
— Да нет же, победителем будет, как всегда, Шумахер, — воскликнул Ник. — А об Алези и говорить нечего, ему не быть первым.
Питер, к которому обратился Ник, возмутился:
— Хиллу не видать первого места, а вот Алези пилотирует самую мощную машину.
По завершении этапа гонок оказалось, что каждое из двух предположений двоих друзей подтвердилось, а оба предположения третьего из друзей оказались неверны. Кто выиграл этап гонки?
Решение. Введем обозначения для логических высказываний:
Ш — победит Шумахер; Х — победит Хилл; А — победит Алези.
Реплика Ника «Алези пилотирует самую мощную машину» не содержит никакого утверждения о месте, которое займёт этот гонщик, поэтому в дальнейших рассуждениях не учитывается.
Зафиксируем высказывания каждого из друзей:
Джон: 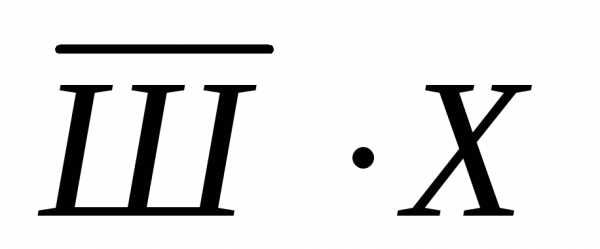 ,Ник:
,Ник: 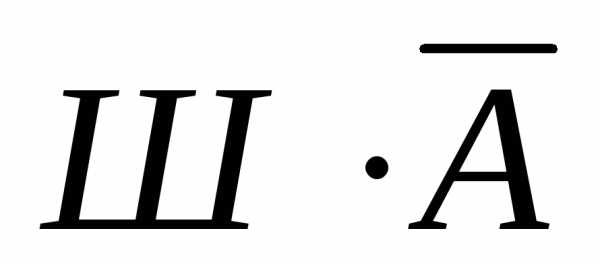 ,
Питер:
,
Питер: 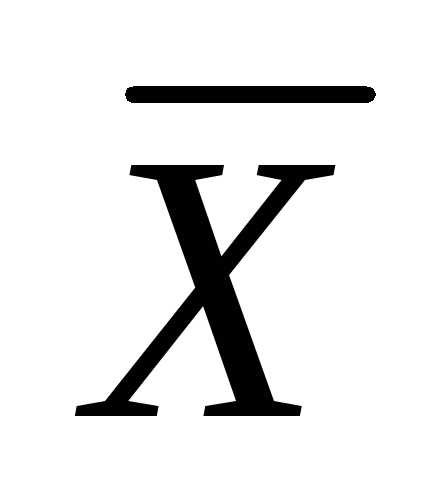 .
.
Учитывая то, что предположения лишь двух друзей подтвердились, а предположения третьего неверны, запишем все возможные комбинации истинности двух из трёх высказываний. Тогда истинное высказывание будет иметь вид:
=1.
Упростим это выражение. Используя (11), установим, что первые два слагаемые тождественно-ложные. Тогда, с учётом формул де Моргана для третьего слагаемого:
Ответ. Победителем этапа гонок стал Шумахер.
studfiles.net
Решение логических задач
Основные приемы и методы решения логических задач
Рассмотрим разные способы решения логических задач.
Каждый из приемов имеет свою область применения.
Логические (или нечисловые задачи) относятся к нестандартным задачам. К ним относят текстовые задачи, в которых необходимо распознать объекты или расположить их в определенном порядке. При этом часть утверждений в условии задачи может быть истинной или ложной. К логическим задачам относят также задачи на переливания и взвешивания (фальшивые монеты и т.п.).
Можно выделить несколько различных способов решения логических задач, которые можно назвать следующим образом:
метод рассуждений;
метод таблиц;
метод графов;
метод блок-схем;
метод бильярда;
метод кругов Эйлера.
Метод рассуждений
Метод рассуждений является самым примитивным способом и его обычно применяют для решения самых простых логических задач. Идея метода заключается в проведении рассуждений при последовательном использовании всех условий задачи, вследствие чего приходят к выводу, который является ответом задачи.
Пример 1
Владимир, Семен и Олег изучают разные иностранные языки: английский, французский и немецкий. На вопрос, какой язык изучает каждый из них, один ответил: «Владимир изучает английский, Семен не изучает английский, а Олег не изучает немецкий». Впоследствии выяснилось, что в этом ответе только одно утверждение верно, а два других ложны. Какой язык изучает каждый из студентов?
Решение:
Имеем три утверждения. Если принять за истину первое утверждение, то правдиво и второе, т.к. студенты изучают разные языки, что противоречит условию задачи. Таким образом первое утверждение ложно.
Если правдивым является второе утверждение, то первое и третье должны быть ложными. В таком случае получаем, что никто не изучает английский. Это противоречит условию, таким образом, второе утверждение также является ложным.
Остается третье утверждение, которое можем считать верным, а первое и второе — ложными. Таким образом, Владимир не изучает английский, его изучает Семен.
Ответ: Семен изучает английский язык, Олег — французский, Владимир — немецкий.
Метод таблиц
Основным приемом для решения текстовых логических задач является метод таблиц. С помощью таблиц можно наглядно представить условие задачи или ее ответ, кроме того их использование значительно помогают в принятии правильных логических решений.
Пример 2
У трех кукол Маши, Даши и Алены были платья трех разных цветов: красного, зеленого и синего. Туфли у них были таких же цветов. У Маши цвет платья и туфель совпадали. У Алены ни туфли, ни платье не были красными. Даша была в зеленых туфлях и в платье другого цвета. Как были одеты куклы?
Решение:
Составим таблицу, в которой отметим возможные цвета платьев и туфель кукол. По условию задачи заполним таблицу:
туфли Даши зеленые, а платье не зеленое. Следовательно, у Маши и Алены туфли уже не могут быть зелеными, так же как не могут быть туфли Даши синими или красными. Отмечаем все в таблице:
туфли и платье Алены не являются красными. Из таблицы видим, что красные туфли могут быть только у Маши, а, следовательно, туфли Алены — синие. Правая часть таблицы заполнена.
Рисунок 1.
- Цвет платья Маши совпадает с цветом ее туфель, значит оно красное. Теперь легко увидеть, что у Алены — зеленое платье, а у Даши — синее.
Рисунок 2.
Таблица полностью заполнена и в ней однозначно установлены цвета туфель и платьев кукол.
Ответ: Маша одета в красное платье и красные туфли, Даша в синем платье и зеленых туфлях, Алена в зеленом платье и синих туфлях.
Метод блок-схем
Этим методом решаются задачи, в которых с помощью сосудов требуется отмерить необходимое количество жидкости или связанные со взвешиванием на чашечных весах. Простейшим приемом решения таких задач является перебор всех возможных вариантов, который не является удобным и не дает возможности выделения общего подхода к решению подобных задач.
Суть метода блок-схем состоит в следующем:
выделяют операции для точного отмеривания жидкости, которые называются командами;
устанавливают последовательность выполнения команд, которая оформляется в виде блок-схемы (как в программировании). Составленная блок-схема является программой, выполнение которой должно привести к решению задачи, в ходе которой достаточно отмечать получаемые количества жидкости.
При выполнении программы удобно заполнять отдельную таблицу, в которую заносится количество жидкости в каждом из имеющихся сосудов.
Метод математического бильярда
Игра в бильярд стала предметом серьезных научных исследований в области механики и математики. Если представить горизонтальный бильярдный стол произвольной формы без луз, по которому без трения будет двигаться точечный шар, абсолютно упруго отражаясь от бортов стола, то возникал вопрос: какой может быть траектория этого шарика. В поисках ответа на этот вопрос появилась теория математического бильярда (теория траекторий).
С помощью данного метода можно очень легко решать задачи на переливание жидкостей.
Пример 3
Дано два сосуда — объемом $3$ л и $5$ л. С помощью этих сосудов необходимо получить $1$, $2$, $3$, $4$, $5$, $6$, $7$ и $8$ литров воды. Имеется водопроводный кран и раковина, в которую можно выливать воду.
Решение:
Построим для данной задачи параллелограмм со сторонами $3$ и $5$ единиц. По горизонтали будет откладываться количество воды в литрах в пятилитровом сосуде, а по вертикали — в трехлитровом. На всем параллелограмме нанесем сетку из одинаковых равносторонних треугольников:
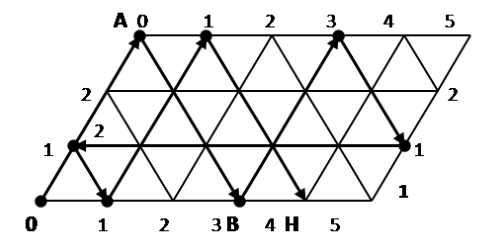
Рисунок 3.
Бильярдный шар может перемещаться только вдоль прямых, которые образуют сетку на параллелограмме. При ударе о сторону параллелограмма шар отражается и движется вдоль борта. При этом каждая точка соударения о сторону параллелограмма полностью характеризует, сколько воды находится в каждом из сосудов.
spravochnick.ru
Решение логических задач и силлогизмов, страница 4
5.[h5] Изобразить первую и вторую фигуры категорического силлогизма. По каждой фигуре построить правильный силлогизм (для этого нужно воспользоваться таблицей правильных модусов) так, чтобы его посылки были истинными суждениями. Убедиться, что полученное заключение тоже является истинным суждением. (Записать текст посылок и заключения.)
Силлогизм, соответствующийIфигуре:
Все студенты данной группы (M) должны решить задачи по Логике (P).
Петров (S) – студент данной группы (М).
Петров (S) должен решить задачи по Логике (P).
Его модус АII является правильным.
Силлогизм, соответствующий II фигуре:
Ни один студент заочного отделения (P) не будет сдавать экзамен по физкультуре (М).
Студент Смирнов (S) будет сдавать экзамен по физкультуре (М).
Смирнов (S) не является студентом заочного отделения заочного отделения (Р).
Его модус ЕIO является правильным.
6. Изобразить третью и четвертую фигуры категорического силлогизма. Далее выполнить задание по условию задачи № 5.
Силлогизм, соответствующий III фигуре:
Все герани (М) – комнатные растения (Р).
Все герани (М) цветут (S).
Некоторые комнатные растения (Р) цветут (S).
Модус данного силлогизма ААI.
Силлогизм для IVфигуры:
Многие спортсмены (Р) являются учащимися высших учебных заведений (М).
Некоторые учащиеся высших учебных заведений (М) участвуют в художественной самодеятельности (S).
Некоторые спортсмены (S) участвуют в художественной самодеятельности (Р).
Модус силлогизма – ААI.
7. III. Проверить тремя способами (по особым правилам фигур, по модусам и по правилам категорического силлогизма), являются ли приведенные ниже категорические силлогизмы правильными, а заключение – истинным суждением.
№ 1. Все рыбы (Р) плавают (М).
Это животное (S) плавает (М).
—————————————————
Это животное (S) – рыба (Р).
Данный силлогизм соответствует правилу II фигуры. Его модус – AII. Его вывод не является истинным, т.к. нарушено правило учетверения терминов.
№ 2. Все ягоды (М) – плоды (P).
Арбуз (S) – ягода (М).
————————————————
Арбуз (S) – плод (P).
Данный силлогизм соответствует правилу I фигуры. Его модус – AAA. Он не противоречит ни одному из правил категорического силлогизма. Его заключение истинно.
№ 3. Во всех городах за полярным кругом (М) бывают белые ночи (P).
Санкт-Петербург (S) не находится за полярным кругом (М).
———————————————————————————————————————————
В Санкт-Петербурге (S) не бывает белых ночей (Р).
Данный силлогизм соответствует правилу I фигуры. Его модус – AOO не является правильным. Заключения не является истинными.
№ 4. Чистый воздух (М) полезен (P) для дыхания человека.
В этой комнате (S) чистый воздух (М).
———————————————————————————————————————-
Воздух этой комнаты (S) полезен (P) для дыхания человека.
Данный силлогизм соответствует правилу I фигуры. Его модус – AII. Он не противоречит ни одному из правил категорического силлогизма. Его заключение истинно.
Литература.
1. Гетманова А.Д. Логика. Учебник. Оега-Л, М., 2006.
2.
[h2]Замечание к оформлению решения задач!
При оформлении решения каждой задачи необходимо придерживаться следующих требований: 1) сначала до конца продумать решение задачи, затем последовательно, чётко изложить весь ход логических рассуждений, приводящих в итоге к окончательному исчерпывающему решению задачи; 2) при оформлении решения задачи следует исключить все лишние, не необходимые для решения данной задачи, рассуждения, т.е. постараться оформить решение задачи так, чтобы в тексте не было ни одного лишнего слова.
[h3] Подчеркнуто преподавателем.
[h4]Замечание.
Следует иметь в виду, что диаграммы Эйлера-Венна не обязательно круги, диаграммами могут быть и эллипсы, и квадраты, и любая другая фигура. При выполнении заданий форма фигур выбирается из соображений удобств.
[h5]Примечание: В задачах 5-10, если ответом будет решение: «рассуждение — неправильно», то для иллюстрации решения с помощью диаграмм Эйлера-Венна, достаточно привести один опровергающий пример, т.е. нарисовать картинку, из которой очевидно следует, что данное рассуждение неверно.
[h5]Замечание. При выполнении заданий №№ 5 и 6 при построении правильных силлогизмов нет необходимости проверять их правильность при помощи девяти правил, т.к., если при построении силлогизмов используются правильные модусы (каждая фигура имеет свои правильные модусы, см. таблицу), то и силлогизм необходимо будет правильным, и из истинных посылок необходимо будет выводиться истинное суждение заключения.
Вообще правильность силлогизмов проверяется тремя способами: по особым правилам фигур (см. учебник Гетмановой, стр. 132), по модусам (см. таблицу правильных модусов) и по девяти правилам категорического силлогизма.
vunivere.ru
Решение задач по логике с ответами для юристов
Правильное мереологическое деление. 9. Таксономическое деление с излишним членом. Упражнение 8 (с. 179) 1. Правильная таксономическая классификация. К ГЛАВЕ VIII. ЛОГИЧЕСКИЕ И МЕТОДОЛОГИЧЕСКИЕ АСПЕКТЫ АРГУМЕНТАЦИИ И КРИТИКИ Упражнения (с. 228—230) 3. Тезис — “Невозможны коляски, которые ездят без лошадей”. Аргументация не является доказательной. 9. Нарушено правило по отношению к тезису. Не определено понятие “лгун”. 11. Правильная доказательная аргументация “от противного”. 13. Решение задач по логике с ответами для юристов Задание 12 Проверьте, правильно ли произведено превращение приведенного ниже суждения; укажите, в чем заключается ошибка, если превращение произведено неправильно: Ни одна демократическая страна не одобряет терроризм. Некоторые демократические страны одобряют не терроризм. Превращение не полное. Все демократические страны одобряют терроризм.
Примеры решения задач по логике (стр. 1 из 2)
Схема превращения: При этом частноутвердительное суждение превращается в частноотрицательное и наоборот, а общеутвердительное суждение превращается в общеотрицательное и наоборот. Выделим два частных способа превращения: — путем двойного отрицания, которое ставится перед связкой и перед предикатом: S есть Р S не есть не-Р.
Некоторые неудачники любят ссылаться на обстоятельстваНа обстоятельства ссылаются некоторые неудачники. — отрицание можно переносить из предиката в связку: Некоторые неудачники любят ссылаться на обстоятельства На обстоятельства ссылаются некоторые неудачники. Обращение – это логическая операция, посредством которого происходит преобразования суждения, в результате которого субъект исходного суждения становится перидикатом нового суждения, а предикат субъектом.
Задачи по логике (24 шт.) с решениями — файл n1.doc
Внимание Физика в задачах: Экзаменационные задачи с решениями (Документ)- Бобровникова Н.Н., Газарян А.С., Шадрина Г.П. Осесимметричный изгиб круглых пластин, устойчивость продольно сжатых стержней (Документ)
ВАРИАНТ II Понятие Задание 1.
Содержание какого понятия богаче в следующих парах понятий? а) Преступление против личности. Клевета. б) Военнослужащий. Сержант. Ответ: а) Ст.129 УК РФ «Клевета» входит в раздел «Преступления против личности», т.е.
первое понятие шире. б) Сержант является воинским званием военнослужащих и поэтому это понятие менее богатое, чем понятие военнослужащий. Задание 2. Дайте полную логическую характеристику понятиям: а) Судимость б) Рязанский кремль Ответ: а) Понятие общее, абстрактное, относительное, отрицательное, собирательное.
б) Понятие частное, конкретное, безотносительное, несобирательное. Задание 3.
Решение задач по логике
Чgиф\ШЗ’#Ѕу}arкіmТkXЮџЗГ2яьЌ wy=%В[l)gXмЮ,њ(рYS i+YyPЫOqy2руЂЇњFвхђ2ЬЗaAFШЛ 2№»аяxDСH brњZІЄ пюф=ч`ч3lHБпС§ЂпОыd!ѓпЅљ]?рж:їЮ\BAъ.TTёГЊ Ді§FЇбAН!іЦSdGRшѓ,і\<ГФ
- Примеры решения задач по логике
- Задачи по логике (24 шт.) с решениями — файл n1.doc
- Решение задач по логике
- Решения задач по логике
- Юридический казус
- Ответы на задачи по логике для юристов
Примеры решения задач по логике Внимание Для его доказательства мы располагаем рядом аргументов:
- Все щелочные металлы различают воду при комнатной температуре.
- Натрий щелочной металл.
- Полученный в лаборатории металл не различает воду при комнатной температуре.
Все перечисленные в качестве аргументов утверждения являются истинными.
Контрольная работа: примеры решения задач по логике
Превращение – вид непосредственного умозаключения, при котором предикат заключения является отрицанием предиката посылки. Как уже отмечалось, по качеству связки («есть» или «не есть») категория суждения делится на утвердительные и отрицательные.
Схема превращения: При этом частноутвердительное суждение превращается в частноотрицательное и наоборот, а общеутвердительное суждение превращается в общеотрицательное и наоборот. Выделим два частных способа превращения: — путем двойного отрицания, которое ставится перед связкой и перед предикатом: S есть Р S не есть не-Р.
Некоторые неудачники любят ссылаться на обстоятельстваНа обстоятельства ссылаются некоторые неудачники. — отрицание можно переносить из предиката в связку: Некоторые неудачники любят ссылаться на обстоятельства На обстоятельства ссылаются некоторые неудачники.
Решение задач по логике с ответами для юристов
ИнфоНатрий различает воду при комнатной температуре» — А. Третий – Б. Натрий (S) различает воду при комнатной температуре (M).
Полученный в лаборатории металл (P) не различает воду при комнатной температуре (M). Задачи по логике (24 шт.) с решениями — файл n1.doc Ответ: Энтимемой, или сокращенным категорическим силлогизмом, называется силлогизм, в котором пропущена одна из посылок или заключение.- пропущена меньшая посылка Всем юристам – важно уметь применять логику Этот человек – юрист Умение применять логику в своей практической деятельности — являются юристы Задание 17 Является ли правильным следующее разделительно-категорическое умозаключение? «Воспитание … дается нам или природой, или людьми, или вещами… из этих трех различных видов воспитания воспитание со стороны природы вовсе не зависит от нас, а воспитание со стороны людей — вот единственное, в котором мы сами – господа…» (Ж.-Ж.
Примеры решения задач по логике
По твоему, на свете только три несчастья и есть: жить зимой в холодной квартире, летом носить узкие сапоги да ночевать в комнате, где пищит ребенок, которого нельзя посыпать персидским порошком; у меня нет ни первого, ни второго, ни третьего. Следовательно, нет у меня несчастья» (И. Тургенев). Ответ: По-твоему, на свете только три несчастья и есть: жить зимой в холодной квартире, летом носить узкие сапоги да ночевать в комнате, где пищит ребенок, которого нельзя посыпать персидским порошком; у меня нет ни первого, ни второго, ни третьего.
Следовательно, нет у меня несчастья Список литературы
- Багаров В.А. Основы логики: Учеб. / В.А. Багаров, В.И. Маркин. М., 1998.
- Берков В.Ф.
Логика / В.Ф. Берков, Я.С. Яскевич, В.И. Павлюкевич. Мн.: НТООО «ТетраСистемс», 1997. 480 с.
- Бузук Г.Л.
Логика в вопросах и ответах: Опыт популярного учеб, пособия / Г.Л. Бузук М.
Ответы на задачи по логике для юристов
Истинное Несовместимое противоположное (контрарное) суждение Ни по каким делам законом не предусматривается проведение экспертиз Ложное Несовместимое (контрадиктарное) суждение Все дела не предусматривают закономпроведение экспертиз Ложное Задание 10 Установите термины, входящие в состав данного сложного сужения и напишите его в символической форме, используя логические знаки конъюнкции, дизъюнкции, импликации и эквиваленции: «В современном обществе печать – это колоссальная сила. Она может и создать и испортить репутацию любому человеку.
Никто не мешает ей назвать лучшего из граждан мошенником и вором и погубить его навеки» (Марк Твен). p V q. p ^ q ^ r. p ^ q ^ r ^ n.
Решение задач по логике с ответами для юристов
Подберите понятия, равнозначные данным: а) Конституция. б) Арест. Ответ: а) Основной закон государства. б) Задержание, взятие под стражу.
Задание 4. Определите отношения между следующими понятиями и выразите эти отношения с помощью круговых схем: а) Юрист; б) Женщина; в) Человек; г) Дочь; д) Адвокат Ответ: в Задание 5. Обобщите понятия: а) общественное порицание б) министр Ответ: а) Наиболее мягкая мера наказания (в старом уголовном кодексе).
б) Член правительства или федеральный государственный служащий. Задание 6. Проверьте правильность следующих ограничений понятий: а) допрос – допрос свидетеля – допрос подозреваемого б) военнослужащий – офицер – лейтенант.
Ответ: а) Неправильное ограничение. Правильно — допрос – допрос участников уголовного процесса – допрос свидетеля. б) Правильное ограничение. Задание 7. Выясните, заключено ли в следующих примерах деление понятий.
Содержание 1.Задание 1 2.Задание 2 3.Задание 3 4.Задание 4 5.Задание 5 6.Задание 6 7.Задание 7 8.Задание 8 9.Задание 9 10. Задание 10 11. Задание 11 12. Задание 12 13. Задание 13 14.
Задание 14 15. Задание 15 16. Задание 16 17. Задание 17 18. Задание 18 19. Задание 19 20. Задание 20 21. Список литературы Задание 1 Дайтеполную логическую характеристикупонятиям: 1) Судимость; 2) Поджог 1) Судимость – абстрактное, положительное, безотносительное, собирательное, пустое, общее, атрибутивное.
2) Поджог – конкретное, положительное, соотносительное, не собирательное, пустое, общее, атрибутивное. Задание 2 Определите отношения между понятиями и выразите эти отношения с помощью круговых схем: 1) Правоотношение, общественное отношение, семейное отношение; 2) Полиция, налоговая полиция, городская полиция.
Оно указывает, чем не является предмет, не указывая, чем он является. б) Неправильное определение, т.к. определение не должно содержать в себе круга . Ошибка в том, что определяющее понятие является повторением определяемого.
СУЖДЕНИЕ Задание 9. Изменяется ли распределенность терминов при переходе от одного примера к другому в следующем случае? Все тела расширяются при нагревании. Почти все тела расширяются при нагревании. Некоторые тела сужаются при нагревании.
Не все тела расширяются при нагревании Ответ: В первом случае, Все S есть P. Общеутвердительное суждение. Субъект распределен полностью, а предикат не распределен или распределен полностью.
Во втором и четвертом случаях имеют место частноутвердительные суждения. В этих случаях оба термина не распределены. Во втором случае – частноотрицательное суждение при котором субъект не распределен, а предикат распределен. Задание 10.
plusbuh.ru
Решения задач по логике
В качестве предисловия. Хотите произвести хорошее впечатление на преподавателя и получить соответствующую оценку? Пробегите глазами книгу Рэймонд Смаллиан — Как же называется эта книга и как-нибудь сошлитесь на нее во время лекции.
Теперь пожалуй перейду к задачам. Некоторые элементы отображаются некорректно, поэтому здесь приведен лишь ряд задач, остальные вы можете скачать из прикрепленного файла ниже.
Скачать
1. Привести примеры нарушения законов логики.
Закон тождества — требует определенности, однозначности и устойчивости любой мысли в процессе рассуждения.
1 пример:
— Ты в Москве бывал ?
— Я на таких озерах рыбу ловил твоей Москве и не снилось.
Говорящие имеют в виду не одно и то же.
2 пример:
— Мне требуется кассовый чек на приобретение у вас чайника.
— Хорошо. Вот вам чек заполненный от руки на бланке с печатью, товарный чек который я вам даю это в общем и есть кассовый чек.
В данном случае совершается нарушение закона тождества способом подмены понятия, так как второй собеседник отождествляет кассовый чек с товарным чеком, а эти понятия не являются тождественными, подобное может происходить как неосознанно, так и целенаправленно.
Закон непротиворечия — требует непротиворечивости мышления. Два несовместимых друг с другом суждения не могут быть одновременно истинными, по крайней мере одно из них ложно.
1 пример:
— Подозреваемый 10.06.2014 года ровно в 6 часов вечера по московскому времени был в Москве и в Санкт-Петербурге.
В данном случае происходит нарушение закона противоречия, как минимум одно из утверждений ложное.
2 пример:
— Я видел сегодня зеленый лист на березе, правда он был бирюзовым.
Аналогично первому примеру.
Закон исключенного третьего — действует только в отношении противоречащих (контрадикторных) суждений. Два противоречащих суждения не могут быть одновременно ложными, одно из них необходимо истинно.
1 пример:
— Обвиняемый все же немножко виновен.
Обвиняемый может быть либо виновным, либо невиновным, третьего не дано.
2 пример:
— Пациент не является ни живым, ни мертвым.
Аналогично первому примеру нарушается закон исключенного третьего.
Закон достаточного основания — требует обоснованности суждения. Достаточным основанием какой-либо мысли может быть другая, уже проверенная и установленная мысль, из которой с необходимостью вытекает истинность данной мысли.
1 пример:
— Я вчера увидел бегавшую по газону собаку с пятью головами. Значит ваш пудель тоже с пятью головами.
Суждение основано на непроверенной информации и соответственно нарушает закон достаточного основания.
2 пример:
— Рассыпать соль — к ссоре.
Суждение необоснованно, поскольку в данном случае за причинно-следственную связь принимается простая последовательность произошедших событий во времени.
2. Привести примеры нарушения правил деления объема понятия.
Правило соразмерности — требует, чтобы объем делимого понятия был равен сумме объемов членов деления.
1 пример:
— Кислота бывает серная и азотная.
Не перечислены иные виды кислот.
2 пример:
Биатлонисты бывают русскими, японцами и индусами.
Аналогично примеру 1.
Правило одного основания — требует, чтобы каждый шаг деления осуществлялся по одному основанию.
1 пример:
— Кошки бывают черными, белыми и пушистыми.
2 пример:
— Вода бывает морской, речной и зеленоватой.
Правило взаимоисключения — требует не указывать такие члены деления, между объемами которых образуется отношение пересечения.
1 пример:
— Люди могут быть любителями кино или любителями театра.
2 пример:
— Кошки могут быть пушистыми или черными.
Правило последовательности деления — требует последовательности деления, без скачков.
1 пример:
— Станция может быть строящейся, построенной и с надземным павильоном.
2 пример:
— Коты могут быть персидскими, невскими маскарадными, сибирскими и с черной шерстью.
3. Привести примеры нарушения правил определения понятия.
Правило соразмерности — требует, чтобы объем определяемого понятия был равен объему определяющего.
1 пример:
— Рецидивист — лицо совершившее умышленное преступление.
Не всякое лицо совершившее умышленное преступление есть рецидивист. Правило соразмерности нарушено так как объем определения шире объема определяемого понятия. Данная ошибка называется ошибкой слишком широкого определения.
2 пример:
— Рецидивист — лицо совершившее умышленное преступление после судимости за ранее совершенное умышленное преступление против личности.
В данном примере объем определяющего понятия уже определяемого. Данная ошибка называется ошибкой слишком узкого определения.
Определение не должно заключать в себе круга. Если при определении прибегают к другому понятию, которое в свою очередь, определяется при помощи первого, то такое определение содержит в себе круг.
1 пример :
— Вращение определяется как движение вокруг своей оси, а ось — как прямая, вокруг которой происходит вращение.
Содержит в себе круг.
2 пример:
— Опиум усыпляем потому, что он имеет усыпляющую силу, а усыпляющую силу он имеет потому, что усыпляет.
Данное определение представляет собой элемент круга — тавтологию.
Определение должно быть ясным.
1 пример:
— Индетерминизм — это философская концепция, противоположная детерминизму.
Ошибка определения неизвестного через неизвестное.
2 пример:
— Вирулентность — это степень патогенности различных изолятов или штаммов конкретного патогенного вида.
Ошибка аналогичная примеру 1.
Определение не должно быть отрицательным — это объясняется тем, что отрицательное определение не раскрывает определяемого понятия, указывая чем не является предмет и не указывая чем он является (правило не распространяется на определение отрицательных понятий).
1 пример :
— Кошка — это не собака.
Из этого определения нельзя понять чем же является кошка, ясно только одно, что кошка не является собакой.
2 пример:
— Огонь — это не вода и не земля.
5. Обобщить понятие (три шага).
5.2 Лев.
Лев — (1) хищное млекопитающее семейства кошачьих — (2) хищное млекопитающее — (3) — хищный зверь
5.5 Цезарь.
Цезарь — (1) выдающийся полководец — (2) выдающаяся личность — (3) древний патриций.
5.8 Береза.
Береза — (1) лиственное дерево — (2) дерево — (3) растение.
6. Ограничить понятие (три шага).
6.4 Книга.
Книга — (1) книга изданная в Москве — (2) учебник логики изданный в Москве — (3) учебник логики изданный в Москве, авторов Кириллова В. И. и Старченко А. А.
6.7 Средство связи.
Средство связи — (1) компактное средство связи — (2) телефон — (3) радиотелефон.
6.2 Искусство.
Искусство — (1) изобразительное искусство — (2) статическое изобразительное искусство — (3) живопись.
7. Дать определение, указав ближайший род и видовое понятие.
7.2 Преступление.
Преступление — общественно — опасное деяние (родовое понятие), влекущее применение к лицу мер уголовной ответственности (видовое понятие).
7.4 Ответственность.
Ответственность — это особое отношение (родовое понятие) между поступками человека, людей , различных институтов, намерениями, а также оценками этих действий другими людьми или обществом (видовое понятие).
7.3 Философия.
Философия — особая форма познания мира (родовое понятие), вырабатывающая систему знаний о наиболее общих характеристиках, предельно обобщающих понятиях и фундаментальных признаках реальности и познания, бытия человека, об отношении человека и мира (видовое понятие).
8. На основе логического квадрата, полагая исходное суждение сначала истинным, затем — ложным, выведите суждения, соотносимые с исходным, и установите их истинностные значения.
8.5 Не все сапожники в сапогах.
Приведем суждение к стандартной форме: Некоторые сапожники есть не имеющие сапоги.
Это частноотрицательное суждение = O
Если O истинное, то соотносимое с ним I = Некоторые сапожники есть имеющие сапоги будет истинным; E = Все сапожники есть имеющие сапоги будет ложным; A = Все сапожники есть не имеющие сапоги будет ложным.
8.1 Коровы не летают.
Приведем суждение к стандартной форме: Все коровы не есть летающие существа.
Это общеотрицательное суждение = Е
Если E истинное, то соотносимое с ним A = Все коровы есть летающие существа будет ложным; O = Некоторые коровы не есть летающие существа будет истинным; I = Некоторые коровы есть летающие существа будет ложным.
klassikaknigi.info
