Поиск решения MS EXCEL (6.1). Задача линейного программирования (ЛП) . Примеры и методы
Решим задачу линейного программирования с помощью надстройки Поиск решения.
В этой статье мы отойдем от формулировки практических задач и решим задачу линейного программирования в абстрактных терминах: вектор переменных х, матрица ограничений Aх, вектор b, целевая функция cTx (вместо более привычных: объем производства, количество комплектующих разного вида, максимальный доход).
Задача линейного программирования (ЛП) есть задача максимизации линейной функции при линейных ограничениях. Задачу ЛП можно записать несколькими стандартными способами. Мы сформулируем ее в форме max{cTx: Ax<b, x>0}
Задача
Необходимо максимизировать целевую функцию cTx: max 50*x1 + 30*x2 + 25*x3 + 30*x4 при условии, что:
2*x1 + 2,5*x2 + 3*x3 + 1,8*x4 <= 800
1,5*x1 + 1,2*x2 + 1,5*x3 + 0,8*x4 <=380
x2 >= 50
x3 >= 30
x1; x2; x3; x4 >= 0
cTx — это векторное произведение векторов cT (транспонированный вектор с) и х.
Примечание: эта задача эквивалентна задаче определения оптимальной структуры производства с целью максимизации дохода (см. статью Поиск решения MS EXCEL (1.1). Оптимальная структура выпускаемой продукции). Сформулируем эту задачу в общем виде:
Предприятие планирует производить n видов продукции, используя m видов ресурсов. Для производства единицы j-го продукта требуется aij единиц i-го ресурса. Стоимость единицы j-го продукта равна cj. В наличии имеется bi единиц i-го ресурса. Нужно определить план производства с целью максимизировать прибыль.
Обозначив хj — объем выпуска продукции j-го вида (j =1;…;n), мы можем записать задачу поиска оптимального производственного плана следующим образом:
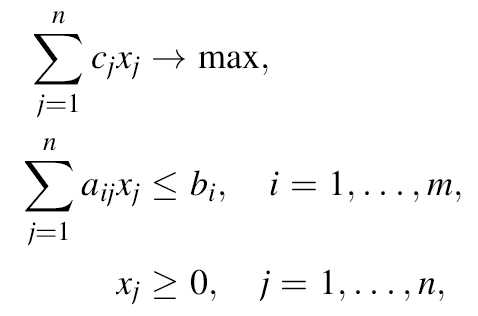
Или в матричной форме:
Получается, что в исходной задаче:
- вектор с (стоимость продукции) равен (50; 30; 25; 30)
- вектор x (количество продукции) необходимо найти для заданных условий
- n=4 (4 вида продукции)
- m=3 (3 вида ресурсов)
- вектор b (количество ресурсов) равен (800; 400; 380)
- матрица A (количество единиц ресурсов для изготовления продукта) равна (2; 2,5; 3; 1,8: 1,2; 1; 2; 0,8: 1,5; 1,2; 1,5; 0,8)
Теперь создадим модель.
Создание модели
На рисунке ниже приведена модель, созданная для решения задачи (см. файл примера).
Для решения задачи на листе MS EXCEL необходимо записать матрицу А, вектора b
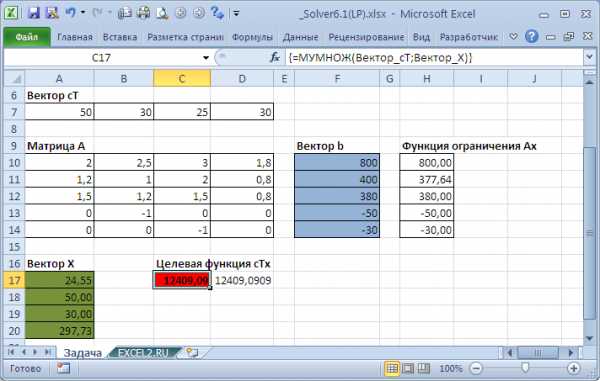
Примечание: для удобства настройки Поиска решения используются именованные диапазоны.
Совет: Вводная статья про Поиск решения в MS EXCEL 2010 находится здесь.
Значение целевой функции cTx получено путем матричного умножения векторов cT и x (используйте функцию МУМНОЖ(), которая вводится как формула массива). Аналогично получена функция ограничений Ах, путем умножения матрицы А на х. Так как матрица Ах имеет размерность 5х1, то перед вводом формулы =МУМНОЖ(Матрица_А;Вектор_Х) необходимо выделить столбец из 5 ячеек, затем после записи формулы в Строке формул, нажмите CTRL+SHIFT
+ENTER для ее ввода.Настроить Поиск решения нужно следующим образом:

excel2.ru
Решение задачи линейного программирования в MS Excel с помощью «Поиск решения»
- Курсы
- Новости
- Статьи
- Excel
- PowerPoint
- Windows
- Word
- Заметки
- Excel
- PowerPoint
- Windows
- Word
- Другие заметки
- Видео
- Excel
- PowerPoint
- Windows
- Word
- Другие видео
- Блог
- Shop
- Доступ к курсам
- Услуги
Поиск
- Главная
- Центр обучения
- Справочник
- Поддержка
- Контакт
- Курсы
- Новости
- Статьи
- ВсеExcelPowerPointWindowsWord
Windows
Windows 10 19h2 (версия 1903) все изменения и новые функции
WindowsЛучшие в октябрьском обновлении Windows 10 (версия 1809)
ExcelГоризонтальная сортировка в Excel
ExcelАвтонумерация внутри составной записи в Excel
- ВсеExcelPowerPointWindowsWord
Windows
- Заметки
- ВсеExcelPowerPointWindowsWordДругие заметки
Excel
Анимация минигана в MS Office
Другие заметкиКак установить шрифты в систему Windows
ExcelСкопировать ячейку Excel, скопировать данные ячейки и скопировать значение ячейки. В…
Другие заметкиПользуемся почтой Gmail без интернета
- ВсеExcelPowerPointWindowsWordДругие заметки
Excel
- Видео
- ВсеExcelPowerPointWindowsWordДругие видео
Windows
Как удалить папку Window.Old?
PowerPointСоздание параллакс анимации в PowerPoint вариант 1
- ВсеExcelPowerPointWindowsWordДругие видео
Windows
msoffice-prowork.com
Решение транспортной задачи линейного программирования в среде MS Excel
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РЕСПУБЛИКИ КАЗАХСТАНКАЗАХСКИЙ ГОСУДАРСТВЕННЫЙ ЖЕНСКИЙ ПЕДАГОГИЧЕСКИЙ ИНСТИТУТ
КАФЕДРА ИНФОРМАТИКИ
Дипломная работа
Выполнила: студентка 4курса,
протокол № о/о, р/о, спец. «Информатика»
Оспанова А.А.
Научный руководитель:
к.т.н., доцент старший преподаватель
Г.И. Салгараева Мусиралиев Ж.А.
Алматы 2008 г.
СОДЕРЖАНИЕ
ВВЕДЕНИЕ
Глава I Задачи линейного программирования
1.1 Общая характеристика задачи линейного программирования
1.2 Математическая постановка задачи линейного программирования
Глава II Основные методы решения транспортной задачи линейного программирования
2.1 Математическая постановка транспортной задачи
2.2 Решение транспортной задачи с помощью программы Ms Excel
2.3 Рекомендации по решению задач оптимизации с помощью надстройки «Поиск решения»
Глава III Двойственная задача линейного программирования
3.2 Математическая постановка двойственной задачи о красках
3.3 Решение двойственной задачи о красках с помощью программы Ms Excel
Заключение
Литература
В некотором географическом регионе имеется фиксированное число пунктов производства и хранения некоторого однородного продукта и конечное число пунктов потребления этого продукта . В качестве продукта может выступать, например, нефть, уголь, песок, цемент, т.д. Для каждого из пунктов производства и хранения известен объем производства продукта или его запаса. Для каждого пункта потребления задана потребность в продукте в этом пункте потребления.
Требуется определить оптимальный план перевозок продукта, так чтобы потребности во всех пунктах потребления были удовлетворены, а суммарные затраты на транспортировку всей продукции были минимальными.
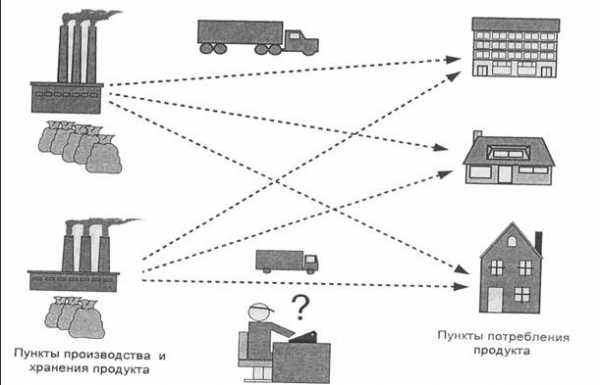
Рисунок1. Иллюстрация транспортной задачи для двух пунктов производства и трех пунктов потребления
Очевидно, оценочной функцией в данной задаче являются суммарные затраты на транспортировку всей продукции, а ограничениями служат объемы производства и потребности в продукте в каждом пункте потребления.
Данная задача также является одной из классических задач линейного программирования, методы ее решения мы будем рассматривать далее. В бизнес приложениях эта задача известна как задача о перемещении товаров со складов на торговые точки или задача о планировании цепочек поставок. В случае штучного товара, например, телевизоры, компьютеры, пылесосы, автомобили и пр., соответствующая транспортная задача относится к классу задач целочисленного программирования.
Транспортная задача: Уменьшение затрат на перевозку.
В этой работе мы рассмотрим решение классической транспортной задачи Excel 7.0 позволяет находить оптимальное решение, сохраняя заданные ограничения.
Транспортная задача является классической задачей исследования операций. Множество задач распределения ресурсов сводятся именно к этой задаче.
1. Математическая постановка транспортной задачи.
Общая постановка транспортной задачи состоит в определении оптимального плана перевозок некоторого однородного груза из т пунктов отправления А1,А2,…,Ат в п пунктов назначения В1,В2,..,Вп. При этом в качестве критерия оптимальности обычно берется либо минимальная стоимость перевозок всего груза. Обозначим через сij тарифы перевозки единицы груза из i-го пункта отправления в j-й пункт назначения, через ai-запасы груза в j-м пункте отправления, через bj-потребности в грузе в j-м пункте назначения , а через xij-количество единиц груза, перевозимого из i-го пункта отправления в j-й пункт назначения. Тогда математическая постановка задачи состоит в определении минимального значения функции:
, [1]
при условиях:
[2] [3] [4]Поскольку переменные
удовлетворяют системам уравнений(2) и (3) и условию неотрицательности (4), то обеспечивается доставка необходимого количества груза в каждый из пунктов назначения (условие (2)), вывоз имеющегося груза из всех пунктов отправления (условие (3)), а также исключаются обратные перевозки (условие (4)).Определение 1. Всякое неотрицательное решение системы линейных уравнений (2) и (3), определяемое матрицей Х=(
) (i=1,…m;j=1,…n), называется планом транспортной задачи.Определение2. План
=() (i=1,…m;j=1,…n), при котором функция (1) принимает своё минимальное значение, называется оптимальным планом транспортной задачи.Обычно исходные данные транспортной задачи записывают в виде (см. таблицу 1.)
Очевидно, общее наличие груза у поставщиков равно:
,а общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, т.е.
единиц.
Если общая потребность в грузе в пунктах назначения равна запасу груза в пунктах отправления, т.е.
=, [5]То модель такой транспортной задачи называется закрытой. Если же указанное условие не выполняется, то модель транспортной задачи называется открытой.
Таблица 1
Теорема 1 . Для разрешимости транспортной задачи необходимо и достаточно, чтобы запасы груза в пунктах отправления были равны потребностям в грузе в пунктах назначения, т.е. чтобы выполнялось равенство (5)
mirznanii.com
| Задача 1 Предприятие выпускает 2 вида продукции А и Б. Ресурсы предприятия ограничены (Таблица 1). Известны также удельные нормы расходов каждого вида ресурсов на производство единицы каждого вида изделий, прибыль от реализации одной единицы изделия. Составьте оптимальный план производства, обеспечивающий максимум прибыли предприятию. Решим задачу средствами Excel. Заполним ячейки исходными данными (в виде таблицы) и формулами математической модели. Вычисляемые ячейки пометим цветом. Таблице в режиме чисел: Вызываем надстройку «Поиск решения» и заполняем параметры: Вносим целевую функцию и ограничения. 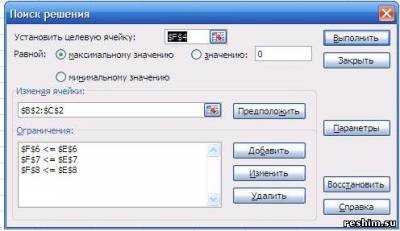 Запускаем решение: Получаем решение: Задача 2 Для изготовления трех видов продукции используют три вида сырья. Составьте оптимальный план производства, обеспечивающий максимум прибыли предприятию. Запасы сырья, нормы его расхода и прибыль от реализации каждого продукта в приведены в таблице 2. Ответьте на вопрос: Вариант 1. Как изменится общая прибыль и план ее выпуска при увеличении запасов сырья I и II видов на 40 единиц каждого? Вариант 2. Как изменится общая прибыль и план ее выпуска при увеличении запасов сырья III вида на 500 единиц? Вариант 3. Как изменится общая прибыль и план ее выпуска при уменьшении запасов сырья I вида на 100 единиц? Вариант 4. Как изменится общая прибыль и план ее выпуска при увеличении запасов сырья II вида на 100 единиц? Вариант 5. Как изменится общая прибыль и план ее выпуска при уменьшении запасов сырья I и II видов на 40 единиц каждого? Вариант 6. Целесообразно ли включать в план изделие Г с прибылью 13 единиц, на изготовление которого расходуется, соответственно, 1, 3 и 2 ед. каждого вида сырья? Вариант 7. Целесообразно ли включать в план изделие Г с прибылью 12 ед., на изготовление которого расходуется по 2 ед. каждого вида сырья? Вариант 8. Целесообразно ли включать в план изделие Г с прибылью 20 ед., на изготовление которого расходуется по 4 ед. каждого вида сырья? Вариант 9. Целесообразно ли включать в план изделие Г с прибылью 5 ед., на изготовление которого расходуется по 1 ед. каждого вида сырья? Вариант 10. Целесообразно ли включать в план изделие Г с прибылью 15 единиц, на изготовление которого расходуется, соответственно, 2, 3 и 3 ед. каждого вида сырья? |
www.reshim.su
